Agent-Based Modelling of Mpox Infection Dynamics: Simulating Disease Transmission and Control Strategies

, , ,
and
aInsight SFI Research Centre for Data Analytics, Data Science Institute, Galway, Ireland; bSchool of Computer Science, University of Galway, Ireland; cSchool of Computer Science, University College Dublin, Ireland; dADAPT Research Centre, Technological University Dublin, Ireland; eHealth Protection Surveillance Centre, Dublin, Ireland; fTrinity College Dublin, Dublin, Ireland
Journal of Artificial
Societies and Social Simulation 27 (2) 6
<https://www.jasss.org/27/2/6.html>
DOI: 10.18564/jasss.5380
Received: 05-Sep-2023 Accepted: 08-Mar-2024 Published: 31-Mar-2024
Abstract
Mpox is a viral disease caused by the monkey pox virus (MPXV) of the Poxviridae family. It is similar to smallpox and cowpox. Mpox is not categorized as a sexually transmitted infection, however, most transmission in the recent global outbreak has been attributed to be through men who have sex with men(MSM). Agent-based modelling (ABM) is an effective approach to simulate the spread of Mpox because it enables the detailed representation of heterogeneity among individuals or sub-populations, including variations in behaviour, susceptibility to disease, and contact patterns. This is crucial for accurately modelling diseases in populations with long tailed distributions of characteristics such as sexual activity, that has been seen in the recent Mpox outbreak. Two ABMs are presented in this paper which simulate the spread of Mpox in an artificial population. The parameters for contact formation and dissolution are drawn fromthe NATSAL-3 dataset (National Survey of Sexual Attitudes and Lifestyles) (Mercer et al. 2013). The presented ABMs are based on the principles of the classic compartmental Susceptible-Exposed-Infected-Recovered (SEIR) model and complexity is further added to break the assumptions of homogeneous mixing and populations. The first ABM is based on an heterogeneous population, consisting of people from two self-identified genders (male and female) and three sexual preferences: homosexual, bi-sexual and heterosexual. The second ABM is a subset of the first ABM, that focuses on the MSM population, which is considered to be at high-risk of Mpox. We report a set of experiments modelling relevant scenarios by number of imported cases, number of super-spreader events, and different vaccination strategies. Our analysis concludes that Mpox infection reaches locally stable disease-free equilibrium in the absence of concurrent partnerships. Our simulations demonstrate that prioritizing vaccines for the MSM population can significantly reduce the effective R value from 1.62 to 0.19, highlighting the potential impact of targeted vaccination strategies in mitigating Mpox transmission.Introduction
Mpox is a zoonotic viral disease caused by MPXV virus (Pauli et al. 2010). It is closely related to the Variola virus, which causes smallpox in humans (Pauli et al. 2010). It was first identified in 1958 in monkeys showing signs of a poxvirus (Pauli et al. 2010). In 1970, the first case of Mpox in humans was detected in the Democratic Republic of Congo (DRC) (Pauli et al. 2010). Since then, it has become endemic in the DRC and other central and west African countries. Prior to the 2022 outbreak, Mpox cases reported from outside these regions were rare and linked to case importations from affected regions. In May 2022, a British resident tested positive for MPXV after returning from Nigera. Within 10 days, 6 news cases were reported by UK Health Security Agency (UKHSA), all of them having no known contact with the index case. This suggested a wider community transmission which had never previously occurred outside of Africa. In July 2022, Mpox was declared as a "Public Health Emergency of International Concern" by the World Health Organisation (WHO) (WHO 2022b). By February 2023, more than 87 thousand confirmed cases of Mpox have been reported globally in 110 different countries (Mathieu et al. 2023).
The resurgence of MPVX in 2022 has has been attributed to various factors including waning effectiveness of small pox vaccines, genetic mutation in the virus that enhance its human-to-human transmission, its better adaptation to humans, the occurrence of super-spreader events, population increase and greater global interaction among other reasons (Forni et al. 2022; Kumar et al. 2022). This current outbreak has primarily affected men who have sex with men (MSM), especially those MSM who have multiple and frequently anonymous partners whom they have met at venues such as saunas, cruising bars, sex clubs, dating apps, and (chem-)sex parties (Bragazzi et al. 2023; CDC 2022; Iñigo Martínez et al. 2022; Thornhill et al. 2022; van Ewijk et al. 2023), collectively referred to as super-spreader events in this paper. In this work, we specifically look at the role of super-spreader events and travel related cases in the spread of Mpox transmission. For more details on transmission routes of Mpox in the 2022 outbreak, see Thornhill et al. (2022), Bragazzi et al. (2023) and references within.
The symptoms of Mpox include fever, rash and swollen lymph nodes (Anwar & Waris 2022). As Mpox is closely related to smallpox, vaccines used to eradicate smallpox can also provide protection against Mpox. However, the vaccine supply during the outbreak was initially limited (HSE 2022; WHO 2022a; Wolff Sagy et al. 2023). Combining this with the fact that the outbreak was the first major Mpox outbreak with person-to-person transmission outside of Africa, there were questions of what was the best way to respond. For example, are there certain vaccination strategies that would prove more beneficial than others? Or are there higher risk individuals in the MSM community that should be targeted for prevention? One method that can be used to provide evidence to public health agencies is infectious disease modelling.
There are several different methods to model the transmission dynamics of an infectious disease. Mathematical models have been extensively used for this purpose. Mathematical models can be classified into two types: deterministic and stochastic. Deterministic models have fixed input parameters (e.g., incubation period or recovery period). Stochastic models consider random parameters and hence provide a range of output trajectories, for example, the worst case and best case scenarios or the probability that a given outcome will occur (Vynnycky & White 2010).
Compartmental models that typically use Ordinary Differential Equations (ODEs) are popular in epidemiological modelling, such as the Susceptible-Infectious-Recovered (SIR) and Susceptible-Exposed-Infectious-Recovered (SEIR) models. One drawback of such models is that they assume homogeneous mixing within different subgroups of a population. In reality, humans tend to mostly mix with a small subset of other humans. Network models are based on mathematical properties of graphs and the social science of human interaction. These have the capability to incorporate non-homogeneous mixing in the population by explicitly modelling permanent or semi-permanent links for infection transmission between pairs of individuals. There are different types of network models: random networks (Erdős & Rényi 1959), lattice models, small world networks (Watts & Strogatz 1998), spatial networks (Eames & Keeling 2002), scale free networks (Barabási & Albert 1999) and agent-based models (also known as individual based simulation) (Vynnycky & White 2010).
Traditional modelling approaches, such as compartmental modelling (Duggan et al. 2024), focus on aggregated data and rely on assumptions about the behaviour of the system as a whole. On the other hand, agent-based modelling is a bottom-up approach to simulate the behaviour of individual agents in a decentralized system, taking into account their unique characteristics, behaviours, and interactions. Agent-based modelling offers a unique perspective on complex systems, as it allows for the modelling of both individual and collective behaviour (Wilensky & Rand 2015). They can exhibit emergent behaviour, where complex and unexpected patterns arise from the interactions between the agents. This can lead to new insights and a better understanding of the system being modelled (Wilensky & Rand 2015). ABMs are often stochastic. This characteristic can be beneficial for modelling infectious diseases because it enables the modeller to simulate a variety of potential outcomes from the same starting conditions. This is crucial for comprehending disease outbreaks since stochasticity allows for the recognition that there are multiple paths that an outbreak may follow, influenced by the individual decisions and interactions of agents and chance events (Hunter et al. 2020). While ABMs offer numerous advantages, they also come with certain limitations and drawbacks, including sensitivity to initial conditions and high computational cost.
ABMs are becoming increasingly popular to model the dynamics of infectious diseases (Hunter & Kelleher 2021). They have been used in the recent years to model the spread of COVID-19 (Cuevas 2020; Kerr et al. 2021; Novakovic & Marshall 2022; Silva et al. 2020), Flu (Arduin et al. 2017; O’Neil & Sattenspiel 2010; Rakowski et al. 2010; Roche et al. 2011), Measles (Hunter & Kelleher 2021), Cholera (Crooks & Hailegiorgis 2014), Ebola (Ajelli et al. 2015; Merler et al. 2015), Tuberculosis (De Espíndola et al. 2011; Kasaie et al. 2014), etc. ABMs can be used to test various scenarios, such as the effectiveness of different intervention strategies (e.g., Merler et al. 2015; Kerr et al. 2021; Novakovic & Marshall 2022), the impact of behaviour changes on disease transmission (e.g. Valle et al. 2012; van Dijck et al. 2022), and the role of demographic and environmental factors (e.g., Alzu’bi et al. 2021; Adiga et al. 2018). This information can help inform public health policies and inform decision-making in response to disease outbreaks.
For Mpox modelling, ABMs offer several advantages over other approaches. They allow us to model individual level heterogeneity: people of different age cohorts, sexual preferences, and sexual activity level. This heterogeneity is crucial in capturing the variability in Mpox transmission dynamics, susceptibility, and response to interventions within a population or sub-groups. Being able to model heterogeneity is critical for understanding a disease such as Mpox where the contact network follows a heavy-tailed distribution (a smaller sub-group of the population with a very dense contact network).
Most ABMs use social contact and epidemiological data to set up the model parameters, for example, Hunter et al. (2018), Rakowski et al. (2010), Crooks & Hailegiorgis (2014). In a data-driven ABM, the behaviour of each agent is determined by rules driven from a data source. In our study, we use the National Survey of Sexual Attitudes and Lifestyles (NATSAL-3) (Mercer et al. 2013) dataset to derive parameters of sexual contact behaviour between the agents.
We present two ABMs to study the transmission of Mpox in an artificial society: the Population Model and the MSM Model. The Population Model comprises heterosexual, homosexual and bi-sexual men and women between ages 16-74. The MSM Model focuses only on the MSM group. For both models, we run simulations assuming different scenarios by varying the number of super-spreader events, number of imported cases and vaccination strategies. We report the daily count of new infections for the population and different sub-groups, an estimate of time-varying reproductive number (\(R_t\)) and effective reproduction number (\(R_e\)) in each scenario. \(R_e\) represents average number of secondary infections caused by a single infected individual in a population where not everyone is susceptible to the disease. \(R_e\) is different from the basic reproductive number \(R_0\), which represents the average number of new infections caused by a single infected individual in a completely susceptible population. \(R_t\) refers to the average number of secondary infections caused by a single infected individual at a specific time during an outbreak or epidemic. In other words, it is an estimation of \(R_e\) at a single specific point in time during the outbreak.
The decision to present both models stems from the iterative nature of our modelling process and the evolving understanding of Mpox dynamics during that process. This research was performed in collaboration with the public health authorities in the Republic of Ireland. The first model aimed to provide a broad overview of potential transmission dynamics and assess the overall impact of the disease on the general population. However, as the spread of Mpox in Ireland continued, it was evident that Mpox was spreading through MSM contacts, therefore, the demand for more targeted and nuanced modelling approaches became apparent. This led to the development of the second model, with modifications tailored to specifically target vulnerable groups identified in the initial analysis. The idea was to gain deeper insights into the dynamics of Mpox transmission within the MSM demographic groups and inform targeted intervention strategies to the public health authorities. Figure 1 shows the flowchart of our modelling process. Both models share a substantial portion of their underlying code and methodologies.
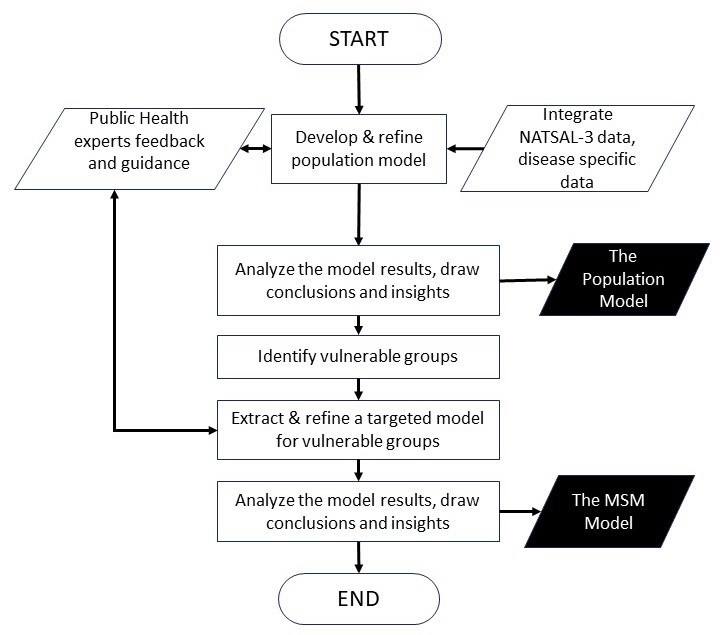
Related Research
To the best of our knowledge, Brainard & Hunter (2019) is the only study that uses ABM to study the spread of Mpox. They examine the impact of misinformation on the severity of influenza, Mpox, and norovirus outbreaks. For a comprehensive review of computational models used to study Mpox transmission dynamics, see Molla et al. (2023) and the references within.
Spicknall et al. (2022) proposed dynamic network models to simulate the sexual behaviour among MSM. The study found that MSM who had multiple sexual partners within the previous 3 weeks had a significantly higher risk (1.8-6.9 times) of acquiring Mpox compared to those with only one partner. Although one-time partnerships constituted less than 3% of total daily partnerships and 16% of sexual encounters between men on any given day, they were responsible for approximately 50% of the transmission of Mpox. The model demonstrated that reducing one-time partnerships by 40% resulted in a 20%-31% reduction in the percentage of infected MSM and slowed down the spread of the outbreak. Research conducted by van Dijck et al. (2022) based on network models is closely related to ours. They use a previously published temporal exponential family random graph model of a Belgian MSM population. Like us, they also categorise MSMs as high-risk and low-risk. They assume 20% transmission probability, while we assume 12.5% (as will be discussed later in Section "The Agent-Based Models"). Their incubation period is drawn form a uniform distribution and infected period is a constant number, whereas we draw these numbers from Weibull and normal distributions respectively. Unlike us, they model the diagnostic delay and sexual behavioural interventions after diagnosis. They consider both pre- and post-exposure vaccination. Like us, they do not take childhood-based smallpox vaccinations into account. The key conclusions drawn from their research indicate that contact tracing, even if only a small proportion can be successfully traced, is valuable. Additionally, the study suggests that pre-exposure vaccination targeting individuals at the highest risk of infection holds greater potential for effectiveness compared to post-exposure vaccination.
Grant et al. (2020) developed a mathematical model for Mpox transmission using historical epidemiological data collected in the DRC during 1980-1984. They calculated the \(R_e\) of Congo basin clade of Mpox at that time to be 0.32 (uncertainty bounds 0.22–0.40). Using 85% for vaccine efficacy, value of \(R_0\) worked out to be 2.13 (uncertainty bounds 1.46–2.67). Gao et al. (2023) identified twenty one Mpox infection risk factors through correlation-based network analysis and multivariate regression and then assessed the risk at the country level using a modified SEIR model. Their SEIR model predicted a declining transmission rates with \(R_0\) ranging between 1.62-7.84 in early stage of the epidemic (before June 23, 2020) and between 0.70-4.13 in the later stage (post June 23, 2020). Ko et al. (2023) developed a model to study the transmission of Mpox in a non-endemic country, taking contact tracing and self-reporting into account. They developed an algorithm based on Gillespie’s stochastic chemical kinetics (Cai 2007) to quantify the number of infections, contacts and the time elapsed between the arrival of a primary case and the detection of an index case. Their findings revealed that the self-reporting behaviour of primary cases had the most significant impact on the size and the duration of the outbreak.
Peter et al. (2023) proposed an ODE based mathematical model to study the interplay of human-human and rodent-human transmission of Mpox. They also incorporated quarantine and isolation measures in the model. They found that the effective contact rate is the most sensitive parameter that, when increased, lead to an increased burden of Mpox in the population. Similarly, Ahmed El-Mesady et al. (2022) developed a Caputo fractional-order non-linear differential equations model (A El-Mesady et al. 2022) to study the spread of Mpox between rodent and human populations. Like us, Endo et al. (2022) developed a transmission model based on NATSAL-3 empirical sexual partnership data. Their findings revealed that the heavy-tailed distribution of sexual partnerships, where a few individuals have a disproportionate number of partners, can account for the continuous spread of Mpox among MSM. Their analysis revealed that projected values of the \(R_0\) in the MSM group sexual network consistently exceeded 1 for various sexually associated secondary attack rates (SAR), indicating sustained transmission of Mpox. In contrast, \(R_0\) in the non-MSM sexual network remained below 1 unless the SAR approached 100%, indicating a lower likelihood of widespread transmission in this population. Spath et al. (2022) use Austrian population data to modify a stochastic spatiotemporal SIR epidemic model in order to evaluate the age-specific protection against human Mpox resulting from previous mandatory smallpox vaccination, as well as the likelihood of infection across different age groups. Some other studies that use compartmental model include Khan et al. (2022), Yuan et al. (2023), Peter et al. (2022), Peter et al. (2021), Bankuru et al. (2020).
Some pre-2022 studies use branching process to model Mpox transmission (Antia et al. 2003; Blumberg et al. 2014; Blumberg & Lloyd-Smith 2013; Kucharski 2015). However, these studies did not account for transmission through sexual contact and did not focus on the MSM population.
Some studies that used ABMs to study the transmission dynamics of STIs using various methods for modelling sexual networks include Chumachenko & Chumachenko (2017), Kasaie et al. (2018), Gopalappa et al. (2023), Rutherford et al. (2012), LeVasseur et al. (2018), Jones et al. (2019), Scott et al. (2018), Goedel et al. (2018), Luo et al. (2018). Various other computational modelling approaches have been proposed to represent sexual partnership dynamics and their impact on the transmission of STIs, see Rao et al. (2021) and the references within.
All of the models discussed above present varying \(R_e\) values. This is not surprising as all are based on varying assumptions and parameters. However, some of the key points to be taken from this literature review are that MSM with multiple recent partners significantly increase Mpox transmission risk (Endo et al. 2022; Spicknall et al. 2022; van Dijck et al. 2022), suggesting that reducing one-time partnerships could effectively slow outbreak spread. Strategies such as pre-exposure vaccination, post-exposure vaccination, interventions in sexual behaviours and self-reporting behaviour can help curb the spread of Mpox. Studies consistently show that interventions focused on high-risk populations, particularly MSM, are crucial for controlling Mpox outbreaks effectively.
The Agent-Based Models
Two agent-based models are presented: The Population Model and The MSM Model. The Population Model presents infection transmission in a population representative of agents from both sexes (male and female) and three types of preferences in sexual partnership (heterosexual, bi-sexual and homosexual). Based on our analysis of the population model (as will be discussed in Section "Results"), we found that the majority of cases were concentrated within the MSM community, with minimal impact on other groups. This corresponds to the real-world data showing a higher prevalence of infections among the MSM population during the 2022 Mpox outbreak. However, due to the relatively small proportion of MSM individuals in the Population Model, the model’s outcomes displayed a low number of cases. Therefore, we decided to develop a separate model exclusively targeting the MSM community. The MSM model only contains an MSM population and female partners of the bi-sexual men.
The details provided in the sections below aim at introducing the ABMs, its application, and main insights. The computer software "Netlogo" (Wilensky 1999) is used to implement an ABM for Mpox transmission dynamics. Netlogo is a powerful and popular programming language and development environment specifically designed for agent-based modelling. Both models are discrete-time models that run on time steps. In our models, each time step equates to one day and the model runs for 180 time steps or days. An ABM for the spread of an infection has typically four main components: disease, society, transportation and environment (Hunter et al. 2017). To simplify, we do not take "geographical/spatial" perspective into consideration, but only disease, transportation and society. That is to say, sexual partners are not selected on the basis of physical location of an agent.
The society component is structured to simulate a population using parameters obtained from the NATSAL-3 survey data. The survey is designed to collect information about sexual behaviour, attitudes, and lifestyles, and has been conducted three times: in 1990, 2000, and 2010. The NATSAL-3 data is widely used by researchers and policy makers to understand the sexual health and well-being of the population and to inform public health policy and practice. The data collected in the NATSAL-3 survey covers a wide range of topics, including sexual behaviour, contraceptive use, sexually transmitted infections, sexual health services, and sexual attitudes and beliefs. The survey is conducted using a sample of the general population and is designed to be representative of the UK population in terms of age, gender, and geographical location. As previously noted, Mpox is not a sexually transmitted infection. However, the current outbreak is primarily traced back to sexual contact among MSM. Therefore, sexual contact parameters are derived from the NATSAL-3 dataset.
Both models presented in this paper simulate the outbreaks of Mpox in a closed population. In a closed population, there are no individuals entering or leaving the population due to migration, birth, death or any other reason. However, the MSM Model ABM is a mixture of open and closed population. The MSM group in that model is a closed population, whereas the female partners of the bi-sexual males are modelled as open population. They enter the model when a new heterosexual relationship is established between a bi-sexual man and a woman. They leave the model when the relationship ends. These models are outlined using the ODD protocol and can be found online in the Netlogo User Community Model Library at https://www.comses.net/codebase-release/bc36f788-2181-42af-9be3-fd993e2c92f6/ and https://www.comses.net/codebase-release/d96f7e11-180b-4b9b-af5f-0618d4bb5d88/.
The key assumptions of the models are presented below:
- Non-homogeneous partnerships: Our model can represent non-homogeneous sexual mixing among the agents. Each agent can have one of the three preferences in sexual partnership: homosexual, bi-sexual and heterosexual. This preference is based on the agent’s age and sex. Each agent has a different rate of formation of new partnerships. This rate is also based on its age and sex. These parameters are derived from the NATSAL-3 data.
- Concurrency. We model two types of sexual partnerships: long-term partnerships are modelled to be strictly monogamous and their parameters are derived from the NATSAL-3 dataset. Short-term partnerships are concurrent and their related parameters are varied to study the transmission dynamics and are based on our assumptions.
- Protection. We assume that vaccination provides complete protection against infection to 85% of the vaccinated individuals (vaccine efficacy = 85%) (Fine et al. 1988; Grant et al. 2020; Rimoin et al. 2010). The vaccination does not wane. Our model also assumes that once a person recovers from Mpox, they acquire permanent immunity.
- Assortativity. Assortativity or assortative mixing is the tendency of individuals to associate (or in this particular context, to develop sexual contact) with others who are similar to them in some way. For simplicity, assortativity is not considered in our model when it comes to long-term partnerships (although in reality, individuals with more social interactions tend to connect with others who have similar levels of social interactions). In our model, an agent who engages in a high number of new sexual partnerships has an equal likelihood of choosing a partner with either a high or low number of new partners annually. However, in the case of short-term casual interactions, which in our model only occur through super-spreader events, assortative mixing does take place since only agents from a specific group attend such venues.
The population model
The different parameters of the full ABM are detailed in Table 1 and explained in the subsequent sections.
| Variable | Description | Value | Source |
|---|---|---|---|
| Minimum Age | Minimum age of an agent in the model | 16 | NATSAL-3 |
| Maximum Age | Maximum age of an agent in the model | 74 | NATSAL-3 |
| Total Population | Size of the population | 10,000 | - |
| Homosexual Males (%) | Percentage of homosexual men | 1.144% | NATSAL-3 |
| Bi-sexual Males (%) | Percentage of bi-sexual men | 3.92% | NATSAL-3 |
| Homosexual Female (%) | Percentage of homosexual women | 0.30% | NATSAL-3 |
| Bi-sexual Females(%) | Percentage of bi-sexual women | 6.04% | NATSAL-3 |
| Initially Infected MSM | Number of infected MSM agents at the start | 5 | - |
| Size of a super-spreader event | Number of people attending an event which has multiple short-term sexual partners | 35 | - |
| Transmission Probability (\(TP\)) | Probability of acquiring infection after sexual contact | \(\frac{1}{8}\) | - |
| Weekly contact rate (\(WC\)) | Number of sexual encounters per week between agents in a long-term relationship | \(\frac{3}{7}\) | - |
| Exposed Period | Number of days an agent is exposed to the disease but not infectious | Weibull distribution with scale parameter \(\eta = 8.4\) and the shape parameter \(\beta= 1.5\) | Ward et al. (2022) |
Society and agents
The model is initialised with a population of 10,000 agents. Each agent is randomly assigned an age from a uniform distribution between 16 and 74 years. These upper and lower limits correspond to the minimum and the maximum ages of the respondents of the NATSAL-3 dataset. Agents are also assigned an age cohort. There are 15 age-cohorts, each with a size of 4 years.
All agents are given a biological sex: male and female. The sex is also assigned randomly, with a 50% probability of being a male. Each agent is also assigned a sexual-preference. There are three types of sexual preferences modelled: heterosexual, homosexual or bi-sexual. The percentages of males and females in these categories of sexual preferences are derived from the NATSAL-3 dataset and are mentioned in Table 1. These percentages are calculated in the following way: the percentage of heterosexual men in the model is equal to the percentage of men in NATSAL-3 survey who reported sexual contact only with the opposite sex in their lifetime, percentage of homosexual men is equal to the percentage of men in NATSAL-3 survey who reported having only same-sex sexual contact in their lifetime and percentage of bi-sexual men is equal to the percentage of men who reported having sexual contact with both sexes in their lifetime. The same method is applied to calculate percentage of heterosexual, homosexual and bi-sexual women.
Each agent has a "number of new partners each year" parameter (denoted by \(k\) in this paper), which is based on its age, sex and sexual preference. This parameter is a random Poisson number which is generated using the means calculated from the NATSAL-3 dataset for each sex, sexual preference and age-cohort. A discrete random variable is said to have a Poisson distribution, with parameter \(\lambda_{s,a,p} > 0\) if it has a probability mass function given by:
| \[f(k;\lambda_{s,a,p}) = Pr(X = k) = \frac{\lambda_{s,a,p}^k \times e^{-\lambda_{s,a,p}}}{k!},\] | \[(1)\] |
For agents who are bi-sexual, the probability of finding a same-sex partner is calculated using relative frequency counts from the NATSAL-3 data. This probability is denoted by \(P(SameSexPartner,C_{bi{\text -}sexual,a,s})\). Here, \(C_{bi{\text -}sexual,a,s}\) represents the cohort an agent belongs to, \(a\) represents the age cohort \(a: a \in [0,1,...,15]\) and \(s\) represents the sex \(s: s \in {male, female}\). \(P(SameSexPartner,C_{bi{\text -}sexual,a,s})\) of each agent in cohort \(C_{bi{\text -}sexual,a,s}\) is given by:
| \[\begin{aligned} P(SameSexPartner,C_{bi{\text -}sexual,a,s}) &= \sum_{i \in C_{bi{\text -}sexual,a,s}}{\frac{NSS_{i}}{N_{i}}} \\ P(OppostiveSexPartner,C_{bi{\text -}sexual,a,s}) &= 1 - P(SameSexPartner,C_{bi{\text -}sexual,a,s}).\end{aligned}\] |
Here, \(NSS_{i}\) represents the sum of same-sex partners of an agent \(i\) in the cohort \(C_{bi{\text -}sexual,a,s}\) in last 12 months and \(N_{i}\) represents the total number of partners of an agent \(i\) in the cohort \(C_{bi{\text -}sexual,a,s}\) in last 12 months. In our model, there are 30 such probability values (15 age cohorts, 2 sexes).
When a bi-sexual agent of age-cohort \(a\) and sex \(s\) seeks a long-term sexual partner, a random number is drawn from a uniform distribution between 0 and 1. If the drawn number is less than \(P(SameSexPartner,C_{bi{\text -}sexual,a,s})\), then the agent forms partnership with another agent of the same-sex. Else, the agent forms partnership with another agent of the opposite sex.
Disease and disease transmission
We study the Mpox disease and have designed a disease model to reflect this. Our model is drawn from an SEIR model. Susceptible agents are vulnerable to infection following sexual contact. Exposed individuals are those who have been exposed to the virus but not showing any symptoms. Infected agents are the ones showing symptoms. Recovered agents are those who have been infected one in their lifetime and are now immune to the disease. An agent can transmit an infection either when they are in an infected state with visible symptoms or up to four days prior to the onset of symptoms. This disease component of our models and the calculations of \(R_0\) and \(R_t\) are based on Hunter et al. (2018) and Hunter et al. (2020).
We assume a transmission probability of \(1/8\). This means that during a sexual encounter between an infected and a susceptible agent, there is 1 in 8 chance that the susceptible agent will become infected. We also assume that in a long-term relationship, there are 3 sexual encounters in a week. Therefore, each day has a 3 in 7 chance of sexual encounter between a couple in a long-term relationship. Both these parameters are assumed and can be varied to study their impact on the outbreak size. Lets say that \(P({S \rightarrow E}_L)\) represents the daily probability that a susceptible long-term partner of an infected agent becomes exposed. \(P({S \rightarrow E}_L)\) is calculated according to the following equation:
| \[P({S \rightarrow E}_L) = TP \times WC = \frac{1}{8} \times \frac{3}{7} = 0.0535,\] | \[(2)\] |
| \[P({S \rightarrow E}_S) = TP.\] | \[(3)\] |
If the infection has been transmitted, the agent remains in an "Exposed" state before the onset of the first symptoms. The incubation period is the time interval between the initial infection and the appearance of symptoms. We take the incubation period parameter from Ward et al. (2022), values of which are shown in Table 1. A person can be infectious for up to four days before symptoms emerge (Ward et al. 2022). To achieve this, a random number is drawn from a uniform distribution \(\mathcal{U}(0,4)\) and subtracted from the incubation period. Assume that \(Inc\) represents the incubation period for an exposed agent. \(Inc - \mathcal{U}(0,4)\) represents the time period an agent remains in the "Exposed" state without becoming infectious. This subtraction is only carried out when the incubation period for an agent is less than 6 days, otherwise the time period in "Exposed" state can get very close to zero or even be negative.
A person is in the "Infected" state between 2 to 4 weeks (CDC 2023). For each agent, an individualised "sick-period" is calculated by drawing a random number from a normal distribution with mean of 21 days (mid-point between 14 and 28 days) and a standard deviation of 3 days. Once infectious, a person can transmit Mpox virus through sexual contact. It is assumed that vaccination efficacy is 85%, similar to the estimates by Wolff Sagy et al. (2023), Grant et al. (2020), Rimoin et al. (2010), Fine et al. (1988). This means that out of every 100 people vaccinated, 85% will not get the disease if exposed. One an infected agent recovers, it is placed into the "Recovered" state. For simplicity, permanent immunity to the disease post-infection is assumed. This is because Mpox infection induces long-term immunity in recovering patients (Mitjà et al. 2023) and only a very few cases of reinfection have been reported so far (Golden et al. 2023; Musumeci et al. 2023).
Sexual network
Transmission is modelled through sexual contact. Two types of sexual contacts are possible in this model: long-term and short-term. Long-term sexual contact that is continued towards the end of a relationship. The short-term contact is a once-only contact modelled to mimic the transmission through super-spreader events or travel. long-term relationships are modelled to be monogamous. These are formed probabilistically using the \(\lambda_{s,a,p}\) parameter derived from the NATSAL-3 dataset. Each agent has a parameter that defines the number of new partners that agent will take in a year. As explained in Section "Society and agents", it is a random Poisson number \(k\) drawn from Poisson distribution with mean \(= \lambda_{s,a,p}\). To get a new long-term partner, the agent has to break-up with the existing partner first. The probability that an agent will breakup on a particular day is drawn from the following exponential distribution function (scaled to a day from a year):
| \[P_{BreakupToday} = 1 - e^{-1 * \frac{k+0.1}{365} }\] | \[(4)\] |
Here, a small number (\(\frac{0.1}{365}\)) is added as a large number of agents will end up with zero probability of finding a new partner otherwise. For each agent, at each timestep/day, a random uniform number is drawn between 0 and 1. If the drawn random number is less than \(P_{BreakupToday}\), the link between the agent’s current long-term partner, if any, is removed, and a new partner is sought for this agent.
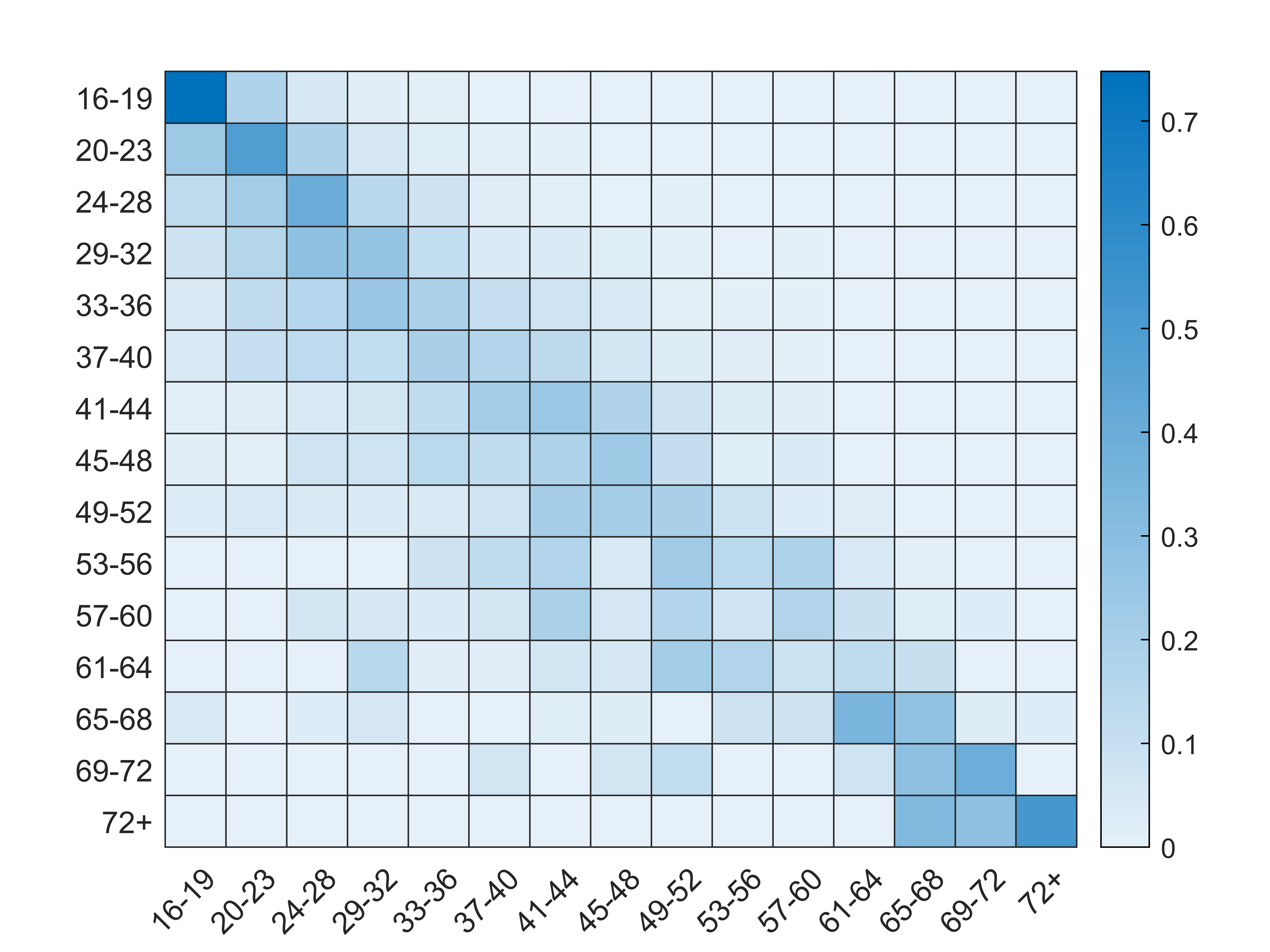
The other component of the model is the contact matrix. This matrix gives the probability that an agent in a age-cohort will form a sexual partnership with another agent in the same or a different age cohort. The age of the partner is recorded within the NATSAL-3 survey dataset. Therefore, an age-mixing matrix is calculated from the NATSAL-3 dataset, using the method presented by Datta et al. (2018). In this paper, the authors determine distributions of the rate of new partners that involve in condomless sex and therefore, facilitate the spread of STIs. Following the methodology proposed by Datta et al. (2018), we aggregate data from individual respondents within each age-cohort, differentiated by sex and sexual preference. Unlike Datta et al. (2018), condom-less sex is not a necessary assumption in this model framework. Each cell in the age-mixing matrix represents the probability of an agent in an age cohort \(C_1\) of forming a sexual partnership with another agent in the age-cohort \(C_2\). Each time a new partner is being sought, the probability that the new partner belongs to a certain age cohort is based on the age-mixing matrix.
The following equation is used to calculate the age-mixing matrix. \(C_{ij}\) represents probability that an agent in cohort \(C_i\) will have sexual partnership with an agent in cohort \(C_j\). The probability that an agent in cohort \(C_i\) will seek a sexual partnership with an agent in cohort \(C_j\), \(P(P_{C_i,C_j})\), is based on the relative frequency counts obtained from the NATSAL-3 dataset, described by the following equation:
| \[P(P_{C_i,C_j}) = \frac{\sum \theta_{i,j}}{\sum \theta_i},\] | \[(5)\] |
| \[P_{AGEMIXING} =\] \[\begin{bmatrix} P_{C_1,C_1} & P_{C_1,C_2} & \dots & P_{C_1,C_N} \\ \vdots & \ddots & & \\ P_{C_N,C_1} & & & P_{C_N,C_N} \\ \end{bmatrix} = \] \[\begin{bmatrix} \frac{\sum \theta_{C1,C1}}{\sum \theta_{C_1}} & \frac{\sum \theta_{C_1,C_2}}{\sum \theta_{C_1}} & \dots & \frac{\sum \theta_{C_1,C_N}}{\sum \theta_{C_1}} \\ \vdots & \ddots & & \\ \frac{\sum \theta_{C_N,C_1}}{\sum \theta_{C_N}} & & & \frac{\sum \theta_{C_N,C_N}}{\sum \theta_{C_N}} \\ \end{bmatrix}\] | \[(6)\] |
The parameters for the short-term casual partnerships are not available through NATSAL-3 dataset as there is scarce data on concurrent relationships. Several assumptions are made about the short-term links. An agent goes to an event where there are multiple one-time sexual contacts are made. These contacts do not last past the event. In the Population Model, only MSMs aged between 16 to 32 years old attend such events, as this is a "high-risk" group in this model. The number of people attending the event is fixed to 35. This is an assumption made for simplicity. They can be many different types of events such as saunas, cruising bars, sex clubs, dating apps, and sex parties (CDC 2022), which have not been explicitly modelled for now, therefore selecting a reasonable estimate that can cover any type of event was necessary. The number of events per year is a variable in our simulations.
The MSM model
After analysing the results of the full population model (discussed in Section "Results"), we determined that the majority of cases in the model were in the MSM community with little spillover to some of the other groups, this seemed to fit with the real data where the majority of infections in the Mpox outbreak are in the MSM population. However, when modelling on the full population data, the portion of agents who were in the MSM community was small relative to the entire population resulting in low case counts in the model results. Based on the fact that there is evidence that suggests that the MSM community is at a higher risk, we develop a second model in which the society solely focuses on the MSM community. This model also contains 10,000 agents, all of whom are homosexual and bi-sexual men. Female partners of the bi-sexual men are added in addition to the MSM agents. The parameters for long-term sexual contacts are derived from the NATSAL-3 dataset, as performed in the previous model. Female partner agents are not a closed population, they enter or leave the model based on the partnership (i.e., once a partnership between a bi-sexual man and heterosexual woman ends, the woman agent leaves the model). There are no heterosexual men in the model.
In this model, some MSM agents are flagged as high-risk. These are the agents who are more prone to acquiring Mpox through travel, attending super-spreader events/venues and having multiple partners. The percentage of high-risk MSMs is set to 1% in our simulations. Top 1% agents with highest number of partners are marked as high-risk. This parameter can also be varied to study its impact on the outbreak size. The parameters specific to this model are presented in Table 2. All other parameters are same as the previous model.
| Variable | Description | Value | Source |
|---|---|---|---|
| Homosexual Males (%) | Percentage of homosexual men | 63.6% | NATSAL-3 |
| Bi-sexual Males (%) | Percentage of bi-sexual men | 36.3% | NATSAL-3 |
| % of high-risk | Percentage of MSM at high-risk behaviour | 1% | - |
Model simulation
We simulate our models using various combinations of the parameters shown in Table 3. For the population model, there are 12 different scenarios. For the MSM model, there are 16 different scenarios modelled.
| Population Model | MSM Model | ||
|---|---|---|---|
| Variable | Values | Variable | Values |
| No. of imported cases per year | 0 or 30 | No. of imported cases per year | 0 or 30 |
| No. of super-spreader events | 0 or 30 | No. of super-spreader events | 0 or 30 |
| Vaccination Strategy | None, Random or Random high-risk | Percentage of vaccinated high-risk agents | 0, 30, 50 or 90 |
- Travel related cases
- Super-spreader events
- Vaccination strategy/Number of people vaccinated
For each combination, we run 100 simulations and present the results with mean and standard deviation. Each simulation is run for 180 ticks (1 tick = 1 day). The following metrics are reported:
- Effective Reproduction number, denoted by \(R_e\), represents the average number of new infections caused by each infected individual in a population made up of both susceptible and non-susceptible hosts. \(R_e\) for each scenario is calculated at the end of the simulation at 180 days.
- Time-varying reproduction number, denoted by \(R_t\). \(R_t\) is the average number of secondary infections generated by an infected individual at each day during the simulation.
- Daily number of new Mpox cases in the entire population and/or in different sub-groups by age, sex and sexual-preferences.
- Total number of infected individuals within each group by sex, age and sexual-preference.
Results
Population model results
Impact of super-spreader events and imported cases
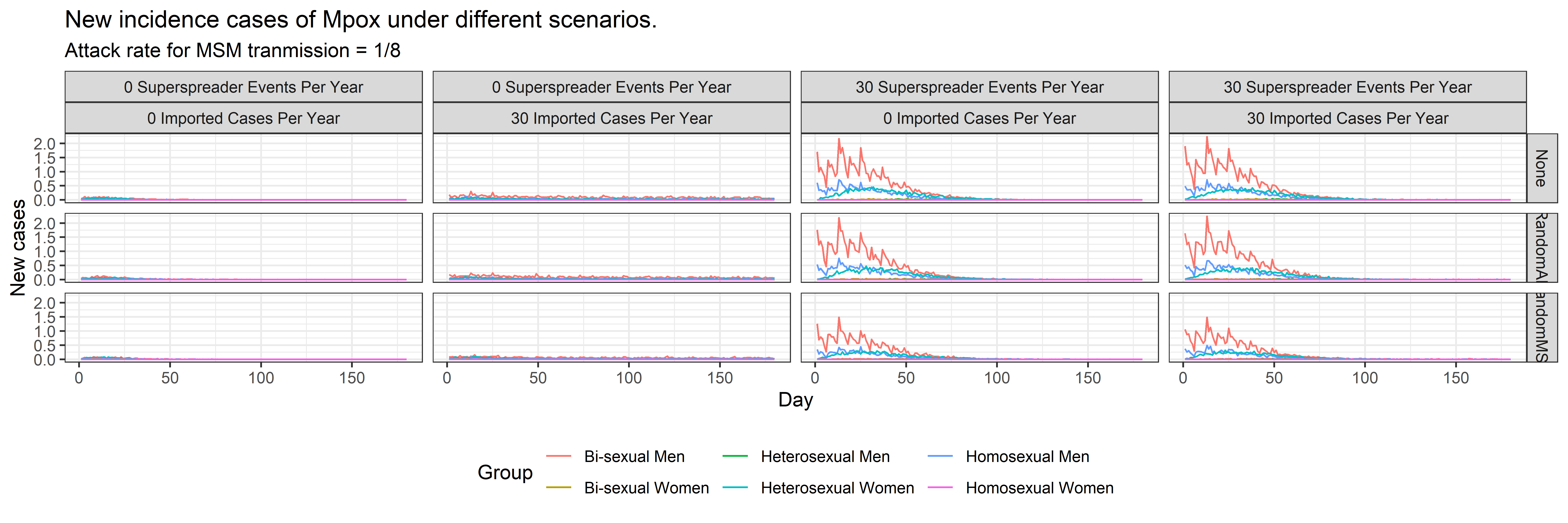
We can observe that when there are no super-spreader events or imported cases, the infection does not persist within the society. The graph in Figure 3 shows the mean and standard deviation of daily new infections in 100 runs for each scenario. It also shows the time-varying reproduction number of the infection. We observe the following from the results:
- In the situation where there are no super-spreader events or imported cases, the infection does not persist for an extended period and is eliminated after 50 days, with the mean time-varying reproductive number \(R_t\) remaining close to zero.
- In the scenario where there are no super-spreader events, but approximately 30 cases imported per year, we observe a low but sustained incidence of new Mpox cases. The mean (\(R_t\)) remains close to zero, but unlike the first scenario, it does not remain exactly zero after 50 days.
- In the scenario where there are no imported cases but 30 super-spreader events per year, we observe a higher rate of new incidences. The average \(R_t\) exceeds 1 on certain days, particularly when no one is vaccinated or when the vaccination is not targeted to the high-risk MSM group.
- In the scenario where there are 30 super-spreader events and approximately 30 imported cases per year, we observe a sustained and heightened incidence of new Mpox cases. Similar to the previous scenario, the mean \(R_t\) exceeds 1 on certain days, particularly when no one is vaccinated or when random individuals are vaccinated.
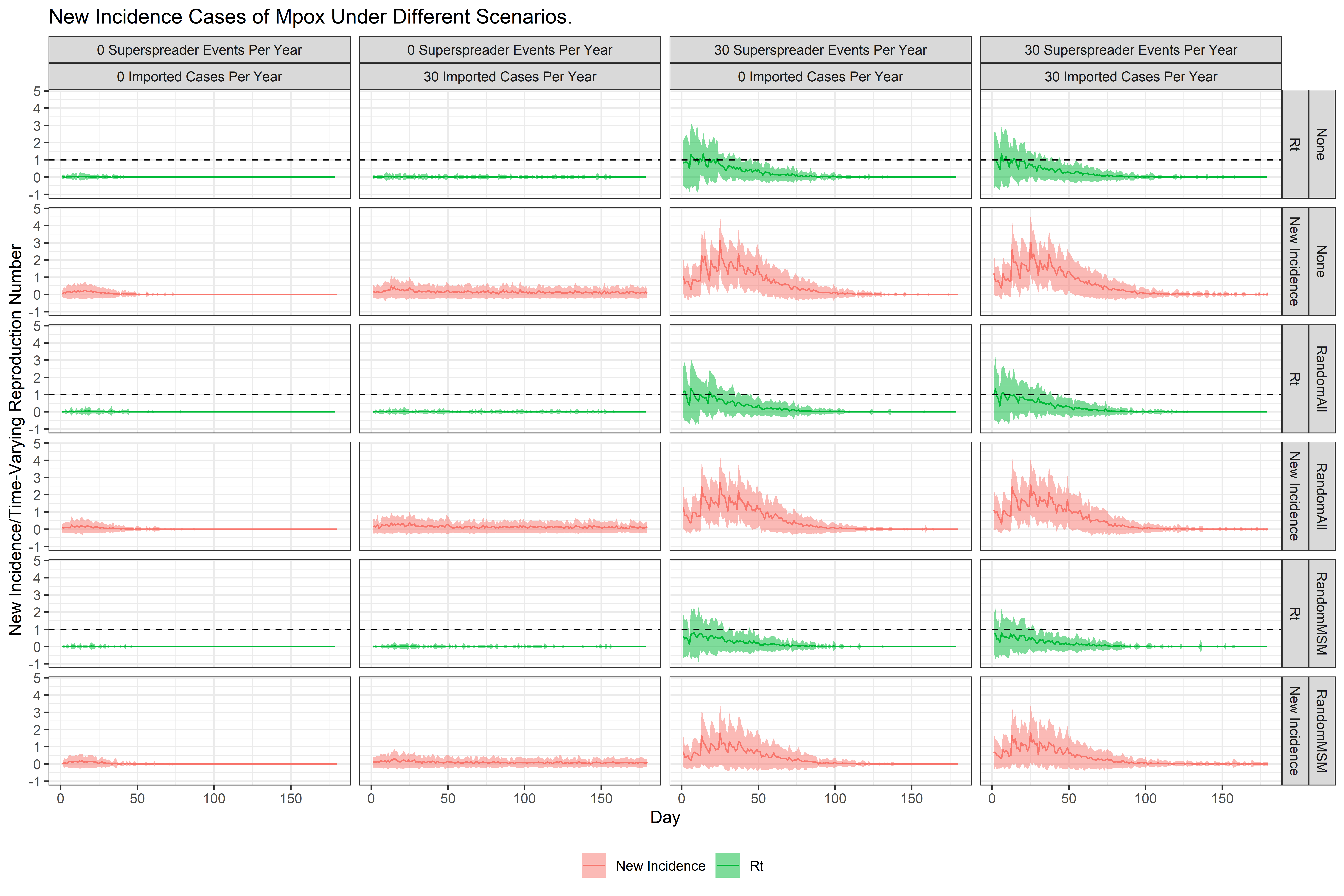
The graph in Figure 4 shows the mean effective reproduction number \(R_e\) calculated for each scenario. The mean \(R_e\) in all scenarios where there are no super-spreader events is less than the mean \(R_e\) when there are 30 super-spreader events.
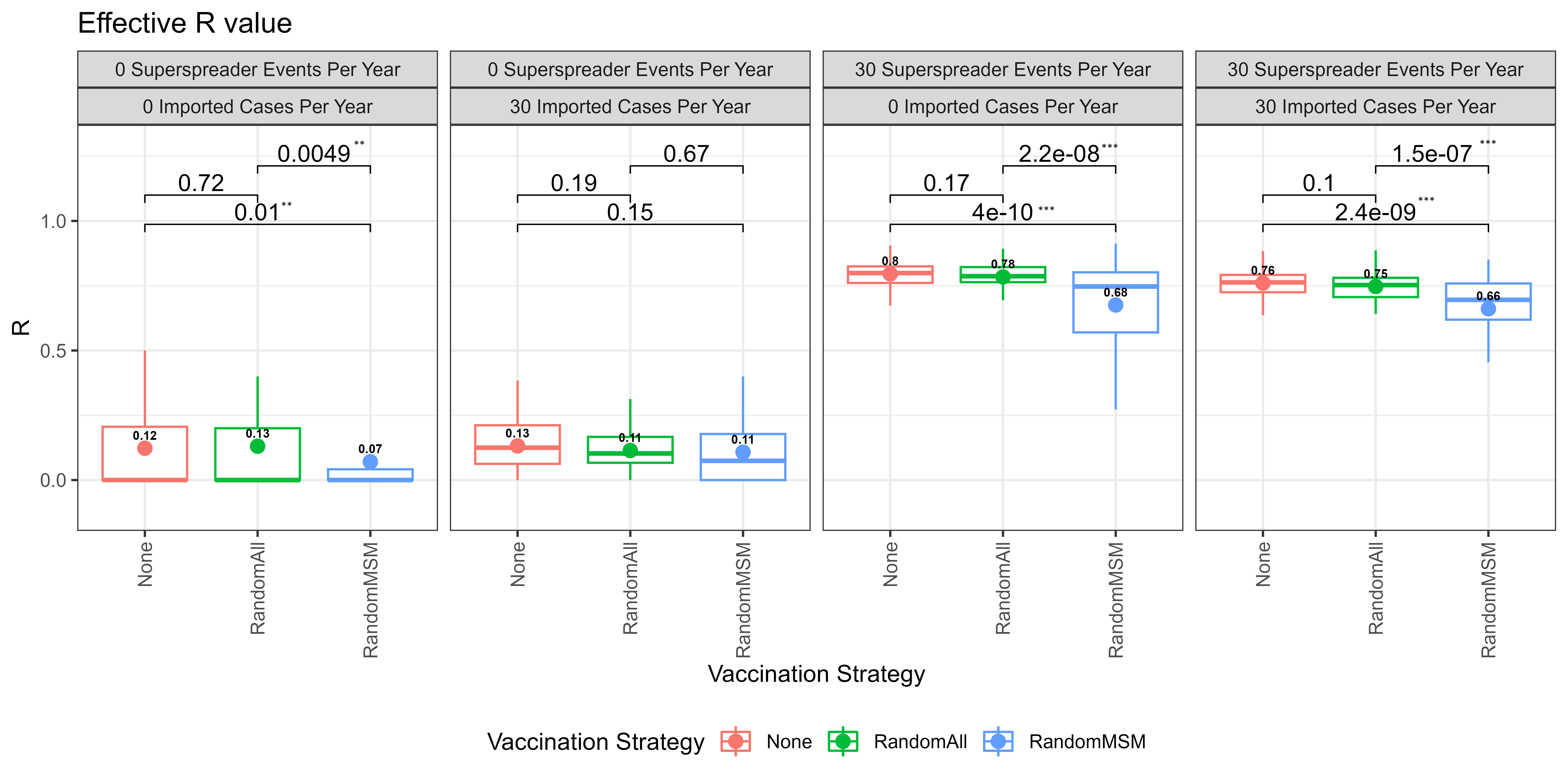
Impact of vaccination strategy
The graph in Figure 4 reveals that in most scenarios, the average \(R_e\) is notably lower when 100 randomly selected individuals from the MSM group are vaccinated, as opposed to scenarios where there is no vaccination or when 100 random people from the entire model are vaccinated. This finding indicates that targeting vaccination efforts towards the high-risk MSM group yields a greater impact compared to random vaccination strategies. Randomly vaccinating the population yields no benefit, especially if the vaccine supply is low.
Transmission in heterosexual, bi-sexual and homosexual men and women groups
Figure 5 depicts the average total number of infections among homosexual, bi-sexual, and heterosexual men and women over a 180-day period. Notably, the MSM group is the most affected, while there are relatively few incidences among heterosexual women, fewer among heterosexual men and bi-sexual women, and none among homosexual women in all scenarios. This is because MSM group is modelled as high-risk: Imported cases and super-spreader events are both modelled to occur exclusively within the MSM group, specifically among individuals aged 16-40 years.
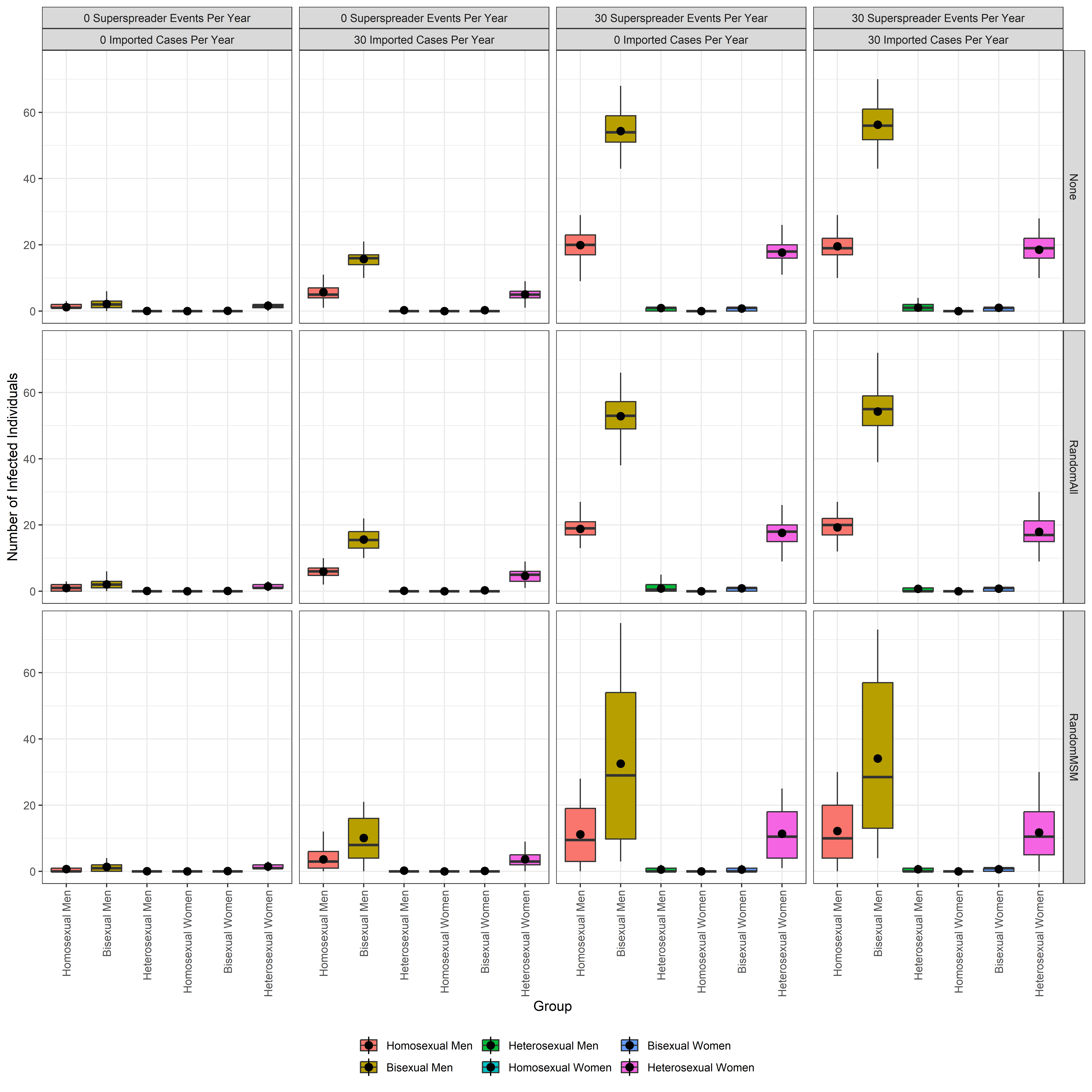
Figure 6 shows the mean new incidence broken down by different groups (sex and sexual preferences) each day. As expected, incidence is low for all groups when there are no super-spreader events and no imported cases. In the scenario when there are 30 super-spreader events, we see that bi-sexual men are most affected. This is because of two reasons: Bi-sexual and homosexual men (MSM) are modelled as high risk and bi-sexual men population is higher than homosexual men population. Heterosexual women is the next affected group. There is low incidence at the start of the simulation but new incidences peak around day 25 for heterosexual women. Incidence rate is close to zero for the rest of the groups. In all scenarios, infected does not sustain after day 100.
Transmission in different age groups
As shown in the graph in Figure 7, people between ages 24 and 40 are most affected by Mpox. This is because these age cohorts have a higher rate of new sexual partnership formation (as calculated through NATSAL-3 data). In our model, as previously explained, age bracket 16-40 is the high risk population and imported cases and super-spreader events are both modelled to occur exclusively within the MSM group of this age bracket.
MSM model results
Impact of super-spreader events and imported cases
Similar to what was observed in the Population Model, when there are no super-spreader events or imported cases in the MSM model, the infection does not persist within the society. The graph in Figure 8 shows the mean and standard deviation of daily new infections in 100 runs for each scenario. It also shows the time-varying reproduction number of the infection. We observe the following from the results:
- In the situation where there are no super-spreader events or imported cases, the infection does not persist for an extended period and is eliminated after 50 days, with the mean time-varying reproductive number \(R_t\) remaining close to zero.
- In the scenario where there are no super-spreader events, but approximately 30 cases imported per year, we observe a low but sustained incidence of new Mpox cases. The mean (\(R_t\)) remains close to zero.
- In the scenario where there are no imported cases but 30 super-spreader events per year, we observe a higher rate of new incidences. The average \(R_t\) exceeds 1 on most days before day 50, particularly when 0 or 30% people from the high-risk are vaccinated.
- Similarly, in the scenarios where there are 30 super-spreader events and approximately 30 imported cases per year, we observe a sustained and heightened incidence of new Mpox cases. Similar to the previous scenario, the mean \(R_t\) exceeds 1 on most days before day 50, particularly when when 0 or 30% people from the high-risk are vaccinated.
- As we increase the percentage of vaccinated high-risk individuals, we observe that mean new incidence and mean \(R_t\) are decreased. When 90% of high-risk individuals are vaccinated, we see that the mean \(R_t\) is close to 0 at all times and the mean new incidence is also close to zero at all times.

The graph in Figure 9 shows the mean \(R_e\) calculated for each scenario. As with the population model, the mean \(R_e\) in all scenarios where there are no super-spreader events is less than the mean \(R_e\) when there are 30 super-spreader events.
Impact of % of vaccinated high-risk individuals
The graph in Figure 9 reveals that when there are 30 super-spreader events in a year, the mean \(R_e\) when 90% high risk population is vaccinated is significantly (p-value < 0.01) less compared to when 50% high-risk individuals are vaccinated. The mean \(R_e\) when 50% high risk population is vaccinated is significantly (p-value < 0.01) less compared to when 30% high-risk individuals are vaccinated and the mean \(R_e\) when 30% high risk population is vaccinated is significantly (p-value < 0.01) less compared to when 30% high-risk individuals are vaccinated. This shows that as we increase the vaccination rate among high-risk individuals, the mean \(R_e\) significantly decreases.
Transmission in bi-sexual men and homosexual men and women groups
Figure 10 depicts the average total number of infections among homosexual men, bi-sexual men and heterosexual women over a 180-day period under different scenarios. In the scenarios when there are 30 super-spreader events and/or 30 imported cases in a year, the MSM group is notably the most affected. There are there are relatively few incidences among heterosexual women in scenarios when there are 30 super-spreader events in a year. In such scenarios, when there are 0 high-risk individuals vaccinated, there are on average around 20 heterosexual women infected over the course of 180 days. In the scenario, when there are 30% high-risk individuals vaccinated, there are on average around 10 heterosexual women infected over the course of 180 days. This mean goes down further between 5-10 when 50% high risk individuals are vaccinated and approaches 0 when 90% high-risk individuals are vaccinated.
Transmission in different age groups
As shown in the graph in Figure 11, in the scenarios when there are 30 super-spreader events in a year and 0-50% high-risk population is vaccinated, people between ages 33 and 48 are most affected by Mpox. This is because these age cohorts have a higher rate of new sexual partnership formation (as calculated through NATSAL-3 data). In contrast to our previous population level ABM, this model does not explicitly mark agents as high-risk based on their age cohorts. Instead, it marks the top 1% of agents with the maximum value of new-partners-per-year parameter and marks them as high-risk.
Discussion
The COVID-19 pandemic placed scientific community under immense pressure to provide rapid, data-driven advice to the policy makers. Squazzoni et al. (2020) emphasize the importance of model transparency, data access, and rigor, alongside faster, responsible data sharing from trusted sources. In this work, we have presented models that are free and open source, whose parameters are informed by public data sources and have been rigorously analysed under various scenarios. In the light of the discussion in Edmonds et al. (2019), the purpose of presented models is ‘Description’ as they have the ability to explore different scenarios. Our presented models can also be used (in current or extended form) for ‘Prediction’ as they have the features to anticipate and compare intervention scenarios, including consequences of no interventions. From a public health point-of-view, these models can make a valuable contribution towards the discussion of interventions and have the potential to inform broader public health policy and practice, in addition to their immediate relevance for Mpox control and prevention efforts. By identifying and prioritizing vulnerable groups such as MSM and their partners, our models provide valuable information for targeted intervention planning and resource allocation (Mpox vaccination was limited in supply in Ireland at the time these models were being developed). Our findings align with global trends of Mpox spread and the use of data from NATSAL-3 further strengthens the validity and generalizability of our results. The insights gained from our work can be extrapolated and adapted to inform strategies for addressing other infectious diseases with similar transmission dynamics, thereby contributing to the broader scientific literature on infectious disease modelling and public health surveillance.
The ABMs proposed in this study provide a valuable framework for studying the spread of Mpox. By simulating the interactions and behaviours of individual agents within a virtual environment, the model captures the dynamics of disease transmission and allows for the exploration of scenarios and mitigation strategies. The models allow for the incorporation of heterogeneity in the sexual networks and disease-specific parameters. These models can be customized to represent specific regions, age groups, or social/sexual networks, enabling a more nuanced understanding of the disease dynamics within specific populations. The proposed models can also facilitate the investigation of different intervention strategies and their impact on Mpox spread, as we investigated the impact of various vaccination strategies in the current study. The framework’s utility to simulate and compare multiple intervention scenarios can aid policy makers in making informed decisions to mitigate the spread of Mpox and allocate resources efficiently. All code is open source and hence other researchers can build upon it.
When interpreting the data provided, it is crucial to consider the model’s design and the underlying assumptions used to establish its parameters. Accurate estimates of some key parameters were not available and some assumptions were made. These include the transmission probability (and how it varies according to the type of sexual contact), weekly sexual contact rate and size of the super-spreader events. These can be estimated from contact tracing data or studies focusing on behaviours of MSM specifically. The results can vary significantly if these fixed parameters are changed. The vaccine efficacy parameter has been derived from data obtained during Mpox outbreaks in regions where the disease is endemic. It remains uncertain whether the assumptions based on such data are applicable to the 2022 epidemic outside the endemic regions (van Ewijk et al. 2023).
Although the model has not yet been scaled to represent an actual population, the observed trends of new incidences in our results align with global patterns, indicating a decline in Mpox cases worldwide. Quick eye-balling of Figure 3 of the Population Model shows that daily new confirmed cases peak around day 25 and fall close to 0 at around day 100 in all scenarios. Similarly, in the MSM model simulation, particularly in the scenario where no high-risk individuals are vaccinated, the daily mean new incidences decrease to close to zero between day 100 and day 125 (Figure 7). While a direct comparison with the actual daily confirmed cases in the UK is not appropriate, it is worth noting that the epidemic curve appears to approach zero around November 1, 2022, approximately 180 days after the identification of the first case. After that, new cases are few and far between. The overall trends are similar, with the infection dying out within the initial 4-6 months.
It is also challenging to directly compare the \(R_e\) we computed and the \(R_0\) reported in various studies as the estimates of \(R_0\) are influenced by factors such as the specific strain of the virus, society structure, population density and the level of immunity within the population (Grant et al. 2020). According to Kwok et al. (2022), the \(R_0\) for England in 2022 is 1.60 [95% (credible interval) CrI, 1.50–1.70]. This number is comparable to the \(R_e\) of our MSM model, in which the number of super-spreader events in a year is set to 30 and percentage of high-risk vaccinated is equal to 0 or 30%. Grant et al. (2020) estimated an \(R_e\) for period 1980-1984 between 0.22-0.40. Our estimates of \(R_e\) for both models in scenarios when there are no super-spreader events are less than this.
While our results confirm some expectations, such as the effectiveness of vaccinations and the impact of reducing concurrent partnerships on achieving a disease-free equilibrium, the validation of these insights through our model provides an important contribution to the field for several reasons. Firstly, the confirmation of public health insights through modelling is in itself significant outcome. Our model’s capability to replicate known outcomes in the context of disease transmission not only confirms its accuracy and reliability but also reinforces the importance of these public health strategies. At the same time, our models also offer insights that go beyond the common-sense understanding. For example, our analysis highlights that certain groups, such as homosexual women and heterosexual men, may be less vulnerable to the spread of the disease. These findings underscore the importance of targeted interventions in disease control and prevention. One of the interesting findings from our model, which is particularly relevant given the constraints on vaccine availability, is the vulnerability of younger heterosexual females to the disease. This analysis highlights the need for vigilance and targeted intervention strategies for this cohort, which might not have been initially considered a high priority. Our study also demonstrates the value of leveraging data from NATSAL-3 in constructing and validating the models. This approach exemplifies how large-scale survey data can be effectively used in epidemiological modelling to inform public health strategies. The purpose of employing agent-based modelling was precisely to guide an investigation into the dynamics of disease spread and to inform decision-making processes with empirical data and nuanced analysis.
The focus of the work we have presented in this paper was the 2022-2023 global Mpox outbreak. While we are aware that the immediate threat of Mpox has subsided for most regions, Mpox remains endemic in many African nations (WHO 2023). Thus, the threat for another global outbreak remains. As such the findings of this work on Mpox remain important until a time when Mpox can be eradicated. Additionally, beyond the findings related to Mpox, due to globally low vaccination rates for many diseases that have previously been controlled, there is a risk of more large-scale outbreaks. This can be seen in the evidence of polio spread in 2022 in New York and the measles outbreaks in the UK in 2023/2024. The framework and modelling process we have developed here will be essential guidance in responding to future disease outbreaks particularly to those disease that spread through high-risk groups.
Limitations and Future Work
The model, currently is not scaled to an actual population. It has been difficult to obtain clearer information about contact tracing and nature of the events through which the infection is spread. The NATSAL-3 data does not have a rich volume of MSM behaviours. To closely match the real scenarios, it is important that the network parameters are derived from the datasets focused on the MSM population. Modelling the sexual networks of MSM is essential for accurately understanding and predicting the spread of Mpox within this population. For future research, we plan to use the EMIS 2017 (Casey et al. 2019) report to derive the parameters of the MSM sexual contact network in Ireland and to scale our models to the Irish population and compare the results with incidence data from Ireland. Several studies focusing on developing MSM sexual networks can be also be used, see Amirkhanian (2014), Glynn et al. (2018) and the references within. By mapping out MSM sexual networks, researchers and public health officials can identify individuals or subgroups with a higher risk of Mpox transmission. This information allows for the development of targeted interventions, such as outreach programs, testing campaigns, or education initiatives, to reach those at greater risk.
Additional data is necessary to gain a deeper understanding of the characteristics and magnitude of super-spreader events. Currently, an assumed count of 35 events is used; however, the actual number may vary. Ideally, this number would be derived from contact tracing data to provide more accurate insights.
Categorizing people as bi-sexual, homosexual and heterosexual is based on their past sexual experiences as reported in the NATSAL-3 data is a crude generalisation. A person with sexual experience with both sexes is bisexual, while someone with sexual experience only with the opposite sex is heterosexual. Therefore, we model sexual preferences instead of sexual orientation. In the NATSAL-3 dataset, there is no information about self-disclosed sexual orientation of a person.
Our model currently does not model childhood smallpox vaccinations, diagnosis or diagnostic delay, behaviour changes after diagnosis (e.g. attending less events, limiting sexual activity, etc) and contact tracing. We plan to extend our model to include these details.
Conclusion
In this paper, we proposed two agent-based models to study the spread of Mpox within an artificial society. Disease parameters were derived from the relevant epidemiological research, and sexual networks were constructed using the NATSAL-3 dataset and methodology described in Datta et al. (2018). Estimates of \(R_e\) and \(R_t\) were presented for various scenarios.
Our analysis revealed that in the absence of super-spreader events and imported cases, the infection does not sustain within the society. Furthermore, our findings highlighted the efficacy of targeting high-risk groups through vaccination compared to random vaccination or no vaccination at all. Vaccinating individuals in the high-risk groups proved to be an effective strategy in limiting the spread of Mpox within the society. Further research and modelling efforts can build upon these findings to develop more robust strategies for managing and containing the spread of Mpox in real-world scenarios.
References
ADIGA, A., Chu, S., Eubank, S., Kuhlman, C. J., Lewis, B., Marathe, A., Marathe, M., Nordberg, E. K., Swarup, S., Vullikanti, A., & Wilson, M. L. (2018). Disparities in spread and control of influenza in slums of Delhi: Findings from an agent-based modelling study. BMJ Open, 8(1), e017353. [doi:10.1136/bmjopen-2017-017353]
AJELLI, M., Parlamento, S., Bome, D., Kebbi, A., Atzori, A., Frasson, C., Putoto, G., Carraro, D., & Merler, S. (2015). The 2014 Ebola virus disease outbreak in Pujehun, Sierra Leone: Epidemiology and impact of interventions. BMC Medicine, 13, 1–8. [doi:10.1186/s12916-015-0524-z]
ALZU’BI, A. A., Alasal, S. I. A., & Watzlaf, V. J. (2021). A simulation study of coronavirus as an epidemic disease using agent-based modeling. Perspectives in Health Information Management, 18.
AMIRKHANIAN, Y. A. (2014). Social networks, sexual networks and HIV risk in men who have sex with men. Current HIV/AIDS Reports, 11(1), 81–92. [doi:10.1007/s11904-013-0194-4]
ANTIA, R., Regoes, R. R., Koella, J. C., & Bergstrom, C. T. (2003). The role of evolution in the emergence of infectious diseases. Nature, 426(6967), 658–661. [doi:10.1038/nature02104]
ANWAR, F., & Waris, A. (2022). Monkeypox virus outbreak: A brief timeline. New Microbes and New Infections, 48, 101004. [doi:10.1016/j.nmni.2022.101004]
ARDUIN, H., Domenech de Cellès, D., Guillemot, D., Watier, L., & Opatowski, L. (2017). An agent-based model simulation of influenza interactions at the host level: Insight into the influenza-related burden of pneumococcal infections. BMC Infectious Diseases, 17(1). [doi:10.1186/s12879-017-2464-z]
BANKURU, S. V., Kossol, S., Hou, W., Mahmoudi, P., Rychtář, J., & Taylor, D. (2020). A game-theoretic model of Monkeypox to assess vaccination strategies. PeerJ, 8, e9272. [doi:10.7717/peerj.9272]
BARABÁSI, A. L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286(5439), 509–512.
BLUMBERG, S., Funk, S., & Pulliam, J. R. C. (2014). Detecting differential transmissibilities that affect the size of self-Limited outbreaks. PLoS Pathogens, 10(10), e1004452. [doi:10.1371/journal.ppat.1004452]
BLUMBERG, S., & Lloyd-Smith, J. O. (2013). Inference of r0 and transmission heterogeneity from the size distribution of stuttering chains. PLoS Computational Biology, 9(5), e1002993. [doi:10.1371/journal.pcbi.1002993]
BRAGAZZI, N. L., Kong, J. D., Mahroum, N., Tsigalou, C., Khamisy-Farah, R., Converti, M., & Wu, J. (2023). Epidemiological trends and clinical features of the ongoing monkeypox epidemic: A preliminary pooled data analysis and literature review. Journal of Medical Virology, 95(1), e27931. [doi:10.1002/jmv.27931]
BRAINARD, J., & Hunter, P. R. (2019). Misinformation making a disease outbreak worse: Outcomes compared for influenza, monkeypox, and norovirus. SIMULATION, 96(4), 365–374. [doi:10.1177/0037549719885021]
CAI, X. (2007). Exact stochastic simulation of coupled chemical reactions with delays. The Journal of Chemical Physics, 126(12), 124108. [doi:10.1063/1.2710253]
CASEY, C., O’Donnell, K., Brady, M., & Igoe, D. (2019). EMIS-2017 Ireland: Findings from the European men who have sex with men internet survey (Ireland). Dublin: HSE HPSC.
CDC. (2022). Safer sex, social gatherings, and Mpox. Available at: https://www.cdc.gov/poxvirus/mpox/prevention/sexual-health.html.
CDC. (2023). Isolation and prevention practices for people with Mpox. Available at: https://www.cdc.gov/poxvirus/mpox/clinicians/isolation-procedures.html
CHUMACHENKO, D., & CHUMACHENKO, T. (2017). Agent-based investigation of sexually transmitted infection. Online Journal of Public Health Informatics, 9(1). [doi:10.5210/ojphi.v9i1.7638]
CROOKS, A. T., & Hailegiorgis, A. B. (2014). An agent-based modeling approach applied to the spread of cholera. Environmental Modelling & Software, 62, 164–177. [doi:10.1016/j.envsoft.2014.08.027]
CUEVAS, E. (2020). An agent-based model to evaluate the COVID-19 transmission risks in facilities. Computers in Biology and Medicine, 121, 103827. [doi:10.1016/j.compbiomed.2020.103827]
DATTA, S., Mercer, C. H., & Keeling, M. J. (2018). Capturing sexual contact patterns in modelling the spread of sexually transmitted infections: Evidence using Natsal-3. PLoS One, 13(11), e0206501. [doi:10.1371/journal.pone.0206501]
DE Espíndola, A. L., Bauch, C. T., Cabella, B. C. T., & Martinez, A. S. (2011). An agent-based computational model of the spread of tuberculosis. Journal of Statistical Mechanics: Theory and Experiment, 2011(05), P05003. [doi:10.1088/1742-5468/2011/05/p05003]
DUGGAN, J., Andrade, J., Murphy, T. M., Gleeson, J. P., Walsh, C., & Nolan, P. (2024). An age-cohort simulation model for generating COVID-19 scenarios: A study from Ireland’s pandemic response. European Journal of Operational Research, 313(1), 343–358. [doi:10.1016/j.ejor.2023.08.011]
EAMES, K. T., & Keeling, M. J. (2002). Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proceedings of the National Academy of Sciences, 99(20), 13330–13335. [doi:10.1073/pnas.202244299]
EDMONDS, B., Le Page, C., Bithell, M., Chattoe-Brown, E., Grimm, V., Meyer, R., Montañola-Sales, C., Ormerod, P., Root, H., & Squazzoni, F. (2019). Different modelling purposes. Journal of Artificial Societies and Social Simulation, 22(3), 6. [doi:10.18564/jasss.3993]
EL-MESADY, A., Elsonbaty, A., & Adel, W. (2022). On nonlinear dynamics of a fractional order monkeypox virus model. Chaos, Solitons & Fractals, 164, 112716. [doi:10.1016/j.chaos.2022.112716]
EL-MESADY, A., Sonbaty, A., & Adel, W. (2022). On nonlinear dynamics of a fractional order monkeypox virus model. Chaos, Solitons and Fractals, 164, 112716. [doi:10.1016/j.chaos.2022.112716]
ENDO, A., Murayama, H., Abbott, S., Ratnayake, R., Pearson, C. A. B., Edmunds, W. J., Fearon, E., & Funk, S. (2022). Heavy-tailed sexual contact networks and monkeypox epidemiology in the global outbreak, 2022. Science, 378(6615), 90–94. [doi:10.1126/science.add4507]
ERDŐS, P., & Rényi, A. (1959). On random graphs. Publicationes Mathematicae Debrecen, 6, 290–297.
FINE, P., Jezek, Z., Grab, B., & Dixon, H. (1988). The transmission potential of monkeypox virus in human populations. International Journal of Epidemiology, 17(3), 643–650. [doi:10.1093/ije/17.3.643]
FORNI, D., Cagliani, R., Molteni, C., Clerici, M., & Sironi, M. (2022). Monkeypox virus: The changing facets of a zoonotic pathogen. Infection, Genetics and Evolution, 105, 105372. [doi:10.1016/j.meegid.2022.105372]
GAO, J., Zhou, C., Liang, H., Jiao, R., Wheelock, A. M., Jiao, K., Ma, J., Zhang, C., Guo, Y., Luo, S., Liang, W., & Xu, L. (2023). Monkeypox outbreaks in the context of the COVID-19 pandemic: Network and clustering analyses of global risks and modified SEIR prediction of epidemic trends. Frontiers in Public Health, 11. [doi:10.3389/fpubh.2023.1052946]
GLYNN, R. W., Byrne, N., O’Dea, S., Shanley, A., Codd, M., Keenan, E., Ward, M., Igoe, D., & Clarke, S. (2018). Chemsex, risk behaviours and sexually transmitted infections among men who have sex with men in Dublin, Ireland. International Journal of Drug Policy, 52, 9–15. [doi:10.1016/j.drugpo.2017.10.008]
GOEDEL, W. C., King, M. R. F., Lurie, M. N., Nunn, A. S., Chan, P. A., & Marshall, B. D. L. (2018). Effect of racial inequities in pre-exposure prophylaxis use on racial disparities in HIV incidence among men who have sex with men: A modeling study. Journal of Acquired Immune Deficiency Syndromes, 79(3), 323–329. [doi:10.1097/qai.0000000000001817]
GOLDEN, J., Harryman, L., Crofts, M., Muir, P., Donati, M., Gillett, S., & Irish, C. (2023). Case of apparent Mpox reinfection. Sexually Transmitted Infections, 99(4), 283–284. [doi:10.1136/sextrans-2022-055736]
GOPALAPPA, C., Balasubramanian, H., & Haas, P. J. (2023). A new mixed agent-based network and compartmental simulation framework for joint modeling of related infectious diseases - Application to sexually transmitted infections. Infectious Disease Modelling, 8(1), 84–100. [doi:10.1016/j.idm.2022.12.003]
GRANT, R., Luong Nguyen, L. B., & Breban, R. (2020). Modelling human-to-human transmission of Monkeypox. Bulletin of the World Health Organization, 98(9), 638–640. [doi:10.2471/blt.19.242347]
HSE. (2022). Update on HSE monkeypox vaccination programme. Available at: https://www.hse.ie/eng/services/news/media/pressrel/update-on-hse-monkeypox-vaccination-programme.html.
HUNTER, E., & Kelleher, J. D. (2021). Adapting an agent-Based model of infectious disease spread in an Irish county to COVID-19. Systems, 9(2), 41. [doi:10.3390/systems9020041]
HUNTER, E., Mac Namee, B., & Kelleher, J. (2018). An open-data-driven agent-based model to simulate infectious disease outbreaks. PLoS One, 13(12), e0208775. [doi:10.1371/journal.pone.0208775]
HUNTER, E., Mac Namee, B., & Kelleher, J. (2020). A hybrid agent-Based and equation based model for the spread of infectious diseases. Journal of Artificial Societies and Social Simulation, 23(4), 14. [doi:10.18564/jasss.4421]
HUNTER, E., Mac Namee, B., & Kelleher, J. D. (2017). A taxonomy for agent-Based models in human infectious disease epidemiology. Journal of Artificial Societies and Social Simulation, 20(3), 2. [doi:10.18564/jasss.3414]
IÑIGO Martínez, J., Gil Montalbán, E., Jiménez Bueno, S., Martínez, F. Martín, Nieto Juliá, A., Sánchez Díaz, J., García Marín, N., Córdoba Deorador, E., Nunziata Forte, A., Alonso García, M., Humanes Navarro, A. M., Montero Morales, L., Domínguez Rodríguez, M. J., Carbajo Ariza, M., Díaz García, L. M., Mata Pariente, N., Rumayor Zarzuelo, M., Velasco Rodríguez, M. J., Aragón Peña, A., … Arnáez, A. A. (2022). Monkeypox outbreak predominantly affecting men who have sex with men, Madrid, Spain, 26 April to 16 June 2022. Eurosurveillance, 27(27).
JONES, J., Weiss, K., Mermin, J., Dietz, P., Rosenberg, E. S., Gift, T. L., Chesson, H., Sullivan, P. S., Lyles, C., Bernstein, K. T., & Jenness, S. M. (2019). Proportion of incident human immunodeficiency virus cases among men who have sex with men attributable to gonorrhea and chlamydia: A modeling analysis. Sexually Transmitted Diseases, 46(6), 357–363. [doi:10.1097/olq.0000000000000980]
KASAIE, P., Andrews, J. R., Kelton, W. D., & Dowdy, D. W. (2014). Timing of tuberculosis transmission and the impact of household contact tracing. An agent-based simulation model. American Journal of Respiratory and Critical Care Medicine, 189(7), 845–852. [doi:10.1164/rccm.201310-1846oc]
KASAIE, P., Berry, S. A., Shah, M. S., Rosenberg, E. S., Hoover, K. W., Gift, T. L., Chesson, H., Pennington, J., German, D., Flynn, C. P., Beyrer, C., & Dowdy, D. W. (2018). Impact of providing preexposure prophylaxis for human immunodeficiency virus at clinics for sexually transmitted infections in Baltimore City: An agent-based model. Sexually Transmitted Diseases, 45(12), 791–797. [doi:10.1097/olq.0000000000000882]
KERR, C. C., Stuart, R. M., Mistry, D., Abeysuriya, R. G., Rosenfeld, K., Hart, G. R., Núñez, R. C., Cohen, J. A., Selvaraj, P., Hagedorn, B., Jastrzębski, M., Izzo, A. S., Fowler, G., Palmer, A., Delport, D., Scott, N., Kelly, S. L., Bennette, C. S., Wagner, B. G., … Klein, D. J. (2021). Covasim: An agent-based model of COVID-19 dynamics and interventions. PLOS Computational Biology, 17(7), e1009149. [doi:10.1371/journal.pcbi.1009149]
KHAN, A., Sabbar, Y., & Anwarud, D. (2022). Stochastic modeling of the Monkeypox 2022 epidemic with cross-infection hypothesis in a highly disturbed environment. Mathematical Biosciences and Engineering: MBE, 19, 13560–13581. [doi:10.3934/mbe.2022633]
KO, Y., Mendoza, V. M., Mendoza, R., Seo, Y., Lee, J., & Jung, E. (2023). Estimation of Monkeypox spread in a nonendemic country considering contact tracing and self-reporting: A stochastic modeling study. Journal of Medical Virology, 95(1), e28232. [doi:10.1002/jmv.28232]
KUCHARSKI, W. J., Adam J. AND Edmunds. (2015). Characterizing the transmission potential of zoonotic infections from minor outbreaks. PLoS Computational Biology, 11(4), e1004154. [doi:10.1371/journal.pcbi.1004154]
KUMAR, R., Singh, S., & Singh, S. K. (2022). A systematic review of 5110 cases of Monkeypox: What has changed between 1970 and 2022? Cureus, 14(10). [doi:10.7759/cureus.30841]
KWOK, K. O., Wei, W. I., Tang, A., Yeung Shan Wong, s., & Tang, J. W. (2022). Estimation of local transmissibility in the early phase of monkeypox epidemic in 2022. Clinical Microbiology and Infection, 28(12). [doi:10.1016/j.cmi.2022.06.025]
LEVASSEUR, M. T., Goldstein, N. D., Tabb, L. P., Olivieri-Mui, B. L., & Welles, S. L. (2018). The effect of PrEP on HIV incidence among men who have sex with men in the context of condom use, treatment as prevention, and seroadaptive practices. Journal of Acquired Immune Deficiency Syndromes, 77(1), 31–40. [doi:10.1097/qai.0000000000001555]
LUO, W., Katz, D. A., Hamilton, D. T., McKenney, J., Jenness, S. M., Goodreau, S. M., Stekler, J. D., Rosenberg, E. S., Sullivan, P. S., & Cassels, S. (2018). Development of an agent-Based model to investigate the impact of HIV self-Testing programs on men who have sex with men in Atlanta and Seattle. JMIR Public Health and Surveillance, 4(2), e58. [doi:10.2196/publichealth.9357]
MATHIEU, E., Spooner, F., Dattani, S., Ritchie, H., & Roser, M. (2023). Mpox (monkeypox). Available at: https://ourworldindata.org/monkeypox
MERCER, C. H., Tanton, C., Prah, P., Erens, B., Sonnenberg, P., Clifton, S., Macdowall, W., Lewis, R., Field, N., Datta, J., Copas, A. J., Phelps, A., Wellings, K., & Johnson, A. M. (2013). Changes in sexual attitudes and lifestyles in Britain through the life course and over time: Findings from the National Surveys of Sexual Attitudes and Lifestyles (Natsal). The Lancet, 382(9907), 1781–1794. [doi:10.1016/s0140-6736(13)62035-8]
MERLER, S., Ajelli, M., Fumanelli, L., Gomes, M. F., Pastore y Piontti, A., Rossi, L., Chao, D. L., Longini, I. M., Halloran, M. E., & Vespignani, A. (2015). Spatiotemporal spread of the 2014 outbreak of Ebola virus disease in Liberia and the effectiveness of non-pharmaceutical interventions: A computational modelling analysis. The Lancet Infectious Diseases, 15(2), 204–211. [doi:10.1016/s1473-3099(14)71074-6]
MITJÀ, O., Ogoina, D., Titanji, B. K., Galvan, C., Muyembe, J. J., Marks, M., & Orkin, C. M. (2023). Monkeypox. The Lancet, 401(10370), 60–74.
MOLLA, J., Sekkak, I., Mundo Ortiz, A., Moyles, I., & Nasri, B. (2023). Mathematical modeling of mpox: A scoping review. One Health, 16, 100540. [doi:10.1016/j.onehlt.2023.100540]
MUSUMECI, S., Najjar, I., Boffi El Amari, E., Schibler, M., Jacquerioz, F., Yerly, S., Renzoni, A., Calmy, A., & Kaiser, L. (2023). A case of Mpox reinfection. Clinical Infectious Diseases, 77(1), 135–137. [doi:10.1093/cid/ciad147]
NOVAKOVIC, A., & Marshall, A. H. (2022). The CP-ABM approach for modelling COVID-19 infection dynamics and quantifying the effects of non-pharmaceutical interventions. Pattern Recognition, 130, 108790. [doi:10.1016/j.patcog.2022.108790]
O’NEIL, C. A., & Sattenspiel, L. (2010). Agent-based modeling of the spread of the 1918-1919 flu in three Canadian fur trading communities. American Journal of Human Biology, 22(6), 757–767.
PAULI, G., Blümel, J., Burger, R., Drosten, C., Gröner, A., Gürtler, L., Heiden, M., Hildebrandt, M., Jansen, B., Montag-Lessing, T., Offergeld, R., Seitz, R., Schlenkrich, U., Schottstedt, V., Strobel, J., Willkommen, H., & Wirsing von König, C. H. (2010). Orthopox viruses: Infections in humans. Transfusion Medicine and Hemotherapy, 37(6), 351.
PETER, O. J., Abidemi, A., Ojo, M. M., & Abosede Ayoola, T. (2023). Mathematical model and analysis of Monkeypox with control strategies. The European Physical Journal Plus, 138(3). [doi:10.1140/epjp/s13360-023-03865-x]
PETER, O. J., Kumar, S., Kumari, N., Oguntolu, F. A., Oshinubi, K., & Musa, R. (2021). Transmission dynamics of Monkeypox virus: A mathematical modelling approach. Modeling Earth Systems and Environment, 8(3), 3423–3434. [doi:10.1007/s40808-021-01313-2]
PETER, O., Oguntolu, F., Ojo, M. M., Oyeniyi, A., Rashid, J., & Khan, I. (2022). Fractional order mathematical model of Monkeypox transmission dynamics. Physica Scripta. [doi:10.1088/1402-4896/ac7ebc]
RAKOWSKI, F., Gruziel, M., Krych, M., & Radomski, J. P. (2010). Large scale daily contacts and mobility model - An individual-based countrywide simulation study for Poland. Journal of Artificial Societies and Social Simulation, 13(1), 13. [doi:10.18564/jasss.1529]
RAO, D. W., Wheatley, M. M., Goodreau, S. M., & Enns, E. A. (2021). Partnership dynamics in mathematical models and implications for representation of sexually transmitted infections: A review. Annals of Epidemiology, 59, 72–80. [doi:10.1016/j.annepidem.2021.04.012]
RIMOIN, A. W., Mulembakani, P. M., Johnston, S. C., Lloyd Smith, J. O., Kisalu, N. K., Kinkela, T. L., Blumberg, S., Thomassen, H. A., Pike, B. L., Fair, J. N., Wolfe, N. D., Shongo, R. L., Graham, B. S., Formenty, P., Okitolonda, E., Hensley, L. E., Meyer, H., Wright, L. L., & Muyembe, J. J. (2010). Major increase in human monkeypox incidence 30 years after smallpox vaccination campaigns cease in the Democratic Republic of Congo. Proceedings of the National Academy of Sciences, 107(37), 16262–16267. [doi:10.1073/pnas.1005769107]
ROCHE, B., Drake, J. M., & Rohani, P. (2011). An agent-Based model to study the epidemiological and evolutionary dynamics of Influenza viruses. BMC Bioinformatics, 12, 1–10. [doi:10.1186/1471-2105-12-87]
RUTHERFORD, G., Friesen, M. R., & McLeod, R. D. (2012). An agent based model for simulating the spread of sexually transmitted infections. Online Journal of Public Health Informatics, 4(3). [doi:10.5210/ojphi.v4i3.4292]
SCOTT, N., Stoové, M., Wilson, D. P., Keiser, O., El-Hayek, C., Doyle, J., & Hellard, M. (2018). Eliminating hepatitis C virus as a public health threat among HIV-positive men who have sex with men: A multi-modelling approach to understand differences in sexual risk behaviour. Journal of the International AIDS Society, 21(1), e25059. [doi:10.1002/jia2.25059]
SILVA, P. C., Batista, P. V., Lima, H. S., Alves, M. A., Guimarães, F. G., & SILVA, R. C. (2020). COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos, Solitons and Fractals, 139, 110088. [doi:10.1016/j.chaos.2020.110088]
SPATH, T., Brunner-Ziegler, S., Stamm, T., Thalhammer, F., Kundi, M., Purkhauser, K., & Handisurya, A. (2022). Modeling the protective effect of previous compulsory smallpox vaccination against human monkeypox infection: From hypothesis to a worst-case scenario. International Journal of Infectious Diseases, 124, 107–112. [doi:10.1016/j.ijid.2022.09.022]
SPICKNALL, I. H., Pollock, E. D., Clay, P. A., Oster, A. M., Charniga, K., Masters, N., Nakazawa, Y. J., Rainisch, G., Gundlapalli, A. V., & Gift, T. L. (2022). Modeling the impact of sexual networks in the transmission of Monkeypox virus among gay, bisexual, and other men who have sex with men - United States, 2022. Morbidity and Mortality Weekly Report, 71(35), 1131–1135. [doi:10.15585/mmwr.mm7135e2]
SQUAZZONI, F., Polhill, J. G., Edmonds, B., Ahrweiler, P., Antosz, P., Scholz, G., Chappin, E., Borit, M., Verhagen, H., Giardini, F., & Gilbert, N. (2020). Computational models that matter during a global pandemic outbreak: A call to action. Journal of Artificial Societies and Social Simulation, 23(2), 10. [doi:10.18564/jasss.4298]
THORNHILL, J. P., Barkati, S., Walmsley, S., Rockstroh, J., Antinori, A., Harrison, L. B., Palich, R., Nori, A., Reeves, I., Habibi, M. S., Apea, V., Boesecke, C., Vandekerckhove, L., Yakubovsky, M., Sendagorta, E., Blanco, J. L., Florence, E., Moschese, D., Maltez, F. M., … Orkin, C. M. (2022). Monkeypox virus infection in humans across 16 countries - April-June 2022. New England Journal of Medicine, 387(8), 679–691. [doi:10.1056/nejmoa2207323]
VALLE, S. Y. D., Mniszewski, S. M., & Hyman, J. M. (2012). Modeling the impact of behavior changes on the spread of pandemic influenza. In Modeling the interplay between human behavior and the spread of infectious diseases (pp. 59–77). Springer New York. [doi:10.1007/978-1-4614-5474-8_4]
VAN Dijck, C., Hens, N., Kenyon, C., & Tsoumanis, A. (2022). The roles of unrecognized Mpox cases, contact isolation and vaccination in determining epidemic size in Belgium: A modeling study. Clinical Infectious Diseases, 76(3), 1421–1423. [doi:10.1093/cid/ciac723]
VAN Ewijk, C. E., Miura, F., VAN Rijckevorsel, G., de Vries, H. J., Welkers, M. R., VAN den Berg, O. E., Friesema, I. H., VAN den Berg, P. R., Dalhuisen, T., Wallinga, J., & others. (2023). Mpox outbreak in the Netherlands, 2022: Public health response, characteristics of the first 1,000 cases and protection of the first-generation smallpox vaccine. Eurosurveillance, 28(12), 2200772. [doi:10.2807/1560-7917.es.2023.28.12.2200772]
VYNNYCKY, E., & White, R. (2010). An Introduction to Infectious Disease Modelling. Oxford: Oxford University Press.
WARD, T., Christie, R., Paton, R. S., Cumming, F., & Overton, C. E. (2022). Transmission dynamics of monkeypox in the United Kingdom: Contact tracing study. British Medical Journal, 379. [doi:10.1136/bmj-2022-073153]
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393(6684), 440–442. [doi:10.1038/30918]
WHO. (2022a). Vaccines and immunization for monkeypox: Interim guidance, 16 November 2022. Available at: https://www.who.int/publications/i/item/WHO-MPX-Immunization
WHO. (2022b). WHO director-General declares the ongoing monkeypox outbreak a Public Health Emergency of International Concern. Available at: https://www.who.int/europe/news/item/23-07-2022-who-director-general-declares-the-ongoing-monkeypox-outbreak-a-public-health-event-of-international-concern. Accessed on May 17, 2023
WHO. (2023). Mpox (monkeypox) - Democratic Republic of Congo, 23 November 2023. Available at: https://www.who.int/emergencies/disease-outbreak-news/item/2023-DON493
WILENSKY, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL. Available at: http://ccl.northwestern.edu/netlogo/
WILENSKY, U., & Rand, W. (2015). An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo. The MIT Press.
WOLFF Sagy, Y., Zucker, R., Hammerman, A., Markovits, H., Gur Arieh, N., Abu Ahmad, K., Battat, E., Ramot, N., Carmeli, G., Mark-Amir, A., Wagner-Kolasko, G., Duskin-Bitan, H., Yaron, S., Peretz, A., Arbel, R., Lavie, G., & Netzer, D. (2023). Real-world effectiveness of a single dose of Mpox vaccine in males. Nature Medicine, 29(3), 748–752. [doi:10.1038/s41591-023-02229-3]
YUAN, P., Tan, Y., Yang, L., Aruffo, E., Ogden, N. H., Bélair, J., Heffernan, J., Arino, J., Watmough, J., Carabin, C., & Zhu, H. (2023). Assessing transmission risks and control strategy for monkeypox as an emerging zoonosis in a metropolitan area. Journal of Medical Virology, 95(1), e28137. [doi:10.1101/2022.06.28.22277038]