Agent-Based Modeling as an Evaluation Tool to Understand the Mechanisms of a Financial Incentives Scheme for Maternal and Child Health in Tanzania

Abdullah Alibrahim; Nicholaus Mziray; Peter Binyaruka; John Maiba; Rachel Cassidy; Zaid Chalabi; Josephine Borghi; Anna M Foss

doi:10.18564/jasss.5793

Introduction

Payment for performance (P4P), or financial rewards to healthcare entities, contingent on their achievement of predefined performance targets, is gaining popularity as a mechanism to improve health service delivery. The assumption underpinning P4P is that health providers will respond to incentives by increasing effort, with additional funds motivating performance, thus resulting in improved health outcomes (Miller & Babiarz 2014). In the context of maternal healthcare, predefined performance targets typically include metrics such as the percentage of institutional deliveries, antenatal care coverage, and immunization rates. The ‘principal-agent problem’ arises when health providers (agents) may not always act in the best interests of policy makers, health system managers, or patients (principal), especially when incentives are not aligned (Smith et al. 1997). By overcoming the principal-agent problem, theory suggests that P4P should improve the desired behavior of the health provider, resulting in better health outcomes (Paul et al. 2021).

P4P has been widely implemented worldwide and, in low- and middle-income countries (LMIC), there has often been a focus within these settings on maternal and child health (MCH) (Diaconu et al. 2021; Witter et al. 2012). Much of the initial evidence in these settings focused on evaluating the impact of P4P on MCH outcomes, with mixed conclusions (Witter et al. 2012). Subsequently, the research focused on exploring the health system mechanisms through which P4P improves outcomes (Diaconu et al. 2021; Renmans et al. 2016; Singh et al. 2021; Witter et al. 2012), reporting improvements in the availability of health workers and drugs (Diaconu et al. 2021), community outreach, patient trust and facility autonomy, and reductions in patient care costs (Singh et al. 2021). Furthermore, the context within which P4P programs are implemented appears to matter, with differences in effects noted depending on the characteristics of the facility and the community (Singh et al. 2021), with a recognized need for more research that explicitly studies this (Binyaruka et al. 2020; Diaconu et al. 2021). P4P design is also known to influence program mechanisms and outcomes (Diaconu et al. 2021; Kovacs et al. 2020; Singh et al. 2021), but design effects can be challenging to examine empirically, as program design is typically homogeneous within a country (Kovacs et al. 2020). An aspect of program design is the role of local authority health managers in P4P schemes. When involved in verification visits, this can strengthen the governance function of the health system and offer an avenue to support providers, especially when they are also incentivized (Singh et al. 2021).

Existing empirical evaluations of P4P and other complex health systems policies are often constrained by factors including their assessment of effects ex-post, limited statistical power that may limit the ability to detect effects or conduct subgroup analysis to explore the heterogeneity of effects, and the lack of data for counterfactual scenarios. Such limitations can significantly hinder the ability to uncover the heterogeneity in the initial conditions and the resulting trajectories. The pressing need to improve MCH outcomes in LMIC and the growth of P4P programs in the region, make a compelling case for additional in-depth evaluations of system-level dynamics and community outcomes. To overcome these limitations, computational systems science tools, such as agent-based modeling, have been proposed as an approach to better understand the functioning of health systems and assess the dynamic effects of health system interventions such as P4P.

Agent-based models (ABMs) are increasingly used as a mathematical modeling method to capture the micro-level behavior of complex systems such as health systems (Alibrahim & Wu 2020; Borghi & Chalabi 2017; Macal & North 2005). The modeling approach simulates agents embedded with decision-making capabilities, progression trajectories, and the interaction within and between agent types (Badham et al. 2018). ABMs have been used to model health systems and their dynamic response to various incentive-based reforms, capture feedback loops between agents and incorporate heterogeneities in the emergent behavioral response to reforms (Alibrahim & Wu 2018, 2020; Cassidy et al. 2019; Shrime et al. 2019). ABM can create virtual replicas of social systems, enabling exploration of the interaction between different program design components and individual agent decision-making, informing more effective program design.

This study conceptualizes, develops, and validates an ABM to recreate and understand the drivers of P4P in institutional deliveries using empirical data from the woman, community, and facility level in Tanzania. The developed model is built as a policy and evaluation tool to disentangle the effects of the unique characteristics of the P4P design over a 3-year study period. Specifically, the model aims to recreate empirical trajectories through a simulated representation of individuals within this setting of care. The model is conceptualized, parameterised, calibrated, and verified using empirical data, published literature, and stakeholder interviews. Empirical data used in the model include household surveys, facility surveys, and program reports. Key endline outcomes, such as the proportion of births in a facility, the patient experiences of facility-based deliveries, and access to drugs, are used for validation. The model was developed to shed light on counterfactual scenarios and help decision makers refine the design of the Tanzanian P4P program for MCH. In the following sections, we explain the conceptual framework for the ABM, methods, results, and conclusions.

Study Setting

Tanzanian maternal and child health system

The MCH care system and the delivery of services need to be strengthened in Tanzania (UNICEF 2024). The availability of drugs and supplies remains challenging, and the referral and transport systems are inadequate. Limited access to insurance schemes and informal payments in health facilities pose financial barriers to access. The achievement of Sustainable Development Goals (SDGs) 1, 3, 5, and 10 depends on the increasing coverage and quality of MCH services in low-income settings (UNDP 2024). In this study, we focus solely on primary care facilities that play a pivotal role in MCH.

Pwani P4P program design

This model focuses on the Pwani Region, one of Tanzania’s 31 administrative regions located along the eastern coast. In this setting, predefined performance targets included specific percentage increases in institutional deliveries and antenatal care visits. The design of the P4P program has been described elsewhere (Binyaruka et al. 2015; Borghi et al. 2013), but a summary follows. The program was implemented in facilities with a bank account, offering MCH services and providing baseline performance data from previous years. Facilities were eligible for incentive payments for deliveries if they met targets for each 6-month cycle: a percentage point increase in performance compared to the previous cycle or an absolute performance target. For primary healthcare facilities (dispensaries and health centers), 75% of this payment was distributed among health workers at the facility and the remaining funds were to be spent on improvements to the facility (25%). Managers at the district and regional levels who were responsible for supporting facilities and verifying facility performance data, the Council Health Management Team (CHMT), the Regional Health Management Team (RHMT), and the district were also eligible for incentives.

In each six-month performance cycle, the performance metrics reported by a participating facility were compared to target performance to determine bonus eligibility. In this analysis, we focus on the number of births in the facility calculated as the percentage of total births in the catchment area of the facility. The target performance value for each indicator is calculated based on a threshold-specific target detailed in section 3.10. If the facility met or exceeded the indicator’s target, it received the full bonus. If the facility met at least 75% of the target performance, it received 50% of the bonus. All achievements below the 75% threshold do not receive incentive payment (Binyaruka et al. 2015). The maximum payout per cycle was US$820 for facility (Binyaruka et al. 2015). If a facility receives the maximum payout, the portion allocated to health workers amounts to approximately 10% of an individual staff member’s salary, when distributed across the average number of staff at a facility.

Facilities regularly reported performance indicators to the Council Health Management Teams. District health managers then verified performance during routine facility visits (every three months) to ensure accurate, complete, and consistent data. District health managers were incentivized based on the performance of the facilities in their areas, the availability of drugs, and the timely submission of performance reports. It was expected that each payment verification cycle would take 2-3 months. The intention was that all facilities receive the P4P incentive payment at most three months after the end of the previous cycle. However, payment delays were common, and the first bonus payment was processed three months later than originally scheduled. Table 1 shows the actual and scheduled bonus payment timelines. Evident delays in bonus payment processing led to challenges in maintaining drug supplies, staff motivation, and outreach activities. Table 1 presents the timeline of performance cycles and bonus payments in the Pwani P4P program, highlighting the critical issue of payment delays that forms a key focus of our research. While all facilities in the study were part of the P4P program, the timing of bonus payments varied significantly from the scheduled dates, allowing us to examine how payment timeliness affects outcomes. Therefore, we focus on delays within the Pwani P4P program as a potential policy lever in the ABM to understand how reductions in delays might improve the rate of in-facility deliveries.

**Table 1:** Performance cycles in the Pwani Region Pay-For-Performance and Bonus Payment Timeline.
Cycle	Start	End	Scheduled Payment	Actual Payment
1	Jan 2011	Jun 2011	Sep 2011	Jan 2012
2	Jul 2011	Dec 2011	Mar 2012	Jun 2012
3	Jan 2012	Jun 2012	Sep 2012	Oct 2012
4	Jul 2012	Dec 2012	Mar 2013	Mar 2013
5	Jan 2013	Jun 2013	Sep 2013	Oct 2013
6	Jul 2013	Dec 2013	Mar 2014	Jun 2014

Methods

The agent-based model

Our agent-based model simulates the complex interactions between three key agent types within the maternal healthcare system in Tanzania: women of reproductive age, healthcare facilities, and district managers. The model explicitly incorporates both supply-side dynamics (facility responses to incentives) and demand-side behaviours (women’s healthcare-seeking decisions). These exogenous demand-side dynamics, including demographic factors, social influences, and previous experiences, play a crucial role in determining outcomes and are modeled based on empirical data from household surveys and stakeholder input.

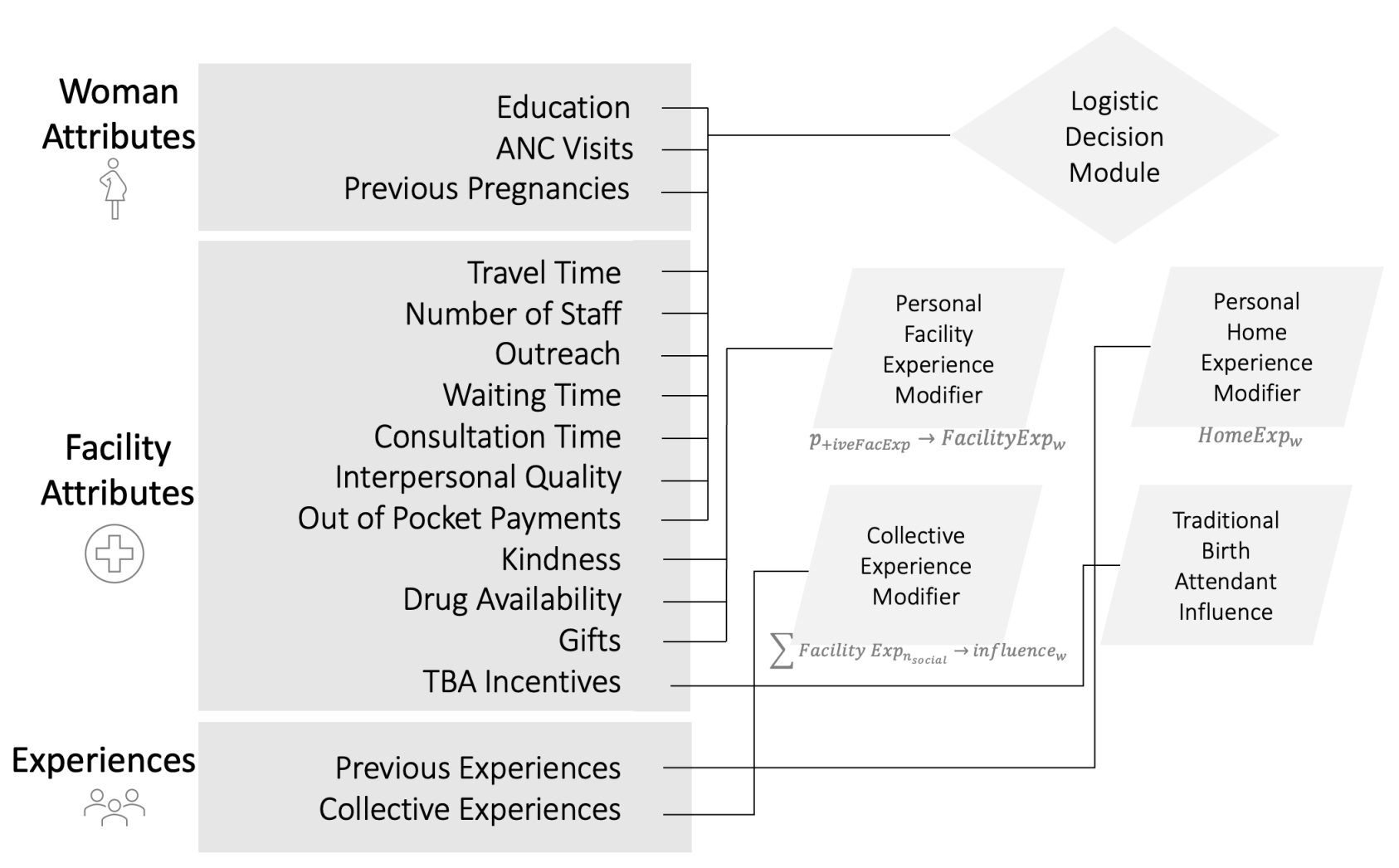
We modeled a representative district within the Pwani Region in Tanzania. Three key types of agents constitute the modeled entities: women of reproductive age ($w$), health facilities ($f$), and a district manager (m). Each type of agent has designated properties, state charts, and capabilities to progress and perform their predefined roles. We describe the building blocks of the ABM using the "PARTE" framework: Properties, Actions, Rules, Time, and Environment described in Hammond (2015). Figure 1 summarizes the key modules with which each agent is equipped to execute key decisions as active participants in the Pwani P4P program. We then proceed with an agent-level description of the modules.

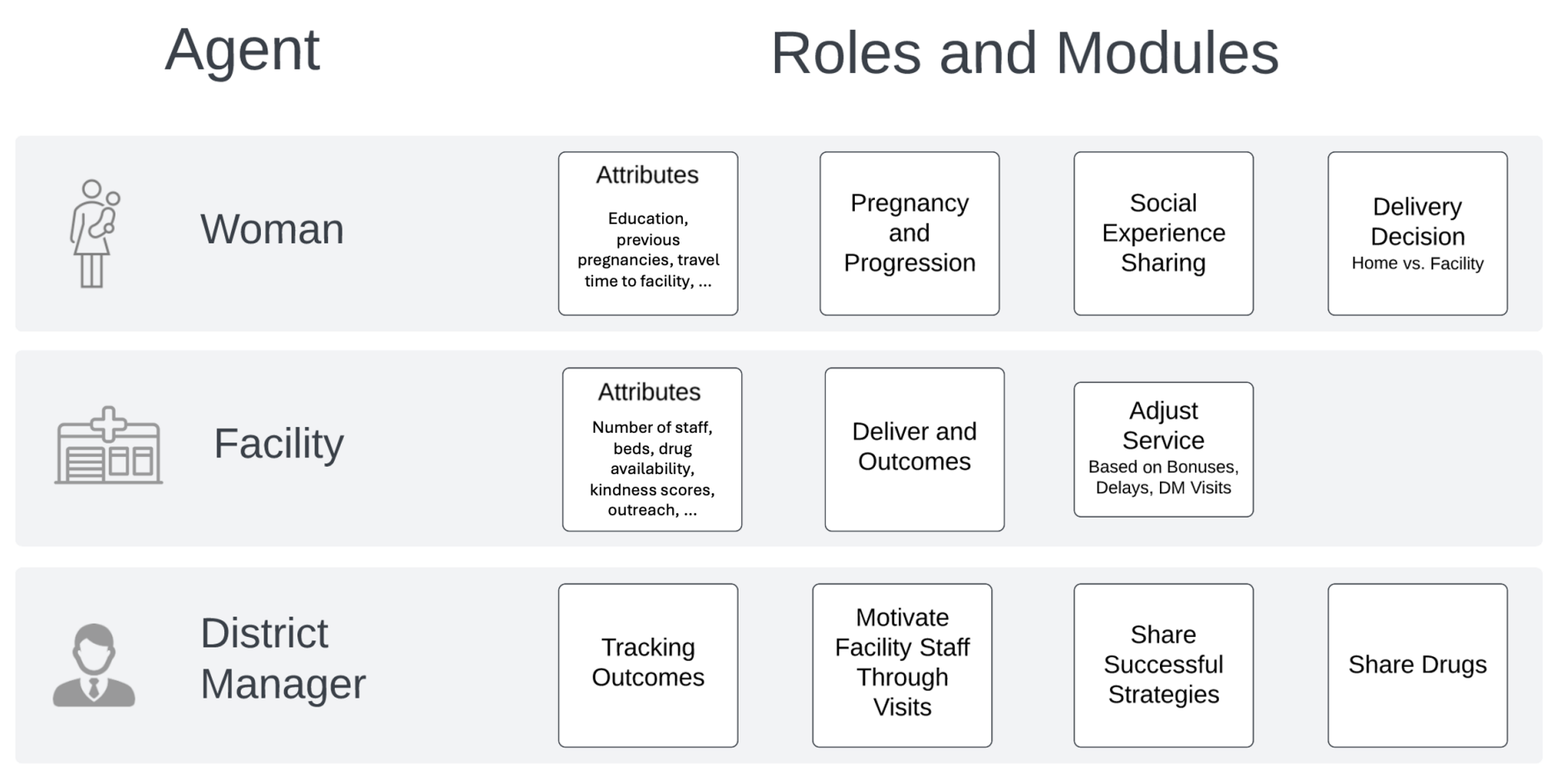
**Figure 1.** Agents and embedded modules coded in the ABM.

Data sources & variable selection

Our study drew on various data sources for model formulation, parameterization, calibration, and validation. To inform the formulation of the model, we considered the demand- and supply-side factors shaping women’s decisions regarding where to deliver and a theory of how P4P would influence these, drawing on existing evidence regarding the supply- and demand-side effects of the P4P program in Tanzania, and the wider literature (Binyaruka et al. 2015; Borghi et al. 2013; Mayumana et al. 2017; Ministry of Health and Social Welfare 2012), and through engagements with stakeholders in Bagamoyo and Chalinze districts councils in Pwani Region, Tanzania, including district managers, facility in-charges and members of the facility governing committees.

Model parameters were derived from government reports on P4P in Tanzania (Ministry of Health and Social Welfare 2012). The modeled characteristics of facilities and the women were selected based on literature, previously described stakeholder engagements, and statistical analysis of P4P evaluation data, focused on facility and patient survey data and a survey of women who recently delivered (Binyaruka et al. 2015; Maiba et al. 2022; Mziray et al. 2022). Facility surveys from the baseline, midline and endline periods of the P4P evaluation were conducted in 2012, 2013, and 2014, respectively. The survey covered 150 facilities, 1,500 patients and women, and 2,846 households in three regions in Tanzania. Eligible women were those who had delivered 12 months before the surveys. The selected facility attributes modeled are selected from the associated published statistical models (Binyaruka et al. 2015, 2018, 2023; Borghi et al. 2013). Facility-reported performance data submitted to the district were used as calibration targets to calibrate unknown facility parameters. The decision to deliver at the facility for childbirth by women was modeled using a multilevel mixed-effects logistic regression based on data from the women’s survey (Binyaruka et al. 2023). This statistical model captures the supply- and demand-side factors that influence women’s choice of delivery. Table 2 summarizes the data sources and uses within the model.

**Table 2:** Data Sources and Their Application in the Study.
Data Source	Use	Reference
Literature Review	To understand healthcare delivery and maternal and child health (MCH) in Tanzania.	Borghi et al. (2013), Binyaruka et al. (2015), Mayumana et al. (2017), Ministry of Health and Social Welfare (2012)
Stakeholder Interviews	To collect first-hand information on the operations of healthcare facilities, establish causal relationships and verify structural validity.	Maiba et al. (2022)
Focus Group Discussion	To gather detailed insights on the implementation of the P4P program.	Mziray et al. (2022)
Government Reports	Used for the model structure and parameterization of the P4P program.	(CHAI and Ministry of Health 2011)
Baseline P4P Survey	To provide model parameters, demographic information, healthcare access data, and health behavior insights.	N/A
Midline P4P Survey	To calibrate unobservable and unmeasured model inputs for improved model representation	N/A
Endline P4P Survey	To validate modeled outcomes against observed endline outcomes of the modeled facilities	N/A
Facility Attributes Data (Obtained from from P4P Survey)	To model facility characteristics related to performance and influencing women’s childbirth location decisions. Facility performance was used for validation and calibration.	Borghi et al. (2013), Binyaruka et al. (2018), Binyaruka et al. (2015), Binyaruka et al. (2023)
Multilevel Mixed-Effect Logistic Regression (Obtained from from P4P Survey)	To model women’s choice of facility for childbirth and verifying model relationships.	Binyaruka et al. (2023)

Causal pathways of Pwani P4P underpinning the formulation of the ABM

There are a variety of pathways through which the Pwani P4P program was envisaged to increase the coverage of institutional deliveries among pregnant women. On the supply-side, incentives for health workers are expected to increase motivation to provide incentivized services, improve the kindness of the provider, and reduce informal fees (such as out-of-pocket fees, or OOP). In addition, the funds for health facilities could be used to increase drug availability, cover transportation costs associated with community outreach activities, pay traditional birth attendants to refer women to facilities, and offer gifts to attending women. Increasing drug availability also reduces OOP for mothers who purchase out-of-stock drugs. These changes to service delivery are expected to increase demand for facility-based care (Anselmi et al. 2017; Binyaruka & Borghi 2017; Mayumana et al. 2017).

To explicitly quantify and model the demand-side effects, our ABM incorporated key drivers of demand increase with specific parameterization based on empirical data from the Pwani region. We estimated that P4P interventions would increase demand for facility-based deliveries through three primary mechanisms: (1) improved perceived experiences and quality of care, based on survey data from Binyaruka & Borghi (2017); (2) better access and reduction in OOP expenses, according to household expenditure data in household survey; and (3) community and word-of-mouth effects from positive experiences. Our model accounts for potential capacity strains through explicit modeling of bed availability and drug stock levels, all of which act as moderating factors that can dampen demand increases when facilities reach capacity constraints. All of these pathways have been confirmed in stakeholder interviews.

Through their involvement in facility performance verification and because of incentives from P4P, district health managers are expected to make more regular visits to facilities enrolled in the Pwani P4P program (Mayumana et al. 2017). This is expected to further motivate the facilities to deliver better care. In addition, district managers can allow the sharing of strategies between providers to encourage the adoption of best practices (i.e., community outreach) (Mziray et al. 2022). Managers are also incentivized to mitigate drug stock outs (i.e., where the facility runs out of essential medications) in facilities that experience high demand or payment delays to the facility. It is expected that managers may support facilities in mitigating stock-outs through, for example, facilitating drug sharing among facilities when supplies are low, further reducing the risk of stock-outs as revealed in stakeholder interviews.

Supply-side changes are expected to increase the acceptance of delivery care services among pregnant women. As women’s experience of care changes, this information is shared with other women, which influences the care-seeking behavior of other women. Alongside these positive causal pathways, there are potentially negative and unintended effects. Delays in expected bonus payments can adversely affect provider motivation and deteriorate experiences of delivering women, reducing future demand (Alonge et al. 2017; Ogundeji et al. 2016). Furthermore, additional demand for in-facility deliveries can reduce future demand through depletion of drug supplies and worsening of delivery experiences at the facility (owing to capacity and supply constraints). The positive and negative pathways to births in the facility associated with the Pwani P4P program are illustrated in Figure 2.

**Figure 2.** Causal feedback structure of the P4P intervention illustrated in two complementary panels. (a) Positive (reinforcing) pathway, read left $\rightarrow$ right. Timely bonus payments and district-manager (DM) visits (green) lift three supply-side service domains – Access, Community Engagement, Experiences (blue) – which in turn raise both the level and the word-of-mouth sharing of favourable care experiences (yellow). The net effect is more in-facility births, which feeds back with a “+” polarity to sustain or increase subsequent bonus payments. (b) Negative (balancing) pathway, read left ← right. When delivery volumes surge without commensurate resources (e.g., because bonus funds are delayed), rising in-facility births erode Access, Engagement, and Experiences (red arrows with “–”), generating worse shared experiences and ultimately fewer in-facility births; the drop in performance lowers future bonus payments, closing a vicious loop. Arrows are annotated with “+” (reinforcing) or “–” (balancing) to indicate the polarity of each causal link. Colours: green = health-system manager levers, blue = supply-side service factors, yellow = demand-side perception/social-network factors.

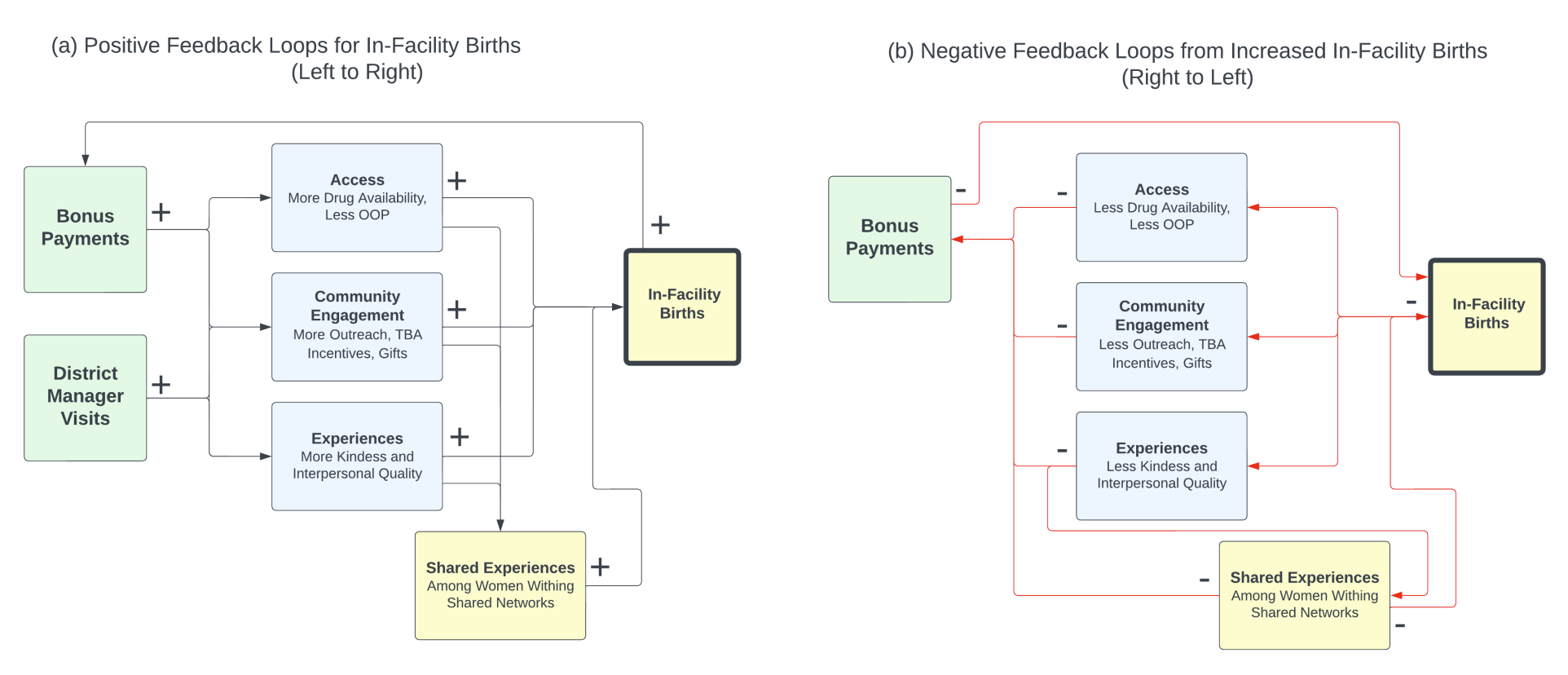
Facility agent

Facility agent properties

We model three facilities, $|F|=3$, in the Bagamoyo district. The modeled facilities were selected to provide diverse characteristics and performance outcomes for the facility and the population in the catchment area. Facility names are masked in this model and are called facilities A, B, and C. At model initiation, the characteristics of each facility agent correspond to the baseline data from the associated facility and the household for their corresponding catchment areas. The selected facility attributes modeled are curated from published analyses ( Binyaruka et al. 2015, 2018, 2023; Borghi et al. 2013). The attributes of a facility agent $f$ are static (remaining unchanged from baseline) or dynamic (changing based on bonuses, delays, and occupancy). The following list describes the attributes and classification of each attribute:

Static Facility Attributes:
1. Number of Staff at Baseline
2. Number of Beds at Baseline
3. Catchment Population (Number of women of reproductive age and their attributes)
4. Average Waiting Time for Antenatal Visits at Facility in Minutes
Dynamic Facility Attributes, Change in Time $t$:
1. Rate of Facility-Based Deliveries $\textit{FB}_{f,t}$
2. Staff Interpersonal Quality $\textit{IPQ}_{f,t} \in [0,1]$
3. Staff Kindness $K_{f,t} \in [0,1]$
4. Drug Availability $D_{f,t} \in [0,1]$
5. Out-of-Pocket Costs $\textit{OOP}_{f,t} \in [0,1]$
6. Outreach Programs $\textit{O}_{f,t} \in \{0,1\}$
7. Traditional Birth Attendant (TBA) Incentives $\textit{TBA}_{f,t} \in \{0,1\}$
8. Gifts to Mothers $G_{f,t} \in \{0,1\}$

Dynamic attributes are updated monthly for each facility through counters of each event type: district births, in-facility deliveries, and delivery outcomes in the facility’s catchment area. Data used to parameterize each of the three facilities at baseline are collected from three data sources: (1) facility survey, (2) stakeholder interviews for baseline TBA incentives and Gifts to mothers ($\textit{TBA}_{f,1}$ and $G_{f,0}$) (3) household survey (for interpersonal quality, kindness, waiting time, and out of pocket payments), and (4) facility performance reported to the Pwani P4P program as described in Section 3.2. The baseline period corresponds to January 2011. The agent’s actions and rules outlined in Section 3.10 dictate what happens in the proceeding periods.

Facility agent actions & rules

Upon initiating and loading baseline values, a facility provides maternal care services in its catchment area and progresses through its performance cycle, bonus cycle, and district manager cycle.

Performance Evaluation and Bonus Cycles. Every six months after initiating the model, facilities undergo an evaluation in which all deliveries in their corresponding catchment area are aggregated over the performance period PP. Then, if a bonus is earned, a bonus payment is made where its effects are observed in the bonus period BP. Figure 3 visually represents the performance and bonus payment cycles.

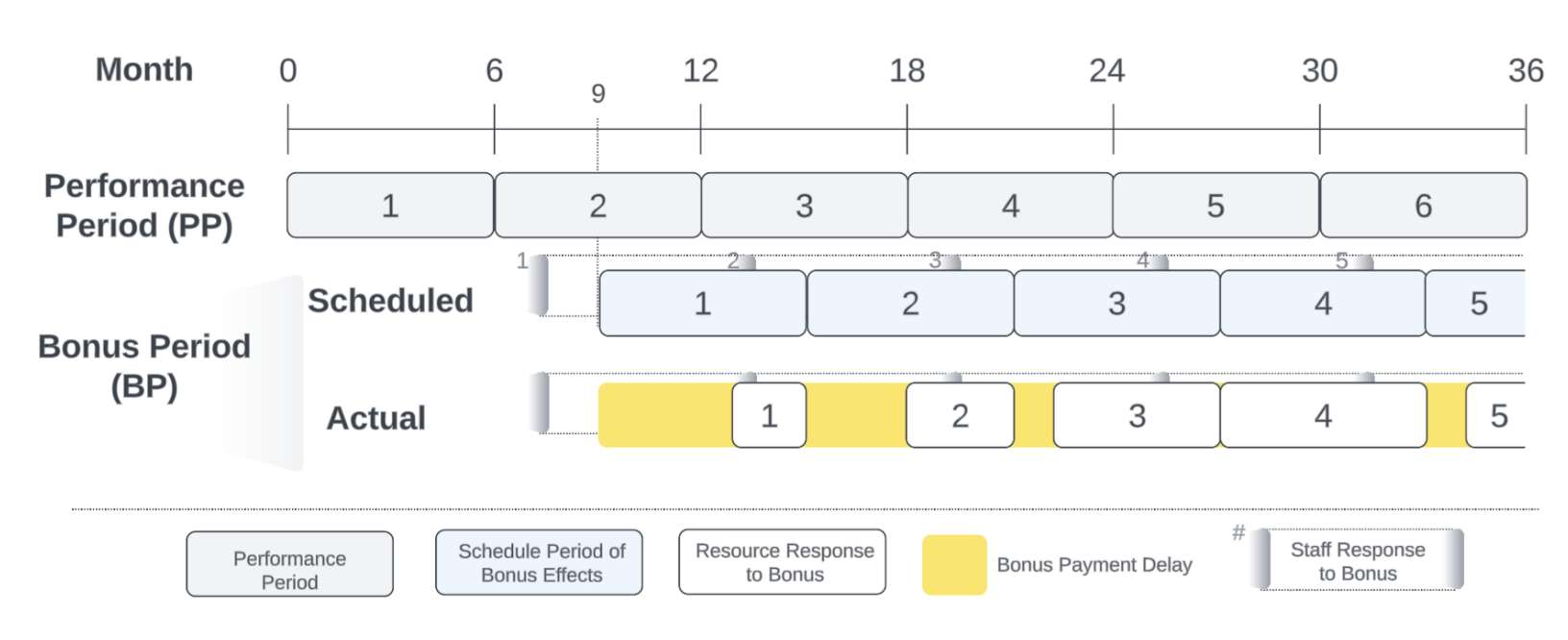
**Figure 3.** Performance and bonus‐payment timeline for each facility agent. Grey blocks mark successive 6-month performance periods (months 0–6, 6–12, 12–18, $\dots$). Blue blocks show the scheduled bonus periods, which start 3 months after the close of every performance period. Yellow bars indicate any payment delays—the gap between the scheduled start of a bonus period and the date on which the funds actually reach the facility. The box with grey sides denotes the staff behavioural response, which begins immediately once the bonus amount becomes known.

The coverage performance of a facility $f$, or proportion of facility-based births at $f$, $\%\textit{FB}_{f,\textit{PP}}$, during the performance period PP is calculated as:

\[\%\textit{FB}_{f,\textit{PP}} = \frac{\textit{# of deliveries at f during PP}}{\textit{# of births in catchment population of f during PP}}\]

\[(1)\]

The difference between $\%\textit{FB}_{f,\textit{PP}}$ and $\%\textit{FB}_{f,\textit{PP}-1}$ determines whether the facility $f$ receives a bonus for its performance during the performance period $PP$. The difference is called the indicator $I_{f,\textit{PP}} = \%\textit{FB}_{f,\textit{PP}} - \%\textit{FB}_{f,\textit{PP-1}}$, and must equal or exceed a target value that depends on the previous performance period’s $\textit{FB}_{f, (\textit{PP}-1)}$, calculated as follows:

\[ \textit{Target}_{f, \textit{PP}} = \begin{cases} 0.15 & \text{if } \textit{FB}_{(f, \textit{PP}-1)} < 0.2\\ 0.1 & \text{if } 0.2 \leq \textit{FB}_{(f, \textit{PP}-1)} < 0.4\\ 0.05 & \text{if } 0.4 \leq \textit{FB}_{(f, \textit{PP}-1)} < 0.85\\ \text{Maintain} & \text{if } 0.85 \leq \textit{FB}_{(f, \textit{PP}-1)} \\ \end{cases}\]

\[(2)\]

If $I_{f,\textit{PP}} \geq \textit{Target}_{\textit{PP}}$, then the facility $f$ receives a full bonus, $\textit{Bonus}_{f,\textit{PP}} = 1$. If not, but $I_{f,\textit{PP}} \geq 0.75* \textit{Target}_{\textit{PP}}$, then the facility $f$ receives half a bonus, $\textit{Bonus}_{f,\textit{PP}}=0.5$. Otherwise, if none of the previous conditions are met, then the facility $f$ does not receive a bonus; $\textit{Bonus}_{f,\textit{PP}}=0$. Note that if $f$ performs in the previous performance period $\textit{FB}_{ (f, \textit{PP}-1)} \geq 0.85$, then $f$ can receive a full bonus by maintaining $\textit{FB}_{(f, \textit{PP})} \geq 0.85$. Note that a facility that achieved $\textit{FB}_{(f, \textit{PP}-1)} \geq 0.85$ can only receive a full bonus in PP after maintaining it above the 0.85 threshold.

Performance Bonus Payment Cycles. At the end of the performance period PP, changes related to the bonus occur. These changes are of two types: (1) resource-dependent changes and (2) motivational responses from the staff to bonuses. In general, gaining a bonus is associated with improving facility characteristics, and losing a bonus is associated with deterioration of facility characteristics. Bonus recipients experience increases in their drug supplies, motivation, and outreach initiatives that last the duration of the performance cycle (6 months). Changes in facility characteristics are dependent on the bonus amount $\textit{Bonus}_{f,\textit{PP}}$. Table 3 describes the bonus-induced changes to the attributes of the facility in month $t+1$ after a facility earns a bonus.

The motivational responses of the staff to bonuses, if earned, occur one month after the end of the performance cycle PP. The motivational responses of the staff manifest themselves in the model as improvements in the kindness kindness and interpersonal quality $\textit{IPQ}$ parameters for the facility, which further improve the rate of in-facility deliveries at the facility. One thing to note is that Kindness $K$ is capped at 0.9 in Table 3; however, it is still possible for Kindness to increase beyond 0.9 during district manager (DM) visits. As mentioned above, the extent of change in these values due to bonuses is primarily informed by the input of stakeholders.

Three months after the end of each performance period $\textit{PP}$, a facility $f$ is scheduled to receive the bonus amount $\textit{Bonus}_{f,\textit{PP}}$. According to Table 1, a bonus period BP is always scheduled three months after the performance period PP. For example, the first PP ends in June 2011, and the first BP is scheduled in September 2011. Resource-dependent changes are assumed to occur at the time a bonus is received because bonus funds immediately enable additional resources. Once a facility $f$ receives the bonus amount, the facility can purchase more drugs, reduce out-of-pocket fees, and provide gifts, traditional birth attendant (TBA) incentives, and outreach activities.

**Table 3:** Consequences of receiving performance bonuses on facility characteristics.
Case	$\textit{Bonus}_{f,\textit{PP}}$	Changes to Facility Attributes at $t+1$
1	0	Incentives for $\text{TBA}_{f,t+1} = \text{TBA}_{f,0}$ Outreach $\text{O}_{f,t+1} = \text{O}_{f,0}$ Staff $\text{IPQ}_{f,t+1} = \text{IPQ}_{f,0}$ Kindness $K_{f,t+1} = K_{f,0}$ Drugs $D_{f,t+1} = D_{f,0}$ Gifts $G_{f,t+1} = 0\%\cdot G_{f,0}$ $\text{OOP}_{f,t+1} = \text{OOP}_{f,0}$
2	0.5	Incentives for $\text{TBA}_{f,t+1} = 1$ Outreach $\text{O}_{f,t+1} = \max(\text{O}_{f,t}, \text{random with 50% chance of }1)$ Staff $\text{IPQ}_{f,t+1} = \max(\text{IPQ}_{f,t}, 0.8)$ Kindness $K_{f,t+1} = \max(K_{f,t}, 0.8)$ Drugs $D_{f,t+1} = \max(D_{f,t}, 0.8)$ Gifts $G_{f,t+1} = 0\%\cdot \max(G_{f,t}, \text{ 50% chance of }1)$ $\text{OOP}_{f,t+1} = \text{OOP}_{f,t} \cdot 0.9$
3	1	Incentives for $\text{TBA}_{f,t+1} = 1$ Outreach $\text{O}_{f,t+1} = 1$ Staff $\text{IPQ}_{f,t+1} = 1$ Kindness $K_{f,t+1} = \max(K_{f,t}, 0.9)$ Drugs $D_{f,t+1} = 1$ Gifts $G_{f,t+1} = 1$ $\text{OOP}_{f,t+1} = \text{OOP}_{f,t} \cdot 0.8$
4	Delay Effects	Incentives for $\text{TBA}_{f,t+1} = 0$ Outreach $\text{O}_{f,t+1} = 0$ Staff $\text{IPQ}_{f,t+1} = \text{IPQ}_{f,t-1} - 0.1 \;\; \text{while } \text{IPQ}_{f,t} \geq 0.6$ Kindness $K_{f,t+1} = K_{f,t-1} - 0.1 \;\; \text{while } K_{f,t} \geq 0.5$ Drugs $D_{f,t+1} = D_{f,t-1} - 0.1 \;\; \text{while } D_{f,t} \geq D_{f,0}$ Gifts $G_{f,t+1} = 0$ $\text{OOP}_{f,t+1} = \text{OOP}_{f,t} + 0.1 \;\; \text{while } \text{OOP}_{f,t} \leq 1$

Delays in Bonus Payments. Performance periods and bonus payments occur according to Table 1 and Figure 3. The changes induced by bonuses occur during the month $t$ when a bonus payment is received. Practically, bonus payments were not always made according to schedule, creating a payment delay. A facility agent $f$ is considered to be experiencing a bonus payment delay at month $t$ if it was scheduled to receive a payment, but no payment was made. Based on staff interviews from sampled facilities, bonus delays affected several aspects of facility performance. During a delay in the payment of the bonus, a facility would have less funds to replenish drug stocks and gifts and would be more inclined to increase informal fees for delivering mothers. Furthermore, facility personnel would be less motivated to provide the same delivery experience. Consequently, a bonus payment delay has a time-related effect on the facility, whereby every month of delay is operationalized in row 4 of Table 3. The changes represent a time-dependent decrease in drug availability, interpersonal quality and kindness of staff, and an increase in OOP. Additionally, incentives for TBAs and outreach programs are stopped if a bonus payment is delayed.

Facility Capacity & Occupancy. Each facility agent is generated with a static number of beds representing its capacity. However, facilities accept delivering women even if the beds are occupied. Therefore, we introduce a capacity variable set to the number of beds plus a capacity relaxation amount so that the capacity of the facility is $C_f = \text{beds} + R$, where $R$ is a relaxation parameter applied uniformly to all facilities. Beyond $C_f$, the facility $f$ cannot accept deliveries, and a pregnant woman agent who wishes to deliver in an at-capacity facility will deliver elsewhere; an out-of-system delivery. These deliveries are recorded and noted, but are not a key outcome of this model. The value of the relaxation parameter $R$ is a calibration parameter where we experiment with $R =$ 1, 2, or 3.

If the number of women who hope to deliver in a facility $f$ exceeds the number of beds available but is $\leq C_f$, the staff of a facility provide less contact time with women (total patient-contact time) during their stay at the facility. This facet represents the demand-capacity balance as shown in Figure 2 in the Worse Experiences red box. An increase in occupancy from 20% to 30% would lead to a smaller decrease in patient contact time than an increase in occupancy from 70% to 80% as we use a logistic function to create an occupancy factor that follows an S-shaped curve to represent this relationship. The function is described in Appendix C.

Woman agent

We generate 1,866 women agents $W$ to represent women of reproductive age who reside in the catchment area of one of the three modeled facilities $f$. Each simulated woman agent $w$ is assigned to a catchment area of a facility $f$ such that $w \in W_f \subset W$. The distribution of each attribute of a woman $w$ is conditional on the facility to which they are assigned. The number of women assigned to each facility $|W_f|$ reflects the actual number of women of reproductive age in the area of the facility. Census data from National Bureau of Statistics (2015) were used to estimate $|W_f|$ of the population in the catchment area $P_f$ multiplied by the proportion of women of reproductive age $\%\textit{WRA}$. $\%\textit{WRA}$ was estimated from national rates applied to local population figures after reviewing census data and consulting local demographers. The formula $|W_f|=\%\textit{WRA} \times P_f$ approximates the number of women agents in each facility’s catchment area.

Woman agent properties

Once a woman $w$ is generated and assigned to a facility $f$, the properties that are relevant to the demand for delivery care are sampled from the conditional distributions shown in Table 4. We consider the demographic and epidemiological characteristics of the catchment area static. Therefore, we used average distributions from the 3 waves of survey data, grouped by facility, to determine static woman properties. For the three categorical variables, education, previous pregnancies, and antenatal visits, a uniform random variable $u$ was sampled and compared to the cumulative distribution of levels to assign a category to the woman agent $w$. The travel time from agent $w$ to assigned facility $f$ is estimated using the average facility-specific travel time $\overline{TT}_{f}$ from the multi-year survey. Approximately 67 observations per facility $f$ are used to estimate $\overline{TT}_{f}$. The travel time of a woman agent $TT_{\textit{w-to-f}}$ is assumed to be uniformly distributed around $\overline{TT}_{f} \pm 50\%$, sampled as $TT_{\textit{w-to-f}} = \overline{TT}_{f} * (u + 0.5)$ where $u \sim$ uniform[0,1]. The correlations between the woman covariate (including travel time) were found to be minimal and assumed to be independent of each other.

**Table 4:** Distributions and means of parameters in the woman agent obtained from a multi-year women survey. The statistics are grouped by facility and aggregated from 3 waves of data.
Variable	Category	Facility A	Facility B	Facility C
Education	No education	12.0%	22.3%	17.4%
	Some primary education	8.8%	16.9%	3.3%
	Primary/some secondary education	68.8%	58.5%	72.4%
	Secondary/above education	10.4%	2.2%	6.9%
Previous Pregnancies	0	24.1%	24.1%	24.1%
Previous Pregnancies	1+	75.9%	75.9%	75.9%
Antenatal Visit (ANC)	4+ ANC visits	67.4%	59.9%	65.3%
Antenatal Visit (ANC)	Less than 4 ANC visits	32.6%	40.1%	34.7%
Travel Time to facility in Minutes		14.67	39.77	46.87

A woman agent’s $w$ decision-making is also influenced by an additional set of factors, referred to as modifiers $(M_{\textit{fExp}}, M_{\textit{hExp}}, M_{\textit{social}}, M_{\textit{TBA}})$ including $w$’s prior delivery care experience at the facility and at home, delivery care experience at the facility among peers within the social network, and TBA influence (TBA incentives to refer women to the facility). Details on how these modifiers shape a woman’s delivery decision are provided in Section 3.32. In each simulation run, a social network is created for each woman agent $w \in W$, connecting the agent to $n_{\textit{social}}$ random women agents within the same area. The mechanisms of influence will be clarified later in Section 3.26.

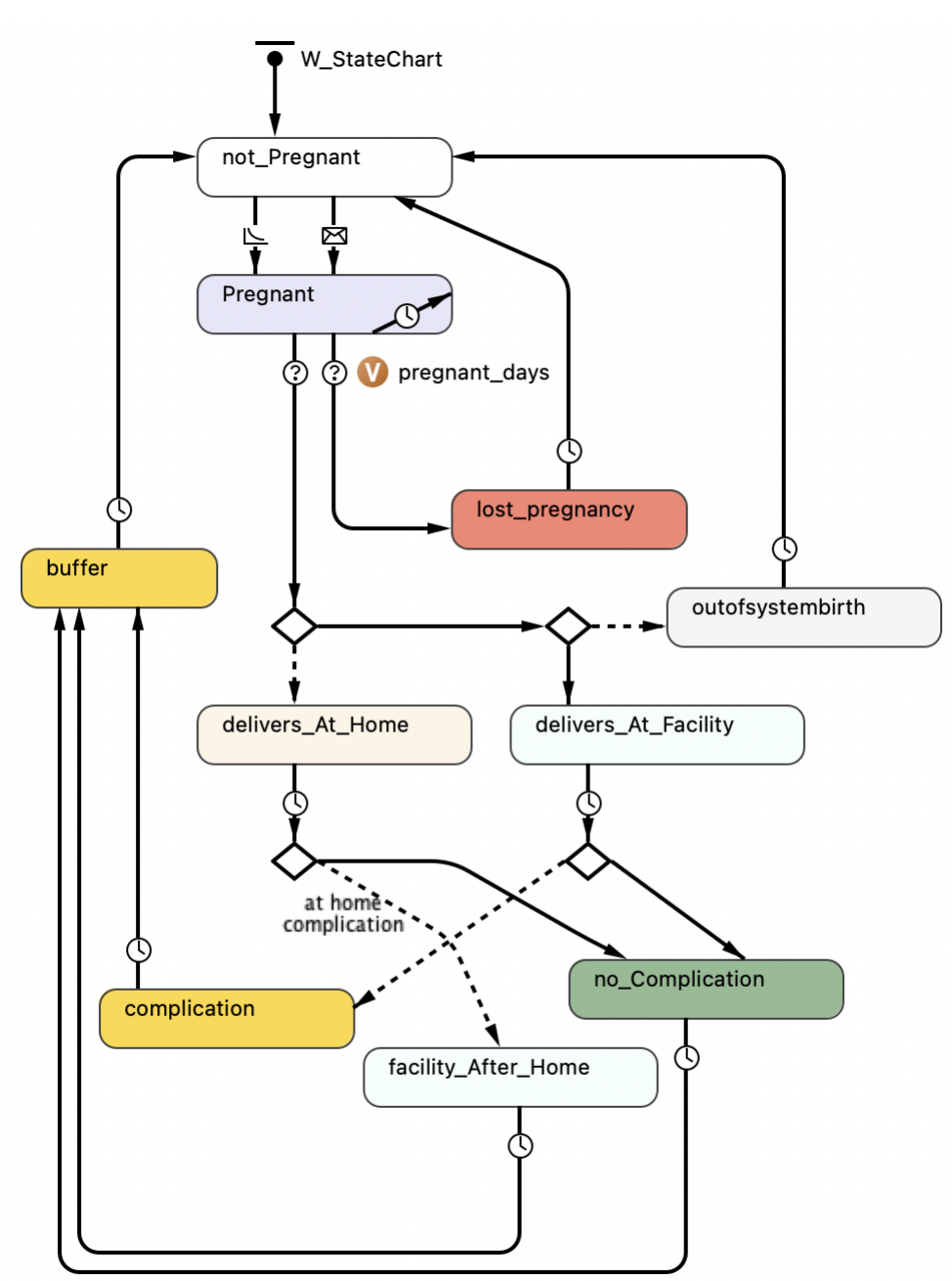
**Figure 4.** A woman agent delivery and pregnancy state chart as modeled in the ABM.

Woman agent actions & rules

A woman agent’s decision regarding the place of delivery is determined by: (1) woman attributes, (2) facility characteristics, and (3) individual and shared experiences. The decision rule is shaped by the probability determined by a predictive logistic regression model (binyaruka et al. 2023), prior to this probability being adapted by the modifiers as detailed below.

Women agents progress through the pregnancy and delivery state chart as in Figure 4. A woman $w$ is initiated as pregnant with probability $p_{\textit{PregnantInitiation}}$. If $w$ is initiated as pregnant, then it has a pregnancy duration of 270 days (9 months) $\textit{pregnantDays} \sim$ uniform(0,270). The pregnancy period is assumed to be deterministic, as it is not directly relevant to the purpose of the model. If a woman is not pregnant at initiation, then the probability of becoming pregnant is set at $p_{\textit{pregnant}} = 0.015$ per month. In other words, 18% of women of reproductive age become pregnant each year (derived during model calibration). During pregnancy, $w$ can experience a lost pregnancy before labor (due to a miscarriage or stillbirth) with a probability of $p_{\textit{lostpregnancy}}=0.2$. This was calculated from the prevalence of stillbirths, which is 0.0217 (21.7 per 1000 is the prevalence of stillbirths in 2019) (Hug et al. 2020). Furthermore, 49% of stillbirths occur before labor ($100\% - 51\%$), where 51% is from Sub-Saharan Africa in Lawn et al. (2016). Multiplying these values together and then adding the 0.189 risk of miscarriage from Dellicour et al. (2016) produces the value of 0.2 as the probability that a pregnancy will be lost. If $w$ experiences a lost pregnancy, $w$ returns to the non-pregnant state after 14 days, as reported in Mayo Clinic (2021) and then experiences the same monthly pregnancy rate $p_{\textit{pregnant}}$.

Mothers of pregnancies that are not lost before labor face the decision of whether to deliver at the facility or at home. At each delivery site (home or facility), the probability of a complication during delivery is $p_{\textit{complication}}=0.46$, as reported in Danilack et al. (2015). If $w$ chooses to deliver at home and experiences a delivery complication, $w$ is referred to the facility (facility-after-home state). If $w$ chooses to deliver in the facility and develops a complication, the delivery is recorded as an out-of-system birth (such events are referred to a higher level of care). All deliveries (including complications, if any) take six weeks before a woman returns to the non-pregnant state, as noted for most women in Jackson & Glasier (2011). The probability of getting pregnant again is then the default $p_{pregnant}$. All deliveries at the facility occupy a bed for one day. In the case of complications, women are referred to the local hospital for further treatment, but for modeling purposes, we still count this as occupying a bed at the original facility for one day before transfer.

Decision-making of a woman agent $w$ is influenced by her previous birth experience. Dynamic variables of the home and facility experience updates based on the latest home or facility experience. The home experience is determined by whether home complications occurred in the past. When a complication occurs during home delivery, $\textit{HomeExp}_w \in \{-1, 1\}$ takes a value of $1$, which makes the woman prefer facility delivery in the future. If a delivery is $w$’s first, $\textit{HomeExp}_w =1$ with probability $p_{\textit{complication}}$. If the woman $w$ had a safe previous home delivery, $\textit{HomeExp}_w$ takes a value of $-1$, which makes the woman prefer home delivery in the future. After $w$ delivers in a facility, $\textit{FacilityExp}_w$ is obtained from $p_{\textit{+iveFacExp}}$; a weighted composite score of the level of drug availability $D_f$, the kindness of the staff $K_f$, and the gifts received $G_f$ when giving birth at $f$. The weights for $p_{\textit{+iveFacExp}}$ are shown in Equation 3 with all $f$ parameters standardized to be between 0 and 1.

\[ p_{\textit{+iveFacExp}} = 0.4*D_f + 0.4*K_f + 0.2* G_f\]

\[(3)\]

For women agents, the baseline facility characteristics are used to calculate $p_{\textit{+iveFacExp}}$ above. The value of $p_{\textit{+iveFacExp}}$ calculated using Equation 3 is then used to sample $\textit{FacilityExp}_w = +1$ with probability $p_{\textit{+iveFacExp}}$, and $\textit{FacilityExp}_w = -1$ otherwise, each time $w$ decides. At the time of a decision, a $w$ requests and aggregates $\sum{\textit{FacilityExp}_n}$ for all $n_{social}$ on the social network. Then, $\textit{influences}_w$ is determined as follows:

\[ \textit{influences}_w= \begin{cases} -1, & \text{if}\ \sum{\textit{FacilityExp}_n}<0 \\ 0, & \text{if}\ \sum{\textit{FacilityExp}_n}=0 \\ 1, & \text{if}\ \sum{\textit{FacilityExp}_n}>0 \\ \end{cases}\]

\[(4)\]

Woman agent delivery decision

The characteristics of the facility closest to $w$ are visible to women in $f$ catchment area as are the occupancy effects. The decision of the woman agent for the delivery site is adapted from Binyaruka et al. (2023) and modified using the insights of the stakeholders. The study by Binyaruka et al. (2023) first included all variables in the multilevel mixed-effect logistic regression model. Then, this model was reduced using backward stepwise regression, dropping the variable with the highest p-value at each step for thirteen steps. Correlation analysis was also performed to explore the collinearity of the supply-side and demand-side determinants of utilizing facility-based delivery care. The correlation analysis used collinearity diagnostics of tolerance $\leq$ 0.1 and VIF $\geq$ 10 as thresholds of concern. However, for each correlated pair identified, at least one variable had already been dropped from the regression as non-significant, so no further variables needed to be removed due to correlations. The final reduced model only includes significant supply-side variables described in Section 3.8 and demand-side variables described in Section 3.24. The coefficients used in the regression are listed in Appendix B.

The decision at delivery is sequenced as follows:

The woman collects the closest facility $f$’s attributes and occupancy level. Specifically, $w$ collect the following for $f$:
1. Number of occupied and unoccupied beds
2. Previous month’s average patient contact time multiplied by an occupancy factor.
3. Previous month’s average waiting time
4. Drug availability
5. Staff interpersonal quality
6. Staff kindness
7. Previous month’s average out-of-pocket costs
then calculate $w$’s new patient experience $\textit{FacilityExp}_w$ sampled using the probability in Equation 3
The woman collects experiences from the $n_{social}$ women agents in her social network to calculate the net $\textit{influences}_w$ of her social network based on their facility experiences (if any) based on the $\textit{influences}_w$ variable (Equation 4).
Run the logistic model using $w$’s properties and information obtained in step 1 and obtain $p_{\textit{facility delivery}}$ as from Equation 5 following Binyaruka et al. (2023).
Aggregate the social and personal experience from
$\textit{influences}_w$, $\textit{HomeExp}_w$, and $\textit{TBA}_f$ in the modifier equation using $w$ weights for each.
Compute the modified probability of giving birth at the facility $p_{w@f}$ using Equation 6.

The pre-modified probability that a woman agent $w$ delivers in a facility is calculated as shown in Equation 5:

\[ p_{\textit{facility delivery}}=\frac{e^y}{1+e^y}\]

\[(5)\]

Where $y$ is the dot product of the values of the variables and the coefficients of the logistic regression vector from the table in Appendix B. Then, the modified and final probability that woman $w$ delivers at facility $f$, $p_{w@f}$, is calculated by adding all the weighted modifiers $\textit{ModSum} = \textit{FacilityExp}_w*M_{\textit{fExp}} + \textit{HomeExp}_w*M_{\textit{hExp}} + \textit{influences}_w*M_{\textit{social}} + \textit{TBAincentive}_f*M_{\textit{TBA}}$ then applying the following to the probability:

\[ p_{w@f}= \begin{cases} p_{\textit{facility delivery}}*(1+\textit{ModSum}), \\ \hspace{3cm} \text{if}\ \textit{ModSum}<0 \\ p_{\textit{facility delivery}}*(1+\textit{ModSum}*(1-p_{\textit{facility delivery}})),\\ \hspace{3cm} \text{if}\ \textit{ModSum}\geq 0 \\ \end{cases}\]

\[(6)\]

Refer to Figure 5 for an illustration of the variables feeding into the logistic regression that would calculate $p_{w@f}$. A pregnant woman agent $w$ delivers in facility $f$ if $u \leq p_{w@f}$ where $u \sim \text{uniform}[0,1]$.

**Figure 5.** A list of all variables that shape a woman agent $w$’s decision either through the logistic regression model from Binyaruka et al. (2023) or as rule-based modifiers.

District health manager

The model generates one m agent to perform the functions of district health managers in the Pwani P4P scheme. The properties that define the m agent are the frequency of facility visits, measured in months between visits, and visit duration. An m visits quarterly (every three months). We assume that m visits happen concurrently (within the same month) for all facilities, and so it is likely they were visited on the same day/week in reality. During visits, the m would induce changes to facility characteristics due to the motivational effect of visits and through the facilitation of resource and knowledge exchange between facilities. The changes associated with m visits are described in the subsection below.

District manager actions & rules

Quarterly Visits to Facilities. During their routine visits, district manager visits induce temporary changes in provider attitudes and motivation around the time of a scheduled visit. Before and after m’s visit, facility agents may be temporarily motivated to provide a higher quality of care manifested in higher kindness $K$ and interpersonal quality IPQ. Therefore, we model a 50% chance a facility would increase its $K$ and IPQ by ten percentage points in response to a scheduled m agent visit. If there is a change, the improvements last for $\textit{VisitDuration}$ in days, starting $\textit{VisitDuration}/2$ days before to $\textit{VisitDuration}/2$ days after, after which $K$ and IPQ revert to pre-visit levels. The duration of m’s agent visit effects, VisitDuration, is a calibration parameter that can vary in the calibration procedure to achieve the best fit to observed facility performance.

Bonus Payment Delay Mitigation. If a district manager agent m visits a facility agent $f$ and the facility is experiencing a bonus payment delay, the m agent can offset the delay-induced decrease in provider motivation by providing assurances of the upcoming payment. Specifically, $f$’s staff interpersonal quality IPQ, staff kindness $K$, outreach $O$, and out-of-pocket OOP will revert to pre-delay levels. For mitigation to occur, the m agent visit and bonus payment delay must occur within the same month. Once the mitigation occurs, changes in the previously listed facility agent attribute restart degrading in the following month of the delay.

Sharing Best Practices. District managers facilitate strategy-sharing across facilities regarding the achievement of bonus targets to promote best practices. In the model, as described in stakeholder interviews, the m agent can share best practices around three demand-inducing strategies: TBA incentives, kindness K, and outreach O. For facilities that do not already have the highest values for these variables, strategy-sharing by the district manager enables the facility to enhance these attributes to match the best performer of the 3 facilities modeled, but only if they receive a bonus payment to fund these enhancements. Facility-level counters track all m mitigation and strategy-sharing events.

Drug Sharing Across Facilities. A district manager visit facilitates drug sharing between facilities when there is a payment delay, provided that specific drug supply conditions are met at both the donor and recipient facilities. The sharing occurs if the donor facility’s drug supply level, known as the Donor Threshold $DT$, is at least as high as the recipient facility’s threshold $RT\%$ plus twice the amount to be shared, i.e., $DT \geq RT\% + 2 \times Sharing\%$. When these conditions are satisfied, the donor facility transfers a portion of its drug supplies, specified by $Sharing\%$, to the recipient facility. Importantly, this transfer ensures that the recipient facility’s drug supply does not surpass the remaining supply at the donor facility after the sharing. The parameters $RT\%$ and $Sharing\%$ are calibration parameters used to fine-tune the model.

Timeline & event sequence

The model runs on a daily time step. Outcomes at the facility level are reported and analyzed monthly. The model time $t$ represents the time in months since model initiation. Model time $t = 0$ corresponds to December 2010, the simulation baseline period. The model begins at time $t = 1$, corresponding to January 2011. The model’s time horizon is 36 months, or three years, ending in January 2014, covering six performance periods, PP, and five bonus payments.

The model initiates by generating the three modeled facilities and reading their baseline attributes. The baseline facility attribute values are shown in Table 11. Then, $|W_f|$ women agents $w$ are generated for each facility with attributes sampled from Table 4. Of the women agents generated, $p_{\textit{PregnantInitiation}}$ of the women agents are generated in the pregnant state and assigned a random stage of pregnancy. The model then makes daily timesteps with women progressing through their statecharts as described in Figure 4. At the end of each month, facility-level attributes (facility-based delivery rates and characteristics) are updated. Then, the time variable updates as time progresses, $t = t + 1$. At the end of a performance period PP, 6-month aggregations occur for bonus evaluations as shown in Equation 2. Where a bonus payment is scheduled and $\textit{Bonus}_{f,PP}>0$, delay effects ensue as described in Table 3. Once the timestep $t$ reaches a month where a bonus payment is made, the bonus effects are manifested according to Table 3. The above-described sequence continues until $t=36$ months.

Model verification, calibration, and validation

Before detailing the analytical steps and experiment design, we first distinguish the three quality-assurance activities applied to the model. Verification asks whether the agent code correctly implements the intended logic; calibration selects parameter values that best reproduce a training data set; and validation evaluates how well the calibrated model explains data that were not used for calibration. The next three subsections describe, in that order, how each task was carried out.

Model verification

During the development of the model, features and agent capabilities were added sequentially. Following each integration, a thorough inspection was conducted to verify the integrity of the coding and the successful implementation of new elements. Debugging was an ongoing process throughout the development journey, ensuring the reliability and efficiency of our model.

To ensure the internal consistency of the ABM, we conducted a series of steps for model verification. Firstly, the mathematical coherence of the deterministic (i.e., bonus effects) and stochastic (i.e., woman agent decisions) components was assessed. This entailed inspection of model equations and their implementation in the simulation software, exploring behavior in terms of model outcomes when varying parameter settings. Inconsistencies were noted, debugged, and addressed. Second, we evaluated the long-term behavior of the ABM and its stability during simulations and emergent behavior. Lastly, we conducted a robustness analysis by testing the model performance under various parameter settings and incorporating small random perturbations. This helped ensure that the model’s results remained consistent despite uncertainties in model parameters, reinforcing the model’s internal validity.

Calibration

To calibrate the ABM, we defined a structured search space comprising twelve input parameters that lack direct empirical estimates. These parameters were varied across discrete, stakeholder-informed ranges to explore plausible behavioral and system dynamics. This is done to align the facility performance metrics generated by the ABM with the empirically reported performance outcomes from the actual facilities in the first 24 months of program implementation. Calibration parameters are listed below and categorized by the agent they relate to:

Facility Agent
- Facility Capacity Relaxation $R$ (1, 2, 3)
- Occupancy Adjustment (0, 1, 2)
Woman Agent
- Facility Experience Modifier $M_{\textit{fExp}}$ (0.3, 0.35)
- Home Experience Modifier $M_{\textit{hExp}}$ (0, 0.025, 0.05)
- Social Network Modifier $M_{\textit{social}}$ (0.3, 0.35)
- Traditional Birth Attendant Modifier $M_{\textit{TBA}}$ ($1-M_{\textit{social}} - M_{\textit{hExp}} - M_{\textit{fExp}}$)
- Size of Social Network $n_{\textit{social}}$ (3, 4, 5, 6)
- Percent of Women Pregnant at Initiation $p_{\textit{PregnantInitiation}}$ (0.025, 0.05, 0.075, 0.10)
District Manager Agent
- Duration of DM Visit Effects $\textit{VisitDuration}$ (0.5, 1)
- Drug Sharing Threshold $RT\%$ (50%, 60%)
- Drug Sharing Rate $\textit{Sharing\%}$ (5, 10)

A total of 13,824 parameter combinations were scanned in the search grid, with 10 replications ran for each combination of parameters. We use least-squares fitting to identify the combination of values of the above parameters that closely match the reported facility-reported delivery rates in the first 4 bonus periods (the last two bonus periods are used for validation purposes). Using a simple search approach based on a grid search methodology, we iteratively evaluated the predetermined combinations of parameter values spanning the plausible parameter space. For each parameter, we defined a range of potential values based on literature and expert input, then systematically tested combinations to identify those that minimized error between simulated and observed values.

Validation

Structural and Face Validity. The structural and face validation of the ABM was carried out through the active participation of stakeholders in the modeling process, according to the principles of participatory modeling. Staketakeholders contributed to the structure of the model by providing information about the real system through workshops organized by the research team in Dar es Salaam, Tanzania. Attendees helped refine the roles and interactions of agents, guided the inclusion of essential processes and behaviours, and provided context-specific information. Multiple iterations of the model were shared with stakeholders, and their feedback was instrumental in refining the model’s structure to align closely with the complexities and nuances of the health system. The involvement of these stakeholders throughout the modeling process not only enhanced the structural validity of the ABM but also promoted the model’s acceptance and future applicability in policy and decision-making.

External and Cross-Validation. After fixing the optimized calibration parameters, external validation involves testing the model against data not used in any part of the model’s development or calibration processes to assess its predictive performance. This helps to verify that the model’s predictions are accurate not just for the data it was calibrated with (which could potentially lead to overfitting) but also for other data in the same domain. We use facility-reported performance from months 30 to 36 (the last modeling performance period) to assess the model’s external validity.

For cross-validation, we compare the output of our model with two other data sources: (1) the outputs of a system dynamics model (SDM) that studies the effects of P4P on drug availability and demand for care delivery in the same context (Cassidy et al. 2025), and (2) the performance data from the control facilities in the Pwani region that did not participate in the P4P program.

In the first stage of cross-validation, we compared the trends and patterns observed in both the ABM and the SDM to gauge the consistency and validity of our findings related to these variables. Any discrepancies identified between the models offer an opportunity to reassess our assumptions and adjust the model parameters.

Second, by comparing our model’s predictions for the control facilities (without P4P) to the actual observed performance in these facilities, we can evaluate the model’s ability to accurately capture the system dynamics in the absence of the P4P initiative. This offers a crucial validity check for our model, enabling us to test its ability to mimic real-world outcomes in different circumstances.

Experiment design and settings

We use the validated simulation model to run several scenarios to identify how changes in P4P implementation (payment delays) and district manager visits affect program outcomes. First, three P4P implementation scenarios are simulated: (1) No P4P, (2) P4P with payment delays, and (3) P4P without payment delays. For scenarios (2) and (3) above, we test a further scenario modification: no $m$ visits (so that the effects of any delays in receiving any bonus payments cannot be mitigated and $m$ cannot facilitate strategy sharing or have any other positive motivational influences), as shown below. We ran 500 replications for each scenario to capture model stochasticity and infer potential divergence in trajectories, if any.

(1) No P4P
(2) P4P, delays
(2.1) P4P, delays, No $m$ visits
(3) P4P, No delays
(3.1) P4P, No delays, No $m$ visits

Model implementation

The implementation of our model was carried out using AnyLogic v8 University Researcher Edition. A model pseudo code can be found in Appendix H. Anylogic’s platform allowed us to implement intricate agent-based configurations, behaviours, and interactions. The platform can also host the model’s user-friendly interface to facilitate interaction and exploration by decision-makers. During model development and analysis, we conduct rigorous sensitivity analysis to ensure the robustness of our findings. This included making structural adjustments based on team deliberations and assessing the resulting changes, as well as systematically varying model parameters.

Results

Model calibration & external validation

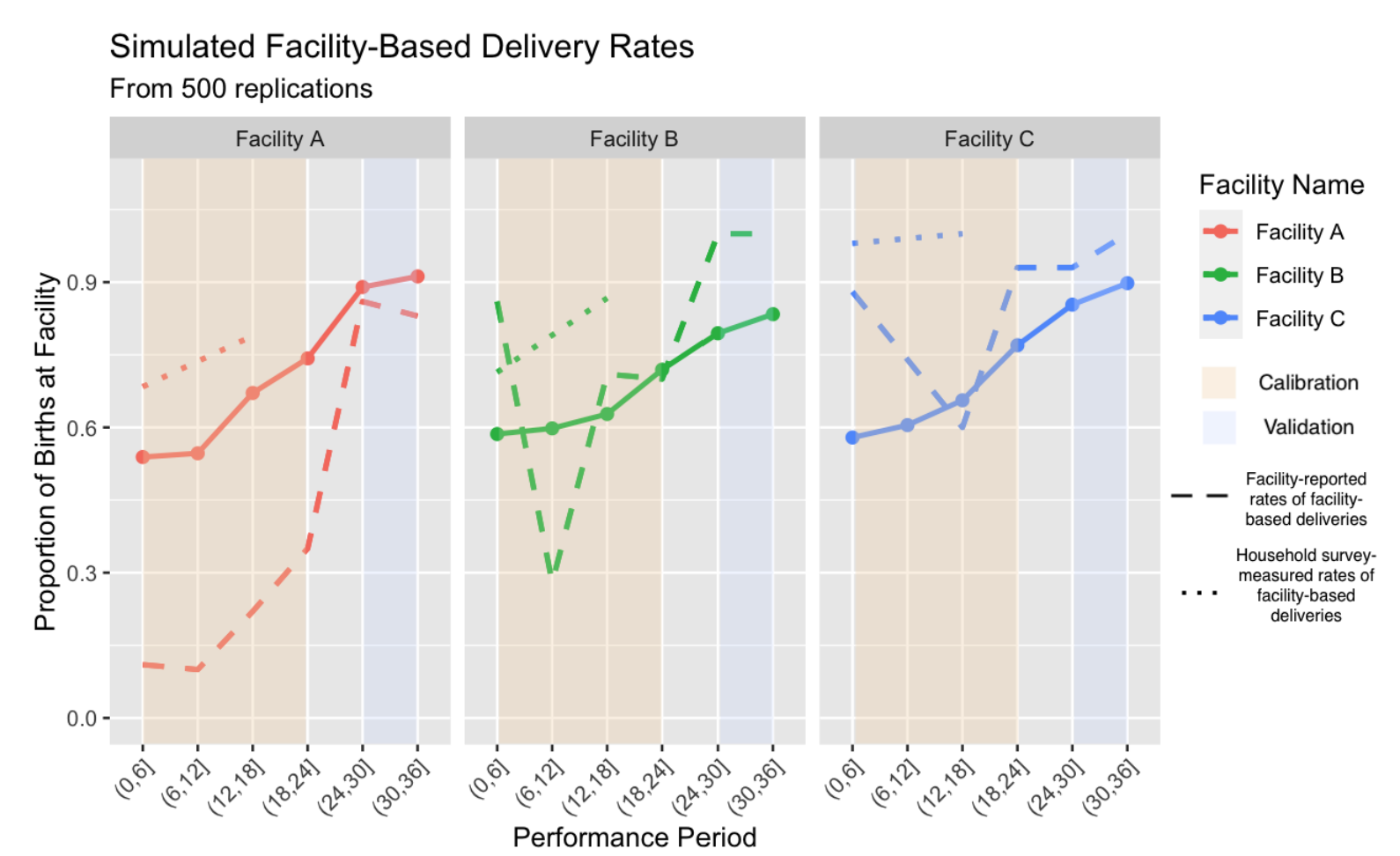
The simulated trajectories produced using the values of the best-fit calibration parameters were relatively well aligned with the rates of facility deliveries as shown in Figure 6. The combinations of parameters associated with the three lowest MSEs are shown in Table 9.

Consistent with the guidance of Nassar & Frank (2016), we focus on overall pattern matching rather than point-wise perfection since the empirical record is imperfect. Facility A records the largest root-mean-square error. This is primarily because empirical series combines two discordant sources: facility reported outcomes (which rise steeply from 13% to over 90%) and household-survey recall (which suggests a flatter trajectory). Reconciling those signals forces the calibration to compromise, leaving a wider gap for that facility while still minimising the pooled error across all sites.

The acceptability of a trajectory discrepancy should be judged in the light of data quality, modelling purpose, and stakeholder needs (Navarro 2019; Robinson et al. 2007). Survey snapshots may miss temporal variability, facility reported data can be incomplete, and both sources may be difficult to verify in low-resource settings. Following the quantitative-fit guidance and recent health-ABM validation supporting practices, we regard relative errors below 10–15% at endline as acceptable for policy-exploratory models (Collins et al. 2024). Using optimized calibration parameter values, the minimum mean squared error (MSE) between observed and simulated in-facility births, summed across the three facilities, was 1.52. For external validation, the difference between model-generated and facility-reported coverage for the last simulation period (months 30 to 36) was 7.7 percentage points (reported: 94.4%, simulated: 87.1%), well within the predetermined error bound limits. At endline, the model underestimated the coverage of two of the three facilities, as shown in Figure 6, which compares the performance of the observed and simulated facilities during the simulation period.

**Figure 6.** Simulated trajectories (in solid lines) produced by the best-fitting calibration parameter values overlayed on rates of facility-based deliveries reported by facilities (dashed lines) and measured through the household survey(dotted lines). The validation period is shaded in blue.

Scenario results

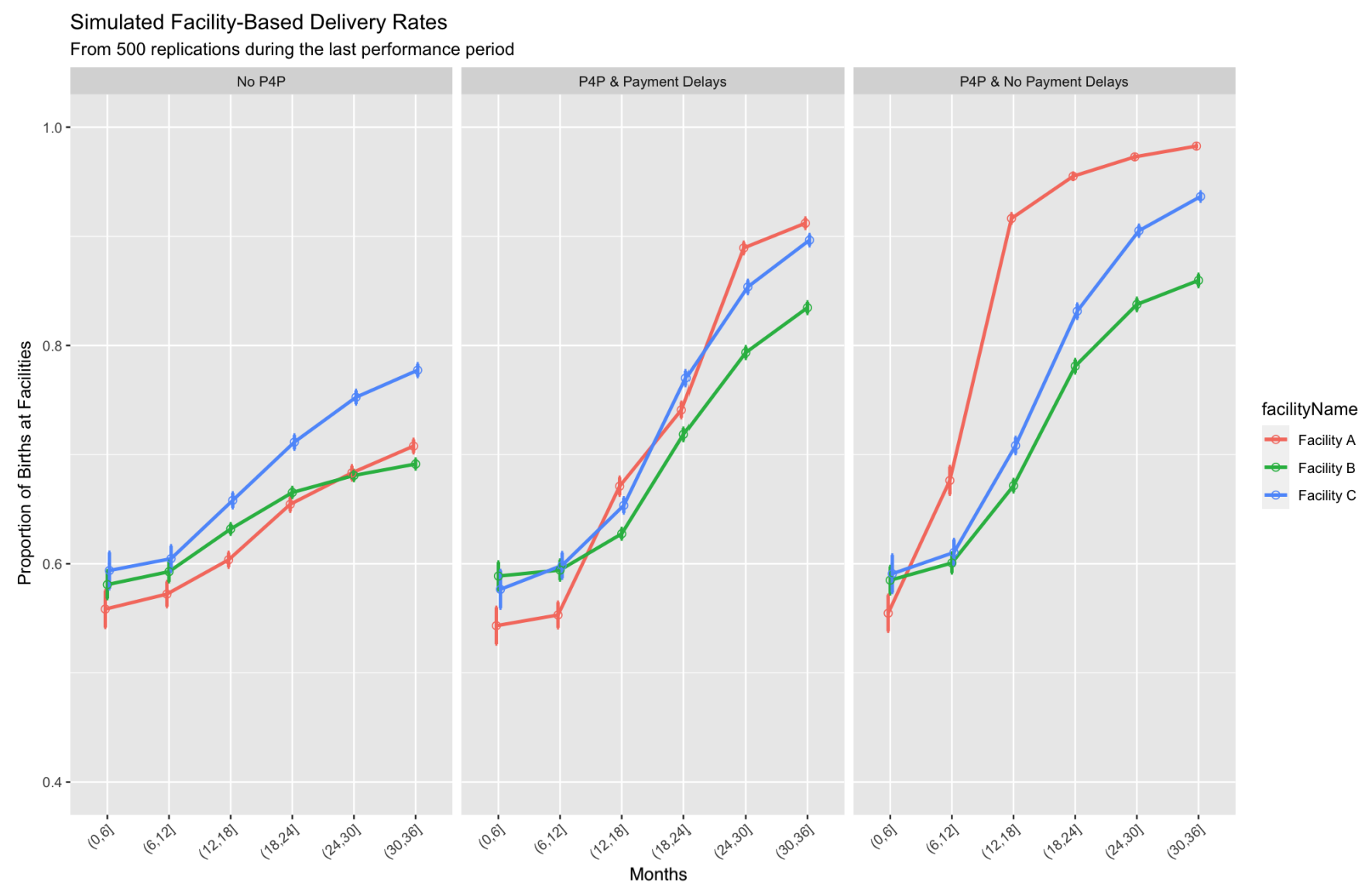
The model estimates that the current implementation of P4P (including DM visits and payment delays) produced a substantial increase in facility-based deliveries compared to the no P4P counterfactual. Specifically, the average facility-based delivery rate rose 15.4 percentage points (95% CI of difference [14.1, 16.7], and a relative increase of 21.5% (95% CI: [19.7%, 23.3%]) over the no P4P baseline ($p<0.001$) (see Table 6 for detailed statistics).

Our simulations indicate that eliminating bonus payment delays would have produced an additional absolute 4.1 percentage point increase in facility-based delivery rates ($p<0.001$) on top of the gains already achieved with the current P4P implementation. This represents a 4.7% relative increase compared to P4P with delays, and a 27.2% relative increase compared to the no P4P scenario (see Table 6).

DM visits showed measurable, though not statistically significant, benefits within the current P4P implementation that includes payment delays ($p=0.55$). However, these benefits were not observed in scenarios where payment delays were eliminated, as the DM’s role in facilitating drug sharing between facilities becomes less relevant. The slight, insignificant decrease associated with DM involvement in the absence of delays may be attributable to random variation.

The results are summarized in Table 5, which shows the coverage of institutional births combined for all three facilities under the three main simulated scenarios (No P4P, P4P with delays, P4P without delays). Consistent with the demand pathways in Sec. 3.6, our one–way sensitivity analysis (Table 13) identifies the home-experience modifier and the traditional birth attendant modifier as the largest contributors to endline coverage; these parameters map respectively to perceived quality/experience, outreach, and peer diffusion, and influence the observed +15.4 percentage-point increase under P4P.

Facility-based delivery rates

We explored individual facility-level performance trajectories in the three scenarios and found variations in the magnitude of effects between facilities.

Facility A, which has the lowest baseline performance, observed the highest increase in the proportion of institutional deliveries compared to the other two facilities under P4P scenarios, shown in Figure 7, though under the no P4P scenario it showed the second-highest increase. Specifically, the model estimates that facility-based deliveries for facility A under the current implementation of P4P with delays are 20.4 percentage points higher relative to the counterfactual where there is no P4P (70.8%, 95% CI = [70.2%, 71.4%] in no P4P vs 91.2% in P4P with payment delays, 95% CI = [90.7%, 91.7%])(Table 6). If P4P payments were made on time, the model estimates that facility A would achieve a facility-based delivery rate of 98.3% (95% CI = [98.1%, 98.4%], a 27.5 percentage point improvement over the counterfactual without P4P), as shown in Table 6.

Facility B, which has the largest catchment population and the lowest number of beds per capita, experienced smaller improvements in the rate of facility-based deliveries from P4P. The model estimates that the rate of facility-based deliveries for facility B under the current implementation of P4P with delays is 14.4 percentage points higher compared to the counterfactual where there is no P4P (69.1%, 95% CI = [68.7%, 69.6%] in no P4P vs. 83.5%, 95% CI = [82.9%, 84.0%] in P4P with delays). If P4P payments were made on time, the model estimates that facility B would achieve a facility-based delivery rate of 86.0%, 95% CI = [85.4%, 86.5%], a 16.9 percentage point improvement over the absence of P4P. In summary, facility B experienced modest benefits from P4P and on-time bonus payments, possibly due to its larger catchment population and high baseline performance.

Facility C experienced the smallest increase in the rate of facility-based deliveries from P4P. Specifically, the model estimates that the rate of facility deliveries for facility C under the current implementation of P4P with delays is 11.9 percentage points higher than the counterfactual where there is no P4P (77.7%, 95% CI = [77.1%, 78.3%] in no P4P vs. 89.6% in P4P with delays, 95% CI = [89.1%, 90.1%]). If P4P payments were made on time, the model estimates that facility C would achieve a facility-based delivery rate of 93.6%, 95% CI = [93.2%, 94.1%], a 15.9 percentage point improvement over the absence of P4P. In summary, facility C experienced the least benefits in performance from P4P and on-time bonus payments, but maintained its baseline high level of facility-based delivery.

**Table 5:** Rates of facility-based deliveries at endline when combined across the 3 facilities modeled for the three modeling scenarios and the baseline period value for reference. From 500 replications during the last performance period.
Experiment Setting	DM Visits	Rate (%)	95% CI
Baseline	No	65.7%	[63.8%, 67.6%]
No P4P	No	71.8%	[71.5%, 72.1%]
P4P & Payment Delays	No	86.3%	[85.7%, 86.9%]
	Yes	87.2%	[86.7%, 87.8%]
P4P & No Payment Delays	No	91.5%	[90.9%, 92.1%]
	Yes	91.4%	[90.8%, 92.0%]

**Figure 7.** Rates of facility-based deliveries across the three modeling scenarios over the modeling period.

**Table 6:** Comparison of simulated endline data across P4P and payment delay scenarios. Percentage improvements are absolute, comparing endline to the no-P4P scenario. All differences between scenarios were statistically significant at $\alpha < 0.05$.
Facility	Facility Characteristics		Simulated Rates of Facility-Based Deliveries
	Static	Dynamic (At Baseline)	No P4P (1)	P4P with Delays (2)		P4P without Delays (3)
			Endline	Endline	$\Delta_{(2)-(1)}$	Endline	$\Delta_{(3)-(1)}$
Average	--	--	71.7%	87.1%	+15.4%	91.2%	+19.5%
95% CI	--	--	[71.4%, 72.0%]	[86.1%, 88.1%]	--	[90.5%, 91.7%]	--
A	Longest wait times, Shortest travel time	Least drug availability, No outreach, Highest Interpersonal Quality, Lowest performance	70.8%	91.2%	+28.9%	98.3%	+38.8%
95% CI	--	--	[70.2%, 71.4%]	[90.7%, 91.7%]	--	[98.1%, 98.5%]	--
B	Largest population, lowest bed capacity, Average staff number	-	69.1%	83.5%	+20.7%	86.0%	+24.3%
95% CI	--	--	[68.6%, 69.6%]	[83.0%, 84.0%]	--	[85.5%, 86.5%]	--
C	Shortest waiting times, Longest travel time	Highest staff kindness score	77.7%	89.6%	+15.3%	93.6%	+20.4%
95% CI	--	--	[77.1%, 78.3%]	[89.1%, 90.1%]	--	[93.2%, 94.0%]	--

Facility characteristics

The three main scenarios (No P4P, P4P with payment delays, and P4P without payment delays) resulted in notable changes in dynamic facility characteristics: drug availability, staff kindness, and out-of-pocket payments. For traceability, we focus on changes in these particular facility characteristics that encompass multiple aspects of patient care. Specifically, drug availability is related to access in terms of medication, staff kindness is related to patient experiences during care provision, and out-of-pocket payments represent financial access barriers.

The implementation of P4P, even with payment delays, led to substantial improvements in drug availability. The model estimates that the current implementation of P4P produced a 47.5 percentage point increase in drug availability compared to the counterfactual without P4P (Drug Availability in No P4P: 38.9%, Drug Availability in P4P with delays: 86.4%). Removing payment delays in the P4P scenario led to a further 2.6 percentage point increase in drug availability (Drug Availability in P4P with no delays: 89.0%).

Staff kindness also increased under P4P conditions, with the current implementation associated with a 16.6 percentage point increase over the no P4P scenario (Kindness in No P4P: 68.6%, Kindness in P4P with delays: 85.2%). This rate improved by 3.3 percentage point with the removal of payment delays (Kindness in P4P with no delays: 88.5%).

Out-of-pocket (OOP) payments showed a somewhat different trend, increasing slightly by $14.0\%$ (relatively) with the introduction of P4P with delays (OOP in No P4P: 18.6%, OOP in P4P with delays: 21.2%), but decreasing by $32.9\%$ (relatively) when payment delays were removed (OOP in P4P without delays: 14.3%).

Facility-Level Characteristics. All facilities observed notable changes modifiable characteristics as shown in Figure 8. Drug availability significantly increased with the implementation of P4P, with Facility A making the largest leap from 33.3% to a full 100.0% in the no-delay scenario. Despite the initial increase, all facilities also benefitted from eliminating payment delays, which signifies the positive impact of timely bonus payments on drug availability.

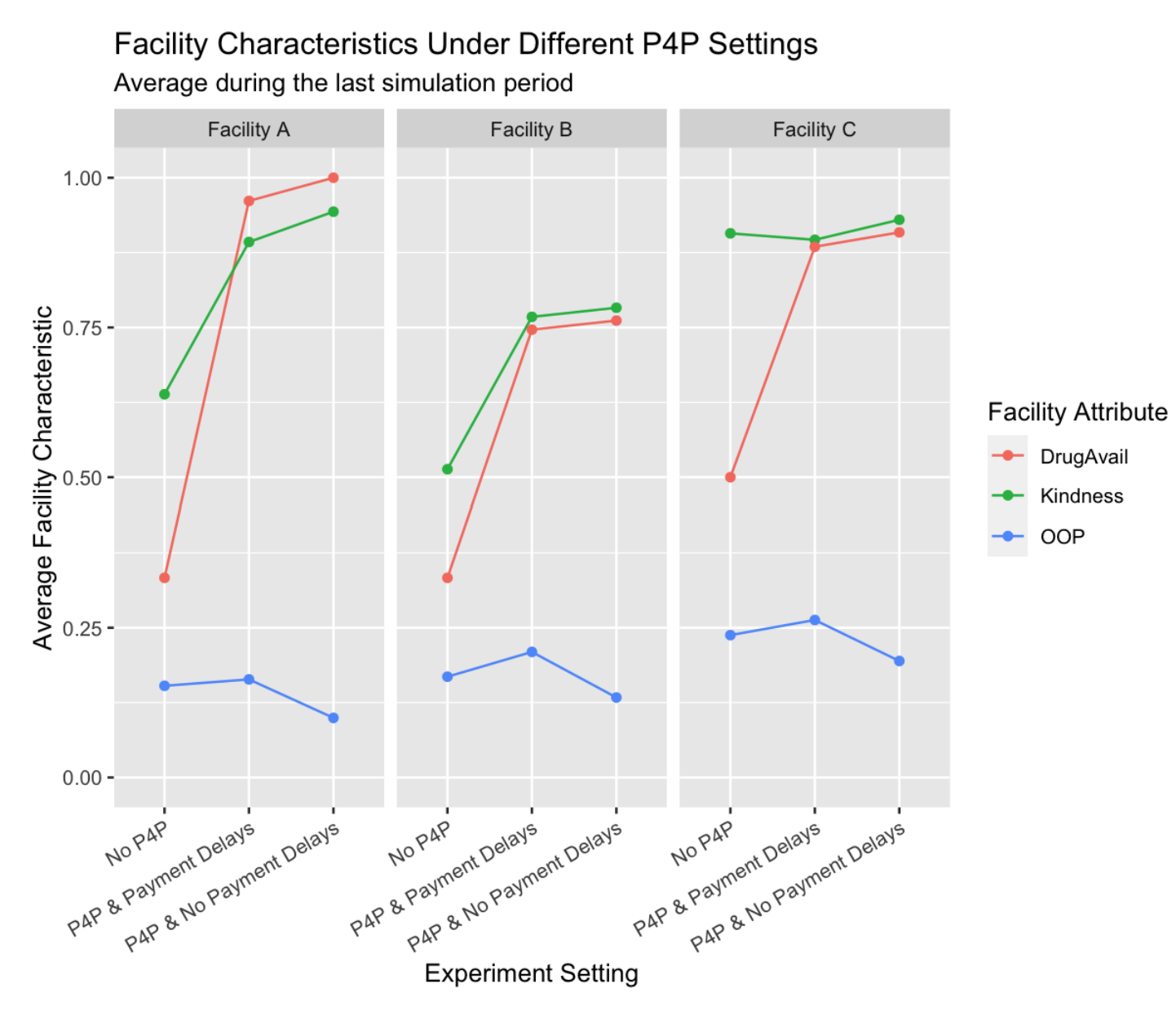
**Figure 8.** Facility-specific differences in endline characteristics across scenarios.

In terms of staff kindness, Facility C maintained a noticeably high baseline, therefore showing the least improvement, albeit a positive increase to 93.0% without payment delays. Meanwhile, Facilities A and B exhibited substantial improvements, highlighting the substantial boost in staff motivation that P4P can bring, further amplified by eliminating payment delays.

For out-of-pocket payments, the initial implementation of P4P with delays led to a surge across all facilities. However, eliminating these delays turned the tide, resulting in significant reductions in out-of-pocket expenses, most notably in Facility A, which fell to 10.0%, demonstrating the significant potential to reduce patient expenses by removing payment delays.

In general, removing payment delays within the P4P framework seems to foster not only improved drug availability but also enhanced staff kindness and lower out-of-pocket expenditures, presenting a more patient-friendly environment across all facilities.

Cross validation

To provide a holistic perspective on P4P implementation effects, we compared our ABM results with findings from (1) complementary modeling approach by our research team and (2) Pwani P4P evaluation experiment (Borghi et al. 2013, 2021). The system dynamics model by Cassidy et al. (2025) modeled a single representative facility using data from 75 evaluation facilities, district-level data, and national statistics. In contrast, our ABM explicitly modeled three specific public facilities (representing around 4% of the 75 facilities in the Pwani evaluation study; Borghi et al. (2021)).

Despite the different modeling approaches and scopes, both models agree on key mechanisms: drug availability serves as the primary demand trigger, and payment delays erode supply-side gains. However, they capture different aspects of the system - the SDM focuses on severe payment delays while our ABM also captures the associated rise in out-of-pocket fees (a variable not represented in the SDM). The SDM treats low baseline drug stocks as a hard ceiling, whereas the ABM shows greater catch-up potential in such settings through its agent-level decision-making framework.

Our ABM’s counterfactual (no-P4P) scenario projects 71.7% facility-based delivery coverage at endline, compared to 89.4% observed in the 75 control facilities in the Pwani evaluation (Borghi et al. 2021). For the P4P-with-delays scenario, our ABM estimates 87.1% coverage, closely aligning with the SDM’s intervention estimate of approximately 89.7% (Cassidy et al. 2025). The lower counterfactual projection in our ABM likely reflects the specific characteristics of the three modeled facilities rather than the broader distribution of all evaluation facilities.

This triangulation across different modeling approaches and program evaluation, each with distinct abstractions and design decisions, strengthens our understanding of P4P dynamics. Like ensemble modeling in climate science or epidemiology, examining these complementary perspectives provides a more comprehensive picture of how payment delays and facility characteristics influence maternal healthcare seeking behavior, even when exact numerical predictions differ.

Sensitivity analysis

The sensitivity analyses demonstrate that our model’s general observed patterns and conclusions may vary slightly with key input variables. Specifically, we run a sensitivity analysis on the key input parameters as well as structural sensitivity analysis to uncover the model’s dependence on key structural assunmptions.

The sensitivity analysis of input parameters revealed varying degrees of influence on the percentage of in-facility births. We varied key model inputs using a scale adapted from Semwanga et al. (2016), which categorizes sensitivity based on the percentage change in model output. Importantly, the relative performance of the facilities remained consistent under these changes for most of the input parameters. The few exceptions were the Traditional Birth Attendant Modifier ($M_{\textit{TBA}}$, range: 0.25–0.4), which exhibited the most substantial impact with a 42.1% change in the average percentage of in-facility deliveries across its range, closely followed by the Home Experience Modifier ($M_{\textit{hExp}}$, range: 0–0.05) at 26.1%. Conversely, parameters such as the Drug Sharing Rate (DrugSharRate, range: 5–10%) and Duration of District Manager Visit Effects (DM $\textit{VisitDuration}$, range: 0.5–1) showed minimal influence, with percent changes of 0.031% and 0.023% respectively. The Facility Capacity Relaxation (Beds, range: 1–3), while not among the most sensitive parameters, still demonstrated a notable effect with a 1.244% change. Other parameters, including the Occupancy Adjustment (OccAdjustor), Percent of Women Pregnant at Initiation ($p_{\textit{PregnantInitiation}}$), Facility Experience Modifier ($M_{\textit{fExp}}$), Social Network Modifier ($M_{\textit{social}}$), Drug Sharing Threshold (DrugSharThres), and Size of Social Network ($n_{social}$), showed less degrees of sensitivity. Appendix H provides detailed results of the sensitivity analysis performed on the calibrated simulation model.

These results highlight the importance of focusing on community-level interventions and women’s prior experiences when designing strategies to increase facility-based deliveries, while suggesting that aspects like drug sharing and the duration of managerial visits may have less immediate impact on this particular outcome. Given the significant influence of certain parameters, particularly those related to community factors, it is important to prioritize the accurate quantification of these input parameters to enhance the model’s predictive power and reliability.

An example of the structural changes made during the model development process involved the bonus effects mechanism. Specifically, we incorporate a dependence of the bonus effects on both the current bonus and the bonus from the previous period. Additionally, we modified the model so that the staff’s motivational response would coincide with the receipt of the bonus, as opposed to occurring at the end of the performance period. Despite these alterations, we observed that the changes in facility performance were not substantial.

Discussion

This paper describes the formulation, parameterization, and validation of an ABM to explore the effects of a P4P program on the delivery care and facility characteristics in a primary care setting. The model also explores the effect of incentive payment delays on outcomes and the heterogeneity of effects across facilities. We demonstrate the feasibility of building an ABM as an ex-post evaluation tool to further unpack program effects, with the model subjected to validity testing. To our knowledge, this is the first ABM to evaluate the effect of a health system strengthening program such as P4P in a low or middle-income setting.

Methodological contribution

For this study, we harnessed the strengths of an advanced ABM that integrated data analytics and regression choice modeling with knowledge from various stakeholders (Binyaruka et al. 2023; Mziray et al., 2022). This innovative approach allowed us to go beyond the conventional applications of ABM and establish it as a potent ex-post evaluation tool capable of dissecting the intricate nuances of health intervention outcomes, going a step beyond its well-trodden path of hypothetical ‘what-if’ analyses in simulation modeling. This evolutionary step in the role of ABM within the healthcare sector unlocks new avenues of understanding, offering a retrospective yet deeply analytical lens to evaluate the actual impacts of interventions on maternal and child health in Tanzania. The study also takes a step towards addressing the lack of examples of advanced computational models used to explore health system policy questions in the context of low- and middle-income countries (Cassidy et al. 2019).

A critical aspect of our approach was the meticulous verification and validation process that we undertook. Using an existing published regression choice model provided a robust starting point (Binyaruka et al. 2023). Furthermore, our approach exceeded standard practice by actively incorporating insights from a spectrum of key stakeholders, policymakers, district managers, and facility staff (Mziray et al. 2022). Their first-hand experiences and perspectives enriched the model’s foundational components and facilitated a deeper understanding of the prevailing challenges and model structures. This engagement nurtured a collaborative spirit, engendering a shared understanding and ownership of the model, thereby enhancing the robustness and reliability of our findings. This holistic approach signifies a significant stride in the continuous evolution of ABM applications in health systems, promising avenues for more insightful and stakeholder-centered research in the future.

The calibration and external validation of the model yielded results closely mirroring the performance at the facility level observed during the first 24 months of implementation of the P4P program. Our approach allowed us to minimize the MSE between simulated and observed delivery rates. Although the model had a minor tendency to underestimate facility-based delivery coverage during the final simulation period, it effectively mimicked reality by generating a plausible performance trajectory. In addition, the simulations of the control scenarios in our model reproduced comparable patterns of service delivery and coverage observed in real-world control facilities. This rigorous validation attests to the utility of an ABM-regression composite approach to understanding complex system dynamics. It illustrates how diverse facility conditions and characteristics of the catchment population can lead to variations in performance under the same operational rules.

A system dynamics model (SDM) of the P4P program in Tanzania was developed concurrently with the ABM described in this article (Cassidy et al. 2021, 2025). The purpose of the SDM was to explore pathways to impact within the program to improve specific maternal and child health outcomes (two doses of intermittent preventative treatment during antenatal care visits and facility-based deliveries) and examine how changes in the design, implementation, and context of the program, affect these key outcomes of service delivery. In contrast to the demand-side focus of the ABM, the main focus of the SDM was on facility-level supply-side dynamics, with reduced inclusion of demand-side elements that may be affected by the program. The focus and results of the two models are complementary, building a complete picture of how health systems are impacted by P4P programs to generate recommendations for future health system strengthening initiatives. The insights gained through the development of each model (program impact on demand-side dynamics and heterogeneous decision-making of agents vs. program impact on supply-side dynamics including medicine procurement) and differential effects of contextual factors on performance (i.e., baseline drug availability) pave the way for hybrid model development in future work, incorporating the benefits of using different types of model approaches in a single simulation while minimizing the limitations of using one methodology.

Model findings

The model indicated that P4P was associated with a considerable increase in facility-based delivery rates, and that, in the absence of payment delays, the effects would have increased rates by almost a third (compared to no P4P). These findings resonate with a recent SDM that explored the effect of payment delays on drug availability and other facility-level characteristics. Although increases were observed in all three facilities, the model illustrates variations in the magnitude of the effect, with the greatest benefits in P4P observed in facility A, with the lowest baseline performance relative to facilities B and C. Facilities B and C benefited less from the P4P program, seemingly due to their higher levels of kindness and drug availability at baseline. The effect of delays also varied between facilities, with the greatest effect on facility A. Also, P4P has greater potential to increase motivation where motivation levels are low at baseline. The model also highlights that effects are not linear over time and, while initially facilities B and C do better than facility A, over time, facility A catches up and surpasses them, consistent with previous findings by Binyaruka et al. (2018).

Our model quantifies the demand-side response to P4P implementation, with facility-based deliveries increasing by 15.4% over the simulation period. This increase was primarily driven by improvements in drug availability, enhanced staff kindness, and reduced out-of-pocket expenses.

Still, our three–facility model already hints at a rich, non-linear interplay between supply-side inputs (drug stocks, staff behaviour, bed capacity) and demand-side responses. Facility A achieved near-maximum drug availability (100%) and high staff motivation, but further improvements became limited by bed capacity (2 beds) and staff numbers (2 staff members). This suggests that P4P programs may need to be coupled with infrastructure investments to achieve sustained improvements beyond certain thresholds. Although these contrasts are instructive, they are necessarily facility-specific. A fuller understanding of how supply–demand feedbacks scale with catchment size, staffing mix, or initial coverage will require an expanded ABM that spans a more diverse set of facilities and referral links. We therefore see the present model as a proof-of-concept and identify the systematic exploration of these relationships across a larger network of facilities as a priority for future work.

The model sheds light on some of the pathways through which these changes came about. Specifically, we observed that P4P, even with payment delays, improved drug availability and staff kindness, consistent with previous studies (Binyaruka et al. 2015). However, there was an increase in OOP payments under P4P with delays, while OOP fell below baseline values once these delays were removed. The greatest effects were observed for facility A, which had the lowest baseline kindness and drug availability. The model results on OOP stand in contrast to our previous research, which reported a reduction in OOP that was sustained over time (Binyaruka et al. 2015; Borghi et al. 2021). We hypothesize that the discrepancy between the model results and actual empirical findings may be due to the way the delays are modeled in this ABM as having time-fixed effects. In reality, the impact of delays can fluctuate over time, particularly as facilities adapt to payment cycles, potentially lessening the immediate effects of subsequent delays. Still, the model suggests that the improvement in OOP would have been greater without delays.

The findings underscore the need to minimize payments delays within the framework of P4P initiatives to realize substantial efficiency gains. Ensuring timely contributions from donors and fostering a timely flow of funds at the subnational level appear to be critical in optimizing the potential benefits of these initiatives. Moreover, our data suggests that facilities with lower baseline performance metrics have a higher propensity to improve. Therefore, crafting incentives targeted at these low performing facilities, potentially based on aspects in addition to baseline coverage, could catalyze a more significant progression over time, aligning incentives with broader community welfare objectives. Our model quantifies the impact of payment delays, estimating an average relative loss of 4.8% in facility-based deliveries, with losses varying between facilities (7.22% for Facility A, 2.91% for Facility B, and 4.27% for Facility C). This significant loss highlights the urgent need to address payment delays to avoid undermining the efficacy of P4P programs and, by extension, the overall delivery of health services.

Furthermore, it is essential to address the inadvertent increase in OOP payments witnessed in scenarios with payment delays to prevent undermining the affordability of healthcare services. Policymakers should support mechanisms to monitor and control informal charges, ensuring that delay in P4P payouts does not inadvertently escalate the financial burden on patients. The findings also highlight the necessity for ongoing monitoring and adjustment of health policies and strategies, capitalizing on the dynamism of healthcare simulation tools and facilitating flexibility and responsiveness in policy implementation based on ongoing studies.

We have demonstrated the potential of ABM for program evaluation, enabling reconstruction of the counterfactual and exploring the effect of past or future policies on outcomes of interest. The findings of this study ultimately illustrate the potential of advanced agent-based modeling to explore and understand the complex dynamics of the health system. By harnessing the power of this approach, we can facilitate the development of more effective, context-specific, and nuanced health policy interventions that consider the diverse and dynamic nature of health systems.

Limitations & future research

The simulation model, while detailed in several aspects, operates within defined boundaries, which entail certain limitations. The model focuses primarily on facility-based services, being the focal point of data measurement in the program, and does not encapsulate patient morbidity, mortality, or other health outcomes. Furthermore, the interactions that occur within healthcare facilities, especially those between providers and patients, have not been modeled in detail. This representation inherently means that a detailed exploration of provider-patient dynamics is omitted.

Moreover, we suppose that a woman agent has perfect information about the nearest facility when making delivery decisions. Our model still accounts for past and shared experiences, but we recommend that imperfect information and perceptions be accounted for in future models. Additionally, while we have attempted to illustrate the relationship between bonus payments and varied facility behaviours and characteristics, it is imperative to acknowledge that these were primarily inferred through stakeholder consultations and calibrations, since explicit data on these relationship were unavailable. Additionally, at present all demand-side pathways (e.g., peer influence, perceived quality, and reduced out-of-pocket costs) are aggregated into a single composite effect. A clear next step is to disaggregate these mechanisms and conduct targeted sensitivity analyses to quantify the relative contribution of each driver to the observed 15 pp demand increase.

The current structure of our model predominantly accommodates microlevel behaviours, not extending to the dynamics that govern aspects such as drug supply chains and staffing nuances that form a key element of healthcare service delivery. In the existing framework, the model does not allow for an in-depth exploration of network effects, bypass decisions, and the decision-making processes of women seeking care in more distant facilities, which could be perceived as an area where the model could benefit from further refinements. We acknowledge that our study did not investigate detailed referral networks, which, although accounted for, have not been modeled to represent the potential cascading effects on the healthcare system. We are addressing this limitation in future work.

As we advance, our research direction encompasses the development of a hybrid model that combines the strengths of the micro-level heterogeneity captured within this ABM with the SDM stocks and flow structures, with the aim of creating a more comprehensive depiction of facility dynamics and drug replenishment cycles – crucial elements in healthcare service delivery. This innovation promises to bridge the gap observed in the present study, offering a fuller portrayal of the interplay between various factors in healthcare settings.

Finally, we envisage expanding our model to include a broader set of policy scenarios, potentially as a versatile tool for studying diverse scenarios and their repercussions in future studies. Through this adaptive approach, we anticipate developing a tool capable of providing deeper insights and nuanced understandings of complex healthcare dynamics, thereby facilitating informed policy decisions and strategies that align with the evolving landscape of healthcare delivery and management.

Conclusion

In conclusion, financial incentives for health workers can significantly increase the percentage of births that occur in facilities. However, overcoming delays in the payments of these incentives would further increase the effects. Programmatic steps to avoid payment delays (and the associated increases in ‘out-of-pocket’ informal charges during delays) should be prioritized. There can be considerable variation between facilities in terms of intervention effects. Policymakers could thus benefit from adopting tailored strategies that account for specific facility and population dynamics, e.g., regarding initial facility performance indicators.

Our study showcases the potential for using agent-based modeling as an ex-post evaluation tool for exploring the intricate dynamics and heterogeneity of health systems. By representing individual behaviours and their interactions within the system, the model provides a unique perspective that can help guide policy making. The model elucidates the pathways to impact and program bottlenecks by virtually reconstructing agents and observing emergent system-level behaviours such as performance improvements and limits to improvements. Our framework has generalizable methodological steps for others seeking to use agent-based modeling to better understand how health system strengthening programs such as P4P affect the behavior of providers and patients.

Acknowledgements

This research was funded by the Medical Research Council under the Health Systems Research Initiative grant (MR/R013454/1). We are immensely grateful to all the key stakeholder participants who helped develop and refine our model. Special thanks go to Dr. Chitalu Chama-Chiliba and Nkenda Sachingongu for their guidance on capacity expansion scenarios, which were crucial to the development of our approach.

We are also thankful to Christa Searle, Agnes Semwanga, Nicky McCreesh, Graham Medley, Karl Blanchet, Neha Singh, Miguel Pugliese Garcia, Maxime Stauffer, and Julia Lohmann for their various contributions, which have been essential to the successful completion of this project.

Supplementary Information

As part of our ongoing commitment to open science and research transparency, we have created a publicly accessible GitHub repository containing an anonymized version of our Agent-Based Model with model documentation. This repository is a comprehensive resource for researchers and policymakers interested in exploring the dynamics of our model and running their test scenarios.

The repository can be found using this link: https://github.com/aalibrahim/COSMIC-ABM-Public-JASSS.git. Once accessed, open the README file for further instructions.

To use this model, a user must first install the free Personal Learning Edition of Anylogic Software (https://www.anylogic.com/downloads/). Please ensure you have the latest version installed for optimal performance and compatibility. Once AnyLogic is installed, you can then clone the contents of our GitHub repository. The repository contains all the necessary files to run the model, including the primary model file, associated scripts, and data files. The data files contain anonymized information about healthcare facilities, ensuring the privacy and confidentiality of the original sources.

To run the model, open the primary model file using AnyLogic. This should load all the necessary components, scripts, and data. From there, you can interact with the model, manipulate its parameters, and run simulations according to your interests.

Data Availability Statement

In compliance with transparency and open science practices, we would like to affirm that all the data and parameters utilized as inputs to this model are readily available. They are either presented directly within this study or can be found in the cited studies. The exact data values for the anonymized facilities used in the model can be found in the corresponding public repository accessible through this link: https://github.com/aalibrahim/COSMIC-ABM-Public-JASSS.git.

Our goal is to facilitate reproducibility and further exploration by providing complete access to the underlying data that support the results, conclusions, and proposed insights of this research. We encourage researchers, policy-makers, and practitioners to leverage this information for extended analysis, ensuring the continual progress of scientific understanding in this domain.

Declarations

The authors of this study declare that they have no conflicts of interest in relation to the research, authorship, and/or publication of this article. They confirm that there are no relevant financial or non-financial competing interests to report. However, it should also be noted that a few of the co-authors were involved in the planning and implementation of the intervention that this model evaluates.

This study received a favorable ethical opinion from the Observational/Interventions Research Ethics Committee at The London School of Hygiene and Tropical Medicine (LSHTM Ethics Ref: 16139 – 3), the Institutional Review Board at Ifakara Health Institute (IHI/IRB/No:17 -2021), and the National Institute for Medical Research (NIMR/HQ/R.8a/Vol. IX/3154) in Tanzania.

Author Contributions

AA led on coding the agent-based model in AnyLogic software, model verification, calibration and validation, undertaking model analyses, and writing the manuscript. NM led on contextualization, model-focused stakeholder engagement (including focus-group discussions and interviews) and model parameterization, and contributed to the conceptualization of the agent-based model and building an earlier version of the model in NetLogo software. PB led on the statistical regression modeling and contributed to the conceptualization of the agent-based model and its parameterization and contextualization (including stakeholder engagement). JM led on broader stakeholder engagement (including data collection and analysis of focus-group discussions and interviews), and contributed to the conceptualization of the agent-based model and its parameterization and contextualization. ZC contributed expert technical modeling experience, guiding the model conceptualization, revising the manuscript, and evaluating internal model validation mechanisms. RC offered her insights from her systems dynamic modeling of the same intervention in the same setting, with valuable foundational work with stakeholders and substantial contributions in guiding the modeling of bonus payment delays. ZC contributed expert technical modeling experience to guide the model conceptualization, model building and documentation of the modeling. JB initiated this project based on her idea to use intervention implementation data within an agent-based model as an ex-post evaluation tool, and led on coordinating the whole team, providing input throughout from conceptualisation, data collection and analysis, modeling and reviewing/writing of the manuscript. AMF led on the conceptualization of the agent-based model and building an earlier version of the model in NetLogo software, contributed to reviewing relevant literature for parameterization and guided/supported the modelling team, having oversight of the modeling project as a whole, including model analysis and manuscript writing. All authors informed the design of the modeling analysis plan and helped with interpretation of the model findings, as well as contributing to the writing/reviewing of the manuscript.

Appendix A: Glossary of Parameters

**Table 7:** Glossary of Model Parameters.
Parameter	Parameter Name	Description
Time
$t$	Simulation Month	Current simulation month, which ranges between 1 and 36
PP	Performance Period	A time segment of 6 months, at the end of which bonus evaluations are conducted.
Facility Agent Parameters
$\textit{Bonus}_{f,PP}$	Facility Bonus	The bonus allocated to a specific facility $f$ at the end of a performance period $PP$.
Sharing%	Sharing Percentage	A calibration parameter that helps to facilitate drug sharing between facilities.
$\textit{O}_{f,t}$	Outreach Activities	Status of outreach activities of a facility at initial time point.
$\textit{OOP}_{f,t}$	Out-of-Pocket Costs	Initial out-of-pocket costs at a facility.
$\textit{TBA}_{f,t}$	TBA Incentives	Traditional birth attendant incentives at a facility during month $t$.
$G_{f,t}$	Gifts to Mothers	Status of gift provision to mothers at a facility during month $t$.
$\textit{IPQ}_{f,t}$	Staff Interpersonal Quality	Staff interpersonal quality of a facility during month $t$.
$D_{f,t}$	Drug Availability	Drug availability at a facility during month $t$.
$K_{f,t}$	Staff Kindness	Staff kindness at a facility during month $t$.
$W_f$	Women of Reproductive Age	Number of women of reproductive age catered by the facility.
$\%\textit{FB}_{f,t}$	Facility Coverage Performance	Percent of facility-based deliveries at the facility during month $t$.
$DT$	Donor Threshold	Criterion for a facility to share drugs.
$RT\%$	Recipient Threshold	Criterion for a facility to be eligible to receive shared drugs.
Woman Agent Parameters
$p_{\textit{pregnant}}$	Pregnancy Probability	Monthly probability that a woman gets pregnant when not initiated as pregnant.
$p_{\textit{PregnantInitiation}}$	Pregnancy Initiation Probability	Probability that a woman agent is assigned a random stage of pregnancy upon generation.
VisitDuration	Visit Duration	Duration in days of an M agent visit.
$p_{\textit{complication}}$	Delivery Complication Probability	Probability of a complication occurring during childbirth.
$p_{\textit{lostpregnancy}}$	Lost Pregnancy Probability	Probability of a pregnancy being lost due to miscarriage or stillbirth before labor.
$\|W_f\|$	Number of Woman Agents per Facility	The number of woman agents assigned to each facility, representing the number of women of reproductive age in the catchment area of a facility.
$\%\textit{WRA}$	Proportion of Women of Reproductive Age	The proportion of women of reproductive age in the catchment area of a facility.
$\overline{TT}_{f}$	Average Travel Time to Facility	Average travel time for a woman agent to reach her assigned facility, based on community survey responses.
$TT_{\textit{w-to-f}}$	Travel Time for Individual Woman Agent	The estimated travel time for a particular woman agent to reach her assigned facility. This is sampled as a uniform distribution around the average travel time $\overline{TT}_{f} \pm 50\%$.
$p_{w@f}$	Delivery Decision Probability	Final probability that a woman $w$ delivers at a facility $f$.
$n_{social}$	Woman's Social Network	The number of woman agents in her social network.
$p_{\textit{facility delivery}}$	Probability of Facility Delivery	Calculated from a logistic model, which is then modified for own and network facility experiences.
$\textit{HomeExp}_w$	Home Experience	Experience of a woman from delivery at home.
$p_{\textit{+iveFacExp}}$	Positive Facility Experience Probability	Probability of a woman having a positive experience at a facility.
$\textit{FacilityExp}_w$	Facility Experience	Experience of a woman from delivery at a facility.
$\textit{influences}_w$	Social Network Influences	Influences on a woman from her social network.

Appendix B: Logistic Regression

**Table 8:** Coefficients of the logistic regression model from (???). Positive coefficient values indicate a positive relationship (More staff is associated with more in-facility deliveries) and negative coefficient values indicate a negative relation (Higher OOP is associated with fewer in-facility deliveries).
	Odds Ratio	Coefficient	z	P>Z
Some Primary Education	1.495	0.402	1.94	0.053
Primary Education	1.821	0.599	4.68	<0.001
Secondary or More Education	6.925	1.935	4.47	<0.001
Previous Pregnancies 1+	1.604	0.472	3.41	0.001
ANC Visits 4+	1.399	0.336	2.94	0.003
Number of Staff	1.012	0.012	3.56	<0.001
Outreach	1.453	0.374	2.88	<0.001
Wait Time (mins)	0.994	-0.006	-3	0.003
patient contact Time (mins)	1.033	0.032	2.71	<0.001
Staff IPQ	4.482	1.5	2.9	<0.001
OOP	0.319	-1.142	-3.98	<0.001
Travel Time	0.988	-0.012	-3.69	<0.001
Constant	0.881	-0.126	-0.26	0.793

Appendix C: Occupancy Effects on Quality of Care

The occupancy rate at the facility $f$ affects the patient contact time a woman agent $w$ receives when delivering at the facility. Beds occupied at the time of delivery, $\textit{BO}_f$, and capacity, $C_f$, are used to calculate the factor occupancyEffects at which patient contact time shortens when the facility is busy. Note that $\textit{BO}_f$ is always less than $C_f$, therefore, Equation 7 will always be $\in [0,1]$ The function is adopted from Alonge et al. (2017) and is shown in the equation using the ABM variables.

\[ \renewcommand{\theequation}{A\arabic{table}} \textit{occupancyEffects} = 1-{(\frac{BO_f}{C_f})}^{3} %-((1-exp(-0.5*(fOccupancy-fCapacity)))/(1+exp(-0.5*(fOccupancy-fCapacity))))+(1+((1-exp(-0.5*(1-fCapacity)))/(1+exp(-0.5*(1-fCapacity)))))))\]

\[(7)\]

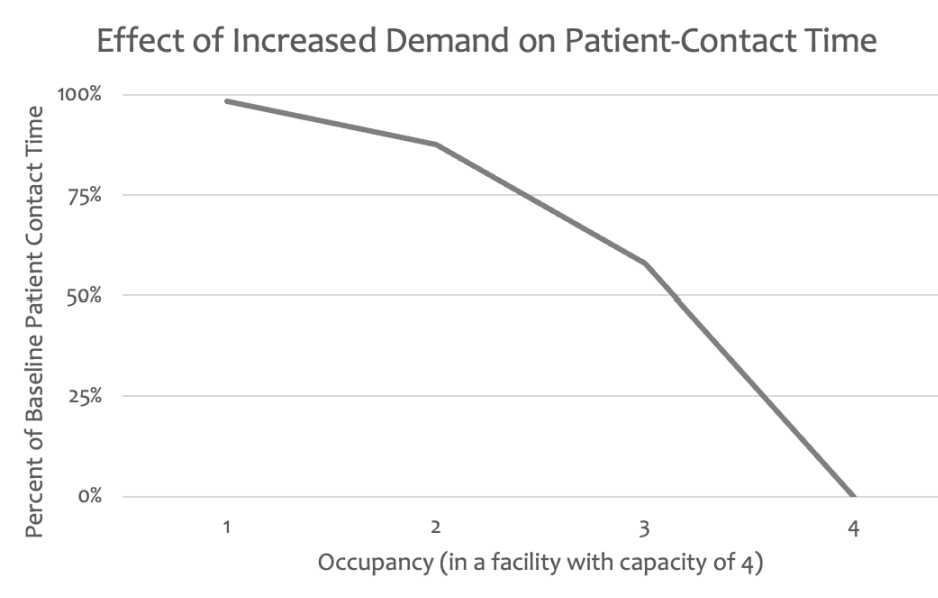
**Figure 9.** Reduction in patient contact time is driven by occupancy at the facility. The figure shows the reduction in patient contact time for different occupancy levels in a facility where capacity $C_f=4$

Appendix D: Calibration Parameter Values

**Table 9:** Calibration experiment results depicting the ten best-performing and ten worst-performing combinations of values for calibration parameters and the corresponding Mean Square Error (MSE) between observed and simulated outcomes over the calibration period.
Best Performing (Lowest MSE)
OccAdjustor	$p_{\textit{PregnantInitiation}}$	Beds	DM $\textit{VisitDuration}$	$M_{\textit{fExp}}$	$M_{\textit{hExp}}$	$M_{\textit{social}}$	$M_{\textit{TBA}}$	DrugSharThres	DrugSharRate	$n_{\textit{social}}$	MSE
2	2.5%	+3	1.0 month	0.30	0.0	0.35	0.35	50%	10%	5	1.521
1	2.5%	+2	0.5 month	0.30	0.0	0.35	0.35	50%	10%	4	1.526
1	2.5%	+3	0.5 month	0.30	0.0	0.35	0.35	50%	10%	5	1.543
1	2.5%	+3	0.5 month	0.30	0.025	0.35	0.325	50%	10%	4	1.562
1	7.5%	+3	0.5 month	0.30	0.05	0.35	0.30	50%	5%	6	1.569
Worst Performing (Highest MSE)
0	2.5%	+1	0.5 month	0.35	0.0	0.35	0.30	50%	5%	6	3.097
0	7.5%	+3	1.0 month	0.35	0.0	0.35	0.30	50%	5%	5	3.115
0	2.5%	+2	0.5 month	0.30	0.0	0.30	0.40	50%	5%	5	3.118
1	2.5%	+1	1.0 month	0.35	0.05	0.35	0.25	50%	10%	6	3.130
0	2.5%	+1	1.0 month	0.35	0.05	0.35	0.25	50%	10%	6	3.158

Appendix E: Internal Validity

**Table 10:** A comparison of the observed baseline performance compared to the simulated endline of the no P4P scenario. The values in the column (1) represent the "Do Nothing" scenario, or the counter-factual to the P4P.
Facility	Differentiating Facility Characteristics		Baseline Empirical Estimates (0)	Simulated
	Static	Dynamic (At Baseline)	Baseline Empirical Estimates (0)	No P4P Endline (1)
	Static	Dynamic (At Baseline)	Endline	Delta
A	Longest wait times Shortest average travel time	Least drug availability No outreach Highest IPQ Lowest performance	13% to 68%	73.6%
B	Largest catchment population size Average bed capacity Average number of staff		71.4% to 100%	68.6%
C	Shortest wait times Longest average travel time	Highest staff kindness score	84.2% to 98%	80.3%

Appendix F: Baseline Facility Characteristics

**Table 11:** Baseline values of facility characteristics in the model correspond to the January 2011 time point.
Attribute	$f=$A	$f=$B	$f=$C
Waiting Time (mins)	91.00	42.50	20.71
Patient Contact Time (mins)	10.17	12.14	14.02
Outreach Activities $\textit{O}_{f,0}$	No	Yes	Yes
OOP (% of Women Paying)	17%	20%	28%
Staff Interpersonal Quality $\textit{IPQ}_{f,0}$	0.97	0.71	0.77
Drug Availability $D_{f,0}$	0.33	0.33	0.50
Staff Kindness $K_{f,0}$	0.64	0.51	0.91
Number of Beds	2.00	1.00	2.00
Number of Staff	2.00	2.00	3.00
Women of Reproductive Age $W_f$	501	903	462
Baseline Performance $\%\textit{FB}_{f,\textit{0}}$	13%	100%	84.2%

Appendix G: Changes in Facility Characteristics

**Table 12:** A comparison of simulation endline data across P4P and payment delay scenarios.
Facility	Category	Scenarios
		No P4P (1)	P4P & Payment Delays (2)	% Change (2-1)	P4P & No Payment Delays (3)	% Change (3-1)
		Endline	Endline	$\%\Delta_{(2)-(1)}$	Endline	$\%\Delta_{(3)-(1)}$
A	Kindness	63.85%	89.27%	39.7%	94.33%	47.6%
	Drug Availability	33.33%	96.13%	188.3%	100.00%	200.0%
	Out-of-pocket Payments	15.30%	16.38%	7.1%	9.95%	-35.0%
B	Kindness	51.33%	76.82%	49.7%	78.29%	52.6%
	Drug Availability	33.33%	74.72%	124.1%	76.15%	128.5%
	Out-of-pocket Payments	16.82%	21.01%	24.9%	13.36%	-20.6%
C	Kindness	90.71%	89.64%	-1.2%	92.98%	2.5%
	Drug Availability	50.00%	88.46%	76.9%	90.88%	81.8%
	Out-of-pocket Payments	23.77%	26.34%	10.8%	19.45%	-18.1%

Appendix H: Agent-Based Model Pseudo Code

This appendix provides essential pseudocode for the agent-based model implementation. Keywords are in UPPERCASE, indentation denotes scope, and // begins comments.

The pseudo-code is available here: https://www.jasss.org/28/4/7/AppendixH.pdf

Key Model Features:

Three agent types: Women (1,866), facilities (3), district manager (1)
Decision model: Logistic regression with behavioral modifiers for delivery location choice
P4P mechanism: 6-month performance periods, bonus payments based on facility-delivery rate improvement
Manager interventions: Quarterly visits, drug sharing, delay mitigation, strategy sharing
Validation: Calibrated to 24 months of empirical data, validated on remaining 12 months

Appendix I: Sensitivity Analysis Results

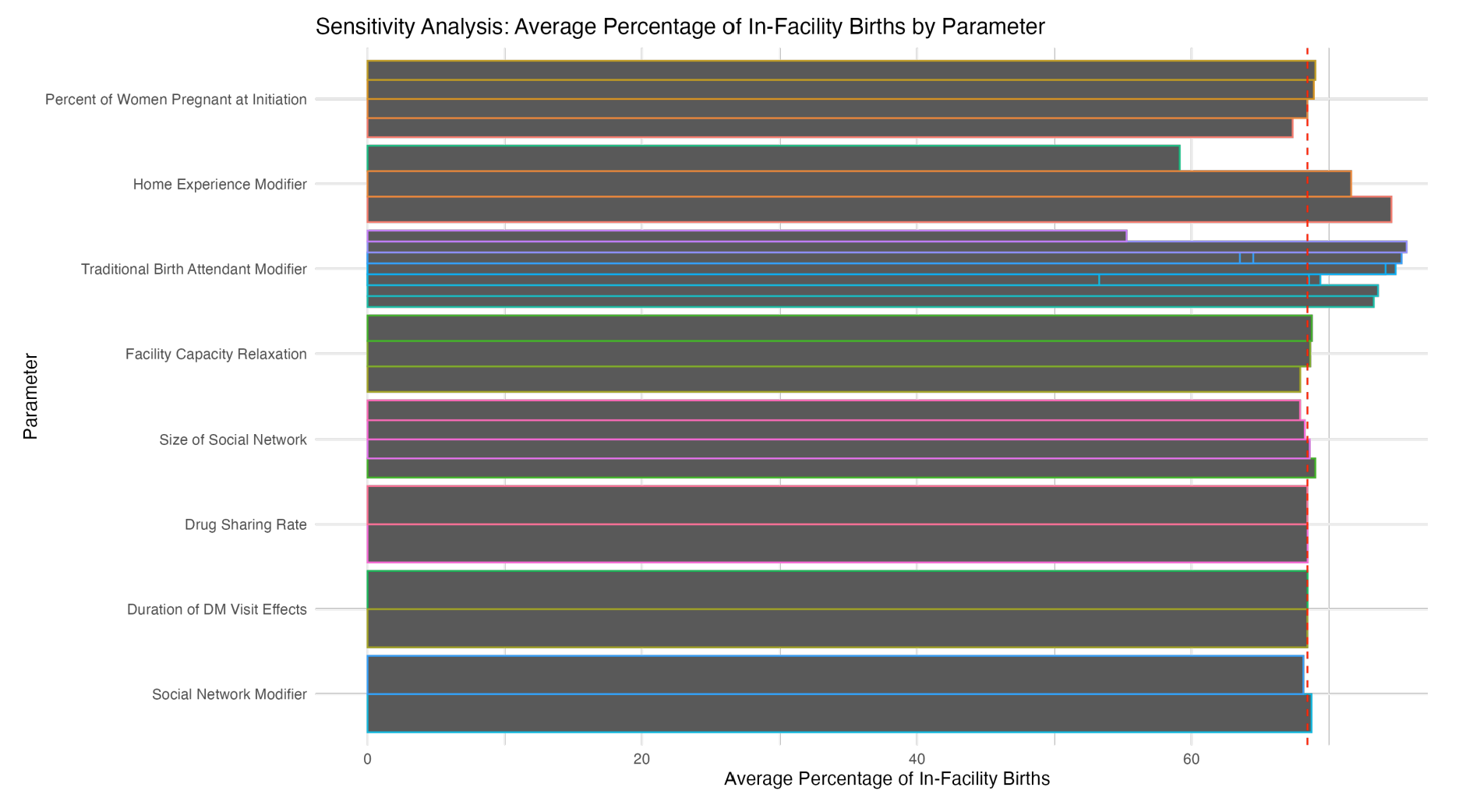
**Figure 10.** A visualization of the change in average average percentage of in-facility births at the system level for each value of the input parameter. The model results are highly sensitive to the values of parameters that vary widely from the red vertical line.

**Table 13:** Classification of Sensitivity Analysis Parameters.
Parameter	param_min_value	param_max_value	min_outcome_percent	max_outcome_percent	range	percent_change	sensitivity
Drug Sharing Rate	5.000	10.00	68.430	68.451	0.021	0.031	Low
Duration of DM Visit Effects	0.500	1.00	68.433	68.448	0.016	0.023	Low
Facility Capacity Relaxation	1.000	3.00	67.916	68.761	0.845	1.244	Low
Home Experience Modifier	0.000	0.05	59.132	74.562	15.430	26.094	Very High
Percent of Women Pregnant at Initiation	0.025	0.10	67.362	69.017	1.654	2.456	Low
Size of Social Network	3.000	6.00	67.901	69.012	1.111	1.637	Low
Social Network Modifier	0.300	0.35	68.143	68.738	0.594	0.872	Low
Traditional Birth Attendant Modifier	0.250	0.40	53.264	75.669	22.405	42.064	Very High

References

ALIBRAHIM, A., & Wu, S. (2018). An agent-based simulation model of patient choice of health care providers in accountable care organizations. Health Care Management Science, 21, 131–143. [doi:10.1007/s10729-016-9383-1]

ALIBRAHIM, A., & Wu, S. (2020). Modelling competition in health care markets as a complex adaptive system: An agent-based framework. Health Systems, 9(3), 212–225. [doi:10.1080/20476965.2019.1569480]

ALONGE, O., Lin, S., Igusa, T., & Peters, D. (2017). Improving health systems performance in low- and middle-income countries: A system dynamics model of the pay-for-performance initiative in Afghanistan. Health Policy and Planning, 32(10), 1417–1426. [doi:10.1093/heapol/czx122]

ANSELMI, L., Binyaruka, P., & Borghi, J. (2017). Understanding causal pathways within health systems policy evaluation through mediation analysis: An application to payment for performance (P4P) in Tanzania. Implementation Science, 12(1), 1–18. [doi:10.1186/s13012-016-0540-1]

BADHAM, J., Chattoe-Brown, E., Gilbert, N., Chalabi, Z., Kee, F., & Hunter, R. F. (2018). Developing agent-based models of complex health behaviour. Health & Place, 54, 170–177. [doi:10.1016/j.healthplace.2018.08.022]

BINYARUKA, P., & Borghi, J. (2017). Improving quality of care through payment for performance: Examining effects on the availability and stock-out of essential medical commodities in Tanzania. Tropical Medicine & International Health, 22(1), 92–102. [doi:10.1111/tmi.12809]

BINYARUKA, P., Foss, A., Alibrahim, A., Mziray, N., Cassidy, R. & Borghi, J. (2023). Supply-side factors influencing demand for facility-based delivery in Tanzania: A multilevel analysis. Health Economics, 13(1), 52. [doi:10.1186/s13561-023-00468-1]

BINYARUKA, P., Lohmann, J., & De Allegri, M. (2020). Evaluating performance-based financing in low-income and middle-income countries: The need to look beyond average effect. BMJ Global Health, 5(8), e003136. [doi:10.1136/bmjgh-2020-003136]

BINYARUKA, P., Patouillard, E., Powell-Jackson, T., Greco, G., Maestad, O., & Borghi, J. (2015). Effect of paying for performance on utilisation, quality, and user costs of health services in Tanzania: A controlled before and after study. PLoS One, 10(8), e0135013. [doi:10.1371/journal.pone.0135013]

BINYARUKA, P., Robberstad, B., Torsvik, G., & Borghi, J. (2018). Does payment for performance increase performance inequalities across health providers? A case study of Tanzania. Health Policy and Planning, 33(9), 1026–1036. [doi:10.1093/heapol/czy084]

BORGHI, J., Binyaruka, P., Mayumana, I., Lange, S., Somville, V., & Maestad, O. (2021). Long-term effects of payment for performance on maternal and child health outcomes: Evidence from Tanzania. BMJ Global Health, 6(12), e006409. [doi:10.1136/bmjgh-2021-006409]

BORGHI, J., & Chalabi, Z. (2017). Square peg in a round hole: Re-thinking our approach to evaluating health system strengthening in low-income and middle-income countries. BMJ Global Health, 2(3), e000406. [doi:10.1136/bmjgh-2017-000406]

BORGHI, J., Mayumana, I., Mashasi, I., Binyaruka, P., Patouillard, E., Njau, I., Maestad, O., Abdulla, S., & Mamdani, M. (2013). Protocol for the evaluation of a pay for performance programme in Pwani region in Tanzania: A controlled before and after study. Implementation Science, 8, 1–12. [doi:10.1186/1748-5908-8-80]

CASSIDY, R., Semwanga, A. R., Binyaruka, P., Blanchet, K., Singh, N. S., Maiba, J., & Borghi, J. (2025). Identifying the active ingredients in payment for performance programmes using system dynamics modelling. SSM-Health Systems, 4, 100040. [doi:10.1016/j.ssmhs.2024.100040]

CASSIDY, R., Singh, N. S., Schiratti, P.-R., Semwanga, A., Binyaruka, P., Sachingongu, N., Chama-Chiliba, C. M., Chalabi, Z., Borghi, J., & Blanchet, K. (2019). Mathematical modelling for health systems research: A systematic review of system dynamics and agent-based models. BMC Health Services Research, 19, 1–24. [doi:10.1186/s12913-019-4627-7]

CASSIDY, R., Tomoaia-Cotisel, A., Semwanga, A. R., Binyaruka, P., Chalabi, Z., Blanchet, K., Singh, N. S., Maiba, J., & Borghi, J. (2021). Understanding the maternal and child health system response to payment for performance in Tanzania using a causal loop diagram approach. Social Science & Medicine, 285, 114277. [doi:10.1016/j.socscimed.2021.114277]

CHAI and Ministry of Health. (2011). Pwani pay-for-performance pilot program design document [Design Document]. CHAI; Ministry of Health.

COLLINS, A., Koehler, M., & Lynch, C. (2024). Methods that support the validation of agent-based models: An overview and discussion. Journal of Artificial Societies and Social Simulation, 27(1), 11. [doi:10.18564/jasss.5258]

DANILACK, V. A., Nunes, A. P., & Phipps, M. G. (2015). Unexpected complications of low-risk pregnancies in the United States. American Journal of Obstetrics and Gynecology, 212(6), 809. [doi:10.1016/j.ajog.2015.03.038]

DELLICOUR, S., Aol, G., Ouma, P., Yan, N., Bigogo, G., Hamel, M. J., Burton, D. C., Oneko, M., Breiman, R. F., Slutsker, L., Feikin, D., Kariuki, S., Odhiambo, F., Calip, G., Stergachis, A., Laserson, K. F., ter Kuile, F. O., & Desa, M. (2016). Weekly miscarriage rates in a community-based prospective cohort study in rural western kenya. BMJ Open, 6(4), e011088. [doi:10.1136/bmjopen-2016-011088]

DIACONU, K., Falconer, J., Verbel, A., Fretheim, A., & Witter, S. (2021). Paying for performance to improve the delivery of health interventions in low- and middle-income countries. Cochrane Database of Systematic Reviews, 2021(5). [doi:10.1002/14651858.cd007899.pub3]

HAMMOND, R. A. (2015). Considerations and best practices in agent-based modeling to inform policy. Assessing the Use of Agent-Based Models for Tobacco Regulation.

HUG, L., Mishra, A., Lee, S., You, D., Moran, A., Strong, K. L., & Cao, B. (2020). A neglected tragedy - The global burden of stillbirths: Report of the UN inter-agency group for child mortality estimation, 2020.

JACKSON, E., & Glasier, A. (2011). Return of ovulation and menses in postpartum nonlactating women: A systematic review. Obstetrics & Gynecology, 117(3), 657–662. [doi:10.1097/aog.0b013e31820ce18c]

KOVACS, R. J., Powell-Jackson, T., Kristensen, S. R., Singh, N., & Borghi, J. (2020). How are pay-for-performance schemes in healthcare designed in low- and middle-income countries? Typology and systematic literature review. BMC Health Services Research, 20(1), 1–14. [doi:10.1186/s12913-020-05075-y]

LAWN, J. E., Blencowe, H., Waiswa, P., Amouzou, A., Mathers, C., Hogan, D., Flenady, V., Frøen, J. F., Qureshi, Z. U., Calderwood, C., Shiekh, S., Bianchi Jassir, F., You, D., McClure, E. M., Mathai, M., Cousens, S., & DipMathstata for The Lancet Ending Preventable Stillbirths Series study group with The Lancet Stillbirth Epidemiology investigator group. (2016). Stillbirths: Rates, risk factors, and acceleration towards 2030. The Lancet, 387(10018), 587–603. [doi:10.1136/archdischild-2016-310863.258]

MACAL, C. M., & North, M. J. (2005). Tutorial on agent-based modeling and simulation. Proceedings of the Winter Simulation Conference, 2005. [doi:10.1109/wsc.2005.1574234]

MAIBA, J., Binyaruka, P., Singh, N., Cassidy, R., Mziray, N., Foss, A., Mtei, G., & Borghi, J. (2022). Strategic purchasing through direct health facility financing mechanisms in Tanzania: Examining the purchaser-Provider relationship. 7th Global Symposium on Health Systems Research, Bogota, Colombia. [doi:10.3389/fpubh.2023.1260236]

MAYO Clinic. (2021). Pregnancy after miscarriage: Trying again. Available at: https://www.mayoclinic.org/healthy-lifestyle/getting-pregnant/in-depth/pregnancy-after-miscarriage/art-20044134

MAYUMANA, I., Borghi, J., Anselmi, L., Mamdani, M., & Lange, S. (2017). Effects of payment for performance on accountability mechanisms: Evidence from Pwani, Tanzania. Social Science & Medicine, 179, 61–73. [doi:10.1016/j.socscimed.2017.02.022]

MILLER, G., & Babiarz, K. S. (2014). Pay-for-performance incentives in low- and middle-income country health programs. In A. J. Culyer (Ed.), Encyclopedia of Health Economics (pp. 457–466). San Diego, CA: Elsevier. [doi:10.1016/b978-0-12-375678-7.00126-7]

MINISTRY of Health and Social Welfare. (2012). The Pwani Region Pay-for-Performance (P4P) pilot design document.

MZIRAY, N., Maiba, J., Binyaruka, P., Cassidy, R., Borghi, J., & Foss, A. (2022). Stakeholders’ engagement in interactive agent-Based model building to explore health system performance. 7th Global Symposium on Health Systems Research, Bogota, Colombia.

NASSAR, M. R., & Frank, M. J. (2016). Taming the beast: Extracting generalizable knowledge from computational models of cognition. Current Opinion in Behavioral Sciences, 11, 49–54. [doi:10.1016/j.cobeha.2016.04.003]

NATIONAL Bureau of Statistics. (2015). Fertility and nuptiality: 2012 population and housing census. Ministry of Finance, The United Republic of Tanzania.

NAVARRO, D. J. (2019). Between the devil and the deep blue sea: Tensions between scientific judgement and statistical model selection. Computational Brain & Behavior, 2(1), 28–34. [doi:10.1007/s42113-018-0019-z]

OGUNDEJI, Y. K., Jackson, C., Sheldon, T., Olubajo, O., & Ihebuzor, N. (2016). Pay for performance in Nigeria: The influence of context and implementation on results. Health Policy and Planning, 31(8), 955–963. [doi:10.1093/heapol/czw016]

PAUL, E., Bodson, O., & Ridde, V. (2021). What theories underpin performance-based financing? A scoping review. Journal of Health Organization and Management, 35(3), 344–381. [doi:10.1108/jhom-04-2020-0161]

RENMANS, D., Holvoet, N., Orach, C. G., & Criel, B. (2016). Opening the “black box” of performance-based financing in low-and lower middle-income countries: A review of the literature. Health Policy and Planning, 31(9), 1297–1309. [doi:10.1093/heapol/czw045]

ROBINSON, D. T., Brown, D. G., Parker, D. C., Schreinemachers, P., Janssen, M. A., Huigen, M., Wittmer, H., Gotts, N., Promburom, P., Irwin, E., Berger, T., Gatzweiler, F., & Barnaud, C. (2007). Comparison of empirical methods for building agent-based models in land use science. Journal of Land Use Science, 2(1), 31–55. [doi:10.1080/17474230701201349]

SEMWANGA, A. R., Nakubulwa, S., & Adam, T. (2016). Applying a system dynamics modelling approach to explore policy options for improving neonatal health in Uganda. Health Research Policy and Systems, 14(1), 1–17. [doi:10.1186/s12961-016-0101-8]

SHRIME, M. G., Iverson, K. R., Yorlets, R., Roder-DeWan, S., Gage, A. D., Leslie, H., & others. (2019). Predicted effect of regionalised delivery care on neonatal mortality, utilisation, financial risk, and patient utility in Malawi: An agent-based modelling analysis. The Lancet Global Health, 7(7), e932–e939. [doi:10.1016/s2214-109x(19)30170-6]

SINGH, N. S., Kovacs, R. J., Cassidy, R., Kristensen, S. R., Borghi, J., & Brown, G. W. (2021). A realist review to assess for whom, under what conditions and how pay for performance programmes work in low- and middle-income countries. Social Science & Medicine, 270, 113624. [doi:10.1016/j.socscimed.2020.113624]

SMITH, P. C., Stepan, A., Valdmanis, V., & Verheyen, P. (1997). Principal-agent problems in health care systems: An international perspective. Health Policy, 41(1), 37–60. [doi:10.1016/s0168-8510(97)00012-2]

UNDP. (2024). Sustainable Development Goals (SDGs). Available at: https://www.undp.org/sustainable-development-goals

UNICEF. (2024). Maternal and Child Health - UNICEF United Republic of Tanzania. Available at: https://www.unicef.org/tanzania/what-we-do/health

WITTER, S., Fretheim, A., Kessy, F. L., & Lindahl, A. K. (2012). Paying for performance to improve the delivery of health interventions in low- and middle-income countries. Cochrane Database of Systematic Reviews, 2012(2012), CD007899. [doi:10.1002/14651858.cd007899]

Case	\(\textit{Bonus}_{f,\textit{PP}}\)	Changes to Facility Attributes at \(t+1\)
1	0	Incentives for \(\text{TBA}_{f,t+1} = \text{TBA}_{f,0}\) Outreach \(\text{O}_{f,t+1} = \text{O}_{f,0}\) Staff \(\text{IPQ}_{f,t+1} = \text{IPQ}_{f,0}\) Kindness \(K_{f,t+1} = K_{f,0}\) Drugs \(D_{f,t+1} = D_{f,0}\) Gifts \(G_{f,t+1} = 0\%\cdot G_{f,0}\) \(\text{OOP}_{f,t+1} = \text{OOP}_{f,0}\)
2	0.5	Incentives for \(\text{TBA}_{f,t+1} = 1\) Outreach \(\text{O}_{f,t+1} = \max(\text{O}_{f,t}, \text{random with 50% chance of }1)\) Staff \(\text{IPQ}_{f,t+1} = \max(\text{IPQ}_{f,t}, 0.8)\) Kindness \(K_{f,t+1} = \max(K_{f,t}, 0.8)\) Drugs \(D_{f,t+1} = \max(D_{f,t}, 0.8)\) Gifts \(G_{f,t+1} = 0\%\cdot \max(G_{f,t}, \text{ 50% chance of }1)\) \(\text{OOP}_{f,t+1} = \text{OOP}_{f,t} \cdot 0.9\)
3	1	Incentives for \(\text{TBA}_{f,t+1} = 1\) Outreach \(\text{O}_{f,t+1} = 1\) Staff \(\text{IPQ}_{f,t+1} = 1\) Kindness \(K_{f,t+1} = \max(K_{f,t}, 0.9)\) Drugs \(D_{f,t+1} = 1\) Gifts \(G_{f,t+1} = 1\) \(\text{OOP}_{f,t+1} = \text{OOP}_{f,t} \cdot 0.8\)
4	Delay Effects	Incentives for \(\text{TBA}_{f,t+1} = 0\) Outreach \(\text{O}_{f,t+1} = 0\) Staff \(\text{IPQ}_{f,t+1} = \text{IPQ}_{f,t-1} - 0.1 \;\; \text{while } \text{IPQ}_{f,t} \geq 0.6\) Kindness \(K_{f,t+1} = K_{f,t-1} - 0.1 \;\; \text{while } K_{f,t} \geq 0.5\) Drugs \(D_{f,t+1} = D_{f,t-1} - 0.1 \;\; \text{while } D_{f,t} \geq D_{f,0}\) Gifts \(G_{f,t+1} = 0\) \(\text{OOP}_{f,t+1} = \text{OOP}_{f,t} + 0.1 \;\; \text{while } \text{OOP}_{f,t} \leq 1\)

Parameter	Parameter Name	Description
Time
\(t\)	Simulation Month	Current simulation month, which ranges between 1 and 36
PP	Performance Period	A time segment of 6 months, at the end of which bonus evaluations are conducted.
Facility Agent Parameters
\(\textit{Bonus}_{f,PP}\)	Facility Bonus	The bonus allocated to a specific facility \(f\) at the end of a performance period \(PP\).
Sharing%	Sharing Percentage	A calibration parameter that helps to facilitate drug sharing between facilities.
\(\textit{O}_{f,t}\)	Outreach Activities	Status of outreach activities of a facility at initial time point.
\(\textit{OOP}_{f,t}\)	Out-of-Pocket Costs	Initial out-of-pocket costs at a facility.
\(\textit{TBA}_{f,t}\)	TBA Incentives	Traditional birth attendant incentives at a facility during month \(t\).
\(G_{f,t}\)	Gifts to Mothers	Status of gift provision to mothers at a facility during month \(t\).
\(\textit{IPQ}_{f,t}\)	Staff Interpersonal Quality	Staff interpersonal quality of a facility during month \(t\).
\(D_{f,t}\)	Drug Availability	Drug availability at a facility during month \(t\).
\(K_{f,t}\)	Staff Kindness	Staff kindness at a facility during month \(t\).
\(W_f\)	Women of Reproductive Age	Number of women of reproductive age catered by the facility.
\(\%\textit{FB}_{f,t}\)	Facility Coverage Performance	Percent of facility-based deliveries at the facility during month \(t\).
\(DT\)	Donor Threshold	Criterion for a facility to share drugs.
\(RT\%\)	Recipient Threshold	Criterion for a facility to be eligible to receive shared drugs.
Woman Agent Parameters
\(p_{\textit{pregnant}}\)	Pregnancy Probability	Monthly probability that a woman gets pregnant when not initiated as pregnant.
\(p_{\textit{PregnantInitiation}}\)	Pregnancy Initiation Probability	Probability that a woman agent is assigned a random stage of pregnancy upon generation.
VisitDuration	Visit Duration	Duration in days of an M agent visit.
\(p_{\textit{complication}}\)	Delivery Complication Probability	Probability of a complication occurring during childbirth.
\(p_{\textit{lostpregnancy}}\)	Lost Pregnancy Probability	Probability of a pregnancy being lost due to miscarriage or stillbirth before labor.
\(\|W_f\|\)	Number of Woman Agents per Facility	The number of woman agents assigned to each facility, representing the number of women of reproductive age in the catchment area of a facility.
\(\%\textit{WRA}\)	Proportion of Women of Reproductive Age	The proportion of women of reproductive age in the catchment area of a facility.
\(\overline{TT}_{f}\)	Average Travel Time to Facility	Average travel time for a woman agent to reach her assigned facility, based on community survey responses.
\(TT_{\textit{w-to-f}}\)	Travel Time for Individual Woman Agent	The estimated travel time for a particular woman agent to reach her assigned facility. This is sampled as a uniform distribution around the average travel time \(\overline{TT}_{f} \pm 50\%\).
\(p_{w@f}\)	Delivery Decision Probability	Final probability that a woman \(w\) delivers at a facility \(f\).
\(n_{social}\)	Woman's Social Network	The number of woman agents in her social network.
\(p_{\textit{facility delivery}}\)	Probability of Facility Delivery	Calculated from a logistic model, which is then modified for own and network facility experiences.
\(\textit{HomeExp}_w\)	Home Experience	Experience of a woman from delivery at home.
\(p_{\textit{+iveFacExp}}\)	Positive Facility Experience Probability	Probability of a woman having a positive experience at a facility.
\(\textit{FacilityExp}_w\)	Facility Experience	Experience of a woman from delivery at a facility.
\(\textit{influences}_w\)	Social Network Influences	Influences on a woman from her social network.