© Copyright JASSS


Barry G. Lawson and Steve Park (2000)
Asynchronous Time Evolution in an Artificial Society Mode
Journal of Artificial Societies and Social Simulation
vol. 3, no. 1,
<https://www.jasss.org/3/1/2.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 6-Dec-99
Accepted: 13-Jan-00
Published: 31-Jan-00
 Abstract
Abstract
-
"Artificial society" refers to an agent-based simulation model used to
discover global social structures and collective behavior produced by simple
local rules and interaction mechanisms. In most artificial society
discrete-event simulation models, synchronous time evolution is used to drive
the actions and interactions of the landscape and agents. Although for some
applications synchronous time evolution is the correct modeling approach,
other applications are better suited for asynchronous time evolution. In this
paper we demonstrate that very different behavior can be observed in a
typical artificial society model if agent events occur asynchronously. Using
an adaptation of the artificial society model defined by Epstein and Axtell,
we describe the implementation of asynchronous time evolution in a
discrete-event simulation model. With output from this model, we show that
the use of asynchronous time evolution can eliminate potential simulation
artifacts produced using synchronous time evolution. Since the use
of discrete-event simulation can produce an associated loss in computational
performance, we also discuss means of improving the performance of the
artificial society simulation model. We provide results demonstrating that
acceptable computational performance for asynchronous time evolution can be
achieved using an appropriate event list implementation.
- Keywords:
-
Artificial society, discrete-event simulation, synchronous time evolution,
simulation artifacts, asynchronous time evolution, next-event simulation, event
list processing
- 1.1
- We use the term "artificial society" to describe an agent-based
discrete-event simulation model used to study social processes as they evolve
on a landscape. Among these processes are agent interaction with the
landscape, population dynamics, economic, cultural and disease interactions,
and combat. The underlying motivation is to define local rules and
interaction mechanisms in an attempt to discover the emergence of
global social structures and collective behavior. An artificial
society model is a "computational laboratory" in which the evolution of
social processes can be systematically examined.
- 1.2
- Epstein and Axtell (1996) define a representative
artificial society model containing comprehensive rules that simulate many
social processes. The authors' artificial society is a model rich with
research topics of interest and provides an important basis for social science
research via computer simulation. Our work was initially motivated by a
careful examination of the results presented by Epstein and Axtell and our
attempt to reproduce those results. We were particularly motivated by our
inability to reproduce the results Epstein and Axtell obtained when agent
movement and reproduction are combined, leading us to consider an alternative
modeling approach. Consistent with the request for interdisciplinary
coordination by Müller et. al. (1998), in this
paper we offer an evaluation of, and suggestions for improvements to, the
simulation techniques used in typical artificial society discrete-event
simulation models.
- 1.3
- Generally, artificial society models employ simple synchronous time evolution,
i.e., all agent events on the landscape are synchronized to a simulation clock
that evolves deterministically at a fixed rate. An alternative approach is to
permit each type of event to occur randomly at its own characteristic rate; in
this way, time evolves asynchronously. While we agree that synchronous
behavior is correct for some applications, such as seasonally motivated
movement, many other applications are modeled more accurately using
asynchronous time evolution. For such asynchronous applications, forcing
events to occur synchronously is unnatural and can produce simulation
artifacts. In addition, forced synchronous time evolution produces an
ambiguity in the order in which events should occur. Because all events occur
randomly at their own characteristic rates, the use of asynchronous time
evolution removes any such ambiguity.
- 1.4
- In this paper, we demonstrate that very different behavior can be observed in
a typical artificial society discrete-event simulation model if agent events
occur asynchronously rather than synchronously. For the results presented, we
use a variation of the artificial society model from Epstein and Axtell, with
only resource growback, agent movement and agent reproduction. The states and
attributes for the landscape cells and agents are real-valued. This variation
of Epstein and Axtell's model provides functionality sufficient to observe
behavior of interest yet remains simple enough to emphasize the difference
between synchronous and asynchronous time evolution. We show that the
use of synchronous time evolution can introduce simulation artifacts and
produce output that is very different from the output obtained using
asynchronous time evolution.
- 1.5
- Asynchronous time evolution in the artificial society model is implemented
using a next-event simulation approach1. For large models, the handling of the
associated event list can incur a substantial loss in computational
performance compared to a simple synchronous time evolution implementation.
However, we discuss means of improving the performance using appropriate data
structures and algorithms for the event list and we provide results
demonstrating that acceptable performance can be achieved. These results
confirm that an asynchronous time evolution implementation is an attractive
approach for artificial society discrete-event simulation models.
- 1.6
- The following is an outline of the remainder of this paper. In Section 2 we
briefly describe the artificial society model used in this paper, specifically
relating our model to the model defined by Epstein and Axtell. In Section 3
we discuss asynchronous time evolution and the corresponding next-event
simulation implementation. In Section 4 we provide results demonstrating the
different results possible when using asynchronous versus synchronous time
evolution. In Section 5 we discuss means of improving the computational
performance of a next-event artificial society simulation model and provide
supporting results. In Section 6 we present conclusions and suggest areas of
future study. In the Appendix we provide definitions of the random variable
models referenced in this paper.
 Model Formulation
Model Formulation
- 2.1
- Since our goal is to promote an alternative approach for artificial society
discrete-event simulation models, not to develop fundamentally new
models, our work is based on an adaptation of the extensive artificial society
model presented by Epstein and Axtell (1996). To
demonstrate that different output can be obtained using asynchronous versus
synchronous time evolution in an artificial society model, we balance
functionality with model complexity by including only a subset of the rules
defined by Epstein and Axtell. Our model can be easily extended to include
additional rules.
- 2.2
- For brevity, we omit a complete description of our artificial society model.
Except for the descriptions to follow, the rules used in our implementation
are the same as those defined by Epstein and Axtell. A comprehensive
description of the artificial society discrete-event simulation model used to
obtain the results in this paper is located at
State and Attribute Notations
- 2.3
- In our artificial society model, both the landscape cells and agents are
characterized by dynamic states, which change with time, and static
attributes, fixed for the lifetime of the model. In the notation to
follow, we adopt the convention of using uppercase letters to represent
cardinality parameters, lowercase letters to represent dynamic states, and
lowercase Greek symbols to represent static attributes.
We denote the model attributes as
| T: |
the maximum simulated time for the model; |
| X, Y: |
the vertical and horizontal landscape dimensions
respectively |
and the model variables as
| t: |
time (0 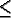 t
t 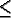 T);
T); |
| A(t): |
the number of agents on the landscape at time
t. |
- 2.4
- When necessary, we use the subscript a = 0, 1,
 , A(t) - 1 to distinguish agents.
, A(t) - 1 to distinguish agents.
- 2.5
- Define
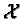 = {0, 1,
= {0, 1, 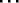 , X - 1} and
, X - 1} and 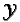 =
{0, 1,
=
{0, 1, 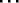 , Y - 1}. Then each
cell in the X
, Y - 1}. Then each
cell in the X  Y landscape is
distinguished by its (x, y) position with (x, y)
Y landscape is
distinguished by its (x, y) position with (x, y)
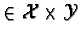 . Each (x, y) cell is
characterized by the attributes
. Each (x, y) cell is
characterized by the attributes
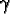 (x, y):
(x, y): |
the resource capacity at cell (x,
y); |
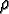 (x, y):
(x, y): |
the resource growback rate at cell (x,
y) |
and the state variables
| r(x, y, t): |
the level of resource at cell (x,
y) at time t; |
| d(x, y): |
the most recent time of resource depletion at cell
(x, y); |
| o(x, y, t): |
the occupancy status of cell (x, y) at
time t. |
- 2.6
- We define the real-valued resource capacity at an (x, y)
landscape cell by the equation
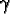
(
x,
y) =
f(x -
X/4,
y -
Y/4
) +
f(x - 3
X/4,
y - 3
Y/4
)
where
f(
x,
y) =
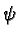
exp
(-(
x /
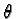 x
x)
2
- (
y /
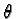 y
y)
2
)
with 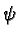 = 4.0,
= 4.0,
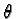 x = 0.3X and
x = 0.3X and
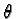 y = 0.3Y.
Although integer-valued but not otherwise explicitly defined, the resource
capacity used by Epstein and Axtell appears to be consistent with this
equation.
y = 0.3Y.
Although integer-valued but not otherwise explicitly defined, the resource
capacity used by Epstein and Axtell appears to be consistent with this
equation.
- 2.7
- Each agent is characterized by the attributes
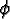 : : |
the field of view (FOV) attribute; |
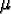 : : |
the metabolic rate of resource consumption; |
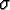 : : |
sex (male or female); |
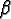 : : |
the time of birth; |
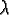 : : |
lifespan; |
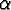 : : |
the age when reproductive capability begins (puberty);
|
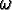 : : |
the age when reproductive capability ends (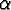 < < 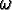 ); ); |
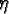 : : |
the gestation period (for females) |
and the state variables
| w(t): |
the amount of resource wealth (holdings) at time
t; |
| (x, y): |
the landscape cell occupied by the agent; |
| m(t): |
pointer to the current mate (if any). |
Behavioral Rule Modifications
- 2.8
- In our artificial society model, only the behavioral rules for resource
growback, agent movement and agent reproduction are included. Resource
growback and agent movement remain as defined by Epstein and Axtell. We have
modified the agent reproduction rule to be more realistic, incorporating a
gestation period 2. The criteria
for agent fertility remains the same, with the addition that for an agent
a to be fertile at time t,
ma(t) must be undefined. The reproduction
rule for a fertile agent is then defined as follows.

- Select one of the four nearest neighbor agents (if any) of
the opposite sex from the von Neumann neighborhood, shown in
Figure 2-1.
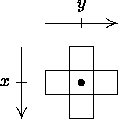
Figure 2-1:
The von Neumann neighborhood for an agent at (x, y)
|

- If the selected neighbor agent is fertile and if there is an unoccupied
cell (for the child) within the von Neumann neighborhood of either agent,
the neighbor agent is a candidate for mating.

- Repeat until the candidate agent with maximum wealth is found or the
nearest neighbor search is exhausted.
- 2.9
- If a mate is found (i.e., there is at least one candidate agent), the female
agent of the pair becomes pregnant. Throughout the gestation period, neither
the male nor the female agent can move or attempt to reproduce. The initial
endowment of wealth (resource) to the child, equal to the sum of half the
initial wealth of each parent, is computed at the time of conception.
Attribute inheritance rules for the child agent remain the same as in Epstein
and Axtell's model. At the time of birth, the unoccupied cell with maximum
resource from the union of the von Neumann neighborhoods of both parents is
selected for the child to occupy. If no such cell is available the child dies
at the time of birth3.
 Model Time Evolution
Model Time Evolution
- 3.1
- Although given little consideration in most artificial society discrete-event
simulation models, time evolution is an important part of our research. We
agree that synchronous time evolution may be appropriate in some artificial
society models if, for example, movement is seasonally motivated. However,
many other models are more accurately modeled using asynchronous time
evolution. In general, we claim that the use of asynchronous time evolution
yields a more realistic simulation model and minimizes simulation artifacts.
Synchronous Time Evolution
- 3.2
- Synchronous time evolution involves fixed-increment time steps, with time
conventionally denoted t = 0, 1, 2,
 , T. All events of interest must occur
precisely at these time steps. For instance, in the Epstein and Axtell model
all agents attempt to move simultaneously, once each time step. All agents
attempting to reproduce must also do so once each time step. For serial
program execution, this kind of parallel activity is not possible and so it is
necessary to randomize the order in which agents act at each time step.
Without this randomization, the agents will always act in the same order,
introducing a bias that can produce artifacts (Epstein and
Axtell, 1996).
, T. All events of interest must occur
precisely at these time steps. For instance, in the Epstein and Axtell model
all agents attempt to move simultaneously, once each time step. All agents
attempting to reproduce must also do so once each time step. For serial
program execution, this kind of parallel activity is not possible and so it is
necessary to randomize the order in which agents act at each time step.
Without this randomization, the agents will always act in the same order,
introducing a bias that can produce artifacts (Epstein and
Axtell, 1996).
- 3.3
- Given the model attribute T, which defines the number of simulated time
steps, the artificial society model evolves synchronously in time according to
the following pseudocode algorithm.
/* initialize the landscape */
/* initialize the agents */
t = 0;
while (t <= T) {
/* move and reproduce the agents */
/* update the landscape */
/* update the agent list */
/* randomize (shuffle) the agent list */
t++;
}
Algorithm 3-1:
Synchronous time evolution algorithm
- 3.4
- Note the ambiguity in the order of events inside the while loop. For example,
should the landscape be updated before or after the agents move?
Asynchronous Time Evolution
- 3.5
- Asynchronous time evolution allows each type of event to occur at random at its
own characteristic rate. In this way, individual agent movement events and
reproduction events occur at distinct times. That is, whereas the order of
agent actions must be specifically randomized at each time step in the
synchronous case, randomization is inherent in the asynchronous case. In
addition, in the asynchronous case there is no ambiguity in the order of
events.
- 3.6
- To facilitate asynchronous time evolution, we construct our artificial society
model using the next-event simulation approach. For a next-event
simulation model, we must clearly define the system state, the event
types, the simulation clock, and a set of algorithms for each event type that
define the state changes that occur when each type of event occurs (Park and Leemis, 1999).
- 3.7
- The simulation clock is the real-valued global time parameter t. As
defined in ¶2.3, at any time 0
 t
t  T, the state of the
system is defined by the following set of variables4.
T, the state of the
system is defined by the following set of variables4.
- A(t);
- o(x, y, t) and r(x, y,
t) and d(x, y) for all (x, y)
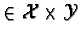 ;
;
- (x, y)a and
wa(t) and
ma(t) for all a = 0, 1,
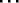 , A(t) - 1.
, A(t) - 1.
- 3.8
- Accordingly, there are four types of events that can change the state of the
system.
- Movement and corresponding resource consumption by agent a will
change (x, y)a and
wa(t) for the agent,
o(x, y, t) and
r(x, y, t) for the departed and newly occupied
landscape cells, and d(x, y) for the departed landscape
cell.
- The death of agent a will change A(t), and
o(x, y, t) and d(x, y) for
(x, y)a.
- A successful mating by an agent a with another agent a' will
change ma(t) and
ma'(t) for the agents.
- The birth of a new agent a" from parent agents a and
a' will change wa(t) and
wa'(t),
ma(t) and
ma'(t). If there is an unoccupied landscape
cell for the new agent to occupy, the birth will change A(t),
create (x, y)a" and
wa"(t), and change o(x,
y, t) and r(x, y, t) for
(x, y)a".
- 3.9
- Because there is a gestation period, the state of the system can change
when agents mate and when a new agent is born. For this reason, the
reproduction rule, as defined in ¶2.8, is
modeled by two distinct types of events. A mating event type initiates the
gestation period if the female agent becomes pregnant. Since a mating event is
an attempt to reproduce, the mating event does not guarantee pregnancy.
A birth event type signals the end of the gestation period when the new agent is
born (if possible). Both of these event types can change the state of the
system as described above.
Asynchronous Inter-Event Times
- 3.10
- For each event type, inter-event times are assumed to be iid Exponential
(1 /
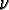 ) where
) where 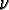 is the rate of occurrence of that event type. Equivalently, each event type is
modeled as a stationary Poisson process with rate
is the rate of occurrence of that event type. Equivalently, each event type is
modeled as a stationary Poisson process with rate 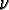 . The Poisson rate for the agent movement process is
. The Poisson rate for the agent movement process is 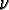 = 1.0
5. The mating event type can either be coupled with the
movement/consumption event type or modeled as a separate stationary Poisson
process. If the two event types are coupled, a mating event occurs for an agent
each time a movement/consumption event occurs for that agent. For all the
results in this paper, if the two event types are uncoupled, the Poisson rate
for agent mating is also
= 1.0
5. The mating event type can either be coupled with the
movement/consumption event type or modeled as a separate stationary Poisson
process. If the two event types are coupled, a mating event occurs for an agent
each time a movement/consumption event occurs for that agent. For all the
results in this paper, if the two event types are uncoupled, the Poisson rate
for agent mating is also 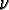 = 1.0.
= 1.0.
Asynchronous Resource Regrowth
- 3.11
- Resource regrowth is not considered an event, but rather an inherent part of the
other events. At t = 0 the resource level at each (x, y)
cell is the same as the resource capacity at that cell. As time evolves, the
cell resources are depleted only when an agent occupies a cell. While the cell
remains occupied, the resources continue to grow, but are continuously gathered
by the occupying agent; at the moment an agent departs, the cell has no
resources. As time evolves, the cell resources can then regrow up to the
resource capacity at the cell, provided the cell does not become occupied again.
Because the onset of regrowth is a direct result of the interaction of an agent
with a landscape cell, we include regrowth as part of the movement, mating, and
birth events.
- 3.12
- For each (x, y) landscape cell, as time evolves d(x,
y) is defined by the last time an agent departed that cell. At time
t > d(x, y), we can compute the current level of
resource at cell (x, y) by the equation
r(
x,
y,
t) = min
{ 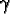
(
x,
y),
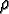
(
x,
y)(
t -
d(
x,
y))
}.
Asynchronous Time Evolution Algorithm
- 3.13
- Given T, the artificial society model evolves asynchronously in time
according to the following pseudocode algorithm. The algorithm presumes the
existence of a procedure GetNextEvent() that returns the event time and
event type of the next (most imminent) event.
/* initialize the landscape */
/* initialize the agents */
t = 0.0;
while (t <= T && A > 0) {
event = GetNextEvent();
t = event.time;
switch (event.type) {
case movement:
/* unoccupy the current cell */
/* select the (x,y) cell within the FOV with maximum resource */
/* occupy the selected (x,y) cell */
/* update the wealth of the agent */
/* schedule the next movement event */
case death:
A(t)--;
/* unoccupy the current cell */
case mating:
/* execute the mating algorithm */
if ( /* the mating is successful */ ) {
/* compute endowments and update the wealths of the parents */
/* update the mate pointers of each parent */
/* schedule a birth event */
/* cancel any parent agent events to occur before the birth */
}
case birth:
/* update the wealths of the parent agents */
/* schedule the next event occurrences for each parent agent */
if ( /* there is an (x,y) cell for the new agent */ ) {
A(t)++;
/* initialize the new agent */
/* occupy the selected (x,y) cell with the new agent */
/* update the wealth of the new agent */
/* schedule the next event occurrences for the new agent */
}
}
}
Algorithm 3-2:
Asynchronous time evolution algorithm
Synchronous Time Evolution Via Next-Event Simulation
- 3.14
- For the purpose of using one program to compare synchronous and asynchronous
time evolution, an attractive alternative to Algorithm
3-1 is to implement synchronous time evolution using next-event
simulation, similar to Algorithm 3-2. Except for the
timing results in Figure 5-2, this is
the approach we use for the results presented herein. The system state, event
types, simulation clock and set of algorithms described for the asynchronous
model remain the same. However, different event types no longer run as
Poisson processes with their own characteristic rates. Instead, we implement
the simultaneous occurrence of synchronous events at fixed time steps by
forcing agent events to occur at random within a small
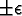 window at times t, t + 1,
window at times t, t + 1,  as shown in Figure 3-1 where bullets denote typical agent
events.
as shown in Figure 3-1 where bullets denote typical agent
events.

Figure 3-1:
Next-event simulation of synchronous events
|
- 3.15
- The movement/consumption and mating events for an agent occur at the same time.
Birth and/or death events, if they are to occur, also take place at this time.
 Results
Results
- 4.1
- The goal of the work by Epstein and Axtell (1996) was to
examine collective social behavior by using a discrete-event simulation model
based on simple rules and initial configurations. Our focus is on the
implementation of the simulation model rather than the development of new
artificial society models or the social interpretation of the results produced
by these models. With this motivation, we now provide results from the
artificial society model defined in Section 2 to
support our claim that, based on the choice of asynchronous or synchronous time
evolution, very different behavior can be observed in the resulting
output.
- 4.2
- The following figures were motivated by an attempt to replicate the results
Epstein and Axtell obtained when combining agent movement with reproduction.
Despite considerable experimentation, we were never able to reproduce the
results in Figure III-4 (Epstein and Axtell,
1996). Since Epstein and Axtell never reveal their model for the
landscape capacity (perhaps for brevity), there is some uncertainty in our
choice of
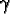 (x, y). However,
we conjecture that the oscillatory behavior shown in Figure III-4 is a
simulation artifact caused primarily by synchronous time evolution. Moreover,
this oscillatory behavior is very much dependent upon initial conditions which
to date we have been unable to determine.
(x, y). However,
we conjecture that the oscillatory behavior shown in Figure III-4 is a
simulation artifact caused primarily by synchronous time evolution. Moreover,
this oscillatory behavior is very much dependent upon initial conditions which
to date we have been unable to determine.
Mating Tied to Movement
- 4.3
- For Figure 4-1, we used an X
 Y = 50
Y = 50  50
landscape. The resource capacity at each cell is given by the equation in ¶ 2.6, and the resource growback rate for each
(x, y) cell is
50
landscape. The resource capacity at each cell is given by the equation in ¶ 2.6, and the resource growback rate for each
(x, y) cell is 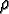 (x,
y) = 1. The landscape is initially occupied with A(0) = 400
randomly placed agents. The initial wealth of each agent is w(0) = 10.
The attributes for each agent are initialized as random variates according
to6
(x,
y) = 1. The landscape is initially occupied with A(0) = 400
randomly placed agents. The initial wealth of each agent is w(0) = 10.
The attributes for each agent are initialized as random variates according
to6
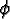 : : |
Equilikely(1, 6); |
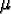 : : |
Uniform(1, 4); |
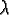 : : |
Uniform(60, 100); |
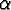 : : |
Uniform(12, 15); |
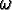 : : |
Uniform(40, 50) for females,
Uniform(50, 60) for males. |
The agents execute the movement/consumption and reproduction rules, with 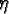 = 0. Reproduction and movement are coupled, i.e.,
the mating event type is not modeled as a separate process.
= 0. Reproduction and movement are coupled, i.e.,
the mating event type is not modeled as a separate process.
- 4.4
- Figure 4-1 depicts the time evolution of the agent
population for five different initial random number generator seeds with
T = 2500. In general, the output produced using synchronous time
evolution is the more oscillatory of the two curves, while asynchronous time
evolution produces the more stable darker curves. Epstein and Axtell propose
explanations of the large oscillatory behavior in terms of population dynamics.
Although in a few atypical cases asynchronous time evolution produced large
oscillations in the population7, we
believe that, in general, the large oscillations produced by Epstein and Axtell
are simulation artifacts produced by the use of synchronous time evolution.
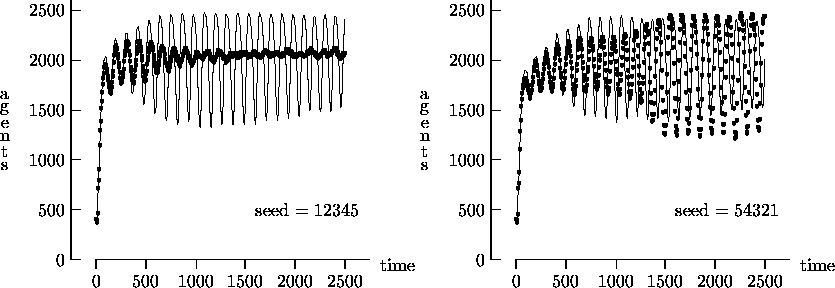
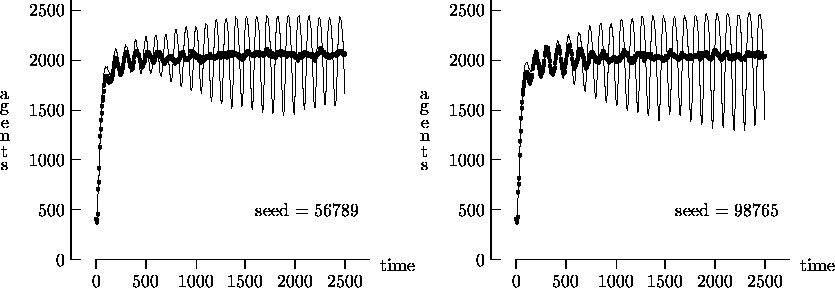
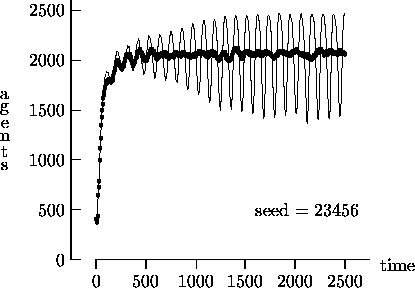
Figure 4-1:
Asynchronous vs. synchronous time evolution,
50  50 landscape
50 landscape
|
- 4.5
- Figure 4-2 depicts the time evolution of the agent
population for an X
 Y = 100
Y = 100
 100 landscape with an initial A(0) =
1600 randomly placed agents. The remaining state and attribute parameters are
the same as in Figure 4-1. Again, undamped
oscillatory behavior is present in the synchronous time evolution output but
not in the asynchronous time evolution output8. While some initial oscillation is present in
the asynchronous time evolution results, the amplitude is damped
considerably. Moreover, for all initial seeds, changes in the output are far
less dramatic in the asynchronous case. That is, unlike the synchronous
results, the asynchronous results are not sensitive to the random variate
sequence of movement and reproduction, as manifested by the choice of initial
seed.
100 landscape with an initial A(0) =
1600 randomly placed agents. The remaining state and attribute parameters are
the same as in Figure 4-1. Again, undamped
oscillatory behavior is present in the synchronous time evolution output but
not in the asynchronous time evolution output8. While some initial oscillation is present in
the asynchronous time evolution results, the amplitude is damped
considerably. Moreover, for all initial seeds, changes in the output are far
less dramatic in the asynchronous case. That is, unlike the synchronous
results, the asynchronous results are not sensitive to the random variate
sequence of movement and reproduction, as manifested by the choice of initial
seed.
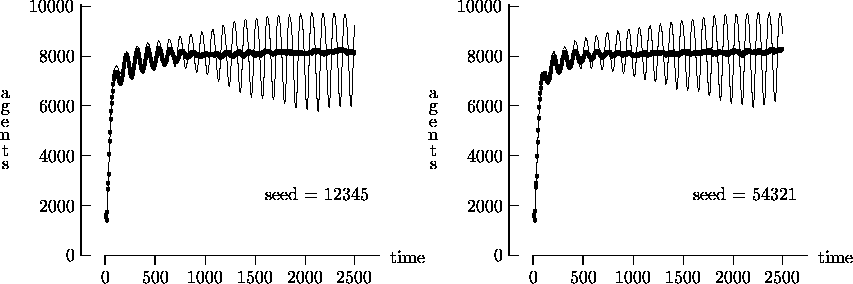
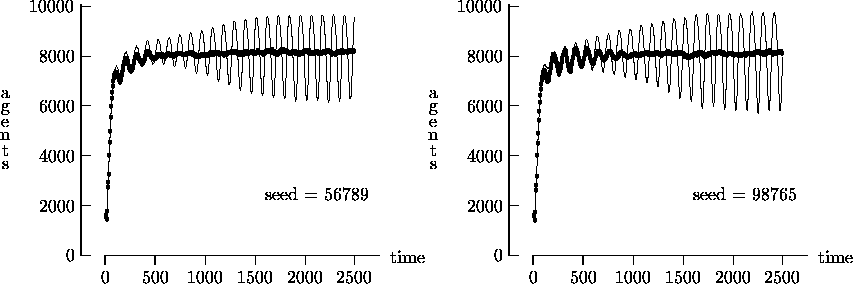
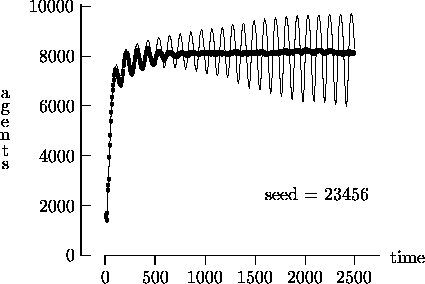
Figure 4-2:
Asynchronous vs. synchronous time evolution,
100  100 landscape
100 landscape
|
- 4.6
- We felt that T = 2500, as suggested by Epstein and Axtell, may not yield
a sufficient measure of the long-term time evolution of the agent population.
For this reason, Figure 4-3 depicts the time
evolution for the same initial conditions as Figure
4-1, but with T = 25,000. In these figures, the highly oscillatory
behavior of the synchronous time evolution output persists, while the
asynchronous time evolution produces a stable agent population in virtually
all cases.
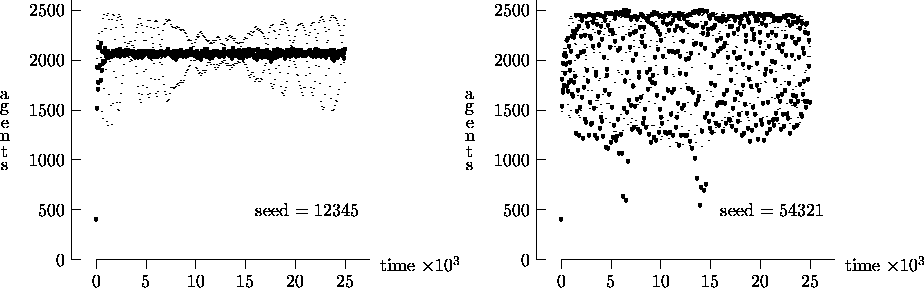
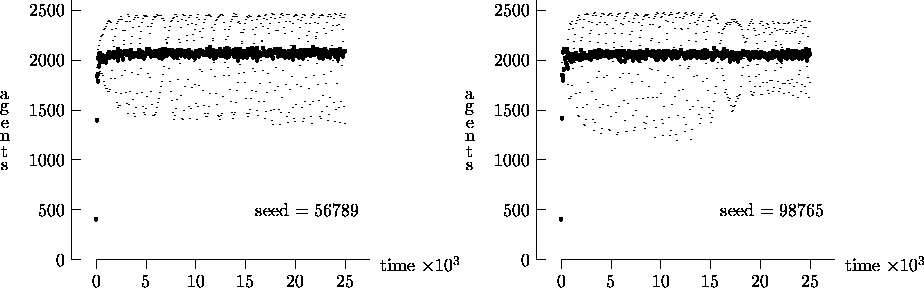
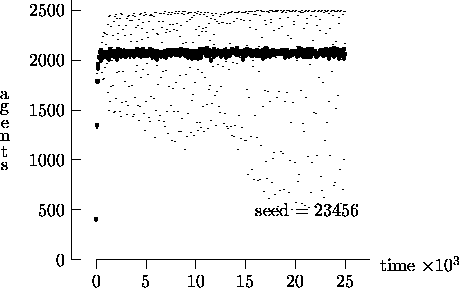
Figure 4-3:
Asynchronous vs. synchronous time evolution,
50  50 landscape
50 landscape
|
- 4.7
- Similarly, Figure 4-4 depicts the time evolution
for the same initial conditions as Figure 4-2, but
with T = 25,000. In this figure, we see the oscillatory behavior
persisting in a majority of the synchronous time evolution output. In contrast,
the asynchronous time evolution quickly produces a stable agent population. We
present the results in Figures 4-1, 4-2, 4-3 and 4-4 as strong evidence that very different behavior
can result from the choice of modeling time evolution as synchronous or
asynchronous.
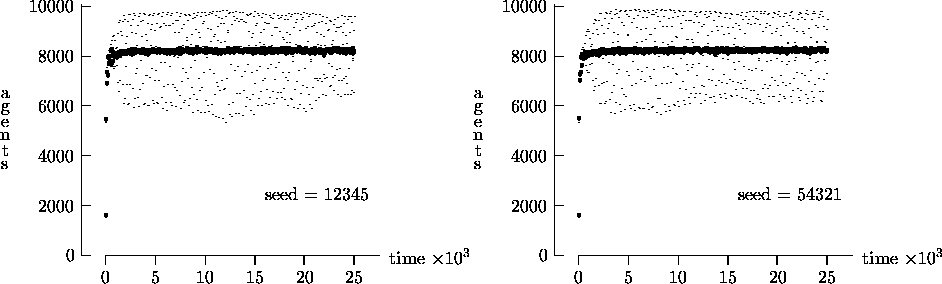
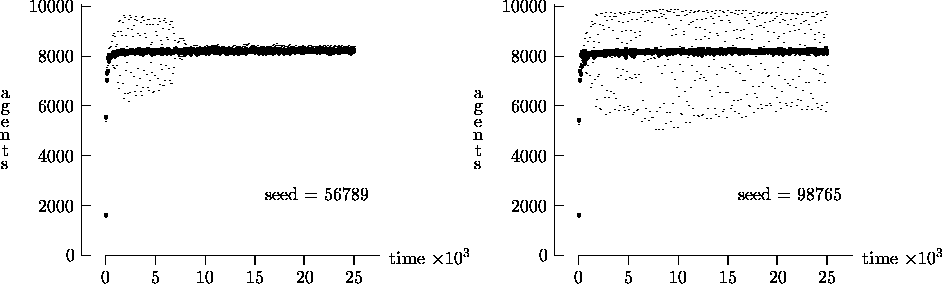
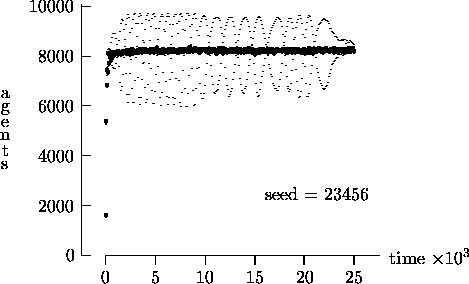
Figure 4-4:
Asynchronous vs. synchronous time evolution,
100  100 landscape
100 landscape
|
Mating Modeled Separately
- 4.8
- For the results in Figure 4-5, the mating event type
is no longer coupled with movement but is modeled as a separate Poisson process
as described in ¶ 3.10. Otherwise, everything is
the same as in Figure 4-1, with the exception that
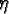 = 1. Again, the darker curves represent
output from the asynchronous time evolution model. We see that not only is the
amplitude of oscillations diminished dramatically using asynchronous time
evolution, but when compared with Figure 4-1 the mean
of the agent population is lowered as well. We reemphasize that we are not
promoting asynchronous time evolution as the best approach for all
artificial society models, but these results show that very different output
can result from modeling time evolution as synchronous or asynchronous.
= 1. Again, the darker curves represent
output from the asynchronous time evolution model. We see that not only is the
amplitude of oscillations diminished dramatically using asynchronous time
evolution, but when compared with Figure 4-1 the mean
of the agent population is lowered as well. We reemphasize that we are not
promoting asynchronous time evolution as the best approach for all
artificial society models, but these results show that very different output
can result from modeling time evolution as synchronous or asynchronous.
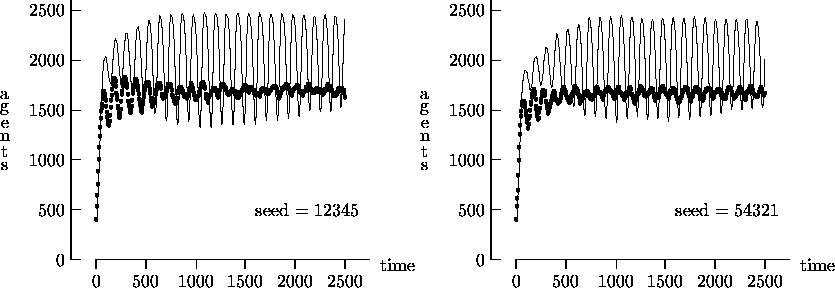
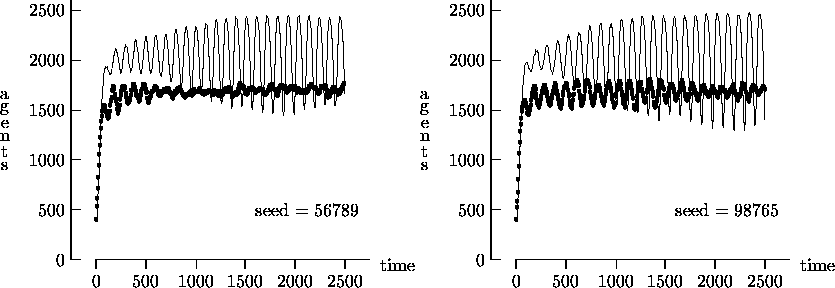
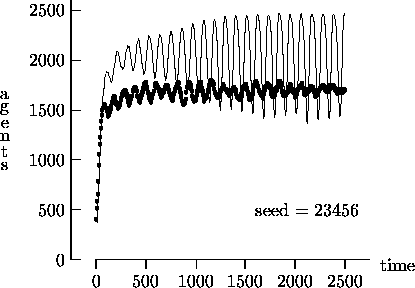
Figure 4-5:
Asynchronous vs. synchronous time evolution, mating uncoupled
|
 Computational Performance Issues
Computational Performance Issues
- 5.1
- Although asynchronous time evolution in an artificial society discrete-event
simulation model can reduce simulation artifacts and sensitivity to initial
conditions, computational performance can suffer significantly unless the
next-event approach is implemented properly. In this section we provide a
discussion of two possible algorithms and data structures for handling the
associated event list. We also demonstrate that acceptable computational
performance can be achieved by a judicious choice of the event list
implementation.
An Initial Event List Approach
- 5.2
- The asynchronous time evolution in the next-event simulation of the artificial
society model is driven by an event list. Each element in the event list
is associated with the future occurrence of a single event, where the type of
that event is exactly one of the four event types defined in ¶ 3.8. For the artificial society model, each
element in the event list contains the time that the associated event is to
occur, the type of event, and a pointer to the corresponding agent.
- 5.3
- Given that each agent can execute only one type of event at a time, we can
simplify the event list by including only the most imminent event for each
agent. In this way, there is one event per agent in the event list. Since
the type of the most imminent event for each agent can be determined from the
agent data structure, we no longer need the type of the event in the event
list. If we use a singly-linked list data structure to represent the event
list and sort the events by increasing time of occurrence, we obtain a sample
event list like the one shown in Figure 5-1.

Figure 5-1:
A typical event list for the artificial society model simulation
|
- 5.4
- Using this approach, the next event to occur in simulated time is always the
first element in the linked list. In this way, the GetNextEvent()
procedure from Algorithm 3-2 is implemented by simply
returning the head of the linked list. However, when a new event is inserted
into the event list, a linear search must be executed from the head of the list
to determine the appropriate insertion point. Similarly, any search for a
canceled event also requires a linear search. For a large number of events,
i.e., as the number of agents grows, such linear searches seriously degrade the
computational performance of the simulation.
- 5.5
- Figure 5-2 depicts sample execution
times9 for a standard synchronous
implementation of the artificial society model and an asynchronous
implementation using the previously described singly-linked list event list
approach. Each value displayed is the average time for five replications along
with the corresponding 95% confidence interval. The simulation was executed
with T = 500 for the increasing landscape sizes shown, each initially
populated with 16% agents10. The
initial values for agent states and attributes were the same as described in ¶ 4.3, except initial agent wealth was
w(0) = 25. Agents were not permitted to reproduce so that the number of
agents monotonically decreased for the duration of the simulation. As shown, as
the initial number of agents increases (with landscape size), the performance of
the sorted linked list implementation degrades quickly.
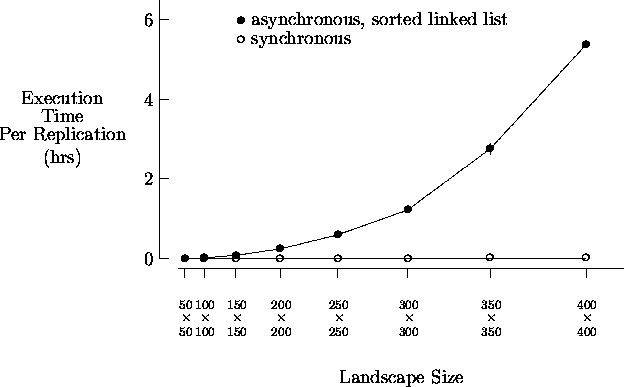
Figure 5-2: Sample execution times
|
An Improved Event List Approach
- 5.6
- To improve upon the sorted singly-linked list approach described in the previous
section, an alternate approach is needed. Of the possible event list algorithms
available, Henriksen's algorithm (1977, 1983) is a natural extension to the sorted linked
list approach. As shown in Figure 5-3, the
linked list is modified to be doubly-linked and includes "dummy" low and
high events at the respective ends. Similar to the previous approach,
retrieving the next event to occur in simulated time, always the second
element in the linked list, remains a simple operation.
- 5.7
- As depicted in Figure 5-3, a linear search is
avoided through the use of an auxiliary search array. Each element in the
search array contains an event time and a pointer to an event in the event list.
The search array is sorted by decreasing event time. A typical binary
search of the search array, a variation on Henriksen's approach, is used to find
the smallest time in the search array greater than the event time sought.
Beginning with the event pointed to by the selected search array element, a
linear search of the event list in descending order ensues until the desired
event time is found. During the binary search, Henriksen's "pull" technique
(1983) is used to keep the search array pointers
evenly distributed throughout the event list. The end of the search array is
maintained, and the size of the array is increased if necessary11.
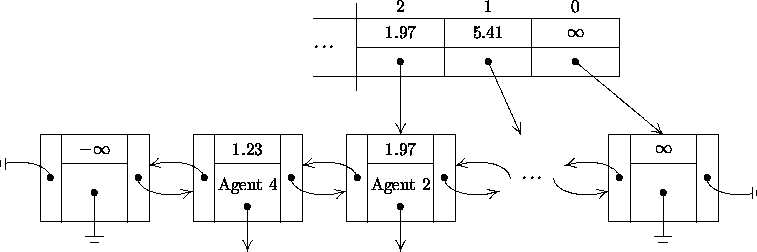
Figure 5-3:
The typical event list improved with search array
|
- 5.8
- Figure 5-4 depicts sample execution times
for an asynchronous implementation of the artificial society model using the
sorted linked list approach and the modified Henriksen's approach. Again, each
value shown is the average time for five replications along with the
corresponding 95% confidence interval. The simulation was executed with
T = 500 for the increasing landscape sizes shown, each initially
populated with 16% agents. As shown, the data structure and algorithm
modifications used in the modified Henriksen's approach yield execution times
comparable to those of the standard synchronous implementation given in Figure 5-2. Also shown are the times
obtained using the modified Henriksen's approach with agents able to reproduce.
Although the number of agents is no longer monotonically decreasing (in time) in
this case, acceptable performance is still achieved. These results show that
when implemented properly, the loss in computational performance resulting from
the use of asynchronous time evolution is minimal in a typical artificial
society discrete-event simulation.
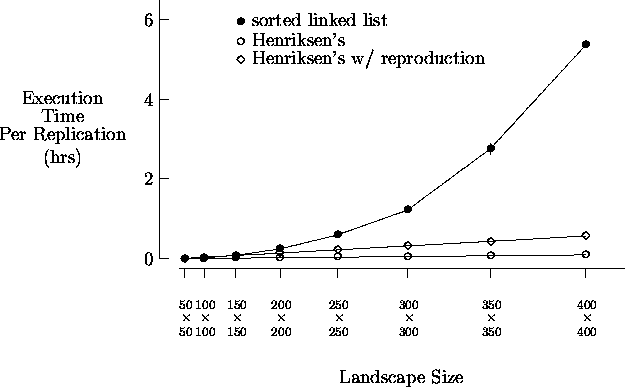
Figure 5-4:
Sample execution times
|
 Conclusions and Future Work
Conclusions and Future Work
- 6.1
- For applications involving natural asynchronous behavior, time evolution in an
artificial society discrete-event simulation model is more appropriately modeled
asynchronously rather than with the typical synchronous approach. In a typical
artificial society model adapted from Epstein and Axtell, asynchronous time
evolution produces output that is very different from output obtained using
synchronous time evolution. Specifically, the use of asynchronous time
evolution reduces simulation artifacts and sensitivity to initial conditions.
- 6.2
- Asynchronous time evolution is implemented using a next-event simulation
approach. If implemented poorly, a next-event artificial society simulation
model can suffer dramatically in terms of execution time. However, through
the use of proper event list data structures and algorithms, execution times
are comparable to those of a typical synchronous time implementation.
- 6.3
- The results in this paper suggest that when judiciously implemented,
asynchronous time evolution in an artificial society discrete-event simulation
model is an attractive alternative to synchronous time evolution in terms of
both the quality of the resulting output and computational performance. Future
work involves the systematic study of both standard and novel event list data
structures and algorithms on a more comprehensive artificial society model. We
also plan to investigate various approaches for executing the artificial society
simulation in parallel.
 Appendix: Random Variable Models
Appendix: Random Variable Models
The following material was taken directly from Park and Leemis (1999). A random variate is an algorithmically generated
realization of a random variable. The purpose of this appendix is to
provide definitions of the random variable models used to generate the
Uniform, Exponential and Equilikely random variates from ¶ 3.5, 3.10 and
4.312.
Uniform
The continuous random variable X is Uniform(a, b) if
and only if
- the real-valued parameters a, b satisfy a <
b
- the possible values of X are
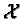 = { x
| a < x < b }
= { x
| a < x < b }
- the probability density function of X is
as illustrated
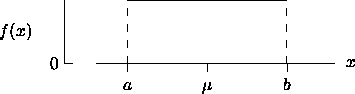
- the mean of X is
- the standard deviation of X is
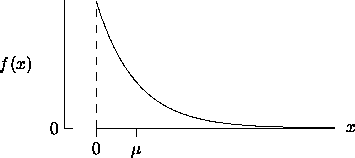
Exponential
The continuous random variable X is Exponential(
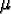 ) if and only if
) if and only if
Equilikely
The discrete random variable X is Equilikely(a, b)
if and only if
 Notes
Notes
-
- 1
For means of comparing asynchronous with synchronous time evolution, the
next-event implementation is easily modifiable to simulate synchronous time
evolution.
2
If the gestation period is 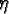 = 0, the
behavior of agents under our reproduction rule is the same as if the gestation
period was omitted from the rule.
= 0, the
behavior of agents under our reproduction rule is the same as if the gestation
period was omitted from the rule.
3
If 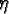 > 0, during the gestation period other
agents may occupy all the cells adjacent to the parents. Consequently,
at the time of birth a cell may not be available for the child to occupy.
> 0, during the gestation period other
agents may occupy all the cells adjacent to the parents. Consequently,
at the time of birth a cell may not be available for the child to occupy.
4
For convenience, the state description includes some variables that could be
determined from other variables. For instance, A(t) can be
determined by summing o(x, y, t) for all (x,
y) 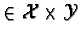 . Accordingly, the state
description is not minimal.
. Accordingly, the state
description is not minimal.
5
It is common to assume that a stochastic process which occurs "at random" is
a stationary Poisson process. The Poisson rate 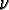 = 1.0 corresponds to the fixed-increment time step rate of the
synchronous approach. Systematically increasing
= 1.0 corresponds to the fixed-increment time step rate of the
synchronous approach. Systematically increasing 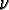 produces time evolutions similar to those presented in Section 4 but with lower population means. We also
experimented with inter-event times as Uniform, Erlang and
Normal random variables, each with a mean of 1.0 (the Normal was
truncated to positive values). These other distributions for the inter-event
times produce results similar to the stationary Poisson process results.
produces time evolutions similar to those presented in Section 4 but with lower population means. We also
experimented with inter-event times as Uniform, Erlang and
Normal random variables, each with a mean of 1.0 (the Normal was
truncated to positive values). These other distributions for the inter-event
times produce results similar to the stationary Poisson process results.
6
An Equilikely random variate is the discrete analog of a continuous
Uniform random variate (Park and Leemis, 1999).
7
The oscillatory behavior associated with the initial seed 54321 never
diminished. Instead, the population swings eventually led to termination at
approximately t = 45,000. We consider this atypical case an outlier
since we were able to produce similar results only four times using 100
different initial seeds.
8
Unlike the 50  50 landscape results,
asynchronous time evolution produced no atypical behavior in any of the
results using 100 different initial seeds on a 100
50 landscape results,
asynchronous time evolution produced no atypical behavior in any of the
results using 100 different initial seeds on a 100  100 landscape. To date we have not performed a more
systematic study of this atypical behavior in either the 50
100 landscape. To date we have not performed a more
systematic study of this atypical behavior in either the 50  50 or 100
50 or 100  100 landscape
case.
100 landscape
case.
9
All timing results were obtained using a dedicated Pentium II 350 MHz processor
with 128 MB of RAM.
10
The effect of landscape size on execution time is negligible. Nearly
identical timings were obtained when the landscape size was increased but the
initial number of agents remained constant.
11
We initially allocate a dynamic search array of size 1024. The end of the
search array is determined by the number of valid entries in the array. When
necessary, the size of the search array is systematically doubled.
12
In the definitions to follow, the use of 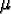 to
represent the mean and
to
represent the mean and 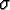 to represent the standard deviation
is consistent with conventional statistical notation and is not to be confused
with the
to represent the standard deviation
is consistent with conventional statistical notation and is not to be confused
with the 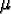 and
and 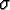 notations
from ¶ 2.7.
notations
from ¶ 2.7.
 References
References
-
- EPSTEIN,
Joshua M. and Robert Axtell. 1996.
Growing Artificial Societies.
Brookings Institution Press, Washington, D.C.
- HENRIKSEN,
J. O. 1977.
An improved event list algorithm.
In Proceedings of the Winter Simulation Conference, pages 547-557.
- HENRIKSEN,
J. O. 1983.
Event list management -- a tutorial.
In Roberts, S., Banks, J., and Schmeiser, B., editors, Proceedings of the 1983 Winter Simulation Conference, pages 542-551. IEEE.
- MÜLLER,
H. J., T. Malsch and I. Shulz-Schaeffer. 1998.
Socionics: Introduction and potential.
Journal of Artificial Societies and Social Simulation, 1(3), https://www.jasss.org/1/3/5.html.
- PARK,
Steve and Larry Leemis. 1999.
Discrete-Event Simulation: A First Course.
College of William and Mary, Williamsburg, VA.

 Return to Contents of this issue
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999
 Abstract
Abstract![]() Introduction
Introduction![]() Model Formulation
Model Formulation
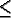 t
t 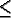 T);
T);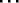 , A(t) - 1 to distinguish agents.
, A(t) - 1 to distinguish agents.
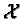 = {0, 1,
= {0, 1, 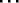 , X - 1} and
, X - 1} and 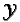 =
{0, 1,
=
{0, 1, 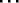 , Y - 1}. Then each
cell in the X
, Y - 1}. Then each
cell in the X  Y landscape is
distinguished by its (x, y) position with (x, y)
Y landscape is
distinguished by its (x, y) position with (x, y)
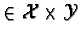 . Each (x, y) cell is
characterized by the attributes
. Each (x, y) cell is
characterized by the attributes
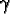 (x, y):
(x, y):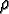 (x, y):
(x, y):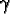 (x, y) = f(x - X/4,
y - Y/4) +
f(x - 3X/4,
y - 3Y/4)
(x, y) = f(x - X/4,
y - Y/4) +
f(x - 3X/4,
y - 3Y/4)
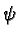 exp(-(x /
exp(-(x /
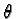 x)2
- (y /
x)2
- (y /
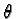 y)2
)
y)2
)
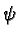 = 4.0,
= 4.0,
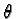 x = 0.3X and
x = 0.3X and
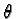 y = 0.3Y.
Although integer-valued but not otherwise explicitly defined, the resource
capacity used by Epstein and Axtell appears to be consistent with this
equation.
y = 0.3Y.
Although integer-valued but not otherwise explicitly defined, the resource
capacity used by Epstein and Axtell appears to be consistent with this
equation.
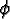 :
: :
: :
: :
: :
: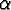 :
: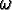 :
: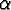 <
< 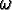 );
);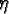 :
:


![]() Model Time Evolution
Model Time Evolution
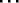 , T. All events of interest must occur
precisely at these time steps. For instance, in the Epstein and Axtell model
all agents attempt to move simultaneously, once each time step. All agents
attempting to reproduce must also do so once each time step. For serial
program execution, this kind of parallel activity is not possible and so it is
necessary to randomize the order in which agents act at each time step.
Without this randomization, the agents will always act in the same order,
introducing a bias that can produce artifacts (Epstein and
Axtell, 1996).
, T. All events of interest must occur
precisely at these time steps. For instance, in the Epstein and Axtell model
all agents attempt to move simultaneously, once each time step. All agents
attempting to reproduce must also do so once each time step. For serial
program execution, this kind of parallel activity is not possible and so it is
necessary to randomize the order in which agents act at each time step.
Without this randomization, the agents will always act in the same order,
introducing a bias that can produce artifacts (Epstein and
Axtell, 1996).
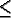 t
t 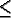 T, the state of the
system is defined by the following set of variables4.
T, the state of the
system is defined by the following set of variables4.
 ;
; , A(t) - 1.
, A(t) - 1.
 ) where
) where  is the rate of occurrence of that event type. Equivalently, each event type is
modeled as a stationary Poisson process with rate
is the rate of occurrence of that event type. Equivalently, each event type is
modeled as a stationary Poisson process with rate 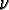 . The Poisson rate for the agent movement process is
. The Poisson rate for the agent movement process is 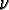 = 1.0
5. The mating event type can either be coupled with the
movement/consumption event type or modeled as a separate stationary Poisson
process. If the two event types are coupled, a mating event occurs for an agent
each time a movement/consumption event occurs for that agent. For all the
results in this paper, if the two event types are uncoupled, the Poisson rate
for agent mating is also
= 1.0
5. The mating event type can either be coupled with the
movement/consumption event type or modeled as a separate stationary Poisson
process. If the two event types are coupled, a mating event occurs for an agent
each time a movement/consumption event occurs for that agent. For all the
results in this paper, if the two event types are uncoupled, the Poisson rate
for agent mating is also 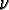 = 1.0.
= 1.0.
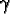 (x, y),
(x, y), 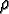 (x, y)(t - d(x, y))
}.
(x, y)(t - d(x, y))
}.
 window at times t, t + 1,
window at times t, t + 1,  as shown in Figure 3-1 where bullets denote typical agent
events.
as shown in Figure 3-1 where bullets denote typical agent
events.
![]() Results
Results
 (x, y). However,
we conjecture that the oscillatory behavior shown in Figure III-4 is a
simulation artifact caused primarily by synchronous time evolution. Moreover,
this oscillatory behavior is very much dependent upon initial conditions which
to date we have been unable to determine.
(x, y). However,
we conjecture that the oscillatory behavior shown in Figure III-4 is a
simulation artifact caused primarily by synchronous time evolution. Moreover,
this oscillatory behavior is very much dependent upon initial conditions which
to date we have been unable to determine.
 Y = 50
Y = 50  50
landscape. The resource capacity at each cell is given by the equation in ¶ 2.6, and the resource growback rate for each
(x, y) cell is
50
landscape. The resource capacity at each cell is given by the equation in ¶ 2.6, and the resource growback rate for each
(x, y) cell is 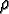 (x,
y) = 1. The landscape is initially occupied with A(0) = 400
randomly placed agents. The initial wealth of each agent is w(0) = 10.
The attributes for each agent are initialized as random variates according
to6
(x,
y) = 1. The landscape is initially occupied with A(0) = 400
randomly placed agents. The initial wealth of each agent is w(0) = 10.
The attributes for each agent are initialized as random variates according
to6
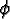 :
: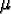 :
: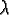 :
: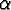 :
: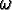 :
: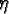 = 0. Reproduction and movement are coupled, i.e.,
the mating event type is not modeled as a separate process.
= 0. Reproduction and movement are coupled, i.e.,
the mating event type is not modeled as a separate process.
 Y = 100
Y = 100
 100 landscape with an initial A(0) =
1600 randomly placed agents. The remaining state and attribute parameters are
the same as in Figure 4-1. Again, undamped
oscillatory behavior is present in the synchronous time evolution output but
not in the asynchronous time evolution output8. While some initial oscillation is present in
the asynchronous time evolution results, the amplitude is damped
considerably. Moreover, for all initial seeds, changes in the output are far
less dramatic in the asynchronous case. That is, unlike the synchronous
results, the asynchronous results are not sensitive to the random variate
sequence of movement and reproduction, as manifested by the choice of initial
seed.
100 landscape with an initial A(0) =
1600 randomly placed agents. The remaining state and attribute parameters are
the same as in Figure 4-1. Again, undamped
oscillatory behavior is present in the synchronous time evolution output but
not in the asynchronous time evolution output8. While some initial oscillation is present in
the asynchronous time evolution results, the amplitude is damped
considerably. Moreover, for all initial seeds, changes in the output are far
less dramatic in the asynchronous case. That is, unlike the synchronous
results, the asynchronous results are not sensitive to the random variate
sequence of movement and reproduction, as manifested by the choice of initial
seed.
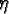 = 1. Again, the darker curves represent
output from the asynchronous time evolution model. We see that not only is the
amplitude of oscillations diminished dramatically using asynchronous time
evolution, but when compared with Figure 4-1 the mean
of the agent population is lowered as well. We reemphasize that we are not
promoting asynchronous time evolution as the best approach for all
artificial society models, but these results show that very different output
can result from modeling time evolution as synchronous or asynchronous.
= 1. Again, the darker curves represent
output from the asynchronous time evolution model. We see that not only is the
amplitude of oscillations diminished dramatically using asynchronous time
evolution, but when compared with Figure 4-1 the mean
of the agent population is lowered as well. We reemphasize that we are not
promoting asynchronous time evolution as the best approach for all
artificial society models, but these results show that very different output
can result from modeling time evolution as synchronous or asynchronous.
![]() Computational Performance Issues
Computational Performance Issues
![]() Conclusions and Future Work
Conclusions and Future Work
![]() Appendix: Random Variable Models
Appendix: Random Variable Models
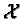 = { x
| a < x < b }
= { x
| a < x < b } 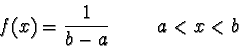
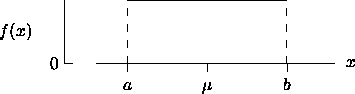
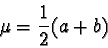
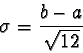
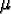 ) if and only if
) if and only if
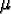 satisfies
satisfies 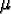 > 0
> 0 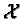 = { x
| x > 0}
= { x
| x > 0} 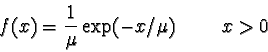
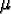
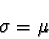
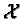 = {a,
a + 1,
= {a,
a + 1,  , b}
, b} 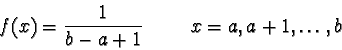

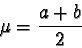
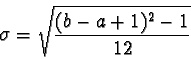
![]() Notes
Notes = 0, the
behavior of agents under our reproduction rule is the same as if the gestation
period was omitted from the rule.
= 0, the
behavior of agents under our reproduction rule is the same as if the gestation
period was omitted from the rule.
 > 0, during the gestation period other
agents may occupy all the cells adjacent to the parents. Consequently,
at the time of birth a cell may not be available for the child to occupy.
> 0, during the gestation period other
agents may occupy all the cells adjacent to the parents. Consequently,
at the time of birth a cell may not be available for the child to occupy.
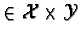 . Accordingly, the state
description is not minimal.
. Accordingly, the state
description is not minimal.
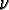 = 1.0 corresponds to the fixed-increment time step rate of the
synchronous approach. Systematically increasing
= 1.0 corresponds to the fixed-increment time step rate of the
synchronous approach. Systematically increasing 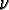 produces time evolutions similar to those presented in Section 4 but with lower population means. We also
experimented with inter-event times as Uniform, Erlang and
Normal random variables, each with a mean of 1.0 (the Normal was
truncated to positive values). These other distributions for the inter-event
times produce results similar to the stationary Poisson process results.
produces time evolutions similar to those presented in Section 4 but with lower population means. We also
experimented with inter-event times as Uniform, Erlang and
Normal random variables, each with a mean of 1.0 (the Normal was
truncated to positive values). These other distributions for the inter-event
times produce results similar to the stationary Poisson process results.
 50 landscape results,
asynchronous time evolution produced no atypical behavior in any of the
results using 100 different initial seeds on a 100
50 landscape results,
asynchronous time evolution produced no atypical behavior in any of the
results using 100 different initial seeds on a 100  100 landscape. To date we have not performed a more
systematic study of this atypical behavior in either the 50
100 landscape. To date we have not performed a more
systematic study of this atypical behavior in either the 50  50 or 100
50 or 100  100 landscape
case.
100 landscape
case.
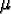 to
represent the mean and
to
represent the mean and 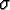 to represent the standard deviation
is consistent with conventional statistical notation and is not to be confused
with the
to represent the standard deviation
is consistent with conventional statistical notation and is not to be confused
with the 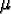 and
and 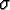 notations
from ¶ 2.7.
notations
from ¶ 2.7.![]() References
References![]()
Return to Contents of this issue