This paper describes the development of a series of intelligent agent simulations based on data from previously documented common pool resource (CPR) experiments. These simulations are employed to examine the effects of different institutional configurations and individual behavioral characteristics on group level performance in a commons dilemma. Intelligent agents were created to represent the actions of individuals in a CPR experiment. The agents possess a collection of heuristics and utilize a form of adaptation by credit assignment in which they select the heuristic that appears to yield the highest return under the current circumstances. These simulations allow the analyst to specify the precise initial configuration of an institution and an individual's behavioral characteristics, so as to observe the interaction of the two and the group level outcomes that emerge as a result. Simulations explore settings in which there is no communication between agents, as well as the relative effects on overall group behavior of two different communication routines. The behavior of these simulations is compared with documented CPR experiments. Future directions in the development of the technology are outlined for natural resource management modeling applications.

Keywords:

Common Pool Resources, Intelligent Agents, Simulation, Bounded Rationality, Communication

Introduction

1.1

The current challenges of environmental management place increasing pressure on policy analysts, ecologists, and resource managers to understand the complex relationships that exist between natural and human systems. Groups of individuals who interact with a natural resource may be described collectively as complex adaptive systems in that: they consist of a network of interacting agents; they exhibit a dynamic aggregate behavior that emerges as a result of the interactions of the individual agents; their aggregate behavior can be described without a detailed knowledge of the behavior of the individual agents (Holland and Miller 1991). Agents operating within this system are described as adaptive if they possess the following criteria: the outcome of the agents actions within its environment can be assigned a value such as utility or fitness; the agent behaves so as to increase this value over time. Complex adaptive systems may operate far from the global optimum or attractor (Holland and Miller 1991). Depending upon the design of the model, these systems may exhibit many different levels of organization and interaction. Agents seek to adapt so as to exploit the local niche to which they have access. This adaptation and evolution in turn creates new niches, or opportunities, to be explored. Such evolution can also result in lock-in, as agents adapt to the actions of other agents pursuing a collective course of action that leads the overall system in a particular direction which may or may not result in the system finding the predetermined global optimum.

1.2

Developing a better understanding of the nature of the complex interactions that exist when humans utilize natural resources is central to the development of effective policies for resource management. In recent years, researchers have turned to modeling and computer simulations to supplement and build on field observations, lab experiments, and theoretical and mathematical models (See for example Berry et al. 1993, Folse et al. 1989, Saarenmaa et al. 1994a, Saarenmaa et al. 1994b, Deadman et al. 1993). Recently, a number of intelligent agent-based simulation efforts have emerged that begin to explore interactions between human and natural systems.

1.3

This paper outlines an effort to develop a series of simulations that are derived from previous experimental research and theoretical developments in policy analysis. These simulations attempt to capture the actions of individuals engaged in a series of common pool resource (CPR) management experiments. Each participant in each experiment is modeled as a separate agent, with its own individual characteristics. The model captures some of the strategies of the agents and includes mechanisms by which they may communicate to govern their appropriation of the common pool resource. The individual agents utilize a simplified learning mechanism in which alternate strategies are evaluated and selected on the basis of the economic return that they earn for the agent. Simulations are developed in which communication is not allowed, and in which two simplified communication routines are allowed.

1.4

The experiments on which this simulation is based were carefully and purposefully designed to capture the dynamic of the "tragedy of the commons", a dynamic that has been repeatedly observed in numerous natural resource settings around the world (Hardin 1968, Ostrom 1990). In natural resource economics, the "tragedy of the commons" dynamic observed in some fisheries was captured and modeled in the work of H.Scott Gordon (1954). The common pool resource experiments are based on Gordon's model (Ostrom, Gardner, and Walker 1994). These experiments have been run hundreds of times in U.S. laboratories and replicated by other researchers (Moir 1995). Furthermore, they are closely related to social dilemma experiments designed and explored by social psychologists (Brechner 1977, Dawes 1980, Bornstein and Rapoport 1988). Thus, the common pool resource experiments provide particularly fertile ground for simulations because they capture real world dynamics, they are widely recognized and accepted in the social sciences, and they have been replicated. These experiments were selected as the subject of these simulations because they are already themselves models of a real world system, and because they have been widely studied. These experiments have been simulated as a step towards the eventual development of simulations based on real world case studies.

1.5

In the remainder of this paper, we describe the CPR experiments that form the basis for these simulations and the structure of the simulations themselves. The behavior of these simulations under different configurations is described, along with an outline of potential future directions for these efforts.

Understanding Common Pool Resources

2.1

Common pool resources are those resources that are subtractable and for which the exclusion of potential users or appropriators is difficult (Ostrom, Gardner, and Walker 1994). Examples of common pool resources include ground water basins, irrigation systems, forests, and fisheries. Interest in the study of CPRs is fueled in part by the desire to understand how the apparent conflict between individual rationality and group rationality, referred to as a CPR dilemma or the tragedy of the commons (Hardin 1968), can be avoided. This tragedy occurs when individuals who use a shared resource over appropriate and produce suboptimal collective benefits. Hardin (1968) indicated that this tragedy was unavoidable. Indeed, new examples of the tragedy seem to appear every day, as fisheries collapse and ground water basins dry up.

2.2

Ostrom (1990) challenged the universality of metaphors such as the tragedy of the commons by outlining numerous real world examples in which individuals were able to organize their collective actions by establishing rules which facilitated a long term improvement in joint outcomes. However, despite the fact that we know that many CPR management institutions are able to function effectively without depleting the resource, it is still difficult to explain how and why some appropriators are able to avoid CPR dilemmas while others are not.

2.3

Researchers have traditionally turned to field studies and laboratory experiments in an effort to gather data to explain commons dilemmas and their institutional solutions. Recent developments in computer technology, such as the development of multi-agent simulation platforms, now make it possible to develop computer experiments designed to improve our understanding of common pool resource situations. However, a well-established theoretical framework must guide the development of such computer simulations if they are to be interpretable and useful. The simulations of common pool resource institutions discussed here are grounded in the Institutional Analysis and Development (IAD) framework (see Ostrom, et al 1994, and Gardner, Ostrom and Walker 1990).

2.4

Numerous parallels exist between the structure of the IAD framework and that of agent-based simulations. Most notably, the IAD framework considers the individual actor as an important unit of analysis. Ostrom, et al. (1994) define four features that influence the behavior of an actor: preferences, information processing capabilities, selection criteria, and resources. These four variables are used to describe the individual agents used in these simulations. The agents are assumed to have a complete and stable set of preferences over the outcomes of the simulation and adequate resources to realize their preferences. Furthermore, the agents select those alternatives that they assess will make themselves best off. However, agents are not completely rational by microeconomics standards. Instead, the agents possess a form of bounded rationality. They use a collection of heuristics that guide their actions.

2.5

The transparency of the agent's inner configuration and explicit way in which an agent is defined facilitates observations between individual attributes and group outcomes. This supports the investigation of the connection between individual behavior and overall system performance. By exploring different configurations of these four variables in a collection of agents, it is possible to evaluate questions regarding the relative effects of these variables on group performance under different institutional configurations.

CPR Laboratory Experiments

3.1

Non-cooperative game theory predicts that individuals in common-pool resource settings will over utilize the CPR, and that even if allowed to communicate with one another, individuals will continue to over harvest the CPR (Ostrom, et al. 1994). Ostrom and colleagues designed a series of laboratory experiments to test these predictions. In the baseline version of these experiments, eight subjects are presented with a choice between harvesting from, or investing in, two alternatives. The first alternative, Market One, presents a constant rate of return for each unit invested in it. It presents an investment opportunity for individuals, so that they do not have to invest all of their resources in the CPR. The second alternative, labeled Market Two, is the common-pool resource. The return that an individual receives from Market Two depends not only on the level of investment of the individual, but also the level of investment of the group, thereby establishing an interdependent situation, or CPR. Each individual receives the full benefit of each unit invested in Market Two, while externalizing the costs of such investment on to all other users.

3.2

From an individual's standpoint the best outcome is to have all other CPR users limit their investment, allowing the individual to invest as much as she can in the CPR, maximizing her income. The second best outcome is for all individuals to collectively invest in the CPR to the point at which the group return is maximized. The third best outcome is for individuals to invest in the CPR so as to maximize their own returns given what all others are doing. This is known as a Nash equilibrium. The final outcome is the reverse of the first. The individual is part of the group of individuals who are limiting their investment in the CPR so that another individual can maximize her income from the CPR. Outcomes 1, 2, and 4, require individuals to explicitly coordinate their investment actions and voluntarily refrain from investing as much as they could in Market Two, the CPR. Outcome 3 requires no explicit coordination. Individuals simply respond to each other's actions. From the point of view of the individual and of the group outcome 3 is suboptimal. The individual could be made better off under outcome 1 and collectively the group would be better off under outcome 2.

3.3

In this setting, in which individuals may invest as much or as little as they choose in Market One or Two, subject only to their own budget constraints, non-cooperative game theory predicts that individuals will not coordinate their actions. In other words, outcome three, the Nash equilibrium will be achieved.

3.4

In the laboratory experiments reported by Ostrom, et al. (1994) each of the eight individuals were endowed with resources that could be invested in the two markets. These endowments consisted of tokens. Two types of experiments were run in which participants were given equal endowments of either 10 or 25 tokens each. Each experiment consisted of a series of rounds. In each round participants made their investment decisions. For each round participants possessed the following information:

1. the average and marginal returns for each token invested in Market Two at different levels of group investment,
2. the returns the individual earned from each market,
3. the number of tokens the individual invested in market two, and
4. the number of tokens the group invested in market 2.

With the information provided in (1) individuals could determine their individual best response to the actions of others as well as the optimal group level investment. Since individuals only knew what the group as a whole invested in the CPR, participants could not determine the individual investment decisions of other participants.

3.5

In the laboratory experiments the optimal level of investment by the group, that is outcome 2, would occur when 36 tokens were invested in Market 2. The Nash equilibrium level of investment, that is outcome 3, would occur when 64 tokens were invested in Market 2. Ostrom and colleagues devised a means by which to measure group performance. They compared what the group of participants actually earned to what the group could have earned had it invested optimally. They call this measure "rent as a percentage of optimum". It consists of the return the group receives from market two, minus the opportunity cost of investing in Market One, compared to the optimal level of investment. The Nash equilibrium returns 39% of the optimum level of rent.

Modeling CPR Experiments

4.1

We approach the simulation of a CPR dilemma in much the same way that researchers have approached the study of CPR management institutions, by considering a collection of autonomous individuals who interact with their environment. In this case, a collection of eight intelligent agents makes decisions regarding the investment of tokens in two alternate markets. These agents possess a collection of heuristics, from which they may draw upon when attempting to determine their appropriate course of action, given past events. The structure of these agents and the overall simulation are described here.

4.2

The simulation system utilized in this study is Swarm, a multi-agent simulation platform developed at the Santa Fe Institute (Minar et al. 1996). Swarm adopts a modeling formalism that consists of a collection of autonomous agents, interacting via a time-stepped series of discrete events. The basic unit of a Swarm simulation is an agent that generates events that can effect it and other agents (Minar et al. 1996). Swarm has been utilized in a variety of applications covering such fields as computational economics, anthropology, and geography.

4.3

The simulations described here contain a number of classes which control the simulation and represent the component parts of the model (see figure 1). At the lowest and most important hierarchical level lie the classes that represent the components of the CPR experiment itself, namely the participants in the experiment, or appropriators, and the CPR. Above these, the simulation contains an instance of a class called CprModelSwarm, which contains the schedule of agent activities, and above that an instance of a class called CprObserverSwarm, which controls the graphic output of the simulation. The classes that represent the CPR itself and the appropriators of the resource are described in detail.

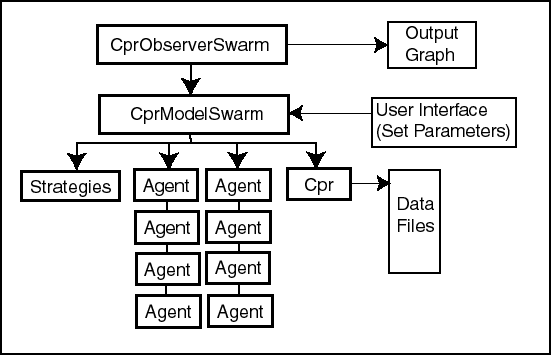
Figure 1. The Swarm Objects and Relationships for the CPR Simulations

The CPR Class

4.4

The methods written for the CPR class specifies the state of the CPR in relation to actions of the appropriators (see Figure 1). Only one instance of this class is created in these simulations. The quadratic production function for Market 2, the CPR, as utilized by Ostrom et al. (1994), is embedded in the code of the CPR and specified as follows:

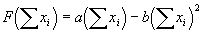
(1)

where   is the sum of all of the Market 2 bids submitted by the agents. By manipulating the a and b parameters, the shape and magnitude of the quadratic production function can be controlled. In addition, the CPR tracks parameters used in the quadratic production function (a and b), the parameter w which is used to calculate the return from Market 1, and the number of agents in the simulation. For all of the simulations explored in this work, the a, b, and w parameters of the production function and Market 1 fixed return were set to 23, 0.25, and 0.05 respectively. These are identical to the settings used by Ostrom, et al. (1994). During the initialization phase of the simulation, the CPR object calculates the optimum group bid as:

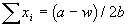
(2)

4.5

During each round of the simulation, the CPR collects the token bids for Markets 1 and 2 from the individual agents. The CPR then calculates the total return from Market 2, group rent as a percentage of optimum for Market 2, and the return to each individual appropriator for that round. In addition, during each round of the experiment the CPR object outputs the bids submitted by each participant, the cumulative rent earned by each participant, and the group rent as a percentage of optimum, to a data file for later analysis.

The Agent Class

4.6

Writing a set of methods for the individual appropriators requires the modeler to specify explicitly the strategies that individual subjects employ when they are engaged in a CPR experiment. How do subjects determine the bids that they will submit in each round of the experiment? What strategies do they employ? How do they adapt to the changing environment in which they find themselves? To what extent are they influenced by different factors such as the behavior of others? In essence, the modeler must decide how rational to make the agents.

4.7

In simple situations, or tight theoretical models, representations of individual behavior that are based on full rationality can be useful tools (Ostrom et al. 1994, Arthur 1994). But real world commons dilemmas are seldom simple. When the environment in which the human agent is situated becomes complex, the information processing capabilities of an individual are exceeded. Individuals are unable to behave in a fully rational manner. In these situations, researchers have argued that individuals display bounded rationality, relying on heuristics or hypotheses to guide their behavior (Ostrom 1998, Ostrom et al. 1994, Arthur 1994). This form of bounded rationality can be captured with intelligent agents that utilize a form of inductive reasoning (Arthur 1994). With this approach, agents follow an iterative sequence of events in which they keep track of the relative performance of a collection of heuristics. At each decision point, the agents utilize the heuristics that appears to be the most credible, or has the greatest strength. The agents update the relative performance of each alternative heuristic (Arthur 1994).

4.8

The simulations described here employ this basic pattern of agent behavior. A knowledge base for each agent is represented by a collection of strategies, composed of different rules. These rules have a condition-action structure of the form, "If such and such, Then so and so" in the manner described by Holland et al. (1986). For each agent, one of these strategies is designated the current strategy, the rest alternates. The agents begin by playing the current strategy. But they also keep track of how the alternate strategies would have performed in each round had the agent used them. At set intervals during the simulation, the agents employ an adaptive mechanism in which they evaluate the performance of these different rules based on information available from the environment. The adaptive mechanism is similar to the adaptation by credit assignment approach discussed by Holland (1995). The agents select a strategy to follow based on their actual or apparent performance over the preceding rounds, and enact that strategy until the next evaluation period. Specifically, all the agents in these simulations attempt to maximize the return they receive from the CPR, with a variety of possible techniques for achieving that goal.

4.9

The agents in these simulations may access up to sixteen alternate strategies (see Table 1). Some of the strategies are derived from documented exit interviews of participants in CPR laboratory experiments (Ostrom, et. al 1994). Six of the strategies simply attempt to maximize the individual return received in each round by comparing investments in Market 2 in previous rounds with the resulting returns. If returns on tokens are increasing, then more tokens are placed in Market 2. If returns on tokens invested in Market 2 are decreasing, then fewer tokens are placed in Market 2. These six strategies vary in the amount that Market 2 bids are incremented or decremented each round. Six additional strategies compare average returns between Market 1 and Market 2, increasing the bid to the market that performs better. This is a strategy that was reported by subjects in CPR experiments during exit interviews (Ostrom, et al. 1994). These six strategies also vary in the amount that Market 2 bids are incremented or decremented in each round. The final four strategies directly compare an individual agent's bid with the bids of the group as a whole.

Table 1: Descriptions of the sixteen strategies employed in the simulations
Strategy Number	Description
1	Total Return Maximizing Strategy - Increment and decrement Market 2 bid by one token.
2	Total Return Maximizing Strategy - Increment and decrement Market 2 bid by two tokens.
3	Total Return Maximizing Strategy - Increment and decrement Market 2 bid by three tokens.
4	Total Return Maximizing Strategy - Increment and decrement Market 2 bid by four tokens.
5	Total Return Maximizing Strategy - Increment Market 2 bid by all available tokens, decrement Market 2 bid by three tokens.
6	Total Return Maximizing Strategy - Increment Market 2 bid by all available tokens, decrement Market 2 bid by 5 tokens.
7	Unit Return Maximizing Strategy - Increment and decrement Market 2 bid by one token.
8	Unit Return Maximizing Strategy - Increment and decrement Market 2 bid by two tokens.
9	Unit Return Maximizing Strategy - Increment and decrement Market 2 bid by three tokens.
10	Unit Return Maximizing Strategy - Increment and decrement Market 2 bid by four tokens.
11	Unit Return Maximizing Strategy - Increment Market 2 bid by all available tokens, decrement Market 2 bid by three tokens.
12	Unit Return Maximizing Strategy - Increment Market 2 bid by all available tokens, decrement Market 2 bid by five tokens.
13	Submit Market 2 bid equal to group average bid in previous round.
14	Submit Market 2 bid equal to group average bid in previous round plus one token.
15	Submit Market 2 bid equal to group average bid in previous round plus two tokens.
16	Submit Market 2 bid equal to group average bid in previous round plus three tokens.

Pseudo Code of Object Actions in Baseline Simulations

The Appropriator Agents	The Cpr Object
Step:
- Calculate Market 1 and 2 token bids
- Update variables
- Submit Market 2 bid to Cpr
	Step:
	- Collect Market 2 Bids from all Appropriators
	- Calculate:	Group Return
		Return per token
		Rent as % of Optimum
Update:
-Get total return for Market 1 and 2 bids from Cpr
-Update variables
	Output:
	- Send to data files:
		Each agent's Market 2 bid that round
		Return earned by each agent that round
		Group rent as a percent of optimum
		Current and alternate strategies of each agent
Eval:
if (this is an evaluation round)
- Send prerequisite data to Strategies object
- Request Market 2 bids for alternate strategies
- Get total return from each alternate strategy's bids from Cpr
- Update average return of each strategy
- Select new current strategy with highest average return

Non-communication Simulations

5.1

In the first series of simulations the agents were not allowed to communicate with one another. In each decision round, the agents had to choose how to allocate their tokens between Markets 1 and 2. In each round agents had information on: the return they received in previous rounds, the number of tokens both they and the group as a whole bid on Market 2 in previous rounds, the average performance of their alternate strategies in all previous rounds.

5.2

Three sets of simulations were run, at 10 and 25 token allotments, in which agents were assigned four, eight, or all sixteen of the possible strategies. Approximately 100 decision rounds were run for each simulation.

5.3

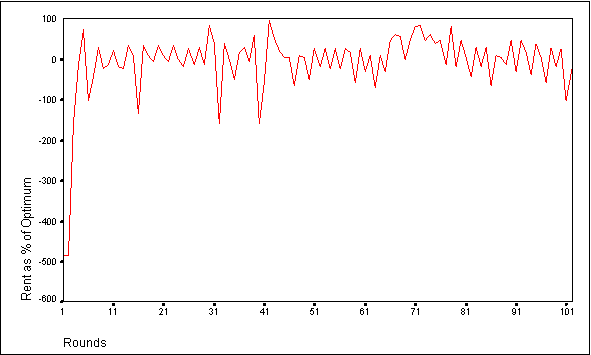
When the agents are endowed with 4 strategies and 10 tokens, group rent as a percentage of optimum fluctuates within a range of values between about -11 and 92 percent (see Figure 2). The same general fluctuating pattern is observed when agents with four strategies are provided with a 25 token endowment, although the range of values is greater (see Figure 3). Both the 10 and 25 token endowment simulations are characterized by occasional plunges in performance as the agents over invest in the CPR. These dips in performance are more noticeable in the 25 token endowment simulations because of the potential for enormous over investment in Market 2. Strategies that prompt the agent to invest all its tokens in Market 2 are the ones that cause these large drops. As a result, they tend to be selected by individual agents less frequently over time.

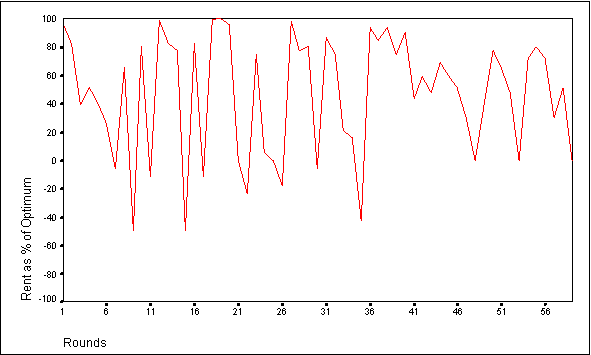
Figure 2. Group Performance for Adaptive Agents with a 10 Token Endowment

Figure 3. Group Performance for Adaptive Agents with a 25 Token Endowment

5.4

The behavior of these agents is similar to those of groups participating in CPR laboratory experiments as observed by Ostrom et al (1994). Specifically, in non-communication lab experiments, human subjects with a ten token endowment achieved group rent as a percentage of optimum performance levels of 37 percent. Group performance for the comparable agent based simulations fluctuated around a mean of 43 percent. At a 25 token endowment, human subjects in the lab achieved group performance levels of about -3 percent (Ostrom et al 1994), whereas in the agent simulations, group performance was about -10 percent. Furthermore, the group performance of the human subjects and the agent based simulations both followed fluctuating patterns as the groups adjusted their bids to Market 2 in an effort to maximize their individual payoffs. The number of strategies available to the agents in these simulations did not significantly alter the group performance (see Deadman 1997).

Discussion of Non-Communication Simulations

6.1

The most interesting observation of these non-communication simulations is the fact that they perform similarly to groups of human subjects in CPR non-communication laboratory experiments. As in CPR experiments, the group performance for the simulations follows an oscillating pattern in which high performance leads to over investment in the CPR and the resultant drop in performance causes a reduction in group wide investment in the CPR. In addition, the mechanism that allows agents to switch strategies is based on a goal of utility maximization. Agents will switch to another strategy if it achieves a higher return. Such a mechanism is likely to cause over investment, as agents seek higher returns from Market 2, followed by reduced investment, as the agents react to the reduced returns caused by over investment.

6.2

Still more interesting is the observation that the simulations perform similarly to subjects in lab experiments in terms of average performance over time. At the ten token endowment, the simulations perform near the Nash equilibrium over time. At the 25 token endowment, the simulations perform near zero percent of optimum over time. Has enough human rationality been captured in these agents to represent the actions of humans in this highly simplified environment? We know that some students in the lab experiments reported following a strategy similar to the unit return strategy described earlier. We know that students would attempt to maximize returns from one round to the next, and submit a variety of bids in an attempt to maximize utility. Perhaps in capturing these behavioral patterns, we have reproduced the essence of human behavior in this simplified game. Although clearly no claim can be made that the agents are reproducing the thought processes of human beings, it appears that in such a simplified environment the simulations do a achieve a reasonable degree of replicative validity at the group level.

Communication Simulations

7.1

Ostrom, et al. (1994) examined the effects of face-to-face communication on the ability of individuals to coordinate their investment strategies in the CPR. Non-cooperative game theory predicts that communication should have no effect on individual behavior. Communication does not change the payoff structure of the game, and individuals have no means of enforcing promises to refrain from overinvesting in the CPR. Consequently, individuals will play their nash equilibrium strategies.

7.2

Ostrom, et al. (1994) explored two communication routines. First, subjects participated in 10 decision rounds in which they could not communicate. They were allowed to communicate face-to-face for 10 minutes. They then participated in another series of decision rounds. Second, subjects participated in 10 decision rounds during which they could not communicate. After that, they were allowed a few minutes of communication after each decision round. The first communication routine produced mixed results. In the first five decision rounds after communication groups earnings averaged 74% of the optimal outcome (Ostrom, et al. 1994:152). From that point earnings declined. One time face-to-face communication promoted cooperation, but the groups could not sustain it. The second communication routine produced clear outcomes. Individuals identified the optimal group investment strategy, which was universally adopted. Repeated communication allowed the groups to sustain cooperation. Groups earned between 97% and 100% of the optimal group outcome (Ostrom, et al. 1994: 154).

7.3

In the simulations two forms of simple communication between agents were explored. In the first, agents employed a very restricted form of information exchange. After five rounds of no communication, each agent submitted to every other agent the Market 2 bid yielding the highest individual return. Following the submission of these bids, each agent individually evaluated each suggestion, determining the one that would yield the highest individual return. Each agent then incorporated the best bid as an additional strategy. Agents utilizing a pool of four strategies in the non-communication rounds prior to the communication round, adopt the best suggestion as a fifth strategy for subsequent rounds. Initially each agent adopts the fifth strategy as the current strategy. Another five decision rounds of no communication are run. As in the non-communication simulations, the agents evaluate the performance of the new strategy against the alternates, and may switch to one of the alternates if it appears to provide a higher return. Following the five no communication decision rounds, agents once again communicated their best performing strategy, and the process repeated itself.

7.4

A second form of communication was explored in which the best bid suggestions of each agent were evaluated by a central authority, rather than by the agents themselves. In this case, during a communication round each agent submitted to the CPR object the bid that provided it with the highest return. The CPR evaluated each bid and determined the one that if followed uniformly by all members of the group would produce the highest group return. The CPR instructed each agent of the bid that would produce the highest group return. Each agent adopted this bid as its current strategy. Then the agents participate in five non-communication rounds. If, during the non-communication rounds, an agent determined that one of its alternative strategies would provide it with a higher individual return than the highest group return strategy it would switch.

Pseudo Code of Object Actions in Communication Simulations

The Appropriator Agents	The Cpr Object
Step:
- Calculate Market 1 and 2 token bids
- Update variables
- Submit Market 2 bid to Cpr
	Step:
	- Collect Market 2 Bids from all Appropriators
	- Calculate:	Group Return
		Return per token
		Rent as % of Optimum
Update:
- Get total return for Market 1 and 2 bids from Cpr
- Update variables
	Output:
	- Send to data files:
		Each agent's Market 2 bid that round
		Return earned by each agent that round
		Group rent as a percent of optimum
		Current and alternate strategies of each agent
Eval:
if (this is an evaluation round)
- Send prerequisite data to Strategies object
- Request Market 2 bids for alternate strategies
- Get total return from each alternate strategy's bids from Cpr
- Update average return of each strategy
- Select new current strategy with highest average return
When best Market 2 bid is calculated by Cpr object:
Comm:
if (this is a communication round)
- Send best Market 2 bid to Cpr
	SetCommBid:
		- Collect best bids from each appropriator
		- Calculate return of each bid if used by all appropriators
		- Select best Market 2 bid
CommEval:
- Retrieve best Market 2 bid from Cpr
- Set best bid as new current strategy
- Update variables
When best Market 2 bid is calculated independently by each agent:
Comm:
if (this is a communication round)
- Send best Market 2 bid to Cpr
	SetCommBid:
		- Collect best bids from each appropriator
CommEval:
- Retrieve all suggested bids from Cpr
- Get total return for each alternate bid from the Cpr object
- Select bid providing highest return as new current strategy
- Update variables

7.5

These communication routines capture some aspects of the communication routine used in the experiments using human subjects and fail to capture others. In the experiments using human subjects, individuals were allowed to engage in face-to-face communication between decision rounds, although agreements were not enforceable. Subjects discussed different investment strategies that they believed if collectively adopted would maximize group returns. Although subjects would publicly commit to following a particular strategy, they made their investment choices in private and could deviate from the strategy that was collectively agreed upon (Ostrom, et al. 1994).

7.6

The agents in these simulations in no way engage in face-to-face communication. However, the communication routines that are explored capture different aspects of the face-to-face communication used among human subjects. The communication routine in which agents submit their best performing strategies to one another is similar to human agents discussing different strategies that they believe will work well. And just like human agents who make their investment decisions privately, the intelligent agents select the suggested strategy that they determine will provide the highest individual payoff. Furthermore, the communication routine in which the CPR object evaluates all submitted strategies and determines which one will produce the highest group payoff if adopted by all agents is similar to human agents publicly agreeing to adopt the strategy that they believe will produce the highest group payoff. And just as the human agents can deviate from what they publicly committed to, so the intelligent agents can deviate from the strategy suggested by the CPR object. However, it must be emphasized that while the communication routines used in these simulations capture aspects of the communication routines used by human subjects, they in no way simulate such communication.

Evaluation of Alternate Bids by Individual Agents

7.7

In these simulations the only communication that occurs among agents is the exchange of information about high performing bids. Each agent is free to adopt any of the Market 2 bids suggested by the other agents that appears to provide it with the highest return. It may switch from that bid at any time. In other words, the agents do not collectively adopt the same strategy that they believe will yield them the highest group return. Instead, after exchanging information about different strategies they individually select the strategy that will individually make them better off.

7.8

The most important observation in this set of simulations is that the groups eventually lock in to a uniform Market 2 bid. All agents eventually converge on a bid that results in the best return, given the events that have occurred previously in that particular simulation run. However, this group-wide uniform Market 2 bid frequently produces group performance levels that are sub-optimal. The amount of time required for the agents to lock into this group-wide uniform bid frequently exceed 100 rounds, and can exceed 200 rounds. Typically, in these simulations, group performance fluctuates as it did in the non-communication simulations. However, unlike the non-communication simulations, eventually a constant group performance level will appear (see Figures 4 and 5).

7.9

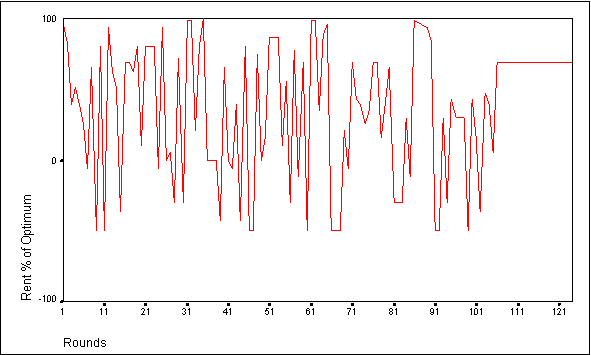
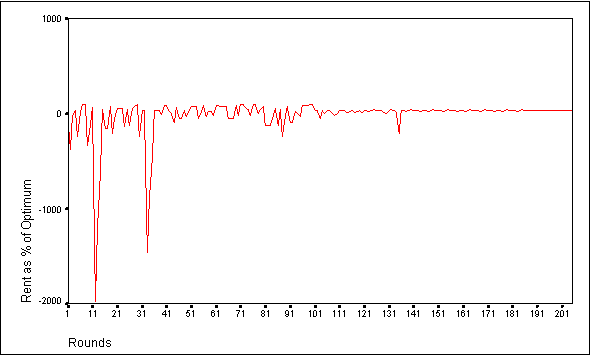
For these simulations, the optimum total group investment in Market 2 occurs at 36 tokens. The closest that the group of agents can come to optimum by submitting uniform bids occurs when they submit either 4 tokens each (total 32) or 5 tokens each (total 40). The Nash equilibrium level of investment for the group occurs at 64 tokens (39% of optimum rent). Examining the bids data file for the agents reveals that all the members of the group settle on a uniform Market 2 bid. This uniform Market 2 bid fluctuates between 4 and 8 tokens per agent across simulations, yielding group rent as a percentage of optimum levels from 98% to 39% respectively. Interestingly, this range of investments indicates that, as a group, the agents never settle on a uniform bid that under appropriates the CPR. In addition, they have never been observed to settle on a group investment that performs worse than the Nash equilibrium.

Figure 4. Group Performance for Adaptive Agents Employing Communication and Individual Evaluation of Bids with a 10 Token Endowment

Figure 5. Group Performance for Adaptive Agents Employing Communication and Individual Evaluation of Bids with a 25 Token Endowment

7.10

Because the agents employ an adaptive mechanism that evaluates the relative strength of each strategy based on the return that it earns for the agent, the performance of any particular strategy depends upon the actions of the other members of the group in each round. Therefore, a strategy that works well for one agent at a particular point in time may result in a considerably poorer performance later in the simulation. Consequently, the strategy is less likely to be used again. Eventually, the agents adopt a bid for which none of them has a better performing alternative, even if this group-wide bid is suboptimal. The actions of the group in previous rounds will determine which bid appears to yield the best performance.

Evaluation of Alternate Bids by a Central Authority

7.11

In the previous communication routine, each agent shared its best Market 2 bid with the group and evaluated the suggestions of others individually. A second communication routine was explored in which the CPR object evaluated each suggestion as if it had been submitted uniformly by all members, and then instructed the agents to adopt the best performing bid. In this case, the agents collectively adopt the same bid - the bid that the CPR object determined would produce the highest group return if played by each agent. Although each member adopted this bid as its current strategy, agents could switch to an alternate strategy later in the simulation if the alternate appears to provide a higher return.

7.12

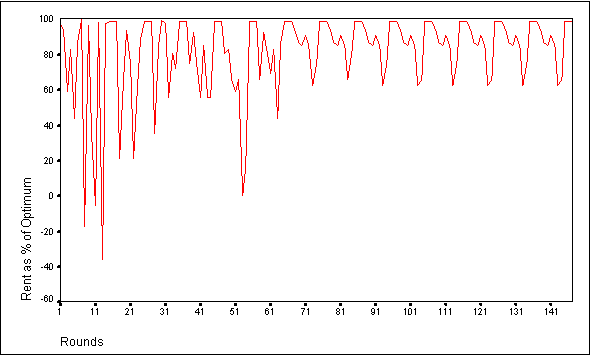
These simulations differ from the previous communication simulations in two important ways. First, the majority of the members of the group tend to lock into a uniform group-wide bid much earlier than in the previous simulations. This group wide bid is frequently near the optimal level. In the majority of simulation runs, the CPR selects a group level of appropriation of 4 or 5 tokens each. On rare occasions, the CPR selects a uniform investment level of 6 or 7 tokens each. Second, one or more members of the group switch away from the group strategy after a few rounds. This behavior results in the establishment of a fluctuating pattern of group performance in which the agents adopt a single group-wide Market 2 investment for the few rounds following communication, followed by a drop in performance as one or two members of the group switch to an alternate strategy (see Figures 6 and 7). In the simulation depicted in Figure 6, the members of the group adopt the near-optimum investment level of 5 tokens each after each communication round. However, shortly thereafter four members of the group switch to an alternate strategy that appears to provide a higher return, thereby lowering group performance. The fluctuating pattern we see is the result of this cycle of group induced compliance at a communication round, followed by subsequent strategy changes by one or more members of the group. The number of strategies provided to each agent or the size of token endowment does not appear to be correlated with the group wide investment level, or the number of agents that will subsequently change strategies.

Figure 6.Group Performance for Adaptive Agents Employing Communication and Centralized Evaluation of Bids with a 10 Token Endowment

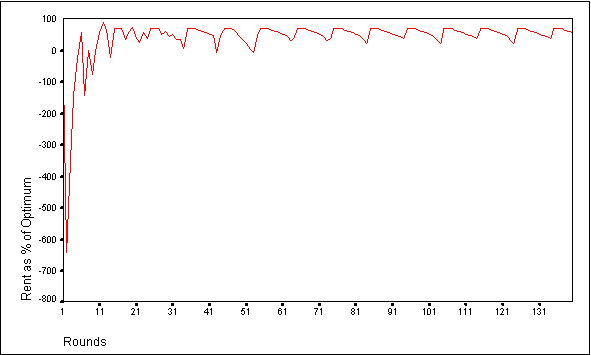
Figure 7. Group Performance for Adaptive Agents Employing Communication and Centralized Evaluation of Bids with a 25 Token Endowment

Discussion of Communication Simulations

8.1

Simulations in which the agents evaluate the suggested bids of the other agents independently are characterized by eventual convergence of the group to a stable group wide uniform investment in Market 2. The emergence of this stable condition usually occurs somewhere between 100 and 250 rounds of the simulation. The length of time required to achieve tacit collusion is a product of the limited rationality of the agents and the mechanism they use to select from amongst the different strategies. Near the beginning of these simulations the agents suggest a wide variety of bids during the communication round. Frequently these bids suggest higher levels of investment in Market 2 than bids that would result in the group optimum level of investment. This occurs because these bids are recorded when the agent submitted a bid higher than the group average. However, when all members of the group implement this bid, group performance drops and the bid is discarded. Over time, the agents continue to implement a variety of strategies, evaluating their performance as they go along. Eventually, a bid is suggested and adopted by some members of the group that provides a return that is higher than the score of any alternate strategy. At this point the agent will continue to submit this bid indefinitely. Over several communication rounds, more agents adopt this bid until all agents find that it performs better than any alternate strategy.

8.2

The communication mechanism changes the simulation significantly from the previous non-communication simulations. It creates a simple self-reinforcing mechanism as discussed by Arthur (1988). According to Arthur, researchers have discovered that systems in many different fields of study, from theoretical biology to physics, tend to possess a multiplicity of asymptotic states, or "emergent structures". The initial configuration of the system, and some early, often random, events tend to push these dynamic systems into the domain of one of these asymptotic states, or attractors, and thus select a state that the system eventually "locks into" (Arthur 1988).

8.3

Arthur points out that such states exist in economic systems as well citing examples from international trade theory, spatial economics, and industrial organization. The evolution of silicon valley in California is one such example from spatial economics. According to Arthur (1988), these systems display four properties; multiple equilibria, possible inefficiencies, path dependence, and lock-in. Each of these properties has been reproduced by these simple simulations. Multiple equilibria are seen in these simulations as the group wide level of investment that the agents eventually agree on changes in successive runs of the simulation. Inefficiencies are demonstrated as the agents settle on uniform group bids that are frequently well below optimum. Path dependence is ensured as the strength of alternate strategies is influenced by past performance. Events early in the simulation may cause certain strategies to be permanently discarded, thus influencing future decisions by individuals and overall group behavior. Finally, lock-in is clearly demonstrated as the agents settle on a uniform group-wide level of investment.

8.4

The agents in this simulation reach a form of tacit cooperation without direct interaction. They only go along with the final group wide equilibrium bid because none of their alternate strategies appears to perform any better. This tacit agreement can take several hundred rounds to evolve as contrasted to the rapid agreement that can be achieved by subjects in the lab.

8.5

In a second communication routine, a central authority evaluates bids and a single group-wide bid is initially imposed on all members. However, despite the fact that the group bids following these communication rounds are frequently near optimum, the group is unable to maintain this arrangement. Individual agents evaluate the imposed strategy and compare it with other strategies, determining which one produces the highest individual payoff. Some agents defect from the prearranged bid in subsequent rounds as they determine that other strategies will produce higher individual payoffs. Fluctuating patterns emerge as near optimal group level performance is repeatedly imposed during every communication round but subsequently declines in the following rounds.

8.6

This form of communication does have some characteristics in common with the CPR experiments in which communication is allowed. As in the lab experiments, communication in these simulations does frequently result in the discovery of the optimal level of investment. However, there is an important difference in the subsequent behavior of human subjects and agents, following communication. Whereas humans in the lab are able to draw upon social norms favoring cooperation and verbal sanctions in subsequent communication rounds to ensure compliance, the agents in these simulations possess no mechanism to represent a social norm favoring cooperation. Therefore they are not encouraged to cooperate with the imposed group bid by any mechanism other than an objective evaluation of the potential payoffs that may be earned by their alternate internal strategies. If it appears that an alternate strategy will yield a higher return in the next round, they switch away from the group strategy without any consideration of the potential actions of the other agents.

Conclusion

9.1

In this modeling approach global level behavior is produced by local level actions, such as the exchange of information between adaptive agents and the CPR. Nothing is included in the code of the simulation, such as a differential equation, that directly specifies global level behavior. However, this simulation system will neither be able to reproduce the structure of the appropriator's strategy generating mechanism (i.e. the functions of an individual's brain) nor the detailed events that occur during an open discussion period in a lab experiment, nor would we necessarily want it to. For in reproducing the actions of a human brain exactly (assuming it could be done) and the behavior of a group of individuals in open discussion (again assuming it could be done), we would fall into the trap of producing a simulation that was too complex to interpret (Zeigler 1976).

9.2

Clearly the simple nature of these early simulations leaves a great deal of avenues open to further investigation. Some future directions in which this work might proceed include; testing alternative learning models including those which employ adaptation by rule discovery (Holland 1995), and exploring the effectiveness of more detailed communication procedures.

9.3

The simulations explored here have focused on modeling CPR laboratory experiments as a prelude to the development of other resource management or institutional models. Eventually the intention is to extend these models to link human systems and natural systems models in resource management applications. Some examples of this already exist. Simulations such as Phoenix (Cohen et al. 1989) combine dynamic models of natural processes (in this case forest fire spread) with dynamic models of human action (the movement of the firefighters and equipment). In these models, agents representing human individuals or organizations will have to deal with constantly changing conditions in the natural system. In addition these models will have to capture the essential components and actions of resource management institutions. Although some theoretical tools exist, such as the IAD framework to assist in this effort, such models will be considerably more complex than the ones explored in the simulations outlined here. However, if these challenges can be met in a series of incremental efforts, then there is a great deal of potential for modeling and simulation as a tool to assist us in our understanding of these social dilemmas.

References

ARTHUR, B.W. (1988), Self-Reinforcing Mechanisms in Economics. in The Economy as an Evolving Complex System. SFI Studies in the Sciences of Complexity. Addison-Wesley Publishing Company.

ARTHUR, B. W. (1994), Inductive Reasoning and Bounded Rationality. AEA Papers and Proceedings. 84(2) pp 406-411.

BERRY, J. S., G. Belovsky, A. Joern, W. P. Kemp & J. Onsager. (1993), Object-Oriented Simulation Model of Rangeland Grasshopper Population Dynamics. in Proceedings of Fourth Annual Conference on AI, Simulation, and Planning in High Autonomy Systems, Tucson, AZ. September 20-22, 1993, pp. 102-108.

BORNSTEIN, G. and A. Rapoport. 1988. Intergroup Competition for the Provision of Step-Level Public Goods: Effects of Preplay Communication. European Journal Social Psychology 18:125-142.

BRECHNER, K. 1977. An Experimental Analysis of Social Traps. Journal of Experimental Social Psychology 13:552-564.

Cohen, P. R., M.L. Greenberg, D. M. Hart & A. E. Howe. (1989). Trail by Fire: Understanding the design requirements for agents in complex environments, AI Magazine 10(3):32-48.

DAWES, Robyn. 1980. Social Dilemmas. Annual Review of Psychology 31:169-193.

DEADMAN, P., R. Brown, H. R. Gimblett. (1993), Modelling Rural Residential Settlement Patterns with Cellular Automata. Journal of Environmental Management. 37. pps. 147-160.

DEADMAN, P. (1997), Modelling Individual Behaviour in Common Pool Resource Management Experiments with Autonomous Agents. PhD Dissertation, The University of Arizona.

FOLSE, L.J., J. M. Packard & W. E. Grant. (1989) AI Modelling of Animal Movements in Heterogeneous Habitat. Ecological Modelling 46, 57-72.

GARDNER, Roy, Elinor Ostrom, and James Walker. (1990), 'The Nature of Common Pool Resource Problems.' Rationality and Society 2:335-358.

GORDON, H. Scott. 1954. The Economic Theory of a Common Property Resource: The Fishery. Journal of Political Economy 62:124-142.

HARDIN, G., (1968). The Tragedy of the Commons. Science. 162:1243-48.

HOLLAND, J. (1995). Hidden Order: How Adaptation Builds Complexity. Addison-Wesley.

HOLLAND, J.H. & J. H. Miller. (1991). Artificial Adaptive Agent in Economic Theory. American Economic Review, 81(2):365-370.

HOLLAND, J.H., Holyoak, K.J., Nisbett, R.E., Thagard, P.R. 1986. Induction: Processes of Inference, Learning, and Discovery. MIT Press, Cambridge, Ma.

MINAR, N., R. Burkhard, C. Langton & M. Askenazi. (1996), The Swarm Simulation System: A Toolkit for Building Multi-Agent Simulations. Overview paper. Santa Fe Institute, Santa Fe, NM.

MOIR, R. 1995. The Effects of Costly Monitoring and Sanctioning Upon Common Property Resource Appropriation. Working Paper, University of New Brunswick, Department of Economics, Saint John, New Brunswick.

OSTROM, E. (1990), Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge University Press.

OSTROM, E., Gardner R., and J. Walker. (1994), Rules, Games, & Common Pool Resources. The University of Michigan Press.

OSTROM, E. (1998) Coping with Tragedies of the Commons. Annual Meeting of the Associate for Politics and Life Sciences in conjunction with the Annual Meeting of the American Political Science Association, Boston, Ma.

SAARENMAA, H., J. Perttunen, J. Vakeva & A. Nikula. (1994a), Object-oriented modelling of the tasks and agent in integrated forest health management. AI Applications in Natural Resource Management. 8 (1), pps. 43-59.

SAARENMAA, H. & H.R. Gimblett. (1994b), Preface to the Special Issue on Object-Oriented Modelling of Natural and Artificial Agents in Ecosystem and Natural Resource Management. Mathematical and Computer Modelling. Volume 19, Number 9, November.

Zeigler, B.P. (1976). Theory of Modelling and Simulation. John Wiley, New York.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 1999