This paper reviews Axelrod's work on the evolution of cooperation in terms of the generality of his findings. It is argued that while his results are to some degree sensitive to changes in the parametric assumptions he made, his and subsequent work provide a valuable general framework for the analysis of the conditions promoting cooperative play. In addition, this literature makes important methodological innovations through the evolutionary analysis of boundedly-rational interaction and learning using computer simulations.

Keywords:

Axelrod, prisoner's dilemma, computer simulations, evolution, bounded rationality

Introduction

1.1

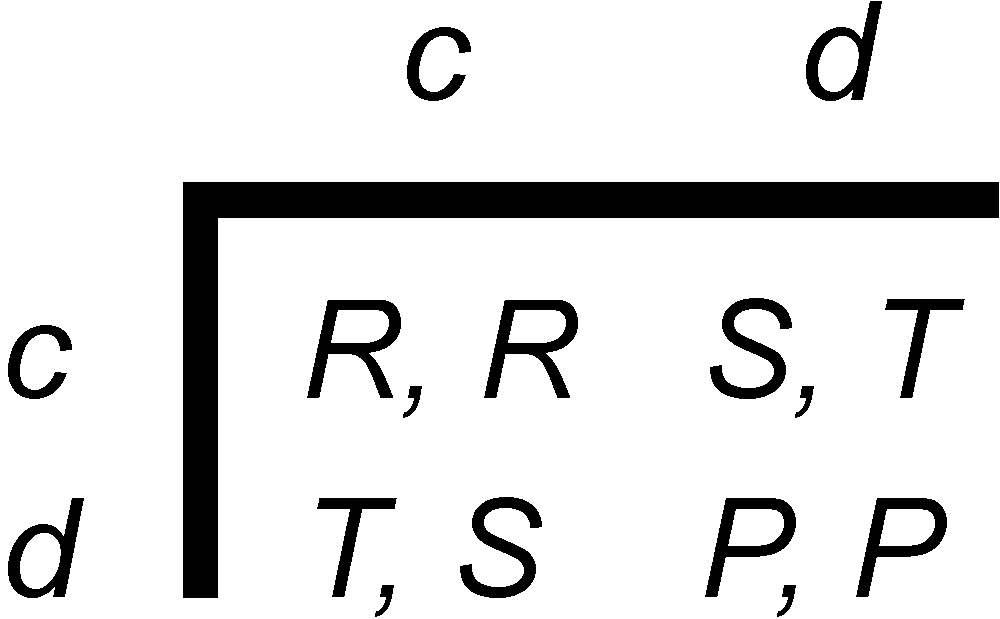
In 1980, the Journal of Conflict Resolution published two papers by political scientist Robert Axelrod (1980a, 1980b) reporting the results of computerised tournaments of the repeated prisoner's dilemma (RPD, figure 1). The game provides a formal representation of a ubiquitous type of collective action problem that arises when individual interests undermine the collective welfare of the group. As many writers before, Axelrod wanted to identify the conditions under which cooperative behaviour could emerge in groups of this kind in the absence of central enforcement.^[1]

Figure 1. The Prisoner's Dilemma. The payoffs obey T>R>P>S. Players have a choice between cooperation (c) and defection (d). The dominant strategy equilibrium (P,P) for the one-shot game is Pareto-dominated by (R, R)

1.2

Axelrod's work on this issue culminated in a book containing the results of his first four articles (Axelrod 1984) followed by a number of further contributions reprinted in another single volume (Axelrod 1997). His approach turned out to be extremely influential. According to the Social Science Citation Index, his work had been quoted more than one thousand times by 1992 (Axelrod 1992) and more than 2500 times to date.

1.3

Axelrod's work has also been subjected to a number of criticisms (see Binmore 1994, 1998). In particular, subsequent authors have called the generality of his results into question. Since computer simulations are known to be sensitive to the parametric assumptions made, a literature has emerged over the last twenty years that tests the robustness of Axelrod's findings with respect to changes in seven key assumptions he made. This article is a review of Axelrod's contribution based on the discussion of subsequent work on the seven parameters.^[2] A summary of Axelrod's main findings is contained in the next section. Subsequent literature is examined in section three. Section four concludes with a summary and a number of general observations.

The Evolution of Cooperation

2.1

Axelrod was interested in the circumstances which permit cooperation in groups of agents playing the RPD. His approach was to identify and explore the following general conditions for cooperative behaviour: first, cooperative strategies must generate success in a given environment in order to be adopted by individual agents. Second, these strategies must generate success in changing environments of learning players to be capable of spreading. Finally, populations of cooperative players thus established must be immune to the adoption of alternative forms of behaviour.

2.2

To find out what strategies would yield success in play, Axelrod invited selected specialists to enter strategies for a computerised round-robin computer tournament which could use the entire past history of the current game to determine moves. Tit-for-Tat (TFT)^[3], submitted by Anatol Rapoport, obtained the highest overall score both in the initial and a subsequent tournament with additional, nonspecialist entrants. TFT's success is based on its ability to differentiate between and adapt to opponents. It resists exploitation by defecting strategies but reciprocates cooperation.

2.3

Next, Axelrod simulated a learning process by allowing a replicator dynamic to change the representation of tournament strategies between successive generations according to relative payoffs.^[4] The result was that after one thousand generations, reciprocating cooperators accounted for about 75% of the total population. TFT itself displayed the highest representation among all. The reason is that in addition to its differentiating nature, TFT does well against itself and other cooperative strategies. In contrast, defecting strategies fare badly when their own kind spreads and their victims begin to die out.

2.4

In a later, less well-known article, Axelrod (1987) used a computational search heuristic, the Genetic Algorithm (GA, see Holland 1992) to simulate agent learning. The GA uses operators based on evolution such as mutation and crossover, to 'breed' increasingly efficient solutions to a set computational problem which are represented as bit strings. Axelrod encoded backward-looking game strategies in this way and pitted them against the entries of his (1984) tournament. He then employed a GA to introduce a selection process among the strings using average game payoffs as a fitness criterion. The GA finally yielded a population which was highly adapted to the tournament population and scored near best-reply payoffs against it. In most simulations the GA generated strings that resembled TFT.

2.5

In real learning populations, agents adapt their behaviour against opponents who are in turn continually changing as they learn. In order to allow the GA to capture this type of mutual adaptation, Axelrod (1987) allowed the strings' opponents to change with them, i.e. they played one another as opposed to a specified niche. Axelrod found that under this type of coevolution, defecting strategies were able to spread in the population initially. However, as the defectors became more numerous and their potential victims diminished in number, their fitness declined. Soon, conditional cooperators displaced the defectors and spread as before.

2.6

Axelrod argued that a homogeneous population thus established is resistant to invasion when the strategy concerned is 'collectively stable', i.e. is a best reply to itself. Any alternative strategy would therefore be unable to score strictly higher payoffs upon emerging in the population. Axelrod goes on to prove that TFT can be collectively stable.

The Robustness of Cooperation

3.1

Axelrod's results thus demonstrate that TFT can be viable for individual use, capable of spreading in learning populations and resists invasion once adopted by an entire population. Subsequent authors have expressed reservations about the generality of TFT's success in particular and the evolution of cooperation in general with respect to alternative initial conditions in the tournament. Seven key simulation parameters can be identified in this context (Axelrod and Dion 1992, Hoffmann 1996).

Agent Representation

3.2

The way strategies are encoded in the computer program reflects the model's assumption concerning individual decision making. In his initial quest for successful strategies, Axelrod (1984) imposed few restrictions on the entries to his tournament. However, TFT's initial success may be sensitive towards the model's assumption concerning this parameter.

3.3

The first issue is agent memory. Reciprocal behaviour requires an element of agent recollection of previous rounds. In Lindgren's (1992, see also Andersen 1994, p.176) simulation, learning agents increasingly adopt strategies with longer memory components allowing more complex behaviours. By the same token, however, sufficiently long memories allow strategies to recognise the game's final round and may generate backward induction endgame behaviour (see Nachbar 1992, Binmore 1994, 1998). This issue is discussed further in paragraph 3.21.

3.4

While complexity may have benefits in terms of efficacy, a number of authors follow the psychological literature and model the resulting mental effort.^[5] Hirshleifer and Coll (1988) study populations consisting only of ALL-D, ALL-C and TFT-players.^[6] They find that increasing complexity cost harms the chances of cooperation due to the relative complexity of reciprocal behaviour. A similar finding is made by Linster (1992), in whose simulations ALL-D behaviour benefits in relative terms from complexity costs due to its own simplicity as well as its ability to exploit other equally simple strategies such as ALL-C. Hoffmann and Waring (1998) show that complexity cost increases the stability of converged populations by unmasking distinct, but behaviourally identical invaders which may randomly spread and open the door for conditional cooperation (see 3.17).

3.5

Other authors investigate strategies which generate probabilistic rather than history-dependent moves. Kraines and Kraines' (1993) 'Pavlovian' strategies are able to support the evolution of cooperation in tournaments where players are assumed to make errors (see section 3.24). In contrast to TFT, they are able to exploit naive cooperative strategies.

3.6

The evolution of cooperation is sensitive to assumptions made concerning agent rationality. In particular, agent memories need to be sufficient to allow conditional strategies, insufficient to identify the game's end and must not be accompanied by prohibitive complexity cost.

Initial Population

3.7

Axelrod's tournament population reflects no systematic selection criterion (Marinoff 1992).^[7] However, since strategy success depends on opponent behaviour, results such as Axelrod's may depend on the composition of the initial population (Axelrod 1984, p.48). In particular, the outcome of a learning process may be path dependant on the types and representation of strategies present at the outset. Hirshleifer and Coll (1988) use initial populations with alternative proportions of ALL-C, ALL-D and TFT. They show that a sufficient number of conditional cooperators relative to defecting strategies are required for cooperation to spread.

3.8

There are two ways to overcome arbitrary or biased population selection. Many authors employ learning dynamics capable of creating novelty in the population to allow the introduction of strategies not included originally.^[8] Using suitable dynamics of this kind, both Lomborg (1996) and Hoffmann (2000) observe the evolution of cooperation in initially defecting populations. The evolution of cooperation has also been detected by authors selecting randomly or exhaustively from the background pool of possible strategies belonging to their chosen agent representation (e.g. Linster 1992, Lindgren 1992, Miller 1996, Fogel 1993).

3.9

In addition to its selection, the size of the initial population may matter (see Olson 1965 for the theoretical argument). Fogel (1993) conducted round-robin simulations with mutually-adapting agents in which he varied the total number of players with little effect on simulation results. Simulations of this type do not model factors such as social pressure identified in the theoretical literature to be responsible for group size effects.

Population Structure

3.10

Simulation results may be sensitive to the way in which players are matched for interaction and learning. Axelrod considered population structures other than the round robin such as matching on the basis of player labels and location and detected changes in his results (Axelrod 1984, chapter 8). More recent work has followed this line of investigation.

3.11

Some authors examine games where interaction is based on player identity. Vanberg and Congleton (1992) analyse a model in which agents have the option not to interact with a given opponent. Similarly, Stanley, Ashlock and Tesfatsion (1994) consider a game in which agents select and refuse potential opponents on the basis of their expected behaviour. Exit options promote cooperation as cooperative players may refuse to interact with defectors. However, this feature arguably dissolves the nature of the RPD (Axelrod 1984, p.12, Vanberg and Congleton 1992).

3.12

Hirshleifer and Coll (1988) consider an elimination contest from which defeated players are removed. Compared with the round robin, the elimination population structure is harmful to the evolution of cooperation. The reason is that defecting strategies such as ALL-D have the ability to outscore their opponents, while conditional cooperators such as TFT can never 'win' a game (Kraines and Kraines 1993).

3.13

A number of authors introduce spatial dimensions to the matching process (Nowak and May 1992 and 1993, Routledge 1993, Oliphant 1994, Kirchkamp 1995, Grim 1997, Hoffmann 1999). Axelrod (1984, see also Mueller 1988) suggested that in many realistic scenarios, agents interact and learn mainly within territorial proximity. Nowak and May (1992 , 1993) show that clusters of cooperation can persist among agents located in squares on a torus.^[9] The agents interact with players in all neighbouring squares and imitate the best-performing one. The localised imitation operator generates the formation of monomorphic strategy clusters on the torus which aid cooperative players due to the insulation they afford from defecting players outside. Cooperative players on the border of such a cluster can sustain their cooperation by imitating their successful neighbours inside the cluster. Hoffmann (1999) shows that this type of result is driven by local imitation rather than local interaction.

3.14

These contributions demonstrate that Axelrod's initial results are sensitive to population structure. While elimination contests seem to harm cooperative play, agent exit opportunities and local dimensions seem to promote it. However, it would seem that more realistic matching structures such as random or localised matching promote cooperative behaviour. Elimination structures imply player preferences over others' payoffs and require more justification. The issue of population structure has clear implications for other literatures and has been discussed in subsequent theoretical work (e.g. Ellison 1993).

Population Dynamics

3.15

Results can be sensitive towards the learning dynamic used to propagate strategies in the population. As seen, a dynamic's ability to introduce novelty is significant. Axelrod's replicator dynamic has the undesirable conservative feature that new or extinct strategies cannot emerge, amplifying path dependence on the initial population make-up. In contrast, Linster (1992) uses the replicator dynamic in conjunction with a number of alternative mutation operators which introduce random changes to selected strategies. The application of these dynamics to a population of all possible one-round memory strategies generated the spread of TRIGGER^[10] and to a lesser extent ALL-C and TFT. The use of different mutation schemes had some quantitative impact in terms of relative strategy representation. Lomborg's (1996) mutation dynamic also afforded cooperation in a simulation with an initial ALL-D population.

3.16

Many writers followed Axelrod's use of a co-evolutionary GA. In Miller's (1996) population, this dynamic evolved reciprocal cooperation after few generations. About 44% of final behaviour traits reciprocate cooperation, and about 70% reciprocate defection. Only 3% of traits expressed trigger attributes that generate sequences of unconditional behaviour for the rest of a given game once activated.

3.17

Hoffmann (2000) uses a similar GA to examine thousands of generations of learning and detects oscillating evolutions of cooperation and defection. In particular, this study shows that these phases of convergence can be undermined by the arrival of distinct but behaviourally identical invaders that open the door for other strategies. For example, a TFT or TRIGGER-population can be neutrally invaded by mutations generating ALL-C players until the population is unable to resist further invasion by ALL-D. This result demonstrates the ultimate instability of both cooperation and defection which some forms of learning can generate.^[11]

3.18

One question concerns the issue whether these types of result are sensitive to the use of alternative evolutionary dynamics and to alternative GA-parameter settings, such as mutation rates. Routledge (1993), for example, finds that the GA's strategy replacement rate has a negative impact on the evolution of cooperation. Hoffmann (2000) shows how the process of neutral population invasion is aided by higher GA mutation rates. Fogel (1993) employs his own evolutionary algorithm which uses an alternative mechanism to select behavioural traits to be spread. Fogel's results are quantitatively and qualitatively similar to those of GA studies in showing the evolution of cooperation.

3.19

These studies provide mixed evidence for Axelrod's (1984, 1987) findings. Although the evolution of reciprocal cooperation is evident under a number of alternative learning assumptions, it is also apparent that defection may evolve. These results confirm theoretical work in this area which suggests no strategy can ultimately repel invasion in RPD-playing population under normal conditions (Boyd and Lorberbaum 1987). In addition, this work shows that the evolution of cooperation may be generated by conditional cooperators other than TFT, such as TRIGGER, or a mixture of them.

Payoff Variation

3.20

A number of writers are concerned about the robustness of Axelrod's result with respect to other closely related games as well as to payoff variations within the confines of the prisoner's dilemma. Nachbar (1992, p.320) selects a payoff setting strongly favouring the relative reward of cooperating and finds that this setting elicits an increased degree of cooperation. Fogel (1993) finds that smaller values for T promote the evolution of cooperative behaviour. Kirchkamp (1995) finds that the value of S becomes less important with longer strategy memory as this permits conditional cooperation which is less susceptible to exploitation. Finally, Mueller (1988) finds that payoff settings with increasing values of T relative to P promote cooperative behaviour.

Repetition

3.21

Repetition intuitively promotes cooperation as in the long term players can establish reputations, build trust and engage in reactive behaviour. Axelrod investigated this parameter theoretically (Axelrod 1984, p.12-16, 126-132, see also Mueller 1988). In addition, short repetition coupled with long player memories can enable players to engage in endgame behaviour.^[12] Nachbar's (1992) simulations included the two-round and the six-round game. In both games, the agents' memories were as long as the game and the populations converged on mutual defection. Routledge (1993) compares games with more rounds than his players can remember, and ones with fewer rounds than their memory. Routledge's populations generate mutual defection in the finite game but manage some amount of mutual cooperation in the infinite version.

Noise

3.22

Results are sensitive to the extent to which players make mistakes either in the execution of their own strategy (misimplementation noise) or in the perception of opponent choices (misperception noise).^[13] In particular, cooperation is vulnerable to noise as it is supported by conditional strategies. For example, in a game between two TFTs, a single error would trigger a series of alternating defection. Axelrod (1984) repeated his initial round-robin tournament with added 1% chance of players misunderstanding their opponent's move in any round. He found that TFT still came first despite some echoes of retaliation between cooperative strategies.

3.23

A number of authors confirm the negative effect of noise of TFT and find that more forgiveness promotes cooperation in noisy environments (Bendor, Kramer and Stout 1991, Mueller 1988). These results imply a trade-off between the resistance to exploitation and the ability to maintain mutual cooperation in the presence of errors.

3.24

Kraines and Kraines' (1993) agents generate moves according to probabilities which are updated according to a conditioning process. Once trained, these 'Pavlovian' strategies are able to support the evolution of cooperation with themselves and are more successful than TFT against a variety of opponents. Specifically, they are less likely to become stuck in ruts of defection through misunderstanding a conditional cooperator. A similar strategy does well in Marinoff's (1992) noisy tournament.

3.25

Other authors find that noise makes little qualitative difference in learning populations. In Miller's (1996) simulation, 5% misperception noise lowered the amount of cooperation among a reciprocating population but did not generate defecting strategies. A similar finding was made by Lomborg (1996) for 12.5% noise.

3.26

Noise has the additional effect of bringing out differences between strategies that neutrally coexist in convergence (Boyd 1989). In Hirshleifer and Coll's (1988) noisy simulation, ALL-C is driven to extinction by ALL-D and also TFT-players. The presence of noise generated fewer unused behaviour traits in Miller's (1996) simulation. Hoffmann and Waring (1998) find that the oscillating evolutions of cooperation and defection found by Hoffmann (2000) cease when noise is present. Noise exposes neutral invaders, such as ALL-C in TFT-populations.

Conclusion

4.1

The literature has confirmed the sensitivity of Axelrod's results with respect to alternative initial simulation conditions. The following conclusions emerge from this work. First, the evolution of cooperation is a phenomenon observable in a wide variety of circumstances. It has been demonstrated under alternative representations of agents, in a variety of initial populations, with a number of agent learning and interaction structures, under alternative learning dynamics and noise conditions. This evolution is not, however, limited to TFT, but general to conditionally cooperative strategies. Conversely, however, in line with theoretical work, a number of simulations have demonstrated that defection can evolve in the RPD.

4.2

The results of this literature therefore confirm a number of key findings of theoretical work. First, cooperation is possible in equilibrium when players do not take account of the game's end.^[14] Secondly, in evolutionary frameworks, any strategy that spreads to fixation can ultimately be displaced by alternative forms of behaviour (Boyd and Lorberbaum 1987). As a result, the question arises whether Axelrod's approach provides any new insights.

4.3

Axelrod (1984) is aware that cooperation is only one of many possible outcomes of evolutionary play in the RPD. He is explicit about his interest not in the demonstration of the possibility, but in the conditions necessary for cooperative play (e.g. Axelrod 1984, p.3, 15). In addition to highlighting the role of reciprocation in this context, Axelrod points to a number of factors that have an impact on cooperation. Interestingly, his 1984 book includes speculation and some amount of initial analysis of most of the simulation parameters subsequently studied.^[15] In this sense, Axelrod's contribution lies in the identification of the factors that influence whether cooperation is possible. His work and subsequent literature have established a comprehensive menu of the conditions of cooperation. This general framework is applicable to a host of realistic scenarios both in the social and natural worlds (e.g. Milinski 1987).

4.4

In addition, Axelrod's work has arguably made important contributions in terms of the approach and methodology he used to analyse the RPD. First, Axelrod is an early author to explicitly consider boundedly-rational play (1984, p.18, p.50). This notion envisages agents with limited information and cognitive skills which make heuristic, procedure-based rather than optimising choices. The strategies in his simulations are algorithmic, are used indiscriminately against all opponents and make no use of the finite nature of the game. Bounded rationality is only recently becoming more widespread in game theory in particular and in economics generally (Conlisk 1996). Axelrod's computational demonstration of cooperation therefore relates to agents of this type. A number of later studies show it using theoretical means (see Aumann 1981, Neyman 1985, Rubinstein 1986, Radner 1986, Aumann and Sorin 1989). Axelrod (1987) and subsequent literature have made some progress in the difficult issue of modelling boundedly-rational behaviour (Holland and Miller 1991).

4.5

Another merit in Axelrod's work consists of his focus on the agent learning process. As Binmore (1998) points out, this type of approach is useful in the RPD since, depending on assumptions, equilibrium multiplicity or nonexistence problems exist. While game theory had made a number of important discoveries relating to the existence and properties of equilibria, little work had been devoted to the question of how they are reached. The analysis of learning affords identification of the processes and conditions governing the spread of alternative strategies (Hoffmann 2000).

4.6

Another novelty is Axelrod's reliance on computer simulation (see Emshoff 1970, Maynard Smith and Price 1973 for other early users of this approach). The coevolutionary GA in particular is a powerful method in the analysis of the experimental and imitative aspects of boundedly-rational learning which has been taken up by a number of subsequent authors. There is considerable debate in the social sciences over the appropriate use of simulation. The approach is generally criticised when the simulation results could in principle be established theoretically. The reason for this is the fact that simulations are sensitive to parametric assumptions, while mathematical results often have a greater degree of generality. Conversely, computer simulations can have advantages over theoretical approaches when the phenomenon at hand resists theoretical analysis (Simon 1981, p.19, Axelrod 1986, p.1089), when there is great model complexity and when either no or a multitude of solutions exist. Computers can be used to monitor a system's behaviour as it unfolds (Holland and Miller 1991). As seen, evolutionary models are often characterised by these types of problems.

4.7

Axelrod's work has sometimes been accused of taking too low-brow an approach to an essentially technical game-theoretic problem (Binmore 1998). In addition, the discussion of his findings especially in popular science circles has sometimes led to exaggerated claims being made on their behalf. While a dilution of scientific content in this way is certainly undesirable, there is merit in the wide appeal of Axelrod's work outside specialist audiences, partly due to his accessible presentation. In the end, academic paradigms such as game theory can only be useful to the extent that they are taken up and applied more generally. In this sense, Axelrod would certainly pass the McCloskey (1983) test of good academic practice. Certainly, this seems to have been part of his intention (Axelrod 1992).

Notes

¹In the social sciences, this fundamental issue is commonly known as spontaneous order (see Taylor 1976, Sugden 1989, Hardin 1982). It has been addressed in various forms by writers since ancient times. It is also of interest for biologists as the question of reciprocal altruism among animals (Trivers 1985, chapter 15).

²The discussion of all literature in this area is beyond the scope of a single review. A overview of this literature up to 1988 is contained in Axelrod and Dion (1988). Axelrod's website at http://pscs.physics.lsa.umich.edu/Software/ComplexCoop.html provides a comprehensive annotated bibliography.

³The strategy that cooperates in round one of any game and subsequently repeats the opponent's previous move.

⁴A lot has been written about this dynamic and its properties in the theoretical literature. It was originally developed in theoretical biology. Its first application to game theory is due to Taylor and Jonker (1978). See also Zeeman (1981), Schuster and Sigmund (1983), Hofbauer and Sigmund (1988), Sigmund (1993).

⁵The effort of decision making has been considered in psychology for some time (e.g. Johnson and Payne 1985). A trade-off between decision efficacy and cognitive effort required is said to exist. In game theory, a strategy's memory requirement provides a natural vehicle for examining this issue (see, for example, Rubinstein 1986, Binmore and Samuelson 1992).

⁶The former two are the strategies that cooperate (ALL-C) and defect (ALL-D) in all rounds of a given game.

⁷Axelrod introduced a bias into the tournaments by pairing all strategies not just with every other strategy, but also with their own respective twins. This favours cooperative strategies that do well against each other, while strategies that defect fare badly against their own kind.

⁸A number of authors have made this point. See Axelrod (1984, p.48), Sigmund (1993, p.196), see also Hirshleifer and Coll (1988, p.370), Dawkins (1989, p.215), Nachbar (1992, p.308), Linster (1992, p.881).

⁹A three-dimensional shape resembling a doughnut.

¹⁰The strategy that cooperates until a single act of defection by its opponents causes it to defect for the remainder of the game. It is sometimes known as the GRIM-strategy.

¹¹Axelrod (1984) follows Taylor (1976) to claim that strategies that are best replies to themselves can resist invasion. However, alternative best replies can emerge and spread neutrally until a third form of behaviour can emerge and prosper. As a result, only strategies that are strictly their own unique best replies (or better replies to alternative ones) can be evolutionary stable (Maynard Smith 1982). In the standard RPD, no pure strategy has this quality (Boyd and Lorberbaum 1987). However, noise and complexity cost generate payoff differentials between alternative best replies and may therefore re-establish evolutionary stability (Sugden 1986, May 1987, Boyd 1989).

¹²The backward induction argument suggests that defection in every round is the only rational outcome of the finite RPD with complete information. The reason is that the identification of the final round leads to defecting endgame behaviour which ultimately unravels the game.

¹³See, for example, Axelrod and Dion (1988, p.1387), Sigmund (1993 p.192), Bendor (1993), Bendor, Kramer and Stout (1991), Hirshleifer and Coll (1988), Molander (1985), Sugden (1986 p.109), Mueller (1988), Lomborg (1996).

¹⁴In the paper first mentioning the prisoner's dilemma, Flood (1958, p.16) reports a private communication with John Nash in which the latter explains that two TRIGGER-strategies are in equilibrium in the infinite version of the game. The general result pertaining to infinite games is known as the Folk Theorem.

¹⁵The parameters considered by Axelrod (1984) include the initial population (p.48), population structure (chapter 8), payoff variation (p.133), repetition (p.59, p.126) and noise (p.182-183). The issues of population dynamics and agent representation are examined in his later article (Axelrod 1987).

References

ANDERSEN, ES (1994) Evolutionary Economics. Pinter

AUMANN, RJ (1981) "Survey of Repeated Games". In Aumann, RJ et al, Essays in Game Theory and Mathematical Economics, Bibliographisches Institut

AUMANN, RJ and Sorin, S (1989) "Cooperation and Bounded Recall". Games and Economic Behaviour 1, pp.5-39

AXELROD, R (1980a) Effective Choice in the Prisoner's Dilemma. Journal of Conflict Resolution, vol.24. pp.3-25

AXELROD, R (1980b) More Effective Choice in the Prisoner's Dilemma. Journal of Conflict Resolution 24. pp.379-403

AXELROD, R (1984) The Evolution of Cooperation. Basic Books

AXELROD, R (1986) An Evolutionary Approach to Norms. American Political Science Review 80. pp.306-318

AXELROD, R (1987) The Evolution of Strategies in the Iterated Prisoner's Dilemma, in Davis, L (ed.) Genetic Algorithms and Simulating Annealing. Pitman

AXELROD, R (1992) Citation Classic: How to Promote Cooperation. Social and Behavioral Sciences 44. p.10

AXELROD, R and Dion, D (1988) The Further Evolution of Cooperation. Science 242. pp.1385-1390

AXELROD, R (1997) The Complexity of Cooperation. Princeton University Press

BENDOR, J (1993) Uncertainty and the Evolution of Cooperation. Journal of Conflict Resolution 37(4). pp.709-734

BENDOR, J, Kramer, RM and Stout, S (1991) When in Doubt Cooperation in a Noisy Prisoner's Dilemma. Journal of Conflict Resolution 35(4). pp.691-719

BINMORE, K (1994) Playing Fair Game Theory and the Social Contract I. MIT Press

BINMORE, K (1998) Review The Complexity of Cooperation. Journal of Artificial Societies and Social Simulation 1(1). https://www.jasss.org/1/1/review1.html

BINMORE, KG and Samuelson, L (1992) Evolutionary Stability in Repeated Games Played by Finite Automata. Journal of Economic Theory 57. pp.278-305

BOYD, R (1989) Mistakes Allow Evolutionary Stability in the Repeated Prisoner's Dilemma Game. Journal of Theoretical Biology 136. pp.47-56

BOYD, R and Lorberbaum, JP (1987) No Pure Strategy is Evolutionarily Stable in the Repeated Prisoner's Dilemma Game. Nature 327. pp.58-59

CONLISK, J (1996) Why Bounded Rationality. Journal of Economic Literature 34. pp.669-700

DAWKINS, R (1989) The Selfish Gene. Oxford University Press

ELLISON, G (1993) Learning, Local Interaction, and Coordination. Econometrica 61(5). pp.1047-1071

EMSHOFF, JR (1970) A Computer Simulation Model of the Prisoner's Dilemma. Behavioural Science 15. pp.304-317

FLOOD, MM (1958) Some Experimental Games. Management Science 5. pp.5-26

FOGEL, DB (1993) Evolving Behaviors in the Iterated Prisoner's Dilemma. Evolutionary Computation 1(1). pp.77-97

GRIM, P (1997) The Undecidability of the Spatialized Prisoner's Dilemma. Theory and Decision 42(1). pp.53-80

HARDIN, R (1982) Collective Action. Johns Hopkins University Press

HIRSHLEIFER, J and Coll, JM (1988) What Strategies Can Support the Evolutionary Emergence of Cooperation?. Journal of Conflict Resolution 32(2). pp.367-398

HOFBAUER, J and Sigmund, K (1988) The Theory of Evolution and Dynamical Systems. Cambridge University Press

HOFFMANN, R (1996) The Evolution of Cooperation Revisited. UNBS Discussion Paper 96/6

HOFFMANN, R (1999) The Independent Localisations of Interaction and Learning in the Repeated Prisoner's Dilemma. Theory and Decision 47. pp.57-72

HOFFMANN, R (2000) The Ecology of Cooperation.Theory and Decision. forthcoming

HOFFMANN, R and Waring, N (1998) "Complexity Cost and Two Types of Noise in the Repeated Prisoner's Dilemma". In Smith, G.D., Steele, N.C. & Albrecht, R.F. (eds), Artificial Neural Nets and Genetic Algorithms. Springer Verlag

HOLLAND, JH (1992) Genetic Algorithms. Scientific American, July 1992. pp.44-50

HOLLAND, JH and Miller, JH (1991) Artificial Adaptive Agents in Economic Theory. American Economic Association Papers and Proceedings 81(2). pp.365-370

JOHNSON, EJ and Payne, JW (1985) Effort and Accuracy in Choice. Management Science 31(4). pp.395-413

KIRCHKAMP, O (1995) Spatial Evolution of Automata in the Prisoners' Dilemma. University of Bonn SFB 303 Discussion Paper B-330, http://www.sfb504.uni-mannheim.de/~oliver/spatEvol.html

KRAINES, D and Kraines, V (1993) Learning to Cooperate with Pavlov An Adaptive Strategy for the Iterated Prisoner's Dilemma with Noise. Theory and Decision 35. pp.107-150

LINDGREN, K (1992) "Evolutionary Phenomena in Simple Dynamics". In Langton, CG (ed.) Artificial Life II. Addison-Wesley

LINSTER, BG (1992) Evolutionary Stability in the Infinitely Repeated Prisoner's Dilemma Played by Two-State Moore Machines. Southern Economic Journal 58. pp.880-903

LOMBORG, B (1996) Nucleus and Shield: The Evolution of Social Structure in the Interated Prisoner's Dilemma. American Sociological Review 61. pp.278-307

MCCLOSKEY, D (1983) The Rhetoric of Economics. Journal of Economic Literature 21. p.481-517

MARINOFF, L (1992) Maximizing Expected Utilities in the Prisoner's Dilemma. Journal of Conflict Resolution 36(1). pp.183-216

MAY, RM (1987) More Evolution of Cooperation. Nature 327. pp.15-17

MAYNARD SMITH, J (1982) Evolution and the Theory of Games. Cambridge University Press

MAYNARD SMITH, J and Price, GR (1973) The Logic of Animal Conflict. Nature 246. pp.15-18

MILINSKI, M (1987) Tit for Tat in stickleback and the evolution of cooperation. Nature 325. pp.434-435

MILLER, J (1996) The Coevolution of Automata in the Repeated Prisoner's Dilemma. Journal of Economic Behavior and Organization 29. pp.87-112

MOLANDER, P (1985) The Optimal Level of Generosity in a Selfish, Uncertain Environment. Journal of Conflict Resolution 29(4). pp.611-618

MUELLER, U (1988) Optimal Retaliation for Optimal Cooperation. Journal of Conflict Resolution 31(4). pp.692-724

NACHBAR, JH (1992) Evolution in the Finitely Repeated Prisoner's Dilemma. Journal of Economic Behavior and Organization 19. pp.307-326

NEYMAN, A (1985) Bounded Complexity Justifies Cooperation in the Finitely Repeated Prisoners' Dilemma. Economics Letters 19. pp.227-229

NOWAK, MA and May, RM (1992) Evolutionary Games and Spatial Chaos. Nature 359. pp.826-829

NOWAK, MA and May, RM (1993) The Spatial Dilemmas of Evolution. International Journal of Bifurcation and Chaos 3(1). pp.35-78

OLIPHANT, M (1994) "Evolving Cooperation in the Non-Iterated Prisoner's Dilemma: The Importance of Spatial Organization". In Brooks, R and Maes, P (eds.) Proceedings of the Fourth Artificial Life Workshop, MIT Press

OLSON, M (1965) The Logic of Collective Action. Harvard University Press

RADNER, R (1986) "Can Bounded Rationality Resolve The Prisoners' Dilemma?". In Hildenbrand, W and Mas-Colell, A (eds.) Contributions to Mathematical Economics in Honor of Gérard Debreu, North-Holland

ROUTLEDGE, BR (1993) Co-Evolution and Spatial Interaction. manuscript. http://sulawesi.gsia.cmu.edu/papers/Coevolution/

RUBINSTEIN, A (1986) Finite Automata in the Repeated Prisoner's Dilemma. Journal of Economic Theory 39. pp.83-96

SCHUSTER, P and Sigmund, K (1983) Replicator Dynamics. Journal of Theoretical Biology 100. pp.533-538

SIGMUND, K (1993) Games of Life. Oxford University Press

SIMON, HA (1981) The Sciences of the Artificial. MIT Press

STANLEY, EA, Ashlock, D and Tesfatsion, L (1994) "Iterated Prisoner's Dilemma with Choice and Refusal of Partners". In Langton, CG (ed.) Artificial Life III. Addison-Wesley

SUGDEN, R (1986) The Economics of Cooperation, Rights and Welfare. Basil Blackwell

SUGDEN, R (1989) Spontaneous Order. Journal of Economic Perspectives 3(4). pp.85-97

TAYLOR, M (1976) Anarchy and Cooperation. John Wiley

TAYLOR, PD and Jonker, LB (1978) Evolutionarily Stable Strategies and Game Dynamics. Mathematical Biosciences 40. pp.145-156

TRIVERS, R (1985) Social Evolution. Benjamin/Cummings

VANBERG, VJ and Congleton, RD (1992) Rationality, Morality and Exit. American Political Science Review 86(2). pp.418-431

ZEEMAN, EC (1981) Dynamics of the Evolution of Animal Conflicts. Journal of Theoretical Biology 89. pp.249-270

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 1998