Colm O' Riordan (2000)

A forgiving strategy for the Iterated Prisoner's Dilemma

Journal of Artificial Societies and Social Simulation vol. 3, no. 4,
<https://www.jasss.org/3/4/3.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary

Received: 24-Jul-00      Accepted: 12-Oct-00      Published: 31-Oct-00

This paper reports results obtained with a strategy for the Iterated Prisoner's Dilemma. The paper describes a strategy that tries to incorporate a technique to forgive strategies that have defected or retaliated, in the hope of (re-)establishing cooperation. The strategy is compared to well-known strategies in the domain and results presented. The initial findings, as well as echoing past findings, provides evidence to suggest a higher degree of forgiveness can be beneficial and may result in greater rewards.

Keywords:

game theory, classical iterated prisoner's dilemma, cooperation.

---

Introduction

1.1

This paper adds yet another strategy to the existing collection of strategies studied in the domain. The proposed strategy contains a technique which forgives defecting strategies in the hope of re-establishing cooperation. The motivations behind the design decisions are discussed with an explanation of the different features. We compare the strategy to well-known strategies and present results.

1.2

Section 2 discusses the Prisoner's Dilemma and the Iterated Prisoner's Dilemma. Section 3 discusses well-known strategies and discusses the properties found that render strategies successful. Section 4 introduces forgiving, a strategy that incorporates most of the salient features of the well-known successful strategies, but attempts to improve performance by overcoming some of the shortcomings of these strategies. Section 5 discusses our results which compare forgiving to other strategies in an evolutionary environment. The final section presents some conclusions drawn from this work and outlines some future potential work.

Prisoner's Dilemma and the Iterated Prisoner's Dilemma

2.1

In the prisoner's dilemma game, there are two players who are both faced with a decision: to either cooperate or defect. The decision is made by the player with no knowledge of the other players choice. If both cooperate, they receive a specific punishment or reward (R). If both defect they receive a larger punishment(P). However, if one defects, and one cooperates, the defector receives a large reward (T) and the cooperator a punishment (S, the sucker's payoff). The game is often expressed in the canonical form in terms of pay-offs:

	Cooperate	Defect
Cooperate	R = 3 R = 3	S = 0 T = 5
Defect	T = 5 S = 0	P = 1 P = 1

The prisoner's dilemma is a much studied problem due to it's far-reaching applicability in many domains. The prisoner's dilemma and applications has been described in Dugatkin (1988), Dugatkin (1990), Lombardo (1990) (biology), Sober (1992) (economics) and Bendor (1987) (politics).

2.2

The game becomes more interesting in the iterated version; 2 players will play numerous games (the exact number not known to either player). Note that some research has indicated that it is not necessary to look to the iterated versions for more interesting behaviour to occur. Work by Epstein (1997) into spatial zones indicate that cooperative behaviour can emerge and exist in the non-iterated version of the game.

2.3

A computer tournament (Axelrod, 1984) was organised to pit strategies against each other in a round-robin manner. The winning strategy was tit-for-tat; this strategy involved cooperating on first move and then mirroring opponents move on all subsequent moves.

2.4

No best strategy exists; the success of a strategy depends on the other strategies present. For example, in a collection of strategies who defect continually ALL-D the best strategy to adopt is ALL-D. In a collection of strategies adopting a tit-for-tat strategy, an ALL-D strategy would not perform well.

Strategies

3.1

It is instructive to look at other approaches and classify the strategies. This list is by no means exhaustive:

• periodic strategies play C or D in a periodic manner. Common strategies: ALL-C, ALL-D, (CD)*, (DC)*, (CCD)*, etc.
• random: strategies that have some random behaviour. Totally random, or one of the other types (e.g. periodic) with a degree of randomness.
• based on some history of moves tit-for-tat (C initially, then D if opponent defects, C is opponent cooperates), spiteful (C initially, C as long as opponent cooperates, if opponent defects then D forever), probers (play some fixed string, example (DDC) and then decides to play tit-for-tat or ALL-D (to exploit non-retaliatory)), soft-majo (C initially, then cooperate if opponent is not defecting more than cooperating).

There are many variations on the above types of strategies.

3.2

The initial results and analysis (which were echoed in later tournaments) showed that the following properties seemed necessary for success: niceness (cooperate first), retaliatory, forgiving and clear.

3.3

Beaufils et al (1996) question that last property and develop a strategy gradual which performs like tit-for-tat, in that it cooperates on the first move. It retaliates upon defection. On the first defection it responds with a defection, followed by 2 cooperations. Following the second defection, it responds with 2 Ds, followed by 2Cs and so forth which is far more complex than tit-for-tat and has outperformed tit-for-tat in experiments.

3.4

In a second tournament (Axelrod, 1984), of the top 16 strategies, 15 were found to be nice. These results seem to indicate that cooperative strategies are useful if there is a high chance the strategies will meet again.

The forgiving strategy

4.1

The benefits of initial cooperation, retaliation and forgiveness are clear from the initial experiments.

4.2

If we look at tit-for-tat, we can identify techniques to overcome it's shortcomings. There are certain aspects where new heuristics (with parallels in human interactions in the real world) could be used to improve upon `weak' parts of tit-for-tat's performance.

4.3

If we consider (CD)* against tit-for-tat, we get:

tit-for-tat	C C D C D C D C D C . . .
per-cd	C D C D C D C D C D . . .

4.4

The per-cd repeatedly plays a C followed by a D irrespective of tit-for-tat's move. This results in the two strategies alternating between receiving the maximum payoff and the sucker's payoff.

4.5

Tit-for-tat and other strategies could improve performance by recognising non-nice, naive strategies. Upon recognition of these strategies, a less forgiving approach can be adopted. The goal here is to be more far-sighted with respect to clearly non-nice strategies.

4.6

Another (and possibly more serious) shortcoming of tit-for-tat is the prevalence of spiraling into ongoing retaliation. Consider tit-for-tat player against nasty-tit-for-tat (tit-for-tat but attempts to exploit non-retaliatory strategies by playing a DD with some probability. Note this can also happen with tit-for-tat in noisy environments.)

tit-for-tat	C C C C C C C C C C C D D D...
nasty-tit-for-tat	C C C C C C C C C C D D D D . . .

4.7

Once nasty-tit-for-tat plays 2 Ds, the two strategies are locked in a spiral of mutual defections. This will not be broken until one of the two strategies plays two Cs.

4.8

We can also improve upon tit-for-tat by attempting to identify spirals and trying to re-establish cooperation via playing CC. This represents a type of forgiveness not present in other strategies. A CC is played following a set of mutual Ds. It is also important to limit the amount of times an effort should be made to re-establish cooperation.

4.9

Our strategy attempts to take these two factors into account:

• Don't be exploited by periodic strategies
• Try to re-establish cooperation by forgiving

4.10

Note that the above modifications do not violate the first three recommendations (generally accepted) forwarded by Axelrod - never defect first, be retaliatory, be forgiving. There are cases when the exploitation of periodic strategies can damage performance: where a pattern is recognised as a periodic strategy and we adopt an ALL-D approach to avoid exploitation. This can quickly result in a spiral of mutual defections if the opponent is not really periodic (but appears to be).

4.11

The degree of forgiveness in our strategy is of length 2, i.e we play two consecutive Cs. The length of the DD strings is set to 5. (i.e once 5 pairs of defections are encountered an effort is made to re-establish cooperation).

4.12

In summary, our strategy is tit-for-tat like, with the following amendments - exploit periodic strategies and forgive when interactions are spiraling into ongoing defections.

Results

5.1

The initial experiments carried out with the strategy was in a round-robin tournament with 37 other well-known strategies. The strategies chosen were those included as default in the simulation package created by Beaufils and Delahaye, available at http://www.lifl.fr/IPD/ipd.frame.html.

This very useful package allows experiments in a round-robin and an evolutionary setting. A set of well-known strategies are included in the package and the addition of new strategies is facilitated. We added our strategies to the pool of strategies provided.

5.2

The initial results, Table 1, showed that the strategy performed well, reaching a position of second. The only strategy that outperformed it was the gradual strategy. We see, however, in the next section that in an environmental setting the forgiving strategy performs better. (Note: strategies (soft_spiteful etc.) not explained in the text of paper are explained in the appendix of strategies.)

Top Ten Results
1	gradual	106277
2	forgiving	104086
3	soft_spiteful	102553
4	soft_joss	102487
5	c_then_per_dc	102345
6	hard_prober	102341
7	tit_for_tat	100319
8	doubler	99409
9	prober4	97761
10	worse_and_worse3	95484

5.3

In the evolutionary simulation, each successive generation contains strategies with frequency proportional to their score in the current generation. Again, 38 strategies were included initially. The performance of the strategies over a number of generations was plotted (Figure 1). We also include the top ten results following the first and twenty-first generations:

	Strategy	Proportion in next generation
1	gradual	119
2	forgiving	116
3	soft_spiteful	115
4	soft_joss	114
5	c_then_per_dc	114
6	hard_prober	114
7	tit_for_tat	112
8	doubler	111
9	prober4	109
10	worse_and_worse3	107

	Strategy	Proportion in next generation
1	forgiving	449
2	gradual	419
3	soft_joss	393
4	soft_spiteful	388
5	tit_for_tat	335
6	doubler	309
7	c_then_per_dc	263
8	soft_tf2t	206
9	hard_prober	155
10	worse_and_worse3	143

5.4

This trend continues as illustrated in Figure 1, with forgiving's representation in the population greater than that of any of the others.

5.4

Following these initial results we wished to investigate which of the two aspects of the forgiving strategy accounted for its good performance (its exploitation of periodic strategies or its ability to re-establish cooperation).

5.5

The performance of the strategy in the environmental setting indicate that its exploitation of periodic strategies, while useful, is not necessary for its success as the strategies (periodic) upon which it preys die off at a relatively early stage (e.g., (ALL-D), per-ddc).

5.6

To provide empirical evidence, we also include two variations - forgiving-1 which does not exploit periodic strategies but attempts to re-establish cooperation and forgiving-2 which attempts to exploit periodic strategies only. The graph in Figure 2 shows their performance.

5.7

As can be seen, the two strategies that attempt to forgive and re-establish cooperation flourish.

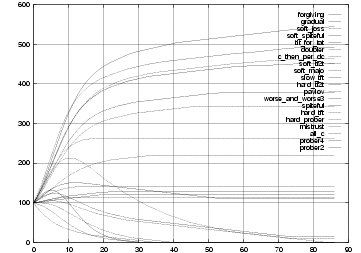
Figure 1. Evolutionary Simulation 1

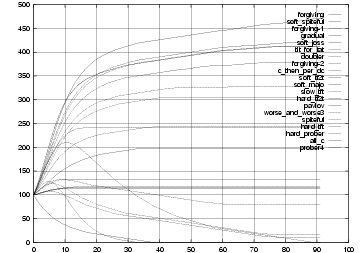
Figure 2. Evolutionary Simulation 2

We believe that the ability to re-establish cooperation is a more important feature than avoiding exploitation by periodic strategies for two reasons:

• the advantage conferred by not being exploited by periodic strategies can be reduced if there exist strategies in the environment which appear to be periodic but in reality are not.
• more importantly, in the early generations of the evolutionary simulation there exist periodic strategies; overtime these strategies will die off. This result has been shown in our experiments and also in the simulations of Axelrod (1984). Strategies that are not nice will tend to die off. Hence the advantage conferred by recognising these strategies is less noticeable as the simulation continues. The second feature of re-establishing cooperation will succeed with strategies that are retaliatory and not nice. Sophisticated strategies (like prober) may result in a spiral of defections when played against well-known strategies like tit-for-tat. The ability to re-establish cooperation will result in a greater score being obtained.

Conclusion

6.1

This paper presents another strategy for the Iterated Prisoner's dilemma. The strategy outperforms other well-known strategies by introducing two new ideas to the strategy. The first extension is that of attempting to prevent exploitation by naive periodic strategies. This is found to be a useful addition.

6.2

A more useful extension is that of breaking spirals of defection by re-establishing cooperation by playing a CC. This provided a greater advantage in the experiments and we conclude that it is this feature that gives the advantage to this strategy.

Future Work

7.1

Ongoing and proposed work include further experimentation with length of strings of Cs to be used to re-establish cooperation. The number of times a strategy should attempt to re-establish cooperation is also under investigation. A genetic algorithm is being used to breed strategies to help identify optimal values for this variable in different settings.

7.2

Another strand of work stemming from this study of forgiving, is the study of strategies working in an environment with a certain degree of noise. In this setting, there is a higher potential for mutual defection. Hence, it seems plausible that the type of forgiveness described in this paper may be of greater benefit.

References

AXELROD R (1984) Evolution of Cooperation, , Basic Books.

BEAUFILS B, Delahaye J.P. and Mathieu P (1996) Our Meeting with Gradual, A Good Strategy for the Iterated Prisoner's Dilemma , in Artificial Life, Proc. 5th International Workshop on the Synthesis and Simulation of Living Systems, editor C. Langton.

BENDOR, J and Mookherjee D (1987) Institutional Structure and the Logic of Ongoing Collective Action, American Political Science Review, 81, pages 129-154.

DUGATKIN, L.A. (1988) Do Guppies Play TIT FOR TAT during Predator Inspection Visits?, Behavioral Ecology and Sociobiology, 23, pages 395-399.

EPSTEIN, J (1997) Zones of Cooperation in Demographic Prisoner's Dilemma, Technical Report, Santa Fe Institute.

DUGATKIN, L.A. (1990) N-person Games and the Evolution of Co-operation: A Model Based on Predator Inspection in Fish, Journal of Theoretical Biology, 142, pages 123-135.

LOMBARDO, M. (1990) Tree Swallows and TIT FOR TAT: Response to Koenig, Ethology and Sociobiology, 11, pages 521-528.

SOBER, E. (1992) Stable Cooperation in Iterated Prisoner's Dilemmas, Economics and Philosophy, 8, pages 127-139

---

Appendix

Strategy	Description
soft_spiteful	Cooperates if opponent cooperates; otherwise retaliates with 4Ds followed by 2Cs
soft_joss	Tit-for-tat but defects with a probability of 0.9
hard_prober	Probes opposing strategy with 2Ds followed by 2Cs. If opposing strategy cooperates on move 2 and 3 hard_prober defects from then on. Otherwise plays as tit-for-tat
doubler	Cooperates on first move. Defects if opponent has defected (provided the opponent has defected more than twice as often as not). Otherwise cooperates.
prober_4	Probes opponent with a string of Cs and Ds of length 20. Depending on opponent's response to this string, prober responds with Ds or settles on tit-for-tat
worse_and_worse3	Cooperates on initial move. Probability of defecting following a defection increases as opponent defects.
soft_tf2t	Behaves like tit-for-tat, but only defects following 2 consecutive defections by opposing strategy.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 1998