Sophie Thoyer, Sylvie Morardet, Patrick Rio, Leo Simon, Rachel Goodhue and Gordon Rausser (2001)

A Bargaining Model to Simulate Negotiations between Water Users

Journal of Artificial Societies and Social Simulation vol. 4, no. 2,
<https://www.jasss.org/4/2/6.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary

Received: 01-Nov-00      Accepted: 01-Feb-01      Published: 31-Mar-01

Abstract

The French water law of 1992 requires that regulations on water use and water management be negotiated collectively and locally in each river sub-basin. Decision-makers therefore need new tools to guide the negotiation process which will take place between water users. A formal computable bargaining model of multilateral negotiations is applied to the Adour Basin case, in the South West of France, with seven aggregate players (three "farmers", two "environmental lobbies", the water manager, the taxpayer) and seven negotiation variables (three individual irrigation quotas, the price of water, the sizes of three dams). The farmers' utility functions are estimated with hydraulic and economic models. A sensibility analysis is conducted to quantify the impact of the negotiation structure (political weights of players, choice of players...) on game outcomes. The relevance of the bargaining models as negotiation-support tools is assessed.

Keywords:

game theory, bargaining, water management, negotiation, decentralisation

Introduction

1.1

A growing number of conflicts involving collective goods is resolved through negotiations between stakeholders. The water management issue is one of the most striking examples : many countries have adopted a decentralised approach in order to design water policies which are both politically acceptable and environmentally sustainable. The 1992 French water law has formalised this process by setting the negotiation framework within which local water management rules^[2] must be decided. There is therefore a growing need for analytical instruments which could help to guide the negotiation process and the choice of the negotiation procedure. Within this perspective, the objectives of this paper are fourfold :

1. To assess to what extent a bargaining model is appropriate to simulate the negotiation process which is expected to take place between water users within the context of the 1992 French water law.
2. To identify and to assess well-behaved utility functions reflecting the hierarchy of the stakeholders' preferences with regard to the negotiated variables.
3. To measure how the solutions of the bargaining game are affected by the negotiation structure
4. To examine the conditions of the model validation and its usefulness for negotiation support.

1.2

Our approach is based on a case study which we have explored extensively and for which we have conducted a series of simulations in order to compare negotiation solutions under different negotiation structures (Rio et al. 1999). However, the bargaining model which is presented here has not been used to guide the negotiation process although the authors are intending to use a revised version as a negotiation-support tool on another case study. This paper will draw from the work and conclusions of this case study to highlight the main difficulties involved in seeking to design a useful tool for accompanying the difficult process of setting up an efficient negotiation mechanism.

Bargaining games and natural resources management

Collective action in the management of natural resources

2.1

The over-exploitation of free access resources is a well-known issue for which the traditional remedies are the privatisation of the resource or the regulatory control by a legitimate authority. However, none of these solutions work satisfactorily in the case of water management. Water is a partially renewable natural resource moving through an intricate hydrological network, and it is inherently variable and uncertain in time. Moreover, water uses are manifold: the three types of sectoral demands are agricultural, municipal and industrial, to which must be added ecological demand. They encompass production and consumption objectives as well as recreational, aesthetic and moral^[3] purposes. Water demands are therefore a combination of economic uses (water is then a production input) and non economic uses (water is then the argument of a utility function). Moreover the competition between uses is often difficult to identify and technically complex to quantify^[4].

2.2

The consequences are threefold:

1. In most cases, water rights are not proper property rights but are user (or usufructuary) rights which allow the use of water for a given period of time under pre-determined conditions (often designed for preserving minimal thresholds of ecological sustainability or to enforce the fulfilment of certain reciprocal obligations to society^[5]) but do not allow the transferability of the right. It makes difficult the implementation of the market solution, which is expected to ensure water allocation efficiency.
2. Despite the availability of specific methods such as contingent valuation, the quantification in economic terms of non economic uses remains controversial. It is therefore impossible to calculate objectively a social utility function which the central authority would be expected to maximise.
3. Due to technical difficulties, the state of the resource and the cross effects of its uses are imperfectly known and monitored. It may generate information asymmetries between different stakeholders and more specifically between the centralised management unit and water users.

For all the reasons listed above, water conflicts are often very complex and sometimes outstrip the capabilities of even the best institutional arrangements. Although there have been enormous efforts to improve the ability of allocation and management systems, it is increasingly acknowledged that new solutions must be found outside the established processes of centralised public decision-making .

Benefits expected from decentralised decision-making and devolution mechanisms

2.3

One of the responses has been to promote collective negotiated decision-making procedures: more than simple decentralisation, which is a transfer of responsibility from the central government to its local agencies, it implies an explicit political process by which more autonomy and independence is granted to local authorities and stakeholders. It refers to the ideas of empowerment of local people and devolution of government.

2.4

The expected positive effects of a locally negotiated decision-making procedure for water management rely on four hypothesis: a better informed decision leading to management choices which are better adapted to local conditions; improved accountability of stakeholders; and higher legitimacy of the decisions. According to Caldart and Ashford (1998), negotiated decision-making translates into easier implementation, less litigation and improved stability of the agreements. However, it is still at an experimental stage and decision-makers are seeking guidance on the kind of negotiation structure they should set-up to get the best solution. The rapidly growing literature in environmental sociology (Pellow 1999) promotes the "veto-right" rule as a powerful incentive to build a consensus as well as to attract stakeholders prone to make a "hit and run"-type demonstration. It is consistent with the theoretical finding that the convergence of a bargaining game can only be proved with unanimity rules (which are formally equivalent to a veto right system). This kind of literature therefore suggests that game theory is one of the economic approaches which can be efficiently mobilised and which offers new perspectives by analysing the negotiations as a bargaining game.

The case of water management in France

2.5

The new French water law promulgated in 1992 specifies that water is a national resource and that water management should be organised so as to reconcile water user needs and environmental uses. It requires that specific development plans be set up to tackle water issues (SDAGE^[6]) at the scale of each hydrological basin and that new water regulations be progressively enforced at the much smaller scale of catchment areas (SAGE^[7]). SAGE regulations have to be negotiated locally between all stakeholders under the supervision of local authorities.

2.6

The decentralisation of water management in France is the outcome of a general trend towards the integration of local authorities into the process of policy formulation and application. The former water management system was a top-down centralised system. It gives now place to a management system based on policies defined in a progressive way, at different nested levels. However, the role of the state remains prominent for several reasons (Goodhue et al. 1998):

• The SAGE negotiations take place within a given set of constraints which are set up by the SDAGE under state supervision and which define the acceptable domain of negotiated variables: for example, objective discharge (corresponding to an average desirable discharge at various points of the river) are defined within the SDAGE, limiting therefore the maximum water quantities which can be pumped from the river (and therefore the total amount of quotas which can be granted to farmers).
• SAGE negotiations must be initiated locally and must be conducted within an ad-hoc committee (the Commission Locale de l'Eau CLE) bringing together water users (25% of the CLE embers), members of local councils (50%) and state representatives (25%) . The state is the last resort decision-maker: it has veto power on all collective decision and it imposes its own solution when no compromise can be found between negotiating parties. Thus, the water law does not undermine the role and responsibilities of the central state. From this point of view, the SAGE is more a dialogue committee than a negotiation committee. It can also be interpreted as a mechanism of information revelation by stakeholders to the benefit of the state
• The SAGE procedure is still fairly recent and only three SAGE have been officially ratified in France since 1992. However many SAGE negotiations have been launched with mixed success and with very different outcomes. They lack necessary experience and the CLE are proceeding without guidance. There is a growing need for negotiation-support models which would fulfil two objectives: (i) help to identify the best negotiation structures; (ii) accompany the negotiation process and help stakeholders to reach a stable compromise.

Description of the bargaining model

3.1

The French water law establishes a new decision-making procedure for water management which is halfway between a simple decentralisation process and a complete devolution system. However, despite the constraints imposed by the water law , the SAGE negotiations can be interpreted as a bargaining game in which players try to reach a compromise over the sharing out of a pie - the allocation of " user " rights over a common-pool resource.

The bargaining game

3.2

The game model is documented in Rausser and Simon (1991) and Adams, Rausser and Simon (1996). It is a non cooperative model of multilateral bargaining which is an extension of the Stahl-Rubinstein game (Rubinstein 1982): it incorporates multiples players and multidimensional issue spaces. The structure is the following: N players gather to negotiate over a given set of K policy variables x_k. Each player is characterised by a pre-defined payoff function (called utility function) with respect to the negotiated variables. The negotiation is organised as a sequence of games with finite bargaining horizon: at each round t, a proposer j amongst the N players is chosen randomly with a given access probability a_j and makes a proposal X^j_t = (x^j_1,t,... ,x^j_k,t,... ,x^j_K,t) over the policy variables. All other players i#j calculate the utility Uⁱ they derive from this proposal and compare it with their reservation utility EUⁱ. A player's reservation utility is the utility he can expect from the following round t+1: it is the sum of the player's utilities derived from each player's proposals (including himself) in the next round, weighted by their access probability:

3.3

Players choose to move on to the next round when their reservation utility is higher than the utility derived from the proposer's offer. A compromise is reached when all players agree on a proposed set of policies X. The game then ends. It has to be noted that such game structure implies perfect information between players. It is a strong assumption which is of course not verified in real-life negotiation processes. Such discrepancy with reality will be taken into account when interpreting the model's outcomes.

3.4

One of the characteristics of the model is that there is a sufficiently large finite number of negotiations rounds (sufficient to reach convergence before the last round). Convergence of the game is forced by the characteristics of the "disagreement outcome": if no compromise is reached in the last round, then a pre-specified disagreement outcome is implemented which yields for all players lower utilities than any negotiated outcome. Therefore, the player selected in the last round can get his preferred point. Players in the previous rounds anticipate this outcome and the bargaining game is therefore theoretically solved in the first round by rational expectation of the first player who selects right away the equilibrium solution. However, contrary to the Rubinstein model, this model does not introduce a last-mover advantage because players do not play in turn: at each round, they all make a proposal which maximises their utility with respect to their participation constraint in the next round. The multilateral bargaining model allows the endogenous formation of coalitions when the decision rule is not unanimity.

The solving procedure and the formal algorithm

3.5

Formally, the game is solved recursively by backward induction. In the last round T of the game (round 1 of the computable model), we know that the proponent i will select a final set of policies Xⁱ_T which maximises his utility : other players will have to accept it because the disagreement outcome is even worse for them. At round T-1 (round 2 of the computable model), each player j will make a proposal X^j_T-1 with probability a_j which maximises his utility with respect to the reservation utility constraint: his proposal must provide to all players (including himself) a level of utility superior to their expected utility in round T.

3.6

Of course, the proposal must also be consistent with exogenous constraints. The same procedure is repeated until the proposals made by all players converge towards a limit point which is the equilibrium solution of this sequence of negotiation games.

3.7

Figure 1 is a simple illustration with three players and a two-dimensional issue space presented in Adams et al. (1996). Player's best choices in the last round T are at the vertices of the triangle. The participation frontiers in round T-1 are the indifference curves of the players corresponding to their reservation utility in round T-1: in this particular example, the lower access probability of player 1 is represented by a greater distance between his preferred point and his participation constraint in the preceding round. In round T-1, the acceptable domain is thus limited to the area ABC. Round after round, we could draw the new indifference curves of players and the tighter possible set until finding the limit Z of these sets which, in this particular case, is the weighted centre of the initial triangle.

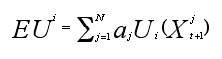
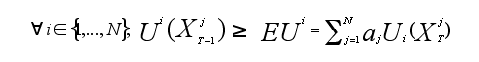
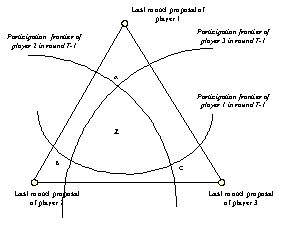
Figure 1. Simplified representation of the multilateral bargaining model from Adams et al. (1996)

3.8

Conditions for convergence are (Rausser and Simon 1991):

• X, the set of K possible policy alternatives must be a convex compact subset of the K-dimensional Euclidian space,
• Player's payoff functions Uⁱ(X) must be strictly concave (this assumption can be weakened under certain conditions).

Convergence cannot be reached in two situations:

• When the decision rule is not unanimity, it may happen that cyclical coalitions impede convergence
• When the negotiated variables hit the constraints, there is no solution in the realisation domain.

Parameters for the model specification

3.9

The initial specifications of the game are: the identification of authorised players, the definition of the negotiated variables, the choice of the pay-off functions of players. However, the structure of the negotiation is also defined by other exogenous variables:

• The vector of access probability (a_i) can be interpreted as the vector of players' political weights. In many negotiation cases, players with the highest influence are able to push forward efficiently their proposals. The political influence of a group is usually associated to its electoral weight (number of voters in the constituency) or/and to its economic power, but it is also very often linked to the individual influence of the group leaders.
• The decision rule can refer to the unanimity, to the majority rule, or to any other rule. In the latter case, a list of admissible coalitions is defined, the admissible coalition being a subset of players that can impose a solution on the rest of the group.

Model implementation: the Adour case

Description of the issues at stake

Water scarcity

4.1

Our research work focuses on the upstream part of the Adour Basin (south-west of France), from its source in the Pyrenées to its confluence with the Midouze river. During the last twenty years, irrigation has become the main water use in the region (170 millions cubic meters, mainly diverted in summer, for 47500 ha of irrigated land). This massive growth of irrigation has led to a net deficit of water in the basin (31.8 millions cubic meters). It has triggered the anger of environmental pressure groups which have become increasingly vocal on the issue of aquatic life and landscape protection.

From regulatory to integrated water management

4.2

Water management in the Adour sub-basin is controlled by a top-down administrative procedure: agricultural producers ask for an annual authorisation to pump water in the river. The authorisation is specified for a given area (the official irrigated area^[8]) and for a given discharge (the authorised discharge for pumping). Farmers pay water fees proportionally to their irrigated area and to the authorised discharge obtained. Local authorities are entitled to forbid irrigation when the river discharge drops below "crisis discharge thresholds" (débits de crise DCR) which are theoretically defined so as to preserve the aquatic life in the river and domestic use. In the early nineties, this regulatory water management failed in ensuring water balance between uses and resources, first because authorizations of pumping have been delivered to farmers without control, and also because of the lack of control instruments to measure water quantities used by farmers (most agricultural producers pump water directly from the river or from affluent rivers).

4.3

Another type of water management is now developing, which is organised at decentralised levels in order to take into account the viewpoints of all stakeholders. The 1992 national water law states a number of principles on decentralised water use regulation, but enforcement of the law and details of implementation are decided and controlled by regional and local administrative entities.

4.4

In the Adour zone:

1. The main scheme for water development and management (SDAGE) has been devised at the scale of the Adour-Garonne region: it defines reference values for crisis discharge (DCR) and objective discharge (DOE) at various points of the river (Estirac, Aire-sur-Adour, Audon). Local state representatives are expected to make these threshold flows enforceable.
2. A management plan for low waters (Plan de Gestion des Etiages PGE) was negotiated^[9] in 1998 and approuved in march 1999, and is to become the key piece of low water management in this basin. This plan is a contract negotiated by all stakeholders. It settles, for the Adour river and its tributaries, areas and water volumes that can be dedicated to irrigation. This collective volume will then be shared out between individual farmers on a per hectare basis^[10]. This plan also assesses the needs for additional dam capacity in order to balance water supply and water demand. It was initially planned to build successively three reservoir dams in the Adour area (see Figure 2): the Ousse dam (dam 1) above the midstream sub-basin (5 million m³), the Eslourenties dam (dam 2) on the Gabas river to increase the discharge of the rivers Lees and Gabas and increase the Adour discharge upstream the Aire-sur-Adour town (20 million m³) and finally the upstream Adour dam (dam 3^[11], 20 million m³). Investments costs for dam construction should be financed jointly by the central state (ministry of agriculture and ministry of environment), and by local councils and water agencies provided an agreement is reached between all stakeholders on the allocation of water quotas and on the price of water charged to users. The contribution of public finance to the construction project is contingent upon the implementation of a new water tariff system ensuring that water fees cover all maintenance and management costs induced by the new dams (Faÿsse and Morardet 1999).

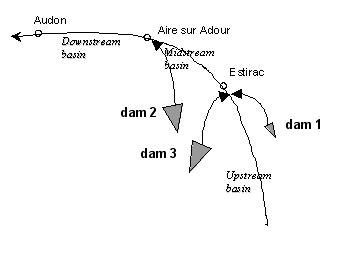
Figure 2. Projects for new dams in the Adour river basin

Stakeholders in the Adour basin

4.5

Discussions and negotiations over water quotas and water fees take place within the Basin committee which gathers:

• representatives of the central state ,
• local representatives of the ministry of agriculture and of the ministry of environment
• elected representatives of agricultural producers
• local councils
• a group representing the interests of all water users in the Adour Basin (urban consumers, industries, environmental lobbies)
• the water manager: in the Adour basin, it is a semi-public institution, in charge of maintaining existing reservoir dams, of delivering water to farmers and of providing a steady flow in the river.

From reality to model

Choice of players

4.6

Due to the large number of stakeholders involved in the real process of negotiation, and since it is rather difficult to identify their respective preferences over the negotiated variables, we have chosen to simplify the structure of the Adour negotiation game by taking into account only seven players: one "aggregated" farmer in each of the three sub-basins, two environmental groups, the water manager and a representative of all elected local councils with the generic name of taxpayer.

4.7

In the case of farmers (1332 farms for 47174 ha in the studied area), the main difficulty was to define the aggregation procedure. Three types of aggregation were possible:

1. according to their organisation as interest groups: in the real negotiation process, their interests are defended in each administrative area by the elected representative of all farmers;
2. according to their preferences over the negotiated variables, which could possibly depend on the type of irrigated production, the localisation of the farm and its size. For example, farmers producing high value added products would accept more easily a high water price. On another hand, upstream farmers would not accept easily restrictions on their water consumption because they are not used nor organised to face severe water shortages.
3. according to a geographic division which reflects the hydraulic system. We have chosen this last option because the negotiated variables are also defined at the sub-basin scale. The research area is thus divided into 3 sub-basins^[12] (see appendix I) (i) the upstream Adour, between Tarbes and Estirac (ii) the midstream Adour, between Estirac and Aire-sur-Adour, (iii) the downstream Adour, between Aire-sur-Adour and Audon.

This aggregation step is quite crucial: according to the way they are aggregated, farmers might have to defend more or less divergent positions.

Negotiated variables

4.8

The Adour negotiations are primarily focused on the sharing out of available water (quantity of water in the river after deducting the quantities necessary to respect the crisis flow) between agricultural uses and environmental needs. Since crisis flow constraints are defined for each sub-basins, the negotiated variables are the levels of irrigation quotas per hectare which can be granted to each of the three sub-basins (Qu for the upstream quota, Qm for the midstream quota and Qd for the downstream quota), residual flows being attributed to the player "environmentalist" to protect aquatic wildlife. Moreover, since the condition for state participation in the financing of new dams is that the water management agency covers the maintenance and operation costs with water sale receipts, another negotiated variable is introduced: the price of water (P). In the simulations presented in this paper, the assumption was made that a uniform water price would be charged in the whole Adour Basin^[13]: agricultural producers will seek the lowest price which satisfies the budgetary constraints whereas the environmentalist groups will try to push up the price so as to induce a decrease in water use. The third category of negotiated variables is the respective sizes of the three dams (DC1 dam capacity for the first dam, DC2 dam capacity for the second dam and DC3 dam capacity for the third dam). The building-up of new dams may have negative consequences on the landscape quality. On the other hand, dams provide additional water storage capacities which contribute to relieve the water constraint in summer. It is assumed in the following simulations that the dam size is a continuous variable between zero (no dam) and the maximum dam capacity specified in the management plan^[14].

Hydraulic constraints

4.9

We have previously pointed out that minimum low water flows (crisis discharge), defined at reference points, should be respected. It is therefore crucial to check in the game structure that negotiated quotas allocated to farmers do not exceed the total quantity of water available and that crisis flows (which are the minimum flow acceptable) are maintained in the river. This condition is written as follows for each sub-basin :

Natural water stock + stock provided by will-be dams + stock provided by existing dams - water used by basins which are not included in the negotiation - total quotas given to farmers = residual stock in the river

residual stock in the river > crisis stock

Hydraulic models have been developed in order to estimate natural flows for a set of climatic years.

Budgetary constraint

4.10

The budgetary constraint requires that water charges paid by farmers cover operation and maintenance costs of the new dams. It is assumed that water fees are calculated on the basis of authorised quotas. The constraint therefore is:

Sum for all three sub-basins (Quotas * Price) (operating and maintenance costs of new dams

Operating and maintenance costs have been estimated on the basis of data for existing dams as a function of the new dam capacities.

Estimation of players' utility functions

Economic use: the profit functions of farmers

4.11

Irrigation is the only economic use of water considered in the game. We make the assumption that the utility functions of farmers are well represented by their profit functions. By doing this, we assume that farmers have no other concerns than the maximisation of their own financial interest.

4.12

To evaluate this profit function, we modelled farmer behaviour with micro-economic linear programming techniques. The objective was to generate a set of data on profits, quotas and prices in order to finally estimate the parameters of their profit function with an econometric least square regression method.

4.13

Micro-economic farm models (Gleyses and Morardet 1997) were built and calibrated on the basis of eight representative farms, identified with a typology procedure designed so as to avoid "arithmetic" aggregation bias^[15] (see Appendix I). Such a bias comes from resources aggregation over several farm types, which may disable some constraints active in a specific kind of farms. Farm models are stochastic linear programming models which take into account risks on water resource availability and on crops water requirements.

4.14

Simulations were then conducted for each farm type, for quotas varying between 500 cubic meters/ha and 2000 cubic meters/ha, and for water prices varying between 0.02 F/cubic meter and 3 F/cubic meter to calculate total gross margin and total water demand. Results were aggregated for each sub-basin: the three data bases obtained were then used to estimate the parameters of the profit functions of each sub-basin's aggregate farmer.

4.15

In our simulations, all prices and fixed factors are held constant but the price of water and the quota (similar to a fixed factor of production): therefore the translog^[16] functional form which was estimated does only include these two variables:

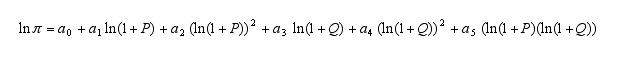
with π aggregate profit in million francs in sub-basin i
P price of water in francs/m³
Q total quota given to the sub-basin (in million m³)

Non-economic use: preferences and trade-off between variables

4.16

The others players present in our bargaining game are designated players. They are expected to summarise and defend the interests of real individual stakeholders who may have various motivations and preferences over negotiated variables. For instance, among environmental pressure groups one can distinguish those who, in the downstream part of the basin, wish a high level of minimum flow and are then in favour of dams, from those, upstream, who oppose dam building for nature preservation reasons. Likewise, some taxpayers are ready to accept a high level of tax to finance water preservation, although some others give priority to the reduction of public expenditures.

4.17

We have tried to build ad-hoc utility functions which reflect as well as possible their hierarchy of preferences upon the negotiated variables and the trade-off they are ready to accept between the variables.

4.18

We adopted a procedure based on an intuitive reasoning translating the player's preferences into a functional form, having the "good" mathematical properties. Qualitative interviews were simultaneously conducted with stakeholders (Faÿsse 1998). However, this process leaves unanswered the question of the validation of such utility functions. In another case study, the Central Valley in California, direct approach "à la Keeney-Raiffa " (1976) is considered, to elicit parameters and functional forms of the stakeholders utility function, which is a worthwhile way to homogenise the building utility functions.

4.19

It has to be emphasised that no interpersonal comparison of utilities is conducted in the bargaining model: at each round, each player only compares his utility with the utility he can expect at the following round. Therefore, we need not establish comparable utility functions.

Environmentalists

4.20

It is observed that environmentalists can be classified into two groups : the priority of the first group, located downstream, is the quality of aquatic life whereas the priority of the second group is the preservation of landscape. We therefore chose to introduce two environmental groups with similar functional forms for their utility functions but different parameters: the utility functional form is characterised by a constant elasticity of substitution (CES) with respect to the residual flow in the river and the gaps between maximum dam capacity and negotiated dam capacity.

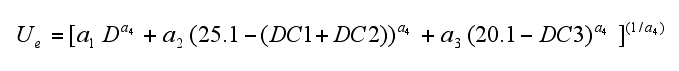
with D residual flow in the downstream basin. DC3 is assigned a different coefficient from DC1 + DC2 because the third dam would be located in the mountains and there is a stronger aversion for this dam due to landscape preservation concerns than for the first two dams.

4.21

The first environmentalist (the "river environmentalist") is more sensitive to the quantity of water left in the river and is therefore relatively more mobilised by the fate of fishes and the sustainability of aquatic life, whereas the priority of the second category of environmentalist (the "landscape environmentalist") is the preservation of landscape and he battles against dam construction. We have chosen values for the parameters of the utility function which reflect these differences in priorities (see appendix II).

Taxpayer

4.22

The assumption is made that the taxpayer is averse to public spending and therefore its utility decreases when new dam capacity is built. Besides, the taxpayer has also some concern for the quantity of water left in the river, which can be used for different purposes (recreational use, drinking water etc.). This double preference is translated by a Constant Elasticity of Substitution function (CES) with two input arguments "residual flow D" and the gap between maximum investment costs (MIC) and effective investment costs (IC):

Manager

4.23

It is assumed that the utility of the manager increases when his level of activity (for which two dummies are total water provided to farmers and total dam capacity) increases and his utility decreases when the budget imbalance (positive or negative) increases. As a first approximation we assumed that the manager is averse to any positive or negative deviation from the budget balance since it is in his mandate to balance out expenses and receipts. The utility function of the manager is written as a CES between three series of arguments: quotas, dam capacities and the gap between maximum potential losses and the actual budget

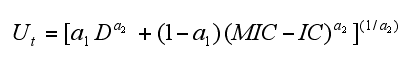
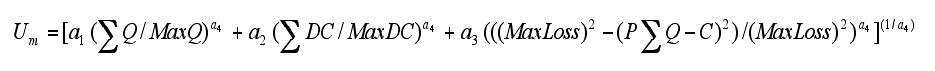
with C operating and maintenance costs in million francs
MaxQ maximum sum of quotas which can be allocated given the exogenous constraints
MaxDC maximum dam capacity
MaxLoss : maximum potential losses by the manager

4.24

In the three cases (environmentalists, taxpayer and manager cases), the "verification" procedure for these utility functions follows three steps:

1. check with the stakeholders that their level of satisfaction is effectively related to the identified variable
2. check that the chosen functional form is strictly concave with respect to the negotiation variables
3. estimate the relative range of values taken by the parameters by assessing players' order of preferences between variables and the level of substitution which they are prepared to accept. Contingent valuation methods and revealed preference methods can be useful tools at this stage.

This method is fairly crude and needs to be refined. However, there are very few examples of empirical work which try to characterise the "satisfaction" function of stakeholders which do not make a direct economic use of water.

Simulations, validation and use

Which simulations ?

Reference simulation

5.1

The reference simulation includes seven negotiated variables and seven players: the three groups of agricultural producers (upstream, midstream and downstream), the two environmentalists, the manager and the taxpayer with equal political weights (1/7^th each). Table 1 provides the outcomes of the negotiation and the consequence in terms of water left in the river (which is compared to the crisis discharge defined in the SDAGE).

Table 1: reference simulation
	Reference simulation : 7 players, equal weights
Upstream quota	1665 m3/ha
Midstream quota	2501 m3/ha
Downstream quota	2787 m3/ha
Dam capacity 1 (in millions m3)	5 Mm3
Dam capacity 2 (in millionsm3))	0 Mm3
Dam capacity 3 (in millions m3))	14 Mm3
Water price (FF/m3)	0.077
Quantity of water left in the river	11 m3/s
Crisis discharge	2.8 m3/s

Changes of political weights

5.2

Since the "access probability" parameter - the probability for a player to be chosen to make a proposal - expresses the opportunity for a player to obtain a compromise, it can be interpreted as a "political weight". The political weight can be used as a parameter to tackle the issue of lack of information concerning the true preferences of players. For example, if one ignores whether the environmentalist group belongs to the landscape group or to the river group, it is interesting to conduct a series of simulations in order to explore to what extent his proposals are changing when various linear combinations (through changes in the political weight) of the two utility functions are considered.

5.3

In the following simulations, the political weight of one of the players is increased from 0 to 1 whereas the other players share out equally the remaining political weight^[17]. The following graphs show the pattern of negotiated water allocation between the agricultural producers and the river, as well as the negotiated total dam capacity.

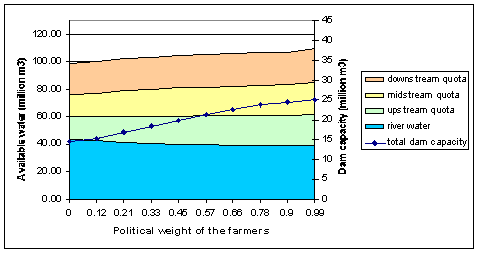
Figure 3. Negotiation outcomes when the political weight of farmers increases

5.4

As expected, the higher the weight of the farmers, the greater the quantity of water dedicated to irrigation. The upstream and midstream farmers gain proportionally more than the downstream farmer when their collective political weight increases. The dam capacity increases from 15 Mm³ to 25 Mm³. It is interesting to notice that farmers are not willing to push for the construction of the third dam: although it would provide more irrigation water, it would also require a significant increase in water prices which farmers are not prepared to pay.

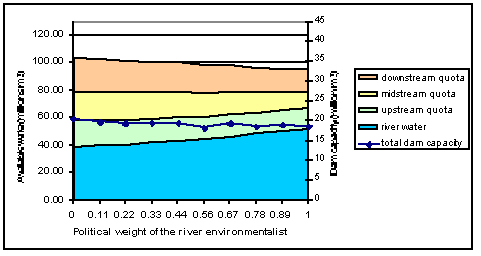
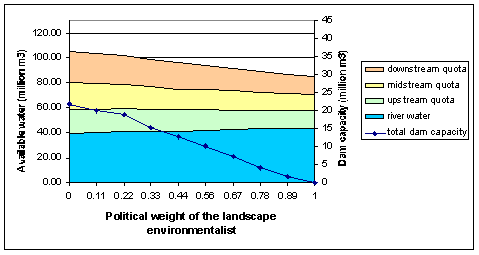
Figures 4 and 5. Negotiation outcomes when the political weight of environmentalists increases

5.5

The reinforcement of the environmentalists' weight induces a steady decline in irrigation water. However, the interests of the two environmentalists diverge on the issue of dam capacity. Whereas the growing influence of the "landscape environmentalist" reduces the dam sizes (down to zero when he is in a "dictatorial position"), the "river environmentalist" is fairly indifferent to dam capacity and allows that up to a 20 million m³ new dam capacity to be built.. In both cases, the quantity of water left in the river increases, more significantly when the "river environmentalist" becomes more powerful.

5.6

The negotiation outcomes observed when the taxpayer political weight increases are very similar to the outcomes obtained for the simulations conducted with the landscape environmentalist (Figure 6). It is justifiable by the similarity of their respective utility functions.

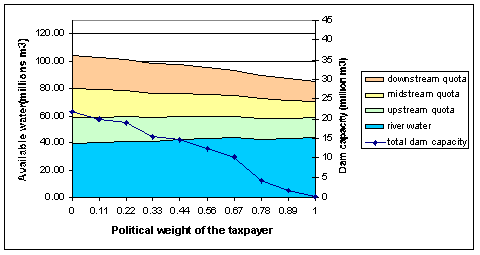
Figure 6. Negotiation outcomes when the political weight of the taxpayer increases

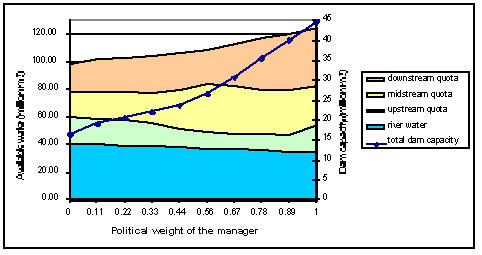
Figure 7. Negotiation outcomes when the political weight of the manager increases

5.7

Figure 7 shows that the consequences of the growing influence of the manager at the negotiation table are: (i) a slight decline in the quantity of water left in the river, which reflects the conflicting interests of the manager and the environmentalists (confirmed by Figure 8), (ii) the realisation of the planned maximum dam capacity, (iii) and a large increase of water allocated to irrigation, which reveals the converging interests of farmers and the manager.

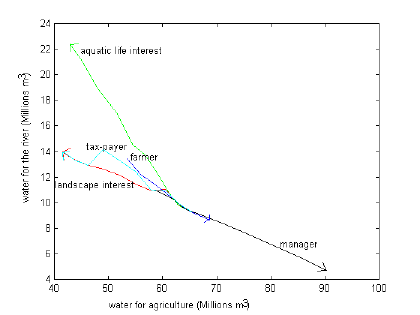
Figure 8. Trajectories of negotiation outcomes

5.8

This figure summarises the preceding results. Each trajectory is associated to a player and shows the changes in the sharing out of water between irrigation needs and aquatic life needs, when his political weight increases separately from zero to 1. No specific interpretation can be made on the local proximity of trajectories. However, the direction of the arrows indicates unambiguously how the negotiation outcomes change when the political weight of the player considered increases.

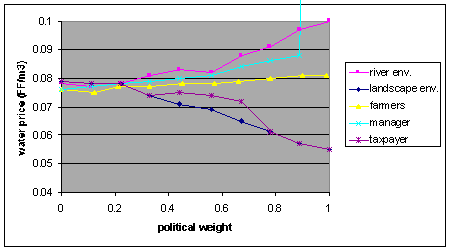
Figure 9. Changes in water prices when players' political weights change

5.9

The opposite interests of the manager and the landscape environmentalist are the main sources of conflict within the negotiation: both are equally indifferent to the water dedicated to the aquatic life. Their opposition highlights the contrasted options defended by the two types of environmentalists. On the price issue (Figure 9), the convergence between the landscape environmentalist and the taxpayer is confirmed. However, the manager and the river environmentalist which conflict over the water dedicated to the river, find common grounds to defend high water prices. Farmers accept a slight price rise in order to get larger irrigation water quantities. Farmers share common goals with the manager as long as the price constraint remains non effective.

Scope for negotiation manipulation

5.10

The previous simulations have enlightened the nature of conflict between players and the narrow domain of potential agreement. Let's assume that the negotiation is organised by a mediator working like a central decision-maker. We demonstrate in the following part how the mediator can manipulate the negotiation structure in order to pick up the outcome he desires. Two cases are envisaged: (i) the exclusion of a player, (ii) the choice of the initial proposal made to stakeholders.

Exclusion of a player

5.11

A second category of simulations compares the negotiation outcomes for three situations: (1) the player is excluded from the negotiation table, (ii) the player is sitting at the negotiation table but his political weight is zero, (iii) the player has the same political weight as the 6 other players (1/7^th), which is the reference simulation. Figure 10 shows the outcomes of these three simulations for the landscape environmentalist case.

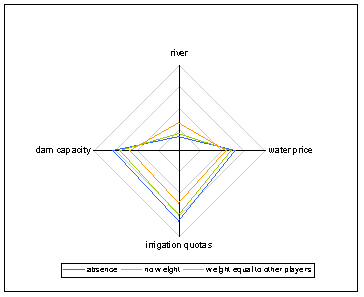
Figure 10. Negotiation outcomes for three negotiation structures - landscape environmentalist

Note: negotiation variables are standardised and the axis scales are all identical

5.12

Figure 10 shows that the negotiation outcomes when the landscape environmentalist is excluded from the negotiation table are different from the negotiation outcomes when his political power is null. Without the environmentalist, the outcome of the negotiation is favourable to the dam capacity and to irrigation quotas. With an inactive environmentalist, the allocation of water is closer to the allocation observed in the reference situation.

5.13

It is therefore very different to exclude a player and to let him participate even without any negotiation power. In the latter case, although the "powerless" player does not intervene in the negotiation process, he does influence the outcome because other players have to take his reaction into account in their proposals. This is the consequence of the unanimity rule. Such situations can be observed in many empirical cases. The multilateral bargaining model translates this situation: other players do not include the zero-weight player's proposal in the calculation of their expected utility but their proposal must respect his expected utility constraint. Therefore the outcome of the game is also influenced by his preferences. It is not the case when he is not at the negotiation table.

Changes in the initial proposal

5.14

In the simulations conducted so far, the initial proposal made by each player is the proposal which maximises his utility with respect to the exogenous constraints. In the following series of simulations, the proposal in the first round of the algorithm is made by a the central decision-maker (who is not a stakeholder) and it initiates the negotiation process.

5.15

Three simulations are conducted for three different initial proposals (Table 2).

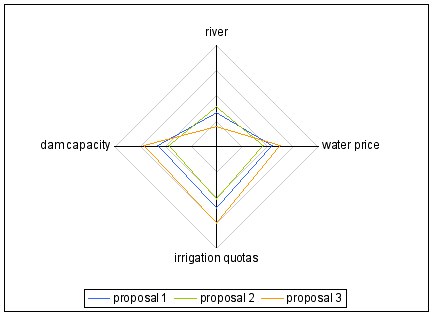
Table 2: Characteristics of the three initial proposals
	Qu (m3/ha)	Qm	Qd	DC1 (Mm3)	DC2	DC3	P (FF/m3)
Proposal 1	1300	1500	1500	5	20	20	0.04
Proposal 2	1300	1500	1500	5	0	20	0.04
Proposal 3	1800	1800	1800	5	20	20	0.04

Figure 11. Negotiation outcomes for three different initial proposals

5.16

The proposal 1 which offers a maximum dam capacity (45 million m³) leads to a final agreement of 19.7 million m³. When the initial proposal is based on lower dam capacities (proposal 2), the final outcome for dam capacity is lower (17.8 million m³). Associated losses in terms of water availability are entirely borne by farmers. Initial proposal 3 which offers higher irrigation quotas leads to much higher dam capacities (22 million m³), higher quotas to farmers but much less water left in the river.

5.17

To conclude, these experiments make clear that it is relatively easy for the decision-maker in charge of organising the negotiations to manipulate the negotiation process in order to pick up the outcomes he prefers. It therefore raises a number of issues concerning the adequate use of this model as a negotiation-support tool. In particular there are risks of misuse by one player at the expenses of others.

Validation and use: which method?

5.18

The question of model validation is multidimensional. The first phase of the validation process is an internal validation of the consistency between the formal model and its Matlab computation: the use of comparative statics can help to detect computing bugs and misspecifications through the identification of absurd or suspiciously counterintuitive results. The relative simplicity of the algorithm developed in the model and the use of the software Matlab allows computational tractability.

5.19

The second phase of the validation is to check the accuracy of the model in simulating and reproducing an historical well-known situation. Only when this experiment is successfully completed (after adjustments and calibration of the model) can one assess the qualities of the model as an extrapolative device. The validation results also give some indications on the order of magnitude of the unavoidable errors which must be expected for the prediction, given the hypothesis made on the value of critical exogenous parameters. The validation procedure is also a good way to identify the possible weaknesses of the model and therefore to define the limitations concerning its potential uses. However, it is obvious that the complexity of agents interactions has led us to adopt necessary simplifications which increase the gap between simulated game solutions and real world outcomes.

5.20

However, the validation procedure should be selected with regard to the objectives of the model. The Adour model has been developed as a negotiation-support tool and not as a decision-support tool. Therefore, the predictive power of the model is not our main concern. Our objective is to provide a better understanding of the complex interrelations between the various components of the modelled system: preferences of stakeholders over negotiated variables, the role of exogenous (hydraulic and budgetary) constraints in the bargaining game, the consequences of the structure of negotiation (decision rule, players' weights, dimension of the issue space etc.) on the bargaining outcome etc. Within this perspective, the model could then be used with two purposes: (i) to provide guidelines to the negotiation organisers, helping them to choose the adequate negotiation structure (ii) to increase the participation of stakeholders and to improve the quality of dialogue by reducing information asymmetries between them. The final objective is to improve the gradual build-up of a common representation of issues at stake which would favour the convergence of views and the emergence of a stable compromise.

5.21

In the former case, it is necessary that the model be validated on its accuracy for schematically simulating the consequences of changes in the negotiation parameters, not in absolute terms but in relative terms. The validation could be conducted by comparing simulated results with expected outcomes by "experts" (neutral observers of the negotiation process with a thorough knowledge of the empirical case). We are intending to conduct this validation in the next phase of our project. In the latter case, the validation is positive when stakeholders themselves acknowledge the accuracy of the model in formalising their perception of the issues at stake. Role playing games can be a useful device both for validation purposes and as a negotiation-support tool through gradual reinforcement of the credibility and the legitimacy of the model (Barreteau and Bousquet 1999).

Conclusion

5.22

In this research work, our attempt to build a model of the negotiation process was driven by a double concern : to analyse the consequences on the outcomes of the negotiation of the structure of the negotiation and to provide an informational framework to all stakeholders in order to improve the quality of the agreement.

5.23

Our objective was also to demonstrate that the objectives of realism can be compatible with the requirements of the modelling process. However, a number of improvements would be necessary to reflect the "procedurality" of the true negotiation process: the bargaining model should include some learning process, path dependency as well as some dynamics in the utility function. In the real world, negotiations take years during which many parameters of the negotiation structure may change including the collective rules but also the utility functions of players integrating some information from the other player's proposals through a learning process we should seek to make explicit. Such an objective calls for more empirical (experimental) research where MAS-experience would be requested but which requires also specific theoretical investment because the concepts of dynamic solutions in differential games are still to be built.

Notes

¹ We gratefully acknowledge the financial support of the France-Berkeley fund and of the Risome fund.

² generally, at the scale of a catchment basin

³ such as obligation to nature and to future generation

⁴ For example, the case of an agricultural producer over-pumping water in the river will be denounced by environmentalists. On the other hand, excess water spread on the field might percolate and improve the level of the watertable. Therefore externalities for other water users are both positive and negative.

⁵ Such as the condition of "beneficial use" in the Californian water right system.

⁶ Schéma Directeur d'Aménagement et de Gestion des Eaux

⁷ Schéma d'Aménagement et de Gestion des Eaux

⁸ Irrigated areas theoretically get specific CAP irrigation premiums, as long as they are officially registered.

⁹ In the Adour case, no SAGE negotiations were initiated. However, the PGE is an equivalent framework, although the state is less involved in the process.

¹⁰ In some basins where a dam already exists, a double-bind contract was signed : farmers commit themselves, on an individual basis, to respecting the allowed quota. The water manager commits itself in return to guaranteeing that the water quota will be made available at least nine years out of ten to farmers, therefore reducing farmers' risk. This kind of contract is only possible when storage capacities allow to reduce short-term fluctuations of water resources (reduce inter-annual and intra-annual variations).

¹¹ Dams are identified by the order in which they are planned to be built.

¹² The limits between two sub-basins correspond to the points for which minimum low water flows were defined in SDAGE. The fourth sub-basin (Lees-Gabas) is not included in the simulations.

¹³ Although we have conducted other simulations in which the price can vary from one basin to another. We could also introduce multiple-tier prices.

¹⁴ Although in reality, there are technical constraints which do not allow perfect continuity.

¹⁵ This bias is the difference between the result of the aggregate model and the sum of the individual models.

¹⁶ We assume that the production function of a farm is given by h(q,x,z) = 0 where q is the vector of output quantities, x is the vector of variable input quantities and z is the vector of fixed factor quantity. If p is the input vector price, then the profit function can be approximated by a translog function :

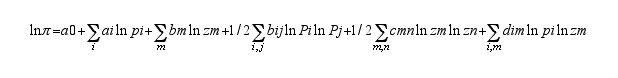
(with given restrictions on parameters : see Sadoulet and de Janvry (1995)

¹⁷ As specified earlier, the political weight is translated into the model by an " access probability ". Therefore the sum of the political weights of all players is equal to 1.

.

APPENDIX I

Repartition of farms, agricultural area (in hectares) and irrigated area (in hectares) according to farm types and sub basins in the Adour Basin
Sub basin	Farm types	traditional cattle farming	dairy farming	pig or poultry farming with cereals	small corn producers	mixed crop-livestock farming	corn producers with seeds or vegetable crops	corn producers with a complementary poultry farming	large corn producers	Together
(1) Upstream sub basin	farm number	75	32	16	357	38	16	0	63	597
	agricultural area	2273	1401	1195	6583	2451	1072	0	4022	18997
	irrigated area	831	573	731	4400	970	744	0	2825	11074
(2) Midstream sub basin	farm number	37	10	28	165	35	39	21	0	335
	agricultural area	1199	709	2096	3181	2311	3296	1570	0	14363
	irrigated area	396	350	1111	1943	1008	2241	1059	0	8108
(3) Downstream sub basin	farm number	34	18	24	240	30	8	46	0	400
	agricultural area	1043	869	1646	4463	2060	587	3145	0	13814
	irrigated area	448	535	1052	2942	991	408	2153	0	8529
(4) Lées Gabas	farm number	105	41	47	216	60	16	44	0	529
	agricultural area	3379	1936	2723	4621	3709	1024	2942	0	20334
	irrigated area	1315	744	1315	2577	1383	567	1591	0	9492
Whole Adour Basin	farm number	251	101	115	978	163	79	111	63	1861
	agricultural area	7894	4915	7660	18848	10531	5979	7657	4022	67508
	irrigated area	2990	2202	4209	11862	4352	3960	4803	2825	37203
Studied area	farm number	146	60	68	762	103	63	67	63	1332
	agricultural area	4515	2979	4937	14227	6822	4955	4715	4022	47174
	irrigated area	1675	1458	2894	9285	2969	3393	3212	2825	27711

NB : the fourth sub basin (Lées-Gabas) is not included in the simulations

APPENDIX II

Parameters of the utility functions
	a0	a1	a2	a3	a4	a5	α
Upstream farmer	3.605	0.421	-0.105	0.506	-0.045	-0.190	0.9
Midstream farmer	3.795	0.424	-0.124	0.346	-0.0161	-0.194	0.75
Downstream farmer	3.69	0.145	0.138	0.498	-0.051	-0.151	0.75
Landscape Env.		0.2	0.08	0.72	-0.5		0.7
River Env.		0.8	0.02	0.18	-0.5		0.7
Manager		0.1	0.4	0.5	0.5		0.7
Taxpayer		0.3	0.8				1

It has to be noted that all utility functions are written U = U^α with α being a risk-aversion parameter.

Investment costs IC

IC = 0.25 (NDC)² + 40

with NDC new dam capacity in million m³
IC in million French Francs

References

ADAMS G, Rausser G and Simon L (1996), Modelling multilateral negotiations: an application to California water policy. Journal of Economic Behaviour and Organisation, 1996, vol. 30, pp. 97-111

BARRETEAU O and Bousquet B (1999), "Jeux de rôles et validation de systèmes multi-agents " in Gleyzes MP and Marcenac P (Eds) Ingénierie des systèmes multi-agents. Actes des 7^ème Journées Francophones d'Intelligence Artificielle et Systèmes Multi-Agents, Hermès Sciences Publications, pp. 67-80

CALDART C and Ashford N. (1998), "Negotiation as a means of developing and implementing environmental policy." Working paper, MIT, draft version, May 1998

FASSE N (1998), "L'eau entre Etat et usager dans le bassin de l'Adour : de la gestion réglementaire à la gestion concertée". DEA-Sciences de l'eau dans l'environnement continental. Montpellier. Septembre. 72p.

FASSE N and Morardet S (1999), "La mise en place d'une gestion négociée de l'eau en France : l'exemple de la gestion des étiages sur le bassin de l'Adour." Contributions to the 17^th International Congress on Irrigation and Drainage "Water for agriculture in the next millennium", Granada, 1999, volume 1F, 29-46

GLEYSES G and Morardet S (1997), "Barrage de Gardères-Eslourenties. Evaluation économique de l'agriculture irriguée". Cemagref, Division Irrigation, Institution interdépartementale pour l'aménagement hydraulique du bassin de l'Adour, Compagnie d'Aménagement des Coteaux de Gascogne, Montpellier, 80 p.

GOODHUE R, Morardet S, Rio P and Thoyer S (1998), "Les formes institutionnelles de la gestion de l'eau en France et en Californie : droits de propriété, décentralisation et délégation." Contribution to the SFER Conference "Irrigation et gestion collective de l'eau en France et dans le Monde", Montpellier, 19-20 november 1998

KEENEY R, Raiffa H (1976) Decision with multiple objective: Preference and value tradeoffs. John Wiley.

RIO P, Morardet S and Thoyer S (1999), "Gestion de l'eau en France : l'efficacité des procédures négociées." Contribution to the Conference "Economie et Environnement", Strasbourg, 2-3 décembre 1999, 30 p.

PELLOW D (1999), Negotiation and confrontation: environmental policymaking through consensus. Society and Natural ressources, Vol 12, pp. 189-203

RAUSSER G and Simon L (1991), "A noncooperative model of collective decision making: A multilateral bargaining approach." Working Paper n°618, Department of Agricultural and Ressource Economics, University of California, Berkeley, 50 p.

RUBINSTEIN A (1982), "Perfect Equilibrium in a Bargaining Model." Econometrica, 50, pp. 97-109.

SADOULET E. and de Janvry A. (1995), Quantitative Development Policy Analysis. Baltimore, MA: Johns Hopkins University Press

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 2001