Günter Haag and Philipp Liedl (2001)
Modelling and Simulating Innovation Behaviour within Micro-based Correlated Decision Processes
Journal of Artificial Societies and Social Simulation
vol. 4, no. 3,
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/4/3/3.html>
Received: 5-Oct-00 Accepted: 13-Mar-01 Published: 30-Jun-01
Modelling of the evolution of technologies as well as structural changes in the management of firms however, require a better understanding of knowledge production and the knowledge transfer process within and between industries, the role and efficiency of transfer institutions such as universities, technology-transfer centres and consulting companies. The paper aims to provide a decision-based framework for this kind of complex interwoven processes.
Technological product and process (TPP) innovations comprise implemented technologically new products and processes and significant technological improvements in products and processes. A TPP innovation has been implemented if it has been introduced on the market (product innovation) or used within a production process (process innovation). TPP innovations involve a series of scientific, technological, organisational, financial and commercial activities. The TPP innovating firm is one that has implemented technologically new or significantly technologically improved products or processes during the period under review.
The term product innovation on the one hand includes technologically new products whose technological characteristics or intended uses differ significantly from those of previously produced products and on the other hand technologically improved products which means that the performance of an existing product is significantly enhanced or upgraded (OECD/Eurostat 1997).
A process innovation is the adoption of technologically new or significantly improved production methods, including product delivery. These methods may be intended to produce or deliver technologically new or improved products, which cannot be produced or delivered using conventional production methods, or essentially to increase the production or delivery efficiency of existing products. (OECD/Eurostat 1997).
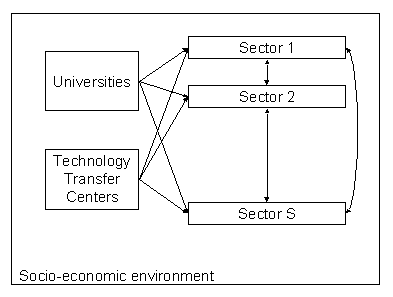
|
| Figure 1. Nested system of economic agent |
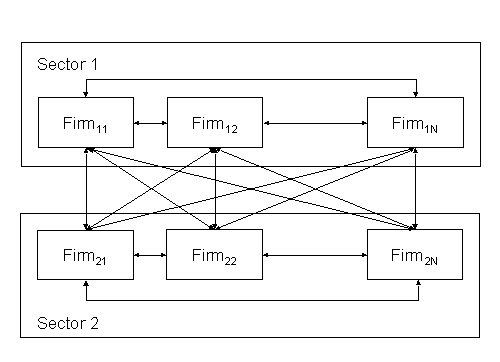
|
| Figure 2. Interdependencies of firms belonging to two industrial sectors |
|
|
(1) |
This means Ii is that part of a mixture of knowledge, innovation and information used by firm i in its production process, whereby the parameter b describes the efficiency of using this mixture for production. Thus, Ii covers knowledge and information with public good character as well as without. Spillover effects will be modelled within Ii and not directly in the production function.
|
|
(2) |
In case of Ii = 0, i.e. if firm i is not innovating and there are no innovation or technology transfers from outside the firm, the chosen production function (1) becomes the neoclassical Cobb-Douglas production function.
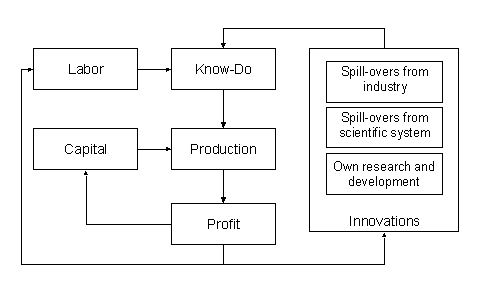
|
| Figure 3. Graphical description of the innovation process in case of one firm |
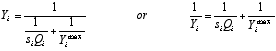
|
(3) |
with a rate of savings si. The rate of savings is viewed as being constant over time in a first approximation. Of course, the rate of savings has to fulfil the conditions 0 ≤ si ≤ 1. According to Figure 4, for small values of siQi, investments Yi become equal to neoclassical investments Yi = siQi. In the case of very high values of siQi, Yi becomes approximately equal to Yimax.
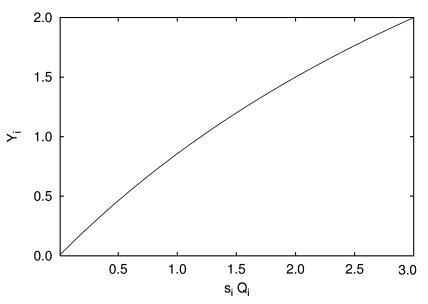
|
| Figure 4. Investments Yi in dependency of siQi with maximal investments of Yimax = 6.0 and a rate of savings si = 0.6 |
|
|
(4) |
|
|
(5) |
where δi is the rate of decrease of the capital stock Ki.
|
|
(6) |
where (i is the rate of decrease of labour force due to natural decreasing factors. This means that investments in labour force are related to the production. If we translate the number of workers in labour hours h afforded in one production period we receive the total labour hours Li used for production in one period:
|
|
(7) |
|
|
(8) |
where wi is the hourly wage rate and n is the number of production periods a worker is employed.
|
|
(9) |
|
|
(10) |
|
|
(11) |
where γi is the rate of decrease in innovation activities Ii and accounts for the obsoleteness of older innovations. N is the overall number of firms regarded, M is the number of scientific institutions taken into account.
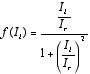
|
(12) |
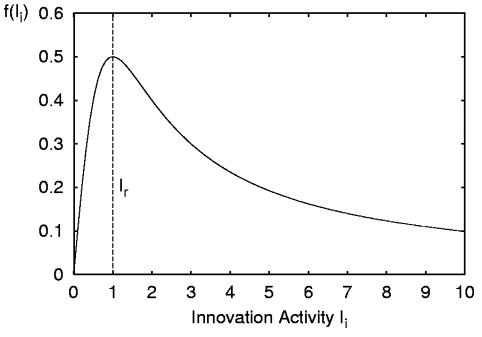
|
| Figure 5. The spillover-function f(Ii) in dependency of innovation activity Ii with a scaling parameter Ir=1 [1/h]. |
|
|
(13) |
Wages wi and the rate of interest r are viewed as being constant for simplicity. Without loss of generality the price of the product can be set to one. Therefore, r and wi are measured in units of the good produced (Zhang 1999).
|
|
(14) |
can be interpreted as utility to invest (Müller and Haag 1996), where m = K, L, I.
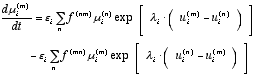
|
(15) |
where εi is the speed of adjustment. The parameter λi describes the intensity of response due to differences in those marginal profitabilities. The parameters f(nm) consider possible barrier effects due to insufficient information between the different investment types. Since we are dealing with the decision behaviour of firms it seems to be justified to assume f (mn) = f (nm) = 1.
|
|
(16) |
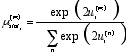
|
(17) |
| Table 1: Parameters for the simulations with fixed ratios of investment | |||||||||
| Global parameters | |||||||||
| a | b | α1 | α2 | r | Disci | Ir | |||
| 1.0 | 1.0 | 0.5 | 0.5 | 0.1 | 1.0 | 1.0 | |||
| Firm specific parameters | |||||||||
| Yimax | si | wi | δi | νi | γi | ||||
| Firm 1 | 6.0 | 0.5 | 0.4 | 0.1 | 1.0 | 0.1 | |||
| Firm 2 | 6.0 | 0.5 | 0.4 | 0.1 | 1.0 | 0.1 | |||
| gi1 | gi2 | gi1sci | µiK | µiL | µiI | ||||
| Firm 1 | 0.00 | -0.30 | Var* | 0.33 | 0.33 | 0.34 | |||
| Firm 2 | 0.78 | 0.00 | 0.0 | 0.33 | 0.33 | 0.34 | |||
|
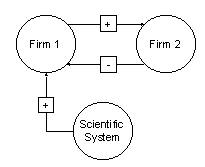
| Figure 6. Interdependencies of the agents regarded in the first simulation |
| Table 2: Initial values for the simulations with different values of g11sci | |||
| Ki(τ = 0) | Li(τ = 0) | Ii(τ = 0) | |
| Firm 1 | 1.0 | 0.5 | 1.0 |
| Firm 2 | 1.0 | 0.5 | 1.0 |
|
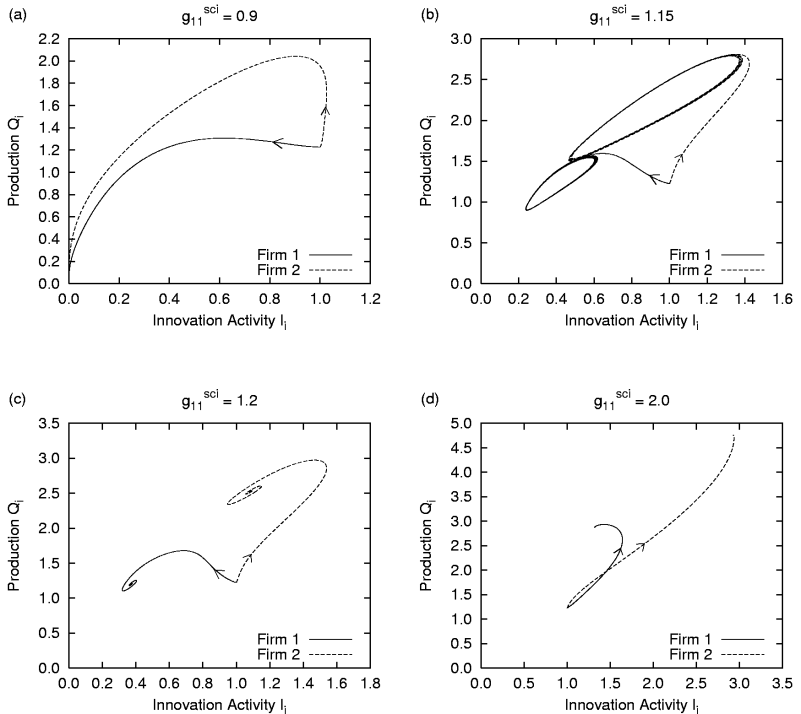
| Figure 7 (a) - (d). Innovation activity Ii and production Qi of both firms for different values of g11sci in the simulation without intra-firm R&D |
|
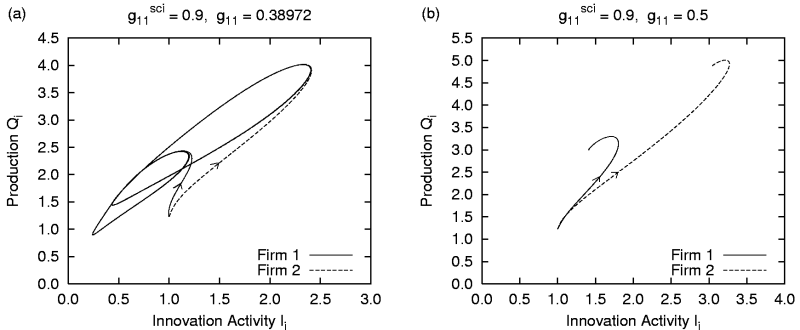
| Figure 8. Innovation activity Ii and production Qi of both firms for g11sci = 1.15 and different values of g11 in the simulation with intra-firm R&D |
| Table 3: Initial conditions for the simulations with g11sci = 1.15 and g11 = 0 | ||||||
| Initial condition | K1(τ = 0) | L1(τ = 0) | I1(τ = 0) | K2(τ = 0) | L2(τ = 0) | I2(τ = 0) |
| A | 3.80 | 1.00 | 1.30 | 5.00 | 1.30 | 2.50 |
| B | 4.20 | 1.20 | 1.00 | 4.20 | 0.40 | 0.80 |
| C | 0.30 | 0.02 | 0.35 | 0.30 | 0.02 | 0.35 |
| D | 0.30 | 0.02 | 0.20 | 0.30 | 0.02 | 0.20 |
| E | 1.00 | 0.50 | 1.00 | 1.00 | 0.50 | 1.00 |
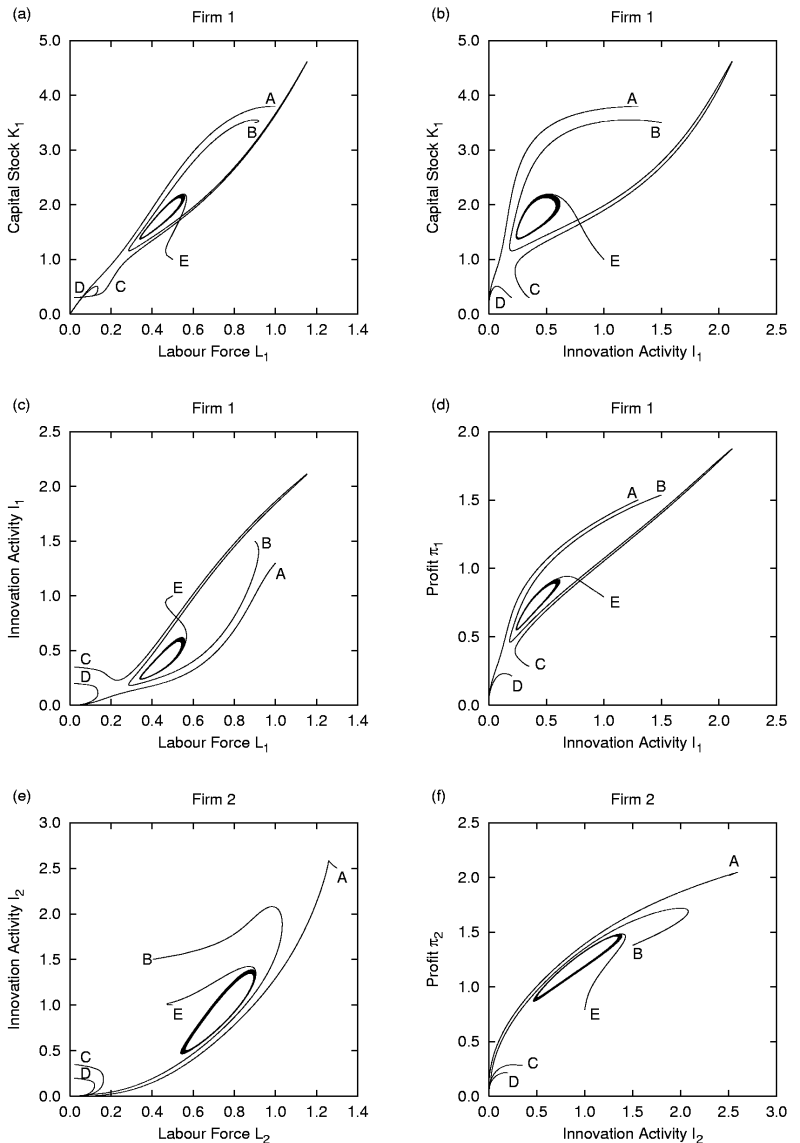
|
| Figure 9 (a) - (f). Simulation of the dynamics of two firms with different initial conditions and g11sci = 1.15 without intra-firm R&D |
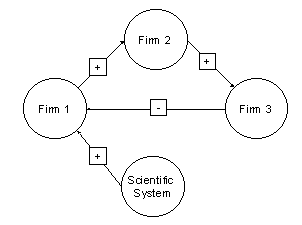
|
| Figure 10. Interdependencies of the agents regarded in the simulation of innovation diffusion |
| Table 4: Parameters in the simulation of innovation diffusion | |||||||||
| Global parameters | |||||||||
| a | b | α1 | α2 | r | D1sci | Ir | |||
| 1.0 | 1.0 | 0.5 | 0.5 | 0.1 | [1.0 ; 1.4] | 1.0 | |||
| Firm specific parameters | |||||||||
| Yimax | si | wi | δi | νi | γi | ||||
| Firm 1 | 6.0 | 0.6 | 0.4 | 0.1 | 1.0 | 0.1 | |||
| Firm 2 | 6.0 | 0.6 | 0.4 | 0.1 | 1.0 | 0.1 | |||
| Firm 3 | 6.0 | 0.6 | 0.4 | 0.1 | 1.0 | 0.1 | |||
| gi1 | gi2 | gi3 | gi1sci | εi | εi | ||||
| Firm 1 | 0.00 | 0.00 | -0.40 | 1.15 | 0.1 | 1.0 | |||
| Firm 2 | 0.21 | 0.00 | 0.00 | 0.0 | 0.1 | 1.0 | |||
| Firm 3 | 0.00 | 0.21 | 0.00 | 0.0 | 0.1 | 1.0 | |||
| Table 5: Initial values for the simulation of innovation diffusion | ||||||
| Ki(τ=0) | Li(τ=0) | Ii(τ=0) | µiK(τ=0) | µiL(τ=0) | µiI(τ=0) | |
| Firm 1 | 3.5 | 0.7 | 1.2 | 0.3 | 0.2 | 0.5 |
| Firm 2 | 3.5 | 0.7 | 1.2 | 0.3 | 0.2 | 0.5 |
| Firm 3 | 3.5 | 0.7 | 1.2 | 0.3 | 0.2 | 0.5 |
|
|
(18) |
whereby the assumption is included that all firms belong to the same industrial sector.
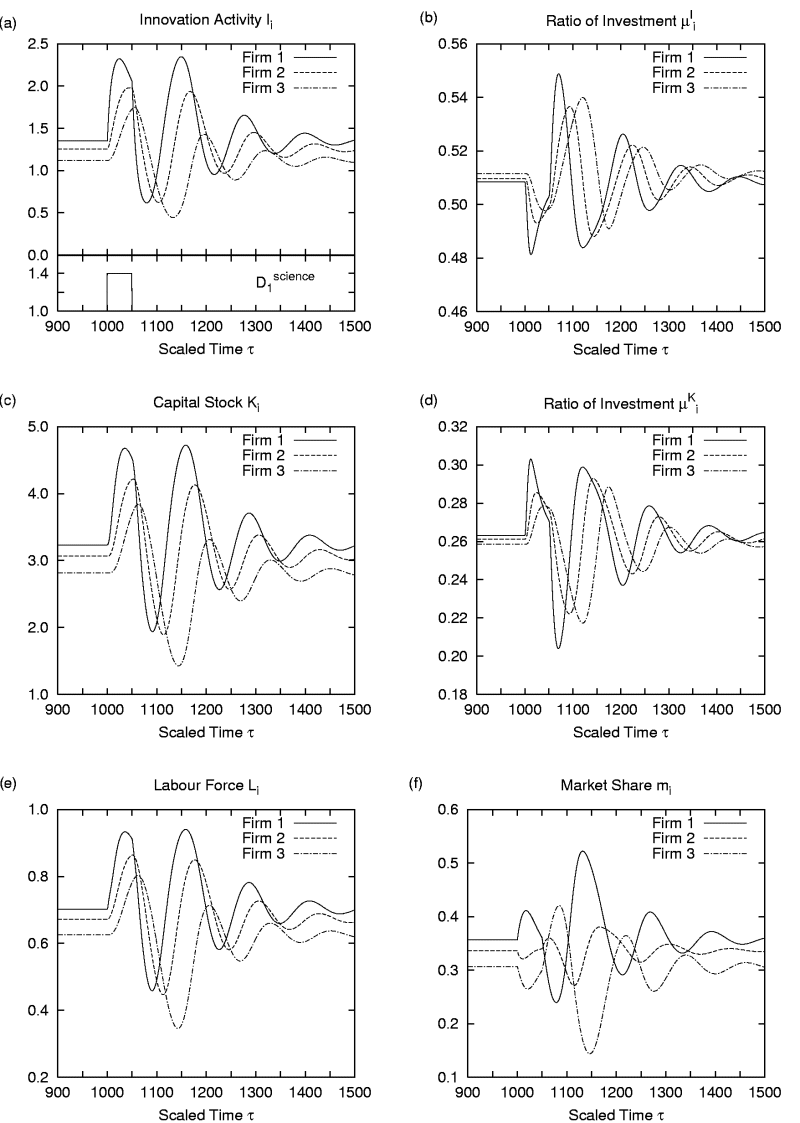
|
| Figure 11. Time evaluation of three firms in the simulation of innovation diffusion |
ANDERSSON, A. E., MATSINEN, J. (1980): Mobility of Resources, Accessibility of Knowledge and Economic Growth. Behavioural Science 25, 353-366.
ARROW, K. J. (1962): The economic implications of learning by doing. Review of Economic Studies 29, 155-173.
ARTHUR, W. B. (1989): Competing Technologies, Increasing Returns, and Lock-In by Historical Events. Economic Journal 99, 116-131.
AUDRETSCH, D. B. (1996), Industrieökonomik. In: Von Hagen, J., Börsch-Supan, A., Welfens, P. (eds.): Handbuch der Volkswirtschaftslehre I. Springer, Berlin Heidelberg New York, pp. 178-218.
CANTNER, U., PYKA, A. (1998): Technological Evolution - An Analysis within the Knowledge-based Approach. Structural Change and Economic Dynamics 9, 85-107.
Cigno, A. (1981): Growth with Exhaustible Resources and Endogenous Population. Review of Economic Studies 48, pp. 281-287.
FISCHER, M. M., MENSCHIK, G.(1994): Innovationsaktivitäten in der östereichischen Industrie: Eine emprische Untersuchung des betrieblichen Innovationsverhaltens in ausgewählten Branchen und Raumtypen. Abhandlungen zur Geographie und Regionalforschung, Band 3. Institut für Geographie der Universität Wien.
FREEMAN, C. (1988): Diffusion: The Spread of New Technology of Firms, Sectors and Nations. In: Heertje, A (ed.), Innovation technology, and Finance. The European Investment Bank. Basil Blackwell, Oxford.
GABISCH G, LORENZ, H. W. (1987): Business Cycle Theory. Lecture Notes in Economics and Mathematical Systems. Vol. 283. Springer, Berlin Heidelberg New York.
GANDOLFO, G. (1980): Economic Dynamics: Methods and Models. Advanced Textbooks in Economics. North Holland publication company, Amsterdam.
HAAG, G. (1989): Dynamic decision theory: Applications to Urban and Regional Topics. Studies in Operational Regional Science. Kluwer Academic Publishers, Dordrecht.
HIPPEL, E. VON (1988): The Sources of Innovation. Oxford University Press, New York.
HIPPEL, E. VON (1989): Cooperation Between Rivals: Informal Know-how Trading. In: Carlsson, B. (ed.): Industrial Dynamics. Kluwer Academic Publishers, Boston, pp. 157-175.
JUNGMITTAG, A., BLIND, K., GRUPP, H. (1999): Innovation, Standardisation and the Long-term Production Function. Zeitschrift für Wirtschafts- u. Sozialwissenschaften 119, 205-222, Duncker & Humblot, Berlin.
KOBAYASHI, K., SUNAO, S., YOSHIKAWA, K. (1993): Spatial Equilibria of Knowledge Production with 'Meeting-Facilities'. In: Andersson (ed.). The Cosmo-Creative Society. Logistical Networks in a Dynamic Economy. Springer Berlin Heidelberg New York, pp. 237-259.
LUCAS, R. (1988): On the Mechanics of Economic Development. Journal of Monetary Economics 22, 3-42.
MAIER, F. H. (1998): New product diffusion models in innovation management - a system dynamics perspective. System Dynamics Review 14 (4), 285-308.
MÜLLER, K. H., HAAG, G. (1996): The Austrian Innovation System, Complex Modelling with NIS-Data. Final report Vol. 5. Institute for Advanced Studies, Vienna.
NELSON, R. R., WINTER, S. G. (1982): An Evolutionary Theory of Economic Change. Belknap Press of Harvard University Press.
NIJKAMP, P., REGGIANI, A. (1998): The Economics of Complex Spatial Systems. Elsevier, Amsterdam.
OECD/EUROSTAT (1997): Oslo Manual: Proposed Guidelines for Collecting and Interpreting Technological Innovation Data.
PYKA, A. (1999): Der kollektive Innovationsprozeß. Volkswirtschaftliche Schriften Heft 498. Duncker & Humblot, Berlin.
ROMER, P. M. (1986): Increasing Returns and Long-run Growth. Journal of Political Economy 94, 1002-1037.
ROMER, P. M. (1990): Endogenous Technological Change. Journal of Political Economy 98, 71-102.
SCHUMPETER, J. A. (1934): Theorie der wirtschaftlichen Entwicklung. 9th edition 1997. Duncker & Humblot, Berlin.
SILVERBERG, G. (1991): Dynamic Vintage Models with Neo-Keynesian Features. In: Technology and Productivity: The Challenge for Economic Policy. The Technology Economy Programme. OECD, pp. 493-507.
SILVERBERG, G. (1997): Is there Evolution after Economics? In Schweitzer, F. (ed.): Self Organization of Complex Structures, From Individual to Collective Dynamics. Gordon and Breach Science Publishers, Amsterdam, pp. 415-425.
SILVERBERG, G., LEHNERT, D. (1994): Growth Fluctuations in an Evolutionary Model of Creative Destruction. In: Silverberg, G. Soete, L. (eds): The Economics of Growth and Technical Change. Edward Elgar Publishing, Aldershot, pp. 74-108.
SOLOW, R. (1956): A Contribution to the Theory of Growth. Quarterly Journal of Economics 70, 65-94.
TEECE, D. J. (1998): Capturing Value from Knowledge Assets: The New Economy, Markets for Know-How, and Intangible Assets. California Management Review 40, 55-79.
WEIDLICH, W, HAAG, G. (1983): Concepts and models of a quantitative sociology. Springer Berlin Heidelberg New York.
WITT, U. (1995): Moralität vs. Rationalität - Über die Rolle von Innovation und Imitation in einem alten Dilemma. In: Wagner, A., Lorenz, H. W. (eds.): Studien zur Evolutorischen Ökonomik III. Schriften des Vereins für Sozialpolotik. Band 195/III. Duncker & Humblot, Berlin, pp. 11-33.
WOECKENER, B. (1993): Innovation, Externalities and the State, a Synergetic Approach, Journal of Evolutionary Economics 3(3), pp. 225 -248.
WOECKENER, B. (1995): Hotelling-Modelle der Konkurrenz und Diffusion von Netzeffektegütern, deterministische und stochastische Ansätze zur Erklärung der Ausbreitung neuer Kommunikations- und Gebrauchgüter-Systeme. Francke-Verlag, Tübingen Basel.
ZHANG, W.B. (1990): Economic Dynamics: Growth and Development. Lecture Notes in Economics and Mathematical Systems. Springer, Berlin Heidelberg New York.
ZHANG, W.B. (1999): Capital and Knowledge: Dynamics of Economic Structures with Non-Constant Returns. Springer, Berlin Heidelberg New York.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 2001