In a paper published in JASSS, Chris Goldspink discusses the methodological implications of complex systems approaches to the modeling of social systems. Like others before him Goldspink advocates the use of bottom-up computer simulations (BUCSs) for examining social phenomena. It is argued therein that computer simulation offers a partial solution to the methodological crisis apparently observed in the social sciences. Though I agree with many of Goldspinkís remarks I personally feel that BUCS has been oversold as a tool for modeling and managing organizational complexity at the expense of other equally legitimate (from a complex systems stance) approaches. I have no doubt that BUCS offer a new and exciting lens on organizational complexity, but we must explicitly recognize that this nonlinear approach suffers from some of the same limitations as its linear predecessors. The aim of this short note is to discuss some of the limitations in more detail and suggest that complexity thinking offers a simulation paradigm that is broader than the new reductionism of BUCS. This alternative interpretation of complexity thinking forces us to reconsider the relationship between our models and "reality" as well as the role of simulation in decision making.

Keywords:

Complexity; Computer Simulation; Exploratory Modelling; Methodology

Introduction

1.1

Richardson & Cilliers (2001) have identified three broad schools of complexity science, namely new reductionism, soft complexity and complexity thinking. In their typology new reductionism is associated with the representationalist view that real life complex systems can best be modeled through the exploration of bottom-up computer simulations (BUCS) often associated with the Santa Fe Institute. This school of complexity science is based on a seductive syllogism (Horgan, 1995):

Premise 1: There are simple sets of mathematical rules that when followed by a computer give rise to extremely complicated patterns.
Premise 2: The world also contains many extremely complicated patterns.
Conclusion: Simple rules underlie many extremely complicated phenomena in the world, and with the help of powerful computers, scientists can root those rules out.

1.2

Simply, because BUCS representations appear to be compositionally similar to the real (observed) world then they must be better representations than others. Though this syllogism was brilliantly refuted in a paper by Oreskes et al. (1994), in which it the authors warned that "verification and validation of numerical models of natural systems is impossible," this position still dominates what has become to be known as complexity studies.

1.3

The term new reductionism is associated with BUCS because, despite the attempt to explicitly build-in the apparent real world complexity to the computer models, these models are still gross simplifications of reality^[1]. Furthermore, many users of BUCS regard their models in a Modernist manner which assumes to some extent that 'what we see is what there is' thereby trivialising the recognition of constituent object boundaries (Richardson, 2001), as well as giving a false sense of realism/objectivity regarding these models. Modernist (or linear) interpretations also focus on the model itself (the computer representation) rather than on the modelling process.

1.4

The aim of this short note is to discuss some of the complexity science inspired limitations to complexity modelling (or, bottom-up computer simulation). In doing so I will consider: the concept of equifinality and its consequences for multiple non-overlapping explanations of the same phenomena (and therefore the validation process, and the potential for knowledge transfer); the status of knowledge derived from the modelling of complex systems; strong exploration versus weak exploration; linear versus nonlinear modelling 'culture', as well as the role that simulation plays in the organisation decision process. The result is a complexity informed modelling paradigm that is considerably broader than the computer-based paradigm.

Equifinality and Multiple Explanations

2.1

The concept of equifinality is defined as "the tendency towards a characteristic final state from different initial states and in different ways" (von Bertalanffy, 1969: 46). Alternatively, there are many paths/trajectories to the same state (see figure 1). Stated in a different way: there are potentially many non-overlapping qualitatively different explanations/models for any particular phenomena resulting from nonlinear interactions or, an infinitude of micro-architectures will give the same subset of macro-phenomena that correspond to our observations. This places some very severe limitations on the usefulness of nonlinear computer simulations. Firstly, given the intractability of the emergent phenomena that occur within the simulation the analyst might not be able to provide any insights into the chain of events that led to a particular (modelled) system state. So, there is the possibility that the simulation itself might not offer any explanatory capability whatsoever even if the final state does indeed resemble 'real' system's behaviour. Potentially worse still is that assuming that the universe is indeed a complex system, there are an enormous number of qualitatively different ways to model the same phenomena. A result of this is that even if our models can be used to develop causal explanations^[2] (within the confines of the model) we cannot be sure that those explanations bear any relationship to reality whatsoever. These are the potentially crippling effects that result from nonlinearity.

Figure 1. Illustration showing that not only can a particular system state (outcome) can be reached via different trajectories from the same starting conditions, but also that different starting conditions may also lead to the same system state. Of course, the reverse case is also a possibility in that different starting conditions may lead to different outcomes and multiple runs from the same starting conditions may also result in different outcomes.

2.2

Figure 2 attempts to illustrate these significant shortcomings by comparing linear systems to nonlinear systems. Figure 2a demonstrates the triviality of linear problems assuming that the universe and our models of it are linear. The thick red line that appears between the two vertical dotted line traces some real world data. Because the system is linear we can be sure that, though we only have data for some subset of all possible contexts, the system will continue to behave linearly in (qualitatively similar) contexts for which we have no data. The thinner coloured lines represent outputs from some of the linear models that might be developed to explain the observed data. Though there is an infinity of possible qualitatively similar models that nearly fit the data (all being of the form y=mx+c) none of them deviate much from the observed data. And, though these models have been validated against a limited set of contexts we can be confident that the models still hold for qualitatively similar contexts for which we have no data. Furthermore, we only need to validate our models against limited data to ensure that they are valid for all qualitatively similar contexts. (All other contexts will of course be qualitatively similar as there are no emergent processes involved). So, the knowledge contained in our models can be easily transferred to other contexts - assuming that the world and our models are linear.

2.3

Figure 2b shows a very different picture. Like before the thick red line depicts actually observed data for a limited range of contexts (delimited by the two vertical dotted lines). Unlike before, the data relates to a particular phenomenon that arises nonlinearly rather than linearly. Now, the thinner coloured lines represent outputs from a selection of qualitatively different nonlinear models (such as BUCS) that have been tuned to account for the observed data. As can be seen, the predictions made by these nonlinear models for contexts of which we have no observations vary wildly. Of course, we could expand our data set by collecting data for an expanded set of contexts, but we would still be left with the same problem. In fact, the only scenario in which one model could be chosen over all others is by validating each model against data collected for all possible contexts. This is absurdly impractical and yet is the case even if the real world system is qualitatively stable. As is well known, real world systems are not necessarily qualitatively stable as new entities can emerge, and the order parameters that describe the key features of a real world (complex) system one day may be qualitatively inaccurate the next^[3]. This would seem to indicate that absolute knowledge concerning a nonlinear universe is impossible. Furthermore, there is no proof that any practical knowledge we might acquire would be at all transferable. Fortunately, these limitations represent an extreme situation. However, it is clear that the relationship between our models and therefore our knowledge of real world systems is not a trivial one-to-one mapping as once assumed - the actual relationship is very complex indeed.

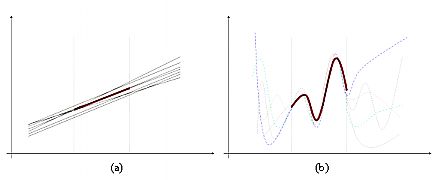
Figure 2. Linear models of a linear universe versus nonlinear models of a nonlinear universe. (For linear systems extrapolation from limited data is a trivial exercise, whereas for nonlinear systems extrapolation from limited data is a highly problematic exercise.

2.4

These limitations concerning the validation of models^[4] of real world complex systems exist for both linear and nonlinear approaches, i.e. these limitations are not overcome through the implementation of BUCS.

Strong versus Weak Exploration

3.1

Though bottom-up computer simulations are susceptible to the some of the same limitations as linear approaches BUCS do allow the exploration of the idealised systems state space which partially mitigates against the limitations discussed above.

3.2

Elsewhere Richardson et al. (2000) identifies two types of exploration: weak and strong exploration where weak refers to intra-perspective (or quantitative) exploration and strong refers to inter-perspective (qualitative) exploration. It is argued therein that both strong and weak explorations are essential in the investigation of complex systems like socio-technical systems. Weak exploration encourages the critical examination of a particular perspective, which is undoubtedly driven by its differences with other perspectives. Strong exploration encourages the sucking in of all available perspectives in the considered development of a situation-specific perspective. These two types of exploration are not orthogonal, and cannot operate in isolation from each other. The greater the number of perspectives available, the more in depth the scrutiny of each individual perspective will be; the deeper the scrutiny the higher the possibilities are of recognising the value, or not, of other perspectives. Essentially complexity-based analysis, Richardson et al. argued, is a move from the contemporary authoritarian (or imperialist - Flood, 1989) style, in which a dominant perspective bounds the analysis, to a more democratic style that acknowledges the 'rights' and value of a range of perspectives. The decision as to what perspective to use is deferred until after a process of contextual and paradigmatic exploration.

3.3

Most of the BUCS-type analysis that I have been involved in focuses mainly on weak exploration (albeit in a form much stronger than traditional linear approaches), i.e. the exploration of the idealised system's state space via the quantitative variation (rather than qualitative variation) of the models underlying assumptions. Essentially this is sensitivity analysis. Such analysis does facilitate the exploration of hypotheses and the checking of robustness of models by an exhaustive search of parameter space (Goldspink, 2002: 2.11). However, throughout such an analysis the qualitative form of the model is more or less static which limits exploration quite significantly - BUCS may well be useful in uncovering qualitatively different behavioural regimes but they are often based upon a qualitatively static assumption set. With the growing availability though of modelling environments that facilitate bottom-up model construction a number of qualitatively different models can be easily constructed and rigorously analysed. So it is becoming increasingly straightforward to perform both strong and weak forms of exploration in BUCS environments.

3.4

However, despite the increased flexibility of the BUCS approach the focus is still on the model itself rather than the modelling process. Furthermore the strong qualitative exploration is still restricted by a preoccupation with mathematical representations which is not necessarily wholly supported by the complex systems view (Richardson, 2002).

Linear versus Nonlinear Modelling Culture

4.1

In running to advocate the complexity perspectives many complexiologists have suggested a move away from linear models in favour of nonlinear models. As argued above, nonlinear models suffer from many of the shortcomings that linear models do. This section aims to shift the focus away from the model itself and onto the modelling process.

4.2

Allen (2001) has suggested that there are two fundamental assumptions that when taken in different combinations, lead to different modelling approaches. The assumptions expressed simply are: (1) no macroscopic adaptation allowed, and (2) no microscopic adaptation allowed. If both assumptions are made, plus an additional one which assumes that the system will quickly achieve an equilibrium state, then we have an equilibrium-type model - a modelling approach that still dominates much of contemporary economics. If neither assumption is made then we have a basic system dynamics model. If assumption (1) is relaxed then the resultant model will have the capacity to self-organisation. And, if both assumptions are relaxed then a truly evolutionary model can be constructed - of which the BUCS approach is a limited example.

4.3

The reason that I bring up Allen's conception of complexity modelling is that it appears to leave no room for linear models. This exclusion seems to support the calls for a complete overhaul of modelling and the disposal of traditional linear tools and methods. To model complex systems well Allen suggests that we should relax both assumptions. In Richardson et al. (2000) presentation of complexity science it was suggested that at times a linear model of a complex system may be perfectly adequate. Why do these two viewpoints disagree? What should be noted is that Allen's fundamental assumptions deal only with the mathematically conceived model that takes shape on a computer. They do not directly deal with the modelling process itself (which includes the interpretation of the model). If the scope of these assumptions were generalised to refer to the modelling process itself and not just the formally developed model then the place for linear modelling (not linear thinking) is retrieved. As an example, consider a decision tree.

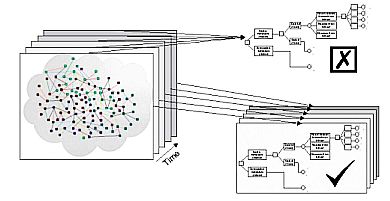
Figure 3. The 'evolution' of a linear 'decision tree' model

4.4

A decision tree is a widely used linear decision-making technique. If one were to build such a tree and populate it with the relevant data then it would spew out a set of numbers that can be used to rank different courses of action. Left to its own devices the tree would not evolve in any way (unless the computer failed, or the piece of paper on which it was drawn burnt - in which case the tree would simply disappear!). The model itself has no intrinsic capability to self-organise or evolve in any way. It is a simple linear model. It would be the same next year as it is today and offer exactly the same output given the same input. According to Allen's typology (when restricted to the model itself) it is worthless as far as complexity modelling is concerned. However, if the tree is used within an environment that does allow for micro and macroscopic adaptation then the tree may also evolve. The modellers can explore possible scenarios by populating the model with different data sets; they can play with the structure of the tree (effecting a re-organisation); and even dispose of the tree and decide to use an alternative method (effecting a true evolution - the tree model 'evolves into' a cellular automata model for example). The 'culture' in which the model is used effectively allows for both micro and macroscopic adaptation of the model. It is for the modellers/decision-makers to judge whether the linear model is appropriate given the currently observed behaviour of the real complex system of interest. In making such a judgement they will necessarily continually question the boundaries of the analysis, and explore the potential of a variety of perspectives. The thinking supporting the model development will be nonlinear, despite the potential linearity of the computer model constructed. Of course, the nonlinear modelling process may equally lead to a nonlinear representation, such as a BUCS.

4.5

In short it is argued that accepting Allen's fundamental assumptions as assumptions regarding the modelling process itself rather than the consequent mathematical representation is a more useful application, which is truer to the analytical requirements inferred from complexity thinking.

4.6

The distinction between a linear and nonlinear modelling 'culture' is crucial as it highlights the different ways in which the models themselves are regarded. The linear 'culture' takes a representationalist view of models in which aspects of reality really are considered to be captured by the model itself - the model becomes an accurate map of reality. Even if the model itself is nonlinear its efficacy tends to be over-estimated. As a brief example (based on the author's personal experience as a government consultant) consider system dynamics 'flight simulators'. 'Flight simulators' are very effective tools for testing out different organisational strategies and tactics by facilitating (weak) exploration of the idealised systems state space. In this case, however, rather than use the simulator to develop a 'feel' for the behaviour of the system of interest, the linear decision makers (regarding the model as an accurate representation, or map, of their organisation) simply set the simulator's 'dials' to achieve a particular outcome and then went away to force the 'dials' of the real system into the same positions. This demonstrated a gross misunderstanding of how exploratory models should be used to support organisational decision making.

4.7

The nonlinear 'culture' takes a very much more pragmatic stance which recognises the model as no more than a rough and ready caricature, or metaphor, of reality. As such the knowledge contained in the model should be regarded with a healthy scepticism, seeing it as a limited source of understanding. The (nonlinear) modelling process is regarded as an ongoing dialectic between stakeholders (modellers, users, customer, decision makers, etc.), the 'model', and observed reality rather than a simple mapping exercise.

4.8

Goldspink (2002: 8.11) does indeed mention a number of analytical philosophies (such as soft systems methodologies and action research) which Richardson et al. (2000) regard as nonlinear analytical philosophies. To Goldspink's list I would definitely add critical systems thinking (Flood & Romm, 1996; Jackson, 2001) and systemic intervention (Midgley, 2000; Flood, 2001). Goldspink suggests that quantitative methods, such as BUCS, "... may, however, be incorporated within these action frameworks." As a result of the discussion thus far I would tend to stress the potential for incorporation of the qualitative and quantitative methods a little differently: it is essential that quantitative methods be incorporated into a qualitative (nonlinear) analytical framework so that the linear application of nonlinear models is avoided.

4.9

Kollman et al. (1997: 463) states that "[a]n ideal tool for social science inquiry would combine the flexibility of qualitative theory with the rigor of mathematics. But flexibility comes at the cost of rigor." This may be the case if we persist in holding on to traditional notions of what rigor is. I would argue that the incorporation of quantitative approaches into one of the available qualitative frameworks mentioned above would achieve the balance of flexibility and rigor that Kollman seeks.

Summary

5.1

BUCS undoubtedly offer a new and exciting view onto the world of social systems. However, they still suffer from some of the same unavoidable limitations that linear approaches do. Complexity science has implications not only for the models used themselves but also for the way in which such models are regarded and the role they play in the development of the understanding that informs organisational related decisions. At the end of the day models are tools that can be used an abused - the best models are worthless in linear hands. The position discussed briefly herein and elsewhere (Richardson et al. 2000; Richardson 2001) alludes to a complexity-inspired modelling paradigm which is significantly broader than the representationalist computer simulation philosophy. With the widespread availability of affordable computing power we have witnessed a modelling revolution. Without an associated cultural revolution decision-makers will continue to make the same mistakes often associated with linear mechanistic philosophies.

Acknowledgements

I would like to thank the Institute for the Study of Coherence and Emergence for supporting this work, and also Michael Lissack for useful comments on an earlier draft.

Notes

¹This is true particularly when considering social systems. The properties of the whole may well emerge from the nonlinear interactions of the parts, but the representation of the parts (people, say) and their interactions is much simpler than real life.

²Which are often no more than statistical correlations rather than causal explanations.

³Even the act of modeling itself may affect the real system in nontrivial ways.

⁴Bankes & Gillogly (1994) and Bankes (1993) recognize the impossibility of validating exploratory models and suggest that we must instead validate our research strategies (i.e. the validation of the modeling process).

References

ALLEN, P. M. (2001). "Economics and the Science of Evolutionary Complex Systems," SysteMexico, Special Edition - The Autopoietic Turn: Luhman's Re-Conceptualisation of the Social, pp. 29-71.

BANKES, S. & GILLOGLY, J. (1994). "Validation of Exploratory Modelling," Proceedings of the Conference on High Performance Computing, Adrian M. Tentner and Rick L. Stevens (eds.), San Diego, CA: The Society for Computer Simulation, pp. 382-387.

BANKES, S. (1993). "Exploratory Modelling for Policy Analysis," Operations Research, Vol. 41 No. 3: 435-449.

FLOOD, R. L. (1989). "Six Scenarios for the Future of Systems 'Problem Solving'," Systems Practice, 2(1): 75-99.

FLOOD, R. L. and ROMM, N. R. A. (eds.) (1996). Critical Systems Thinking: Current Research and Practice, Plenum Press: NY, ISBN 0306454513.

FLOOD, R. L. (2001). "Local Systemic Intervention," European Journal of Operational Research, 128: 245-257.

GOLDSPINK, G. (2002). "Methodological Implications of Complex Systems Approaches to Sociality: Simulation as a Foundation for Knowledge," Journal of Artificial Societies and Social Simulation, Vol. 5, No. 1, <https://www.jasss.org/5/1/3.html>.

HORGAN, J. (1995). "From Complexity to Perplexity," Science, 272: 74-79.

JACKSON, M. C. (2001). "Critical Systems Thinking and Practice," European Journal of Operational Research, 128: 233-244.

KOLLMAN, K., MILLER, J. H. and PAGE, S. (1997). "Computational Political Economy," in Arthur, W. B., Durlauf, S. N. and Lane, D. A. (eds.), The Economy as an Evolving Complex System II, Addison-Wesley: Reading MA, ISBN 0201328232.

MIDGLEY, G. (2000). Systemic Intervention: Philosophy, Methodology, and Practice, Kluwer Academic / Plenum Publishers: NY, ISBN 0306464888.

ORESKES, N., SHRADER-FRECHETTE, K. and BELITZ, K. (1994). "Verification, validation, and Confirmation of Numerical Models in the Earth Sciences," Science, 263: 641-646.

RICHARDSON, K. A. (2001). "On the Status of Natural Boundaries: A Complex Systems Perspective ," Proceedings of the Systems in Management - 7th Annual ANZSYS conference November 27-28, 2001: 229-238, ISBN 072980500X.

RICHARDSON, K. A. (2002). "The Hegemony of the Physical Sciences - An Exploration in Complexity Thinking," submitted for inclusion in a forthcoming edited book Living with Limits to Knowledge. Available here.

RICHARDSON, K. A. and CILLIERS, P. (2001). "What is Complexity Science? A View from Different Directions," Special Issue of Emergence - Editorial, Vol. 3 Issue 1: 5-22.<http://www.kurtrichardson.com/Editorial_3_1.pdf>

RICHARDSON, K. A., MATHIESON, G. and CILLIERS, P. (2000). "The Theory and Practice of Complexity Science - Epistemological Considerations for Military Operational Analysis," SysteMexico, 1: 25-66. <http://www.kurtrichardson.com/milcomplexity.pdf>

VON BERTALANFFY, L. (1969). General System Theory: Foundations, Development, Applications, George Braziller: NY, Revised Edition, ISBN 0807604534.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2002]