Diemo Urbig (2003)
Attitude Dynamics With Limited Verbalisation Capabilities
Journal of Artificial Societies and Social Simulation
vol. 6, no. 1
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/1/2.html>
Received: 15-Nov-2002 Accepted: 13-Jan-2003 Published: 31-Jan-2003
 Abstract
Abstract
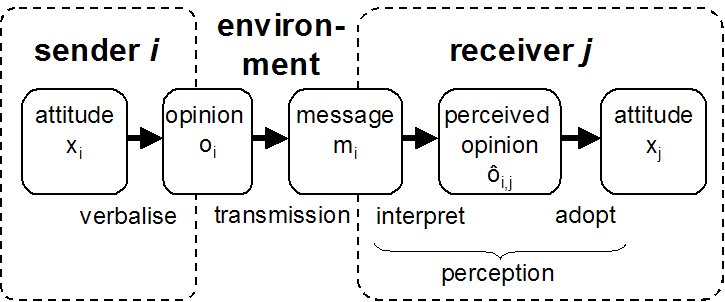
|
| Figure 1. Communication Model |
Definition 1. The attitude x'j of agent j in the next step is changed on the base of the attitude xj of the current step and the four communication-related processes that link agent j with agent i:x'j = adoptj (xj , interpretj (xj, transmission (verbalisei (xi) ) ) )
Definition 2. Assuming agent i communicating its attitude to agent j we define:attitude xi , xj
opinion oi = verbalisei (xi)
message mi = transmission (oi)
perceived opinion ô i,j = interpretj (xj , mi)
new attitude x'j = adoptj (xj , ô i,j)
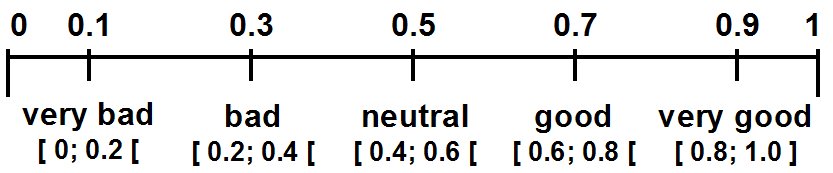
|
| Figure 2. Values of opinion for a precision prec = 5 |
Definition 3. The verbalisation process is given by[10]:
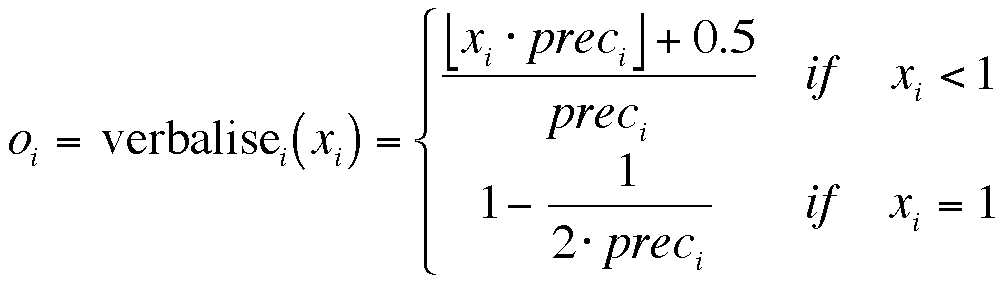
Definition 4. The transmission process does not bias the message, hence the process is given by identity: mi = transmission(oi) = o i
Definition 5. The perceived opinion ô i,j the agent j gets from the interpretation process depends on the received message mi from agent i that is biased by selective interpretation selij of agent j:
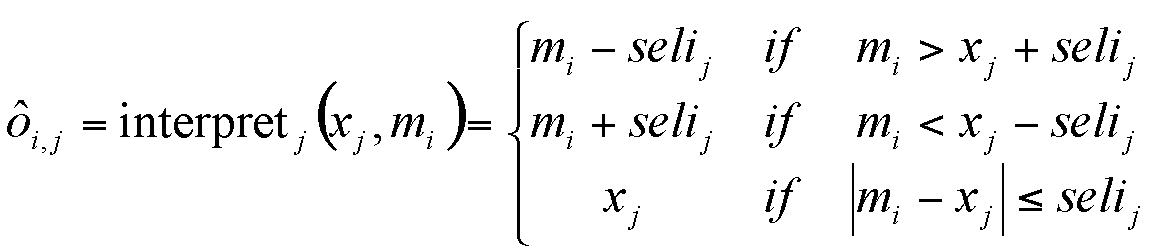
Definition 6. An adoption takes place with the impact (imp) if the perceived opinion is not too far from the own attitude.
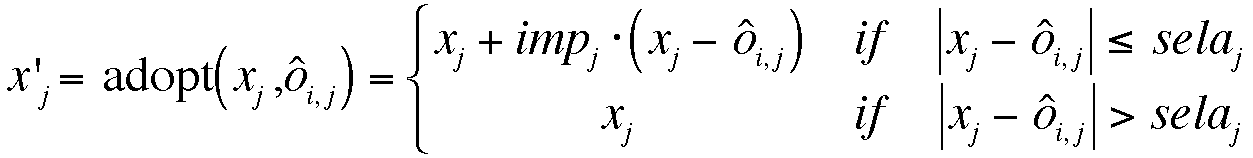
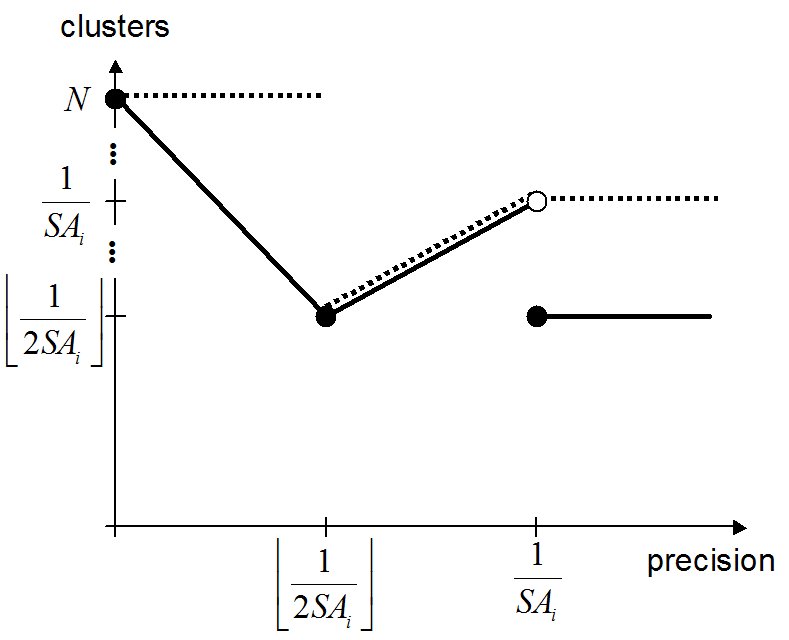
 ) then the area of influential attitudes covers all possible attitudes from 0 to 1. Of course the area of influential attitudes is not equal to the number of influential attitudes, but for our analysis it has proven to be a useful tool[12]. The next paragraphs show how selective attention and selective interpretation influence the area of influential attitudes; it partly reproduces well-known results. The impact of precision is analysed in another section below.
) then the area of influential attitudes covers all possible attitudes from 0 to 1. Of course the area of influential attitudes is not equal to the number of influential attitudes, but for our analysis it has proven to be a useful tool[12]. The next paragraphs show how selective attention and selective interpretation influence the area of influential attitudes; it partly reproduces well-known results. The impact of precision is analysed in another section below.
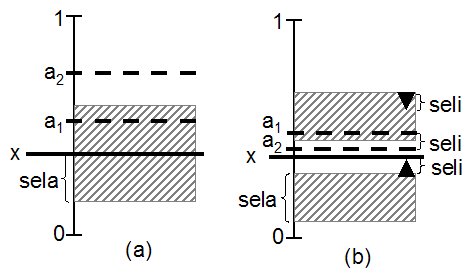
|
| Figure 3. Area influential attitudes: (a) Due to selective attention an agent having the attitude x adopts a1 but ignores a2. (b) Due to selective interpretation an agent having the attitude x perceives the original a1 as a2 and the original a2 as being equal to x. Both, a1 and a2 are adopted. |
|
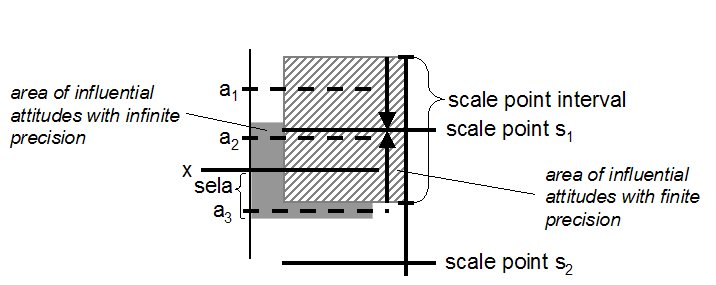
| Figure 4. Area of influential attitudes and precision: Due to the finite precision an agent having the attitude x perceives attitude a1 and a2 as s1 and a3 as s2. Contrary to infinite precision a1 now influences the agent while a3 does not. |
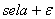 , else an agent from one cluster can adopt a perceived opinion from another cluster, which then means that the clusters by definition have not been clusters[13].
, else an agent from one cluster can adopt a perceived opinion from another cluster, which then means that the clusters by definition have not been clusters[13].
Proposition 1. For many agents, assuming for every agent an infinite precision and no selective interpretation (seli = 0) the maximal number of clusters of attitudes is. The expected number of clusters of attitudes is
.
Proposition 2. For many agents, assuming for every agent an infinite precision and no selective interpretation (seli=0) as well as heterogeneous positive selective attentions (selai> selaj> 0) the maximal number of clusters of attitudes is in the long run. The expected number of clusters of attitudes is
.
|
| Figure 5. Dynamics with heterogeneous selective attentions: (a) shows all attitudes each of the 20 agents adopts during the simulation run, while (b) shows the sequential simulation run. Contrary to agents 1 to 19 that are narrow-minded with an equally small selective attention, agent 20 is open-minded, i.e. has a higher selective attention. |
Proposition 3. For many agents, assuming for every agent an infinite precision and a positive selective interpretation ( seli > 0) the maximal number of clusters of attitudes is. The expected number of clusters of attitudes is
.
|
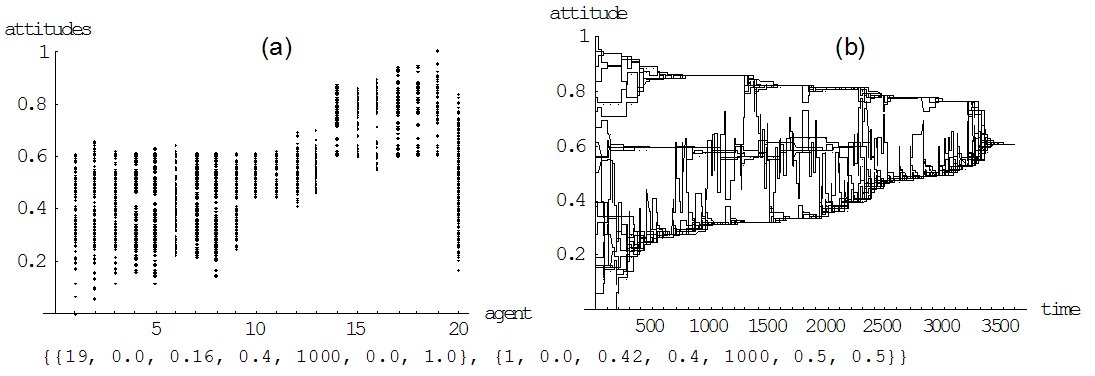
| Figure 6. Zero and positive selective interpretation with homogeneous and heterogeneous selective attentions: (a) is a simulation run with 20 agents that only differ in their initial attitude, but all have no selective interpretation, a selective attention of 0.16, and an impact rate of 0.4. Simulation run (b) is the same as (a) but with one agent being open-minded, i.e. having a selective attention of 0.4 (see also Figure 5). Simulation run (c) is the same as (a) but with a selective interpretation of 0.05. Simulation run (d) changes (c) such that there is one open-minded agent as in (b). |
Proposition 4. For a finite precision () the initial order of attitudes of agents involved in a communication can be inversed after the communication.
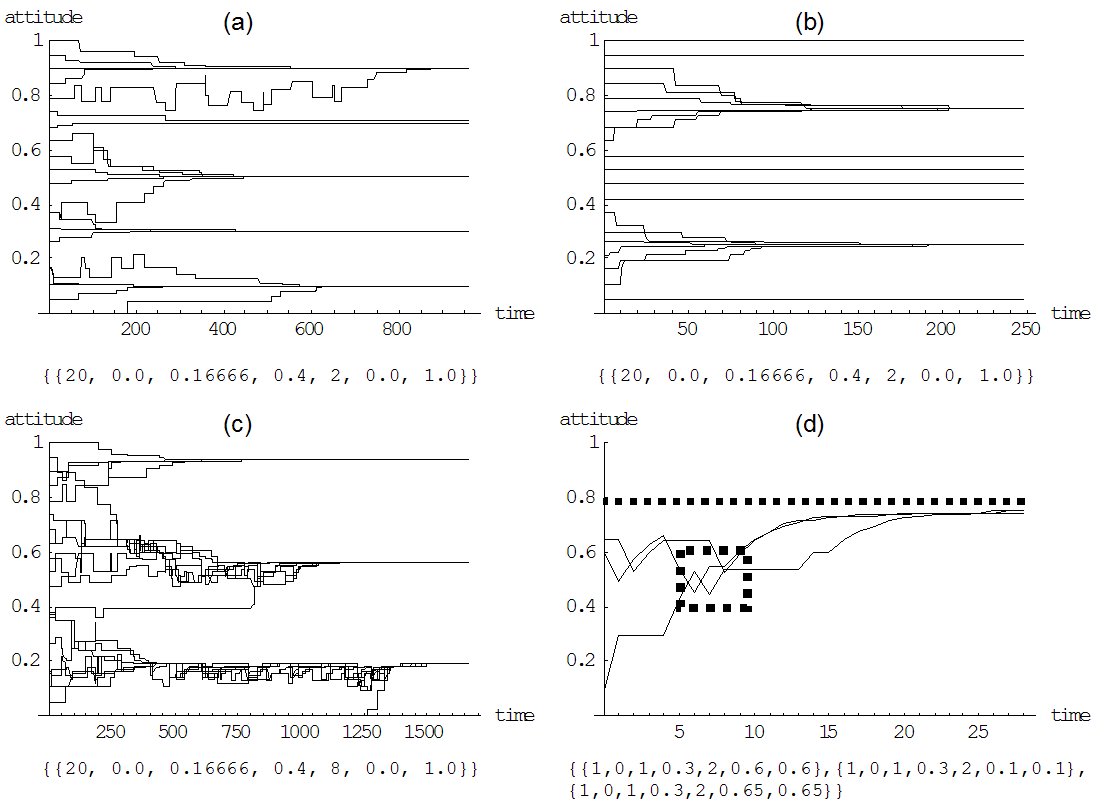
|
| Figure 7. (a), (b), and (c) represent the three important scenarios for the analysis of the impact of precision: low, medium, and high precision. The setting of all three simulation runs is: 20 agents, no selective interpretation, a medium selective attention of 0.16666, and an impact rate of 0.4. Precision is 2 in (a), 5 in (b), and 8 in (c). Simulation run (d) exemplifies over adoption. |
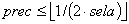 .
.
If the scale has only a small number of scale points, then the smaller the selective attention is the more agents experience a cut of their area of influential attitudes. This leads to a high number of clusters. In fact, there are agents in this scenario between two scale points that have an empty area of influential attitudes. These agents will not change their attitude at all, even if they talk with an agent having an attitude very close to their own. The other agent is forced to verbalise its attitude as a scale point far away. Therefore the maximal number of clusters equals the number of agents, especially if all agents have an initial attitude outside the areas that are set by scale point plus/minus selective attention around each scale point. To get the average number we take into account that on average
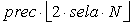 agents lie within such areas and build clusters according to the scale points. The other agents are not influenced, hence being a cluster itself (see proposition 5).
agents lie within such areas and build clusters according to the scale points. The other agents are not influenced, hence being a cluster itself (see proposition 5).
In scenario I every agent has at most one scale point in its area of influential attitudes. Therefore an agent changes its attitude in one and only one direction or it does not change it at all. This leads to an easy way to calculate all attitudes an agent might adopt during a simulation run. An agent can only form attitudes that are in the range between its initial attitude and its attitude in the final stable configuration. The latter is given by the scale point it has in its area of influential attitudes. Proposition 5 summarises the results for scenario I.
Proposition 5. For many agents, assuming a low precision (Figure 7(a) shows a simulation run that fits to scenario I. Proposition 5 predicts a number of ten clusters, which is exactly the number as reached in simulation[16]. One can also see that every agent moves only into one direction.), no selective interpretation (seli = 0), and a positive selective attitude ( sela > 0):
- The maximal number of clusters of attitudes is N
- The expected number of clusters is
.
- For every step from x to x' the difference x-x' has the same sign or equals zero (shift the attitude only in one direction).
- For every scale point s the difference s-x has for every simulation step the same sign or equals zero (no crossing of scale points).
- If
, with x as the attitude of an agent and o(x) as its verbalised attitude, then the agent will never adopt a perceived opinion (some agents might never adopt another attitude).
- If
, with x as the attitude of an agent and o(x) as its verbalised attitude, then the attitudes the agent adopts during the simulation are within the interval [x; o (x)].
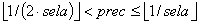 is the assumption of the second scenario, which represents the fact that every agent has at least one and at most two scale points in its area of influential attitudes. Additionally, if an agent has an attitude close to a scale point, it has exactly one scale point in its area of influential attitudes. The meaning of close is determined by being less than sela - 1/(2 · sela). If this difference becomes very small then the probability of coming sufficiently close to a scale point is very small, hence the probability of many agents with oscillating attitudes increases. As the number of oscillating agents increases when selective attention increases or precision decreases such changes increase the time taken until a stable configuration may be reached. As we will see later this is not the only reason why a convergence might be delayed.
is the assumption of the second scenario, which represents the fact that every agent has at least one and at most two scale points in its area of influential attitudes. Additionally, if an agent has an attitude close to a scale point, it has exactly one scale point in its area of influential attitudes. The meaning of close is determined by being less than sela - 1/(2 · sela). If this difference becomes very small then the probability of coming sufficiently close to a scale point is very small, hence the probability of many agents with oscillating attitudes increases. As the number of oscillating agents increases when selective attention increases or precision decreases such changes increase the time taken until a stable configuration may be reached. As we will see later this is not the only reason why a convergence might be delayed.
Proposition 6. For many agents, assuming a medium precision (), no selective interpretation ( seli = 0), and a positive selective attitude ( sela > 0):
- The maximal number of clusters of attitudes as well as the expected number of clusters is given by the precision.
- For every simulation step the difference of any scale point and an agent's attitude has the same sign or equals zero. If it equals zero then this holds forever (no crossing of scale points).
- If the area of influential attitudes of the agent's initial attitude covers only one scale point then the range of possibly formed attitudes of this agent is between its initial attitude and its verbalisation.
- If the area of influential attitudes of the agent's initial attitude covers two scale points s1 and s2 (s1 < s2) and it converges to sj with
then the range of possibly adopted attitudes is given by the following interval [min(sj; s2 - sela ) ; max(sj; s1 + sela)].
Proposition 7. For many agents, assuming high precision, no selective interpretation ( seli = 0), and a positive selective attitude ( sela > 0), proposition 1 holds.
|
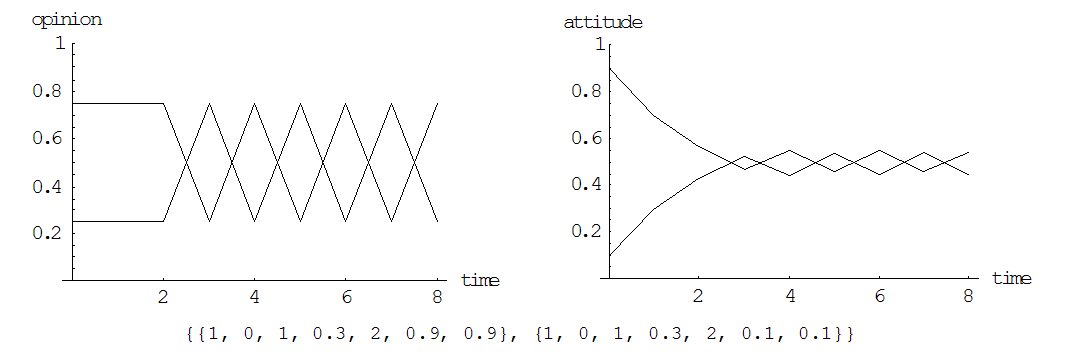
| Figure 8. Cyclic over adoption: Simulation run with two agents, both without selective interpretation, both adopting every perceived opinion, both assigning an impact of 0.3 to perceived opinions, but each with another initial attitude. |
|
| Figure 9. Number of clusters depending on precision for an infinite number of agents with equally distributed initial attitudes. The dotted line marks the maximal number of clusters in a stable configuration |
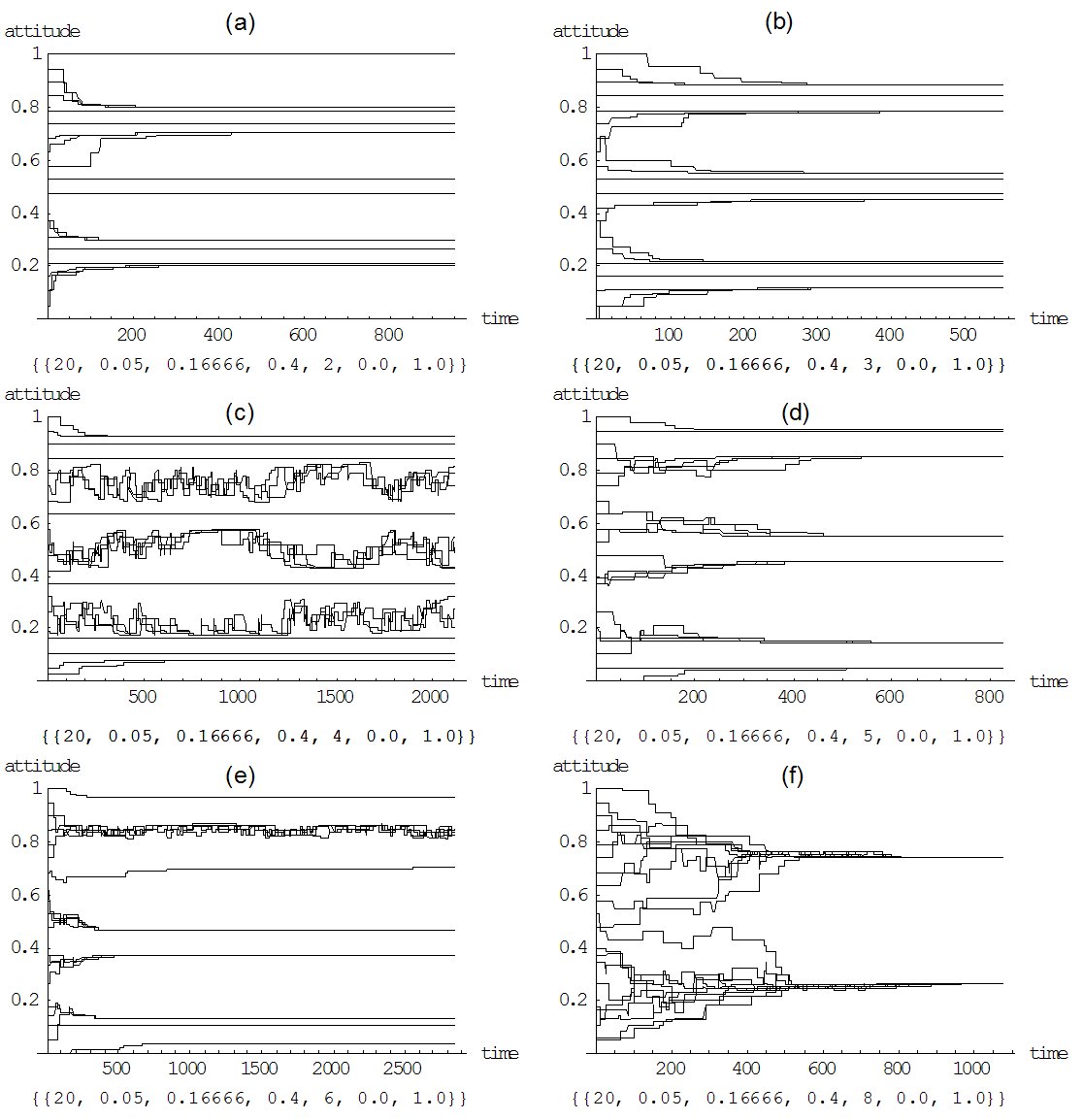
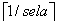 show the same patterns as with an infinite precision, as presented in Figure 10 (f).
show the same patterns as with an infinite precision, as presented in Figure 10 (f).
|
| Figure 10. Limited precision and selective interpretation: Each simulation run is with 20 agents having a selective interpretation of 0.05, a selective attention of 0.16, and an impact of perceived opinions of 0.4. The simulations runs differ in the value of precision: (a) prec = 2, (b) prec = 3, (c) prec = 4, (d) prec = 5, (e) prec = 6, and (f) prec = 8 |
2 Even if opinions are not expressed by words their representation usually contains abstract symbols, i.e. figures or a meaningful position of the body.
3 The interpretation process and the adoption process are also referred to as perceptual processes.
4 The membership of an individual in a specific social network determines the frequency or likelihood of communication with other members of the same net, as well as the impact of the information transmitted within the social net (e.g. Deffaunt 2001). An agent can be part of several social nets.
5 The impact is not included as a parameter that will be varied during the analysis.
6 Diffusion models describe attitudes and opinions usually as a number (see for instance in Deffuant et al. (2001) and Deffuant (2001) and this number is communicated, thus a symbolic channel is used.
7 Asking an individual for his or her opinion very common expressions are "very good", "good", "neutral" or "I do not know", bad, and "very bad", representing the continuum from a very strong tendency towards to a very weak tendency to react positively towards a given object.
8 The term agent refers to a formal representation of an individual. An analysis of agent paradigms can be found in Gilbert and Troitzsch (1999), Conte et al. (1998), and Burkhard (1995).
9 Selecting communication partners arbitrary across the whole society is a strong assumption. But as we do not want to analyse the impact or the emergence of communication networks, this simplification emphasizes the focus on the impact of limited verbalisation capabilities.
10 ![]() means that x is rounded down while
means that x is rounded down while ![]() means that x is rounded up to the next integer value.
means that x is rounded up to the next integer value.
11 For example, {{8, 0.0, 0.5, 0.5, 5, 0, 1},{2, 0.1, 0.5, 0.5, 5, 0.5, 0.7}} describes a multi-agent system with all ten agents having selective attention of 0.5 and an impact of 0,5. They can verbalise their attitudes on a five-point scale. The eight agents in the first group have no selective interpretation, while the two in the second group have that with a value of 0.1. The initial attitudes of the eight agents in the first group are given as 0, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, and 1. The two agents from the second group get the initial attitudes 0.5 and 0.7.
12 We can use the simple tool of area of influential attitudes only because we exclude every concept that distinguishes agents by other attributes than the verbalised attitude.
13 The symbol ![]() is a very small value that has to be integrated because the area of influential attitudes includes its limits.
is a very small value that has to be integrated because the area of influential attitudes includes its limits.
14 For example, the initial configuration of two relatively open-minded agents (sela = 0.9) that have the extreme initial attitudes 0.05 and 0.95 leads to two stable clusters, which is above the expected number of clusters (1).
15 The minimum number of clusters is 1 for all cases, especially in the case of all agents having the same initial attitude.
16 In Figure 7(a) there is one data line identical with the time axis.
CHATTOE E and GILBERT N (1999), Accepting government payment for new agri-environmental practices: A simulation approach to social complexity. In XVIII Congress of the European Society of Rural Sociology: How to be Rural in Late Modernity - Process, Project and Discourse, Lund, Sweden, 24-28 August.
CONTE R, GILBERT N, and SICHMANN J S (1998) MAS and social simulation: A suitable commitment. In J. S. Sichman, R. Conte, and N. Gilbert, editors, Proc. 1st. International Workshop on Multi-Agent Based Simulation, Lecture Notes in Artificial Intelligence, pages 1-9, Berlin. Springer Verlag.
DEFFUANT G, SKERRATT S, AMBLARD F, FERRAND N, CHATTOE E, GILBERT N, and WEISBUCH G (2000). Agent based simulation of decision process mixing rational reasoning and influences from socio-informal networks: case studies of agri-environmental measures adoption by farmers. <http://wwwlisc.clermont.cemagref.fr/ImagesProject/FinalReport/ >.
DEFFUANT G, NEAU D, AMBLARD F, and WEISBUCH G (2001), Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 87-98
DEFFUANT, G. (2001). Final report of project FAIR 3 CT 2092. Improving Agri-environmental Policies: A Simulation Approach to the Cognitive Properties of Farmers and Institutions. <http://wwwlisc.clermont.cemagref.fr/ImagesProject/default.asp >
FISHBEIN M and AJZEN I (1995), Belief, attitude, intention, and behavior: An introduction to theory and research. Addison-Wesley.
GILBERT N, TROITZSCH K G (1999), Simulation for the Social Scientist. Buckingham : Open University Press.
HEGSELMANN R and FLACHE A (1998), Understanding complex social dynamics: A plea for cellular automata based modelling. Journal of Artifical Societies and Social Simulation, 1, 3. <https://www.jasss.org/1/3/1.html >.
HEGSELMANN, R. and KRAUSE, U. 2002. Opinion Dynamics and Bounded Confidence Models: Analysis and Simulation. Journal of Artificial Societies and Social Simulation, 5, 3. <https://www.jasss.org/5/3/2.html >
HOLYST J A, KACPERSKI K, and SCHWEITZER F (2001), Social impact models of opinion dynamics. In Annual Reviews of Computational Physics, volume 9 (Ed. D. Stauffer), pages 253-273. World Scientific, Singapore.
HORNBY A S (1997), Oxford Advanced Learner's Dictionary of Current English. Oxford University Press, fifth edition.
KROEBER-RIEL W and WEINBERG P (1999), Konsumentenverhalten. Vahlen, München, seventh edition.
MOWEN J C and MINOR M (1998), Consumer Behavior. Prentice-Hall, fifth edition.
ROGERS E M (1995). Diffusion of innovations. The Free Press, 4th edition.
SHET J N , MITTAL B, and NEWMAN B I (1999). Customer Behavior. The Dryden Press.
TROMMSDORFF V (1998), Konsumentenverhalten. Kohlhammer, Stuttgart; Berlin; Köln, third edition.
WEISBUCH G, AMBLARD F, and NADAL J P (2001), Interacting agents and continuous opinion dynamics. working paper, Santa Fe Institute, <http://www.santafe.edu/sfi/publications/wpabstract/200111072 >.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]