Paul Vogt and Hans Coumans (2003)
Investigating social interaction strategies for bootstrapping lexicon development
Journal of Artificial Societies and Social Simulation
vol. 6, no. 1
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/1/4.html>
Received: 9-Sep-2002 Accepted: 18-Dec-2002 Published: 31-Jan-2003
 Abstract
Abstract
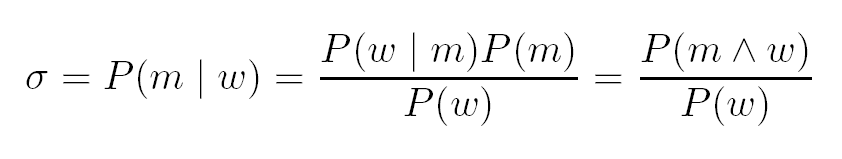
|
| (1) |
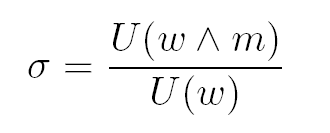
|
| (2) |
Here U(w&m) is the co-occurrence frequency of w with m, and U(w) is the occurrence frequency of w.
1 to 5. are identical to the guessing game.[6]
6. Instead of evaluating the game's success, the agents adapt their lexicon immediately as follows:
- The hearer first makes sure that the word is associated with all meanings in the context. I.e., the hearer adds new word-meaning associations for each meaning in the context that has no existing association with the word. In addition the hearer increments the co-occurrence frequency U(w&m) by 1 for all meanings in the context and increases the occurrence frequency U(w) with the context size, i.e. it increments U(w) by 1 for all meanings in the context.
- The speaker increments both U(w&m) and U(w) by 1 for the topic.
1. A series of X language games are played.
2. Remove all adults, replace them by the set of learners and add N new 'empty' agents to the set of learners.
|
| (a) |
|
| (b) |
|
| (c) |
|
| (d) |
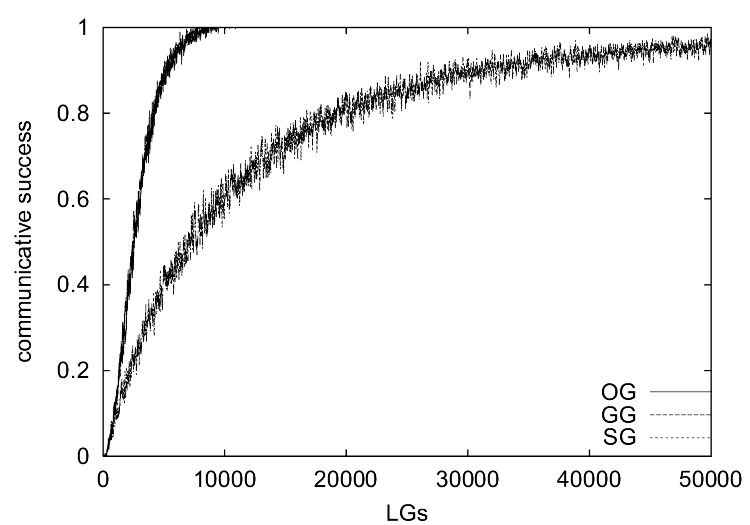
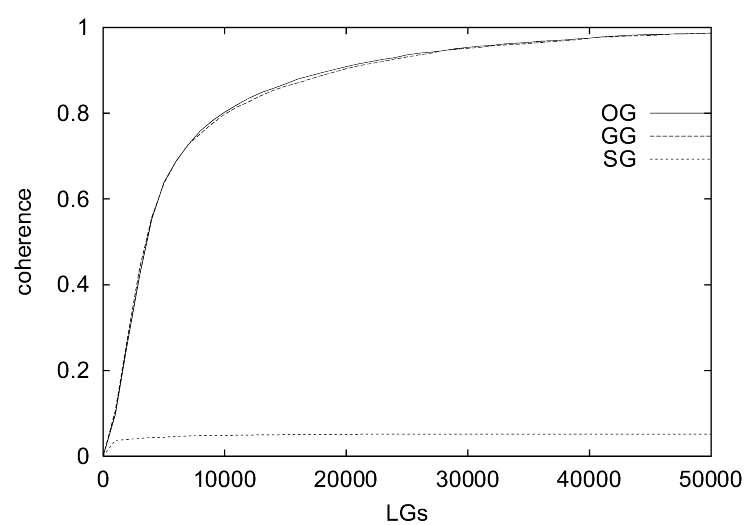
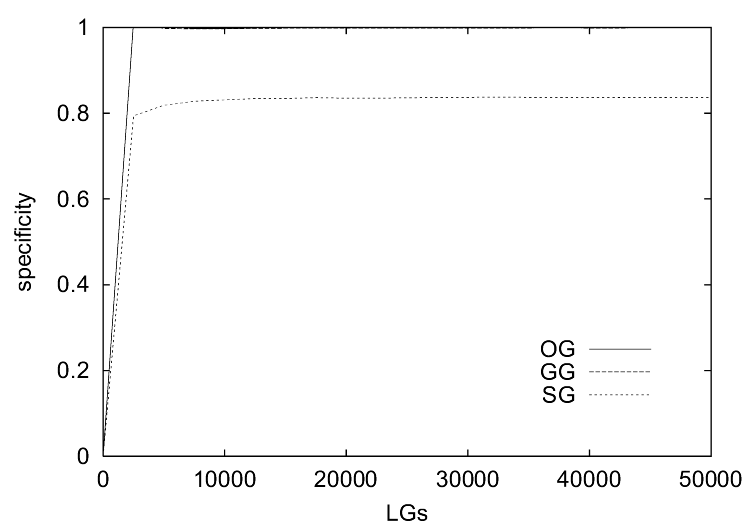
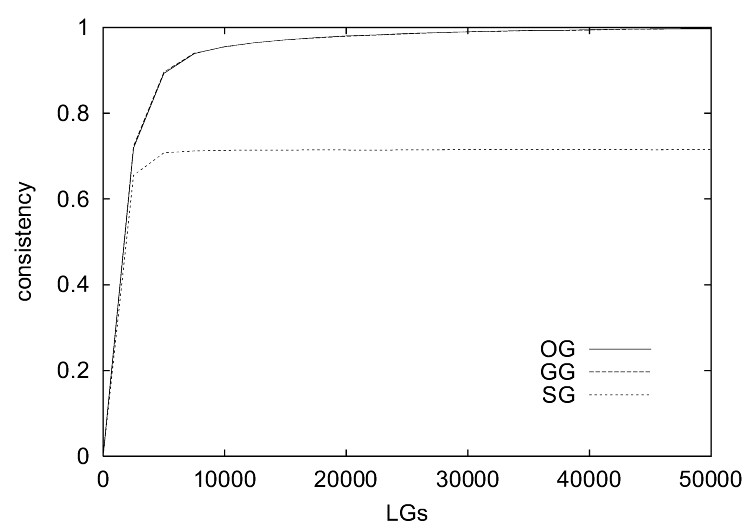
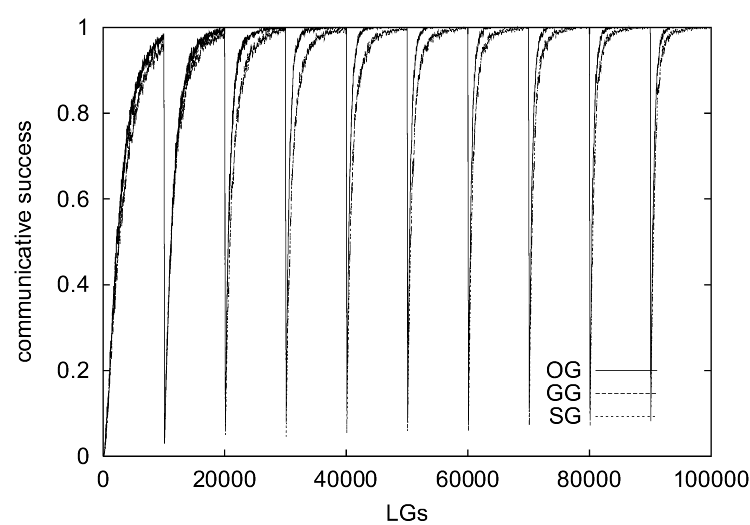
| Figure 1. The results of the simulations without the ILM show (a) the communicative success, (b) the coherence, (c) the specificity and (d) the consistency of the observational games (OG), guessing games (GG) and selfish games (SG) as a function of the number of language games played (x-axis). |
|
| (a) |
|
| (b) |
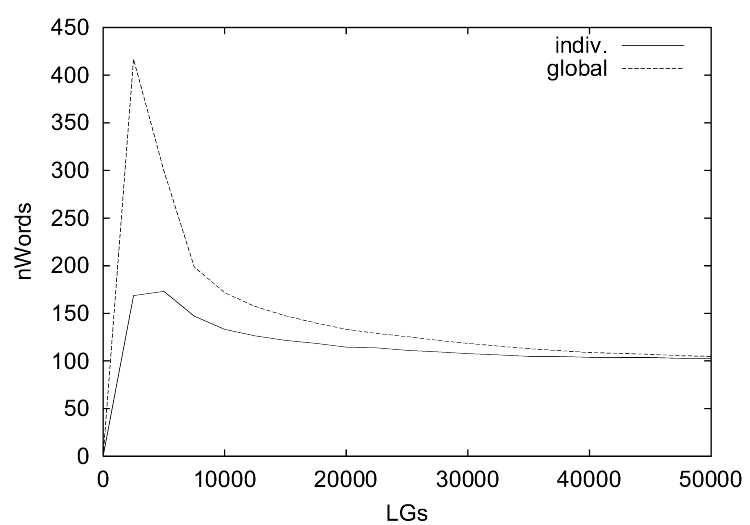
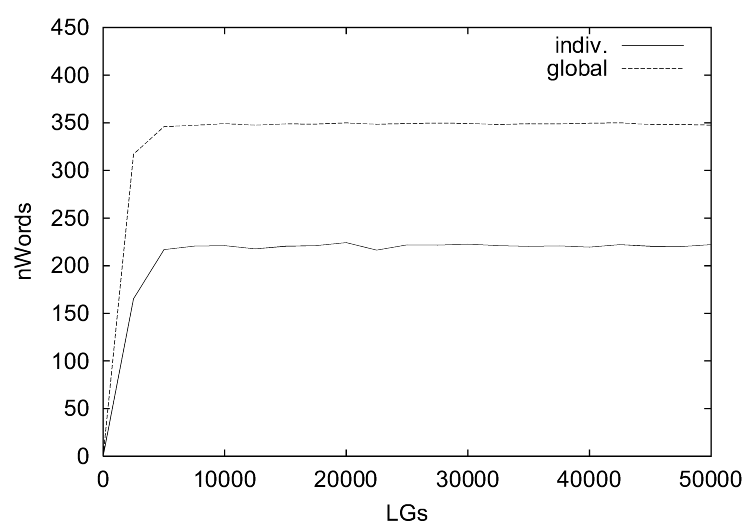
| Figure 2. These figures show the evolution of word use by the global population and an individual agent of (a) the guessing games and (b) the selfish games for the first simulation series. The x-axis shows the number of language games played and the y-axis shows the number of words used in each window of 2,500 games. |
|
| (a) |
|
| (b) |
|
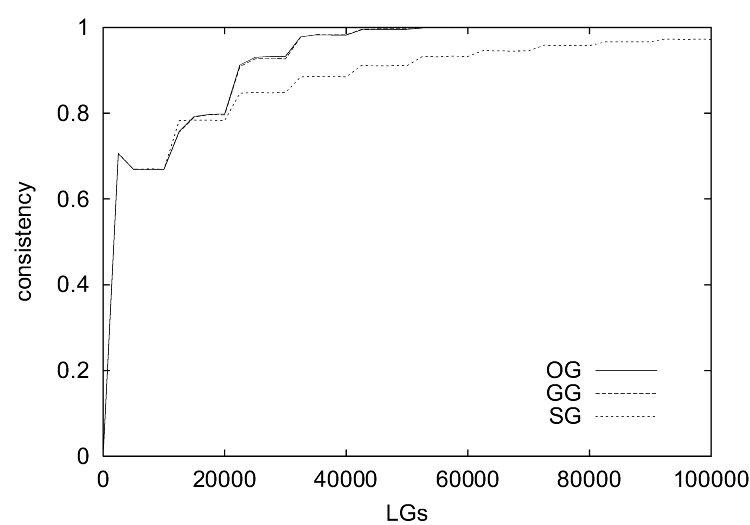
|
| (c) |
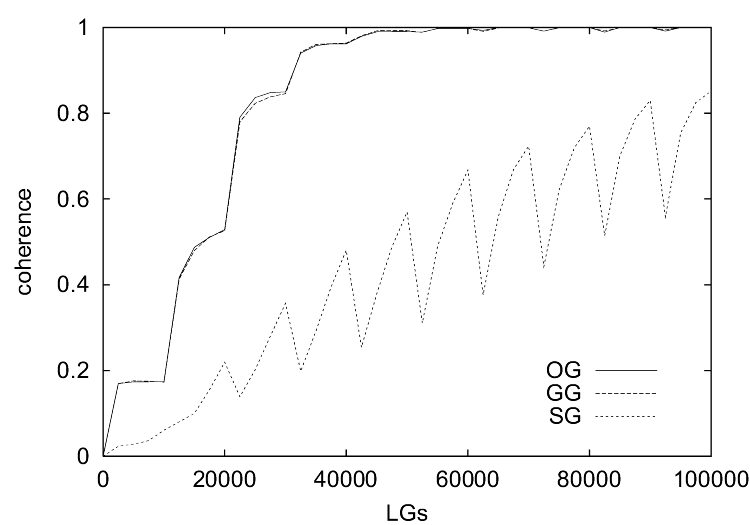
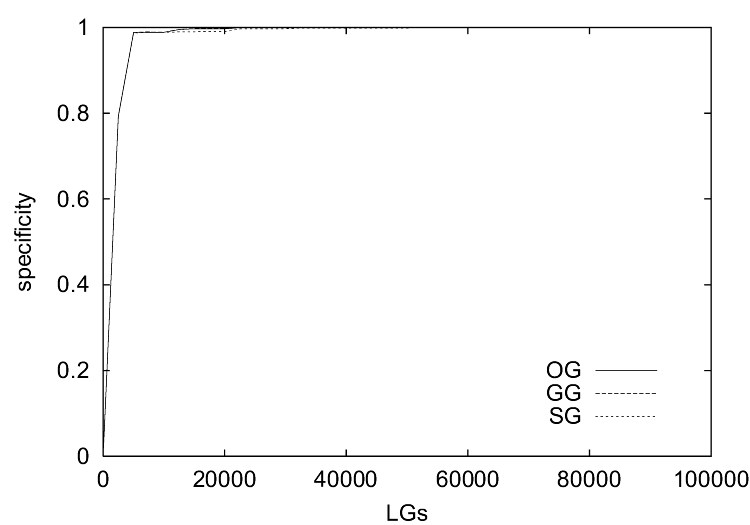
| Figure 3. The results of simulations with the ILM show (a) the communicative success, (b) the coherence, (c) the specificity and (d) the consistency. |
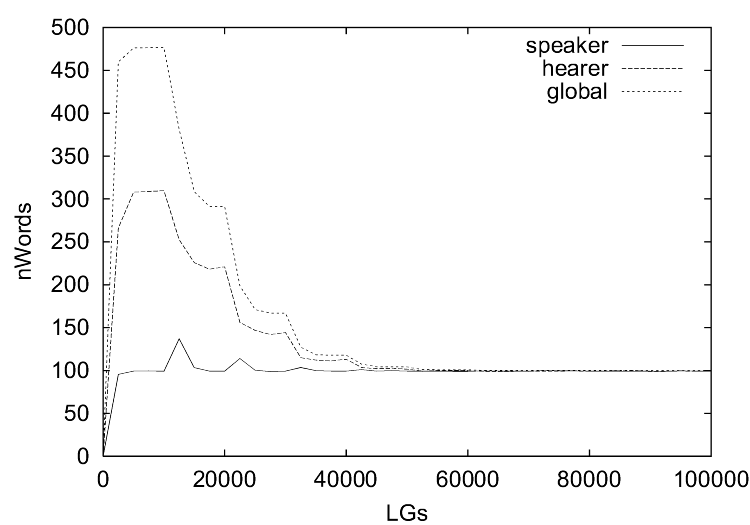
|
| (a) |
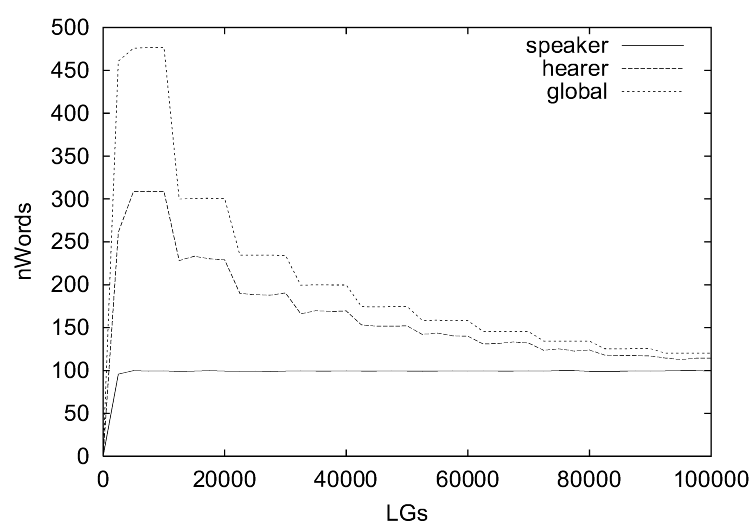
|
| (b) |
| Figure 4. These figures show the evolution of word use by the global population and a typical speaker and hearer of (a) the guessing games and (b) the selfish games for the second simulation series. The x-axis shows the number of language games played and the y-axis shows the number of words used in each window of 2,500 games. |

|
| (a) |
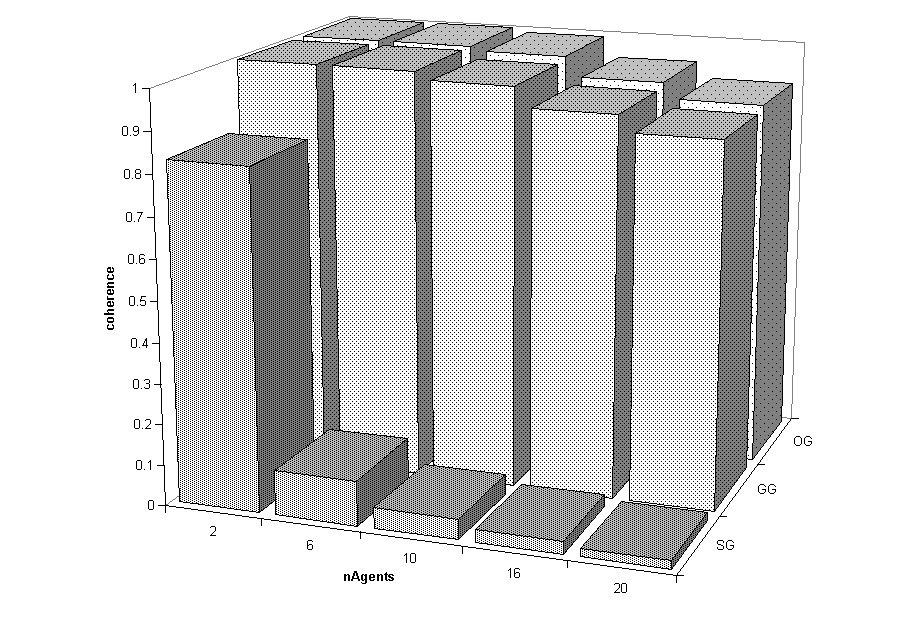
|
| (b) |
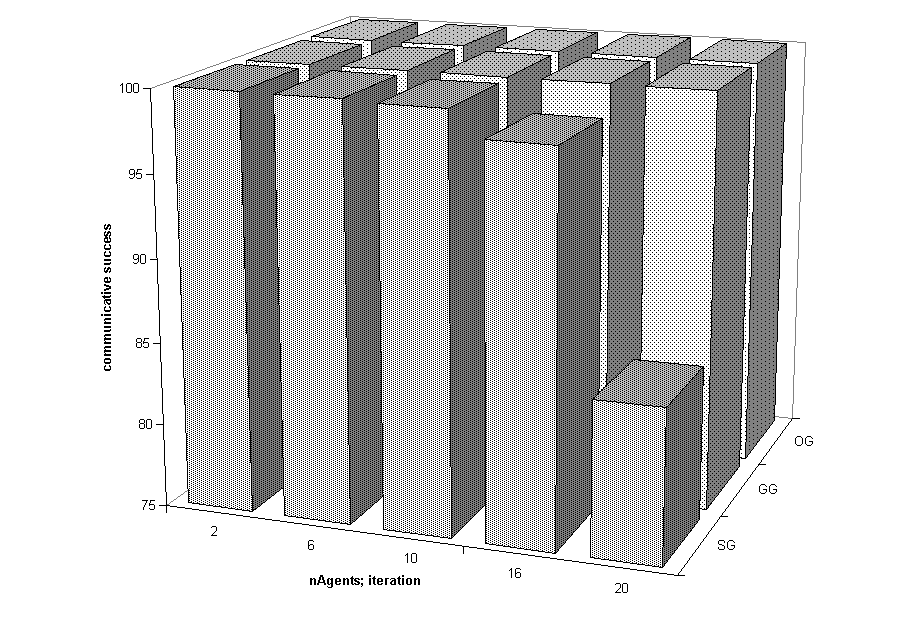
|
| (c) |
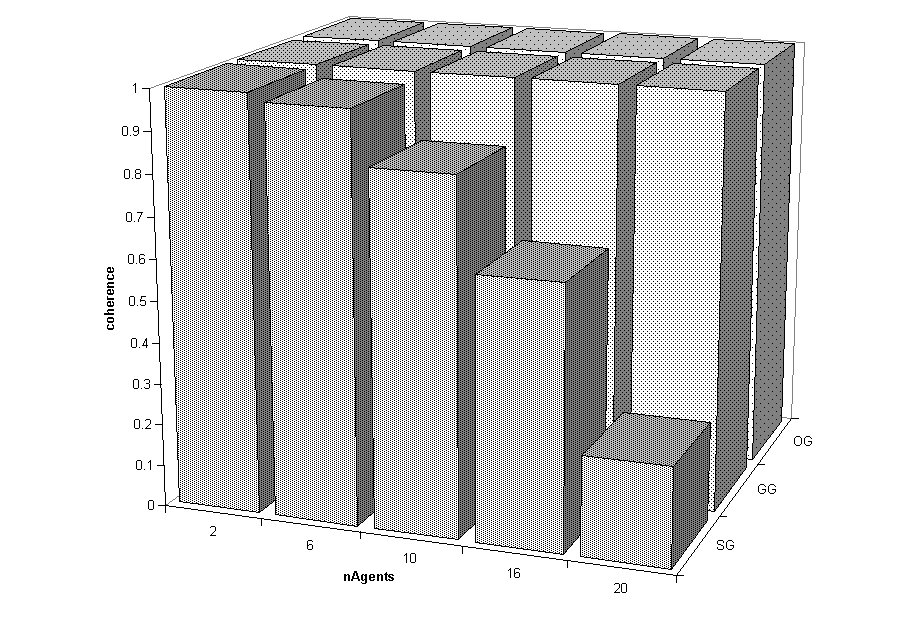
|
| Figure 5. Plots (a) and (c) show the average communicative success (z-axis) during the final 2,500 games as a function of the population size (x-axis) for the observational games (OG), guessing games (GG) and selfish games (SG). The final values of the coherence are presented in Figures (b) and (d). Figures (a) and (b) are from the simulations without the ILM, and Figures (c) and (b) are from those with the ILM. |
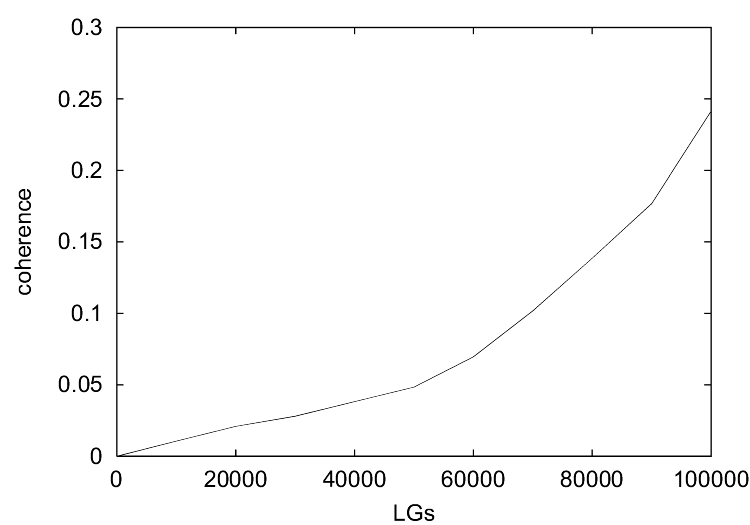
|
| Figure 6. This figure shows the coherence at the end of each iteration (y-axis) for the selfish game with the ILM and a population size of 20. (Note the different scale on the y-axis.) |
2 We can call this 'selfish' learning, because as the agents in this game do not explicitly 'care' whether they communicate about the same meaning, they behave more or less 'selfishly'.
3 Polysemy is the association of one word with several meanings and synonymy is the association of one meaning with several words.
4 Note that when the hearer has an association of the topic and the uttered word, it may select a different association when that one has a higher association score and its meaning is in the context.
5 In the simulations of this paper, the context size was always set to five.
6 When the speaker invents a new association (point 4), U(w& m) and U(w) are initialised with 0; the association score is initially set to σ =1.
7 This means that the population constantly contains 2N agents.
8 It is important to realise that speakers only invent novel words in the first iteration, because the speakers in the successive iterations have already learnt at least one word for each meaning.
9 Understanding each other's intention is required to establish joint attention (Tomasello 1999).
10 Cooperation is required to develop language.
BLOOM, P. (2000). How Children Learn the Meanings of Words. Cambridge, MA. and London, UK.: The MIT Press.
BROWN, R. (1958). How shall a thing be called? Psychological Review, 65, 14-21.
CANGELOSI, A. and Parisi, D. (2002). Simulating the Evolution of Language. London: Springer.
CAREY, S. (1978). The child as word-learner. In M. Halle,J. Bresnan and G. A. Miller (Eds.), Linguistic theory and psychological reality. Cambridge, MA.: The MIT Press.
CLARK, E. V. (1993). The lexicon in acquisition. Cambridge: Cambridge University Press.
COUMANS, H. (2002). The impact of contextual cues on lexicon formation. Unpublished M.Sc. thesis, Universiteit Maastricht.
DE JONG, E. D. (2000). The Development of Communication. Unpublished Ph.D. thesis, Vrije Universiteit Brussel.
DE LARA, J. and Alfonseca, M. (2002). The role of oblivion, memory size and spatial separation in dynamic language games. Journal of Artificial Societies and Social Simulation, 5(2).
DESSALLES, J.-L. (2000). Two stages in the evolution of language use. In J.-L. Dessalles and L. Ghadakpour (Eds.), The evolution of language: 3rd International Conference, Paris 2000. Paris.
HARE, B., Call, J. and Tomasello, M. (2001). Do chimpanzees know conspecifics know? Animal Behaviour, 61, 139-151.
KIRBY, S. (2002). Natural Language from Artificial Life. Paper presented at the Artificial Life.
KIRBY, S. and Hurford, J. R. (2002). The Emergence of Linguistic Structure: An Overview of the Iterated Learning Model. In A. Cangelosi and D. Parisi (Eds.), Simulating the Evolution of Language (pp. 121-148). London: Springer.
LIEVEN, E. V. M. (1994). Crosslinguistic and crosscultural aspects of language addressed to children. In C. Gallaway and B. J. Richards (Eds.), Input and interaction in language acquisition. Cambridge: Cambridge University Press.
MITCHELL, T. M. (1997). Machine Learning: McGraw-Hill.
OLIPHANT, M. (1999). The learning barrier: Moving from innate to learned systems of communication. Adaptive Behavior, 7 (3-4), 371-384.
OLIPHANT, M. and Batali, J. (1997). Learning and the emergence of coordinated communication. Center for Research on Language Newsletter, 11(1).
QUINE, W. V. O. (1960). Word and object. Cambridge: Cambridge University Press.
SAVAGE-RUMBAUGH, E., McDonald, K., Sevcik, W., Hopkins, R. and Rubert, E. (1986). Spontaneous symbol acquisition and communicative use by pygmy chimpanzees (pan paniscus). Journal of Experimental Psychology: General, 115, 211-235.
SHANNON, C. (1948). A mathematical theory of communication. The Bell System Technical Journal, 27, 379-423, 623-656.
SMITH, A. D. M. (2001). Establishing Communication Systems without Explicit Meaning Transmission. In J. Kelemen and P. Sosik (Eds.), Proceedings of the 6th European Conference on Artificial Life, ECAL 2001 (pp. 381-390). Berlin Heidelberg: Springer-Verlag.
STEELS, L. (1996a). Emergent Adaptive Lexicons. In P. Maes (Ed.), From Animals to Animats 4: Proceedings of the Fourth International Conference On Simulating Adaptive Behavior. Cambridge Ma.: The MIT Press.
STEELS, L. (1996b). Perceptually grounded meaning creation. In M. Tokoro (Ed.), Proceedings of the International Conference on Multi-Agent Systems. Menlo Park Ca.: AAAI Press.
STEELS, L. and Kaplan, F. (2002). Bootstrapping grounded word semantics. In T. Briscoe (Ed.), Linguistic evolution through language acquisition: formal and computational models. Cambridge: Cambrige University Press.
STEELS, L. and Vogt, P. (1997). Grounding adaptive language games in robotic agents. In C. Husbands and I. Harvey (Eds.), Proceedings of the Fourth European Conference on Artificial Life. Cambridge Ma. and London: The MIT Press.
TOMASELLO, M. (1999). The cultural origins of human cognition: Harvard University Press.
TOMASELLO, M. and Todd, J. (1983). Joint attention and lexical acquisition style. First Language, 4, 197-212.
VOGT, P. (2000a). Bootstrapping grounded symbols by minimal autonomous robots. Evolution of Communication, 4(1), 89-118.
VOGT, P. (2000b). Lexicon Grounding on Mobile Robots. Unpublished Ph.D. thesis, Vrije Universiteit Brussel.
VOGT, P. (2001). The impact of non-verbal communication on lexicon formation. In B. Kröse,M. De Rijke,G. Schreiber and M. Van Someren (Eds.), Proceedings of the 13th Belgian/Netherlands Artificial Intelligence Conference, BNAIC'01.
VOGT, P. (2002a). Anchoring symbols to sensorimotor control. In H. Blockeel and M. Denecker (Eds.), Proceedings of the 14th Belgian/Netherlands Artificial Intelligence Conference, BNAIC'02.
VOGT, P. (2002b). The physical symbol grounding problem. Cognitive Systems Research, 3(3), 429-457.
VOGT, P. and Coumans, H. (2002). Exploring the impact of contextual input on the evolution of word-meaning. In B. Hallam,D. Floreano,J. Hallam,G. Hayes and J.-A. Meyer (Eds.), Proceedings of the Seventh International Conference of The Society for Adaptive Behavior SAB2002. Cambridge, MA.: The MIT Press.
YANCO, H. and Stein, L. (1993). An adaptive Communication Protocol for Cooperating Mobile Robots. In J.-A. Meyer,H. L. Roitblat and S. Wilson (Eds.), From Animals to Animats 2. Proceedings of the Second International Conference on Simulation of Adaptive Behavior (pp. 478-485). Cambridge Ma.: The MIT Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]