Jürgen Klüver, Christina Stoica and Jörn Schmidt (2003)
Formal Models, Social Theory and Computer Simulations: Some Methodical Reflections
Journal of Artificial Societies and Social Simulation
vol. 6, no. 2
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/2/8.html>
Received: 18-Sep-2002 Accepted: 17-Feb-2003 Published: 31-Mar-2003
 Abstract
Abstract| fn (S1) = S n+1. | (1) |
A point attractor Sa of the trajectory is now simply defined as
| fn (Sa) = Sa, | (2) |
with the corresponding definitions of simple attractors with periods k > 1.
| S = (C, St). | (3) |
| Ro = (r,k). | (4) |
|
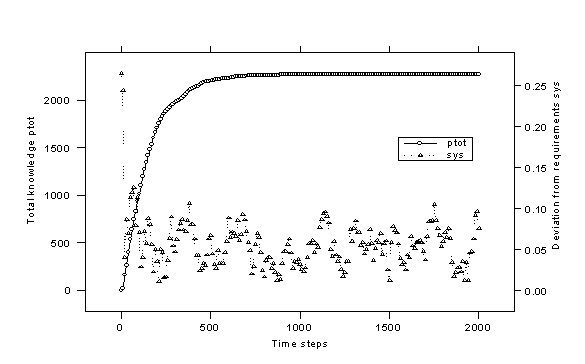
| Figure 1. a Toynbee development with low EP-values: the culture is caught in an attractor |
|
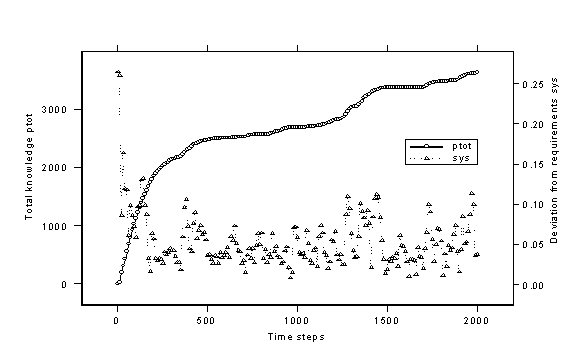
| Figure 2. a modern development: the culture transcends attractors |
|
(1,1) = 1 (1,0) = 0 (0,1) = 0 (0,0) = 0, |
(5) |
then obviously this rule is nothing else than the logical conjunction.
| v = |(OD - ODmin)| / |(ODmax - ODmin)| and 0 ≤ v ≤ 1. | (6) |
ODmin is the outdegree vector, i.e. the vector for the outputs of the units, that contains the maximal possible homogeneous distribution of outputs; ODmax is the outdegree vector with the minimal possible homogeneous distribution and OD is the factual outdegree vector for the BN.
2 To be sure, the use of differential or difference equations does not necessarily mean a top down approach. It is quite possible to model systems with differential equations while going bottom up. For example, Kepler's equations are a typical top down model of the planetary system; Newton's theory of gravitation is strictly speaking a bottom up model.
3 Our translation from the German version
4 We have to make a caveat to this statement: of course there are also theoretical approaches in the social sciences that try to start with the basics of social behaviour and go on from there by enlarging their models. Such a procedure is, e.g., characteristic for Garfinkel and his school of ethnomethodology, the role theory of Goffman or other micro sociological approaches. Therefore our remark is to be understood as a remembrance of methodical procedures that are sometimes neglected.
5 We assume that the determinant of the pay off matrix is the significant parameter. Unfortunately neither Nowak and May nor Fogel did investigate this question.
6 According to a personal remark of Michael Cohen they were inspired to do this by the research of our group.
7 Readers who are acquainted with the famous "limit theorems" of Gödel, Church and Turing may be a bit surprised by our statement, that this procedure has no limits. But it is rather easy to demonstrate that for every single modelling it is possible to construct a sufficient powerful formal system, although for this formal system the limit theorems are also valid (cf. Klüver 2000).
AXELROD, R. 1984: The Evolution of Cooperation. New York: Basic Books
AXELROD, R., 1987: The Evolution of Strategies in the Iterated Prisoner's Dilemma. In: Davis, L. (ed.): Genetic Algorithms and Simulated Annealing. Los Altos: Morgan Kauffman
BAHR, D.B. and Passerini, E., 1998: Statistical Mechanics of Opinion Formation and Collective Behavior. Journal of Mathematical Sociology 23, 1 - 41
BENFER, R.A., Brent, E.E. and Furbee, L., 1991: Expert Systems. Newbury Park-London: Sage
BERGER, J. and Zelditch, M., (eds.), 2002: New Directions in contemporary Sociological Theory. New York: Rowman and Littlefield
BERTALANFFY, L.v., 1951: Zu einer allgemeine Systemlehre. Biologia Generalis. Archiv für die allgemeinen Fragen der Lebensforschung 19, 114 - 129
BRENT, E. E. and Anderson, R., 1990: Computer Applications in the Social Sciences. Philadelphia-London: Basics
BONNEUIL, N., 2000: Viability in Dynamic Social Networks. Journal of Mathematical Sociology 24, 175 - 192
COHEN,M.D., Riollo, R.L. and Axelrod, R., 2000: The Role of Social Structure in the Maintenance of Cooperative Regimes. Rationality and Society 13, 5 - 32
EINSTEIN, A. and Infeld, L., 1958: Die Evolution der Physik. Reinbek: Rohwohlt
EPSTEIN, J.M., 1997: Non-linear Dynamics, Mathematical Biology and Social Science. Redwood: Addison Wesley
FARARO, T., 1997: Reflections on Mathematical Sociology. Sociological Forum 12, 73 - 101
FOGEL, D.B., 1993: Evolving Behaviors in the Iterated Prisoner's Dilemma. Evolutionary Computation 1, 77 - 97
FREEMAN, L. 1989: Social Networks and the Structure Experiment. In: Freeman, L. (ed.): Research Methods in Social Network Analysis. Fairfax: George Mason University Press
GEERTZ, C., 1973: The Interpretation of Cultures. New York: Basic Books
GIDDENS, A., 1984: The Constitution of Society. Outline of the Theory of Structuration. Cambridge: Polity Press
HABERMAS, J., 1981: Theorie des kommunikativen Handelns. Frankfurt (M): Suhrkamp
HANNEMANN, R.A., 1988: Computer-Assisted Theory Building. Newbury Park/London: Sage
HOLLAND, J. R., 1998: Emergence. From Chaos to Order. Reading (MA): Addison Wesley
KAUFFMAN, S.A., 1992: Origins of Order in Evolution. Self-Organization and Selection. In: Varela, F.J. and Dupuy, J.P. (eds.): Understanding Origins. Contemporary Views on the Origin of Life. Dordrecht: Kluwer Academic Publishers
KAUFFMAN, S.A., 1995: At Home in the Universe. New York: Oxford University Press
KAUFFMAN, S.A., 2000: Investigations. Oxford: Oxford University Press
KLÜVER, J. and Schmidt, J., 1999: Control Parameters in Boolean Networks and Cellular Automata Revisited: From a logical and a sociological point of view. Complexity 5, No. 4, 45 - 52
KLÜVER, J. and Schmidt, J., 1999a: Social differentiation as the Unfolding of Dimensions of Social Systems. Journal of Mathematical Sociology 23 (4), 309 - 325
KLÜVER, J. and Stoica, C., 2002: A Model of Cognitive Ontogenesis. In: J. Klüver, J., An Essay Concerning Sociocultural Evolution. Theoretical Principles and Mathematical Models. Dordrecht: Kluwer Academic Publishers
KLÜVER, J. and Schmidt, J., 2003: Historical Evolution and Mathematical Models: A Sociocultural Algorithm. Journal of Mathematical Sociology Vol. 28, issue 1
KLÜVER, J., 2000: The Dynamics and Evolution of Social Systems. New Foundations of a Mathematical Sociology. Dordrecht (NL): Kluwer Academic Publishers
KLÜVER, J., 2002: An Essay Concerning Sociocultural Evolution. Theoretical Principles and Mathematical Models. Dordrecht: Kluwer Academic Publishers
KUHN, T.S., 1962: The Structure of Scientific Revolutions. Chicago: University of Chicago Press
MICHALEWICZ, Z., 1994: Genetic Algorithms + Data Structures = Evolutionary Programs. Berlin: Springer
NOWAK, M.A. and May, R.M., 1993: The Spatial Dilemma of Evolution. International Journal of Bifurcation and Chaos 3, 35 - 78
PARISI, D., Ceconi, F. and Cerini, A., 1995: Kin-directed altruism and attachment behaviour in an evolving population of neural networks. In: Gilbert, N. and Conte, R. (eds.): Artificial Societies. The Computer Simulation of Social Life. London: UCL Press
RASMUSSEN, S., Knudsen, C. and Feldberg, R., 1992: Dynamics of Programmable Matter. In: Langton, C.G., Taylor, C., Farmer, J.D. and Rasmussen S., (eds.): Artificial Life II. Reading (MA): Addison Wesley
TOYNBEE, A., 1934 - 61: A Study of History (12 vols.) Oxford: Oxford University Press
WIPPLER, R. and Lindenberg, S., 1987: Collective Phenomena and Rational Choice. In: Alexander et al. (eds.) The Micro-Macro-Link. Berkeley: University of California Press
WOLFRAM, S. 2002: A new kind of science. Champagne (IL): Wolfram Media
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]