Franziska Klügl and Ana L. C. Bazzan (2004)
Route Decision Behaviour in a Commuting Scenario: Simple Heuristics Adaptation and Effect of Traffic Forecast
Journal of Artificial Societies and Social Simulation
vol. 7, no. 1
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/7/1/1.html>
Received: 10-Feb-2003 Accepted: 14-Aug-2003 Published: 31-Jan-2004
 Abstract
Abstract
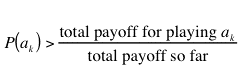
|
(1) |
Therefore, in the near future, each strategy is selected according to its probability. This leads the ESS to be selected asymptotically. It is assumed that the payoffs correspond to changes in fitness, and that the game is played enough times to ensure that the payoffs received after an ESS is reached exceed the payoffs received during the learning period.
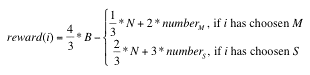
|
(2) |
The parameters numberM and numberS represent the number of commuters in the main and secondary road, respectively. We set N to18 and the total number of rounds to 200, because this was the scenario that was used as an experimental set-up proposed by Selten and colleagues. Later in this paper we also give a brief account on results for N=900.

|
(3) |
The variable rewardM is the reward agent i has accumulated on the main route, while rewardS denotes his success on the side route S. There is a feedback loop - the more a driver selects a route, the more information (in form of reward) he gets from this route. Therefore an important factor is how often and in which intervals the heuristic is updated. This is especially relevant because the reward depends on the other agents. When the agent is learning, he is also implicitly adapting himself to the others. In the experiments described below experiences were collected without any form of forgetting. All previous experience is influencing the dynamics of the heuristic. It is possible to only consider experiences from a restricted window using only the results of the last route choices to compute the new heuristic. We tested experience windows of 10, 50, 100, 200, 500 rounds (the last two values in longer simulation runs of 1000 rounds) resulting in no significant difference between the outcomes in the final heuristics of the agents.
| Table 1: Final heuristics and stability (number of route changes) averaged over all 6 runs and all agents | ||
| Adaptation frequency | Average of final heuristic | Stability: Route Changes |
| 1 | 0.677 ± 0.228 | 70 ± 27 |
| 5 | 0.676 ± 0.322 | 51 ± 39 |
| 10 | 0.679 ± 0.285 | 60 ± 36 |
| 20 | 0.688 ± 0.285 | 60 ± 38 |
| 50 | 0.715 ± 0.191 | 72 ± 29 |
|
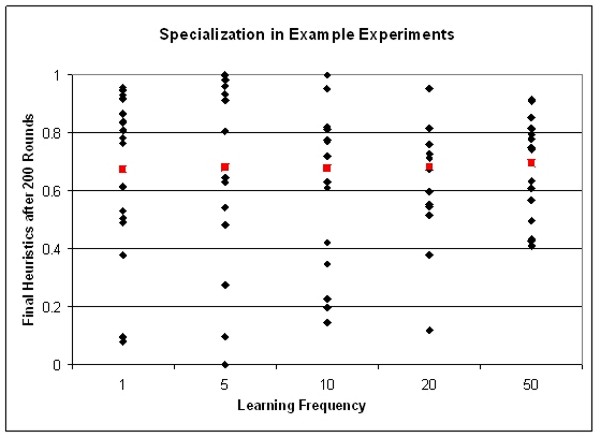
| Figure 1. Final heuristics of all agents in example experiment for all learning frequencies. The red squares denote the mean heuristic for the final heuristics of this run |
|
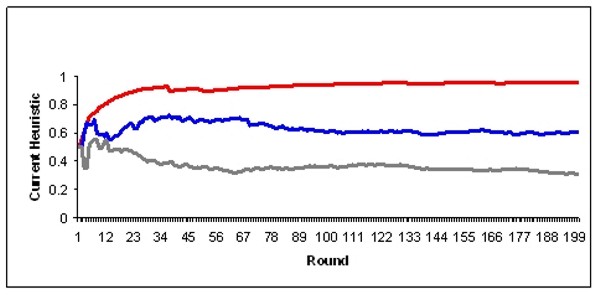
| Figure 2. Development of the heuristics of three selected agents during a simulation run where the agents adapt their heuristic in every round |
A first result of our simulations is the correlation between inertia in learning, the emerging specialisation, and route commitment.
| Table 2: Sum of Reward averaged over all experiments and all agents and average distribution of drivers between the two routes (5 different scenarios) | |||
| Adaptation frequency | Sum of reward | Average number of drivers on main route (last 100 rounds) | Average number of drivers on secondary route (last 100 rounds) |
| 1 | 1784 ± 69 | 12.4 ± 1.7 | 5.6 ± 1.7 |
| 5 | 1824 ± 95 | 12.2 ± 1.5 | 5.8 ± 1.5 |
| 10 | 1810 ± 81 | 12.2 ± 1.5 | 5.8 ± 1.5 |
| 20 | 1691 ± 153 | 12.7 ± 1.6 | 5.3 ± 1.6 |
| 50 | 1641 ± 130 | 13.3 ± 1.7 | 4.7 ± 1.7 |
|
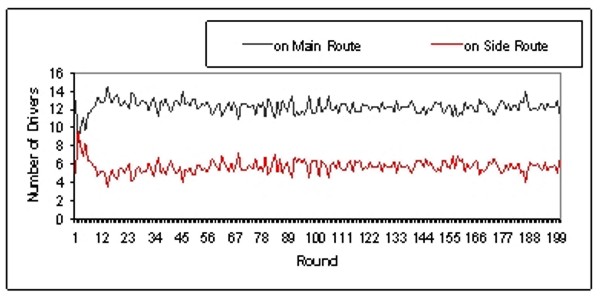
| Figure 3. Development of the distribution of drivers in the Main and Side routes (Learning Frequency = 5, Initial Heuristic = 0.5) |
|
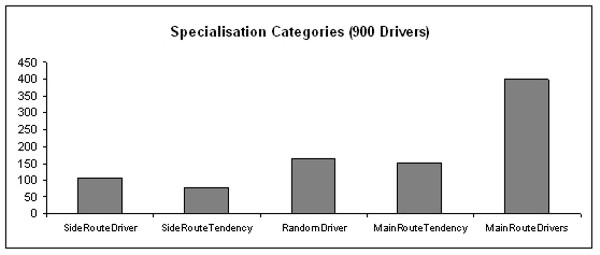
| Figure 4. Number of drivers in each of the five categories; results regard scenario in which the learning takes place about every 5 rounds |
|
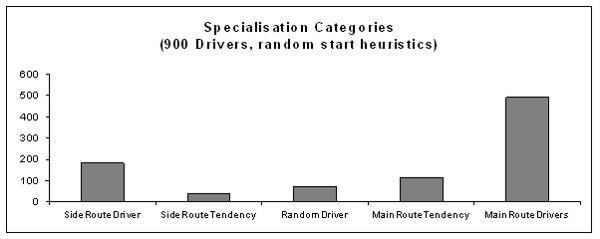
| Figure 5. Number of drivers in each of the five categories; the learning takes place about every 5 rounds; initial heuristic to select main and side routes are equally distributed between 0 and 1 |
|
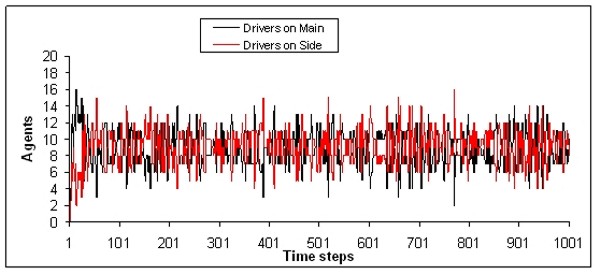
| Figure 6. Example of highly ineffective distribution of drivers on the two routes |
|
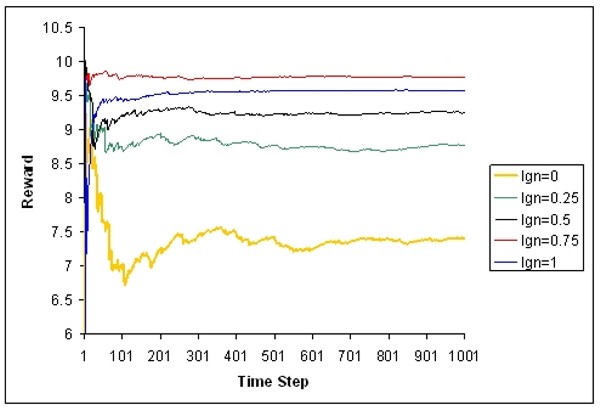
| Figure 7. Development of the average expected reward in five example runs with different shares of drivers who react to traffic forecast |
| Table 3: Mean final heuristics of all drivers in five example runs with different shares of ignorant drivers | |||||
| Share of ignorants | 0 | 0.25 | 0.5 | 0.75 | 1 |
| Final heuristics | 1.06 | 0.80 | 0.67 | 0.67 | 0.68 |
| Table 4: Drivers on main and on side routes (left); final heuristic (mean ± standard deviation) and mean expected reward (right): tolerances 1, 3, and 5, and share of ignorants 0, 0.25, 0.5, and 0.75 | ||||
| tolerance 1 | share of | tolerance 1 | ||
| drivers main | drivers side | ignorants | final heuristic | expected reward |
| 9.11 | 8.84 | 0 | 1.06 ± 0.02 | 7.40 |
| 10.41 | 7.54 | 0.25 | 0.80 ± 0.10 | 8.78 |
| 11.33 | 6.61 | 0.5 | 0.67 ± 0.32 | 9.25 |
| 11.84 | 6.10 | 0.75 | 0.67 ± 0.32 | 9.77 |
| 12.25 | 5.70 | 1 | 0.68 ± 0.42 | 9.58 |
| tolerance 3 | share of | tolerance 3 | ||
| drivers main | drivers side | ignorants | final heuristic | expected reward |
| 11.49 | 6.45 | 0 | 0.73 ± 0.30 | 8.92 |
| 11.48 | 6.47 | 0.25 | 0.70 ± 0.30 | 9.29 |
| 11.84 | 6.11 | 0.5 | 0.68 ± 0.28 | 9.71 |
| 12.01 | 5.93 | 0.75 | 0.67 ± 0.33 | 9.61 |
| tolerance 5 | share of | tolerance 5 | ||
| drivers main | drivers side | ignorants | final heuristic | Expected reward |
| 12.34 | 5.61 | 0 | 0.68 ± 0.31 | 9.23 |
| 12.32 | 5.63 | 0.25 | 0.67 ± 0.29 | 9.29 |
| 11.94 | 6.01 | 0.5 | 0.68 ± 0.25 | 9.83 |
| 12.11 | 5.83 | 0.75 | 0.67 ± 0.28 | 9.27 |
|
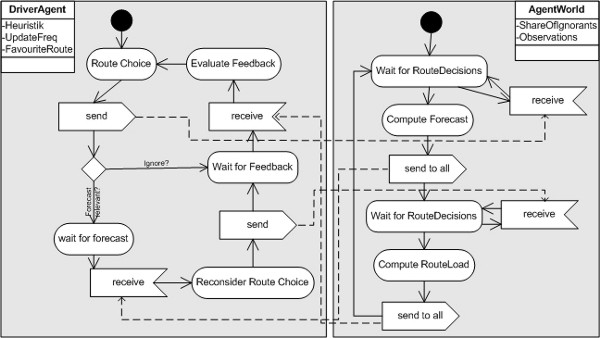
| Figure 8. The specification of the behaviour of a driver agent in combination with the AgentWorld. A driver starts with selecting a route and announcing its choice to the world that computes a forecast for it. After having received the forecast the driver has the chance to reconsider its selection based on the information resulting in a final route choice. The world again acts as a traffic centre and returns travel information as a result of all route choices. Based on this information the driver evaluates its success adapting its route choice heuristic. These two combined graphs form the complete specification of the model with forecast information |
|
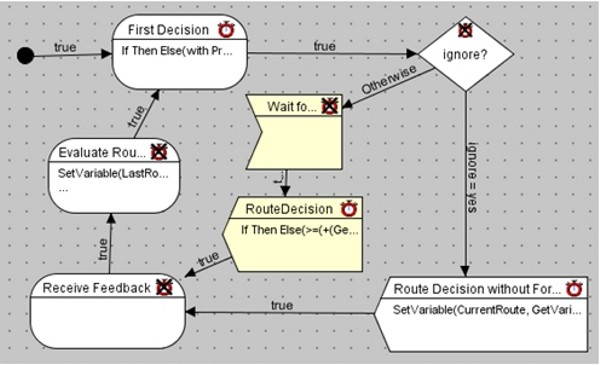
| Figure 9. Screenshot from the SeSAm implementation of a driver agent according to the specification given in figure 8. The yellow nodes are the ones added when extending the scenario without forecast to the scenario with forecast |
BEN-AKIVA,M., de Palma, A. and Kaysi, I. (1991) Dynamic network models and driver information systems. Transportation Research Part A 25(5): 251-266.
BURMEISTER, B., J. Doormann, and G. Matylis. (1997) Agent-oriented traffic simulation. Transactions of the Society for Computer Simulation International, 14(2), June 1997
CASTELFRANCHI, C. (1998) 'Modelling Social Action for AI Agents'. Artificial Intelligence, 103: 157 -182.
DE PALMA, A. (1998) Individual and Collective Decision Making: Applications to Travel Choice. Theoretical Foundations of Travel Choice Modelling, T. Gärling, T. Laitila, and K. Westin, (eds.), pp. 33-50, Elsevier, Oxford.
DIA, H., Purchase, H. (1999) Modelling the impacts of advanced traveller information systems using Intelligent Agents. Road and Transport Research, 8: 68-73.
FISCHER , K., Kuhn N., H.J.Müller, J.P.Müller and M. Pischel (1995) Sophisticated and Distributed: The Transportation Domain. In. Proc. of European Workshop on Modelling Autonomous Agents (MAAMAW 1993), LNAI 975, Springer.
HARLEY, C. B. (1981) Learning the Evolutionary Stable Strategy. Journal of Theoretical Biology, 89: 611-631.
KLÜGL, F.: Multi-Agent Simulation – Concepts, Tools, Application, Addison Wesley, Munich, (in German), 2001.
KLÜGL, F. and Bazzan, A. L. C. (2002) Simulation of adaptive agents: learning heuristics for route choice in a commuter scenario. Proc. of the First Int. Joing Conf. on Autonomous Agents and Multi-agent Systems (AAMAS 2002). ACM Press, 217-218
KLÜGL, F. and Bazzan, A. L. C. (2003) Selection of Information Types Based on Personal Utility – a Testbed for Traffic Information Markets. Proc. of the Second Int. Joing Conf. on Autonomous Agents and Multi-agent Systems (AAMAS 2003). ACM Press, 377-384.
MACY, M. W. and Andreas Flache (2002). Learning dynamics in social dilemmas. PNAS 99: 7229-7236.
MAYNARD-SMITH, J., Price, G. R. (1973) The logic of animal conflict. Nature, 246: 15-18,.
NAGEL, K. and M. Schreckenberg (1992). A cellular automaton model for freeway traffic. J. Phys. I France 2, 2221.
OECHSLEIN, C., Klügl, F., Herrler, R. and F. Puppe (2002). UML for Behavior-Oriented Multi-Agent Simulations. In: Dunin-Keplicz, B., Nawarecki, E.: From Theory to Practice in Multi-Agent Systems, CEEMAS 2001 Cracow, Poland, September 26-29, 2001, (= LNCS 2296), Springer, Heidelberg, pp. 217ff
OSSOWSKI, S. (1999) Co-ordination in artificial agent societies, social structures and its implications for autonomous problem-solving agents. (LNAI, Vol. 1535). Springer, Berlin.
ROSSETTI, R.J.F., Bampi, S., Liu, R., Van Vliet, D., Cybis, H.B.B. (2000) An Agent-Based framework for the assessment of drivers' decision-making. Proc. of the 3rd Annual IEEE Conference on Intelligent Transportation Systems, Oct. 2000 Dearborn, MI, Proceedings, Piscataway: IEEE, p.387-392.
ROTH, A. E. & Erev, I. (1995) Learning in extensive form games: experimental data and simple dynamic models in the intermediate term. Games Econ. Behav. 8, 164-212
SELTEN, R., Schreckenberg, M., Pitz, T., Chmura, T. and Wahle, J. (2003) Experimental Investigation of Day-to-Day Route Choice-Behaviour. R. Selten and M. Schreckenberg (eds.) Human Behavior and Traffic Networks, Springer (to appear).
SRINIVASAN, K. K. and Mahmassani, H. S. (2003) Analyzing heterogeneity and unobserved structural effects in route-switching behavior under ATIS: a dynamic kernel logit formulation. Transportation Research Part B 37(9): 793-814.
WAHLE, J., Bazzan, A. L. C., Klügl, F., Schreckenberg, M. (2000) Decision Dynamics in a Traffic Scenario. Physica A, 287 (3-4): 669 - 681.
WAHLE, J., Bazzan, A. L. C., Klügl, F., Schreckenberg, M. (2002) The Impact of Real Time Information in a Two Route Scenario using Agent Based Simulation. Transportation Research Part C: Emerging Technologies 10(5-6): 73 – 91.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]