Eric Darmon and Dominique Torre (2004)

Adoption and Use of Electronic Markets: Individual and Collective Learning

Journal of Artificial Societies and Social Simulation vol. 7, no. 2
<https://www.jasss.org/7/2/2.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary

Received: 07-Feb-2004    Accepted: 02-Jan-2004    Published: 31-Mar-2004

Abstract

We investigate in this paper the problem of the dynamics of adoption of electronic commerce, focusing on agents expertise and learning patterns in using e-markets. Traders face a double uncertainty. In the traditional channel, intrinsic frictions make uncertain the implementation of an exchange, but the quality of the traded items is perfectly observable. In the electronic channel, exchange always occurs but agents imperfectly appreciate items' quality, because traders and traded commodities are inaccurately observable on e-markets. We develop in this paper a simulation model to deal with this issue. In this model, traders are heterogeneous regarding both their preferences and their ability to trade on the electronic market. We successively sketch two scenarii: i) We first analyse a situation where learning is strictly individual. A trial-and-errors learning pattern may have an ambiguous impact. On the one hand, it is found to improve the diffusion of electronic markets. On the other hand, it may be responsible of a new source of inequalities because some agents may not be able to trade in the electronic channel and are hence excluded from the use of this market either in the short run (temporal unemployment) or in the long run (structural unemployment). As learning is imperfect, the economy converges to a situation where the two markets coexist, inducing coordination costs (frictional unemployment). ii) We then extend our results by exploring the effects of community-based learning practices: such practices are found to enhance the adoption of the electronic channel although inequalities among agents may increase.

Keywords:

Electronic market, e-commerce, Internet, virtual community, search market, learning

Introduction

1.1

The aim of this paper is to build an agent-based framework to analyze the adoption process of electronic markets and to investigate the economic effects of this adoption process. Several arguments have already been raised in order to understand in which conditions "electronic markets" could diffuse and sustain as viable trading institutions. During the e-boom, it had often been suggested that, whatever the initial socio-economic conditions (type of good, market structure, manufacturing process, ability of consumers to transact on these markets), electronic markets should spontaneously develop because of the wide savings on transaction and search costs they should provide, if these costs are compared with those incurred on traditional markets (Strader and Shaw 2000). This speculative hypothesis has failed to understand the current difficulties of the firms operating on electronic markets and has then been replaced by partial arguments: institutional deficiencies such as the absence of any universal secure payment system (Langton et al. 2000), digital procurement or more generally the lack of any unified regulated framework for internal or cross-country commerce (O.E.C.D. 2001), expansive shipment or storage costs for some types of goods (Dumans 2003), existence of prior substitutes for electronic commerce such as EDI for Business-to-Business transactions or Minitel in France, insufficient computer equipment rate, etc. Among others, these factors may be valid in explaining some of the crashes observed on electronic markets. However, we would like in this paper, to emphasize agents' differentiated abilities to use such markets: although search costs are apparently lowered on electronic markets, these markets need to be examined as one particular embodiment of the more generic Information and Communication Technologies (ICT).

1.2

Drawing on this strand of analysis, some evolutionary studies have pointed out the need to study the effects of individual learning patterns on the macroscopic diffusion of ICT (Elliasson 2002). Electronic and traditional markets need to be distinguished according to a qualitative dimension that affects buyers' contact with the traded commodity and the buyer-seller relationship. Electronic markets are technically more fluid than the traditional distribution channels; however, consumers on these markets have to "start from scratch" i.e. identify new trading partners, appreciate the quality of the items provided by these partners, exploit or explore a particular link, etc. Therefore, the utility generated by web transactions is initially uncertain. This type of uncertainty is caused by the specific features of traded goods that are often experience goods, or the frequently-noticed trust lack on electronic markets (Heng et al. 2001, Lee and Turban 2001). This typical feature of electronic markets is rather challenging as it clearly illustrates the difficulties to integrate electronic markets as a new trading institution.

1.3

Few works explicitly introduce the 'out of equilibrium' analysis depicting the transition paths from one type of trading arrangement to another while stressing the crucial role of learning processes. The use of an agent-based methodology seems in this context particularly relevant for three related arguments. First, our main interest lies here in transitional regimes between two trading arrangements. In this context, considering stationary positions is not sufficient and must be complemented by an out of equilibrium analysis. Second, due to the specific type of uncertainty incurred on electronic markets, it is difficult for agents to use stochastic equilibrium predictions to select the most appropriate strategy. Finally, and as a consequence of the two previous arguments, agents are driven to adopt adaptive behaviours in order to appreciate the respective opportunities brought by the two markets, and to select appropriate learning patterns. Learning on this market is a two-dimensional process i.e. both individual and collective: agents can individually learn from their previous transactions (Ratchford et al. 2001). Besides, collective forms of learning are noticeable when agents group into virtual communities defined by Steinmueller as "sites where users interact with one another, gather information and participate in Electronic Commerce" (Steinmueller et al. 2000)^[1].

1.4

The remainder of the paper falls as follows. Section 2 presents the characteristics of the simulation model: we describe the behaviour of a population composed of adaptive buying-selling agents. These agents make sequential choices: first, they need to produce one unit of a differentiated good; then, they try to exchange it by using one of the two markets (electronic or traditional) in order to consume a good that fits their tastes. Section 3 presents the dynamics obtained as agents individually learn how to use electronic markets. By observing and applying a trial-and-error process, agents are thus able to improve their abilities in discovering relevant qualities on the electronic market. As learning is perfect, the out-of-equilibrium analysis generally exhibits two distinct phases driving the process to converge to the full adoption of the electronic market: we distinguish a first learning-stage during which the use of the electronic market is generalized and welfare decreases, from a second stage during which welfare is progressively improving. Finally, it appears that individual learning is not always beneficial for the long term activity rate of the population. Section 4 introduces the effect of collective learning through the existence of communities of agents. The objective of these communities is to share information about the quality of the goods traded on electronic markets. We concentrate on the effects of these virtual communities on the adoption process and on the macroscopic properties of the dynamics of the process as a whole. Section 5 concludes.

Model and Implementation

2.1

This model analyzes the dynamical impacts of sequential choices made by a population of heterogeneous agents who operate on two distinct trading institutions (electronic and traditional markets) along with a productive sector. This section is structured as follows: we first present the structure of agents' production and consumption (2.2). We then describe the characteristics of the traditional (2.9) and electronic (2.10) markets and replace these elements (production and exchange) into the dynamics of agents' choices (2.16). A final section (2.23) gives some technical specifications about the simulation technique.

Agents: production and consumption

2.2

The population of agents (N agents indexed by i) is uniformly distributed on a circle (agents locations are constant during the simulation). Each agent is successively producer and consumer i.e. an agent needs first to produce one unit of consumption goods, and then to exchange it either on the traditional market or on the electronic one in order to get a positive utility y. The qualities produced and consumed depend on the location of the agent on the circle:

Production

2.3

As a producer, each agent i ( i = 1, …, N) supplies a good of quality i. To produce this good at period t , he incurs a unitary production cost c_i,t. This production cost is heterogeneous among agents i.e. each individual production cost is drawn from a uniform distribution (between 0 and y). We focus on two polar cases. In the first case, agents' production costs are renewed at each time step. This situation corresponds to the repeated occurrence of external supply shocks; in the second case, agents' productivities (production costs) are held constant from the initial period t₀ to the end of the simulation. The last case refers to the existence of idiosyncratic producing abilities (due to e.g. the educational system or heterogeneous knowledge-producing capabilities).

ci,t= ζ where ζ is randomly drawn from a uniform distribution between 0 and y.

(1)

Consumption

2.4

As a consumer, agent i gets a positive instantaneous utility (noted y > 0) when he buys a good which quality belongs to the set A_i (where A_i = [ i - a /2, i + a /2] - {i} with a ∈ ]0,1]). In any other cases (trades with agents located on the complementary set noted), he does not get any utility (null payoff). These two sets are represented on Figure 1a.

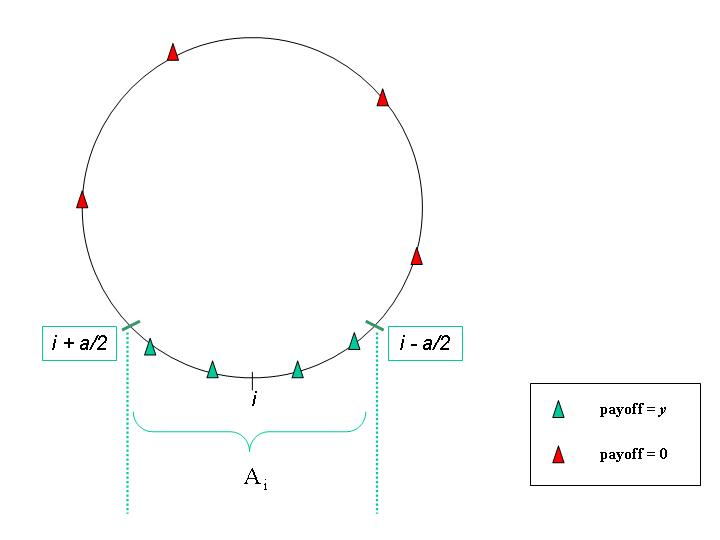Figure 1a. Agent's i preferences and payoffs

2.5

Parameter a is identical for any agent and depicts the accuracy of agents' needs (one can note that this parameter rules the length of the set A_i): as a decreases, the needs of agent i become more and more specific and differentiated.

2.6

Hence, for any agent i, a transaction with agent j (i ≠ j) yields the following payoff:

y if where 0 if where

(2)

2.7

Let us illustrate the preference structure by the following example: we assume that the economy is composed of 100 traders and we consider the agent located at position 50 (Agent 50). This agent needs first to produce a good (of quality '50'). Once he has produced, he will try to exchange this good. Let us suppose first that parameter a is equal to 1. In this case, Agent 50 is willing to transact with any trader on the circle, which means that he will get y with any trader whatever his location (undifferentiated needs). Let us suppose a contrario that a is equal to (0.10). In that case, agents' preferences are more selective and agents will get a positive utility (y) only as they transact with 10% of the traders located around their own location. In other terms, Agent 50 needs to transact with one of the following agents: {45;46;47;48;49;51;52;53;54;55}to obtain y. For any other agent (Agents 1 to 44 and 56 to 100), Agent 50 receives a null payoff.

2.8

Once he has produced, agent i needs to exchange his production good in order to be able to consume. To exchange the produced item, he freely compares the opportunities brought by the electronic market and the traditional market.

The traditional (search) market

2.9

The traditional (i.e. search) market is a typical decentralized market. In this market, agent i is able to clearly identify the quality of the goods he is willing to consume. So, he can perfectly discriminate the producers located on the correct interval A_i from those located on the wrong interval (cf. Figure 1a). However, because this market is decentralized, its underlying matching process is not perfect: a consumer wishing to buy one unit in this market has to bear information costs associated to the visit of each seller. Due to this type of frictions, while he is present on this market, agent i is not sure to meet a correct partner and consequently to implement successfully a transaction. For agent i, a transaction then occurs with probability p^search. This probability depends on two elements. First, it depends on the number of traders present on this market and relevant for agent i ( A_i - traders). Obviously, the more participants to the traditional market, the easier it is to find a trader and make a transaction. This term is noted and measures the relevant fraction of the population present on the search market^[2]. Second, the probability of making a transaction depends on the general efficiency of traditional markets in this economy. This second element is exogenous, common to all agents and modelled by a viscosity parameter τ (τ ∈ [0,1]). As τ is equal to 1, the traditional market is frictionless. As τ decreases, the viscosity of the traditional market increases, and trades are more difficult to implement. We can then write the probability of making a purchase on the search market as follows:

(3)

The electronic market

Characteristics of the electronic market

2.10

In the electronic market, opportunities of exchange are all instantaneously observable. This hypothesis is grounded on the diminishing level of search costs incurred on electronic markets (see Bakos 2001). However, due to the novelty of such markets, agent i can only imperfectly appreciate the qualities exchanged on this market. Consequently, depending on his own expertise, agent i may accept trading irrelevant goods i.e. goods that do fill his preferences and yield a null utility. This situation is illustrated by Figure 1b. Because agent i is only partially able to discriminate qualities, he accepts trading all the goods belonging to the interval A' _i ≡ [ i - a'/2; i + a'/2] - { i } (with a' > a). This set is larger than the correct set A_i. That means that agent i makes an error anytime he trades with another agent located on the set A^err _i,t = { A' _i,t - A_i}. In that case, he cannot resell the traded good and does not get any payoff.

2.11

Because agents are heterogeneous regarding their ability to successfully transact on the electronic market, we assumed that the variable a' is uniformly distributed between a and 1. We can express the expertise of an electronic trader by the ratio (a/a'). As a' is equal to a (expertise ratio equal to 1), the agent evaluates qualities perfectly and never accepts wrong qualities. A contrario, as a' is equal to 1, the agent has the lowest possible expertise and initially accepts trading all the qualities on the circle.

2.12

Again, we can illustrate this by our previous simplified example (a = 0.1; N = 100; case of Agent 50). Let us suppose first that Agent 50 is perfectly expert. In that case, a' = a = 0.1. It follows that the set A^err _i,t is empty and Agent 50 only accepts to trade with Agents {45;46;47;48;49;51;52;53;54;55} which provides a positive payoff y. Let us suppose a contrario, that Agent 50 is weakly expert: a' can then range from 0.1 to 1. Let us set coefficient a' equal to (0.50) for instance. That means that Agent 50 may accept 50% of the goods around his own location (goods or traders A'₅₀ ≡ {25;…;44; 45;46;47;48;49;51;52;53;54;55; 56…75}) on the electronic market. However, anytime Agent 50 transacts with agents {25;26;…44} or with {56;57;…75}, he will trade a wrong quality and get a null payoff.

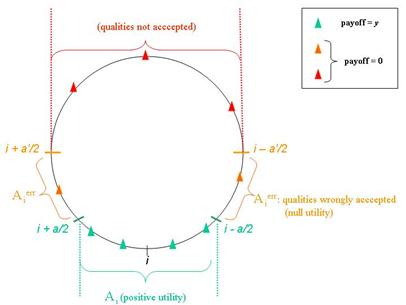Figure 1b. Agent's i errors and payoffs on the electronic market

2.13

From the definition of individual expertise, we can derive the probability of making a successful exchange on the electronic market (noted p^elec) for agent i at time t:

(4)

Learning on the electronic channel

2.14

To model the dynamics of agent i's expertise, we will successively sketch two situations:

1. Individual learning: agent i can increase his expertise by using a simple trial-and-error process. This basic rule-of-thumb can be expressed as follows: as an agent has traded with another agent, and as the quality of the traded good did not match his requirements, the first agent will refuse to trade with the other agent during his future trades. In other terms, as an agent trades a quality that yields no utility, he will not consider anymore the goods provided by the corresponding trader. This simple mechanism implies that the size of the set A^err _i,t decreases as the agent makes errors on the electronic market. In turn, this decrease improves the expertise this agent^[3].

   Going back to our simplified example ( N = 100; a = 0.1; a' = 0.5; choice of Agent 50), let us suppose that Agent 50 trades with Agent 57 on the electronic market. After consuming, Agent 50 can precisely assess the quality provided by Agent 57. As this quality does not fill his needs, Agent 50 will not consider the goods provided by Agent 57 during his future trades. The ex ante uncertainty about quality is then lowered and Agent 50's individual expertise is increased.

2. Collective learning: the potential role of the virtual communities of transaction is here introduced. Although these communities may take various institutional designs (e.g. newsgroups, asynchronous forums, chat-rooms), they all pursue the same objective i.e. sharing information. In our framework, these groups can play a key-role to inform agents about the qualities traded on the electronic market.

   The membership of a community is ruled by an exogenous parameter: the total population is divided in two sub-populations according to the exogenous parameter μ (μ ∈ [0,1]). The first group is composed of (1 - μ) N agents who are not members of any community. These agents then learn individually as described previously. The remaining (μ) agents (uniformly distributed on the quality circle) share transaction experiences in one single community^[4].

   The internal working of this community is very simple: at the end of the period, each member of the community informs all other members about the quality (location) of the good traded over the electronic market. The other members incorporate this information as if they had themselves traded this quality^[5].

   Going back to our simplified example, let us suppose that Agents 50 and 0 are both members of the same community. If Agent 0 trades with Agent 57 on the electronic channel, he will inform Agent 50 about the characteristics of the good traded. Thanks to this description, Agent 50 finds out that the good provided by agent 57 does not fill his needs. During his future search on the electronic market, Agent 50 will then refuse to transact with Agent 57. This learning mechanism is homothetic to the individual one. The only difference is that, unlike the individual learning case, Agent 50 does not need to experience by himself the wrong good and get a null payoff.

"Barriers and bounds to learning"

2.15

As it was defined in the previous section, learning is perfect is the sense that traders are able to store information about qualities provided by others traders without any loss or imperfection. However, individuals' memory performances may be imperfect so that some of the previously identified qualities may be forgotten. To take into account the imperfection of learning processes, we simply assumed that each trader randomly forgets at each period a proportion f of his past experiences^[6].

Agents' choice and dynamics

2.16

We can now describe the whole sequence of agent i's choice: at the beginning of period t, agent i gets a production cost (c_t). The period is then subdivided into two subgames i.e. i) a decisional stage and ii) an implementation stage: during the first (decision) stage, agent i computes the expected utilities attached to his possible actions and chose the best expected action. During the implementation stage, agent i tries to produce and transact, and receive the corresponding payoff.

Decision Stage

2.17

During this stage, agent i evaluates the payoff associated to his three possible actions: (a) "inaction" (no production, no trade); (b) trading on the electronic market, or (c) trading on the traditional market. Each action has a specific reward function: first, if he decides to "do nothing" (inaction, action a), he will simply receive a null payoff (i.e. normalized to 0) and will be considered as unemployed for period t.

(6a)

2.18

Second, trading on the traditional market (action b), yields ( y - c_t), if the exchange occurs during period t, and 0 else. The occurrence of an exchange depends on the previously defined probability . We can then compute the expected gain associated to the traditional market () at period t:

(6b)

2.19

As one can see, we here assume expectations to be grounded on agent's past knowledge as agent i only needs to know the previous frequentation of the traditional market during period ( t - 1).This assumption seems quite reasonable as we are here firstly interested in out-of-equilibrium paths where agents do not have enough information to form rational expectations.

2.20

His third opportunity is to trade on the electronic market (action c). The random event on this market is not the occurrence of exchange: as agent i achieves a transaction with certainty, he will have to bear the production cost, whatever the final outcome of the transaction. But, an electronic trade will yield the positive payoff y only if agent i trades with a 'right' partner. If not, he does not have any benefit (0). Choosing a right partner depends on agent i's expertise on the electronic market at time t and happens with probability . Again, we note that this gain depends on agent's expertise (imbedded in ) which, in turn is related to his past transactions. We can then deduce the expected gain associated to the electronic market ():

(6c)

Implementation Stage

2.21

During the second stage, agent i implements his previous decision. The implementation process is simply modelled by making random draws of the concerned variables: if i selected the electronic market, he receives the payoff ( y - c_t) with probability ( - c_t else). He then eventually, receives and transmits information to his community if he belongs to one, and updates his expertise. If i selected the traditional market, he receives ( y - c_t) with probability . If he failed to meet a suitable partner on the traditional market - which happens with probability - he gets 0 but he will have to trade in order to clear his inventories during the next round. During the next round, he will get the opportunity to switch from one market to another (conditional to the existence of a positive gain to do so).

2.22

The game played by agent i can be summarized by Figure 2.

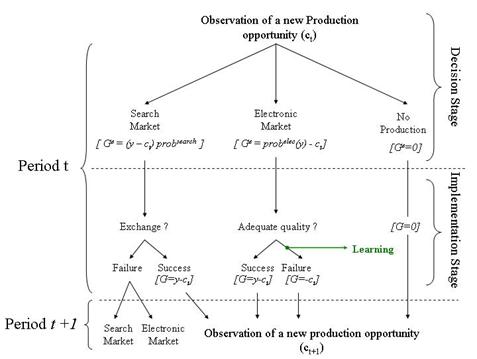Figure 2. Decision Tree of agent i at period t

Model implementation and parameters

2.23

The process has been simulated using the Java-platform: all materials (pseudo-code, code, classes executable on the most current operating systems) are available at http://www.idefi.cnrs.fr/hp/ed/ with a help file on how to launch a simulation. Further details or assistant are available on request. Charts have been implemented using the JFreeChart library (freely available at the URL http://www.jfree.org/jfreechart/). Due to lack of space, we could not report all the configurations into details but complements are also available on request.

2.24

The simulations have been performed with 200 agents and y = 1. The first parameter only changes the absolute convergence time. We mainly chose this scale for technical reasons (computation time). As it can be seen, the second parameter (y) only rules the absolute size of the payoffs. We can then normalize agents' maximal payoff to 1. The initial rate of employment is 100% and we supposed that only 0.01% of the population of agents are initially located on the electronic market. We chose these initial repartitions as we want i) to study the emergence of electronic markets and ii) analyze the perturbation from an initially equilibrated system.

2.25

Without any loss of generality, we set parameters a and τ to (0.2) and (0.8) respectively. These values correspond to a situation where the two types of markets would have coexisted if traders were not able to learn from one period to another (see Appendix 1). Again, the choice of these values does not change the qualitative properties of our conclusions but only the absolute convergence time.

Individual Learning and out-of-equilibrium dynamics.

3.1

We first suppose that learning is both individual and perfect (no virtual community, agents does not need do re-evaluate periodically the qualities distributed on the electronic market i.e. f=0).

Results in the presence of idiosyncratic supply shocks

3.2

As we introduce learning, we obtain the following dynamics in the presence of permanent idiosyncratic supply shocks (Figure 3).

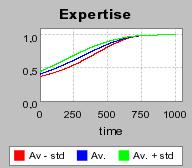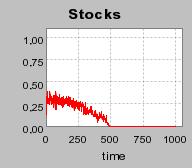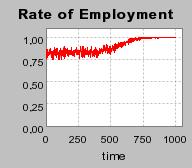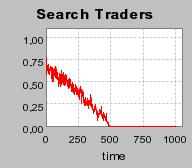
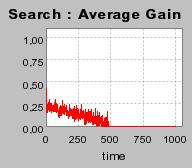
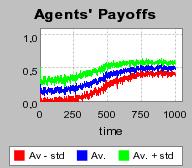
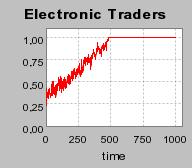
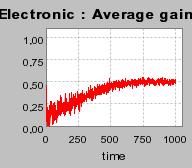
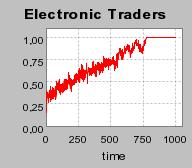
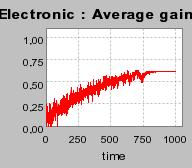
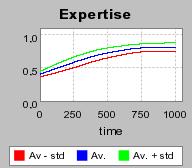
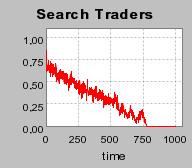
Figure 3. Individual learning; a = 0.2 and τ = 0.8; Permanent idiosyncratic supply shocks: new production cost at each period

3.3

We notice first that the traditional (search) market is gradually crowded out^[7]. The origin of the process is as follows: agents are initially heterogeneously expert in using the electronic channel. Indeed, the most expert agents will first leave the traditional market as they anticipate that the non-purchase cost incurred on the traditional market is higher than the cost associated to trading a wrong quality on the electronic market. As the most expert agents switch to the electronic market, the traditional market is less attractive (as the probability of making a purchase is dependant on the size of this market). This process goes on until all traders have adopted the electronic market and is driven by the effect of learning. Besides, every time an agent uses the electronic market, his expertise potentially increases, which, progressively leads this agent to accept more production opportunities ("higher" production costs) and consequently improves the employment rate of the whole population. The electronic market is not only the single activated institution but all agents are in fine incited to accept all the production opportunities given that the risk of making a wrong transaction (or making no transaction) vanishes.

3.4

Focussing more closely on the dynamics, we can observe two distinct populations: on the one hand, the most expert agents can be considered as early adopters and their expertise is rapidly converging to its maximal level (1). On the other hand, the least expert population will continue using the traditional market until this market is not wholly crowded out (period 500). Until this period, the members of this second population do not improve their expertise. They stop trading on the traditional market only as this market stops generating enough externalities to be profitable. After period 500, they will try to switch to the electronic market, anytime they receive a favourable production opportunities (i.e. a production cost which is sufficiently low to compensate the expected purchase of a wrong quality). On the contrary, as they receive a 'high' production cost, they do not produce and are considered as unemployed. By the way, anytime they wrongly trade on the electronic market, they catch-up their expertise lag. This differentiated timing of adoption may explain the relative slow movement towards a full employment regime. Indirectly, we then observe a 'Ricardo-effect', where the transition from one state to another leads to the apparition of a temporal unemployment^[8].

Results in the absence of idiosyncratic supply shocks

3.5

Considering identical values for parameters a and τ, we assume now that all agents are endowed with a heterogeneous but constant production cost. In other terms, at the initial period t₀, each agent receives a production cost that is held constant during the whole process (no supply shocks).

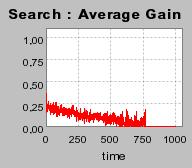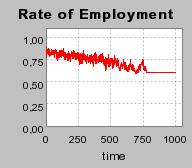
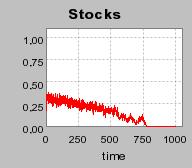
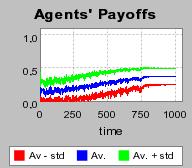
Figure 4. Individual learning; a = 0.2 and τ = 0.8; No supply shock: heterogeneous but constant production costs

3.6

For identical parameters, we observe two important differences from the previous case (see Figure 4):

1. The convergence to the full adoption regime is delayed: switching from the traditional (search) market to the electronic market takes more time, as agents need to fill simultaneously two conditions i.e. a low production cost and a high expertise index, to be able to transact on the electronic channel. In the previous simulation, the first condition was 'soon or later' always filled as costs were randomly redistributed at each time step.
2. More importantly, as costs are not redistributed, a significant part of the whole population does not access to the electronic market because its production costs is not compatible with the use of this market. Hence, this sub-population has no possibility to improve his expertise by learning. Consequently, this economy is converging to a persistent unemployment regime. Inequalities among agents are then maximal as showed by the higher values of average payoffs' standard deviation.

3.7

This second case suggests that introducing learning does not necessarily lead to optimal outcomes despite we have initially set 'optimal' conditions for learning to take place. This scenario attests that learning does not equally apply to all agents: learning processes may benefit to the initially best endowed part of the population (lowest production costs and/or highest expertise), but not to the whole population.

3.8

A final remark applies to the two previous scenarios (with or without supply shocks): the individual trial-and-error learning process takes time in order for the agents to master the electronic channel and this time seems to grow "exponentially" with the values taken by the viscosity parameter (τ) and by the selectivity of agents' needs (a) (see Appendix 2). Another limitation is linked to the agents' bounded memory and will be examined in the next section.

Results with imperfect learning

3.9

Let us suppose now that agents are imperfectly able to store information so that the qualities distributed on the electronic market need to be re-checked periodically. In that case, according to the magnitude of rate f, part of individually acquired knowledge may be forgotten. Using the same set of parameters (a and τ equal respectively to 0.2 and 0.8), we obtain the following representative run (cf. Figure.5):

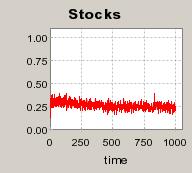
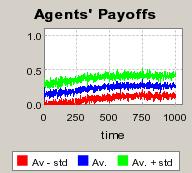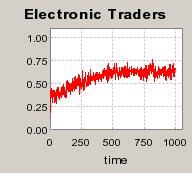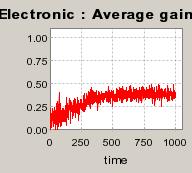
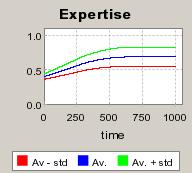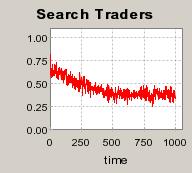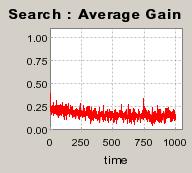Figure 5. Individual learning; f = 1%f = 1%; a = 0.2 and t = 0.8; Supply shocks: new production cost at each period

3.10

The introduction of rate f has an important impact on the trajectory followed by this simplified economy. This leads to three general observations:

1. After an initial diffusion stage (periods 1 to 450), the size of the electronic market is stabilized at a constant but not maximal value. Unlike the two previous cases, this process does not lead to a full adoption regime. After convergence, nearly 40% of the agents chose on average to trade on the traditional search market. That means that the two trading institutions are here complement rather than substitute and coexist over time^[9]. The distribution between the two markets is ruled by the value of parameter f: the size of the electronic market is decreasing as learning is more and more imperfect (cf. Figure 6).

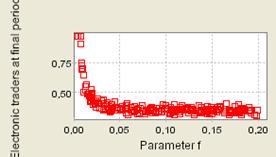   Figure 6. 400 repeated iterations of the process; Supply shocks; depreciation rate f ranging from 0 to (0.2). The chart exhibits the adoption rate of the electronic channel once the economy has reached its stationary position (averaged on the last periods)

2. According to their initial expertise, some agents choose to operate either on the electronic market or on the traditional (search) market. The most expert agents improve their expertise trough learning and transact on the electronic market. The least expert agents are locked to the traditional search market. As in the previous case, the average expertise is not converging to its maximal value (cf. expertise chart). A third category of agents characterized by an intermediate degree of expertise is permanently switching from one market to another (cf. charts representing the size of both markets). In this situation, these switches are due to two combined factors: firstly, if each agent forgets on average f% of the qualities previously checked, the actual individual number of qualities forgotten may randomly vary among agents, causing the expertise of a particular agent to decrease rapidly at one period or to be quite constant at another period. As the expertise of this agent sharply decreases, the use of the electronic channel may be less profitable than the one of the traditional market. Secondly, due to the occurrence of permanent supply shocks, an agent may refuse to produce (and then exchange) as he receives a high production cost. Combined with the previous factor, the induced change in the size of the search market decreases the profitability of this market, causing the switches between the two markets.
3. Dealing with employment, this case mixes some outcomes of the two previous cases. In the first case (periodical supply shocks), we observed the apparition of a temporary unemployment linked to the introduction of the new trading arrangement. In the second case (no supply shocks), we noticed the persistence of a high level of employment associated with a form of exclusion (only a particular category of agents is permanently unemployed). In the case of imperfect learning with supply shocks, the economy is no longer converging to a full-employment regime. However this type of employment is more frictional than structural. Because the search market is not crowded out and because of the periodical occurrence of supply shocks, no specific agent is permanently excluded. The residual unemployment is only caused by the transaction failures on the traditional market: anytime a trader does not find any partner on the traditional market (as shown by the re-apparition of a positive rate of inventories), he has to delay his transaction for the next period and is then considered unemployed.

Collective learning and out-of-equilibrium dynamics

4.1

The learning process introduced in the previous section was strictly individual: agents could only learn from their own past experiences. To study the potential impact of virtual communities of transactions (further VC), we introduce here some collective learning where agents can learn from their own past experiences but also from the experiences of other agents. We here suppose that one part of the population is grouped into a single community. As was stated in Section 2, the working of this community is simply caught: at the end of each period, electronic traders inform all community members about the quality exchanged during their last transaction. By this means, Community-members share their current experiences at each period. The shared information is always truthfully transmitted: because payoffs are not directly dependent. There is no strategic incentive to lie on particular qualities or to hide some others. The shared information is however not always valuable for a particular agent: it can be sometimes either redundant (as this agent already discovered this quality) or irrelevant (as this agent is not interested in buying such quality).

4.2

To study the potential impacts of VC, we now distribute the total population in two groups: the first set (noted VC) is composed of all agents belonging to a single virtual community while the other set (noted ) collects all agents that do not belong to any community. At each time step, VC-agents get the opportunity to collectively learn while -agents are constrained to learn individually. We will first analyse the impact of the presence of this community of agents on the adoption of the electronic market and on the employment rate and then focus more precisely on its effects on welfare.

Virtual Community, timing of adoption, and employment effects

4.3

The following charts present the evolution of the process as 20% of the total population decides to engage in the virtual community (cf. Figure 7).

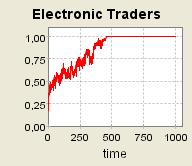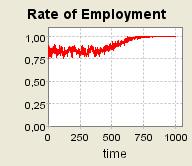Figure 7. τ = 0.8 and a = 0.2 ; 40 agents are grouped into one single community (μ= 0.2) ; Supply shocks

4.4

As can be seen, the convergence to an "optimal" position (full activity rate, minimum payoff dispersion, zero stocks) is accelerated if compared to that of the individual-learning case. Increasing population's involvement in Virtual Communities (i.e. increasing parameter µ) reinforces this statement (Figure 8).

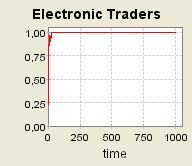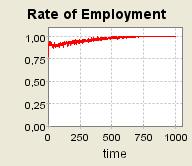Figure 8. τ = 0.8 and a = 0.2 ; 160 agents are grouped into one single community (μ= 0.8) ; Supply shocks

4.5

We can conclude that the presence of virtual communities fosters the adoption process and hence has a positive effect on the global employment rate. In fact, as already noticed, coexistence periods (i.e. situations where electronic and search markets are simultaneously either temporary or permanently activated) lead in most cases, to inferior outcomes compared to a single-trading institution regime (either traditional or electronic market) because coordinating the two trading institutions requires higher inventories rates implying a persisting positive rate of unemployment. By revealing qualities traded on the electronic market more rapidly, the activity of the virtual community contributes to shorten the transition period and then to diminish these negative transitional effects on employment.

Virtual Community and welfare effects

4.6

To assess welfare effects more accurately, we need to identify a proxy variable describing the efficiency of the whole process. The simplest one consists in estimating the average values of all relevant time series. We are then able to measure the efficiency of the whole process (i.e. from Period t₀ until the last period) and confirm the first observations made (Table 1).

Table 1: τ = 0.8 ; a = 0.2 ; Supply shocks.
	No Learning	Individual Learning	Social Learning [μ = 0.2]	Social Learning [μ = 0.8]
Average Employment Rate	0.81	0.89	0.9	0.96
Average Payoff (whole population)	0.14	0.34	0.39	0.47
Average participation rate of the electronic market:	0.37	0.82	0.85	0.99
Average Payoff VC (members of the Community):	--	--	0.46	0.49
Average Payoff (non members of a VC)	--	--	0.34	0.38

4.7

As we did previously, we need to complete these observations by supposing that the considered economy is no longer disrupted by idiosyncratic supply-shocks at every period. Again, we suppose individuals to be characterized by heterogeneous but constant production costs. The following table compares the efficiency of the different configurations (Table 2).

Table 2: τ = 0.8 ; a = 0.2 ; Constant production costs.
	No Learning	Individual Learning	Social Learning [μ = 0.2 ]	Social Learning [μ = 0.8 ]
Average Employment Rate	0.83	0.71	0.74	0.87
Average Payoff (whole population)	0.16	0.28	0.32	0.45
Average participation rate of the electronic market:	0.37	0.75	0.82	0.99
Average Payoff VC (members of the Community):	--	--	0.42	0.51
Average Payoff (non members of a VC)	--	--	0.29	0.25

4.8

These results extend our previous findings: similar to the individual learning case, we note the emergence of a specific subgroup of agents which are de facto excluded from both markets: the search market does not emit a sufficient amount of externalities to be activated while the access to the electronic market requires a minimum initial expertise. The final outcome of such process cannot therefore be perfect. Nevertheless, introducing some community-based learning has a positive effect on global employment rate. As VC-members are randomly selected at period t₀ among the whole set of agents, the VC-membership of a particular agent is by no means linked to his initial expertise^[10]. Moreover, inside the community, the access to the shared information is identical to all agents, whichever their initial expertise. As a consequence, some agents to which electronic trade did not suit as long as they acted separately will be reintegrated among the active population, thanks to their involvement in a VC. From that last point, we infer the apparition of a new source of inequalities.

4.9

Inequalities are closely but not perfectly correlated to the "VC-membership versus non-membership criterion. In fact, we can divide the population in three categories: 1) the first category of agents relates to VC-set. Leaving aside production costs heterogeneity, we infer that members of Virtual Communities achieve the best average payoffs as their expertise grows faster than those of other categories; 2) the second category includes agents that do not belong to any virtual community (i.e. subset of ) but that are endowed with low production costs and/or high expertise indexes. During the convergence stage, these agents experience lower payoffs compared to those of the first category. Yet, the average instantaneous gains of the first two categories converge in the long run, once all agents have acquired perfect expertise; 3) The last category (remaining subset of ) is composed of agents which can be roughly described by three characteristics: i) they do not engage in any virtual community; ii) incur the highest production costs, and iii) are endowed with the lowest initial expertise. Unlike Category 1 and 2, the payoffs of Category 3-agents will be damaged by the presence of virtual communities (Table 2: 0.25 < 0.28). Indeed, the activity of VC contributes to crowd out the search market more rapidly. Due to their characteristics, Category 3- agents are not able to transact electronically. Consequently, the rapid eviction of the search market increases Category 3- average unemployment. As the economy was continuously hit by supply shocks, the last two categories of population were confounded. In that case, the "unlucky" agents (i.e. non VC-members and endowed with a weak expertise) left the traditional market prematurely; but unlike the fixed cost-situation, they were given the opportunity to trade electronically every time they picked-up a favourable production opportunity. This is no longer the case as production costs are fixed from the beginning to the end of the process. In that case, the activity of the community may be responsible of a new source of inequalities arising between members and non members.

Conclusion and future research

5.1

We have explored in this paper the conditions of adoption and of use of electronic markets. We emphasised the effects of two different types of learning on the transition from decentralised to electronic markets. Introducing individual learning via a simple trial-and-error process both enlarges the size of the electronic market and boosts its adoption. In the perfect learning case, traders fully adopt the electronic market. Concerning 'welfare' properties, we highlighted two equally possible scenarios: in the first one, as the economy is permanently hit by idiosyncratic supply shocks, the economy is converging to a regime characterized by a minimal level of inequalities and full employment. The introduction of the new trading technology however induces temporary unemployment induced by the initial inability of agents to use the new technology. In the second scenario, the economy is not hit by supply shocks and we noticed the emergence of a structural unemployment. The least endowed agents do not have the opportunity to learn how to use the electronic market and are finally excluded from this market. Turning to imperfect learning, we have pointed out that the two institutions are more complement that substitute. In that case, agents are distributed on the two markets according to their initial heterogeneous expertise. As a consequence of the coordination costs between the two markets, a frictional unemployment is associated to this situation. We then enlarged our conclusions by studying collective learning through community-based practices. As agents are perfectly able to accumulate knowledge, the main impact of the activity of a virtual community is to favour the adoption process of the electronic channel, which in turn increases community-members' fitness, while decreasing for some cases, the fitness of non members agents.

5.2

We now need to enrich our analysis of community-based practices. More precisely, one challenging issue is to improve our understanding of the factors ruling agents' membership, while this decision is treated as an exogenous parameter in the present model. In that way, further research should concentrate on a precise identification of the various motives for an individual to engage in a community but also to leave it in order to define the dynamics of such communities and their impact on electronic markets.

---

Appendix 1

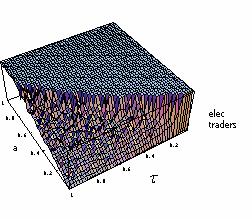Figure 9. Results of 2500 iterations with Parameters a and τ both ranging from 0 to 1. The chart presents the share of electronic traders (among the employed population) at Period 1000 (after convergence); No learning.

A.1

This chart exhibits the size of the electronic market (number of transactions on the electronic channel over the total number of transactions) as agents' expertise is held constant (no learning). We can distinguish two different regimes depending on parameters a (selectivity of agents' needs) and τ (exogenous viscosity of the traditional market): in one case (agents' need are highly selective and/or frictions on the traditional market are low) the two types of markets coexist (partial adoption of the electronic market); in the other case, the electronic market crowds out the traditional market (full adoption). As it can be seen, the electronic channel cannot be totally crowded out. The explanation is as follows:

A.2

As agents cannot individual expertises are exogenous on the electronic market, we can notice that the electronic market is never totally evicted (i.e. the traditional market is activated alone). This is explained by the specification of the payoff' function and the range of individual expertises. We can illustrate this by a simple example: let us suppose that all agents are located on the traditional market. In that case, the probability of implementing a successful purchase is equal to τ(1) = τ (cf. equation 3). Once excluded extreme values such as τ = 1 , this probability is then always inferior to 1. On the electronic market, the probability of trading the right quality in equal to the agent's individual expertise. Hence, it is distributed from 0 to 1. The most expert population (i.e. agents whose individual expertise is greater than τ) always choose to trade on the electronic market. The electronic market would have been crowded out only if we had set an arbitrary superior bound to individual expertises.

Appendix 2: Learning and the timing of adoption

A.3

As individual learning capabilities are perfect, we can observe the progressive generalization of the electronic market, for any values of Parameters a and τ , using the same R³-plot (cf. Appendix 1):

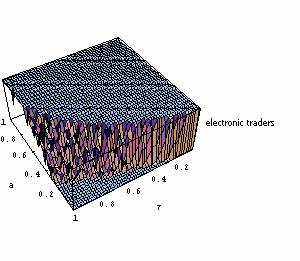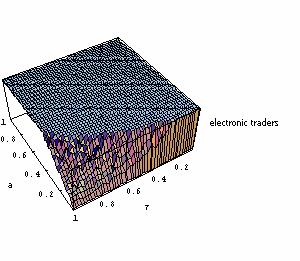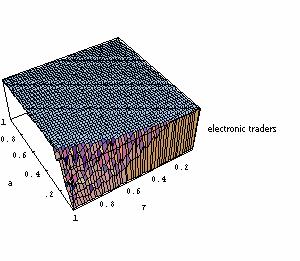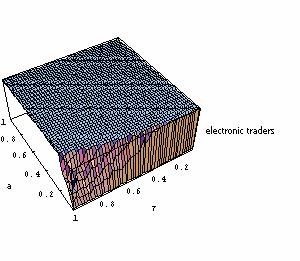Figure 10. Repartition of agents after 250 (top left), 500 (top right), 750 (bottom left) and 1000 (bottom right) periods; individual learning; production costs randomly drawn at each period

A.4

We have plotted the repartition of traders between the adoption rate of the electronic market for different periods (250, 500, 750 and 1000), for 50 values of each parameters t and a. As time goes on, the electronic market diffuses to all range of parameters a and t. As can be noticed, this process does not appear to be linear with respect to time. For example, if we qualitatively compare the two first charts, we notice that the electronic channel tends to impose in a relatively short time scale. Looking at the two last charts, we see that the marginal increase is slower. It is hence proportionally more and more difficult for the electronic market to impose as a and t increase. In other terms, the final position can only be reached by exponentially increasing the total number of market sessions. Although, it can be checked that for any values of the two parameters, the process converge (in a finite time) to the full adoption rate.†

Appendix 3: Generalization for any values of coefficient μ

A.5

The two following charts extend the above conclusions to a wider range of coefficient μ.

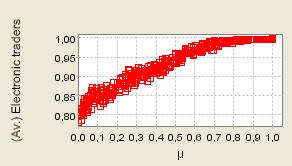Figure 11. 400 repeated iterations of the process with μ randomly selected from 0 to 1; Supply shocks (We only report here the process as production costs are renewed at each time step. The charts depicting the second case - heterogeneous but constant production costs - (available on request) are qualitatively similar)

A.6

VC-agents experience higher payoffs as the population is more widely involved in virtual communities (i.e. as Parameter μ grows) as it is shown by the two next charts. We notice i) that the payoff gap is increasing as μ increases and ii) that the average payoff of "isolated agents" (i.e. non members) is less predictable for extreme values of μ. This heterogeneity is caused by the agents' heterogeneity regarding expertise. The "isolated agents" population includes Category 2 and Category 3 agents. As μ increases, the size of this population mechanically decreases, and the average payoff is more dependant on particular random draws of the initial expertise degrees.

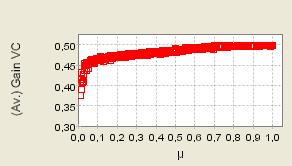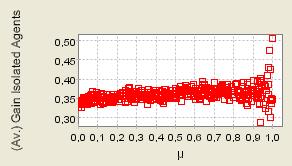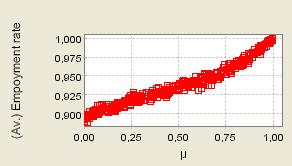
Figure 12. 400 repeated iterations of the process with μ randomly selected from 0 to 1; Supply shocks

Acknowledgements

We would like to thank Nicolas Curien, Bernard Dachs, Gunnar Elliasson, Michel Gensollen, an anonymous referee of JASSS and the participants of the EMAEE 2003 Conference (Augsburg, April 10-12^th 2003) for helpful comments and discussions. The usual disclaimer applies.

Notes

[1] Cf. also (Balasubramanian and Mahajan 2001, Bughin and Hagel 2000) for a general assessment. See also for several sector-based studies - e.g. finance, insurance and tourism - (Barnatt 1998, Kardaras et al. 2003, Wang et al. 2002) or by firm-related case studies (Rothaermel and Sugiyama 2001, Schubert and Ginsburg 2000).

[2] The term is numerically equal to where if agent j chose to operate at period t on the traditional market, 0 else.

[3] Formally, every times he trades with an -agent, agent i will be definitely remove this -agent from the set . If i meets j at period t on the electronic market:

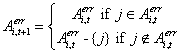[5.i]

This procedure decreases the risk of making a null-payoff trade for the next periods. As the size of the set is decreased, agent i's expertise mechanically increases.

/ = # / # where "#" denotes the cardinal of the set, with by definition # aN.

[4] We only present here the results as agents are belongs to one single community. We have simulated other cases where agents are distributed into several communities. These results are available on request.

[5] Formally, we model a community V as a set of agents. Let k and k' be two members of this community and let us suppose that agent k has traded with agent j on the electronic market. At the end of the period, agent kupdates his own expertise according to the individual learning pattern (see equation [5.i]). He then informs all the other members belonging to his community about the quality traded. Let k' (k' ≠ k) be one of these members. Agent k' will then incorporate the delivered information in his own set of information i.e. as if he had traded himself with agent j.

Formally, this leads to an expression of the learning mechanism close to the individual one: agent k has met agent j at period τ on the electronic market, and transmits the information to agent k':

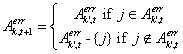[5.ii]

This process is then repeated for each members k' of the community.

[6] Technically, each piece of information belonging to the initial interval is forgotten with probability f. The size of the set is then no longer strictly decreasing with time t.

[7] The explanation provided in this paper focuses on the problem of the use of ICT embedded in electronic market. Of course, this factor is not exclusive from other factors mentioned in the introduction.

[8] We could further notice that, after convergence, the average payoff is not stable over time but permanently oscillates around a constant average, despite the repartition of the population among the three possible states (i.e. unemployment, traditional and electronic market) is constant. The observed fluctuations are mainly due to the random draws of a new production costs at each period: as the size of the sample of agents is finite, the inter-periodic variations has to be assimilated to some supply shocks. The average payoff fluctuates around 0.5 or equivalently (y ñ average production cost). This value is maximal when the economy has reached a full-employment state and remaining inequalities are only caused by heterogeneous producing capacities distributed among agents.

[9] This finding has to be related to what happens in the "no learning" case (see Appendix 1).

[10] We could have done differently by assuming that the most individually-expert agents participate to VC more than less expert. This new assumption would however only reinforce our conclusions.

References

BAKOS Y (2001) The Emerging Landscape for Retail E-Commerce. Journal of Economic Perspectives, Winter 2001. pp. 69-80.

BALASUBRAMANIAN S and Mahajan V (2001) The Economic Leverage of the Virtual Community. International Journal of Electronic Commerce, Spring 2001, pp. 103-138.

BARNATT C (1998) Virtual Communities and Financial Services - Online Business Potentials and Strategic Choice. International Journal of Bank Marketing, pp.161-169.

BUGHIN J and Hagel J (2000) The Operational Performance of Virtual Communities - Towards a Successful Business Model? Electronic Markets, pp.237-246.

DUMANS M-E (2003) Concurrence Entre Commerce Electronique Et Commerce Traditionnel (Competition between Online Retailers and Traditional Shops). Revue Economique, May 2003. pp. 687-696.

ELLIASSON G (2002) "The Macroeconomic Effects of Computer and Communications Technology." 170. Report of the Royal Institute of Technology (KTH): Stockholm

HENG S H, Creemers M and Verhagen T (2001) Some Pre-Requisites for Electronic Commerce. Vrije Universiteit WP.

KARDARAS D, Karakostas B and Papathanassiou E (2003) The Potential of Virtual Communities in the Insurance Industry in the U.K. and Greece. International Journal of Information Management, pp. 41-53.

LANGTON C S, Roghè F and Shaw M (2000) "Consumer Mass Market Online Payment Solutions" In Handbook on Electronic Commerce. M Shaw, R Blanning, T Strader and A Whinston (Eds). Heildelberg: Springer Verlag, pp. 273-288.

LEE M K O and Turban E (2001) A Trust Model for Consumer Internet Shopping. International Journal of Electronic Commerce, Fall 2001. pp. 75-91.

O.E.C.D. (2001) Electronic Commerce. Policy Brief, July 2001.

RATCHFORD B T, Talukar D and Lee M-S (2001) A Model of Consumer Choice of the Internet as an Information Source. International Journal of Electronic Commerce, Spring 2001. pp. 7-21.

ROTHAERMEL F T and Sugiyama S (2001) Virtual Internet Communities and Commercial Success: Individual and Community-Level Theory Grounded in the Atypical Case of Timezone.Com. Journal of Management, pp. 297-312.

SCHUBERT P and Ginsburg M (2000) Virtual Communities of Transaction: The Role of Personalization in Electronic Commerce. Electronic Markets, pp.

STEINMUELLER E W, Shenk I and Mansell R (2000) Net Compatible: The Economic and Social Dynamics of E-Commerce. Communications and Strategies, pp. 241-276.

STRADER T J and Shaw M J (2000) "Electronic Markets: Impact and Implications" In Handbook on Electronic Commerce. M Shaw, R Blanning, T Strader and A Whinston (Eds). Heilderberg: Springer Verlag, pp. 77-100.

WANG Y, Yu Q and Fesenmaier D R (2002) Defining the Virtual Tourist Community: Implications for Tourism Marketing. Tourism Management, pp. 407-417.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2004]