Luis R. Izquierdo, Nicholas M. Gotts and J. Gary Polhill (2004)

Case-Based Reasoning, Social Dilemmas, and a New Equilibrium Concept

Journal of Artificial Societies and Social Simulation vol. 7, no. 3
<https://www.jasss.org/7/3/1.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary

Received: 28-Dec-2003    Accepted: 03-Apr-2004    Published: 30-Jun-2004

Abstract

In this paper social dilemmas are modelled as n-player games. Orthodox game theorists have been able to provide several concepts that narrow the set of expected outcomes in these models. However, in their search for a reduced set of solutions, they had to pay a very high price: they had to make disturbing assumptions such as instrumental rationality or common knowledge of rationality, which are rarely observed in any real-world situation. We propose a complementary approach, assuming that people adapt their behaviour according to their experience and look for outcomes that have proved to be satisfactory in the past. These ideas are investigated by conducting several experiments with an agent-based simulation model in which agents use a simple form of case-based reasoning. It is shown that cooperation can emerge from the interaction of selfish case-based reasoners. In determining how often cooperation occurs, aspiration thresholds, the agents' representation of the world, and their memory all play an important and interdependent role. It is also argued that case-based reasoners with high enough aspiration thresholds are not systemically exploitable, and that if agents were sophisticated enough to infer that other players are not exploitable either, they would eventually cooperate.

Keywords:

Social Dilemmas, Case-Based Reasoning, Prisoner's Dilemma, Agent-Based Simulation, Analogy, Game Theory, Aspiration Thresholds, Equilibrium

Introduction

1.1

Life is full of social dilemmas. When confronted with a social dilemma, we have the temptation to behave selfishly at the expense of the others, but such non-cooperative behaviour leads to outcomes that are undesirable for all if undertaken by enough people. Social dilemmas are at the heart of pollution and resource depletion problems, but they are by no means exclusive to these situations: in any context where collective action can lead to a common benefit we may find that individuals have incentives to undermine the collective good for their own ends.

1.2

Social dilemmas have been studied from different perspectives, including empirical approaches (both experimental and field studies), discursive theoretical work, game theory, and computer simulation. Within the domains of these four approaches there has been much work devoted to the study of the paradigmatic Prisoner's Dilemma (PD) or variations of it, often leading to conflicting conclusions (particularly relevant is the conflict between empirical work and orthodox game theory). The PD is the most elementary formalisation of a social dilemma. In the two-player PD, players can either cooperate or defect; both players are better off defecting given any opponent's action, but they both prefer bilateral cooperation to bilateral defection.

1.3

The most widespread results about the PD come from orthodox game theory. Orthodox game theory is a branch of mathematics devoted to the logic of decision making in social interactions (Colman 1995, p. 3). It is not intended to account for how people actually behave, but for how instrumentally rational ^[1] players should behave in order to attain their clearly defined goals. Therefore orthodox game theory itself is incapable of being empirically tested and falsified (Colman 1995). What we can clearly infer from the combination of empirical research and game theory is that, if empirical observations clash with game theoretical solutions, then (a) the observed real-world situation does not correspond to the abstracted game, or (b) at least one assumption made by game theory does not hold (or both (a) and (b)).

1.4

When the PD is played once by instrumentally rational agents, the expected outcome is bilateral defection: rational players do not cooperate since there is no belief that a player could hold about the other player's strategy such that it would be optimal to cooperate (the cooperative strategy is strictly dominated by the strategy of defecting). The situation is very different when the game is played repeatedly. In the (finite or infinitely) repeated game, the range of possible strategies and outcomes is much wider and defecting in every round is no longer a dominant strategy. In fact, in the repeated PD, there is not necessarily one best strategy irrespective of the opponent's strategy. As an example, Kreps et al. (1982) showed that a cooperative outcome can be sustained in the finitely repeated PD if a rational player believes that there is at least a small probability that the other player is playing "Tit for Tat" (TFT).

1.5

Since assuming players are instrumentally rational was not enough to narrow the set of solutions of the repeated PD sufficiently, orthodox game theorists were obliged to make a further assumption: common knowledge of rationality (see Aumann 1976 for a formal definition). If common knowledge of rationality is assumed, it can be proved using backwards induction that a series of bilateral defections is the only possible outcome of the finitely repeated PD (Luce and Raiffa 1957)^[2]. Put differently, any two strategies which are an optimal response to each other necessarily lead to a series of bilateral defections in the finitely repeated game. However, when the number of rounds is not limited in advance, a very wide range of possible outcomes where the two players are responding optimally to each other's strategy still exists, even when assuming that the two players have detailed pre-planned strategies and these are common knowledge. Specifically, the "Folk Theorem" states that any individually-rational outcome can be a Nash equilibrium in the infinitely-repeated PD if the discount rate of future payoffs is sufficiently close to one. In this case, orthodox game theory has little to say about the dynamics leading a set of players to one among many possible equilibria.

1.6

When game theoretical solutions on the PD and related games have been empirically tested, disparate anomalies have been found (see, for example, work reviewed by Colman (1995) in chapters 7 and 9, Roth (1995), Ledyard (1995), and Camerer (2003)). Generally, empirical studies have found that there is a wide variety of factors in addition to economic payoffs that affect our behaviour, and also that, while it is not easy to establish cooperation, levels of cooperation tend to be higher than would be expected if the agents concerned were the computationally unlimited and entirely self-interested agents of neoclassical economics. The explanation of the clash between orthodox game theory and empirical evidence is, of course, that the assumptions required to undertake a game theoretical analysis do not hold: economic payoffs do not readily correspond to preferences (e.g. considerations of fairness frequently influence behaviour); actual preferences are sometimes neither consistent nor static nor context-independent; players' cognitive capabilities are indeed limited, and players' assumptions of others' preferences and rationality assumed by game theory are therefore often wrong.

1.7

Concerns about the strong assumptions made by orthodox game theory, about its limitations in selecting from among multiple equilibria, and certainly about the applicability of its results in the real world, led to new directions of research within the domain of game theory. These new branches of game theory lie somewhere in the spectrum between: (a) the general and (sometimes) precise, but non-empirically-based and introspective mathematical system of orthodox game theory; and, (b) detailed empirically-driven studies of how a certain group of agents played a specific game under some given circumstances, or behaved in a given real-world situation that could be formalised as a game. In a journey from (a) to (b) we would find at least the following broad and interacting lines of research: development of several refinements of the Nash equilibrium concept (see van Damme 1987), evolutionary game theory, cognitive game theory (also called learning game theory), psychological game theory, and behavioural game theory. The boundaries between these different branches of game theory are not clear nor is there any reason why they should be, so they often overlap. The distinction between them is made here for convenience, and is not intended to be prescriptive.

1.8

In evolutionary game theory (see Weibull 1995 for an introduction), players, who are boundedly rational by assumption, are randomly drawn from large populations to play a game recurrently. These individuals are usually unsophisticated and need not know much about the game, but they can adapt their decisions according to other players' actions. Equilibria may then arise in the long run, as dynamically or stochastically stable states at the population level. Research on evolutionary game theory was boosted by the computer simulations and empirical studies undertaken by Axelrod (1984). Axelrod's work represents a key event in the history of research on the PD. By inviting entries to two repeated PD computer tournaments, Axelrod studied the success of different strategies when pitted against themselves, all the others, and the random strategy. The strategy TFT won both tournaments and an extension of the second one. The extension, called ecological analysis, consisted of calculating the results of successive hypothetical tournaments, in each of which the initial proportion of the population using a strategy was determined by its success in the preceding tournament. Axelrod explains that TFT's success is due to four properties: TFT is nice (it starts by cooperating), provocable (it retaliates if its opponent defects), forgiving (it returns to play cooperatively if the opponent does so), and clear (it is easy for potentially exploitative strategies to understand that TFT is not exploitable). TFT's success is even more striking when one realises that it can never get a higher payoff than its opponent. Though severely criticised by some game theorists for drawing excessively on computer simulation and being partially flawed, Axelrod's work is widely accepted to have greatly stimulated analytical work within the domain of evolutionary game theory and further research on the PD using computer simulation. Findings on the repeated PD from evolutionary game theory are summarised by Gotts et al. (2003), who conclude that the assumptions about the dynamics of competition between strategies make the analytical results much less plausible as good approximations in social than in biological contexts. Gotts et al. (2003) have also extensively reviewed work on social dilemmas using computer simulation.

1.9

Like evolutionary game theory, most approaches within cognitive (or learning) game theory represent backward-looking alternatives to the deductive, forward-looking, rationality of orthodox game theory, which appears to be highly demanding for human agents and remains undefined in the absence of strong assumptions about other players' behaviour. However, not all learning is purely backward-looking (e.g. anticipatory learning theory focuses on learning how to predict). In cognitive game theory, agents learn from their experience using adaptive mechanisms which need not involve the kind of random variation and probabilistic selection found in biological evolution (Fudenberg and Levine 1998). Learning models have been reported to outperform orthodox game-theoretic predictions on experimental data (see chapter 6 in Camerer 2003; Erev and Roth 1998; Macy 1995; Roth and Erev 1995).

1.10

In learning theory (Flache and Macy 2002):

1. Players base their decisions on experience of past events as opposed to logical deductions about the future. Such approaches require fewer assumptions about other players and may be easier for human agents, but they do not lead to true conclusions with logical necessity even if the evidence used is accurate. Therefore, they can potentially lead to suboptimal behaviour (just as deductive reasoning can when its assumptions are not true).
2. Players must have feedback on their actions; otherwise learning cannot occur. Learning takes many forms, depending on the available feedback, the available knowledge, and the way these are used to modify behaviour. Two examples of learning models in the PD are individual learning by reinforcement (see Flache and Macy 2002 for a general model), and social learning by imitation (a controversial^[3] example on the spatial PD can be found in Nowak and May 1992). In reinforcement learning, actions that lead to satisfactory outcomes tend to be repeated, while those that lead to unsatisfactory outcomes are avoided. Imitation is usually biased towards the most successful neighbours, although this is not necessarily the case (see Chavalarias 2003 for an endogenous approach to imitation).
3. The fact that players learn from experience means that they often cannot undertake an optimal behaviour. An optimal approach requires knowledge that sometimes has to be inferred from experience. In the process of acquiring the necessary knowledge, suboptimal behaviour can occur as a result of exploring different actions or having drawn imperfect conclusions from experience. When agents learn from experience it seems more plausible that they look for satisficing rather than optimal solutions. The concept of 'satisficing' was introduced by Simon (1957) to indicate that agents often seek for a solution to a problem until they have found one which is 'good enough', rather than persisting in the hope of finding an optimal solution (which could be inexistent, incalculable, or unidentifiable). The 'good enough' solution is usually defined by setting a certain aspiration threshold.

1.11

Theoretical work on evolutionary game theory, on cognitive game theory, and on their relationship, has been developed to a point where the integration of the two approaches is now within reach (Weibull 1998).

1.12

Although most of the research on cognitive game theory is theoretical, there are a number of learning models that have been proposed to explain experimental data (see chapter 6 in Camerer 2003). The transition from theoretical learning models to psychological game theory and behavioural game theory is very smooth. We still find it useful to distinguish between cognitive, psychological, and behavioural game theory because their aims are usually different. In the context of social dilemmas, cognitive game theory has been mainly concerned with identifying a set of model-independent learning principles that are necessary and sufficient to generate cooperative solutions (Flache and Macy 2002). Psychological game theory is a term coined by Colman (2003).

Psychological game theory [...] overlaps behavioral game theory but focuses specifically on non-standard reasoning processes rather than other revisions of orthodox game theory such as payoff transformations. Psychological game theory seeks to modify the orthodox theory by introducing formal principles of reasoning that may help to explain empirical observations and widely shared intuitions that are left unexplained by the orthodox theory (Colman 2003)

1.13

Overlapping psychological game theory, behavioural game theory is completely driven by empirical (especially experimental) data, and models are assessed according to how well they are fitted to data. While models in cognitive game theory are designed to help us reflect on a certain process, behavioural game theory builds on models which are usually designed to represent the actual process.

Behavioral game theory is about what players actually do. It expands analytical theory by adding emotion, mistakes, limited foresight, doubts about how smart others are, and learning to analytical game theory. Behavioral game theory is one branch of behavioral economics, an approach to economics which uses psychological regularity to suggest ways to weaken rationality assumptions and extend theory. Camerer (2003, p.3)

1.14

The broad aim of the work reported here is similar to that of previous work in cognitive and psychological game theory as explained above: to identify conditions that can lead to more plausible solutions in social dilemmas. For that, we follow a common methodology in cognitive game theory: computer simulation inspired by research in cognitive science, rather than by specific data from the laboratory. In particular, we explore the outcome of the PD and one of its n-player versions when played repeatedly by adaptive computational Agents^[4] that learn from experience. The Agents use a form of case-based reasoning. Case-Based Reasoning (CBR) is a type of analogical reasoning in which specific cases from past experience are used as the basis of inference in the present. We consider CBR plausible as at least a partial representation of how people make use of past experience, that they recall circumstances similar to those they now face and remember what they did and with what outcome (see for example Kahneman et al. 1982).

1.15

The specific objective of this paper is to study how and under what conditions CBR as individual decision mechanism may entail cooperation (and to what extent). The structure of the paper is as follows: section 2 outlines the experiment setup, CBR is explained in more detail in section 3; section 4 describes the design of simple computational case-based reasoners; the results of several simulations are presented in sections 5 and 6, and discussed in section 7. In section 8 we compare our results with those obtained from a general reinforcement learning model of cooperation, and finally, conclusions are provided in section 9.

The experiment setup

2.1

We model social dilemmas in an abstract way by setting our Agents to play a 2-player and an n-player version of the Prisoner's Dilemma. Table 1 shows the 2-player Prisoner's Dilemma Payoff matrix. Payoffs on the bottom left of each cell are for Player 1 and Payoffs on the top right are for player 2.

Table 1: Payoff matrix for the 2-player Prisoner's Dilemma
		Player 2
		Cooperate	Defect
Player 1	Cooperate	Reward	Temptation
		Reward	Sucker
	Defect	Sucker	Punishment
		Temptation	Punishment

2.2

Because of the decision making algorithm of our Agents (explained in section 4), the actual values of the Payoffs are not relevant as long as they satisfy:

Temptation > Reward > Punishment > Sucker

In the n-player social dilemma every agent gets a reward as long as there are no more than M defectors (M < n). The Payoff that defectors get is always higher than the Payoff obtained by those who cooperate (Def-P > Coop-P). However, every player is better off if they all cooperate than if they all defect (Coop-P + Reward-P > Def-P). Table 2 shows the Payoff matrix for a particular agent:

Table 2: Payoff matrix of the "Tragedy of the Commons game" for a particular agent
	Fewer than M others defect	M others defect	More than M others defect
Agent cooperates	Coop-P + Reward-P	Coop-P + Reward-P	Coop-P
Agent defects	Def-P + Reward-P	Def-P	Def-P

2.3

This game has been called in the literature the "Tragedy of the Commons game" (TC) (Kuhn 2001) after the influential paper written by Hardin (1968). When the maximum number of defectors M for which the reward is given is high, it represents a version of the "volunteer's dilemma" (Brenan and Lomasky 1984; Diekmann 1985): a group needs a few volunteers, but each member is better off if others volunteer. If the number of players is large enough, the case when exactly M others defect is sufficiently unlikely that for all intents and purposes it can be ignored. Assuming the latter, we have a "social dilemma" as defined by Dawes (1980): "all players have dominating strategies that result in a deficient equilibrium". In any case, we have a "problematic social situation" (Diekmann 1986; Raub and Voss 1986), or social dilemma in a broader sense, which can be defined in game theory terms as a game with Pareto inefficient Nash equilibria.

2.4

The TC game differs from the two-player PD in three important ways:

1. In the TC game, for a small number of players, the state of "minimally effective cooperation" (exactly M defectors) is not negligible, so there is not a dominating strategy.
2. In the TC game, using pure strategies, there are two Nash equilibria: everyone defecting (universal defection^[5]) and exactly M defectors (minimally effective cooperation).
3. In the two-player PD, universal cooperation is a Pareto optimal outcome since no player can be better off without making the other player worse off. However, in the TC game the only Pareto optimal outcome is the state of minimally effective cooperation.

2.5

These two games allow us to model a particular type of social interdependence: interdependence in payoffs, as opposed to social interdependence in actions (Agents' actions conditioning other Agents' space of possible actions) or in goals (Agents' achievement of goals conditioning other Agents' achievement of their goals).

2.6

In the work reported below, each of these two games will be played repeatedly for an indefinite number of periods (until a cycle in the output of the simulation is reached) according to the following schedule of events:

1. Agents decide whether to cooperate or defect.
2. The Payoff is calculated for each Agent.

Case-based reasoning

3.1

The history of orthodox game theory (and neoclassical economics) has been marked by the assumption that agents are instrumentally rational. However, except in strictly competitive games, defining rational behaviour in games is by no means easy (Colman 1995). The outcome of a player's decision in a game depends on the other players' decisions, and these decisions cannot be rationally inferred a priori (specifically, it seems quite irrational to assume something that is not supported by empirical evidence). In fact, it seems sensible to think that everyone's decisions could be heavily influenced by everyone's previous decisions. To overcome that problem, the usual approach in orthodox game theory is to assume common knowledge of rationality, and to focus on equilibria. We want neither to assume common knowledge of rationality nor to study only the existence of possible equilibria. While we find it useful to explore how rational agents would behave in social dilemmas, we believe that common knowledge of rationality is such a strong assumption that it can hardly be sustained in a useful model of any real-world situation. Similarly, we are also interested in how different equilibria are reached (if they are indeed reached) and how probable each of them is (or, synthesising that information, how probable a certain level of cooperation is).

3.2

Once we have decided to remove any explicit a priori assumption about other players' behaviour from our Agents' decision making algorithm^[6], we are bound to model other types of reasoning apart from (or in addition to) deductive arguments^[7]. Inferences about other players' strategies, or about future payoffs, can then only be made in the light of the history of the game, and therefore they can only lead to probable —rather than necessarily true— conclusions. There are many types of non-deductive arguments^[8], such as 'generalisation by induction' (from now on we will call it just 'induction'), analogy, or abduction.

3.3

Our Agents use a form of analogy in their decision-making algorithm. According to the Collins English Dictionary (2000), analogy is "a form of reasoning in which a similarity between two or more things is inferred from a known similarity between them in other respects". In the context of problem solving, analogy can be defined as the process of reasoning from a solved problem which seems similar to the problem to be solved (Doran 1997). When analogical reasoning is undertaken within a single domain it is usually called Case-Based Reasoning (Aamodt and Plaza 1994; Nicolov 1997). Our Agents use Case-Based Reasoning (CBR) in their decision making algorithm.

3.4

CBR basically consists of "solving a problem by remembering a previous similar situation and by reusing information and knowledge of that situation" (Aamodt and Plaza 1994). The "known similarity" in the first definition of analogy is the problem situation in CBR, whereas the "inferred similarity" is the causal link between solution and outcome. The rationale is that if a solution turned out to be satisfactory when applied to a certain problem it might work in a similar situation too.

3.5

CBR arose out of cognitive science research in the late 1970s (Schank and Abelson 1977; Schank 1982). Schank and Abelson (1977) proposed that the general knowledge that we gain from experience is encoded in episodic memory as "scripts" that allow us to set up expectations and inferences. New episodes are processed by using dynamic memory structures which contain the episodes that are most closely related to the new episode; this process is called "reminding". Schank (1982) develops the idea that, far from being an irrelevant artefact of memory, reminding is at the root of how we understand and how we learn. Reminding occurs during the normal course of understanding, or processing some new information, as a natural consequence of the processing of that information. He argues that "we understand in terms of what we already understood".

3.6

There are several psychological studies that provide support for the importance of CBR as problem-solving process in human reasoning, especially for novel or difficult tasks (see Ross 1989 for a summary). Klein and Calderwood (1988) studied over 400 decisions made by experienced decision makers performing a variety of tasks in operational environments and concluded that "processes involved in retrieving and comparing prior cases are far more important in naturalistic decision making than are the application of abstract principles, rules, or conscious deliberation between alternatives". Drawing on their empirical studies, they also developed a descriptive model of decision making in which the attempt is to satisfice rather than optimise.

3.7

There are also a number of industrial applications of CBR (Watson 1997), particularly in domains where there is a need to solve ill-defined problems in complex situations; in such situations, it is difficult or impossible to completely specify all the rules (if they exist at all) but there are cases available.

3.8

Within the domain of economics, a case-based decision theory has been proposed by Gilboa and Schmeidler (1995 ; 2001). Gilboa and Schmeidler (1995) do not see case-based decision theory (CBDT) as a substitute for expected utility theory (EUT), but as a complement. They argue that CBDT may be more plausible than EUT when dealing with novel decision problems, or in situations where probabilities cannot easily be assigned to different states of the world (uncertainty, as opposed to risk), or if such states of the world cannot be easily constructed (ignorance). They also highlight that CBDT naturally gives rise to the notions of satisficing decisions and aspiration levels.

The decision making algorithm

4.1

This section describes the design of Agents which use a simple form of CBR to decide whether to cooperate or defect. They satisfice in the sense that, for a given state of the world and once they have undertaken a certain action, they will explore the other action only if the decision already taken led to an outcome which was not good enough.

4.2

In CBR, a case is a contextualised piece of knowledge representing an experience (Watson 1997). In general the experience could be the Agent's own, or a neighbour's. In the latter case we would be implementing a type of social learning (Conte and Paolucci 2001). However, in the experiments reported in this paper Agents only use cases that they have experienced themselves. If Agents cannot share cases, CBR becomes less plausible as a decision-making algorithm in very harsh environments, where an Agent has very little chance of learning from its own failures but can learn from others' failures. The scope of this model is therefore restricted to environments in which Agents can learn from their own failures.

4.3

A case for an Agent, i.e. the experience they lived in time-step t, comprises:

1. The time-step t when the case occurred.
2. The perceived state of the world at the beginning of time-step t, characterised by the factors that the Agent considers relevant to estimate the Payoff. These are:
   • Descriptor 1 (D1): the number of other defectors.
   • Descriptor 2 (D2): the decision that the Agent made.
   Agents are able to remember ml time-steps back (e.g. if ml = 2, the perceived state of the world for the Agent will be determined by the number of other defectors and the decisions made, both in time-step t-1 and in time-step t-2).
3. The decision they made in that situation, i.e. whether they cooperated or defected in time-step t, having observed the state of the world in that same time-step.
4. The Payoff that they obtained after having decided in time-step t.

4.4

Thus the case representing the experience lived by Agent A in time-step t has the following structure:

t	dft-ml … dft-2 dft-1	dt	pt
	dt-ml … dt-2 dt-1

where

dfi	is the number of defectors (excluding agent A) in time-step i,
di	is the decision made by Agent A in time-step i, and
pt	is the Payoff obtained by Agent A in time-step t.

The number of cases that Agents can keep in memory is unlimited. It is also worth noting that no cases are available for any Agent until (ml + 1) time-steps have gone by in the simulation. Agents make their decision whether to cooperate or not by retrieving two cases: the most recent case which occurred in a similar situation for each of the two decisions (i.e. each of the two possible values of d_t). A case is perceived by the Agent to have occurred in a similar situation if and only if its state of the world is a perfect match with the current state of the world observed by the Agent holding the case. The only function of the perceived state of the world is to determine whether two situations look similar to the Agent or not.

4.5

In a particular situation (i.e. for a given perceived state of the world) an Agent must face one of the following three possibilities:

1. The Agent cannot recall any previous situations that match the current perceived state of the world. In CBR terms, the Agent does not hold any appropriate cases for the current perceived state of the world. We distinguish three different possibilities here:
   1. The Agent defects. This model will be called D-Model from now on.
   2. The Agent cooperates. This model will be called C-Model from now on.
   3. The Agent chooses at random. This model will be called R-Model from now on.
2. The Agent does not remember a previous similar situation when they made a certain decision, but they do recall at least one similar situation when they made the other decision. In CBR terms, all the appropriate cases the Agent recalls have the same value for d_t. In this situation, Agents will explore the non-applied decision if the Payoff they obtained in the last previous similar situation was below their Aspiration Threshold; otherwise they will keep the same decision they previously applied in similar situations.
3. The Agent remembers at least one previous similar situation when they made each of the two possible decisions. In this situation, the Agent will focus on the most recent case for each of the two decisions and choose the decision that provided them with the higher Payoff^[9]. In this way, Agents adapt their behaviour according to the most recent feedback they got in a similar situation.

4.6

The UML activity diagram of the Agents' decision making algorithm in the R-model is outlined in Figure 1. In the experiments reported in this paper, all the Agents share the same Aspiration Threshold and the same Memory Length ml. These are the two crucial parameters in this CBR decision-making algorithm, determining when an outcome is satisfactory and when two situations are similar, respectively. The behaviour of a slightly more advanced socioeconomic Agent which also uses CBR in their decision-making algorithm but takes into account social approval is explored in Izquierdo et al. (2003).

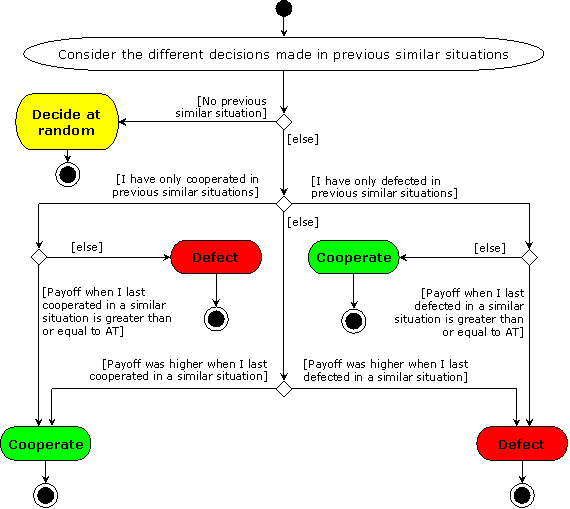
Figure 1. UML activity diagram of the Agents' decision making algorithm in the R-model

4.7

An alternative to CBR would be a rule-based system. One could induce the appropriate generalisations (rules) from the cases, and, in this view, CBR can be seen as a postponement of induction (Loui 1999). However, when dealing with systems that are adaptive themselves (in the sense that they are constituted by adaptive agents), the 'rules' of the system vary as the system evolves and therefore agents must constantly revise their perceptions about the system. This could be done by constantly updating the set of induced rules or by using CBR. Agents who use CBR store the original cases without building rules that summarise them. In that way, cases can suggest solutions even to ill-defined problems, such as those arising in social dilemmas, for which there may not be an adequate set of rules.

Results of the deterministic models

Results using D-Model

5.1

Prisoner's Dilemma : The outcome of the D-Model in the PD is stable bilateral cooperation (a cycle in which Agents cooperate forever) if the Aspiration Threshold of the Agents is greater than Punishment, and stable bilateral defection otherwise, for any value of ml > 0 if the model is run for long enough. The explanation of these outcomes is simple. If the Aspiration Threshold is greater than Punishment, the outcome of each round can be either bilateral cooperation or bilateral defection, but nothing else: the D-Model has no random component at all, every Agent has the same decision-making algorithm, and the game is symmetric; therefore every Agent will make the same decision at any given time^[10]. Bilateral cooperation gives a higher Payoff than bilateral defection and therefore the former will be preferred for any given state of the world. The situation of stable bilateral cooperation is then reached sooner or later (depending on the actual value of ml). If the Aspiration Threshold is not greater than Punishment, Agents will always defect and they will be satisfied with that outcome.

5.2

Tragedy of the Commons Game : Similarly, the outcome of the D-Model in the TC game is stable bilateral cooperation if the Aspiration Threshold of the Agents is greater than Def-P, and stable bilateral defection otherwise, for any value of ml > 0 if the model is run for long enough.

Results using C-Model

5.3

Prisoner's Dilemma : The outcome of the C-Model in the PD is stable bilateral cooperation for any value of ml > 0 if the model is run for long enough. In this model, even if the Aspiration Threshold is low, the final result is stable bilateral cooperation since Agents start by cooperating (contrary to what happens in the D-model).

5.4

Tragedy of the Commons Game : Similarly, the outcome of the C-Model in the TC game is stable bilateral cooperation for any value of ml > 0 if the model is run for long enough.

Results using the stochastic model

6.1

The software used to conduct the experiments reported in this section was written in Objective-C using the Swarm libraries (http://wiki.swarm.org/) and is available online together with a user guide at http://www.macaulay.ac.uk/fearlus/casd/ under GNU General Public Licence. The program is known to work on a PC using Swarm 2.1.1 and on a Sun Sparc using Swarm 2001-12-18.

6.2

As might be expected, the R-Model is very sensitive to the decisions that are made at random. Since the model has stochastic components, the results for a given set of parameters cannot be given in terms of assured outcomes but as a range of possible outcomes, each with a certain probability of happening. The probability of each outcome can either be estimated by running the model several times with different random seeds or, under certain circumstances, can be exactly computed.

6.3

Agents in the stochastic model make decisions at random only when they perceive a novel state of the world. Since the number of different states of the world that an Agent can perceive is finite, so is the number of random decisions the Agent can make. Therefore, simulations using the stochastic model must end up in a cycle. To study how often Agents cooperate in the PD we define the 'cooperation rate' as the number of times bilateral cooperation is observed in a cycle divided by the length of the cycle. Similarly, we define the 'reward rate' in the TC game as the number of times the reward is given in a cycle divided by the length of the cycle.

Prisoner's Dilemma

Aspiration Thresholds

6.4

It is important to realise that when our Agents play the PD, they share the same perception of the state of the world (defined by the last ml moves of the two Agents) in the sense that any two situations that look the same for one Agent will also look the same for the other Agent and any two situations that look different for one Agent will also look different for the other Agent. Therefore, at any given time in the simulation our Agents will have visited any given state of the world the same number of times. This shared perception of the state of the world means that, for a certain state of the world, the only relevant factor is the random decision that they make when they first experience that situation.

Table 3: Decisions made by each of the two Agents in the PD when visiting a certain state of the world for the i-th time. In the first column, Payoffs are denoted by their initial letter. In columns 2 to 5, the first letter in each pair corresponds to the decisions of one Agent, the second letter to those of the other. C is cooperation and D is defection. The first imbalance between CC and DD for every value of AT has been shadowed. The meaning of x and y is explained in the text. The results shown in this table are independent of the Memory Length
Aspiration Thresholds (AT)	1st visit (random)	2nd visit	3rd visit	4th visit and onwards	x	y
T < AT	CC	DD	CC	CC	1	-
	CD	DC	DD	DD	-	2
	DC	CD	DD	DD	-	2
	DD	CC	CC	CC	1	-
R < AT ≤ T	CC	DD	CC	CC	1	-
	CD	DD	DC	DD	-	2
	DC	DD	CD	DD	-	2
	DD	CC	CC	CC	1	-
P < AT ≤ R	CC	CC	CC	CC	0	-
	CD	DD	DC	DD	-	2
	DC	DD	CD	DD	-	2
	DD	CC	CC	CC	1	-
S < AT ≤ P	CC	CC	CC	CC	0	-
	CD	DD	DD	DD	-	1
	DC	DD	DD	DD	-	1
	DD	DD	DD	DD	-	0
AT ≤ S	CC	CC	CC	CC	0	-
	CD	CD	CD	CD	-	-
	DC	DC	DC	DC	-	-
	DD	DD	DD	DD	-	0

6.5

The decision dynamics for a certain state of the world are summarised in Table 3. Consider for now the first four rows of the table (T < AT). These represent the case where the Aspiration Threshold (for both Agents) exceeds T. The first time any particular state of the world occurs, both Agents will choose C (Cooperate) or D (Defect) at random (column headed "1^st visit"). When the same perceived state occurs a second time, the responses will be as shown in the "2^nd visit" column, and so on. The table shows that by the third visit to that state, either both Agents are cooperating or both Agents are defecting, and both will then continue to make the same response. The other four sets of rows in the table show what happens when the AT is in each of four lower ranges of values.

6.6

There are two states of the world that appear to be particularly important in the dynamics of the game. One is that where there have been ml successive bilateral cooperations (let us call it mlBC); the other is where there have been ml successive bilateral defections (let us call it mlBD). Whenever bilateral cooperation follows a visit to mlBC, then mlBC is immediately revisited (since the Agents observe again that they both cooperated in the last ml time-steps). Similarly, whenever bilateral defection follows a visit to mlBD, then mlBD is immediately revisited (since the Agents observe again that they both defected in the last ml time-steps). We can then define x as the number of times that mlBC has to be revisited after it has been abandoned before stable cooperation is reached, and y as the number of times that mlBD has to be revisited after it has been abandoned before stable defection is reached. As an example, when AT > T, if both Agents happen to cooperate when they observe mlBC for the first time, then they will both experience mlBC for the second time in the following time-step. Both of them will then defect (2^nd visit to mlBC), and in doing so will abandon mlBC. If mlBC is then revisited (3^rd visit), it will never be left again. In this hypothetical example, the number of times x that mlBC had to be revisited after it was abandoned before stable cooperation was reached was 1. This information is included in Table 3 and its significance will be explained later.

6.7

When the simulation locks in to a cycle (and it necessarily does), the states that make up the cycle are repeatedly visited, leading to outcomes shown in the "4^th visit and onwards" column in Table 3. Looking at that column, we can identify two values for the Aspiration Threshold AT that make a particularly important difference: Sucker and Punishment.

• When AT > Sucker, simulations lock in to cycles which are necessarily made up of bilateral decisions (both Agents cooperate or defect at the same time), since if an Agent receives the Sucker Payoff in any situation, they will never cooperate again in that situation. In this sense our Agents are particularly unforgiving. Agents with Aspiration Thresholds greater than Sucker cannot be systemically exploited. The importance of this will be discussed later.
• When AT > Punishment, there is a qualitative jump in terms of average cooperation rates. This is because if AT > Punishment, when both Agents defect the first time they experience a certain state of the world, they will end up cooperating in that state, but they will end up defecting if AT ≤ Punishment.

6.8

Taking into account the two previous points and looking at the "4^th visit and onwards" column in Table 3, one could then think that average cooperation rates should be 25% if AT ≤ Punishment and 50% if AT > Punishment regardless of the Memory Length, but one would be wrong. Figure 2 shows the importance of Aspiration Thresholds and how they can modify the effect of the Memory Length.

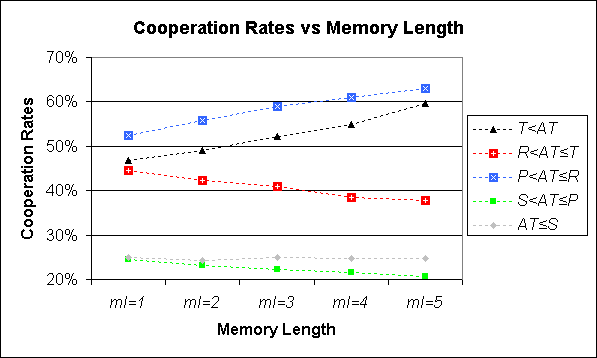
Figure 2. Average cooperation rates when modelling two agents with Memory Length ml and Aspiration Threshold AT, playing the PD. The average cooperation rate shows the probability of finding both Agents cooperating once they have finished the learning period (i.e. when the run locks in to a cycle). The values represented for ml = 1 have been computed exactly. The rest of the values have been estimated by running the model 10,000 times with different random seeds. All standard errors are less than 0.5 %

6.9

The interactions between the Aspiration Threshold and the Memory Length can be explained by taking into account two factors. Both factors are related to the fact that, as the Memory Length becomes larger, the number of possible perceived states of the world grows exponentially and it becomes less likely for any given state of the world to be revisited. From now on let us refer to each Payoff by its initial letter.

1. The first factor concerns only the relative frequency of stable bilateral cooperation and stable universal defection^[11]. This factor is present for any AT > S and represents a bias towards cooperation. Looking at Table 3, one could expect stable bilateral defection to be three times more likely than stable bilateral cooperation if S < AT ≤ P, and as likely as stable bilateral cooperation if AT > P. However, as the Memory Length increases, there is a certain bias towards stable bilateral cooperation. For the simulation to lock in to stable bilateral cooperation, it is required that a bilateral decision (a bilateral cooperation if S < AT ≤ P) follows the first visit to the state of the world formed by ml bilateral cooperations (mlBC) and that the same state of the world mlBC is revisited x more times after it is abandoned; similarly, stable bilateral defection requires a unilateral decision (or bilateral defection if S < AT ≤ P) following the first visit to the state of the world formed by ml bilateral defections (mlBD) and y more visits to that state of the world mlBD after it is abandoned. As we can see in Table 3, except for the trivial case^[12] where AT ≤ S, the average x is always less than the average y for any given Aspiration Threshold. For high values of the Memory Length, revisiting a state can take a very long time and the fact that stable bilateral cooperation needs fewer visits (x) to settle down than stable bilateral defection does (y) is an important bias towards the frequency of stable bilateral cooperation.
2. The second factor explains why average cooperation rates not only fail to increase, but actually decrease with Memory Length for S < AT ≤ P and R < AT ≤ T. This factor is present for S < AT ≤ T and it represents a bias towards cooperation if P < AT ≤ R, and a bias towards defection if S < AT ≤ P or R < AT ≤ T. For any AT > S, the simulation ends up in a cycle of bilateral decisions. Therefore, it is crucial to study whether there is a bias towards cooperative bilateral decisions (CC) or towards defective bilateral decisions (DD) in the Agents' learning process. Table 3 shows the history of decisions made by the Agents having observed any particular state of the world for different Aspiration Thresholds. The first imbalance between CC and DD for every value of AT has been shadowed (e.g. if S < AT ≤ P the first imbalance occurs in the second visit, where DD is three times more likely to happen than CC). Imbalances in the early visits to a state of the world are more important because they occur before those in later stages, which might never materialise if a cycle has been reached before. Imbalances in the component parts of the state of the world (CC and DD) make certain states of the world more likely to occur than others, hence leading to biases in the cooperation rate. What is not obvious is why the importance of such imbalances (in terms of reward rates) increases with the value of Memory Length. This is so because, even ignoring the fact that some states of the world are more likely to occur than others, not all states of the world are equally likely to form part of a cycle; some states can form cycles more easily than others^[13], and their relative frequency depends on the Memory Length. This is certainly the case of mlBC and mlBD. Not only are they the only states of the world that can form cycles just by themselves (assuming AT > S), but they also need fewer revisits to settle than the rest of states of the world (see previous paragraph). Roughly half of the simulation runs reported in this paper with AT > S ended up in cycles made up by either mlBC or mlBD. This means that an imbalance between the frequency of mlBC and mlBD can affect the reward rate substantially. The imbalance between mlBC and mlBD given an imbalance between CC and DD does depend on the Memory Length. To clarify this, assume that DD is always z times more likely than CC; then mlBD will be z^ml times more likely than mlBC. This analysis is not a proof since successive states of the world are not independent, but it clarifies why imbalances gain importance as the value of Memory Length increases. As we can see in Table 3, if S < AT ≤ P or R < AT ≤ T, the imbalance is towards the defective bilateral decision, making mlBD more likely to occur relative to mlBC as Memory Length increases, and thus reducing the average cooperation rate. On the other hand, if P < AT ≤ R, the imbalance is towards cooperation.

6.10

The summary of the effect of each of the two factors depending on the AT outlined above is shown in Table 4, together with the total effect found in the simulations. We have not yet proved that the two effects explained here are the only operating factors.

Table 4: Effect on average cooperation rates of each of the two factors outlined in the text above depending on the value of AT, and results from the simulation runs
	AT ≤ S	S < AT ≤ P	P < AT ≤ R	R < AT ≤ T	T < AT
Effect of Factor 1	No bias	Bias towards cooperation	Bias towards cooperation	Bias towards cooperation	Bias towards cooperation
Effect of Factor 2	No bias	Bias towards defection	Bias towards cooperation	Bias towards defection	No bias
...	...	...	...	...	...
Total effect	No bias	Bias towards defection	Bias towards cooperation	Bias towards defection	Bias towards cooperation

6.11

It is clear that in CBR, not only what is learnt, but the actual process of learning can have a major importance, and Aspiration Thresholds play a crucial role in that process. Consider, for example, the difference between the cases where P < AT ≤ R and where R < AT ≤ T. In both cases, Agents will learn to cooperate in any given state of the world if they happen to make the same decision the first time they visit that state, and they will end up defecting in that situation otherwise. Therefore, for those two values of AT, we could expect average cooperation rates to be the same or at least similar. However, because the actual process of learning is different, differences in average cooperation rates are substantial and get larger as the Memory Length increases (see Figure 2).

Importance of a common representation of the state of the world

6.12

To study the importance of having a shared perception of the state of the world in the PD, we studied the outcome of the game when played by Agents with partial representations of the state of world: Agents who only look at the other player's actions (only descriptor D1) and Agents who only look at their own actions (only descriptor D2). In both these cases, the two Agents may perceive the state of the world differently. Figure 3 shows the results obtained for AT > T. The results for other Aspiration Thresholds are very similar^[14] so they are omitted.

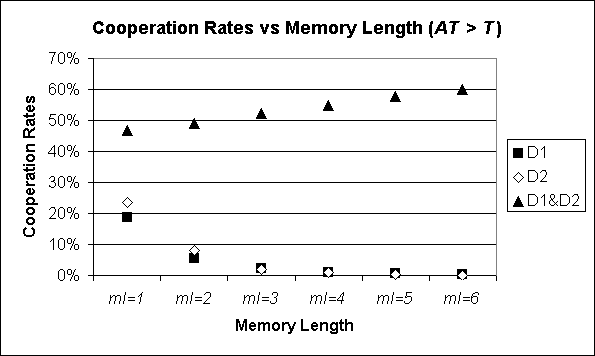
Figure 3. Average cooperation rates when modelling two agents with Memory Length ml, Aspiration Threshold greater than Temptation, and with 3 different representations of the state of the world (D1, D2, and D1&D2), playing the PD. The values represented for ml = 1 have been computed exactly. The rest of the values have been estimated by running the model 10,000 times (ml = 2, 3, 4) or 1,000 times (ml = 5, 6) with different random seeds. All standard errors are less than 1%

6.13

The difference in terms of average cooperation rate between the complete representation of the state of the world (D1&D2) and the two incomplete representations of the state of the world (D1, and D2) is clear and it becomes larger the greater the value of Memory Length ml is. When both the Agent's own decisions and the other player's decisions form the perceived state of the world (D1&D2) the average cooperation rate is much higher than in the other cases. As we saw in Table 3, except in the trivial case where AT ≤ S, Agents will never cooperate again in a given state of the world after having received the Sucker Payoff in that state. When using either of the two incomplete perceptions of the state of the world, there are sets of situations that are represented by the same perceived state of the world for one Agent but by different perceived states of the world for the other. The size of such sets of situations increases as the Memory Length ml increases. In these sets of situations, one of the Agents will make several decisions at random in situations which they perceive as novel, but which are represented by one single perceived state of the world for the other Agent. This fact strongly increases the chances of the latter Agent getting a Sucker Payoff and therefore not achieving a cooperative outcome.

The Tragedy of the Commons game

Aspiration Thresholds

6.14

The TC game is more complex to analyse than the PD since at any given time in the simulation Agents have not necessarily visited what they perceive as a distinct situation the same number of times^[15]. Therefore, in a given time-step some Agents may be making decisions at random while some others may not. This means that we cannot build a table like Table 3 for the TC game.

6.15

Figure 4 shows the results obtained in the TC game when played by 10 Agents with Memory Length ml = 1, for different values of M (maximum number of defectors for which the reward is given). Similar results have been obtained when the game is played by 5 and by 25 Agents.

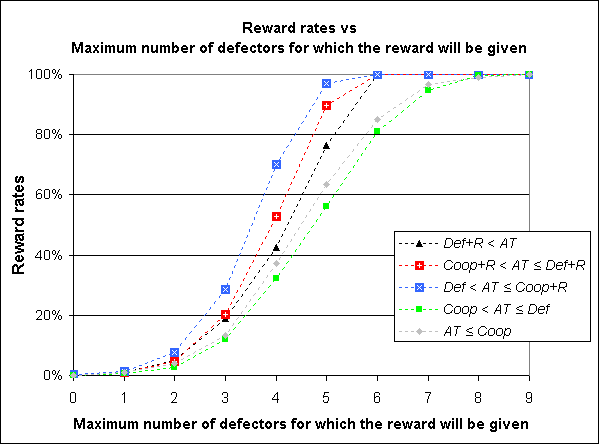
Figure 4. Average reward rates for different values of M in the Tragedy of the Commons game played by 10 Agents with Memory Length ml = 1. Each represented value has been estimated by running the model 1,000 times. All standard errors are less than 1.5%

6.16

Figure 4 shows that levels of cooperation strongly depend on the maximum number of defectors for which the reward is given (M). When the requirement is too demanding (low values of M), levels of cooperation tend to be low and the reward is not usually given. On the other hand, for moderate and high values of M (M ≥ 6), the reward is almost always given^[16]. If Agents have Aspiration Thresholds greater than Def-P then the reward will be given more often than if they choose at random (AT ≤ Coop-P). The highest levels of cooperation are achieved when the Aspiration Thresholds are just above Def-P. Levels of cooperation then decrease as Aspiration Thresholds separate from the optimal value.

Importance of a common representation of the state of the world

6.17

To test the importance of a common representation of the state of the world, we put our Agents on a toroidal 2 × 5 grid so they could only observe their most immediate five neighbours in their Moore neighbourhood of radius 1. Results are shown in Figure 5.

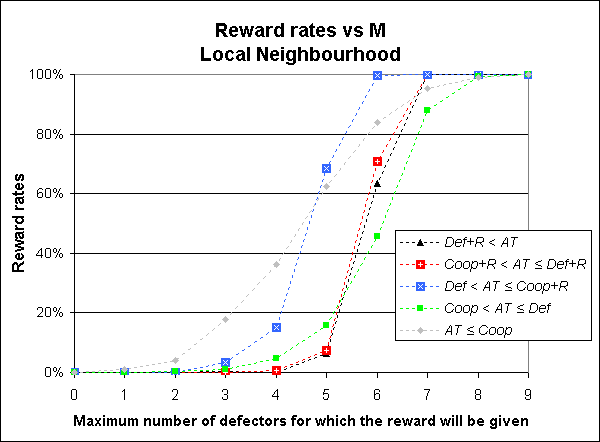
Figure 5. Average reward rates for different values of M in the Tragedy of the Commons game played by 10 Agents with Memory Length ml = 1. Every Agent A can observe other 5 Agents only, who are the only ones that can observe Agent A. Each represented value has been estimated by running the model 1,000 times. All standard errors are less than 1.5%

6.18

When Agents can observe only their local neighbourhood, the range of values of M to which the reward rate is sensitive is shifted and squeezed to the right. The use of local neighbourhoods sharpens the global movement from defection to cooperation. When Agents can only observe their neighbours, their global response to changes in the reward programme (parameterised by M) is not smooth anymore. Instead, the global behaviour is now better characterised by a hard threshold whose particular value depends on the Aspiration Threshold of the Agents forming the society. When Agents can only observe their neighbours there is a very narrow range of values for M where a very small change can make a huge difference.

6.19

As in the previous case, the highest levels of cooperation are achieved when the Aspiration Thresholds are just above Def-P. It is once again clear from these results that in CBR, not only what is learnt is important, but also how it is learnt, and that Aspiration Thresholds play a crucial role in that process.

Discussion

7.1

The experiments conducted show that cooperation can emerge from the interaction of selfish and unforgiving case-based reasoners. It is interesting to note that if Agents tried to anticipate other Agents' actions they would always defect, since defection is always preferred given the other agents' actions^[17]. However, when Agents try to anticipate the outcome of their actions using their experience, the history of the game can be such that cooperating proves to be a better strategy even in the short term.

7.2

We are aware that the assumption that Agents make their decisions at random when confronted with a new situation is difficult to maintain. However, the deterministic models (and Table 3) show that when AT > Maximin, any positive correlation between the random decisions taken by the Agents will tend to increase levels of cooperation. Similarly, we would expect negative correlations to lead to less cooperative outcomes.

7.3

The experiments have also shown that the optimal value of the Aspiration Threshold is just above Maximin, and that sharing a common representation of the state of the world strongly increases levels of cooperation.

7.4

More importantly, the experiments conducted have revealed a concept of equilibrium which is more relevant than the Nash equilibrium for repeated games played by case-based reasoners: strictly undominated outcomes. The concept of strictly undominated outcome is defined for one single stage of any game. Its defining property is that no player can be guaranteed a higher payoff by changing their decision^[18] (i.e. every player is getting at least their Maximin). The concept of strictly undominated outcome is weaker (i.e. less restrictive) than the Nash equilibrium: A Nash equilibrium is always a strictly undominated outcome but the reverse is not necessarily true. In particular, in the one-shot PD, bilateral cooperation is a strictly undominated outcome while it is not a Nash equilibrium.

7.5

As opposed to the concept of Nash equilibrium (which makes the assumption that the other players will keep their strategies unchanged), the concept of strictly undominated outcome accounts for every possible action that the other players might take. A strictly undominated outcome as equilibrium concept is best defined by negation: if a certain player perceives that by changing their strategy they will always get a higher payoff no matter the other players' response, then the player has a clear incentive to deviate from that outcome, so that outcome cannot be an equilibrium (it is strictly dominated by other outcomes). If, on the contrary, no player has such incentive, the outcome could be an equilibrium.

7.6

In the PD, the only strictly undominated outcomes are the two bilateral decisions. In the TC the only strictly undominated outcome in which the reward is not given is universal defection; all the outcomes in which the reward is given are strictly undominated.

7.7

We now define a broad set of decision–making algorithms used to select one action from a finite set (e.g. Cooperate or Defect). Let us call Case-Based Reasoning Exploratory (CBRE) algorithms those decision-making algorithms in which an action is selected by undertaking the following steps (or as if these steps had been undertaken):

1. Identify a set of possible outcomes, Z, in which every action available to the decision maker is represented at least once (hence the modifier "exploratory").
2. Select an outcome in Z that provides the decision maker with a payoff which is no lower than the decision maker's payoff in any other outcome in the set Z.
3. Return the action undertaken by the decision maker in the outcome selected in step 2.

7.8

We are now ready to state that: a) the outcome of any game played by Agents using a CBRE algorithm is necessarily a strictly undominated outcome; and, b) any strictly undominated outcome can be the outcome of a game played by Agents using a CBRE algorithm. These two statements are proved in Appendix B. It comes as no surprise that this equilibrium concept is based on outcomes rather than strategies, since case-based reasoners place the emphasis on the case rather than on the rule.

7.9

The decision-making algorithm presented in section 4 becomes a CBRE algorithm when the simulation locks in to a cycle (and it necessarily does) except in the trivial cases where Aspiration Thresholds are too low. Therefore, we can guarantee that all the non-trivial simulations reported in this paper ended up in cycles made up of strictly undominated outcomes. As we have seen in the previous section, the actual selection among different strictly undominated outcomes can be strongly path-dependent and depends on the specific type of CBRE algorithm that players use.

7.10

Our Agents have shown that they will not accept outcomes in which they are guaranteed a higher Payoff by changing their decision once their learning process is finished if their Aspiration Threshold is high enough. However, they are quite naive in the sense that they are not able to infer that the game has locked in to a persistent cycle. In other words, they are not able to infer that the other players will not accept outcomes where they are not getting their Maximin either.

7.11

We can conjecture what would happen if our Agents were sophisticated enough as to infer, through repeated interaction and learning, the fact that the rest of the Agents are also non-exploitable (i.e. they do not accept outcomes where they get a payoff lower than Maximin). Assuming (or learning) that the rest of the players are not exploitable can then enable a player X to infer that certain outcomes which give payoffs higher than Maximin to this player X will not be sustainable (because they do not yield payoffs higher than Maximin to some other player). This inference can make an outcome which was not initially strictly dominated in effect be dominated. In other words, the concept of strict dominance can be applied to outcomes iteratively just as it is applied iteratively to strategies.

7.12

As an example, we have seen that Agents with a high enough Aspiration Threshold who play the PD will end up in a cycle made up of bilateral cooperations and/or bilateral defections (the only two strictly undominated outcomes (see Figure 6b). If through repeated interaction the Agents were able to infer that the game will not have any other outcome (because one of the players will not accept it), then they could eliminate the unilateral outcomes from their analysis and apply the concept of outcome dominance for the second time to the (two) remaining possible outcomes. For this to happen, it would have to be mutual belief that the opponent is not exploitable either. When only bilateral decisions are confronted, the only strictly undominated outcome is bilateral cooperation (see Figure 6c). When confronted with bilateral cooperation as the only alternative, bilateral defection is not a strictly undominated outcome anymore, since the two players are guaranteed a higher Payoff by changing their decision. In other words, bilateral cooperation is the only outcome that survives two steps of outcome dominance in the PD. In the TC game all the outcomes in which the reward is given survive two steps of outcome dominance, and they are the only outcomes that do so. It can be shown that in any game, after applying any number of steps of outcome dominance, the remaining outcomes are not Pareto-dominated by any of the outcomes which have been eliminated.

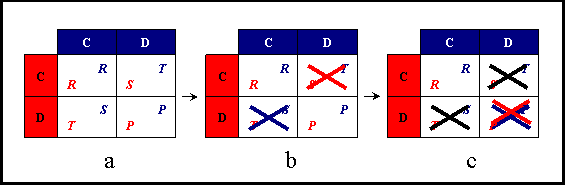
Figure 6. Elimination of dominated outcomes. Figure b shows the remaining outcomes after having applied one step of outcome dominance. Figure c shows the remaining outcomes after having applied two steps of outcome dominance. Red crosses represent outcomes which are unacceptable for player Red (row), blue crosses represent outcomes which are unacceptable for player Blue (column), and black crosses represent outcomes eliminated in previous steps

7.13

How Agents would be able to move from bilateral defection to bilateral cooperation, if indeed they were, is not clear and is a matter for further research. We conjecture that this could be achieved by signalling processes to promote cooperation, or it could emerge from a form of learning by induction, since once the simulation has locked in to a cycle, it does show a general rule or pattern (Agents get a higher Payoff when they cooperate than when they defect). Perhaps induction would then be produced by the simple forgetting of an episode's details and the consequent blurring together in memory of that episode with other similar episodes (Reisberg 1999). In any case, the movement from bilateral defection to bilateral cooperation would require a non-trivial degree of coordination.

7.14

We have seen that if our Agents have a high enough Aspiration Threshold they are not exploitable in the sense that they do not accept outcomes where they are not getting at least Maximin. We find that a more useful definition of rationality in games is that of non-systemic-exploitability. Rational players are not systemically exploitable. According to this definition, cooperation emerges among selfish rational players as soon as it becomes mutual (not necessarily common) belief (not necessarily knowledge) that the game is being played among rational players. Using Macy's words, cooperation would then emerge among self-interested agents "not from the shadow of the future but from the lessons of the past" (Macy 1998).

Case-based reasoning and reinforcement learning

8.1

Some further insights can be gained by comparing the equilibrium concept explained in the previous section with learning-theoretic solution concepts in social dilemmas identified by Macy (1990; 1991) and Macy and Flache (2002), and further developed by Flache and Macy (2002) using their General Reinforcement Learning (GRL) model. In the GRL model, Agents decide stochastically whether to cooperate or defect. After every decision, they observe the resulting outcome and evaluate it as satisfactory or unsatisfactory depending on whether the payoff obtained was greater or less than their Aspiration Threshold respectively. This evaluation, in turn, determines whether the probability of taking the associated action increases (if the outcome was satisfactory) or decreases (if the outcome was unsatisfactory) and how much the probability changes. Figure 7 outlines the GRL model. The specific algorithm used to update probabilities is such that the probabilities approach asymptotically their natural limits, but never reach them^[19].

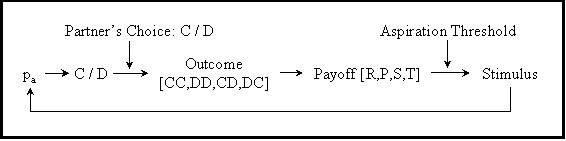
Figure 7. Schematic model of reinforcement learning (Flache and Macy 2002). pa is the probability of making decision 'a', where 'a' can be either cooperate (C) or defect (D)

8.2

A possible way of relating the GRL model to the CBR model is to say that in the GRL model every situation experienced by the Agents looks the same to them (i.e. there is no perceived state of the world), so we could say that there is one single set of similar situations which includes all of them. However, as opposed to what occurs in the CBR model, in which Agents decide at random only when they perceive a novel state of the world, Agents in the GRL model decide always stochastically whether to cooperate or defect.

8.3

Assuming fixed Aspiration Thresholds, Macy and Flache (2002) have characterised two types of attractors that govern the dynamics of the simulations in the GRL model: self-reinforcing equilibria (SRE) and self-correcting equilibria (SCE)^[20]. These two concepts are not equilibria in the static sense of the word, but pairs of probabilities to cooperate (one for each player) which act as "basins of attraction" that pull the dynamics of the simulation towards them.

8.4

SRE are absorbing states in the simulation where Agents' probability to cooperate is either 1 or 0 and the certain outcome resulting from those pure strategies ensures that probabilities will not change (e.g. when probabilities to cooperate are 1 and Agents' Aspiration Thresholds are below Reward). Since the learning algorithm used by Flache and Macy (2002) is such that probabilities cannot reach 1 or 0 from any other value, SRE are unreachable from any other state^[21]. SRE are, however, "basins of attraction" which are more likely to be approached the closer the Agents' probability to cooperate gets to them (although escape from their 'gravitational' attraction is always possible). The number of SRE in a social dilemma depends on the number of outcomes which both players consider satisfactory (i.e. on their Aspiration Thresholds). Regarding SCE, Macy and Flache (2002) have proved that there can be at most one SCE in a social dilemma and there may be none. The SCE obtains when the expected change of probabilities is zero and the Agents' probability to cooperate is neither 1 nor 0.

8.5

The concept of strictly undominated outcomes after applying one step of outcome dominance is closely related to SRE in any game. An outcome is strictly undominated if and only if every player is getting at least their Maximin . An outcome is an SRE if and only if every player is getting at least their Aspiration Threshold (and is using pure strategies). Therefore, if Aspiration Thresholds equal Maximin, the two concepts are equivalent.

8.6

However, as Aspiration Thresholds move away from Maximin, the two concepts diverge. While the concept of strictly undominated outcomes is independent of Aspiration Thresholds, some SRE are eliminated as Aspiration Thresholds increase, while new SRE appear when Aspiration Thresholds decrease, always in a cumulative fashion.

8.7

The main difference between the concepts of SRE and strictly undominated outcomes after applying one step of outcome dominance stems from the different meaning that Aspiration Thresholds have in the GRL model and in the CBR model. In the GRL model, Agents will never be satisfied with a Payoff less than their Aspiration Threshold; on the contrary, in the CBR model Agents will be satisfied with a Payoff below their Aspiration Threshold as long as the last time they applied any other possible decision in a similar situation they got an even lower Payoff. The latter interpretation of the Aspiration Thresholds can be aligned with the former by assuming that:

1. Agents in the CBR model have a different Aspiration Threshold for each distinct set of situations they perceive as different (this set is defined by a certain perceived state of the world).
2. After every possible decision has been explored at least once in a certain set of similar situations, the corresponding Aspiration Threshold is updated according to the following habituation rule:
   AT = sup _i{ last(Payoff_Di) }
   where
   AT is the updated Aspiration Threshold for a given set of similar situations.
   Di is a possible decision made by the Agent
   last(Payoff_Di) is the payoff obtained by the Agent when they last made decision Di

The outcomes resulting from applying more than one step of outcome dominance are not directly related to SRE or SCE.

Conclusions

9.1

We have explored the outcome of social dilemmas when played by case-based reasoners. CBR is a method of inference that is believed to be commonly used by real people when they face novel or difficult problems in which they cannot easily compute a satisfactory solution (Ross 1989). Social dilemmas are clearly ill-defined and difficult problems since the payoff for any player depends on the other players' actions and these actions are not necessarily known by the deciding agent, nor can they be rationally inferred a priori. However, when playing the game repeatedly, agents can adapt their behaviour by observing the other players' actions, and find a satisficing solution within the constraints that the other players' actions impose. By implicitly anticipating the outcome of their actions, our selfish case-based reasoners arrive at a cycle in which all of them can justify every decision they make by appealing to a previous past experience. In this paper we have proved that the decision they make is very often to cooperate, even though they only pursue their own benefit. In determining how often cooperation occurs, aspiration thresholds, the Agents' representation of the world, and their memory length all play important and interdependent roles.

9.2

The experiments conducted have also revealed a new concept of equilibrium which is especially relevant for a broad class of case-based reasoners: strictly undominated outcomes. Case-based reasoners with high enough Aspiration Thresholds do not accept outcomes which are strictly dominated, i.e. they do not accept outcomes where the decision making Agent is guaranteed a higher payoff by changing their decision. Moreover, it is conjectured that if Agents were sophisticated enough as to grasp the fact that other Agents do not accept strictly dominated outcomes, then the outcome of the game would be always cooperative.

Acknowledgements

This work is funded by the Scottish Executive Environment and Rural Affairs Department. We wish to thank Bruce Edmonds and three anonymous referees for some very useful comments. We also would like to thank two anonymous reviewers that commented on an earlier version of this paper submitted to the first European Social Simulation Association Conference.

Notes

¹ Terms in bold are defined in Appendix A.

² For a detailed analysis of the finitely repeated Prisoner’s Dilemma, see Raub (1988).

³ The controversy concerns the effects of synchrony in the spatially embedded PD and, though fascinating, is not relevant here.

⁴ The word ‘Agent’ will be written starting with a capital ‘A’ when it refers to the computer implementation.

⁵ Universal defection is a Nash equilibrium as long as M < n-1.

⁶ Obviously there are always implicit assumptions in any model. Learning depends upon the contextual knowledge and the framework that the learning algorithm provides (the so-called logical, or model, bias).

⁷ Valid deductive arguments are those whose conclusions follow from their premisses with logical necessity (Copi 1986, p. 169).

⁸ Non-deductive arguments are not claimed to demonstrate the truth of their conclusions, but to support their conclusions as probable, or probably true. Arguments of this type are called inductive arguments in some textbooks (e.g. Copi 1986, p. 404, or Salmon 1984, p. 32) and should not be confused with the inference process of generalisation by induction (which is a particular type of non-deductive argument).

⁹ A tie is impossible in either of the two games reported in this paper.

¹⁰ This also applies to the Tragedy of the Commons Game: when Agents cannot recall any cases, they make the same decision by model design. When Agents can recall only one case in which they either cooperated or defected, they all recall the same case, and therefore they all make the same decision. Finally, when Agents can recall one case for each possible decision, those cases necessarily show a situation in which all of them cooperated or all of them defected. When given universal cooperation and universal defection as the only two possible options, they all cooperate.

¹¹ This effect is explained in detail by Izquierdo et al. (2003).

¹² If the Aspiration Threshold does not exceed Sucker, Agents repeat the same decision that they made at random the first time they visited a certain state of the world whenever they visit the same state again.

¹³ Or, conversely, some cycles comprise fewer different states of the world than others.

¹⁴ Except, again, for the trivial case where AT ≤ S, in which the average cooperation rate is always 25%.

¹⁵ Recall that our Agents know only whether they cooperated or defected, and how many others defected. In the TC game, the information provided to the Agents is thus not complete in the sense that they cannot identify who is defecting, as they could in the PD (since there was only one other player).

¹⁶ When the game is played by 25 Agents, average reward rates are greater than 80% if M ≥ 15 and greater than 99% if M ≥ 19, for any Aspiration Threshold.

¹⁷ Except in the case of minimally effective cooperation in the “Tragedy of the Commons” game.

¹⁸ A slightly more restrictive concept is that of an undominated outcome, in which no player can be guaranteed the same or a higher payoff by changing their decision. The concept of undominated outcome as equilibrium implies that Agents deviate from an outcome only if it is certain that they will not be worse off by doing so, whereas the strictly undominated concept implies that Agents move away from an outcome only if it is certain that they will be better off by doing so. The concept of undominated outcome as equilibrium is neither weaker nor stronger than the Nash equilibrium.

¹⁹ Probabilities might reach their natural limits in the implementation of the conceptual model due to floating-point rounding errors.

²⁰ Bendor et al. (2003) have proved that any pure outcome of the stage game can be SRE when Aspiration Thresholds are not fixed.

²¹ Floating-point inaccuracies might make SRE reachable in certain implementations of the model.

²² If we consider undominated outcomes as opposed to strictly undominated outcomes, then statement a) is only true for games in which players never get the same payoff when they select different actions. In those games (e.g. the Prisoner’s Dilemma and the Tragedy of the Commons game), the two equilibrium concepts are equivalent. We find the concept of undominated outcomes more appealing than its strict version, particularly when outcome dominance is to be applied iteratively. However, in this paper we have focused on the latter because the relation of the former with the Nash equilibrium and with CBRE algorithms is not so clear.

Appendix A

Boundedly rational:

A boundedly rational agent acts as if they have consistent preferences, but limited computational capacity (compare with the definition of instrumentally rational below).

Deficient equilibrium:

An equilibrium is deficient if there exists another outcome which is preferred by every player.

Common knowledge of rationality (CKR):

CKR means that every agent assumes: (a) that all agents are instrumentally rational, and (b) that all agents are aware of other agents' rationality-related assumptions (this produces an infinite recursion of shared assumptions).

Individually-rational outcome:

An outcome giving each player at least the largest payoff that they can guarantee receiving regardless the opponents' moves.

Instrumentally rational:

An instrumentally rational agent acts as if they have consistent preferences and unlimited computational capacity.

Maximin:

the largest possible payoff a player can guarantee themselves. This is Punishment in the Prisoner's Dilemma and Def-P in the Tragedy of the Commons game.

Mutual belief:

A proposition A is mutual belief among a set of agents if each agent believes that A. Mutual belief by itself implies nothing about what, if any, beliefs anyone attributes to anyone else (Vanderschraaf 2002).

Nash equilibrium: (Nash 1951):

a set of strategies such that no player, knowing the strategy of the other(s), could improve their expected payoff by changing their own.

Outcome:

a particular combination of strategies, one for each player, and their associated payoffs. In the one-shot games studied in this paper, an outcome corresponds to a cell in the payoff matrix.

Pareto inefficient:

An outcome is Pareto inefficient if there is an alternative in which at least one player is better off and no player is worse off.

Strictly dominated strategy:

For an agent A, strategy S_A is strictly dominated by strategy S^*_A if for each feasible combination of the other players' strategies, A's payoff from playing S_A is strictly less than A's payoff from playing S^*_A (Gibbons 1992, p. 5).

Tit-for-Tat (TFT):

This is the strategy consisting of starting cooperating, and thereafter doing what the other player did on the previous move.

Appendix B

Statement a):

The outcome of any game played by Agents using a CBRE algorithm is necessarily a strictly undominated outcome^[22].

Proof.

If an Agent has selected a certain action using a CBRE algorithm, it means that for any other feasible action A there exists an outcome in which the decision-making Agent selects A and gets an equal or lower payoff, so the Agent cannot guarantee a higher payoff by switching action. Every Agent has used a CBRE algorithm, so it is true that no player can be guaranteed a higher payoff by switching to another action. Therefore the outcome is strictly undominated.

Statement b):

Any strictly undominated outcome can be the outcome of a game played by Agents using a CBRE algorithm.

Proof.

The statement is proved by construction. In a given strictly undominated outcome Φ, any player can identify at least one outcome for each of the non-selected actions in which their payoff would be equal to or less than their payoff in Φ. For each player i, let T_i be the set of outcomes made up of: (1) the given strictly undominated outcome Φ; and, (2) one outcome for each of the non-selected actions in which the payoff for the decision maker is equal to or less than the payoff for the decision maker in Φ. For each player i, let D_i be the decision making algorithm that uses the set of outcomes T_i and returns the action selected by player i in the strictly undominated outcome Φ. For every i, D_i is a particular type of CBRE algorithm and the outcome of the game when played by Agents using D_i would be the given strictly undominated outcome Φ.

References

AAMODT A and Plaza E (1994) Case-Based Reasoning: Foundational Issues, Methodological Variations, and System Approaches. AI Communications. IOS Press, Vol. 7, no. 1, pp. 39-59.

AUMANN R (1976) Agreeing to disagree. Annals of Statistics, no. 4, pp. 1236-1239.

AXELROD R (1984) The Evolution of Cooperation. Basic Books, USA.

BENDOR J, Diermeier D and Ting M (2003) The Predictive Power of Learning Models in Social Dilemma Research. Working Paper, Stanford University.

BRENAN G and Lomasky L (1984) Inefficient Unanimity. Journal of Applied Philosophy, 1, pp. 151-163.

CAMERER C F (2003) Behavioral Game Theory: Experiments in Strategic Interaction. Princeton University Press.

CHAVALARIAS D (2003) Human's Meta-cognitive Capacities and Endogenization of Mimetic Rules in Multi-Agents Models. Presented at the First Conference of the European Social Simulation Association, Groningen, The Netherlands, 18-21/9/03. Conference proceedings available online.

COLLINS (2000) The Collins English Dictionary. HarperCollins Publishers.

COLMAN A M (1995) Game Theory and its Applications in the Social and Biological Sciences. 2nd edition. Butterworth-Heinemann, Oxford, UK.

COLMAN A M (2003) Cooperation, psychological game theory, and limitations of rationality in social interaction. The Behavioral and Brain Sciences, 26, pp. 139-153.

CONTE R and Paolucci M (2001) Intelligent social learning. JASSS - the Journal of Artificial Societies and Social Simulation, Vol. 4, no. 1. Website publication as at 9th March 2004: https://www.jasss.org/4/1/3.html

COPI I M (1986) Introduction to Logic. Seventh Edition. Macmillan, New York.

DAWES R M (1980) Social Dilemmas. Annual Review of Psychology, pp. 161-193.

DIEKMANN A (1985) Volunteer's Dilemma. Journal of Conflict Resolution, 29, pp. 605–610.

DIEKMANN A (1986) Volunteer's Dilemma. A Social Trap without a Dominant Strategy and some Empirical Results. In Diekmann A and Mitter P (Eds.), Paradoxical Effects of Social Behavior — Essays in Honor of Anatol Rapoport, pp. 187-197. Heidelberg: Physica.

DORAN J (1997) Analogical Problem Solving. In: Bundy A (Ed.) Artificial Intelligence Techniques: A Comprehensive Catalogue. Springer-Verlag, fourth revised edition, p. 4.

EREV I and Roth A E (1998) Predicting How People Play Games: Reinforcement Learning in Experimental Games with Unique, Mixed Strategy Equilibria. American Economic Review, 88, 4, pp. 848-881.

FLACHE A and Macy M W (2002) Stochastic Collusion and the Power Law of Learning. Journal of Conflict Resolution, Vol. 46, no. 5, pp. 629-653.

FUDENBERG D and Levine D (1998) The Theory of Learning in Games. MIT Press, Cambridge, MA.

GIBBONS R (1992) A Primer in Game Theory. FT Prentice Hall, Harlow (England).

GILBOA I and Schmeidler D (1995) Case-Based Decision Theory. The Quarterly Journal of Economics, 110, pp. 605-639.

GILBOA I and Schmeidler D (2001) A Theory of Case-Based Decisions. Cambridge University Press, Cambridge, UK.

GOTTS N M, Polhill J G and Law A N R (2003) Agent-Based Simulation in the Study of Social Dilemmas. Artificial Intelligence Review, 19, pp. 3-92.

HARDIN G (1968) The Tragedy of the Commons. Science, 162, pp. 1243-1248.

IZQUIERDO L R, Gotts N M and Polhill J G (2003) Case-Based Reasoning and Social Dilemmas: an Agent-Based Simulation. Presented at the First Conference of the European Social Simulation Association, Groningen, The Netherlands, 18-21/9/03. Conference proceedings available online.

KAHNEMANN D, Slovic P and Tversky A (Eds.) (1982) Judgement Under Uncertainty: Heuristics and Biases. Cambridge University Press.

KLEIN G A and Calderwood R (1988) How Do People Use Analogues to Make Decisions?. In: Kolodner J L, (Ed.) Proceedings of the DARPA Case-Based Reasoning Workshop, Morgan Kaufmann, Calif., US.

KREPS D, Milgrom P, Roberts J and Wilson R (1982) Rational Cooperation in the Finitely Repeated Prisoners' Dilemma. Journal of Economic Theory, 27, pp. 245-252.

KUHN S (2001) Prisoner's Dilemma. The Stanford Encyclopedia of Philosophy (Winter 2001 Edition), Edward N Zalta (Ed.). Website publication as at 9th March 2004: http://plato.stanford.edu/archives/win2001/entries/prisoner-dilemma/

LEDYARD J O (1995) Public Goods: A Survey of Experimental Research. In Kagel J H, and Roth A E (Eds.), The Handbook of Experimental Economics. Princeton University Press.

LOUI R (1999) Case-Based Reasoning and Analogy. The MIT Encyclopedia of the Cognitive Sciences, Wilson R A and Keil F C (Eds.), pp. 99-101.

LUCE D and Raiffa H (1957) Games and Decisions. New York: Wiley.

MACY M W (1990) Learning Theory and the Logic of Critical Mass. American Sociological Review, Vol. 55, pp. 809-26.

MACY M W (1991) Learning to Cooperate: Stochastic and Tacit Collusion in Social Exchange. American Journal of Sociology, Vol. 97, pp. 808-43.

MACY M W (1995) PAVLOV and the Evolution of Cooperation. An Experimental Test. Social Psychology Quarterly, Vol. 58, No 2, pp. 74-87.

MACY M W (1998) Social Order in Artificial Worlds. JASSS - the Journal of Artificial Societies and Social Simulation vol. 1, no. 1. Website publication as at 9th March 2004: https://www.jasss.org/1/1/4.html

MACY M W and Flache A (2002) Learning Dynamics in Social Dilemmas. Proceedings of the National Academy of Sciences, vol. 99, Suppl. 3, pp. 7229-7236

NASH J (1951) Non-cooperative Games. Annals of Mathematics, 54, pp. 285-295.

NICOLOV N (1997) Case-based Reasoning. In: Bundy A (Ed.) Artificial Intelligence Techniques: A Comprehensive Catalogue. Springer-Verlag, fourth revised edition, 1997, pp.13-14.

NOWAK M A and May R M (1992) Evolutionary Chaos and Spatial Games. Nature, 359, pp. 826-829.

RAUB W (1988) An Analysis of the Finitely Repeated Prisoners' Dilemma. European Journal of Political Economy, 4 (3), pp. 367-380.

RAUB W and Voss T (1986) Conditions for Cooperation in Problematic Social Situations. In Diekmann A and Mitter P (Eds.), Paradoxical Effects of Social Behavior — Essays in Honor of Anatol Rapoport, pp. 85-103. Heidelberg: Physica.

REISBERG D (1999) Learning. The MIT Encyclopedia of the Cognitive Sciences, Wilson R A and Keil F C (Eds.), pp. 460-461.

ROSS B (1989) Some Psychological Results on Case-based Reasoning. In Hammond, K (Ed.), Proceedings of the Case-Based Reasoning Workshop, pp. 144-147 San Mateo. DARPA, Morgan Kaufmann, Inc.

ROTH A E (1995) Introduction to Experimental Economics. In: Kagel J H and Roth A E (Eds.), The Handbook of Experimental Economics. Princeton University Press.

ROTH A E and Erev I (1995) Learning in Extensive-Form Games: Experimental Data and Simple Dynamic Models in the Intermediate Term. Games and Economic Behavior, Special Issue: Nobel Symposium, vol. 8, pp.164-212.

SALMON M (1984) Introduction to Logic and Critical Thinking. Harcourt Brace Jovanovich.

SCHANK R (1982) Dynamic Memory: a Theory of Reminding and Learning in Computers and People. Cambridge University Press, Cambridge, UK.

SCHANK R and Abelson R P (1977) Scripts, Plans, Goals and Understanding. Lawrence Erlbaum Associates, Hillsdale, New Jersey.

SIMON H A (1957) Models of Man: Social and Rational; Mathematical Essays on Rational Human Behavior in a Social Setting, John Wiley and Sons, New York.

VAN DAMME E (1987) Stability and Perfection of Nash Equilibria. Springer Verlag, Berlin (2nd ed. 1991).

VANDERSCHRAAF P (2002) Common Knowledge. The Stanford Encyclopedia of Philosophy (Summer 2002 Edition), Edward N Zalta (ed.). Website publication as at 9th March 2004: http://plato.stanford.edu/archives/sum2002/entries/common-knowledge/

WATSON I (1997) Applying Case-Based Reasoning: Techniques for Enterprise Systems. Morgan Kaufman Publishers.

WEIBULL J W (1995) Evolutionary Game Theory. MIT Press.

WEIBULL J W (1998) Evolution, Rationality and Equilibrium in Games. European Economic Review, 42, pp. 641-649.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2004]