P.C. Buzing, A.E. Eiben and M.C. Schut: Emerging communication and cooperation in evolving agent societies

P.C. Buzing, A.E. Eiben and M.C. Schut (2005)

Emerging communication and cooperation in evolving agent societies

Journal of Artificial Societies and Social Simulation vol. 8, no. 1
<https://www.jasss.org/8/1/2.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary

Received: 12-Dec-2003 Accepted: 20-Sep-2004 Published: 31-Jan-2005

Abstract

The main contribution of this paper is threefold. First, it presents a new software system for empirical investigations of evolving agent societies in SugarScape like environments. Second, it introduces a conceptual framework for modeling cooperation in an artificial society. In this framework the environmental pressure to cooperate is controllable by a single parameter, thus allowing systematic investigations of system behavior under varying circumstances. Third, it reports upon results from experiments that implemented and tested environments based upon this new model of cooperation. The results show that the pressure to cooperate leads to the evolution of communication skills facilitating cooperation. Furthermore, higher levels of cooperation pressure lead to the emergence of increased communication.
Keywords:: Social Simulation, Communication, Cooperation, Artificial Societies

Introduction

1.1: The research presented in this paper is concerned with the emergence of communication and cooperation in an artificial society. The main objective is to investigate the evolution of communication between agents under various levels of "cooperation pressure".
1.2: Our experiments take place in a specific artificial world. This world is based on the standard SUGARSCAPE (Epstein and Axtell 1996) model, but differs from it in many aspects. For instance, sugar is periodically redistributed, thereby forcing agents to explore the sugar landscape in search for food. Furthermore, the world is set up in such a way that it includes a cooperation pressure. This feature is based on two premises regarding cooperation. First, we want a model where cooperation does not result in producing new resources (sugar). As such, cooperation here has a mixed positive-negative effect. On the one hand, acting in concert enables agents to consume resources that they could not consume alone. On the other hand, each act of cooperation means that resources (a "meal") have to be shared. Thus, in some sense we are modelling a society of hunters and gatherers rather a society of farmers. Our second requirement is that the model allows for scaling the cooperation pressure by a parameter. This is motivated by the intention of studying the effects of a varying cooperation pressure in a systematic way. The model we invented to satisfy these requirements is based on postulating that an agent alone can only harvest small amounts of sugar and it takes at least two agents to consume a large pile. If two or more agents are at such a large pile, they eat the sugar together, sharing the total amount equally. The cooperation pressure parameter here is the maximum amount of sugar an agent can consume alone. Lower values of this parameter imply a heavier pressure for cooperation.
1.3: Agents are equipped with special new features to meet the challenges of this world. The traditional SUGARSCAPE vision system to obtain information about the world is extended with the capability to communicate. In particular, agents are given the possibility to "call for assistance'' if they encounter a sugar pile too large to be eaten alone. By agents reporting their location and the amount of sugar there, communication facilitates cooperation: it enables purposeful as opposed to random encounters at large sugar piles. The main assumption of our approach regarding this feature is that the possibility to "talk" is hard-wired in the system by a communication protocol, but agents might not use this feature. "Talkativeness" is an agent property that is subject to adaptation through evolution. In other words, a "talkativeness gene" determines to what extent a given agent is willing to talk to others. The populations' communication attitude develops according to an artificial evolution approach by variation (crossover and mutation) and natural selection. The same holds for "listening" on the other end of the communication channel. Here the agents that do receive information from others might or might not use this information when deciding where to go next. This feature is also controlled by a gene that is evolving over time.
1.4: Our main research objective can now be specified as follows: To study the development of the agents' communication attitude (talk/listen gene distributions) and cooperative behaviour (eating together) under varying levels of cooperation (maximum amount of sugar they can eat alone).
1.5: Our notion of cooperation is rooted in the environment. It is interesting to mention that our approach is complementary to some of the classics. Namely, we study the emergence of communication under fixed properties of cooperation (hard-coding its mechanics), while many studies focus on the emergence of cooperation under fixed properties of communication (see for instance Axelrod (1997), which assumes there is none.
1.6: While existing work concentrates on how cooperation emerges (as mentioned above) or how agents actually (have to) cooperate (coordination in multi-agent systems), our work focuses on the emergence of communication. In follow-up studies, we are interested in when, what and how agents have to communicate when the environment in which they are situated requires this. The work presented here is a first step towards this research goal. From this perspective, the investigation in this paper studies when agents communicate in an environment under varying levels of cooperation pressure. Although we have now fixed the content and how they communicate, this is an area to be explored in future in combination with social sciences and evolutionary linguistics.
1.7: Our work can be interpreted from a societal perspective. Our system models (some facets of) real-life situations, where there is no conflict of interest, the benefits of cooperation are equal for all agents involved, and cooperation does not lead to creating new resources. In this sense, our model of cooperation does not cover agriculture, but rather hunting together where the prey must be shared afterwards. Furthermore, communication has no costs, the language is extremely simple (signalling) and talking is mainly unintentional. That is, whether an agent talks in a certain situation does not depend on the situation, but solely on the genetically encoded "talkativeness'' of the agent and a random choice. All in all, our model reflects features of animal or pre-human collectives and allows investigating the evolution of talkativeness under varying levels of hardness of the world, i.e. varying levels of pressure to cooperate. We distinguish the willingness to talk and the willingness to listen and introduce separate genes for these properties. Consequently, we can independently monitor the evolution of talking and listening preferences under the different circumstances.
1.8: This paper is organised as follows. In Section 2 we briefly discuss background work on cooperation and communication in artificial intelligence and artificial societies. Section 3.1 presents the experimental platform JAWAS, while Section 3.2 describes our present model of the artificial world and the agents. In Section 4 we lay out the methodology and parameter settings of the experiments and Section 5 presents the experimental results and their analyses. Finally, Section 6 discusses further work and Section 7 concludes the paper.

Background

2.1: Our research can be positioned in a broader context, that of artificial societies. We let artificial societies be agent-based models of social processes (Epstein and Axtell 1996). This definition brings with it some notion of agents (the "people'' of the artificial society), simulation (models are computationally executed to explore societal phenomena) and social structures (the macroscopic behaviour of a group of interacting individuals).
2.2: Studies of artificial societies have two aims (Gilbert and Conte 1995). Firstly, they demonstrate the practice of using computer simulation to develop ideas and theories in a range of social science disciplines. Secondly, they explore the methodological implications of using computers to create societies of computational agents whose properties can be investigated.
2.3: A number of different sets of properties of artificial societies have been identified. For example, Artikis and Pitt (2001) have adopted a society model on the basis of the following requirements: 1) a need to make the organisational and legal elements of a multi-agent system externally visible, 2) open societies should be neutral with respect to the internal architecture of their members, and 3) communication and conformance of behaviour are at least as important as intelligence. An agent society based on this model consists of 1) a set of agents, 2) a set of constraints on the society (norms and rules), 3) a communication language, 4) a set of roles that agents can play, 5) a set of states the society may be in, and 6) a set of owners of the agents. In addition, Davidsson (2001) has extended this set by 7) the owner of the society.
2.4: Epstein and Axtell (1996) let an artificial society consist of 1) agents, 2) an environment or space, and 3) rules. An agent then has internal states and behavioural rules, which each can be fixed or flexible. Interactions and changes of internal states depend on rules of behaviour for the agents and the space. Environments can be abstractly defined (e.g., a communication network) or more resemble our own natural environment (e.g., a lattice of resource-bearing sites). The environment is a medium separate from agents, on which the agents operate and with which they interact. Rules can be defined to describe the behaviour of agents and the environment on different interaction levels, i.e., agent-environment (e.g., agents looking for and consuming food), environment-environment (e.g., growing resources), and agent-agent (e.g., combat and trade). Our work belongs to this view of an artificial society.
2.5: Finally, properties can be identified that an artificial society must support to different degrees (Davidsson 2001). These properties are 1) openness - possibility for agents to join the society, 2) flexibility - degree to which agents are restricted in their behaviour by the environment, 3) stability - predictability of the consequences of actions, and 4) trustfulness - extent to which agents trust the society. With this properties, it is possible to categorise societies. A society that has each of these properties to high degrees is an information ecosystem. Two more differentiated types of societies are open and closed ones. An open society is normally one with high degrees of openness and flexibility and low degrees of stability and trustfulness. A closed society is one which excels in stability and trustfulness and scores lower on openness and flexibility. Extremes on both ends are anarchic and fixed societies, respectively. Davidsson (2001) coins the idea of semi-open and semi-closed societies attempting to bridge the two extremes. A semi-open society is one in which the agents are implemented and run locally. Such a society has one particular type of agent (called the gate-keeper) that regulates how agents join the society. A semi-closed society is one in which the agents are implemented and run on remote servers. In this society, external agents may not join the society, but can initiate a new agent that acts on their behalf.
2.6: As mentioned in the Introduction, our interpretation of cooperation differs from that of the main stream, which is oriented to evolving cooperation strategies. This "conventional" stream started with the early developments of game theory in the 1940s and 50s. The phenomenon of cooperation was put onto strong footing by the social scientist Axelrod in his seminal work The Evolution of Cooperation (Axelrod 1984). The model under investigation in Axelrod's simulation is the (iterated) prisoner's dilemma game (PD) (Rapoport and Chammah 1965). This game involves two players who can cooperate or defect. Each must choose without knowing the other's choice. Independent of what the other does, defection gives a higher payoff than cooperation. The dilemma is that if both defect, they both are worse off than if they both cooperated. An important aspect of the PD is that the interests of the players are not strictly opposed, cooperation may mean mutual benefit, and cooperation comes at some individual cost.
2.7: Axelrod extends the game to a n-person game in Axelrod (1997). In the context of this paper, this places the game into the field of artificial societies. The n-person game is one in which a society of agents interacts through the iterated PD. The apparent problem with this extension is one of stability: as individuals are not constantly playing with the same player, it is not possible to 'punish' or 'reward' (the same) opponents. This would make stability of cooperation impossible. However, it is observed that nevertheless social norms emerge, enabling the sustaining of cooperation in such societies. For a detailed game-theoretical review of Axelrod's work, see Binmore (1998).
2.8: The research described in this paper assumes the existence of a simple communication system and looks at the interaction of this system with the cooperation between agents. Much research on the evolution and emergence of communication is focused on investigating the development and evolution of the syntax and semantics of communication systems. A recent review by Perfors (2002) of the simulation of language evolution distinguishes between theories of languages and simulations; additionally, within the area of simulations a distinction is made between the evolution of syntax and the evolution of communication and coordination. Our research falls into the last category. However, the review considers individual (reinforcement) learning as the evolution of communication and coordination. Our work concerns this evolution in a truly evolutionary sense - by means of evolutionary learning, communication is learned by the society.
2.9: Perfors concludes that just by theorizing on the innate versus acquisition questions, it is difficult to provide clarity on what is exactly evolving and what characteristics of the environment and organism are necessary to explain observations. Thus computational simulation tools are necessary. Much of the work on computational simulation of language evolution can be categorised into the emergence of syntax, the emergence of coordinated communication, or, more generally, on the innateness of language. The emergence of coordinated communication is most related to our work described here. This body of work is concerned with questions like how stable systems of communication arise, given constraints that influence the agents and their environment.
2.10: As far as the coordination of communication is concerned, the work of Oliphant and Batali (1996) is closely related to our work. They have researched the emergence of coordinated communication and developed a number of learning procedures to be used by new members of a society for communicating. Motivated by questions on coordinated communication in animal societies, e.g. vervet monkeys, the authors present a formal investigation of the emergence of communication among animals capable of producing and responding to simple signals. Additionally, computational simulations illustrate how such coordination can be maintained when new members learn to communicate by observation. This formal model consists of a population of individuals that can recognise a set of situation types with a distinct, appropriate response to each. A set of 'signals' is available to the individuals containing a set of distinct types of actions recognizable by others. The communication system is simple - the signals are produced and responded to as individual tokens. (More complex systems, e.g. human communication, involve a more complex and syntactic communication.) To measure the effectiveness of communication, a measurement called 'accurate communication' is introduced. Assuming that agents have send and receive functions to facilitate communication, accurate communication is the probability that signals sent by an individual using its send function will be correctly interpreted by an individual using its receive function.
2.11: Their learning procedures turn out to perform well, because they explicitly take into account the communicative aspects of behaviour, i.e., acquiring appropriate transmission and reception behaviours. Oliphant states that "the most basic explanation for why only humans have language may not lie in the ability of learning a complex syntactic form of communication, but rather in the ability to learn any communication at all" (Oliphant 1997, p. xii). This statement re-emphasises the anthropological motivation of our research rather than the social one.
2.12: Finally, Noble (1999) presents a signalling model assuming some necessary cooperation between signaller and receiver. This cooperation may be with or without conflict. Noble proposes a cost-based model for signalling in order to reconsider the findings of Krebs and Dawkins (1984) stating that conflicts of interest results in ever more costly signals; common interests lead to cheap signals. Experimental investigation of a sequence of signalling games showed that communication does not evolve when there is a conflict of interests between signallers and receivers. Even when signallers and receivers share a common interest, the evolution of communication is still not straightforward. In the common interest cases, the agent strategies are observed to fall into sub-optimal equilibria. Noble also subscribes to the complex nature of cooperation (as described in the introduction) by relating it to communication costs. This basically means that a signaller does not know how its signal will be interpreted by the receiver and, by definition, this always leads to a conflict of interests in communication.
2.13: In conclusion, although the literature on cooperation and communication includes many pointers to related work, we fix the necessity for individuals to cooperate in the environment and investigate the emergence of communication; secondly, we study the evolution of communication itself rather than the evolution of syntax and/or semantics.

VUScape

3.1

The artificial world used in this paper is a generic test bed for social simulation called VUSCAPE (Buzing et al. 2003), which is based on SUGARSCAPE (Epstein and Axtell 1996). For the purpose of the study described in this paper, we altered the physical and biological laws of SUGARSCAPE world in a number of ways. The adaptations extend the SUGARSCAPE domain in an interesting generic way, opening up the possibility of investigating SUGARSCAPE worlds in wider perspectives. The VUSCAPE model was investigated in the JAWAS^[1] software environment, which has been developed to function as a test bed to investigate artificial societies.

The JAWAS System

3.2

The JAWAS system (version 1.2.3 was used here) can be compared with existing social simulation software like Ascape (Parker 2000), Repast (Collier 2000) and Swarm (Daniels 1999). All settings in JAWAS can be specified either in configuration files or by command line arguments. This enables the user to automate experiments, which substantially speeds up the time needed for, for example, investigating effects of varying experimental parameters (often requiring a large number of runs). Data are automatically saved at specified locations, enabling detailed experimental logging. Thorough statistically based experimental research on complex systems that depend on numerous parameters requires a large number of runs. Facilitating this is one of the main design objectives of JAWAS. It is very easy to add, replace or delete code when changes or extensions to the model need to be implemented. No direct connection is necessary between the program and the graphical user interface. Initial exploration can use the graphical user interface; for automated experimentation, the system can be run solely with configuration files or from the command line. JAWAS is implemented in Java. We intended for JAWAS to be such a flexible and modular system that it will allow the user to implement different world and agent models easily.

3.3

In the research described here, we monitor a selected number of variables to generate our findings. Although a number of monitors have been predefined, it is possible in JAWAS to put a monitor on every numeric variable in the source code. If a variable is monitored, this means that every execution cycle, the value^[2] of the variable is recorded. In Table 1 we briefly enumerate the predefined monitors. Generally, monitors refer either to variables within the agent or within the world.


Table 1: An overview of VUSCAPE monitors

Type	Name	Denotes	Domain
Agent	age	age of the agent	[0:100]
Agent	listenPref	whether agent listens	[0:1]
Agent	talkPref	whether agent talks	[0:1]
Agent	sugarAmount	sugar contained by an agent	[0:∞]
Agent	inNeedOfHelp	percentage of agents on sugar > coopThresh	[0:1]
Agent	cooperating	percentage of agents that cooperates	[0:1]
Agent	exploreCell	percentage of agents that moved to a new cell	[0:1]
Agent	hasEaten	amount of food that agent has eaten	[0:4]
World	numberOfAgents	number of agents	[0: ∞]
World	numberOfBirths	number of just born agents	[0: ∞]
World	numberOfDeaths	number of just died agents	[0: ∞]

The Model

3.4

This section describes the VUSCAPE artificial world from three different viewpoints, those of the simulation, the world and the agent. Firstly, the extensions that VUSCAPE makes to the traditional SUGARSCAPE are explained. Secondly, the simulation part of VUSCAPE is discussed, including the simulation execution cycles and monitors that can be set. Thirdly, we present the world as it exists within the simulation. Finally, we explain the agents that live in the world.

Extensions to SugarScape

3.5

Like SUGARSCAPE, the VUSCAPE world is a two dimensional grid, wrapped around the edges. Each position corresponds with an area which can contain multiple agents and pieces of sugar. We made the following physical (world) and biological (agents) adaptations to the SUGARSCAPE world:

Randomised sugar distribution (physical) - The conventional sugar distribution in SUGARSCAPE is based on two sugar-hills that are located in the world at some distance from each other. In this world sugar is concentrated and grows back at the given location making passive (i.e., not too mobile) agents viable. As we are interested in exploration behaviour, we initially distribute so called sugar seeds randomly over the grid and move a seed to another random location if its sugar has been eaten.
Co-location (physical) - We allow for multiple agents to be at a single grid-point in VUSCAPE, whereas this is not allowed in SUGARSCAPE.
Cooperation (physical) - Cooperative behaviour of agents is stimulated by means of setting a maximum amount of sugar that an agent can eat on its own. This puts a restriction on sugar consumption. The maximum amount of sugar can be set by the cooperation threshold (CT) parameter. A single agent can only harvest small amounts of sugar (less than CT sugar units) and it takes at least two agents to consume a large pile (more than CT sugar units). If two or more agents are at such a large pile, they share the sugar equally.
Randomised age initialisation (biological) - In SUGARSCAPE models, the age parameter of agents is initialised uniformly (at 0). This brings with it some surprising phenomena that are not necessarily realistic. Additionally, the effects of such a setup echoes through the whole simulation until finished. We initialise the ages of agents randomly (between fixed minimum and maximum values), thereby preventing methodological errors resulting from initialisation at 0.
Communication (biological) - Agents receive information from other agents about amounts of sugar at their locations (listen) and multicast (talk) about the amount of sugar at their own location.
Explorative Behaviour (biological) - In VUSCAPE agents randomly move around where they do not know of any sugar to move to or to eat. In SUGARSCAPE, agents do not exhibit such behaviour but stay at their locations in such situations.

3.6

We have investigated the effects of each of the items above experimentally (Buzing et al. 2003). For example, it can be hypothesised that the consequences of a uniform initialisation (as in SUGARSCAPE) include the population growing old simultaneously, generating offspring simultaneously, generations dying out simultaneously, etc. Hence, observations of oscillating phenomena may be explained as an artefact, rather than having a realistic counterpart in natural societies.

3.7

We can divide the extensions according to whether a change is methodological or experimental. For example, the moving sugar seeds and randomised age initialisation are methodological, and we do not explore their effects, but only investigate worlds that work according to these modifications. On the other hand, the cooperation pressure parameter and communication are experimental extensions, and we describe their effects in Section 4.

Execution Cycles

3.8

The VUSCAPE world evolves with discrete time steps, called cycles. The following stages take place in chronological order within a single execution cycle (see Figure 1). During a single cycle, all stages are executed for each agent in parallel^[3].

An agent gathers information about the distribution of sugar in the world. This is done by means of listening (to other agents) and looking (at the directly surrounding locations and the current location). Upon completion of this stage, the agent has at its disposal an array of locations and amounts of sugar on these locations.
Based on this array, the agent makes a decision about its next action. In particular, it chooses a location and moves to this location. This location chosen is always the one containing the largest amount of sugar. If there are more than one such location, the agent chooses a random one^[4].
Having arrived at the sugar, this sugar is harvested in case the amount is under the cooperation threshold. If the amount is above the cooperation threshold, the agent cooperates immediately if there are more agents at the location. Otherwise, it multicasts (with some probability) to other agents that it needs help.
If possible, the agent reproduces and generates offspring. For this, it is (at least) necessary that there is another agent of the opposite sex at the location. (There are also other conditions for reproduction, and these are discussed in detail below.)

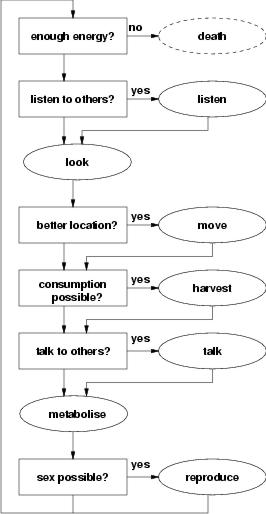Figure 1. The agent control loop in VUSCAPE

World Variables

3.9

A world in VUSCAPE has specific features that can be set as parameters. The initial population size can be set. As in SUGARSCAPE, this is set to 400. An initial population is usually half female, half male. The width and height of the world can be set, our default is 50 × 50 . Finally, the sugar grow-back rate determines at the rate which sugar grows back in the world.

3.10

Sugar is randomly distributed over the world during initialisation. The amount of sugar can be set by the sugar richness parameter: this is the average amount of sugar at each location. A sugar richness of 1.0 means that 2,500 units of sugar are distributed. Sugar grows from sugar seeds. Each sugar seed has a maximum amount of sugar it can grow back to after consumption. For example, when a sugar seed with maximum 4 is consumed, it grows back to 4 until consumed again. This can be set by a parameter; usually, one allows for sugar seeds with maximum levels 1, 2, 3 and 4. It is possible that there are more seeds per location. Each seed is initialised with its maximum sugar amount, achieving the initial sugar richness as desired. We initialise in such a way that the number of sugar seeds is equal for all maximum grow-back values^[5].

3.11

A parameter allows to switch on or off whether seeds are moved to another location after consumption. By doing this, we stimulate agents to travel more to other locations. For example, when the parameter is on, it is not possible for an agent to stay put at a sugar seed that is sufficient to feed the agent; instead, the agent is challenged to find better locations.

Agent Variables

3.12

An agent consists of and possesses some particular features. A number of these features have been taken directly from the original SUGARSCAPE model including metabolism, gender, child bearing, death, vision, reproduction and selection. Additionally, we extended these features by including a reproduction threshold and an initial amount of sugar.

3.13

As agents need energy (here: sugar) to reproduce, VUSCAPE offers the possibility to set the amount of sugar needed for mating by setting the reproduction threshold. If the amount of sugar contained in an agent is over this threshold, then (in prevailing circumstances) this agent is able to reproduce. The offspring of two parents receives half of each parent's sugar at birth. Whereas in SUGARSCAPE, the reproduction threshold (called endowment in SUGARSCAPE) has the same value as the initial amount of sugar an agent received, the VUSCAPE implementation enables one to set this parameter independently of the initial amount of sugar.

3.14

Our agent society forms an evolving system because the individual agents undergo environmental selection and reproduction (Eiben and Smith 2003). The system has environmental selection because agents that run out of sugar die. Agents reproduce as in the original SUGARSCAPE. Reproduction is not subject to individual decisions, nor is there any mate selection. If all conditions are satisfied for two agents, they will always mate and generate offspring. These conditions are that firstly two agents are on the same location or next to each other (vertically or horizontally, not diagonally). Additionally, it is required that the genders differ, both their sugar levels are above the reproduction threshold, they are both in the fertile age range, and there is a vacant cell in the vicinity for placing the offspring. Reproduction takes place by crossover applied to two parents yielding the child, followed by a mutation operator on the child. The talk and listen genes express probabilities and are formally real valued numbers between 0 and 1. The value of a gene in a child is determined by applying recombination and thereafter a Gaussian mutation. That is, the final value is x + d, where x is the inherited value and d is a random number drawn from a Gaussian distribution with zero mean and standard deviation σ (similar to Hales (2002)). The preferences for talking and listening are both inherited from the wealthiest parent (the one with most sugar). Finally, the child receives from each of the parents half of their sugar. The child inherits each of the values for vision, age of death, metabolism, and child bearing independently from one of the parents without change as by uniform crossover. After mating, each agent has a so-called recovery period, which is the number of cycles after mating that an agent cannot mate.

3.15

To illustrate the process of reproduction, consider the following example (without mutation). Two agents are next to each other — one with 24 sugar units, a listen preference of 0.7 and a talk preference of 0.55; the other has 16 sugar units, a listen preference of 0.6 and a talk preference of 0.5. A child of these two agents gets its listen and talk preferences from the first agent (0.7 and 0.55 respectively). Its initial sugar amount is the sum of half of the sugar amounts of each of the parents, thus 12 from the first parent and 8 from the second parent — its initial sugar amount is thus 20.

3.16

Finally, two features of an agent determine its communicative behaviour, namely the features to talk and to listen. The listen feature is used in the observation process of the agent. By listening, the agent receives information from other agents about the amounts of sugar at the locations of those agents. The talk feature determines whether the agent performs a communicative action itself, namely multicasting to other agents: 1) the amount of sugar that is at its location, and 2) the coordinates of its location. After initialisation, the average talk preference over all agents is 0.5. With a preference p, an agent multicasts the amount of sugar at its location with probability p if it needs help to harvest the sugar at its location.

Experiments

4.1

We describe a series of experiments in which we investigate the complex relation between communication and cooperation in the VUSCAPE test bed. This Section presents the experimental methodology and the parameter settings used.

Method

4.2

The aim is to investigate the response of the agent population (in term of communication skills) to an increased need for cooperation. As described above, agents in VUSCAPE have communicative capabilities with which they can multicast local information about the amount of sugar at their location and receive global information about amounts of sugar at other locations. The need for cooperation is imposed in that agents cannot consume large amounts of sugar on their own, but rather need other agents to consume such large quantities together. Next, we describe in more detail our definitions of communication and cooperation as implemented in the experiments.

Communication

Figure 2. Communication in VUSCAPE over the axes. In this example, agent A multicasts information, which can be received by agents B and C

4.3

Communication between agents in the series of experiments described here is implemented by messages from agents which travel only parallel to the axes. The reason for this is that the agents can only move horizontally or vertically but not diagonally. The agents can therefore only receive messages from locations to which they could jump. Figure 2 shows agent A multicasting a message, which is subsequently received by agents B and C. If there are other agents in the world that are not on the same row or column as agent A, they will not receive messages from agent A.

4.4

The communication is implemented through a centralised message-board. Agents can post their messages to this board (talking) and they can read messages from this board (listening).

4.5

We decided on three ways for messages to be removed from the message-board in these series of experiments^[6]. The first method (henceforth called COM1) removes a message from the board once it has been listened to by another agent. In the example shown in Figure 2, assume that agent B receives the message from agent A first^[7]. After agent B has received it, it is removed from the board, and agent C never receives it. The second message removal method (henceforth called COM2) deletes a message from the board when the request contained in the message is fulfilled. Again, assume agent B receives the ''call for assistance'' from agent A first. Furthermore, assume that agent B does not travel to agent A to help out (because, for example, it also knows of another location with more sugar where it prefers to move). In this case, the message is not removed. Next, agent C receives the message, and it subsequently does travel to agent A to help out. Now, the request from agent A has been fulfilled and the message is removed from the board. The third message removal method (henceforth called COM3) deletes a message from the board after a fixed time interval.

Parameter Settings

4.6

In this Section we describe experiments in which the cooperation threshold CT was varied from 0 (every piece of food must be eaten by at least two agents) to 4 (cooperation is never necessary). The values of the other parameters are listed in Table 2.


Table 2: Experimental settings. Parameters not explained in this article are identical to those in SUGARSCAPE

Parameter	Value	Parameter	Value
Height of the world	50	Minimum death age	60
Width of the world	50	Maximum death age	100
Initial number of agents	1000	Minimum begin child bearing age	12
Sugar richness	1.0	Maximum begin child bearing age	15
Sugar growth rate	1.0	Minimum end child bearing age male	50
Minimum metabolism	1.0	Maximum end child bearing age male	60
Maximum metabolism	1.0	Minimum end child bearing age female	40
Minimum vision	1.0	Maximum end child bearing age female	50
Maximum vision	1.0	Reproduction threshold	0
Minimum initial sugar	0.0	Mutation sigma	0.1
Maximum initial sugar	100.0	Sex recovery	0

4.7

As mentioned above, in addition to varying the CT, we also test three options for the communication facility (COM0, COM1 and COM2). Runs with communication use the talk and listen features (COM1 and COM2), runs without communication have them disabled (COM0). In COM3 we ran experiments where messages were removed after some fixed time interval. We fixed these intervals from 1 up to 10 and ran separate experiments for each interval. However, the results of these experiments show that none of the populations survive with any fixed interval and the results have not been included here.

4.8

In the setup presented here, agents in a communicating society evolve their ''talkativeness'' and ''listening'' genes. The independent (fixed) variables are 1) the cooperation threshold CT with values 0, 1, 2, 3, and 4 and 2) the message removal method with methods COM0, COM1 and COM2. The dependent (measured) variables are the population size (Population), the proportion of cooperations of all performed eating actions (Cooperating), the talk preferences of agents (talkPref) and their listen preferences (listenPref). The dependent variables are measured at every time-point. The talk and listen preferences are averaged over the whole population.

Results and Analysis

5.1

In this section, we present and discuss our results arranged by the communication mechanisms. The graphs shown in Figures 3, 4 and 5 each show the outcomes of 10 independent runs superimposed. To save space, only small graphs are plotted to reveal the trends. The reader can find large versions of these and some additional Figures at http://www.cs.vu.nl/ci/eci/. Our experimental data clearly show that turning the ''knob of cooperation pressure" from light to heavy (varying the cooperation threshold from high to low), indeed gradually makes the world a more difficult place for the agents to survive. Furthermore, it is also clear that the populations respond to this effect by evolving increasing skills of communication.

Without Communication (COM0)

	Population	Cooperation
CT=0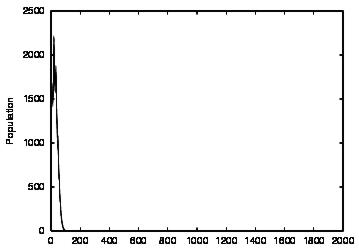
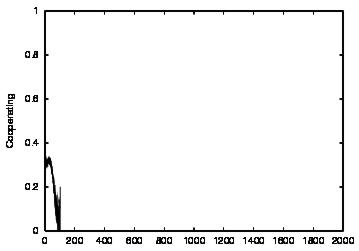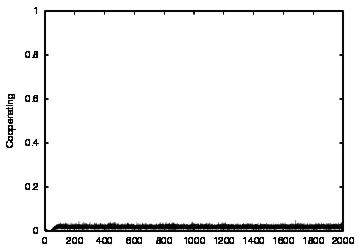
CT=4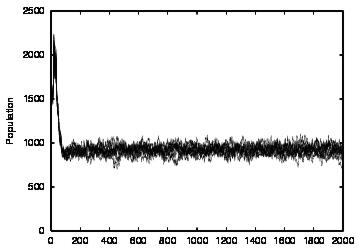
	(a)	(b)
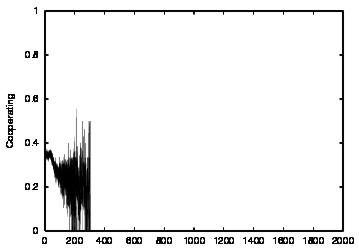
Figure 3. Results for non-learning agents with communication suppressed (COM0). The results are shown for CT = 0 (first row) and CT = 4 (second row). The population size over time is shown in column (a) and the cooperations as a proportion of all performed actions over time is shown in column (b)

5.2

Figure 3 shows the results of the experiments where we suppressed communication. If two agents cooperate in this case, it is by mere chance. Recall that evolution only influences the talk and listen genes. Consequently, in these experiments the populations are non-evolving. We have only selected the plots for CT = 0 (first row in Figure 3) and CT = 4 (second row in Figure 3) for presentation here. For other values the results are very similar to those corresponding to CT = 0, and the populations always die out. For CT = 3, the population dies out around time-step 200; for CT = 2 and CT = 1 the extinction point is around time 120.

5.3

The most important observation here is that even the slightest cooperation pressure makes it impossible for a population to survive. To be more precise, within the range of CT values we consider here (0 - 4), there is only one (CT = 4) that produces viable worlds. When the CT value is lowered, agents are unable to organise themselves and populations die out rapidly. All ten independent runs with different random initial sugar and agent distribution show essentially identical behaviour, indicating that this is a general effect, i.e., the influence of the initial shape of the scape and the agent orientation is negligible.

With Communication (COM1 and COM2)

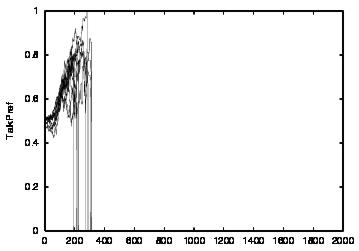
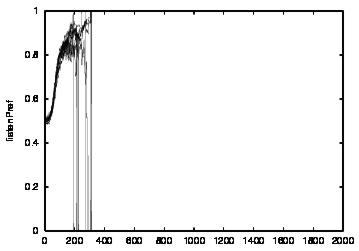
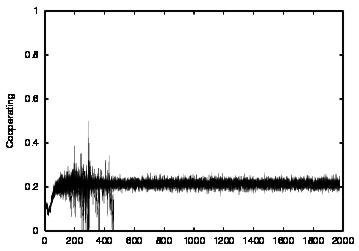
	Population	Cooperation	talkPref	listenPref
CT=0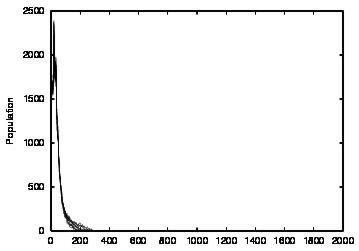
CT=1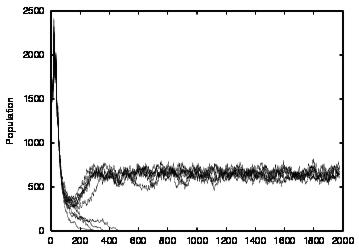
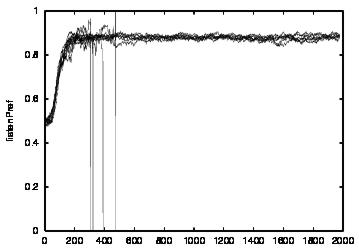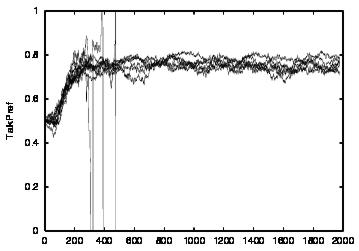
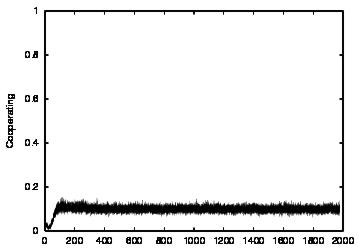
CT=2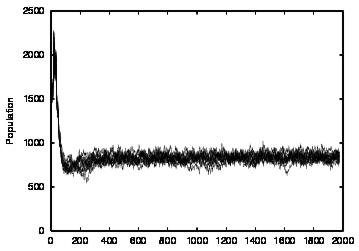
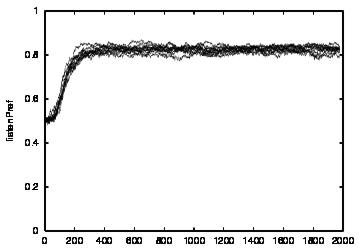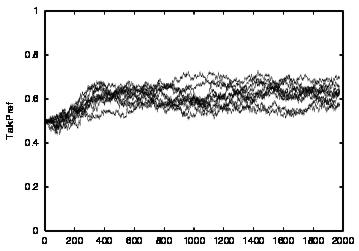
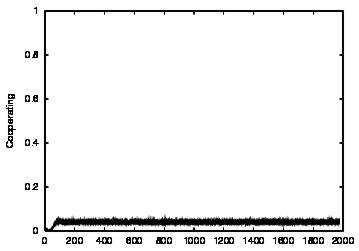
CT=3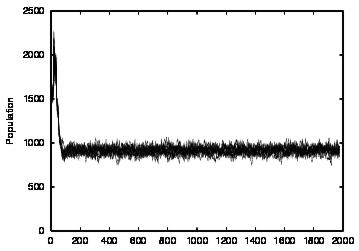
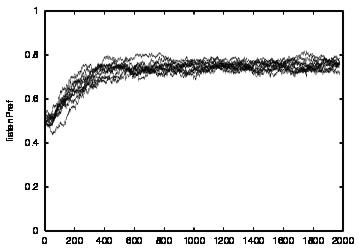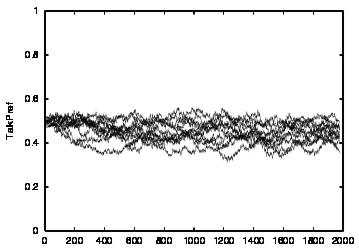
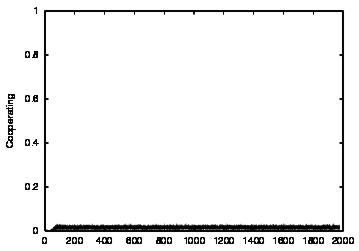
CT=4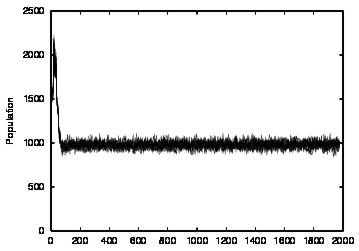
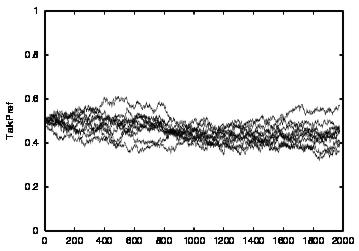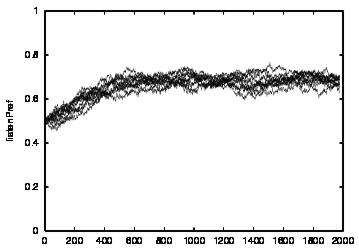	(a)	(b)	(c)	(d)
Figure 4. Results for learning agents with communication enabled and message removal method COM1 active. From top to bottom, the results are shown for CT = 0, 1, 2, 3 and 4. The population size over time is shown in column (a), the proportion of cooperations of all performed actions over time is shown in column (b), the average talk preference of agents is shown in column (c) and the average listen preference is shown in column (d). Each Figure exhibits the results of 10 independent runs overlaid

5.4

Figure 4 shows the results of the experiments where communication is enabled and agents evolve their talk and listen genes. The results shown here are from the series of experiments where we used the COM1 method removal message, thus messages are removed promptly after they have been listened to. The results for CT = 0, 1, 2, 3, and 4 are shown from top to bottom. The population size over time is shown in 4.(a), the proportion of cooperations of all performed actions over time is shown in 4.(b), the average talk preference of agents is shown in 4.(c) and the average listen preference is shown in 4.(d).

5.5

For population size, we observe the same behaviour for CT = 4 of this society as in the society without communication: a short population growth period, followed by a decline and finally leading to a rather constant population size of approximately 1,000 individuals. However, it seems that the population sizes in societies with communication have less variance in the population oscillations. The level of cooperation is consistently near zero, indicating that very little cooperation occurs. Lowering the cooperation threshold (CT = 3) shows an increase in cooperativeness, which is a logical consequence of the increased cooperation pressure. The population sizes are roughly similar to the societies with CT = 4. Further lowering the cooperation threshold (thus increasing the cooperation pressure) results in lower population sizes (approximately 800) that stabilize somewhat later. Furthermore, cooperation levels become consistently higher. For the extreme case in which CT = 0, no population can survive after time 100.

5.6

For talking and listening we observe similar trends as we vary the cooperation pressure. Starting with CT = 4, we see that talkPref tends to decrease slightly, while listenPref grows from 0.5 initially to 0.65 at the end. Apparently, being very talkative does not provide an evolutionary advantage when the cooperation threshold is so high, while listening is a good thing to do. Putting it differently, utilizing information is ''discovered" here as viable strategy, while producing information is not.

5.7

At CT = 3, we observe a marginal drop (with much variance) for talkPref from 0.5 to 0.45. Listening increases strongly during the first 400 iterations, then stabilises at approximately 0.75. We conclude again that talkativeness does not pay off, while listening slowly grows in importance. When we set CT to 2, talkativeness rises, indicating that talkers have an advantage over non-talkers. Listening again grows stronger and stabilises at roughly 0.8 after 300 iterations. For CT = 1, talkPref grows quickly to 0.8 after 300 iterations, and listenPref grows faster to 0.85. In the extreme case where CT = 0, even communication cannot prevent populations from dying out under such high cooperative pressure.

5.8

Summarizing, we observe that communication can really be a matter of life and death. Societies that have the ability to communicate (to talk and to listen) are viable in a significantly wider range of circumstances (surviving for 4 out of 5 CT values) than those without this ability (surviving for 1 out of 5 CT values). With listen cooperation pressure, the population goes through a critical point around iteration 100, but (in most cases) re-establishes itself at around iteration 1,000 at a stable population size of approximately 1,000.

5.9

The populations' behavioural response to increasing cooperation pressure is visible through the increasing number of cooperative acts between agents (shown in Figure 4) and the increasing number of communication acts (not shown here).

5.10

The populations' response on the genotypic level is measured by the average willingness to talk and to listen. Conforming to our intuitive expectations, there is an observable link between increased cooperation pressure and a more positive communication attitude. Roughly speaking, harder worlds cause more communicative populations. However, a surprising outcome of these experiments is that the willingness to listen emerges earlier than the willingness to talk. Note the double meaning of "earlier" here. On the one hand we mean that listening emerges for lower levels of cooperation pressure, while to have talking emerge we need to raise this pressure. On the other hand, for a given CT value, the average values of the listen genes increase faster than those of the talk genes. We plan further work to investigate these outcomes.

	Population	Cooperation	talkPref	listenPref
CT=0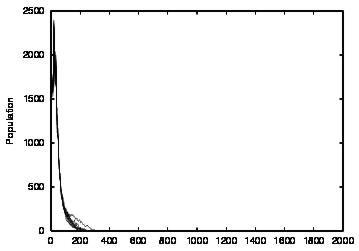
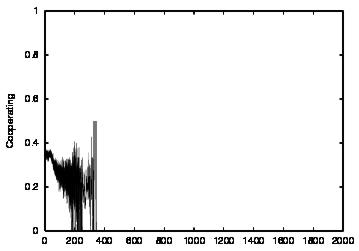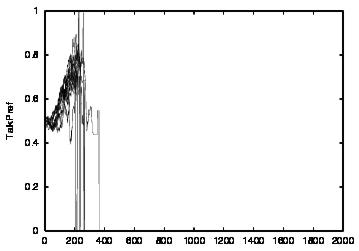
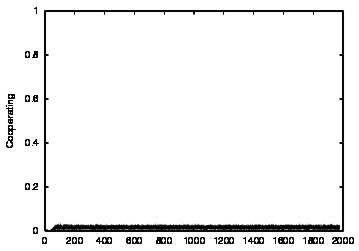
CT=4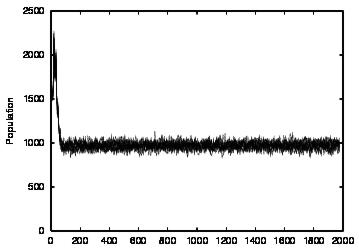
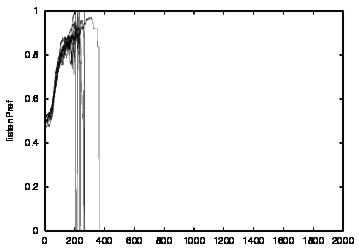
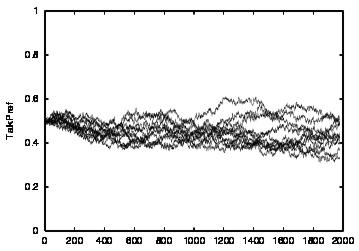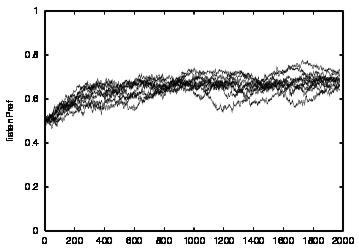	(a)	(b)	(c)	(d)
Figure 5. Results for learning agents with communication enabled and message removal method COM2 active. The results are shown for CT = 0 (first row) and CT = 4 (second row). The population size over time is shown in column (a), the proportion of cooperations of all performed actions over time is shown in column (b), the average talk preference of agents is shown in column (c) and the average listen preference is shown in column (d) overlaid

5.11

Finally, Figure 5 shows the results of the experiments where communication is enabled, agents evolve their talk and listen genes, and the message-board uses message removal method COM2. Thus messages are removed after the required ''call for assistance'' has been responded to. There are no significant differences between the results for removal message methods COM1 and COM2, and out previous observations also hold for this setting.

Summary

5.12

To summarise, we observe significant differences between societies that are able to communicate and those that are not. Societies without communication are not able to survive if there is a necessity to cooperate, while societies with communication survive. Secondly, for the communicating societies we find no significant differences between removing the messages on the board after help has been received and when the message has only been listened to. Finally, to our surprise, we see that the willingness to listen emerges earlier than the willingness to talk.

5.13

We briefly relate our findings to results from the literature that we discussed in Section 2. The main difference between our work and Noble (1999) is the inclusion of a cost-based model for signalling, while we do not include this in ours. As for communication serving either a conflict of interest or common interest, our definition of cooperation is such that the agents need to communicate for a common interest and conflicts of interest are not considered. Noble concludes that with a common interest communication may evolve, with a conflict of interest it will not. In the work of Noble, the evolution of communication is analysed by means of the costs/payoffs of signalling. Our results show that without an explicit cost model, communication also emerges under direct influence of the environment in which the agents are situated. In the anthropological sense, it may be reasonable to assume that communication evolved as a direct consequence of agents interacting with their environment. As such, an explicit cost model might then not be necessary.

5.14

Secondly, our results can be compared with the work of Oliphant (1996, 1997). Oliphant investigated the emergence of coordinated communication and presented a series of learning procedures for communication. The send and receive functions that Oliphant presents are very similar to the probability functions that we used in the controllers of the agents for talking and listening. However, our talking and listening functions are somewhat simpler because only one appropriate action is related to incoming messages (message "I need help'' leads to action to move there). We have not included Oliphant's measurement of communicative accuracy, but will consider this for future work. In agreement with the work of Noble and our work here, Oliphant remarks that his model is most relevant to social individuals where the accurate exchange of information is often mutually beneficial (common interest). Although we do not have explicit learning procedures within our agents compared to those of Oliphant (1996), the population learns to communicate by means of evolution. We consider the most important similarity to be the idea of separating the learning problem into acquiring appropriate transmission and reception behaviours. Our results show that agents have a tendency to acquire appropriate reception (listen) behaviours earlier than transmission (talk) behaviours.

Further Work

6.1: The research described in this paper extends to further work that we are currently undertaking. We distinguish between future communication and cooperation research tracks.
Communication
6.2: The communication model in the research described here is a multicast model, implemented as a centralised message-board. This method brings with it some advantages such as efficiency and regulation. However, the method also comes with disadvantages such as lack of robustness, inflexibility and limited scalability. Domains requiring high degrees of robustness and flexibility may profit more from a distributed type of message casting. Many such distributed methods have been developed, and we are currently investigating the newscast model (Jelasity and van Steen 2002).
6.3: The newscast model is a message casting model defined between distributed individuals without a central message-board. The basic process is as follows. Each individual maintains a cache of 'friends'. Every time an individual creates a message, this is sent to its cache of friends. The reception of messages may be used to update the individuals that are in one's cache. Preliminary results indicate that one difficulty with this approach is that outdated information cannot easily be removed. So far, we have not found a reasonable solution to this problem. Neither can we justly classify it as a problem inherent to the newscast model or to the VUSCAPE model.
6.4: Another option we have considered for the implementation of communication is a spatial casting of messages. Currently we let messages travel along the axes of the world. Instead, we may let messages travel as a circle around agents. This method is more like sound which naturally travels and slowly die out at larger distances.
Cooperation
6.5: As opposed to individual and evolutionary learning, social (or collective) learning is based on the ability of agents to communicate and exchange knowledge. Whereas evolutionary learning can be considered a 'vertical' transfer of knowledge (over generations), social learning is the 'horizontal' transfer of knowledge (within a generation). From the knowledge transfer point of view, individual learning is a sink, since (in a non-Lamarckian system) the learned knowledge disappears when the agent dies. Social learning can be seen as a way to prevent this waste and pass on knowledge learned by an individual.
6.6: This type of learning directly relates to the creation, distribution and transfer of knowledge in our own human society. We propose a novel approach to social learning in artificial societies based on an entirely decentralised knowledge transfer mechanism without any global synchronisation. The motivation for this approach is its expected robustness and scalability. Technically, such a learning situation can be viewed as distributed machine learning, i.e., machine learning where data are distributed over many sites and cannot be directly shared and integrated. Under these circumstances it is the locally learned models of the data (here: the knowledge of individual agents) that are shared and processed. The first steps on this research path have already been made in the form of the newscast model (Jelasity et al. 2004).

Conclusions

7.1: This paper introduced an artificial world where some resources can only be utilized by cooperating agents. The cooperation pressure in this model is scaleable by a parameter. Traversing the range of this parameter we can systematically investigate worlds where cooperation is a nicety and worlds where it is a must. Using this model we performed a number of experiments in which we investigated the evolution of communication under varying levels of cooperation pressure. We endowed agents with the capabilities to talk and listen to each other and observed that they evolved talking and listening skills over time. The experiments showed that the population responds to a heightening level of cooperation pressure with increasingly positive attitude to communication. Conforming to our expectations, the observed level of cooperation (measured by the number of agents eating together) followed the increase of the cooperation pressure. These results also embody a confirmation of our cooperation model, in the sense that the scaling parameter has a significant effect.
7.2: It is a surprising outcome of our experiments that the willingness to listening emerges earlier than the willingness to talking. We observe this both if we lower the cooperation pressure as well as for a given cooperation pressure: the values of the listen genes increase faster than those of the talk genes. However, we do not yet have an exploration for this phenomenon.

Notes

¹JAWAS stands for Java Artificial Worlds and Agent Societies and can be downloaded from http://www.cs.vu.nl/ci/eci/.

²Each variable can be monitored as average, minimum, maximum, sum, variance, standard deviation, frequency, or any combination of these.

³Conceptually, all agents execute these stages in parallel. However, technically, the stages are partially executed in sequence. Therefore, the order in which agents perform their control loop, is randomised over the execution cycles to prevent order effects.

⁴Choosing the closest (and breaking ties randomly) is the method used in SUGARSCAPE. We have the option in VUSCAPE to either choose a random one or the closest. Since a move action does not have a cost associated with it, we do not consider choosing the closest as having a reasonable rationale.

⁵For 2,500 sugar units, this means that there are 250 seeds with maximum 1, 250 with maximum 2, etc. amounting to 2,500 in total.

⁶The JAWAS software offers more possibilities for methods to remove messages than were researched in this series of experiments.

⁷This means that within a single world execution loop, agent loop B is executed before agent loop C. This conceptually means that agent B receives the message from agent A before agent C does. Note that with COM1, agent C never receives the message.

References

ARTIKIS, A. and Pitt, J. (2001). A formal model of open agent societies. In Mueller, J., Andre, E., Sen, S., and Frasson, C., editors, Proceedings of the Fifth International Conference on Autonomous Agents, pages 192-193, Montreal, Canada. ACM Press.

AXELROD, R. (1984). The Evolution of Cooperation. Basic Books, New York.

AXELROD, R. (1997). The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration. Princeton University Press, New Jersey.

BINMORE, K. (1998). Review of the Complexity of Cooperation. The Journal of Artificial Societies and Social Simulation, 1(1). https://www.jasss.org/1/1/review1.html.

BUZING, P., Eiben, A., and Schut, M. (2003). Evolving agent societies with VUScape. In Banzhaf, W. and Christaller, T., editors, Proceedings of the Seventh European Conference on Artificial Life.

COLLIER, N. (2000). Repast: An extensible framework for agent simulation. Technical report, Social Science Research Computing, University of Chicago, Chicago, Illinois.

DANIELS, M. (1999). Integrating simulation technologies with swarm. In Proceedings of the Workshop on Agent Simulation: Applications, Models, and Tools, University of Chicago, Illinois.

DAVIDSSON, P. (2001). Categories of artificial societies. Lecture Notes in Computer Science, 2203.

EIBEN, A.E., and Smith, J.E. (2003). Introduction to Evolutionary Computation. Springer, Berlin, Heidelberg, New York.

EPSTEIN, J. and Axtell, R. (1996). Growing Artificial Societies: Social Science From The Bottom Up. Brookings Institute Press.

GILBERT, N. and Conte, R. (1995). Artificial Societies: the computer simulation of social life. UCL Press, London.

HALES, D. (2002). Evolving specialisation, altruism and group-level optimisation using tags. In Sichman, J., Bousquet, F., and Davidsson, P., editors, Multi-Agent-Based Simulation II. Lecture Notes in Artificial Intelligence 2581, pages 26-35. Berlin: Springer-Verlag.

JELASITY, M. and van Steen, M. (2002). Large-scale newscast computing on the internet. Technical report, Department of Computer Science, Vrije Universiteit, Amsterdam, The Netherlands.

JELASITY, M., van Steen, M., and Kowalczyk, W. (2004). An Approach to Massively Distributed Aggregate Computing on Peer-to-Peer Networks. In Proceedings of the 12th Euromicro Conference on Parallel, Distributed and Network-based Processing, pages 200-207, IEEE Computer Society.

KREBS, J. and Dawkins, R. (1984). Animal signals: Mind reading and manipulation. Behavioural Ecology: An Evolutionary Approach (Second edition), pages 380-402.

NOBLE, J. (1999). Cooperation, conflict and the evolution of communication. Journal of Adaptive Behaviour, 7(3/4):349-370.

OLIPHANT, M. (1996). The dilemma of saussurean communication. Biosystems, 37(1-2):31-38.

OLIPHANT, M. (1997). Formal Approaches to Innate and Learned Communication: Laying the Foundation for Language. PhD thesis, University of California, San Diego.

OLIPHANT, M. and Batali, J. (1996). Learning and the emergence of coordinated communication. Center for research on language newsletter, 11(1).

PARKER, M. (2000). Ascape: Abstracting complexity. Technical report, Center on Social and Economic Dynamics, The Brookings Institution, Washington D.C.,Washington, USA.

PERFORS, A. (2002). Simulated evolution of language: a review of the field. Journal of Artificial Societies and Social Simulation, 5(2). https://www.jasss.org/5/2/4.html.

RAPOPORT, A. and Chammah, A. (1965). Prisoner's Dilemma. University of Michigan Press, Ann Arbor.

Button Return to Contents of this issue