Gary Polhill and Luis Izquierdo: Lessons Learned from Converting the Artificial Stock Market to Interval Arithmetic

Gary Polhill and Luis Izquierdo (2005)

Lessons Learned from Converting the Artificial Stock Market to Interval Arithmetic

Journal of Artificial Societies and Social Simulation vol. 8, no. 2
<https://www.jasss.org/8/2/2.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary

Received: 17-Dec-2004 Accepted: 08-Feb-2005 Published: 31-Mar-2005

Abstract

: This paper describes work undertaken converting the Artificial Stock Market (LeBaron et al., 1999; Johnson, 2002) to using interval arithmetic instead of floating point arithmetic, the latter having been shown in an earlier article to be the cause of changed behaviour in the ASM (Polhill et al., in press). Results of both a naive (potentially automatable) conversion and one involving a more in-depth analysis of the code are presented that suggest that interval arithmetic may not be the best approach to dealing with the issue of numeric representation in the ASM. We also find that there are good reasons to suspect that floating point errors are not a significant issue for the ASM.
Keywords:: Floating Point Arithmetic, Artificial Stock Market, Interval Arithmetic, Reimplementation

Introduction

1.1: The Artificial Stock Market (ASM) is a stochastic discrete event agent based model that simulates a market in which a number of agents choose between investing in a risk-free bond with a fixed interest rate, and a stock with an autoregressive stochastic dividend. In contrast to mathematical models of stock markets based on unrealistic assumptions of agents' knowledge and processing power, the ASM (in its earlier incarnation as the Santa Fe Stock Market) has been shown to demonstrate features observed in real markets, such as weak forecastability and volatility persistence (LeBaron et al. 1999). The original software, written in Objective-C for the NeXTstep architecture, was converted by Paul Johnson (2002) for use with Swarm. Both are open source and obtainable at http://sourceforge.net/projects/artstkmkt/. The Swarm version has been converted to Java (Pajares et al. 2003).
1.2: In earlier work (Polhill et al. 2005), we have shown how floating point arithmetic errors caused significant problems in FEARLUS, an agent-based model of land use change (Polhill et al. 2001; Gotts et al. 2003). We also showed in the case of the ASM that simply reversing the order in which the terms of a sum are computed can change the output of the model. Whilst the issues with floating point arithmetic errors were largely solved in the case of FEARLUS using interval arithmetic, the application of interval arithmetic to the ASM was not explored. This paper outlines the work undertaken to achieve this conversion, and the lessons learned from it.
1.3: The motivation for using interval arithmetic with the ASM was to gauge the magnitude of floating point errors accumulating in the ASM. This would give us some idea about the degree of influence that floating point errors have on the model behaviour. After all, if floating point errors hardly accumulate at all, then there is little need to concern ourselves with the potential effect they are having on the behaviour of the model.
1.4: We find that floating point arithmetic errors do accumulate in the ASM through the interaction between the agents in the market. We also find that the ASM has processes in it that do not convert to interval arithmetic straightforwardly, and as a consequence interval arithmetic gives a rather pessimistic impression of the extent of the impact of floating point arithmetic errors. We argue that in the ASM, this impact is not significant.

The Artificial Stock Market

2.1

In this artificial market, agents trade two different assets:

a risk-free bond, which is offered in infinite supply and pays a constant interest rate, and
a risky stock, which is issued in a constant number of units and pays a dividend that follows an exogenous stochastic process not known to the agents. The stock price emerges from the supplies and demands of the agents in the market.

2.2

At the beginning of the simulation, each agent has a certain amount of risk-free bonds and a given number of stock units. In every time-step, each agent attempts to optimise their allocation between the risk-free bond and the stock by forecasting the next period's stock price and dividend. To make their forecasts, agents use general information on the state of the market, which includes the historical dividend sequence and price sequence. In particular, every agent has a certain number of forecasting rules called "predictors". A predictor is an IF-THEN statement such as: IF a certain state of the market occurs (condition part) THEN a certain forecast function is used (forecasting part).

2.3

The condition part of each predictor is a bitstring where each bit indicates whether a certain statement about the market is true, false, or irrelevant. Some of these statements may be: "the price has risen in the last 3 periods" or "the dividend has dropped in the last time-step". The forecasting part of the predictors is made up of two constants that determine the forecast for next period's price plus dividend as a linear function of the sum of the previous price and the previous dividend.

2.4

In order to form their expectations about the next price and dividend, agents select one or several predictors whose condition part matches the current state of the world, and whose forecasting part has proved to deliver the most accurate predictions in the past. Once the forecast function is formed, agents can calculate their desired holdings for any given price using a constant absolute risk aversion (CARA) utility function.

2.5

The clearing of the market in each time-step is performed by an extra agent, which can use a number of different techniques to declare the market price. After the price is set, agents are able to assess their performance in that period. Learning in this model takes place in two ways:

Agents update the accuracy of their active predictors (i.e. predictors whose condition part matched the current state of the market), so most accurate predictors will be more likely to be used the next time they are active.
Agents also learn on a slower time scale using a genetic algorithm. The genetic algorithm discards the least fit predictors and creates new ones. A predictor's fitness is determined by its accuracy and by how specific it is (the genetic algorithm has a bias against specific predictors, i.e. those whose condition part consider a greater number of statements about the market to be relevant). New predictors are created by applying the genetic operators of mutation and crossover to the most successful predictors in the agent's predictor pool.

Interval arithmetic and conversions from floating point arithmetic

3.1

Floating point arithmetic errors are most often ignored in agent-based models (and possibly in computer models in general). This is reflected in the fact that many programming languages (e.g. Java, SmallTalk, Perl, Visual Basic) do not provide facilities to access the information provided by floating point hardware pertaining to floating point errors that is stipulated by the IEEE 754 (1985) standard.

3.2

Nonetheless, computer models are programmed to follow mathematical equations, often under the misguided belief that floating point arithmetic follows the same laws as arithmetic with real numbers. Several basic laws of real number arithmetic do not apply with floating point arithmetic, such as the associativity of addition (Knuth 1998, p. 230).

3.3

These problems arise because a digital computer has to squeeze an infinity of real numbers into a finite number of bits. Each calculation using floating point numbers thus potentially has a small rounding error associated with it. These small rounding errors can, over a series of calculations each depending on the result of an earlier one, accumulate to such an extent that the floating point result bears little relation to the exact one. According to Higham (2002, p. 14), this more often happens through propagation of a single error through a series of subsequent exact operations than through many thousands of inexact calculations. In agent-based models, over the course of a simulation, agents may find that they are often in the same context relative to a piece of code, with the consequence that exactly the same calculation is repeated many times. This would potentially make such models particularly vulnerable should such a calculation be inexact.

3.4

Accumulation of floating point error does not necessarily occur: rounding errors can cancel each other out. Equally, however, rounding errors do not necessarily cancel each other out, and it should not be assumed that they do. By not monitoring the accumulation of floating point errors, most computer modellers are effectively making this assumption.

3.5

One way of coping with and assessing the rounding errors associated with floating point arithmetic is to use interval arithmetic, which bounds the exact result of a calculation with the two nearest representable floating point numbers. In a series of calculations, the gap between the bounds may get larger, though they do not necessarily do so.

3.6

The method used here is to create an Objective-C class (Interval) to manage interval arithmetic, with methods to replace arithmetic operations, comparison operations, and some (monotonic) functions from the math library. Non-monotonic functions create implementation complexities for interval arithmetic, as the bounds of the range do not necessarily correspond to the images of the bounds of the domain. Consider, for example, calculating the cosine of an interval [-0.01, +0.01]; the cosine of -0.01 is equal to that of +0.01, but the interval result of this function is not a singleton since there is a maximum at 0. For non-monotonic functions, therefore, it is necessary to inspect the images of points between the extremities of the input interval.

3.7

Alefeld and Herzberger (1983) prove various properties of interval arithmetic implemented on computers. The code using floating point arithmetic is then converted to interval arithmetic by replacing the double datatype declaration for a floating point variable with one pertaining to the Interval class, and substituting the appropriate method call in all expressions in which that variable is used. Though this is a rather laborious process when conducted by hand, the Interval class is designed in such a way that the conversion process could be done automatically given an appropriate parser.

3.8

Interval comparison operations work a little differently from those of real numbers. For two intervals, A (with minimum a1, maximum a2) and B (b1, b2), the greater-than operation, for example, can be interpreted in two ways akin to modal logic (Kripke 1963). A is possibly-greater-than B if there exists a member of A's interval that is greater than a member of B's interval, i.e. if a2 > b1. A is necessarily-greater-than B if all members of A's interval are greater than all members of B's interval, i.e. if a1 > b2. It is not always clear which of these two should be used. For example consider a piece of code using floating point arithmetic:

	if(A > B)
	  {
	    /* do something */
	  }
	else
	  {
	    /* do something else */
	  }

3.9

When converting this to interval arithmetic there are two possibilities for converting the comparison of A and B, each with consequences that may not make sense in the set of actions following the condition:

	if(A possibly > B)
	  {
	    /* but A possibly <= B */
	  }
	else
	  {
	    /* OK */
	  }

or:

	if(A necessarily > B)
	  {
	    /* OK */
	  }
	else
	  {
	    /* but A possibly > B */
	  }

To get round this problem, the Interval class stores the floating point arithmetic result (e.g. a_fp and b_fp, for A and B above) as well as the interval arithmetic result. The default replacement comparison operators return the result of comparing a_fp and b_fp, but make a check using the intervals and issue a warning if the comparison result could be wrong. For example, when checking if A > B, the result returned is the comparison of a_fp > b_fp. If this comparison is True, then a warning is issued if A is possibly ≤ B; if False, then a warning is issued if A is possibly > B. This deals with the two 'buts' in the conversion example above, and also allows a warning to be generated if the floating point arithmetic result has sufficient error in it that the program would potentially be following a different branch in the code if it were using real numbers.

3.10

Converting FEARLUS to interval arithmetic dealt with the problems it had with floating point arithmetic effectively (Polhill et al. 2005). Firstly, we were able to confirm that no warning is issued with parameter settings used for earlier results (Polhill et al. 2001; Gotts et al. 2003), and secondly, for those cases where parameter settings did create floating point issues, the interval arithmetic always issued a warning before any invalid state of the model was reached. The expectation was that the ASM would also benefit, though perhaps not to the extent that the model could be run safely for the hundreds of thousands of cycles the authors use in their experiments.

Results and analysis

4.1

The first conversion, using only the default comparison operators, issued many hundreds of warnings from the comparisons during the initialisation phase of the ASM. It managed just six cycles of trading before aborting with an error due to a division by an interval containing zero. In an interval division operation, the result is not defined if the divisor contains zero (i.e. has zero or negative minimum and zero or positive maximum), for the same reason that division by zero is undefined for real arithmetic (Alefeld and Herzberger 1983).

4.2

Divisions by zero occur in the interval ASM where they did not in the floating point version because of converting situations like the following, which are deliberately programmed to avoid this problem:

	if(X > 0)
		/* X is known independently to be positive or zero */
	  {
	    Y = Z / X;
	  }
	else
	  {
	    /* Set Y to some other value */
	  }

The default greater-than operator works as described above, the test depending on a comparison of x_fp with zero. Although X is known by the programmer to be positive or zero, this is not reflected in the code anywhere (there being no unsigned double datatype), meaning that x1 could be ≤ 0, and x_fp > 0. The Interval class will issue a warning in the comparison operation, but the result will nonetheless be that Y is divided by a range containing zero. The way to deal with these problems is to use one of the interval comparison operators instead, in this case:

	if(X necessarily > 0)
	  {
	    Y = Z / X;
	  }
	else
	  {
	    /* set Y to some other value */
	  }

This, however, will have an effect on the behaviour of the model if floating point errors accumulate sufficiently, as the more stringent requirement that x1 > 0 means that we should expect the consequent to be evaluated less often than when requiring that x_fp > 0.

4.3

The naive conversion of the code directly from floating point to interval arithmetic has therefore not produced a viable model, which raises a question mark over the usefulness of building a tool to automate this. However, this conversion could form the foundation of a conversion effort based on a more in-depth understanding of the code and what it is doing, albeit that such a conversion will potentially affect the behaviour of the model.

4.4

By using modal comparison operators appropriately, we were able to build a version of the ASM using interval arithmetic that did not crash due to division by zero, though it did still issue warnings from comparison operations not converted to modal form. In this version of the ASM, however, trading continues for only a few tens of cycles before stopping altogether. The reason for this behaviour proved difficult to unpick.

4.5

The ASM computes a demand for the agents using a demand function that generates a negative result if the agent is to sell shares, and a positive result if the agent is to buy them. To avoid a division by zero, we had to use the modal operators, meaning that the agent buys if the demand is necessarily positive, and sells if necessarily negative. As these impose more stringent conditions, if the accumulated error in the demand becomes too large, then it becomes more likely that an interval will contain zero, causing the agent to neither buy nor sell. This is the immediate cause for the cessation of trade, the question then is how floating point errors are accumulating so rapidly.

4.6

The market clearing process sets a price that balances the demand of the agents with the supply. The demand of an agent depends on their current holding of shares and the forecast of the sum of the price and the dividend according to the particular rule they have chosen to use. The market then takes portions of shares from the sellers and distributes them among the buyers in proportion to their demand. As a consequence, the holding of shares an agent has at time t depends on their holding at time t - 1, their demand, and the demands of all the other agents. If any agent has an interval demand where the minimum is not equal to the maximum, that uncertainty propagates to all the other agents' holdings, and thus to all agents' demands and holdings in the subsequent cycle. The interaction of the agents in the market thus causes a rapid rise in the uncertainty (the gap between the minimum and maximum in the interval) of the demand (figure 1).

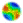
Figure 1. Uncertainty in the demand of agents for the risky stock after just seven cycles of trading in one run of the interval arithmetic ASM. The yellow region shows where the supply and demand ranges intersect, meaning that the price to clear the market could be anywhere between 67 and 87.

4.7

This rise in uncertainty is rather pessimistic. The total holding of shares across all agents is known to remain a constant throughout the simulation. This means there is a correlation between all the agents' holdings. For example, if there are two agents in the market, then if the holding of one agent is known exactly, the holding of the other agent is also known exactly. There is no way to reflect this in the intervals, however. It could also be argued that the market clearing process is not particularly susceptible to floating point errors in the first place. The supply and demand curves are smooth, and thus a small error in the demand of an agent means a small error in the clearing price. Even if there is a consistent bias in the demand due to floating point errors, such as all agents consistently over-estimating their demand by a nano-share or a pico-share, the effect on the clearing price will be correspondingly negligible unless there are an unfeasibly large number of agents.

4.8

To investigate this, we conducted a test that, with hindsight, would have been better done before the conversion to interval arithmetic. Since the total holding of shares across all agents is a known constant, but also a constant that depends on the interaction of the agents in the market, by plotting this constant we can take a measurement of the effect of floating point arithmetic. We ran the original model for 250000 cycles^[1], noting the total holding of shares at each time step to 30 significant figures. Since there are 30 shares for the 30 agents to own, the total holding of shares should remain constant at 30. The graph in figure 2 shows that this is not quite true, not even always to the 15 significant figures of accuracy that a single double precision floating point operation guarantees. The errors also accumulate to an extent, though not necessarily in a consistent direction. In general, however, it is clear that the deviation from the constant is small enough to be ignored.

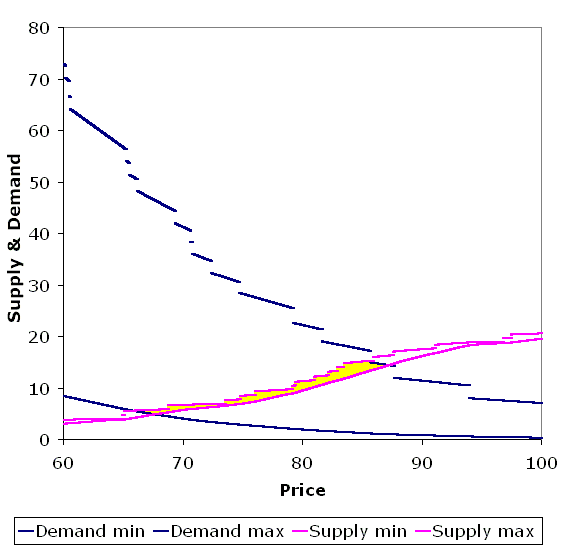
Figure 2. Graph showing the total holding of shares in the floating point arithmetic version of the ASM every 1000 cycles over a period of 250000 cycles. A negligible deviation from the correct constant value of 30 is observed.

4.9

One check we were able to make with the interval arithmetic version of the model was of the accumulation of floating point error in the dividend. The dividend at time t is a linear function of that at time t - 1. With no agents in the model, we checked for accumulation of floating point error by measuring the gap between the minimum and the maximum of the dividend interval in each time step. By inspection, the gap showed no increasing trend over 250000 time steps. (Indeed a regression of the data in figure 3 has a slightly decreasing trend, but with such a small value for R² that this can be ignored.) We therefore concluded that the accumulation of floating point error in the dividend was negligible.

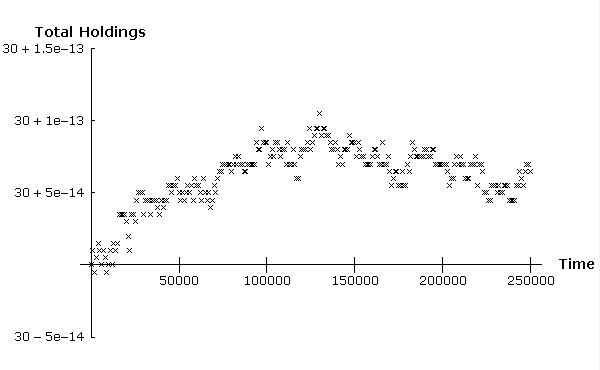
Figure 3. A scatter graph of difference between the maximum and the minimum of the dividend interval (the dividend gap) in the interval arithmetic version of the ASM every 1000 time steps.

4.10

The ASM does contain agent-based decisions with hard-thresholded consequences in the choice of forecasting rule that will be applied to calculate the demand of the agent for the risky stock. Should floating-point errors cause a forecasting rule to be selected that would not have been chosen with real numbers, the effect on the demand is potentially significant. However, the rules that determine which forecasting rule is selected are adapted by the agent in the GA. If the floating-point errors consistently cause a forecasting rule to be selected with poor performance, the rule will eventually be dropped. The GA finds rules that work within the system it is being applied to, floating point errors included, and in this way it could be argued that it mitigates against these problems. Floating point errors are thus potentially significant only if the major point of interest in the ASM is the set of forecasting rules selected, with a much reduced impact on the wealth of the agents and the properties of the market — the last of these being the subject of LeBaron et al.'s (1999) study.

Conclusion

5.1

Oddly, though interval arithmetic has proved not to be an effective tool for representing numbers in the Artificial Stock Market, we have achieved in part what we originally set out to do: gauge the impact of floating point arithmetic errors on the behaviour of the ASM. Though the interval arithmetic implementations initially indicated a seemingly devastating impact — the non-viability of a model such as the ASM in a digital computer — it can be argued that floating point errors do not significantly affect the behaviour of the ASM, even though they undoubtedly result in actions that would not occur were it to be using real numbers. In particular, an agent may buy shares in the floating-point case when they would have sold them with real numbers (and vice versa), and an agent may select a different forecasting rule when making a bid. In the former case, the lack of hard thresholds in the supply and demand curves means that the impact is negligible. In the latter case, the impact is mitigated by the fact that the agents adapt the rules that determine which of the forecasts they will use.

5.2

The fact that the initial impressions were so different from the final conclusions is down to the former being based on a naive conversion of the code that could potentially be automated. The mere fact that we considered automating such an activity is, perhaps, a reflection of the temptation to view re-implementing agent-based models as a more mundane activity than other avenues of research. This case serves as an example of how succumbing to such a temptation would be a mistake. Indeed, re-implementing models requires an in-depth understanding both of the model and of the code originally used to implement it, in some cases (though not here) to the extent that the investigators understand the model better than the original authors (Edmonds and Hales 2003).

5.3

For interval arithmetic, we have learned that whilst in the case of FEARLUS it was very effective at coping with the problems that were caused by floating point arithmetic, in the case of the ASM it became apparent that interval arithmetic makes things worse. Where there is correlation between variables, it is too pessimistic in its estimation of the potential accumulated floating point error. Future work should focus on developing a suite of techniques for examining and mitigating the accumulation of floating point errors in agent-based models, together with heuristics for recognising the features of an agent-based model that make it more susceptible to problems with floating point arithmetic, and the cases in which one technique for dealing with them will be better than another.

5.4

For now, however, the lessons learned for investigating floating point issues with models from this exercise and earlier work can be summarised in the UML activity diagram in figure 4. Detecting floating point errors can be achieved simply and quickly for any model written in C, C++ or Objective-C by adding the following to the file containing the main function:

	#include <ieeefp.h>
	
	/* ... */
	
	int main(int argc, char **argv) {
	  /* variable declarations */
	
	  fpsetmask(FP_X_INV, FP_X_IMP, FP_X_DZ, FP_X_UFL, FP_X_OFL);

The fpsetmask() function^[2] ensures that a floating point signal (SIGFPE) will be generated whenever an issue has arisen with a floating point operation. According to the POSIX standard (IEEE and Open Group 2004), the default action on receiving SIGFPE is to abort. With this line of code at the beginning of the main function, if the program runs without aborting, it is unquestionably free of floating point errors. This is so trivial to implement there is little excuse for not doing it.

5.5

If the model does abort, the offending line can be identified using a debugger. If the line is associated with displaying some information to the user, or for some other reason is not instrumental to the accuracy of the model, then the SIGFPE signal can be temporarily disabled for that piece of code using the signal() function:

	#include <signal.h>
	
	/* ... */
	
	  signal(SIGFPE, SIG_IGN);	// ignore SIGFPE
	
	  /* offending unimportant line(s) of code */
	
	  signal(SIGFPE, SIG_DFL);	// handle SIGFPE

5.6

Should the above fail to verify the model is free of floating point errors, which is likely, this is not in itself a reason to reject the model. Not all floating point errors are harmful, and some are even beneficial (Higham 2002). Instead, the model needs to be checked thoroughly for the potential effects of those errors. Possibly the simplest check to make is to identify mathematical properties of the model that are known to hold in theory, and to confirm that they hold in practice. The mathematical properties should include variables that are integral to the model and are involved in a number of mathematical expressions in the code. The total holding of shares in the ASM is a good example of such a check, and arguably there is no significant deviation from the constant value that it should have from our investigation.

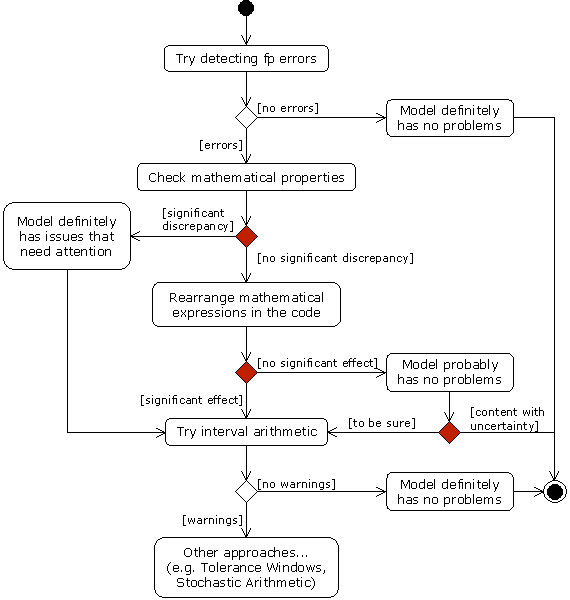
Figure 4. Suggested flow of activity for investigating possible floating point number representation issues in a model. Red decisions (diamonds) represent a judgement of the investigator.

5.7

Having checked the mathematical properties, a further check that can be made is to rearrange mathematical expressions in the code and observe the effect on the output, focusing on those expressions using combinations of operators where floating point arithmetic does not guarantee that the laws of conventional arithmetic will apply (e.g. associativity of addition). This has been done for the ASM by Polhill et al. (in press). Our judgement then, and now, is that the effect on the output is not significant for any reasonable purpose the model might be used, provided that any conclusions are based on several runs of the ASM using different random seeds. Though the interval arithmetic conversion did not enable us to be sure of this, it did enable us to make a further check for accumulation of floating point error in the dividend autoregressive process. Together with our other findings, we may conclude that though floating point errors certainly occur in the ASM, they do not significantly affect its behaviour.

Acknowledgements

: This work was funded by the Scottish Executive Environment and Rural Affairs Department.

Notes

¹This is the number of cycles that LeBaron et al. (1999) use in their paper to allow the agents to learn (p. 1499).

²Note that on Cygwin, the ieeefp.h functions are not implemented. An implementation is provided for Intel CPUs at http://www.macaulay.ac.uk/fearlus/floating-point/download.html.

References

ALEFELD, G and Herzberger, J (1983), Introduction to Interval Computations. Academic Press

GOTTS, N M, Polhill, J G and Law, A N R (2003), Aspiration levels in a land use simulation. Cybernetics & Systems 34, pp. 663-683

EDMONDS, B and Hales, D (2003), Replication, replication and replication: Some hard lessons from model alignment. Journal of Artificial Societies and Social Simulation 6 (4), https://www.jasss.org/6/4/11.html.

HIGHAM, N J. (2002), Accuracy and Stability of Numerical Algorithms. 2nd ed. Philadelphia: Society for Industrial and Applied Mathematics

IEEE (1985), IEEE Standard For Binary Floating-Point Arithmetic. IEEE 754-1985, New York, NY: Institute of Electrical and Electronics Engineers

IEEE and Open Group (2004), The Open Group Base Specifications Issue 6, IEEE Std 1003.1. 2004 ed. http://www.unix.org/single_unix_specification/

JOHNSON, P (2002), Agent-based modeling: What I learned from the Artificial Stock Market. Social Science Computer Review 20, pp. 174-186

KNUTH, D E (1998), The Art of Computer Programming. Vol. 2. Semi-Numerical Algorithms. 3rd ed. Boston: Addison-Wesley

KRIPKE, S (1963), Semantical considerations on modal logic. Acta Philosophica Fennica 16, 83-94

LEBARON, B, Arthur, W B and Palmer, R (1999), Time series properties of an artificial stock market. Journal of Economic Dynamics & Control 23, pp. 1487-1516

PAJARES, J, Pascual, J A, Hernandez, C, and Lopez, A (2003) A behavioural, evolutionary and generative framework for modelling financial markets. Presented at the First Conference of the European Social Simulation Association, Groningen, The Netherlands, 18-21 Sept 2003. Conference proceedings available online.

POLHILL, J G, Gotts, N M and Law, A N R (2001), Imitative versus nonimitative strategies in a land use simulation. Cybernetics & Systems 32, pp. 285-307

POLHILL, J G, Izquierdo, L R, and Gotts, N M (2005), The ghost in the model (and other effects of floating point arithmetic). Journal of Artificial Societies and Social Simulation, https://www.jasss.org/

Button Return to Contents of this issue