Anselm Fleischmann (2005)
A Model for a Simple Luhmann Economy
Journal of Artificial Societies and Social Simulation
vol. 8, no. 2
<https://www.jasss.org/8/2/4.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 20-Sep-2004 Accepted: 28-Feb-2005 Published: 31-Mar-2005
 Abstract
AbstractIn order to secure future access to a finite set of goods, people provisionally access (store, own) these goods. Access as a solution to the problem of scarcity creates further scarcity. This is referred to as the scarcity paradox. The ownership code (to own or not to own) gets established. To own something (desirable) is better that not owning it. The code is asymmetrical.
The money-code (to pay or not to pay) superimposes the ownership-code when the usage of money becomes established. It is not necessarily better to pay than not to pay (or vice versa). This code is symmetrical. Payments enable further payments. Solvability is passed into one direction. Insolvability is passed into the other direction. This is referred to as the double cycle. The economic system gains autonomy, as the value of money (interest) is determined within the economic system. Niklas Luhmann points to the similarity to meaning, because meaning is determined within the social system society[7].
Markets are observation horizons where consumers can efficiently observe (many) other consumers, suppliers can efficiently observe many other suppliers using prices.
Dangers, attributed to events in the environment, are converted to risks, attributed to decisions in the economic system[8].
Remark: Psychic and social systems evolve by means of Co-evolution [19]
| ai,k,t+1 = ai,k,t + Σj di,j,k,t - Σj dj,i,k,t for all i, k and t |
Given the definitions above, the clearing of deals can be expressed in matrix notation as a one-to-one map clear: A × Δ → Δ giving the identity At+1 = clear(At,Dt).
| Flows: | Dt = trade(At, Dt-1) = deal(At, propose(At, Dt-1, showoff(At))) |
| Stocks: | At+1 = clear(At, Dt). |
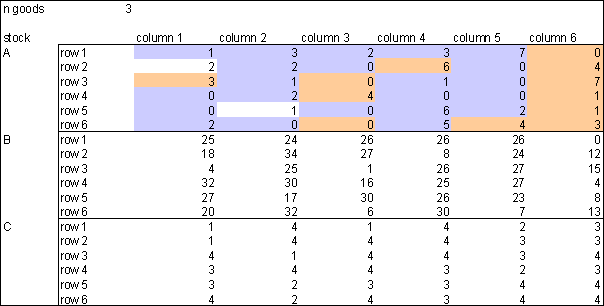
|
| Figure 1. Initial wealth with 3 Goods in a 6 × 6 world, Spreadsheet |
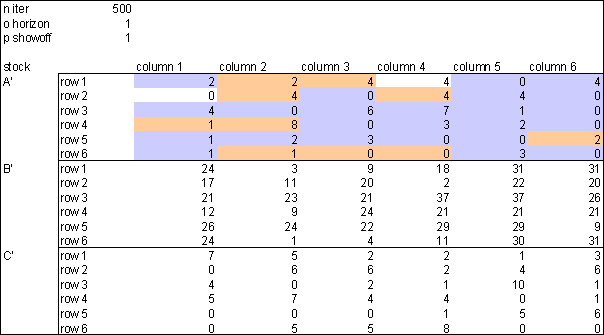
|
| Figure 2. Stock after 500 trade runs, observation horizon 1, show off probability 100% |
Note that the evenness of distribution of wealth of good C has been lost.
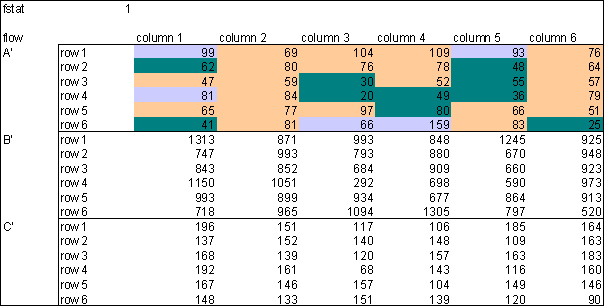
|
| Figure 3. Flow in 500 trade runs, observation horizon 1, show off probability 100% |
The figure is obtained by adding the absolute value of goods flows throughout the trade runs. The colours now refer to 3 clusters. Blue is again the cluster which ranks highest in Euclidean norm of the cluster centre, green ranks lowest. So blue agents trade most, green ones trade lowest. Not surprisingly, the given case clusters show a cohesive pattern, as deals are only made with direct neighbours.

|
| Figure 4. Stock after 500 (137) trade runs, observation horizon 2, show off probability 100% |
As an immediate consequence the system reaches equilibrium (a fixed point) after 137 trade runs. Equilibrium is defined as a situation in which no more deals occur or when a cycle is reached.
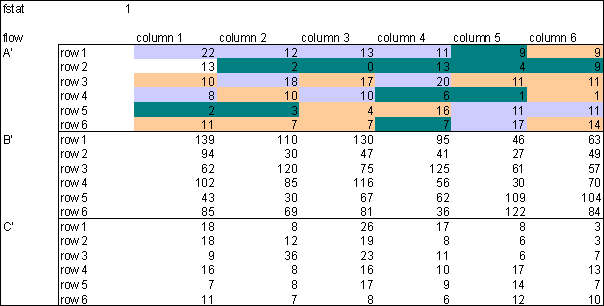
|
| Figure 5. Flow in 500 (137) trade runs, observation horizon 2, show off probability 100% |
It is worth mentioning that a further increase of the observation horizon to 3 does not give a different result to observation horizon 2. In a 6 × 6 world observing other agents that are no more than 2 rows or columns apart (in each direction) is a situation that nearly amounts to "every agent observes every other agent".
|
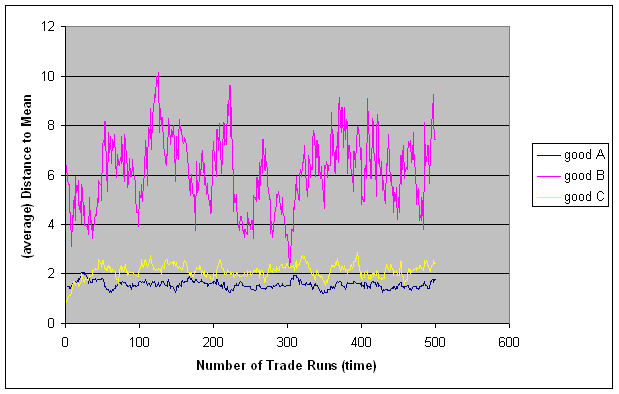
| Figure 6. Distance to mean (even distribution), observation horizon 1; only the first 500 trade runs are shown |
|
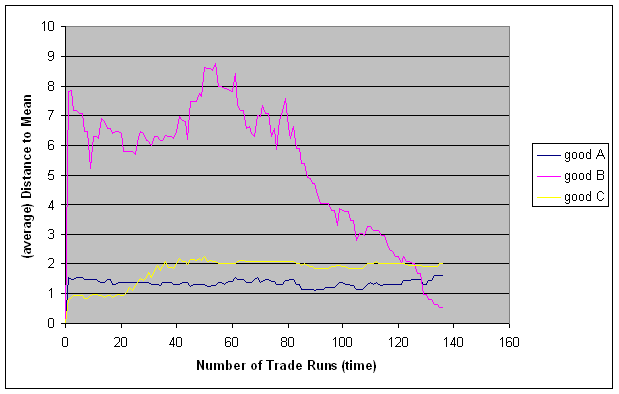
| Figure 7. Distance to even distribution, observation horizon 2 |
The difference between observation horizon 1 and 2 is, that the irregular phase lasts about 150.000 trade runs given observation horizon 1, and merely 80 trade runs given observation horizon 2.
|
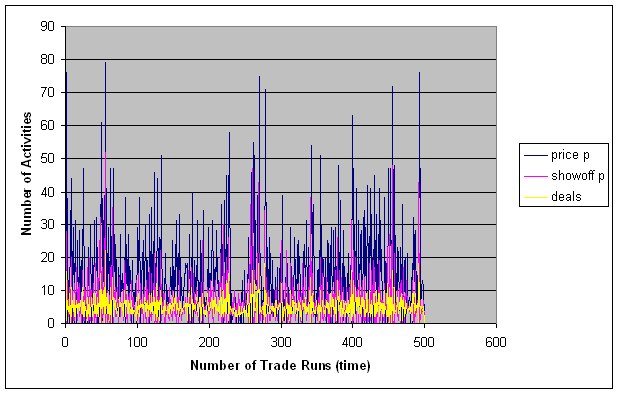
| Figure 8. Activities statistics, observation horizon 1; first 500 trade runs |
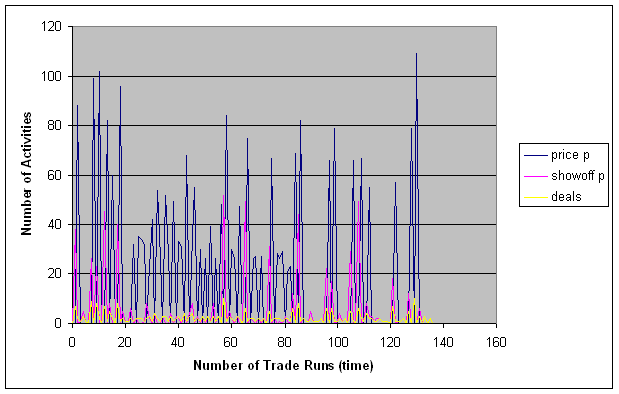
|
| Figure 9. Activities statistics, observation horizon 2 |
|
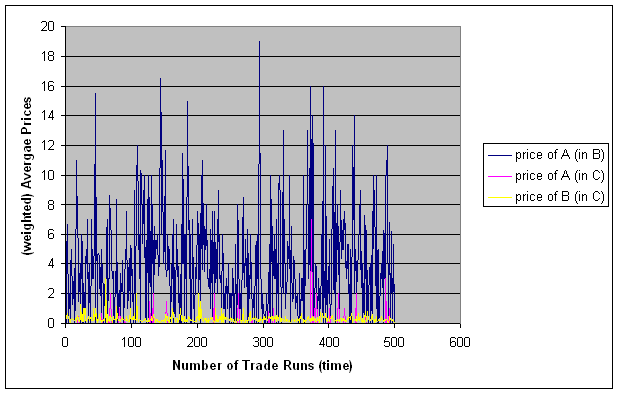
| Figure 10. Price statistics, observation horizon 1; first 500 trade runs |
|
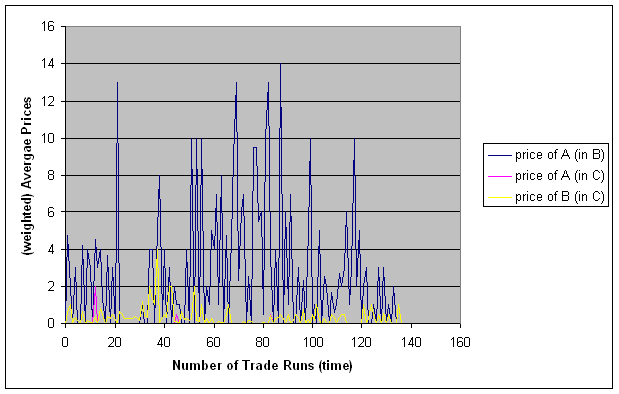
| Figure 11. Price statistics, observation horizon 2 |
The qualitative behaviour appears to be the same in observation horizon 1 and 2.
| Table 1: Aggregated results scenario 1 | ||||
| last run no deals | number no deals | episode length | total A+B+C | |
| mean | 37 | 7 | 7 | 326 |
| median | 35 | 6 | 6 | 325 |
| std deviation | 12 | 4 | 5 | 22 |
| std deviation in % | 32% | 56% | 73% | 7% |
|
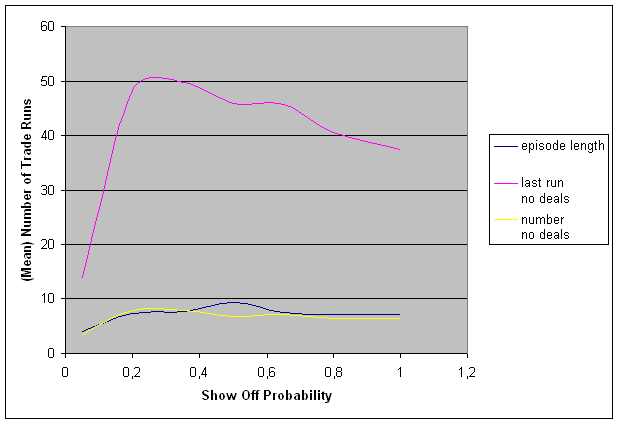
| Figure 12. Means of characteristics varying with showoff probability |
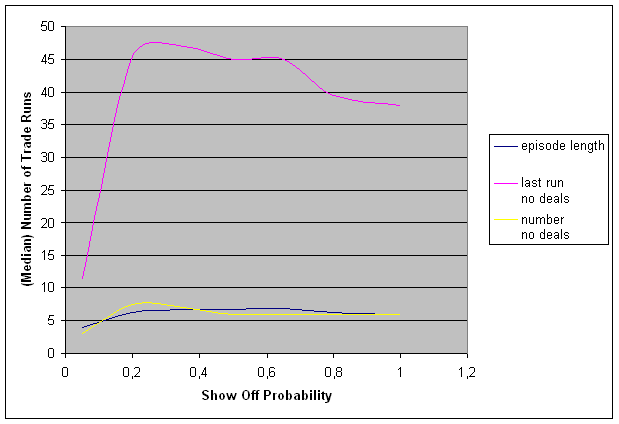
|
| Figure 13. Median of characteristics varying with showoff probability |
|
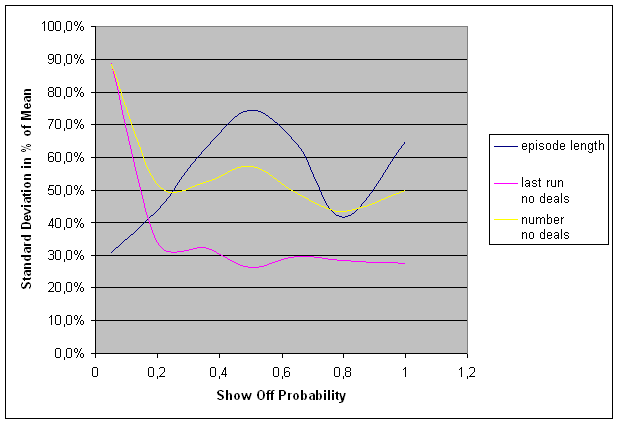
| Figure 14. Relative Standard deviation of characteristics varying with showoff probability |
| Table 2: Aggregated results scenario 2 | ||||
| last run no deals | number no deals | episode length | total A+B+C | |
| mean | 75 | 8 | 10 | 361 |
| median | 55 | 7 | 8 | 364 |
| std deviation | 82 | 5 | 5 | 25 |
| std deviation in % | 109% | 62% | 55% | 7% |
|
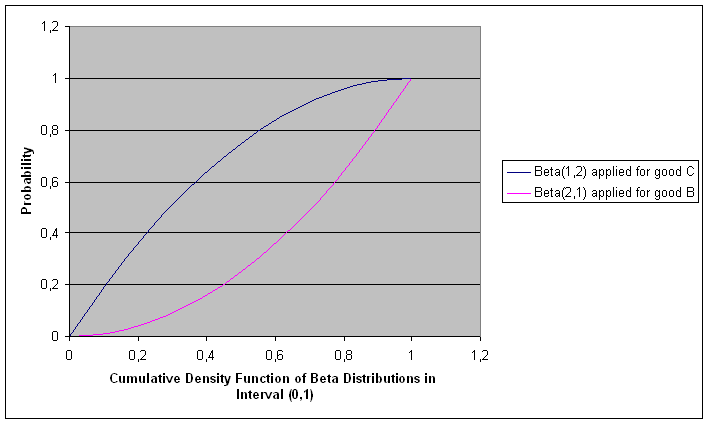
| Figure 15. Cumulative Β(1,2) and Β(2,1) distribution functions |
| Table 3: Aggregated results scenario 3 | ||||
| last run no deals | number no deals | episode length | total A+B+C | |
| mean | 151 | 11 | 12 | 397 |
| median | 97 | 9 | 11 | 397 |
| std deviation | 190 | 9 | 7 | 22 |
| std deviation in % | 126% | 76% | 54% | 6% |
|
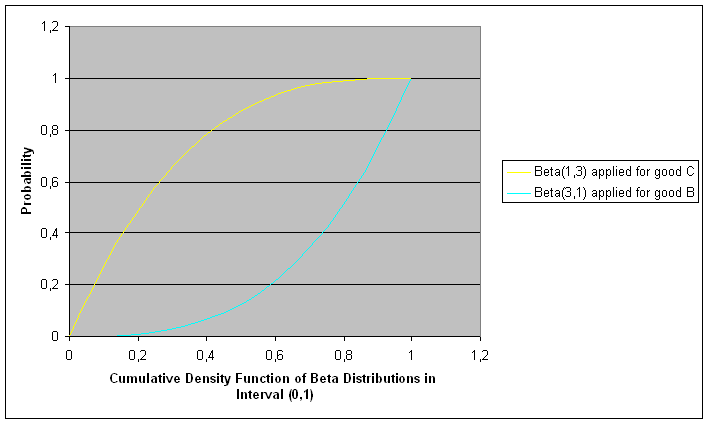
| Figure 16. Cumulative Β(1,3) and Β(3,1) distribution functions |
The following results were obtained:
| Table 4: Aggregated results scenario 4 | ||||
| last run no deals | number no deals | episode length | total A+B+C | |
| mean | 291 | 16 | 15 | 414 |
| median | 180 | 13 | 14 | 414 |
| std deviation | 332 | 12 | 9 | 17 |
| std deviation in % | 114% | 78% | 62% | 4% |
2see Luhmann (1995), p. 446-447: Self-referential, autopoietic reproduction would not be possible without an anticipatory recursivity.
3Luhmann (1989) includes a glossary of the most frequent terms in English.
4see Luhmann (1989) for a concise description of societal function systems. The differentiation of (world) society into function systems (and its primacy) is among the core theorems of Niklas Luhmann's theory. Note that both society as a whole and its function systems are defined as social systems.
5see Luhmann (1995), p. 412: Society is a system for which an encompassing system does not exist
6see Luhmann (1988), p. 413: society is the result of evolution. One does also speak of “ermergence”. ... there is today no other theory (except evolution) that can explain the emergence and reproduction of structures of the social system society
7see Luhmann (1988), p. 232: One can oppose the theorem of a certain structural isomorphism of meaning and money - if one means something different by meaning. But insights, that are worth to be preserved are possibly lost in this case.
8see further Luhmann (1993), pp 175-186
9see Axelrod (1997) p. 3: Agent-based modelling is a third way of doing science. Like deduction, it starts with a set of explicit assumptions. But unlike deduction, it does not prove theorems. Instead, an agents-based model generates simulated data that can be analysed inductively
10see Luhmann (1995), p. 43: An element is, what for a system functions as a not further dissoluble unity;
11see further Luhmann (1995), p. 240: To the Question, what are the parts of social systems, we give a double answer: Communications and their attribution as action.
12see further Luhmann (1995), p. 78: The system builds itself from instable elements, that last only a short amount of time - or as in the case of action have no duration by themselves. ... A stable system consists of unstable elements. The stability is a consequence of itself being a system, not of the elements. Still the system is constituted by its elements - in this case events. It has no basis for duration outside of these events (this is why we experience the present necessarily as short)
13see Luhmann (1995), p. 398: The theory of events and structures plus the theory of expectations are put together by the proposition that structures of social systems are made of expectations, that they are structures of expectations, and that for social systems - because they temporalise their elements as events of action - there are no other options to build structures. That means: structures do only exist as present structures
14see further Luhmann (1995), p. 363: Expectations are a primitve technique. This technique can be used nearly without prerequisites. It is not necessary to know who you are or what you know about your environment. One can have an expectation, without knowing the world - for pure luck. It is solely important, that the expectation can be used by the autopoiesis, so that the access to connecting reality constructions (“Vorstellungen”) is sufficiently pre-structured.
15See further Luhmann (1995), p. 149: In a somewhat different formulation, one can say: communication transforms the difference between information and utterance into the difference between acceptance or rejection of the utterance.
16see Luhmann (1995), p. 203: If communication is defined as synthesis of three selections (the unity of information, utterance and understanding), it is realised when and to what extent understanding happens. Everything further happens outside the unity of an elementary communication. This is not to be confused with the acceptance of refusal of the (communicated, i.e. understood) selection as a basis for own behaviour. But it cannot be ignored.
17For the definition of information (what was said?), utterance (was it said?) and understanding (selection of meaning) see Luhmann (1995), pp.137-175
18See Luhmann (1988), p. 26: that means, the structures of a system can only be varied by the systme's own operations. These operations themselves depend on the structures of the system.
19see Luhmann (1995), p. 92: Psychic and social systems evolved by means of Co-evolution
20Psychic systems are like social systems defined as autonomous systems processing meaning. Their elements are thoughts, not communications, see Luhmann (1995), p. 59
21The term n-to-m refers to n agents performing the task of Alter, m agents performing the task of Ego. Note that in Luhmann's terminology Ego is the agent that understands information and utterance of the agent Alter. Alter is the agent that has provided an offer for communication (an action), as attributed (understood) by Ego.
22The choice of the lexicographic smallest index (instead of random) was preferred at this stage of model development to be able to reproduce results.
23The motivation to show-off lies outside the economic system. It is not governed by bounded rationality focussed on ownership of goods. Probability is used to separate autonomous system dynamics and environmental dynamics. The same holds for the initial distribution of wealth, which is also outside the dynamics of the economic system.
24see xxii
25see xxii
26see xxii
27The term larger environment refers to the environment of agents as observable to the constructer of the model, who has - compared to the agents within this model - superior observation capacity
28see Devaney (2003), p. 60: Let f:R into R be continous. Suppose f has a periodic point of period 3. Then f has periodic points of all other points.
AXELROD, Robert M. (1997), The Complexity of Cooperation. Princeton
DEVANEY, Robert L. (2003), An Introduction to Chaotic Dynamical Systems, 2nd Edition. Westview Press
DUNBAR, Robin I. M. (1996), Grooming, Gossip and the Evolution of Language. Harvard University Press, 1998
JOAS, Hans and KNÖBL Wolfgang (2004), Sozialtheorie, Zwanzig einführende Vorlesungen. Suhrkamp, 2004.
KRON, Thomas and DITTRICH, Peter (2002), "Kontingenz nach Luhmann - ein Simulationsexperiment" in Kron, Thomas (Ed.) (2002), Luhmann modelliert. Leske+Budrich
LAWVERE, F. William and Schanuel, Stephen H. (1997), Conceptual Mathematics. Cambridge University Press, 2002
LEYDESDORFF, Loet (2004), "Meaning, Anticipation and Codification in Functionally Differentiated Systems of Communications" in Kron, Thomas, Schimank, Uwe, Winter, Lars (eds), Luhmann simulated - Computer Simulations of the Theory of Social Systems. Hamburg, LIT-Verlag (in Vorbereitung) 2005.
LUHMANN, Niklas (1973), Zweckbegriff und Systemrationalität, 6. Auflage. Suhrkamp, 1999
LUHMANN, Niklas (1975), Macht. Lucius & Lucius. Suhrkamp, 2003
LUHMANN, Niklas (1984), Soziale Systeme, Grundriß einer allgemeinen Theorie. Suhrkamp, 1999
LUHMANN, Niklas (1988), Die Wirtschaft der Gesellschaft. Suhrkamp, 1999
LUHMANN, Niklas (1989), Ecological Communication (translated by John Bednarz, Jr.). The University of Chicago Press
LUHMANN, Niklas (1993), Risk: A Sociological Theory (translated by Rhodes Barrett). Aldine De Gruyter
LUHMANN, Niklas (1995), Social Systems (translated by John Bednarz, Jr.). Stanford University Press
LUHMANN, Niklas (1997), Die Gesellschaft der Gesellschaft. Suhrkamp, 1999
MEHLMANN, Alexander (1997), Wer gewinnt das Spiel. Vieweg
MILGROM, Paul (2003), Putting Auction Theory to Work. Cambridge University Press
MOOD, Alexander M. and Graybill, Franklin A. and Boes, Duane C. (1974), Introduction to the Theory of Statistics. McGraw Hill, 1983
NELSON, Richard R. and WINTER, Sidney G. (1982), An Evolutionary Theory of Economic Change. The Belknap Press of Harvard University Press
PINGLE, Mark and TESFATSION Leigh, 2003, "Evolution of Worker-Employer Networks and Behaviors Under Alternative Non-Employment Benefits: An Agent-Based Computational Study", pp. 253-284 in Anna Nagurney (ed.), Innovations in Financial and Economic Networks. Edward Elgar Publishers, 2003.
SIMON Herbert A. (1951), "A Behavioural Model of Rational Choice", Quarterly Journal of Economics 69, pp. 99-118. Reprinted in Models of Man. Wiley, New York, 1957
WOLKENHAUER, Olaf (2001), Data Engineering. Wiley
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]