Günter Küppers and Johannes Lenhard (2005)

Validation of Simulation: Patterns in the Social and Natural Sciences

Journal of Artificial Societies and Social Simulation vol. 8, no. 4
<https://www.jasss.org/8/4/3.html>

For information about citing this article, click here

Received: 02-Oct-2005    Accepted: 02-Oct-2005    Published: 31-Oct-2005

Abstract

In most cases, the meaning of computer simulation is strongly connected to the idea numerical calculations. A computer simulation is a numerical solution of a complex mathematical problem. Therefore, the problem of validation of its results should be only a problem of judging the underlying computational methods. However, it will be argued, that this is not the case. It is consensus in literature that validation constitutes one of the central epistemological problems of computer simulation methods. Especially in the case of simulations in the social sciences the answers given by many authors are not satisfactory. The following paper attempts to show how the characteristics of simulation, i.e. the imitation of a dynamic, constitute the problem of validation even in the case of the natural sciences and what consequences arise. Differences as well as common grounds between social and natural sciences will be discussed.

Keywords:

Generative Mechanism, Imitation, Patterns, Simulation, Validation

Introduction

1.1

Generally speaking, a malingerer is a person who simulates the symptoms of a specific disease in a way that even doctors are not able to see through the perfect performance. Felix Krull is a literary figure in a novel of Thomas Mann who played the game as exact as it was possible. He studied medical literature about a specific neural disease which could not be healed and practiced the symptoms in a perfect way. He misled the doctors of a military commission and became for this reason liberated from the military service.

1.2

This example may illustrate some of the problems which arise when the validity of computer simulations has to be judged. In the case of Felix Krull it is the performance of the symptoms which decide about the quality of a simulation. This might be different in the case of computer simulations, which are going to become an important tool of knowledge production, especially in cases, where theoretical or experimental strategies fail because of complexity. To get an answer in this case one has to determine the epistemic status of the knowledge produced by a computer simulation. If it is a numerical solution of an underlying mathematical model, i.e. the calculation of the variables defined by it, the quality of a computer simulation depends on the quality of calculation, especially on the ability to handle unavoidable calculation errors. But if a computer simulation is not merely a calculation of variables but rather an imitation of a model's behaviour in space and time, its quality is an open question which has to be answered if one wants to rely on its results.

1.3

The problem of validation of computer simulation will be the topic of this paper. Even if one believes that simulations are numerical calculations, there seems to be a difference between simulation models based on a mathematical model which, e.g. represents the physical laws of hydrodynamics as it is the case in climate research, and simulation models based on a few qualitative assumptions about the leading mechanisms as for instance in so called agent based simulation models in the social sciences. In the first case there should be no doubt about the validity of the model and the results of the simulation. The only open question will be whether the physical model is complex enough to produce the dynamics in which one is interested in. In other words: The reliability of the knowledge produced by computer simulation is taken for granted if the physical model is correct. In the second case of social simulations in general there is no theoretical model on which one could rely. The knowledge produced in this case seems to be valid if some of the characteristics of the social dynamics known from experience with the social world are reproduced by the simulation. In this case the simulation might be seen as a proof for the basic assumptions of the underlying phenomenological model.

1.4

In literature it is consensus that validation constitutes one of the central problems of computer simulation methods. There is a wide variety of accounts of different strategies for validating simulations in social sciences. Nevertheless, there can be distinguished a common starting point. In the following, it is called the common view on validation. It is based on the assumption of a double correspondence, or analogy.

1. First, the social sciences are structurally equivalent to the natural sciences. Hence, considerations about validity in the social sciences can draw directly on knowledge and practices of validation in the natural sciences.
2. Second, computer simulations are analogous to theories in general.

1.5

Combining these two components, the common view holds that the discussion on validating simulations in the social sciences has to follow the lines of the discussion about confirmation of scientific theories, referring mainly to theories in physics. Two examples out of many:

The validation problem is an explicit recognition that simulation models are like miniature scientific theories.
(Kleindorfer and Ganeshan 1993, 50)

Validation of simulation models is thus the same as (or least analogous to) validation of theories. (Troitzsch 2004)

1.6

A few words on terminology are appropriate. The technically oriented literature discerns between verification, validation, and certification which build different aspects of confirming a simulation model.

Assessment of transformational accuracy (verification), assessment of behavioral or representational accuracy (validation), and independently assuring sufficient credibility (certification) of complex models and simulations pose significant technical and managerial challenges. (Balci 2003)

1.7

There is a huge amount of literature on the more technical aspects of "V,V&C" (Balci 2003). Verification procedures afford in some cases highly sophisticated approaches. Certification is a somewhat different case. What can count as certified simulation-based knowledge depends strongly on the purposes and goals of the simulation. It is difficult to give a general treatment on those issues, because they are to a great extent case-sensitive. The central concern in this article will be the third relation, validity, that is connected to "representational and behavioural accuracy". In other words: A simulation is valid because it relies on laws which represent reality. In the following, the argumentation will bring to the fore that in the case of simulation it is the difference between representation and behavioural accuracy that makes validation of simulation an intriguing subject matter. In particular, simulations ask for additional ways of modelling to overcome for instance numerical instabilities. Sometimes it is even unclear what the appropriate model is which produces the dynamics in which one is interested in. Therefore, simulations are models of models and the question is whether this implies a new, or at least modified, account of validation.

1.8

The common view treats simulations as analogous to scientific theories in general. Consequently, the problem of validation is debated in close connection to the classical standpoints of philosophy of science regarding confirmation of theories. By and large, the discussion about validation of simulation is reflecting the development of the now "classical" positions in philosophy from logical empiricism over Popper to Kuhn and Lakatos, cf. the early attempt of Naylor and Finger (1967), or the extensive contributions of Sargent, e.g. (1992), who adds positive economics as a further "historical" approach to validation.

1.9

This is not the place to discuss these arguments in more detail. In physics a distinction is made between a general theory like electrodynamics and the equations of motion which are an application of the theory. Sometimes artificial concepts like 'boundary layer' have to be introduced to get a model which can be solved in a specific case. Currently a discussion takes place in the philosophy of science that centres around this problem, i.e. the role and function of models and its relationship to theories. Models, so the main point, are essentially different from theories. Models play a mediating role between theory and phenomena ("models as mediators", cf. Morgan and Morrison 1999) and can be interpreted as "(partly) autonomous agents" (Morrison 1999). This discussion has had no impact yet on the literature about simulation in the social sciences. Nevertheless it is highly relevant for the subject matter. Recently, it has been argued that simulation models are a specific kind of models and that the simulation method can be seen as associated with a characteristic realisation of the mediating role — be it "semi-autonomous" (Winsberg 2003) or as "modelling of second order" (Küppers and Lenhard 2005). The main claim of the next chapter will be that simulation modelling can not be conceived of as a mode of calculation but as an attempt for imitation (cf. Küppers and Lenhard 2005).

1.10

In the following we want to discuss in more detail the problem of validation of computer simulations with respect to the natural as well as to the social sciences. Our aim is to show that the validation problem of computer simulation is the same in both cases. However, contrary to the common view on the validation problem, this is by no means an argument that the social sciences can participate on the success story of the natural sciences. Our argument will be that computer simulations are even in the case of exact mathematical models imitations of a complex — social or natural — dynamics by the means of an adequate generative mechanism. Thus, even in strongly theory-driven sciences, simulations are not numerical solutions of a theoretical, albeit complex, model. For this reason neither in the natural sciences nor in the social sciences computer simulations can be validated by theoretical arguments. In the next section, our argument will be developed drawing on a case study in meteorology. The consequences for the validation problem are discussed in the last chapter.

Simulation as Imitation — A Case Study from Climate Research

Phillips' Experiment

2.1

In 1955, Norman Phillips, working at Princeton's Institute for Advanced Studies, succeeded with the so-called first experiment in simulating the dynamics of the atmosphere, i.e. in reproducing the patterns of wind and pressure of the entire atmosphere in a computer model. (Phillips 1956. For more details of the experiment, cf. Lewis 1998, for a broader history of ideas of the modelling of the general circulation of the atmosphere, cf. Lorenz 1967.) This development of a simulation model of the general circulation of the atmosphere was celebrated as a major breakthrough. It surprised the experts, because it was generally accepted that a theoretical modelling approach would hardly be possible — the complexity of the processes that determine atmospheric circulation was judged insurmountable for an approach via a simple model.

2.2

This first attempt to build a simulation model of the entire atmosphere was considered an "experiment". This underlines how uncertain the success of this project was. At the same time, the conception of "experiment" expresses an important aspect for the methodology: in simulations, scientists use their models like an experimental set-up. Hence, the results of simulations acquire a quasi-empirical character.

2.3

Phillips had to introduce the physical laws that govern the dynamics of the atmosphere. He used only six basic equations (PDEs) which since then are called the "primitive equations". They are generally conceived of as the physical basis of climatology. These equations express well-known laws of hydrodynamics — the surprising thing was that only six PDEs were sufficient to reproduce the complex behaviour, and Phillips had the skill and luck of making an adequate choice.

2.4

The physical basis had to be adapted to the grid. The construction of a discrete model is a typical task of simulation modelling. The global and continuous equations of hydrodynamics had to be reformulated in order to calculate the time evolution of the relevant variables — pressure, temperature, wind speed — at the grid nodes step by step. The dynamics was started and the atmosphere settled down in a so-called steady state that corresponded to stable flow patterns.

2.5

The tantalizing question was whether the model was able to reproduce the global flow patterns of the real atmosphere well-known from observations. For instance, one criterion was the complex pattern of the so-called surface westerlies, winds blowing continuously north the equator. The result was positive — everyone was impressed by the degree of correspondence. As we mentioned before, the experts were sceptical about the possibility of a global (and not far too complicated) model, but the empirical success was convincing. The decisive criterion for success was the adequate imitation of the phenomena, i.e. the flow patterns, not the derivation from theoretical principles.

2.6

The continuous primitive equations of the atmosphere were not solved in the strict sense during Phillips' experiment, rather, the phenomena of the atmosphere were imitated by the generative mechanism of the discrete difference equations. The success of the imitation was judged by its correspondence to the flow patterns observed. Insofar, the validation of simulation results relies on a quasi-empirical strategy.

The Problem of Instability — Arakawa's Trick

2.7

There is a certain condition that simulations have to fulfil, a condition that you will certainly be well-acquainted with, namely stability. The generative mechanism chosen that is to imitate a certain dynamics, must "run" on the computer. It must not become instable because of discretization errors and truncation errors building up. Numerical instabilities are a severe and fundamental problem of simulation modelling.

2.8

Phillips simulation experiment was a tremendous success, but it exhibited also an important failure of the simulation model: the dynamics of the atmosphere were stable only for a few weeks. After about four weeks, the internal energy blew up, and the system "exploded" — the stable flow patterns dissolved into chaos. "After 26 days, the field … became very irregular owing to large truncation errors, and is therefore not shown." (Phillips 1956, 145)

2.9

Nevertheless, the experiment was seen in general as a success. The possibility of simulating the atmospheric circulation was not doubted. Instead, it was acknowledged as a challenge for further research to achieve a stable model. Questions of stability were important for climate research, as it was interested in long-time predictions. And they were of equal importance for the simulation method in general, because it is a rather general and typical task of replacing the "natural" dynamics of a system of PDEs by the "artificial" dynamics of a discrete system in a stable way. Phillips was well aware of the superior importance of stability issues and he suggested the truncation errors as the cause of instability.

2.10

Years of intensive and highly competitive research followed. The solution of the problem was assumed to consist in adequate smoothing procedures to cancel out the errors before they could blow up. This strategy was obviously oriented at the ideal of calculating as correctly as possible. Instabilities were seen as resulting from errors, inaccurate deviations of the discrete model from the true solution of the continuous system.

2.11

The decisive breakthrough, however, was achieved by a different approach, one pursued by Akio Arakawa, a mathematically highly gifted meteorologist who was developing a GCM at the University of California in Los Angeles (UCLA). For him, imitating the dynamics was of prime importance, and less the precise calculation of a solution.

2.12

At heart, Arakawa had realised that one could set aside a strict solution of the basic equations. One even should do so! If the time development of the simulation was reproducing the patterns of the atmosphere in a sufficiently adequate manner, and if the simulation was stable, then it was not obliged to be a solution of the basic equations — not even in the limit! To put the whole thing in a nutshell, the point of Arakawa's approach was: imitation of the phenomena beats solution of the equations.

2.13

Of course, this does not imply that one can simulate a given dynamics by completely arbitrary mechanisms. Far from that. And Arakawa very wisely adhered to the given equations. BUT he applied what later was to be known as "Arakawa's computational trick". The basic equations define a generative mechanism whose development over time is formally described by the Jacobi operator. Arakawa replaced the Jacobian by another operator he himself had constructed, later called Arakawa-Jacobian. The construction of the Arakawa operator is full of highly sophisticated mathematical arguments. The details do not matter in our context here (cf. Arakawa 1966, and the reconstruction in Arakawa 2000.) The pivotal fact is that the Arakawa operator permitted a stable long-time integration because he avoided the non-linear instability Phillips had had to face. Arakawa was able to prove this property mathematically.

2.14

To guarantee the stability of the simulation procedure, Arakawa had to introduce further assumptions, partly contradicting experience and the physical theory. He had to assume that the kinetic energy in the atmosphere would be preserved. This is definitely not the case in reality, where part of this energy is transformed into heat by friction. Moreover, dissipation is presumably an important factor for the stability of the real atmosphere. So we can summarize that Arakawa, in assuming the preservation of kinetic energy, "artificially" limited the blow-up of instabilities. In the real atmosphere, friction is responsible for that effect. Incidentally, John von Neumann had employed a very similar strategy. He introduced an "artificial viscosity" to bring about a realistic behaviour while simulating the propagation of "shock waves" (cf. Winsberg 2003).

2.15

Utilizing conservation assumptions that obviously went against theory and experience was taken up very sceptical by the community. As Arakawa remembered, the tenor was: "Why require conservation while nature does not conserve?" (Arakawa 2000, 16) While most researchers were convinced that the promising path was to find a solution of the primitive equations as accurate as possible, Arakawa had made an additional modelling step. This step was not derived from the theoretical basis, and was justified only by the results of simulation runs that showed quasi-empirically that the Arakawa operator led to a successful imitation. The success of his approach was eventually generally accepted, and his initially controversial approach, is today conceived of as a "computational trick" (cf. Weart 2001).

2.16

It is an illustrative fact that Arakawa's approach proved to be superior in the course of a simulation experiment. At first, in the 1960s, Arakawa had a couple of scientific rivals that tried to develop different smoothing procedures to avoid the problem of non-linear instabilities. Again, an experiment brought about a decision. In 1978, Jule Charney conducted a simulation experiment that consisted in the competition of different GCMs. They ran in parallel, starting with the same initial conditions. Three GCMs took part: Leith/ Lawrence Livermore Lab; Smagorinsky/ GFDL Princeton und Arakawa/ UCLA. The first had implemented smoothing procedures, while the UCLA-model was based on the Arakawa-operator. Phillips describes the outcome:

three general circulation models (…) were used for parallel integrations of several weeks to determine the growth of small initial errors. Only Arakawa's model had the aperiodic behaviour typical of the real atmosphere in extratropical latitudes, and his results were therefore used as a guide to predictability of the real atmosphere. This aperiodic behaviour was possible because Arakawa's numerical system did not require the significant smoothing required by the other models, and it realistically represented the nonlinear transport of kinetic energy and vorticity in wave number space. (Phillips 2000, xxix)

Performance Beats Theoretical Accuracy

2.17

Let us take stock of the case study. We have seen that there is no common theoretical ground which would permit to relate a simulation model directly to its underlying mathematical model. Simulation modelling has to transfer a mathematical model into algorithms which can be implemented on a computer. This necessitates to introduce artificial, non-realistic effects in order to overcome numerical instabilities. Therefore, even in the case of natural sciences, the validation of the outcome of a simulation can not be judged on the basis of the validity of the mathematical model on which the simulation model is grounded. Only the experience, i.e. existing data can be used to validate computer simulations. For this reason performance beats theoretical accuracy. This is the point where adequacy of representation and successful imitation of behaviour fall apart. That is, simulations can achieve behavioural accuracy without being structurally accurate.

2.18

Similar claims have been made with regard to the social sciences. For instance, Hegselmann (1996) applies percolation models to the dynamics of opinions not based on accurate assumptions, rather aiming at a reproduction of the experiences made in pattern formation. Most prominently, Milton Friedman (1953) argued in favour of an "as-if" account, i.e. judging models according to their behaviour, not according to the assumptions made. The present case, however, exceeds those claims, because here the theoretical mathematical model is taken to be a highly accurate description that is, nevertheless, ruled out by the behaviour of the simulation.

2.19

Because of the partial autonomy of the simulations from the theoretical basis, simulations are not merely numerical calculations. Rather, they are models of second order in the sense of iterated model construction. This result does not seem to be restricted to simulation models that stem from a system of continuous PDEs. They constituted the extreme case where simulation as calculation seemed to be most plausible. Other simulation procedures employ generative mechanisms in a similar way to imitate a certain dynamic.

2.20

Therefore, the adequacy of a simulation model cannot be theoretically deduced, nor derived from general principles. Simulation results have to be judged by experience. The quasi-empirical approach, that permits to tune the models in face of theoretical model experiments, is a necessary methodological condition for simulations of that kind. Theoretical alternatives can be compared empirically. Hence, it is justified to speak of computer simulations as of experimenting with theories. This provides simulations an independent status in knowledge production, they combine traits both of experiment and theory. (For similar theses concerning the autonomous status of simulations cf. Rohrlich 1991, Humphreys 1991, Galison 1996.)

2.21

This seems to be a result that forms (at least) an important part of an epistemic characterization of simulations, and of the knowledge they provide. What does this imply for our initial question concerning the validity of simulation results?

Epistemic Characteristics

2.22

Simulation models constitute a particular class of models, distinct from theoretical models that are tractable by analytical methods. Admittedly, simulations often are based on theoretical models, e.g. a system of non-linear PDEs, but they require further steps of formal treatment because they have to be implemented into a computer. In this sense simulation models are partly independent from the underlying theoretical model. Therefore, simulations are no mere calculations. On the contrary, they should be viewed as imitation of a dynamics by a generative mechanism. Therefore the analogy between simulation and microscope makes sense: the simulation is a method to look at the dynamics which is encoded in a formal mathematical model. This provisional definition includes both physical and social objects. In social science, simulations often compensate the lack of a general theory. Simulations employ computational experiments to investigate whether the chosen generative mechanism produces the characteristics described by the theoretical model. In the natural sciences, however, in many cases one has a more or less detailed theory from which a set of differential equations can be obtained in a concrete application which could be of theoretical as well as of practical interest. The common view on simulations states that they provide numerical solutions of such a set of equations — a specific model of the given theory — that are not tractable with analytical means. We have seen that this view is wrong. Simulations are not numerical solutions of those models, rather the imitation of their underlying dynamics.

2.23

This claim is nicely backed by agent-based simulation modelling, forming a rapidly expanding class of simulation models in the social sciences. (Cf. Rosenwein and Gorman (1995) and their discussion in Fuller (1995), Halpin (1999), or Hegselmann (1996) that provide an insight into the variety of recent approaches.) Agent-based models simulate a dynamic without claiming that they are implementing the fundamental laws of interaction. In the contrary, one typically starts with a huge amount of data and a simulation counts as successful, if the implementation of some interaction rules lead to a reproduction of structural characteristics of the data, cf. Ahrweiler and Gilbert (1998), Hegselmann (1996), Axelrod (1997), or Gilbert and Troitzsch (1999). A famous example is the kind of patterns sugarscape produces.

2.24

It is important that the pattern maintains a polarity between positive and negative. By this fact one learns about rules that are sufficient to produce such patterns, rather than aiming at concrete predictions in real situations. From the simulation one can gain insights about which interactions and structural presuppositions may be good candidates for explaining observed patterns of behaviour. Obviously, the model is only "imitating" the behaviour of agents — a realistic representation is not aimed at!

2.25

One would hardly find any reasoning in this field that would make concrete predictions based on such simulations. This is fairly typical. (Some authors doubt that any correct predictions were ever achieved in economics, cf. Moss 2003.) The claim that simulations can be viewed as imitation via generative mechanisms is more or less obvious in this context. Admittedly, there exists a quite different species of simulation models in the social sciences that do not much resemble sugarscape and its kinship. Many simulations in social sciences and politics aim at prediction, e.g. to discuss different scenarios of tax policy. These models are oriented at the predictive success of the engineering and the natural sciences. Our case study in meteorology is relevant here, because it treats the "hard" case for our claim, i.e. simulation models that are indeed based on theoretical models.

2.26

Even here, it has been shown, simulations are imitations of complex processes by generative mechanisms. Admittedly, these mechanism are guided by theory, but not determined by theory. At the end, we shall argue that the performance of the model on the computer is more important than its theoretical derivation and its accuracy of calculation — performance beats accuracy.

Validation of Patterns — Patterns of Validation

3.1

Are there any specific differences between simulations in the natural sciences and those in the social sciences? And, moreover, what are the implications for validation of the different simulation models?

3.2

The situation in climate research can be considered as rather typical for the natural sciences. The simulation squeezes out data from a theory, or, in other words it uses a generative mechanism which is be based on a theoretical model to produce data. But at the beginning of simulation within climate research the reproduction of the well-known global patterns of the atmosphere like the "westerlies" was important for believing in power of computer simulation. That was the breakthrough of Phillips' experiment with the 'primitive equations'.

3.3

For validation, the comparison between simulated and observed patterns of the atmosphere was pivotal, and, of course, remains to be so. A main interest of climate research concentrates on data about the dynamics of the climate system in terms of the global average temperature. The enormous efforts of palaio-climatology to reconstruct data about the past climate can be used to validate the models retrospectively. The goal is not to find general structural patterns of climate dynamics, but rather "the right" description of the actual dynamics of the climate. A quite representative statement from interviews (conducted in 2002/2003 at several centres of climate research in the US and Germany) was that confidence in the validity of the model is mainly based on retrospective validity:

"It is my goal to take the best models and compute the last hundred thousand years. And if they succeed to simulate the rapid changes, ice-ages, that occurred in the past, yes, then I have hundred percent confidence" (transcript from interview).

3.4

The overall goal is, clearly, to make predictions of the future development of the climate system. A valid model should produce confidence in its predictions. One of the most cited pictures in climate research is the so-called hockey racket:

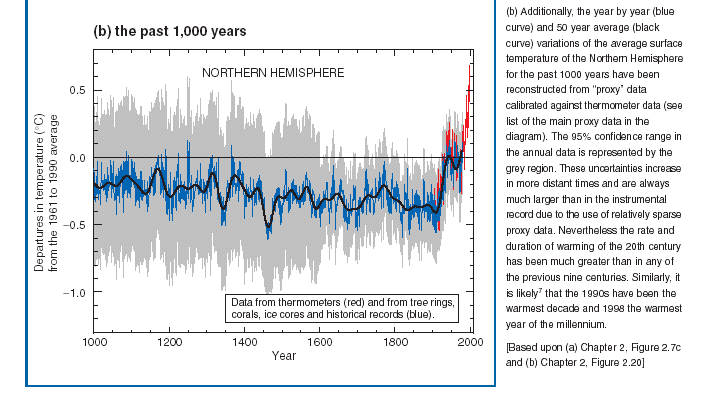
Figure 1. Mean global temperature, observed and estimated, from IPCC Assessment Report

The shaft shows a good fit between observed and retrospectively predicted data. This fit is taken to validate the prediction — the substantial rise of the mean temperature.

3.5

In social science, simulations are often applied where general theories are lacking, while a vast amount of data or a phenomenological description of social dynamics may be available. The goal of simulations is typically to reproduce certain patterns or aspects of observed data. A famous example, among quite a few, is sugarscape, the dynamic of an "artificial social life". Simulation models of this kind do not aim at predictions about what will happen with a concrete system. Moss has pointed in a very similarly direction:

There has never in the history of Economics and Management Science been a correct forecast of macroeconomic or financial market turning points or turning points in retail market sales. I know less about sociology, but my reading of the journals in that field suggests that no sociological theory offers systematically well validated predictions, either. (Moss 2003)

3.6

To state the things clearly, this observation does not propose any fundamental differences between the objects of social models and those of physics. Moreover, the simulation method proceeds rather similar — Phillips' experiment parallels that of Epstein and Axtell to a great extent. The essential point is that (often) in the natural sciences one has a general theory about the objects and simulation models are used as instruments to generate data and to make predictions about the behaviour of these objects. On the other side, agent-based models are instruments to explore the theoretical structure of the data.

3.7

The common view on validity of simulation models seems to neglect these differences between social and natural sciences. The latter are taken as paradigm for both. Zeigler, for instance, discerns different types of validity: replicative, predictive and structural validity. A model is said to be structurally valid if "it truly reflects the way in which the real system operates to produce this behaviour." (Zeigler 1976, 5)

3.8

It is obvious that simulation modelling in the social sciences would hardly be able to reach these stages of validity. It is, however, a misconception to take this as a shortcoming of the simulation models: the goal is different. Hence, the classical hierarchy of validity is not an adequate measure for validity of simulations in the social sciences. Moreover, it was shown in the last chapter that even in the natural sciences behavioural imitation is the key concept. (Troitzsch 2004 has observed a similar point, but he seems to make the objects (not the goals) of the sciences responsible for the differences.) The orientation at the natural sciences suggests that the social sciences would be in a kind of transition, or in a state of infancy compared to, e.g., physics. This is, in our view, a misconception. It is far more convincing to view the criteria of validation as depending on the purpose of the model (cf., e.g., Lehman 1977). This view can be exemplified by model-to-model (M2M) analysis, a validation strategy of growing importance in the context of simulation modelling. It is applied in climate research as well as in agent-based models of social dynamics. It is a general observation that simulation approaches bring with it a plurality of models that can be compared each with the other in a simulation setting.

3.9

To carry forward the already mentioned examples, consider again climate research. How valid are the predictions of different models? In 2000, researchers were taking stock by comparing the predictions of different models concerning the climate in the US (Allen et al. 2000). The models' results are patterns like those of figure 2.

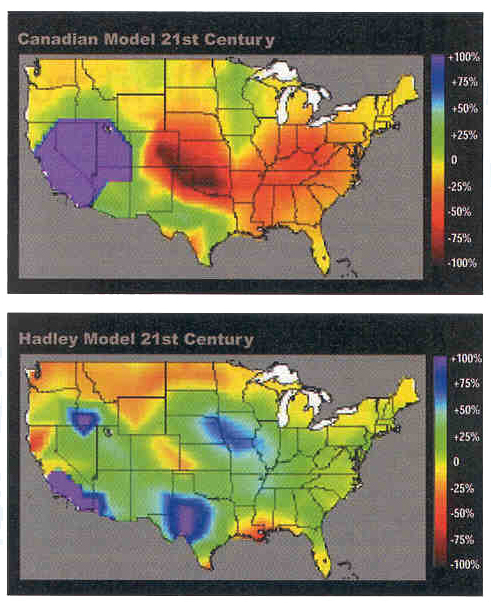
Figure 2. Predicted precipitation in US according to Canadian (upper part) and UK (lower part) simulation model

3.10

The comparison was reported as "dueling models" (Kerr 2000) and it showed that a great variability exists if one is considering the predictions for individual regions, e.g. whether the Middle West of the US will experience dry or rather wet summers. The background assumption, however, is that on a theoretically fundamental level the dynamic of the climate is stable. Consequently, according to the assumption, the difference in the predictions will disappear when the models are refined. In short, M2M is employed to estimate the range of uncertainty of the currently available models' predictions.

3.11

Recently, also in multi-agent based simulation models (MABS) of social systems, the M2M analysis has been strongly advocated (Hales et al. 2003, 1.6). The strategy is similar to that followed in the natural sciences and M2M analysis is a widely applicable method for validating simulation models. But while the strategies of validation are analogous in the social and natural sciences, the goals are not. The statement of Hales et al. that "the ultimate aim of such work [re-analysing models by comparison, J.L.] is to approach a level of rigor and reproducibility that has become the norm in the natural sciences." (ibid., 1.17) is right but can be easily misinterpreted.

3.12

One should have in mind that the rules of validation in the natural sciences concern mainly the reproducibility of results with regard to experiences, i.e. existing data. In climate science, this means the reproduction of the climate history. This strategy does not apply to the social sciences where "to uncover rules that generate patterns" often is the main goal. What can be an adequate strategy to achieve that goal? No substantial answer can be given here. One would have to take into account various treatments of that problem in literature, among them Epstein's and Axtell's slogan "Can you grow it?" (1996) and considerations about the construction and plausibility of those rules (cf. Macy and Willer 2002, or Conte et al. 2001).

3.13

The characteristics of the validation problem in simulation become even more obvious when real systems are discussed whose parts do not share common theoretical ground. In climate research, example continued, there are voluminous projects of model intercomparison, like the currently conducted CMIP (coupled model intercomparison project) that involves the leading simulation centres worldwide. It is aiming to determine the range of uncertainty in the recent predictions of the climate change. The CMIP is part of the hybrid scientific and political effort undertaken by the IPCC (Intergovernmental Panel on Climate Change), a global institution in close connection to the UN, to gather and prepare the currently available scientific knowledge on climate change. The leading scientists as well as political stakeholders are part of the IPCC. In short, the validity of simulation models plays a crucial role as a presupposition of a (possible) consensus about climate change.

3.14

When social situations are modelled, a particular twist may come up turning the additional validation problem into an advantage: the agreement of participants or stakeholders may be an indicator of the validity of a simulation model (cf. Troitzsch 2004). This supports the view that the very meaning of validity is dependent on the purpose of the simulation models under examination.

Acknowledgements

We kindly acknowledge the financial support of the project by the Volkswagen Foundation.

References

AHRWEILER, P. and G. N. Gilbert, Eds. (1998). Computer simulations in science and technology studies. Berlin, Springer.

ALLEN, M. R., P. A. Stott, et al. (2000). "Quantifying the uncertainty in forecasts of anthropogenic climate change." Nature 407: 617-620.

ARAKAWA, A. (1966). "Computational Design for Long-Term Numerical Integration of the Equations of Fluid Motion: Two-Dimensional Incompressible Flow. Part I." J. Comp. Phys. 1: 119-143.

ARAKAWA, A. (2000). A Personal Perspective on the Early Years of General Circulation Modeling at UCLA. General Circulation Model Development. D. A. Randall. San Diego, Academic Press: 1-66.

AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. Simulating Social Phenomena. R. Conte and R. Hegselmann. Berlin, Springer: 21-40.

BALCI, O. (2003). Verification, Validation, and Certification of Modeling and Simulation Applications. Proceedings of the 2003 Winter Simulation Conference. Piscataway, NJ, IEEE: 150-158.

CONTE, R., B. Edmonds, et al. (2001). "Sociology and Social Theory in Agent Based Social Simulation: A Symposium." Computational and Mathematical Organization Theory 7(3): 183-205.

EPSTEIN, J. M. and R. Axtell (1996). Growing Artificial Societies. Cambridge, MIT Press.

FRIEDMAN, M. (1953). Essays in Positive Economics. Chicago, University of Chicago Press.

FULLER, S. (1995). "Symposium on social psychological simulations of science. On Rosenwein's and Gorman's simulation of social epistemology." Social Epistemology 9(1): 81-85.

GALISON, P. (1996). Computer Simulations and the Trading Zone. The Disunity of Science: Boundaries, Contexts, and Power. P. Galison and D. J. Stump. Stanford, Calif., Stanford Univ. Press: 118-157.

GILBERT, G. N. and K. G. Troitzsch (1999). Simulation for the Social Scientist. Buckingham, Open University Press.

HALES, D., J. Rouchier, et al. (2003). "Model-to-Model Analysis." Journal of Artificial Societies and Social Simulation 6(4).

HALPIN, B. (1999). "Simulation in Sociology." American Behavioral Scientist 42(10): 1488-1508.

HEGSELMANN, R., Ed. (1996). Modelling and Simulation in the Social Sciences from the Philosophy of Science Point of View. Dordrecht, Kluwer.

HUMPHREYS, P. (1991). Computer Simulations. PSA 1990. Fine, Forbes and Wessels. East Lansing, Philosophy of Science Association. 2: 497-506.

KERR, R. A. (2000). "Dueling Models: Future U.S. Climate Uncertain." Science 288: 2113.

KLEINDORFER, G. B. and R. Ganeshan (1993). The Philosophy of Science and Validation in Simulation. Proceedings of the 1993 Winter Simulation Conference. G. W. Evans, M. Mollaghasemi, E. C. Russell and W. E. Biles: 50-57.

KÜPPERS, G. and J. Lenhard (2005). "Computersimulationen: Modellierungen zweiter Ordnung." Journal for General Philosophy of Science, to appear.

LEHMAN, R. S. (1977). Computer Simulation and Modeling : an Introduction. Hillsdale, NJ, Erlbaum.

LEWIS, J. M. (1998). "Clarifying the Dynamics of the General Circulation: Phillips's 1956 Experiment." Bull. Am. Met. Soc. 79(1): 39-60.

LORENZ, E. (1967). The Nature of the Theory of the General circulation of the Atmosphere. Geneva, World Meteorological Organization WMO, Technical Paper No. 218, 115-161.

MACY, M. W. and R. Willer (2002). "From Factors to Actors: Computational Sociology and Agent-Based Modeling." Annual Review of Sociology 28: 143-166.

MORRISON, M. and Morgan, M. S. (1999). Models as autonomous agents. Models As Mediators. Perspectives on Natural and Social Science. M. S. Morgan and M. Morrison. Cambridge, Cambridge University Press: 38-65.

MOSS, S. (2003). "Simulation and Theory, Simulation and Explanation. Contribution to the SIMSOC mailing list." www.jiscmail.ac.uk/archives/simsoc.html 14 November 2003.

NAYLOR, T. H. and J. M. Finger (1967). "Verification of Computer Simulation Models." Management Science 14: B92-B101.

PHILLIPS, N. (1956). "The General circulation of the Atmosphere: a Numerical Experiment." Quat. J. R. Met. Soc. 82(352): 123-164.

PHILLIPS, N. (2000). Foreword. General Circulation Model Development. D. A. Randall. San Diego: xxvii-xxix.

ROHRLICH, F. (1991). Computer Simulation in the Physical Sciences. PSA 1990. F. Forbes, Wessels. East Lansing, Philosophy of Science Association. 2: 507-518.

ROSENWEIN, R. and M. Gorman (1995). "Symposium on social psychological simulations of science. Heuristics, hypotheses, and social influence: a new approach to the experimental simulation of social epistemology." Social Epistemology 9(1): 57-69.

SARGENT, R. G. (1992). Validation and Verification of Simulation Models. Proceedings of the 1992 Winter Simulation Conference. J. J. Swain, D. Goldsman, R. C. Crain and J. R. Wilson. Arlington, Virginia: 104-114.

TROITZSCH, K. G. (2004). Validating Simulation Models. Networked Simulations and Simulated Networks. G. Horton. Erlangen and San Diego, SCS Publishing House: 265-270.

WEART, S. (2001). Arakawa's Computation Trick, American Institute of Physics. 2001, http://www.aip.org/history/climate/arakawa.htm.

WINSBERG, E. (2003). "Simulated Experiments: Methodology for a Virtual World." Philosophy of Science 70: 105-125.

ZEIGLER, B. P. (1976). Theory of Modelling and Simulation. Malabar, Krieger.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2005]