Scott Wheeler: It Pays to Be Popular

©Copyright JASSS

Scott Wheeler (2005)

It Pays to Be Popular: a Study of Civilian Assistance and Guerilla Warfare

Journal of Artificial Societies and Social Simulation vol. 8, no. 4
<https://www.jasss.org/8/4/9.html>

For information about citing this article, click here

Received: 15-Feb-2005 Accepted: 09-Jul-2005 Published: 31-Oct-2005

Abstract

: This paper presents a study into the benefits imparted by friendly civilian populaces in assisting peacekeepers to conduct operations under the threat of guerrilla warfare. In this study, civilians report observed insurgent activity to peacekeepers with varying levels of enthusiasm depending on the reputation of the peacekeepers with the local populace. A simulation model is developed using an agent-based approach and a statistically significant number of Monte Carlo simulations conducted to measure the success of the peacekeeping operations and the benefits of civilian assistance.
Keywords:: Peacekeeping, Insurgency, Agent-Based

Introduction

1.1: The disbandment of the Iraqi Army in May of 2003 by the Coalition Provisional Authority following the occupation of Iraq during Operation Iraqi Freedom has been described in Cordesman (2003) and Record and Terrill (2004). This disbandment had ensuing consequences ultimately leading to an increase in the animosity expressed by the Iraqi people to the United Nations (UN) coalition occupying forces and in particular the United States (US) contingent. In this single act, a trained fighting force had been dispersed into the civilian population while simultaneously inflicting loss of morale and removing the soldier's means of self-support - that is, their income. It can be argued that, this in turn increased anti-US sentiment and subsequent insurgent activity. We are left, after the fact, to ask whether this sequence of events could have been predicted a priori and if so whether any of the undesirable consequences could have been avoided. Many studies have been conducted to answer such questions with the purpose of avoiding the mistakes of the past. In particular, the study of civilian behaviours and reactions in war is considered of upmost importance within the Defence community.
1.2: Ryan and Grisogono (2004) studied the consequences of intolerant government policies in response to terrorist bombings. This study was loosely modelled on the current socio-political environment in the Gaza Strip. In Ryan and Grisogono's model, terrorist suicide bombers inflicted casualties upon both civilian populace and law enforcement officials in a manner similar to Palestinian suicide attacks against the State of Israel. In retaliation to terrorist activity, the government was presented with the option to deploy land and air based tactical missile systems. For example, armed helicopter gunships and ground based mobile missile launchers. Ryan and Grisogono found that this response immediately reduced terrorist activity in the short term, it also increased future terrorist activity. Alternatively, the government was presented with the option to increase the presence of law enforcement officials. These officials did not prevent terrorist attacks from occurring but reduced the rate at which terrorists were recruited from the civilian population. Within the context of Ryan and Grisogono's model, it was determined that this passive response to terrorism was more effective in the long term than active anti-terrorist strikes but no other contributing factors were identified or studied.
1.3: Yiu et al. (2003) studied the methods of crowd control based on the Epstein et al.s' (2001) Civil Violence Model. A centralised authority was provided with two means of dealing with dissident civilians. First, insurgents could be gaoled for terms of varying duration. Second, the number of police could be increased. It was shown that, insurgents are most dangerous when they avoid the police force for the greater proportion of the time but mix with a passive population to incite civilians a small but significant proportion of the time. The optimal policy for the civil authority was shown to be to increase the size of the police force rather than the gaol sentences.
1.4: This study seeks to better understand guerrilla warfare, insurgence activity, terrorism and asymmetric warfare by investigating the benefit of civilian assistance in conducting peacekeeping operations under threat of guerrilla warfare. An agent-based model, originally modelled on the conditions of the Vietnam War 1957-1973, is developed in Section 2 to simulate a UN peacekeeping operation in complex terrain including urban constructions and vegetation restricting line-of-sight. This model is designed to be indicative of the type of environment in Vietnam over the course of the war and not specific to any single historical battle. Simulation results and a statistical analysis of these results are presented in Section 3. A discussion of the further findings of this study and extensions to the study assessing danger levels to peacekeepers and optimal team sizes for peacekeepers is provided in Section 4. Conclusions are offered in Section 5.

Agent-Based Model

Aim

2.1

NetLogo (Wilnesky 1999), an agent-based simulation tool belonging to a class of simulation techniques commonly referred to as agent-based distillations (Grieger 2002), is evaluated in this study for its usefulness and suitability in modelling guerrilla warfare. Agent-based distillations differ from large-scale, time-expensive and complex agent-based models in that they trade sophistication for speed and lower simulation costs. As a result simulations tend to be less scripted with less user input than high-fidelity high-cost combat simulation software or seminar wargames. In such models, the emergent behaviour of the system as a whole is considered more important than the behaviour of any single constituent part of the system. This emergent behaviour is a characteristic of complex adaptive systems resulting from combined low-level interactions between numerous low-level entities in the system. These entities act according to comparatively simple rules but their behaviours combine in synergy to exhibit complex dynamic behaviour.

2.2

This study evaluates the use of NetLogo for use in modelling guerrilla warfare and civilian assistance. The assumption is made, under the methodology of agent-based distillations, that a representative generic model can be constructed by encapsulating the key features of the reality being modelled. In this study, these key features are: terrain which includes line-of-sight restrictions based on vegetation; agents or protagonists to inhabit the terrain, including UN peacekeepers, civilians and insurgents; and behaviours for these agents loosely based on accomplishing simple tasks or objectives as appropriate to each agent. Development of the model was influenced by and based on the Australian Defence Force's warfighting publications and in particular the physical, human and information aspects of warfighting in Complex Warfighting (Commonwealth of Australia 2004) and aspects of the Vietnam War 1957-1973. Feedback on the realism of the model and was provided by Australian Army Officers posted at Australia's Defence Science and Technology Organisation (http://www.dsto.defence.gov.au/ accessed 20th May 2004).

2.3

A single instantiation of our model is used for a preliminary study. The relative success or failure of this model then provides insights into the limitations and strengths of NetLogo, and may provide insight into the application of similar agent-based approaches, for the modelling of guerrilla warfare and civilian assistance. Technical assistance in the development of the model and the application of Agent-based distillations was provided and inspired in part by the US Marine Corps Warfighting Laboratory's Project Albert (http://www.projectalbert.org/ accessed 20th May 2004) and personal communication.

Terrain

2.4

Simulations are conducted on a two-dimensional 500 by 500 unit board divided into 10 by 10 unit grids. Each grid is designated as containing either an urban construction or vegetation. Grids containing vegetation are associated with a density rating between 0 and 100, representing cleared ground or grasslands through to densely packed foliage of at least 6 foot in height.

2.5

The board is initialised by randomly assigning vegetation ratings to the grids and subsequently smoothing these ratings by averaging the scores at each grid, processing grids in random order, with the eight immediate neighbouring grids and appropriate consideration at the boundary of the board. This smoothing operation is repeated a total of three times.

2.6

Urban constructions are initialised by throwing out nb constructor agents a random distance between 0 and 300 from the center of the board at a random angle between 0 and 360 degrees. These constructors designate the grid in which they land as an urban construction and each of the eight immediate neighbouring grids as an urban construction independently with a probability of 0.8, again with appropriate adjustments made for the boundary of the board. Grids residing adjacent to urban constructions, that are not themselves urban constructions, are designated cleared ground and their vegetation ratings are reset to 0.

2.7

The effect vegetation has on line-of-sight and movement is described in subsequent sections. Grid elevation ratings, representing hills and valleys for example, are not modelled in this study.

Agents

2.8

Three groups of agents are modelled in this study:

a coalition UN peacekeeping team, denoted the blue force;
an armed insurgent faction, denoted the red force; and
the local civilian populace, denoted the white force.

The objectives of the UN peacekeepers are to locate and eliminate the insurgent threats, minimise blue force casualties and protect civilians. In contrast, the insurgents seek to avoid detection for as long as possible and to kill UN peacekeepers should the opportunity present itself. Civilians assist the UN peacekeepers by reporting known insurgent threats but do not actively seek out insurgents. The role each agent type plays in simulations is described in more detail in subsequent sections where their behaviours, interactions and objectives are explained.

2.9

Let v_max denote the maximum vegetation rating of all grids on the board after smoothing. Then, a total of n_p UN peacekeepers, n_c civilians and n_i insurgents are initialised as follows. The UN peacekeepers are placed upon the board at the coordinate point x = 250, y = 250. That is, the center of the board. The civilians are independently placed upon the board at random points within grids denoted as urban constructions. Insurgents are initially randomly placed upon the board at random points within grids with vegetation ratings greater than v_max/2. Insurgents then successively employ a steepest ascent algorithm, by calculating the gradients between their current positions and the eight immediate neighbouring grids, to take up position at local peaks of highest vegetation ratings. That is, they conceal themselves in the densest vegetation reachable from their initial positions without ever compromising their positions by travelling through grids with less coverage than their current positions. While it is realistic for insurgents to take into account the positions of urban constructions and possible vantage points in choosing initial starting positions, this behaviour requires a more sophisticated approach than used in this model.

2.10

An example of the board is provided in Figure 1. In this figure, grids are coloured in increasingly dark shades of green (gray) to denote regions of increasing vegetation from white (light gray), signifying little vegetation, to deep green (dark gray), signifying dense vegetation. Black grids represent urban constructions. Agents are represented by stick figures.

Figure 1. Example board

Behaviours

2.11

Agents behave, act and react in accordance to the four base operations conducted in order: detection, movement, communication and engagement. Agents are not simulated using a turn based or iterative approach. Instead, agents receive roughly the same amount of simulated run time to carry out actions. There is no priority ordering or predefined sequence in which agents are simulated and only one agent may be simulated at any instance in time. The agent currently in simulation may be pre-empted by another agent between each of the four base operations but not during an operation. For example, an agent in simulation may not be interrupted in the act of detection but may be interrupted before beginning a movement operation. Simulations are terminated once either all n_p UN peacekeepers or n_i insurgents are killed. The four operations require different amounts of physical time to complete so that the actual order in which agents are simulated depends upon which operations the agents are performing, how often the operations are performed and random factors within the simulation. For example, agents who are not currently engaging an enemy can effectively spend more time detecting, moving and communicating while agents who spend most of the simulation stationary can spend more of their allotted time performing detection, communication and engagement operations. Agents may skip one or more base operations when those operations do not apply to their current circumstances. For example, an agent cannot engage another without first knowing of the enemy's location. However, the operations are sequenced and not event or context based. For example, an agent who is fired upon does not immediately return fire. If that agent has just completed a detection operation it will instead move towards the enemy. In most instances, the agent will in fact be able to return fire before being fired upon a second time but this is not explicitly guaranteed.

2.12

Detection is conducted by a counter-intuitive process of identifying all potential target agents for some given observer agent and then inquiring of the target agents whether or not they can see the observer. To explain this process, suppose that a UN peacekeeper is looking for insurgents. First, a line-of-sight agent is spawned at the current position of each insurgent with 3v_max units strength. Next, the line-of-sight agents successively move forward 10 units at a time (the width and height of 1 grid), or less if the distance between the line-of-sight agent and the observer is less than 10 units, towards the observer. The line-of-sight agents' strength is the reduced by v(x,y) units for each grid traversed, where v(x,y) denotes the vegetation rating of the grid at the coordinate (x,y). Line-of-sight agents' strength is reduced after moving and not before. Each (x,y) co-ordinate maps to a single grid so that an agent on the boundary between 2 or more grids strictly resides in one of those grids. If the line-of-sight agent manages to reach the UN peacekeeper without reducing its strength to 0 then, we say that the UN peacekeeper can see the insurgent from which that line-of-sight agent originated. The insurgent is not detectable by the UN peacekeeper otherwise. This means that agents are better able to see out of densely foliated grids than to see into them. Hence, insurgents have a noticeable advantage in taking up positions in grids with high vegetation ratings. Furthermore, for the purpose of detection, grids containing urban constructions are considered to have vegetation ratings of v_max. This means that agents can see out of an urban construction normally but are severely penalised when trying to look into and past an urban construction. Line-of-sight agents are removed from the board at the conclusion of each detection operation.

2.13

Civilian and insurgent detection operations are conducted identically as for the UN peacekeepers with suitable changes in the observer and observee roles. Recall also that base operations cannot be pre-empted and only one operation is conducted at any time. Thus, insurgents cannot move while UN peacekeepers are performing a detection operation. Both insurgents and peacekeepers perform detection operations so there is no significant bias introduced between the agent types. Civilians, however, will only scan for insurgents with probability p_scan meaning in general they spend more time moving as p_scan increases. The exact values of p_scan vary between 0% and 100% to model the level of support for the UN peacekeepers and are presented together with the results of the study in Section 3.

2.14

Agents are initially randomly assigned a compass bearing between 0 and 360 degrees. This bearing is modified during agents' movement operations according to the type of agents undergoing movement. Agents' positions are coded as real numbers and are not linked to fixed points in or at the edges of grids. When choosing to move, agents do so on their bearings 10 units in distance.

2.15

Agents' bearing adjusting movement algorithms are as follows.

UN peacekeepers: Peacekeepers have two movement behaviours based on whether or not peacekeepers are tracking a known insurgent threat. First, if no known threat exists then, agents follow a classic bird-flocking algorithm (Reynolds 1987) designed to model simple agent teaming. The exact details of this algorithm are omitted for brevity. In essence, the UN peacekeepers attempt to match the speed and direction of neighbouring peacekeepers with a fixed distance separation. Introducing variation in the peacekeepers velocity and acceleration in accordance with some random process keeps the flock from forming into a single static mass. We implement the algorithm such that UN peacekeepers have a tendency to travel in small groups of two to three agents, which is designed to provide enhanced safety to the agents under insurgent attack. The parameters used in the flocking algorithm are chosen such that agents form several small groups of agents rather than a single grouping and to occasionally diverge from their current group. Second, if agents possess knowledge of a insurgent threat then, those agents track that threat by changing their bearings to converge upon the threat.
Civilians: Civilians also have two movement behaviours based on whether or not they possess knowledge of a known insurgent threat. First, if agents have no knowledge of a insurgent threat then, those agents move on their current heading so long as that heading would not take them into an area of high vegetation. With probability 0.8, the agents will "bounce" off of a grid according to the laws of physics, as a billiard ball would against a wall of a billiards table for example, with vegetation rating exceeding v_max/2. Urban constructions, for the purpose of movement, are defined to have a vegetation rating of 0 and may be occupied by agents. Otherwise, with probability 0.2, the agents will move into that grid without changing their bearings. Hence, civilians have a preference for urban constructions, well-travelled trails and pathways. Second, if agents have detected a insurgent threat then, those agents move towards the closest UN peacekeeper in sight and on a direct 180 degree bearing away from the threat otherwise.
Insurgents: Insurgents follow only a single movement algorithm and do not move unless a civilian is sighted and within 30 units distance. In this situation the insurgent will attempt to move on a direct 180 degree bearing away from the civilian but prefer to remain in position if it is reasonable to believe it has not been sighted by the civilian and hence move only if the civilian passes within 20 units of their position. Insurgents move in a similar manner to civilians but unlike civilians have a preference for grids with a vegetation rating exceeding v_max/2 and will bounce off of other grids with a probability of 0.8. This behaviour reduces, but does not eliminate, the likelihood of moving to a densely vegetated region by moving across a sparsely vegetated region. Such movement is reasonable because exposure to open areas substantially increases the risk of insurgents being detected.

All agents bounce off the edges of the board. Hence, when using these movement behaviours it is sensible to make the board as large as possible and to scale the numbers of agents accordingly. This minimises any possible bias introduced by reflections off the board boundaries. Introducing board boundaries is not in itself unrealistic. The board represents a village or some other basin of attraction for civilians. Civilians do not in general need to or want to go wandering off alone in the jungle outside the village.

2.16

After movements, agents have the opportunity to perform a communication operation conducted as follows.

UN peacekeepers: UN peacekeepers communicate known insurgents threats with all peacekeepers within 10 units distance. This limitation is designed to restrict all peacekeepers from responding to a threat. Due to the flocking behaviour of the UN peacekeepers, a single group of UN peacekeepers will respond to the insurgent threat in the majority of cases.
Civilians: Civilians communicate with UN peacekeepers to provide them information on known insurgent threats. A civilian at a distance of 10 units or less from a peacekeeper will report sighting an insurgent to that peacekeeper. Each civilian reports a sighting once only per sighting upon which case the civilian is satisfied that it has upheld its civic duty and forgets the location of the insurgent.
Insurgents: Insurgents act independently and without organisation and do not communicate in this study. This assumption is reasonable under a number of circumstances. First, this study is conducted at the tactical level and not the operational or strategic level so we abstract away from high-level planning and coordination. Insurgents are modelled under decentralised command and control in dispersed conditions with little coordination. In our model, insurgents are akin to solitary gunmen concealed in bunker and tunnel networks or waiting in the foliage of trees for UN peacekeepers to pass by. Second, the intent of insurgents is to avoid detection. As such, insurgents try to minimise their footprint and maintain a low emissions profile. Last, it can be that the insurgents simply do not possess the technology for effective radio communication.

2.17

Engagement is conducted on a line-of-sight basis. However, an agent firing a weapon reveals its location to all agents within 30 units distance. UN peacekeepers engage insurgents as soon as sighted. Insurgents ambush UN peacekeepers at 30 units distance or less and will return fire when fired upon. Insurgents ambushing a UN peacekeeper receive a flat 80% probability of successfully killing the peacekeeper if the peacekeeper is unaware of the insurgent. Other weapons fire is resolved on a flat 30% kill probability per engagement for UN peacekeepers. Insurgents are assumed to be poorly armed and trained in comparison to peacekeepers and receive and a flat 20% kill probability per engagement. Civilians are not armed and do not engage in combat.

Results

3.1

To investigate the effect of changing n_c and p_scan and the relative importance of each, 20 independent simulations were conducted for each of the values of n_c ranging between 2 and 20 in increments of 2 and each of the values of p_scan ranging between 0% and 100% in increments of 10%. The parameters n_p = 10 and n_i = 5 were fixed. The terrain and starting locations of all agents were generated anew in each simulation with n_b = 10. 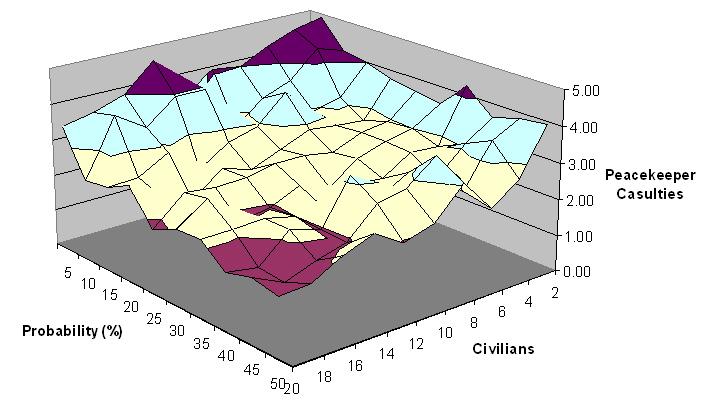The average number of UN peacekeeper casualties over these 20 simulations is displayed in Figure 2.

Figure 2. UN peacekeeper casualties with n_c and p_scan varying

3.2

Figure 2 is useful in that it demonstrates the elasticity between n_c and p_scan. In consultation with subject matter experts, it can be used to select parameters of interest for more detailed investigation. A further two hundred independent simulations were conducted for n_p = 10, n_i = 5 and n_c = 20 where p_scan ranged between 0% and 100% in increments of 10%. The mean number S_avg of UN peacekeepers surviving until the end of the each operation and the standard deviation StDev(S_avg) for the mean over these two hundred simulations is provided in Table 1.


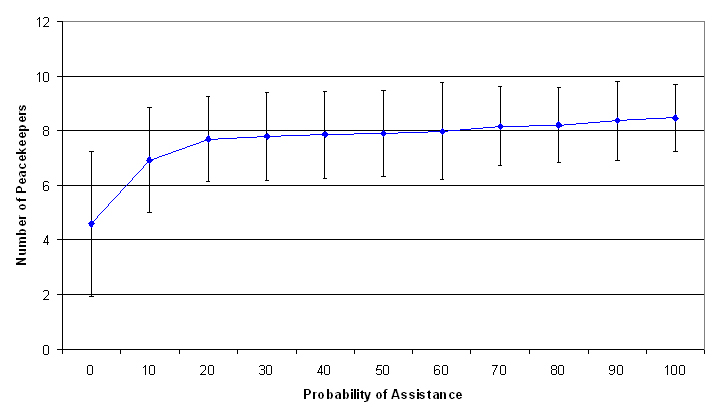
Table 1: Simulation results

p_scan	S_avg	StDev(S_avg)
0	4.585	2.673
10	6.935	1.931
20	7.700	1.566
30	7.790	1.615
40	7.851	1.606
50	7.917	1.573
60	7.985	1.769
70	8.155	1.453
80	8.215	1.363
90	8.365	1.432
100	8.465	1.231

3.3

Figure 3 plots S_avg against p_scan with error bars of length StDev(S_avg) on either side of S_avg. While increasing the number of simulations conducted will certainly reduce the size of the error bars, we first conduct a statistical significance test to determine if this is necessary. Furthermore, computational time and effort prohibits the use of arbitrarily large numbers of simulations for this model.

Figure 3. Plot of S_avg against p_scan

As indicated in Figure 3, the number of UN peacekeepers surviving the peacekeeping operation exhibits a non-linear relationship to p_scan. Hence, we propose to explain how survival rates for UN peacekeepers relate to p_scan by testing for significant differences between the values of interest for p_scan of 0, 10, 20, 60 and 100. The differences between the two values for p_scan of 10x and 10x+10, x = 2,...,9, for example between 40 and 50 or 50 and 60, are not significant at the 90% confidence level.

3.4

Let μ_x denote the true population mean for the average number of peacekeeper casualties for simulations conducted with p_scan = x (as opposed to the sample mean S_avg for each value of x). From Figure 3, the differences between the sample means at 20 and 60 look, to the eye, to be minor. Then to statistically test the hypothesis H₀ : μ_0.2 = μ_0.6, for example, against the alternative hypothesis H_a : μ₆₀ > μ₂₀, a two sample t-test is conducted with 392 degrees of freedom. A t-statistic of 2.389 is calculated. The null hypothesis is rejected at a significance level of α = 0.1. Hence, we are 99% confident that the true population mean for the average number of peacekeeper casualties for simulations conducted with p_scan = 60 exceeds that of simulations conducted with p_scan = 20. Similarly, the null hypotheses that μ₀ = μ₁₀, μ₁₀ = μ₂₀ and μ₆₀ = μ₁₀₀ are all rejected in favour of the alternative hypotheses μ₁₀ > μ₀, μ₂₀ > μ₁₀ and μ₁₀₀ > μ₆₀ respectively with greater than 99% confidence.

3.5

Changing the number of civilians and the probability p_scan is the most direct way of gaining insight into the benefit of civilian assistance to UN peacekeepers. However, there are more factors at play in this model than can be explained by varying these two parameters alone. The less tangible aspects of civilian assistance are explored by varying the number of UN peacekeepers and insurgents in the model. A parameter space exploration was conducted with n_p and n_i ranging from 1 through 10, with n_c = 20 and p_scan = 20 fixed. 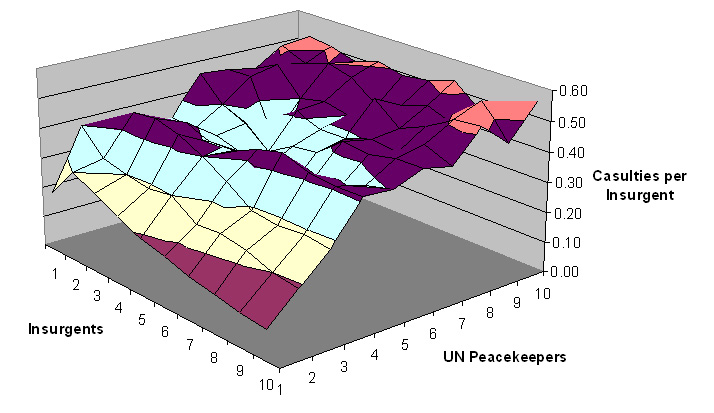Figure 4 depicts the average number of UN peacekeeper casualties per insurgent over the 20 simulations.

Figure 4. UN peacekeeper casualties per insurgent with n_p and n_i varying

3.6

Although twenty simulations are too few for rigorous statistical analysis, a number of useful insights about civilian assistance can be elucidated from the emergent behaviours displayed by the model when interpreted in context of Figure 4.

The comparative value of civilians detecting insurgents is greater for low values of n_p and n_i than high values. This arises because it simply less likely, and thus takes longer, for insurgents and UN peacekeepers to meet by chance alone. Civilians have more time to observe insurgents and report those insurgents to UN peacekeepers. It is then less likely for UN peacekeepers to be assassinated by insurgents because they are more likely to receive information about insurgents from the civilians.
Increasing the number of UN peacekeepers in close proximity to each other through flocking behaviour increases the safety of the UN peacekeepers in that flock. The probability that insurgent threats are eliminated even when the flock sustains casualties is also increased. However, the law of diminishing returns applies in that the comparative benefit between a team of one member increasing to a team of two substantially exceeds the benefit obtained in increasing the size of a team from ten to eleven say.

3.7

The two impacts above are somewhat in opposition. On the one hand, it is obviously a benefit to hold back the UN peacekeepers and wait for the civilians to locate insurgents, therein increasing the relative ratio between insurgents located by civilians to those located by peacekeepers. On the other, it is desirable that the peacekeepers are in both sufficient numbers to flock and that the flock sizes themselves sufficiently large. Varying n_p and n_i can give us a comparative idea of which effect is more important in each scenario, flocking and group behaviour for UN peacekeepers or civilian assistance.

3.8

Across all cross-sections for fixed numbers of insurgents, the value low numbers of UN peacekeepers and hence better relative civilian assistance is consistently greater than the benefits of flocking. Flocking does not eliminate the insurgents' ability to assassinate one unlucky member of the flock. To reduce casualties the team should simply not search for insurgents and instead shout wait for civilian assistance. Furthermore, in theory a meta-team consisting of all UN peacekeepers, however impractical and unrealistic, will reduce the vulnerability of the UN peacekeepers. However, both of these suggestions necessarily mean that large proportions of the board are insecure and unguarded because the frequency of patrols in grids on the board decreases as team sizes increase due to the fixed number of total UN peacekeepers. Inclusion of a penalty function taking into account how often grids are patrolled, and possibly generating new insurgent threats in grids that are not patrolled frequently, could lead to a practical study of optimal team sizes.

3.9

While larger flock sizes reduce UN peacekeeper casualties, it is not immediately apparent why this effect is easier to see in Figure 4. The answer is that increasing the number of UN peacekeepers does not necessarily increase the average flock size. In simulations, typical flock sizes range from unity to four men. Doubling the number of UN peacekeepers does not double the flock size but tends to spawn twice as many flocks. Although it is possible for larger flocks to arise, these tend to fragment into two small flocks quickly. For example, five UN peacekeepers might split into two groups of sizes three and two while nine UN peacekeepers might split into three groups of sizes four, three and two. Of course, this behaviour is by design a direct consequence of the parameters of the flocking algorithm. In simulations, there is a limit to the benefit gained by flocking, irrespective of the total number of UN peacekeepers. In simulations, values of n_p = 5 and n_p = 6 is just large enough to attain reasonable benefits from flocking behaviours and small enough that the ratio of insurgents reported to UN peacekeepers to those located directly by the UN peacekeepers is reasonable.

3.10

Finally, there is at least one undesirable effect at play in these simulations. Flocking between UN peacekeepers requires time after the simulations start to form cohesive groups. The UN peacekeepers are more vulnerable as individuals than as flocks, resulting in a higher average number of casualties before flocking than after. This bias is most prevalent with large n_p and n_i because in these simulations the UN peacekeepers are more likely to encounter one or more insurgents before flocking can occur. For each fixed number of peacekeepers, there is exists a stationary distribution of different flocking configurations. The consequence of this bias is that this stationary distribution is a poor estimation to the empirically observed configurations early in the simulations. For example, one might set n_p = 5, knowing that two groups of sizes three and two are reasonably likely in the stationary distribution. However, if n_p or n_i is too large then, it's more likely that at least one peacekeeper is killed before flocking and the measured proportion of time spent in configurations of five men with low flock sizes will be significantly higher than predicted in the stationary distribution for five men. While this effect is unfortunate, it does emphasise the necessity of teamwork and cooperation between UN peacekeepers.

Discussion

4.1

The greatest potential improvement to this model is to calibrate it to the real world. Terrain, for example, could be initialised from a topological map of some given region of interest. When the dimensions of this map are scaled appropriately in the model, agents' behaviours can be implemented to represent actual behaviours in the field. Of particular relevance are agents' movement rates, which should be influenced by terrain, because these rates have a measurable impact on the results of the model - that is, the results of the model are sensitive to agents' movement rates. Furthermore, these rates must be based upon actual recorded movement rates in combat operations from either field trials or historical data. Other improvements include alterations to the weapons and engagement code to calibrate the model to recorded combat casualty data. For example, the Close Action Environment (CAEn) wargame (Dexter 2004b), initially developed by the United Kingdom Ministry of Defence's Defence Science and Technology Laboratory, does this by detailed ballistics modelling down to individual rifle rounds. Alternatively, tools such as the Janus wargame (Chapman et al. 2002), initially developed by the US Army TRADOC Analysis Center White Sands, models fire-fights between units and groups with expectation-based casualty calculations to adjudicate the outcome of combat. Historically, Lanchester (Taylor 1983) type force-on-force attrition models have been used. Potentially, the model can also be expanded to include additional features and thus better represent guerrilla warfare and civilian assistance.

Figure 5. Example danger levels on a 500 by 500 unit board

4.2

A number of insights are derived beyond the scope of this study. For example, by observation it is apparent that UN peacekeepers are at risk of insurgent attack when travelling near grids of dense vegetation, in which insurgents are most likely to reside, increasingly so when the UN peacekeepers are unaware a priori of any concealed insurgents residing in those grids. Although such an observation seems trivial, this immediately suggests a way to assess the danger or risk to UN peacekeepers in occupying every grid in the map, measured as the distribution of UN peacekeeper casualties over the grids. This distribution is approximated by conducting a large number of independent simulations on a board with fixed vegetation, measuring the number of UN peacekeeper casualties that occur in each grid and normalising the result. See Figure 5 for an illustrative example in which grids coloured in increasingly dark shades of red (gray) to denote danger to peacekeepers from white (clear) signifying no danger to deep red (black) signifying extreme danger. This approach, as well as a number of alternative sophisticated analytic and empiric measurements of danger, are suggested by Stephens et al. (2004).

4.3

The greatest potential use of the "danger map" presented in Figure 5 is to facilitate more complex and meaningful behaviours in the agents, particularly the UN peacekeepers. Given the danger map, it is easy to determine say the safest approach route towards any given insurgent location, which in general is not the direct path taken in this study. Simple classical algorithms such as the shortest path algorithm, see Ahuja et al. (1993), are easily adapted to provide the safest route between two grids. This path is useful in the following context. Suppose that a single peacekeeper, currently residing in location A, is informed by a civilian of an insurgent at location B. The peacekeeper now has knowledge of this insurgent so that peacekeeper cannot be caught unaware and ambushed by the insurgent. The immediate objective for this UN peacekeeper is then to reach point B, starting at A, without being ambushed by yet unlocated insurgents on route. In general, every insurgent threat that can be identified through civilian assistance reduces the risk of peacekeeper casualties, so long as that threat is reached safely. The danger map has limited use when peacekeepers are not forewarned of insurgent threats because insurgents typically inhabit the areas of highest danger. The danger map is more useful when the objective of the peacekeepers is to control and protect civilians and not eliminate insurgents. In this case, it is beneficial to avoid insurgents wherever possible and to keep civilians in protected areas.

4.4

A future extension to this study, requiring significant development of the base model as well as a review of its underlying assumptions, is for both the UN peacekeepers and insurgents to continually co-adapt to the grid danger levels. For example, if at some instance in time, the UN peacekeepers learn that the safest route to some fixed position is via a northern approach then the insurgents may in turn make use of this knowledge by deliberately lying in wait to ambush along this northern approach, hence negating any safety the northern approach might promise but perhaps leaving an eastern approach unguarded. A complex two-sided game emerges as the UN peacekeepers and insurgents attempt to out-play the other.

Conclusion

5.1: This study has supported a greater program of research (Dexter et al. 2005; Hobbs et al. 2005) into understanding guerrilla warfare, insurgent activity, terrorism and asymmetric warfare at the Land Operations Division of the Defence Science and Technology Organisation. In context of this program, we presented a contribution focused on the study of civilian assistance in peacekeeping operations with broader implications to the Defence community as a whole. The agent-based approach employed here has proven a valuable technique for conducting preliminary low-fidelity studies, in minimal time and with minimal effort, and is amenable to subsequent studies at a higher level of fidelity. It has been shown well capable of modelling a subset of the physical, social, and behavioural interactions in guerrilla warfare.
5.2: We have demonstrated, within the limits of this study, the benefit of civilian assistance under threat of insurgent action. This study has shown, with statistical significance over those values of p_scan sampled that, fewer casualties are sustained when peacekeepers are forewarned of insurgent threats by the local populace. Further studies, using a number of different techniques, including higher fidelity simulations, military seminar wargames and historical analysis of actual peacekeeping operations, are planned as alternatives to the agent-based approach used here to verify the results of this study. See for example, the urban combat model (Millikan et al. 2003), the Army Experimental Framework's series of seminar wargames (Commonwealth of Australia 2002) and Land Operations Division's analysis of civilian response to combat (Dexter 2004a).
5.3: The limited nature of this study is insufficient in and of itself to support any greater inference or generalisation of results beyond the case presented in Section 3. However, it is reasonable to infer within the context of all work conducted at Land Operations Division on insurgence and terrorism that, the insights of Land Operations Division's research program may well apply to real-world peacekeeping operations. It is therein recommended that the Australian Defence Force carefully consider the socio-political environment in which Australian peacekeepers deploy and that, when deployed, all due care is taken to assure the continued goodwill of friendly civilian populaces towards peacekeepers in the field.

References

AHUJA R K, Magnanti T L and Orlin J B (1993) Network Flows. Theory, Algorithms, and Applications. Upper Saddle River, New Jersey: Prentice Hall.

CHAPMAN T, Mills V, Kardos M, Stothard C and Williams D (2002) The Use of the Janus Wargame Simulation to Investigate Naturalistic Decision-Making: A Preliminary Examination. DSTO-TR-1372. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

COMMONWEALTH OF AUSTRALIA (2002) Bringing Rigour to Army Experiment in Getting It Right. Australian Defence Science, 10 (1). p. 12.

COMMONWEALTH OF AUSTRALIA (2004) Complex Warfighting. Puckapunyal, Australia: Future Land Warfare, Land Warfare Development Centre.

CORDESMAN A H (2003) Lessons of the Iraq War: Main Report. Washington D C: Center for Strategic and International Studies. 11th working draft dated July 21.

DEXTER P (2004a) Historical Analysis of Population Reactions to Stimuli - A Case Study of Aceh. DSTO-TR-1592. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

DEXTER P, Hobbs W S R and Grieger D (2005) Preliminary Modelling of Asymmetric Warfare and the Contemporary Conflict Environment. DSTO-TR-1621. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

DEXTER R M (2004b) The Close Action Environment (CAEn) V9.2 Training Manual, Part One: Graphical User Interface Overview. DSTO-GD-0404. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

EPSTEIN J, Steinbruner J and Parker M (2001) Modelling Civil Violence: An Agent-Based Computational Approach. Working paper. Washington D C: Center on Social and Economic Dynamics, Brookings Institution.

GRIEGER D (2002) Using Agent Based Distillations to Support Land Warfare Studies. Unpublished publicly released General Document. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

HOBBS W S R, Dexter P, Egudo M and Grieger D (2005) An Analytical Framework for the Study of Asymmetric Warfare. DSTO-TR-1670. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

MILLIKAN J A, Castles T D and Brennan M J (2003) Close Action Environment Modelling of a Combined Arms Sub-Unit in an Urban Environment. DSTO-TN-0485. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

RECORD J and Terrill W A (2004) Iraq and Vietnam: Differences, Similarities, and Insights. Pennsylvania: United States Army War College, Strategic Studies Institute.

REYNOLDS C W (1987) "Flocks, Herds, and Schools: A Distributed Behavioural Model". In Stone M C (Eds.), Computer Graphics, Proceedings of the ACM SIGGRAPH '87 Conference, Anaheim, California, July 1987, 21 (4). pp. 25-34.

RYAN A and Grisogono A-M (2004) "Hybrid Complex Adaptive Engineered Systems: A Case Study in Defence". In Proceedings of the International Conference on Complex Systems, Boston.

STEPHENS A K W, Connell R B and Davies P J (2004) Urban Intelligence Preparation of the Battlespace: Methods for Determining Spatial Vulnerability in Urban Environments. DSTO-TR-1541. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.

TAYLOR J G (1983) Lanchester Models of Warfare. Arlington: Operations Research Society of America.

WILNESKY U (1999) NetLogo User Manual, Version 2.1. Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University.

YIU S Y, Gill A W and Shi P (2003) Using Agent Based Distillations to Model Civil Violence Management. Journal of Battlefield Technology, 6 (1). pp. 1-6.

Button Return to Contents of this issue