Victor Palmer (2006)
Deception and Convergence of Opinions Part 2: the Effects of Reproducibility
Journal of Artificial Societies and Social Simulation
vol. 9, no. 1
<https://www.jasss.org/9/1/14.html>
For information about citing this article, click here
Received: 31-Jul-2005 Accepted: 07-Oct-2005 Published: 31-Jan-2006
 Abstract
Abstract| q = f(Ra | p, a, b) = pa + (1-p)(1-b) | (1) |
| q = f(Ra | p,e,d,a,b) = ed + (1-e)[pa + (1-p)(1-b)] | (2) |
|
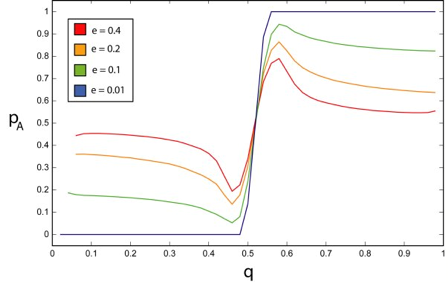
| Figure 1. This figure shows our replication of the Martins results for the infinite article limit. Notice that for small deception (small e and small e variation), the p versus q graph is almost a step function whereas for even for small amounts of deception unity p is never reached. This trend continues monotonically, with less and less step-like behavior observed for increasing e. In all cases a = b = 0.55. |
|
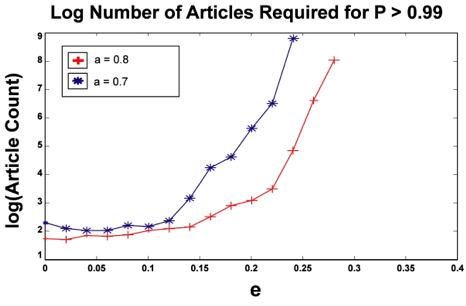
| Figure 2. For two values of a, we plot the number of articles our agent observer must read to be 99% sure that Theory A is correct. For this series of simulations we set q = a since that is always the point of maximum p in the "p versus q" graph. Our simulation did not converge for e > 0.24 for the a = 0.7 case and for e > 0.28 for the a = 0.8 case. |
| q = f( {Ra ,Ra} | p,e,d,a,b) = (ed)2 + 2(ed)(1-e)[pa + (1-p)(1-b)] + (1-e) 2 [pa + (1-p)(1-b)] | (3) |
Where each term is justified below:
| (ed)2 | The probability that both the article and its replication are deceptions and that both support Theory A |
| 2(ed)(1-e)[a + (1-p)(1-b)] | The probability that the article is a deception and supports Theory A, but its replication is NOT a deception and also happens to support Theory A. The factor of 2 is to account for an identical term (since ordering is not important) that occurs when the article is honest and its replication is a deception in support of Theory A. |
| (1-e)2[pa + (1-p)(1-b)] | Both the article and its replication are honest and both support Theory A. Notice that the factor [pa + (1-p)(1-b)] is not squared in the expression — as we said earlier, this factor determines the likelihood of a randomly selected experiment coming up in favor of Theory A — once the experiment is selected (by the initial article), its replication will always come out in favor of the same theory. |
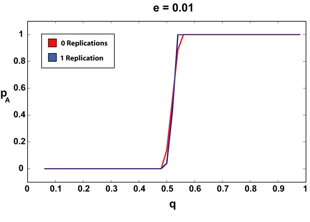
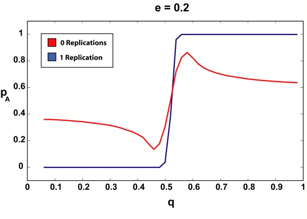
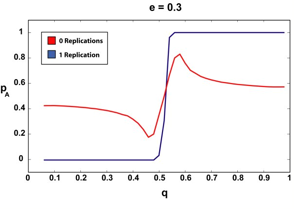 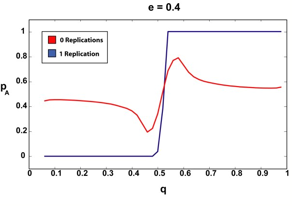
|
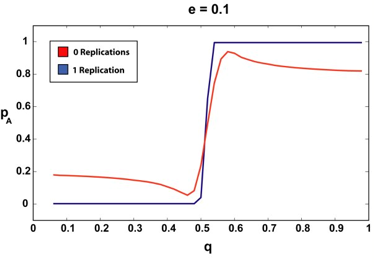
| Figure 3. The infinite article (2000) limit for 0 and 1 replications and various e. The sharper, step-like curves correspond to the 1-replication case. Notice how the 1-replication p curve is relatively unchanged as we increase the amount of a priori suspected deception (e). |
We can see that if our agent requires that the articles it reads have been replicated, even once, the "p versus q" curve remains more or less a step function, regardless of the amount of assumed deception. There are no doubt pathological cases (perhaps an a very, very close to 0.5, for example) where requiring a second replication could offer our agent additional advantages, but since in all the cases we tested, step-function type behavior was observed for the single-replication case, we were not able to test this.
|
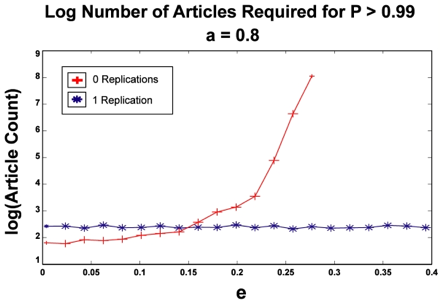
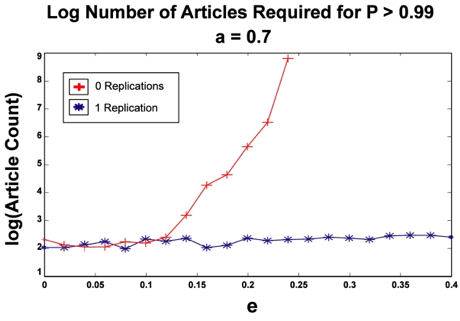
| Figure 4. The sparse article limit simulation for 0 and 1 replications. For the no replication case (strongly increasing curve), as we increase e, the number of articles that our observer agent must read to be 99% sure that Theory A is correct grows super-exponentially. However, for even a single replication, the number of required articles remains more or less constant with increasing e. Notice that once again, our 0-replication simulation never converged for several values of e. |
In the cases we tested, the presence of deception had no visible effect on the number of articles required by our agent to reach certainty — while the 0-replication case diverged super-exponentially with deception as before, the single-replication case remained relatively constant. However, it seems unreasonable that we should observe a true shift from super-exponential scaling to no scaling just by requiring a single replication — instead, we hypothesize that the scaling of our results was still super-exponential in nature, only with a drastically smaller scaling constant. In other words, we guess that the number of required articles still grows super-exponentially under replication, but just very, very slowly. Again, there are probably some pathological conditions where two or more replications would yield additional scaling benefits, but since we never saw a situation where the single-replication case scaled at all, this was not testable.
HEGSELMANN, R. and Krause, U. (2002) Opinion Dynamics and Bounded Condence Models, Analysis and Simulation, Journal of Artificial Societies and Social Simulations, vol. 5, no. 3.
JAYNES, E.T. (2003) Probability Theory: The Logic of Science.Cambridge: Cambridge University Press.
LANE, D. (1997) Is What Is Good For Each Best For All? Learning From Others In The Information Contagion Model, in The Economy as an Evolving Complex System I (ed. by Arthur, W.B., Durlauf, S.N. and Lane, D.), pp. 105-127. Santa Fe: Perseus Books.
MARTINS, A. (2005) Deception and Convergence of Opinions, Journal of Artificial Societies and Social Simulations, vol. 8, no. 2.
SZNAJD-WERON, K. and Sznajd, J. (2000) Opinion Evolution in Closed Communities, Int. J. Mod. Phys. C 11, 1157.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]