Marco Janssen (2006)
Evolution of Cooperation when Feedback to Reputation Scores is Voluntary
Journal of Artificial Societies and Social Simulation
vol. 9, no. 1
<https://www.jasss.org/9/1/17.html>
For information about citing this article, click here
Received: 13-Mar-2005 Accepted: 24-Aug-2005 Published: 31-Jan-2006
 Abstract
Abstract| Table 1: Pay-off table of the Prisoner's Dilemma with the option to withdraw from the game | ||||
| Player B | ||||
| Cooperate | Defect | Withdraw | ||
| Player A | Cooperate | R,R | S,T | E,E |
| Defect | T,S | P,P | E,E | |
| Withdraw | E,E | E,E | E,E | |
| Table 2: Utility pay-off table of the Prisoner's Dilemma with the option to withdraw from the game | ||||
| Player B | ||||
| Cooperate | Defect | Withdraw | ||
| Player A | Cooperate | R,R | S+ β A,T- α B | E,E |
| Defect | T- α A,S+ β B | P,P | E,E | |
| Withdraw | E,E | E,E | E,E | |
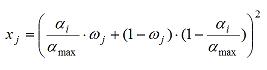
|
(1) |
where α max is used to scale the symbol value between 0 and 1. In order to represent the assumed nonlinear relationship between the preferences of the agent and the symbols, the equation is squared.
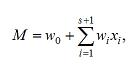
|
(2) |
where w0 is the bias, wi is the weight of the ith input, and xi is the ith input. Initially, all weights are zero, but during the simulation the network is trained, when new information is derived, by updating the weights as described below in equation (4).
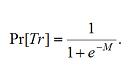
|
(3) |
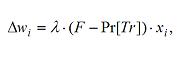
|
(4) |
where Δwi is the adjustment to the ith weight, λ is the learning rate, F is the feedback, F-Pr[Tr] is the difference between the agent's level of trust in the other agent and the observed trustworthiness of the other agent, and xi is the other agent's ith symbol. In effect, if the other agent displays the ith symbol, the corresponding weight is updated by an amount proportional to the difference between the observed trustworthiness of an agent and the trust placed in that agent. The weights of symbols associated with positive experiences increase, while the weights of those associated with negative experiences decrease, reducing discrepancies between the amount of trust placed in an agent and that agent's trustworthiness.
|
|
(5) |
|
|
(6) |
Given the two estimates of expected utility, the player is confronted with a discrete choice problem which addressed with a logit function. The probability to cooperate, Pr[C], depends on the expected utilities and the parameter γ, which represents how sensitive the player is to differences in the estimates. The higher the value of γ, the more sensitive the probability to cooperate is to differences between the estimated utilities.
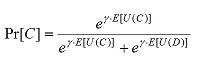
|
(7) |
Logit models are used by other scholars to explain observed behavior in one-shot games such as the logit equilibrium approach by Anderson et al. (forthcoming). Although the functional relation is similar, their approach differs from the one used here since they assume an equilibrium and perfect information of the actions and motivations of other players. Moreover, in the games in this paper agents do not play anonymously but can observe symbols of others in order to estimate the behavior of the opponent.
| Table 3: List of parameters and their default values | |
| Parameter | Value |
| Population size (n) Number of symbols (s) Conditional cooperation parameter α Conditional cooperation parameter β Learning rate (λ) Number of round Steepness (γ) Length of memory (lm) Probability of getting feedback when cooperate. Probability of getting feedback when defect. | 100 0 [ β ,3] [0, α ] 0.1 106 4 100 pC pD |
|
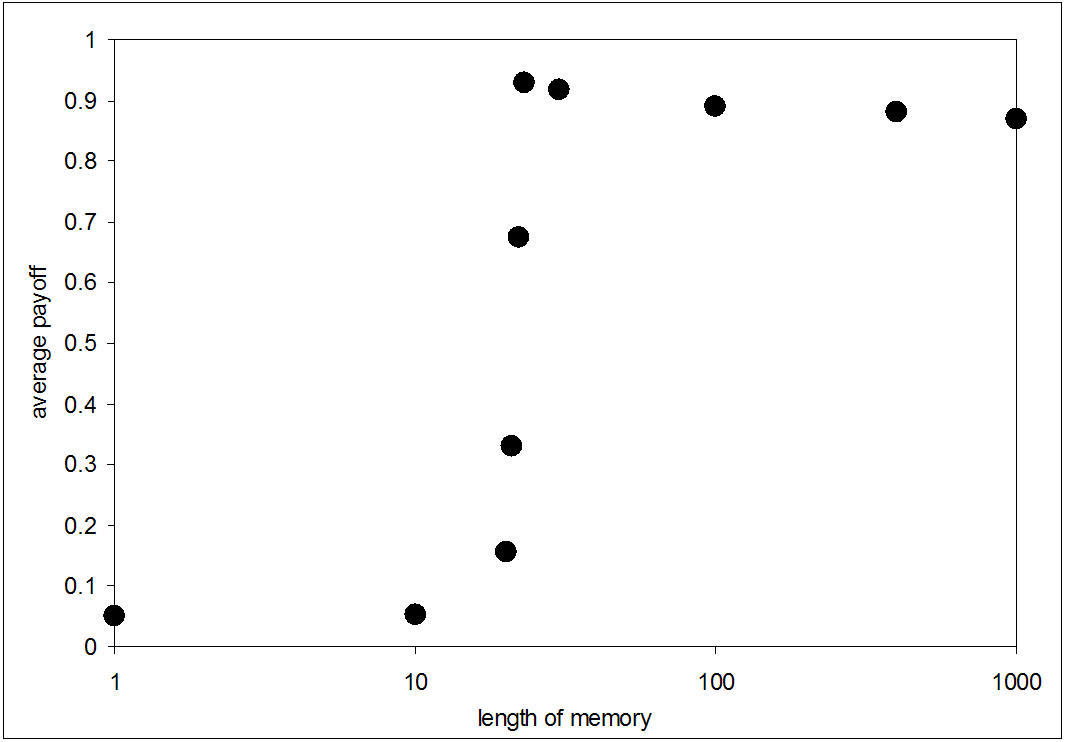
| Figure 1. Average payoff per agent per game for different length of history. The dots represent the average payoffs over 105 interactions over 25 simulations |
|
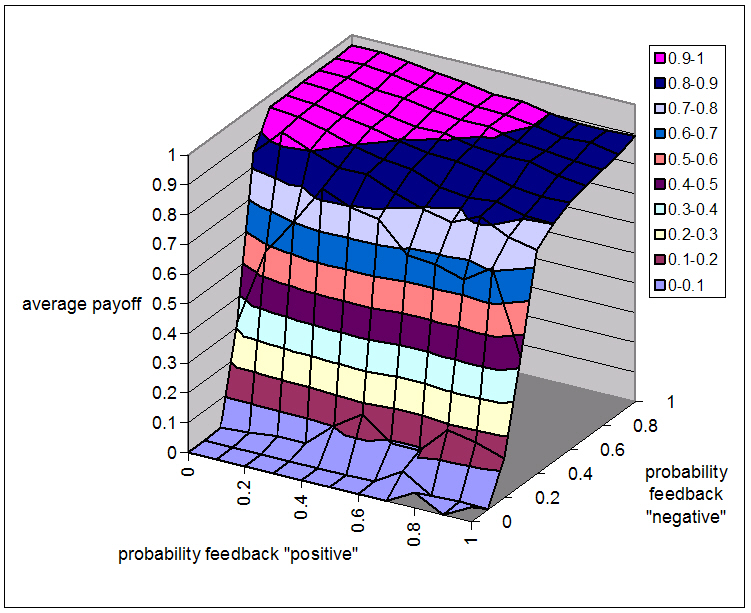
| Figure 2. The average payoff per agent per game for different levels of pC and pD, when agents express only reputation score. The historical memory length is 100 interactions |
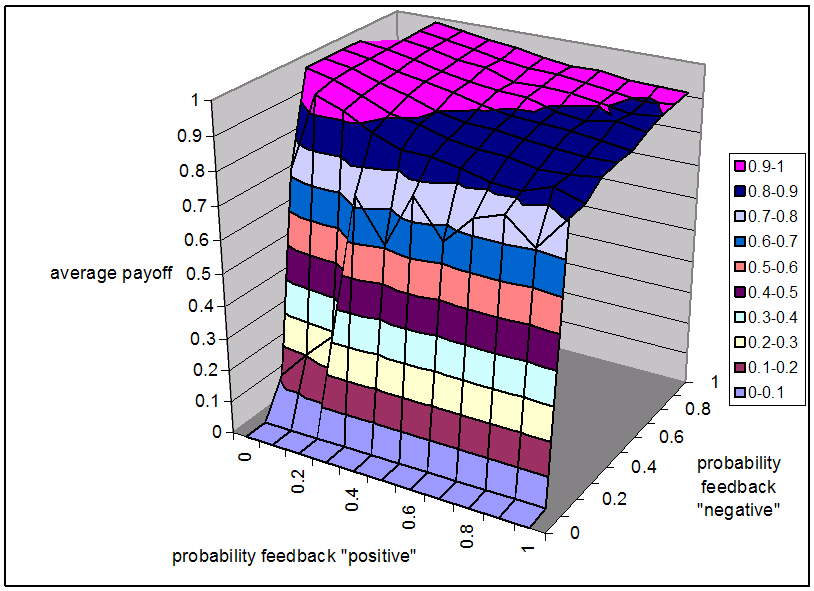
|
| Figure 3. The average payoff per agent per game for different levels of pC and pD, when agents express only reputation score and retaliate. The historical memory length is 100 interactions |
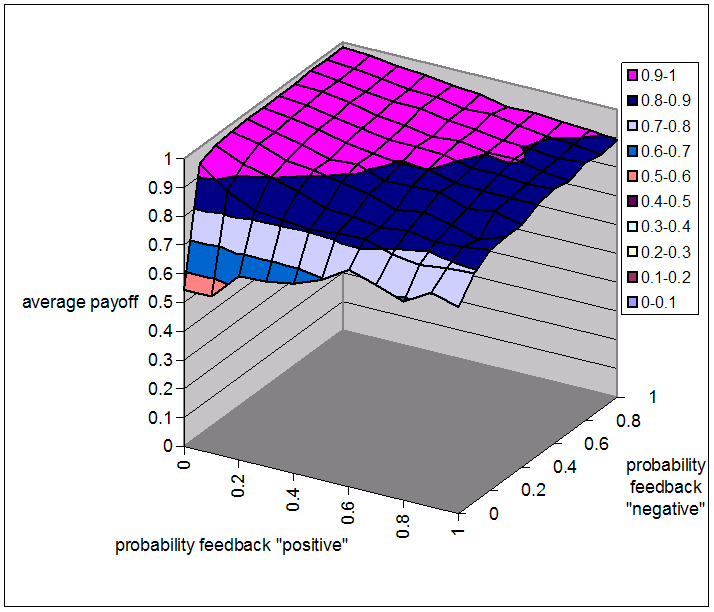
|
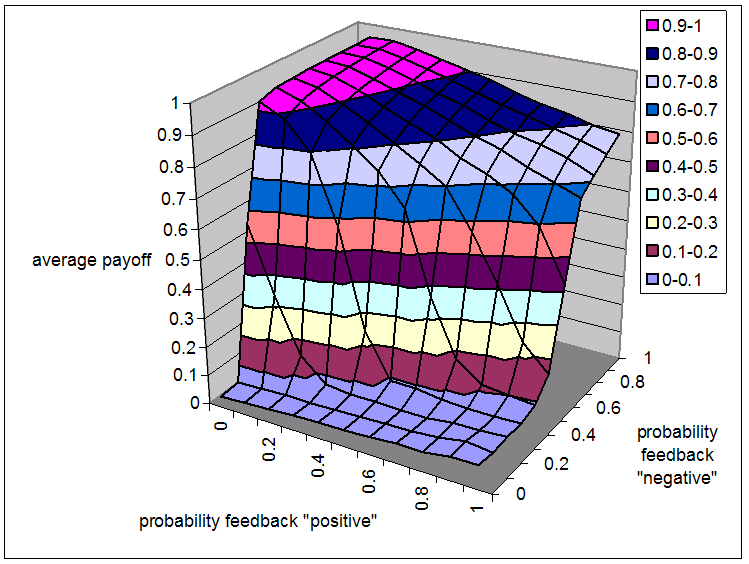
| Figure 4. The average payoff per agent per game for different levels of pC and pD, when agents express reputation scores and 10 additional symbols. The historical memory length is 100 interactions |
|
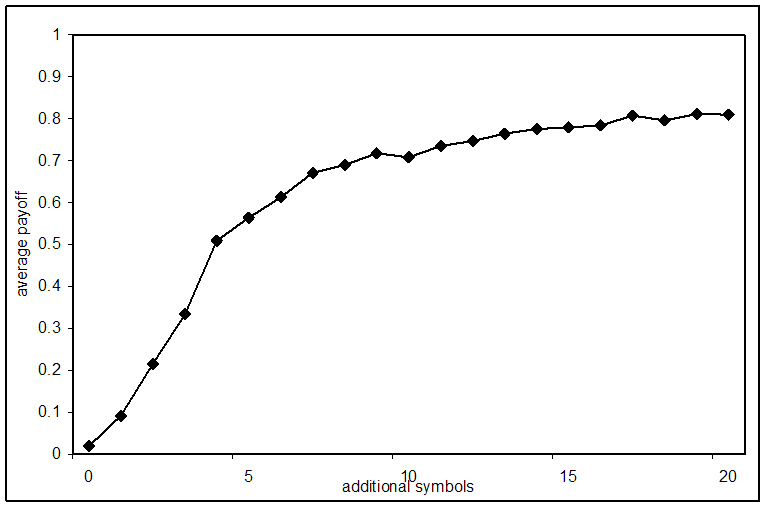
| Figure 5. The average payoff per agent per game when pC =1 and pD =0, for different numbers of additional symbols. The historical memory length is 100 interactions |
|
| Figure 6. The average payoff per agents per game for different levels of pC and pD, when agents express reputation scores and act strategically. The historical memory length is 100 interactions |
AHN T.K, Ostrom E and Walker J (2003), Incorporating motivational heterogeneity into game theoretic Models of collecive action. Public Choice, 117. pp. 295-314.
ANDERSON S P, Goeree J K and Holt C A (Forthcoming), Logit equilibrium models of anomalous behavior: What to do when the Nash equilibrium says one thing and the data something else. In C. Plott & V. Smith (Eds.) Handbook of Experimental Economic Results. New York: Elsevier.
AXELROD R (1984), The Evolution of Cooperation. New York: Basic Books.
BA S and Pavlou P A (2002), Evidence of the effect of trust building technology in electronic markets: Price premiums and buyer behavior, MIS Quarterly 26(3). pp. 1-26.
BOLTON G E, Katok E, and Ockenfels (2004) How effective are electronic reputation mechanisms? An experimental investigation. Management Science 50(11). Pp. 1587-1602
DELLAROCAS C (2003a), The digitization of worth of mouth: promise and challenges of online feedback mechanisms, Management Science 49(10). pp. 147-1424.
DELLAROCAS C (2003b), Efficiency and Robustness of Binary Feedback Mechanisms in Trading Environments with Moral Hazard, Working paper 4297-03, MIT Sloan School of Management.
GINTIS H, Smith E and Bowles S (2001), Costly signaling and cooperation. Journal of Theoretical Biology, 21. pp. 103-119.
GRABNER-KRÄUTER S and Kaluscha E A (2003), Empirical research in on-line trust: a review and critical assessment, International Journal of Human-Computer Studies 58. pp. 783-812.
HAMILTON W D (1964), Genetical evolution of social behavior I and II. Journal of Theoretical Biology, 7. pp. 1-52.
JANSSEN M A (in review), Evolution of Cooperation in a One-Shot Prisoner's Dilemma Based on Recognition of Trustworthy and Untrustworthy Agents.
LEDYARD J O (1995), Public Goods: A Survey of Experimental Research," in Handbook of Experimental Economics, J. Kagel and A. Roth (eds.), Princeton University Press.
MALAGA R A (2001), Web-based reputation management systems: problems, and suggested solutions, Electronic Commerce Research 1. pp. 403-417.
MEHROTA K, Mohan C K and Ranka S (1997), Elements of Artificial Neural Networks. Cambridge, MA: MIT Press.
NOWAK M A and Sigmund, K (1998), Evolution of indirect reciprocity by image scoring. Nature, 393. pp. 573-577.
RESNICK P and Zeckhauser R (2003), Trust among strangers in Internet transactions: Empirical analysis of eBay's reputation system. M.R. Baye (ed.). The Economic of the Internet and E-Commerce. Advances in Applied Micrieconomics, 11. JAI Press, Greenwich CT.
RESNICK P, Zeckhauser R, Swanson J and Lockwood K (2002), The value of reputation on eBay: A controlled experiments. Working paper, University of Michigan, Ann Arbor, MI.
STANIFIRD S S (2001), Reputation and e-commerce: eBay auctions and the asymmetrical impacts of positive and negative ratings, Journal of Management 27. pp. 279-295.
TRIVERS R (1971), The evolution of reciprocal altruism. Quarterly Review of Biology, 46. pp. 35-57
TULLOCK G (1985), Adam Smith and the Prisoner's Dilemma. Quarterly Journal of Economics, 100. pp. 1073-1081.
VANBERG VJ and Congelton R D (1992), Rationality, morality and exit. American Political Science Review, 86. pp. 418-431.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]