Andreas Schlosser, Marco Voss and Lars Brückner (2006)
On the Simulation of Global Reputation Systems
Journal of Artificial Societies and Social Simulation
vol. 9, no. 1
<https://www.jasss.org/9/1/4.html>
For information about citing this article, click here
Received: 13-Mar-2005 Accepted: 22-Jul-2005 Published: 31-Jan-2006
 Abstract
AbstractReputation is the collected and processed information about one entity's former behavior as experienced by others. "Trust is a measure of willingness to proceed with an action (decision) which places parties (entities) at risk of harm and is based on an assessment of the risks, rewards and reputations associated with all the parties involved in a given situation." (Mahoney 2002)
Figure 1: Architecture of a reputation system
| Ea | : = {e |
|
All encounters between a and b with a valid rating for a are: | ||
| Ea, b | : = {e |
|
Furthermore we define | ||
| Ea* | : = |
|
| r(a) | = |
(eBay) | ||
With consideration of transaction values, the reputation in the Value-system computes with: | ||||
| r(a) | = |
(Value) | ||
Adding multiple ratings, we get the SimpleValue-system with the following reputation computation: | ||||
| r(a) | = |
(SimpleValue) | ||
The Simple-system considers multiple ratings, but no transaction values. Thus the reputation for an agent a | ||||
| r(a) | = |
(Simple) | ||
| r(a) | = 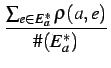 |
(Average) | ||
The reputation of an agent a | ||||
| r(a) | = 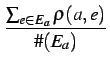 |
(AverageSimple) | ||
The reputation of an agent a | ||||
| r(a) | = 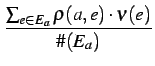 |
(AverageSimpleValue) | ||
The reputation of an agent a | ||||
| r(a) | = 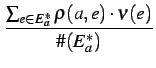 |
(AverageValue) | ||
| r(a) | = ![$\displaystyle {\frac{{\rho(a,\overline{E_a}[i])}}{{\char93 (\overline{E_a})-i+1}}}$](4/img34.png) |
(Blurred) | ||
and with consideration of transaction values: | ||||
| r(a) | = ![$\displaystyle {\frac{{\rho(a,\overline{E_a}[i])\cdot \nu(\overline{E_a}[i])}}{{\char93 (\overline{E_a})-i+1}}}$](4/img35.png) |
(BlurredValue) | ||
| r(a) | = |
(OnlyLast) | ||
With consideration of the transaction value in the OnlyLastValue-system the reputation of an agent a | ||||
| r(a) | = |
(OnlyLastValue) | ||
| (mij) | = 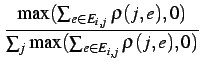 |
|||
= 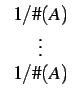 |
||||
| = (M)T |
||||
| r(ai) | = |
(EigenTrust) |
| Ni(a) | = r(a, i - 1)/D | |||
= 1 - 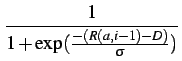 [0] [0] |
||||
| r(a, 0) | = 1 | |||
| r(a, t) | = r(a, t - 1) + |
|||
| . r(b, t) . ( |
(Sporas) |
= 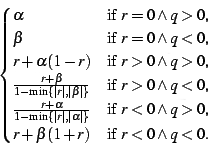 |
||||
| r(a, 0) | = 0 | |||
| r(a, t) | = |
(YuSingh) |
| ra | = |
|||
| sa | = |
|||
| r(a) | = 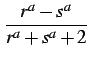 |
(Beta) | ||
where 0 | ||||
| ra | = |
|||
| sa | = |
|||
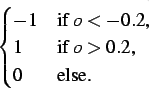
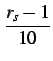 s,
s,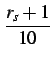 s
s
| System | Reputation s |
|---|---|
| eBay | 120 |
| Simple | 100 |
| SimpleValue | 2000 |
| Value | 2000 |
| Average | 1 |
| AverageSimple | 1 |
| AverageSimpleValue | 40 |
| AverageValue | 40 |
| Blurred | 6 |
| BlurredValue | 250 |
| OnlyLast | 0.8 |
| OnlyLastValue | 40 |
| EigenTrust | 2 |
| Sporas | 30 |
| YuSingh | 1 |
| Beta | 0.8 |
| BetaValue | 0.8 |
Honest Agent This agent initiates only good transactions (i.e. he serves his trade partner what he expected he would get). His ratings are always correct (good transactions are rated good, and bad transactions are rated bad).
Malicious Agent This agent initiates good, neutral and bad transactions by chance. He tries to undermine the system with his rating behavior and rates every transaction negative.
Evil Agent or Conspirative Agent These agents try to gather a high reputation by building a group in which they know each other. If an evil agent finds another evil agent to trade with, they always give each other a good rating. If an evil agent does not find another evil agent, after seeking for a while, he transact neutral and rates neutral.
Selfish Agent This agent is a so called freerider. He blocks all inquiries by other agents and refuses to rate his transaction partners. He just initiates neutral to good transactions by himself.
Disturbing Agent This agent tries to build a high reputation, such that the other agents trust him, with making good transactions and correct rating. Then he switches to a malicious behavior until his reputation gets too bad and then starts from the beginning.
| System | Dist. | Evil | Mal. | Self. |
|---|---|---|---|---|
| eBay | - | 50 | 60 | + |
| Simple | - | 30 | 70 | + |
| SimpleValue | - | 30 | 70 | + |
| Value | - | 50 | 60 | + |
| Average | - | 60 | 70 | + |
| AverageSimpleValue | - | 60 | 70 | + |
| AverageValue | - | 60 | 60 | + |
| Blurred | - | 50 | 70 | + |
| Blurred-Value | - | 50 | 70 | + |
| OnlyLast | + | + | 50 | + |
| OnlyLastValue | + | + | 30 | + |
| EigenTrust | - | + | 60 | 30 |
| Sporas | - | 30 | 70 | 60 |
| YuSingh | - | 50 | 50 | 60 |
| Beta | - | 50 | 70 | + |
| BetaValue | - | 60 | 70 | + |
| + | : | resistent up to 80% of this type |
| x | : | at an amount of x% of this type, the system fails |
| - | : | the system does not protect against this attack |
| : A x E |
||
| r(a) | = ![$\displaystyle {\frac{{\rho(a,\overline{E_a}[i])}}{{(\char93 (\overline{E_a})-i+1)^2}}}$](4/img75.png) |
J. Carbo, J. M. Molina, and J. Davila. (2003) Trust management through Fuzzy Reputation. In Int. Journal of Cooperative Information Systems, 12(1): 135-55.
E. Damiani, S. D. C. di Vimercati, S. Paraboschi, P. Samarati, and F. Violante. (2002) A Reputation-based Approach for Choosing Reliable Resources in Peer-to-Peer Networks. In Proc. of the 9th ACM Conference on Computer and Communications Security, Washington, DC, USA, November, pp. 207-16.
C. Dellarocas. (2000) Immunizing Online Reputation Reporting Systems Against Unfair Ratings and Discriminatory Behavior. In ACM Conference on Electronic Commerce, pp. 150-7.
C. Dellarocas. (2003) Efficiency and Robustness of eBay-like Online Feedback Mechanisms in Environments with Moral Hazard. Working paper, Sloan School of Management, MIT, Cambridge, MA, January.
eBay Homepage. (2004) http://www.ebay.com.
E. Friedman and P. Resnick. (2001) The Social Cost of Cheap Pseudonyms. Journal of Economics and Management Strategy, 10(2): 173-99.
K. K. Fullam, T. B. Klos, G. Muller, J. Sabater, A. Schlosser, Z. Topol, K. S. Barber, J. Rosenschein, L. Vercouter, M. Voss. (2005) A Specification of the Agent Reputation and Trust (A R T) Testbed: Experimentation and Competition for Trust in Agent Societies. In Autonomous Agents and Multi Agent Systems (AAMAS 05), July, pp. 512-8.
T. D. Huynh, N. R. Jennings, and N. Shadbolt. (2004) Developing an Integrated Trust and Reputation Model for Open Multi-Agent Systems. In Autonomous Agents and Multi Agent Systems (AAMAS 04), Workshop on Trust in Agent Societies, July, pp. 65-74.
ITO. Project Reputation Homepage. (2004) http://www.ito.tu-darmstadt.de/projects/reputation.
A. Jøsang and R. Ismail. (2002) The Beta Reputation System. In Proc. of the 15th Bled Conference on Electronic Commerce, Bled, Slovenia, 17-19 June 2002, pp. 324-37.
R. Jurca and B. Faltings. (2003) Towards Incentive-Compatible Reputation Management. In Trust, Reputation and Security, AAMAS 2002 International Workshop, volume 2631 of Lecture Notes in Computer Science. Spinger, pp. 138-47.
S. D. Kamvar, M. T. Schlosser, and H. Garcia-Molina. (2003) The Eigentrust Algorithm for Reputation Management in P2P Networks. In Proceedings of the twelfth international conference on World Wide Web. ACM Press, pp. 640-51.
G. Mahoney. (2002) Trust, Distributed Systems, and the Sybil Attack. PANDA Seminar Talk, University of Victoria, Canada.
E. M. Maximilien and M. P. Singh. (2003) An Ontology for Web Service Ratings and Reputations. In S. Cranefield, T. W. Finin, V. A. M. Tamma, and S. Willmott, editors, Proceedings of the Workshop on Ontologies in Agent Systems (OAS 2003) at the 2nd International Joint Conference on Autonomous Agents and Multi-Agent Systems, Melbourne, Australia, July 15, 2003, volume 73 of CEUR Workshop Proceedings, pp. 25-30.
L. Mui, M. Mohtashemi, C. Ang, P. Szolovits, and A. Halberstadt. (2001) Ratings in Distributed Systems: A Bayesian Approach,. In Proceedings of the Workshop on Information Technologies and Systems (WITS'2001).
L. Mui, M. Mohtashemi, and A. Halberstadt. (2002) Notions of Reputation in Multi-Agents Systems: a Review. In Proceedings of the first international joint conference on Autonomous agents and multiagent systems, ACM Press, pp. 280-7.
RePast Homepage. http://repast.sourceforge.net.
P. Resnick and R. Zeckhauser. (2000) Reputation Systems. Communications of the ACM, 43: 45-8.
P. Resnick and R. Zeckhauser. (2002) Trust Among Strangers in Internet Transactions: Empirical Analysis of ebay's Reputation System. The Economics of the Internet and E-Commerce. Advances in Applied Microeconomics, 11: 127-57.
J. Sabater. (2002) Trust and reputation for agent societies. PhD thesis, Universitat Autonoma de Barcelona.
J. Sabater and C. Sierra. (2001) REGRET: A Reputation Model for Gregarious Societies. In Proceedings of the Fifth International Conference on Autonomous Agents, pp. 194-5.
J. Sabater and C. Sierra. (2002) Reputation and Social Network Analysis in Multi-Agent Systems. In Proceedings of the First International Joint Conference on Autonomous Agents and Multiagent Systems, pp. 475-82.
A. A. Selçuk, E. Uzun, and M. R. Pariente. (2004) A Reputation-based Trust Management System for P2P Networks. In Proceedings of the 4th IEEE/ACM International Symposium on Cluster Computing and the Grid (CCGrid04).
A. Whitby, A. Jøsang, and J. Indulska. (2004) Filtering out Unfair Ratings in Bayesian Reputation Systems. In Autonomous Agents and Multi Agent Systems (AAMAS 04), Workshop on Trust in Agent Societies, July.
L. Xiong and L. Liu. (2004) PeerTrust: Supporting Reputation-Based Trust in Peer-to-Peer Communities. In IEEE Transactions on Knowledge and Data Engineering (TKDE), Special Issue on Peer-to-Peer Based Data Management, pp. 843-57.
B. Yu and M. P. Singh. (2000) A Social Mechanism of Reputation Management in Electronic Communities. In Proceedings of the 4th International Workshop on Cooperative Information Agents IV, The Future of Information Agents in Cyberspace, pp. 154-65.
G. Zacharia and P. Maes. (2000) Trust Management through Reputation Mechanisms. Applied Artificial Intelligence, 14: 881-907.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]