Victor Palmer (2006)
Simulation of the Categorization-Elaboration Model of Diversity and Work-Group Performance
Journal of Artificial Societies and Social Simulation
vol. 9, no. 3
<https://www.jasss.org/9/3/3.html>
For information about citing this article, click here
Received: 28-Oct-2005 Accepted: 17-Apr-2006 Published: 30-Jun-2006
 Abstract
Abstract
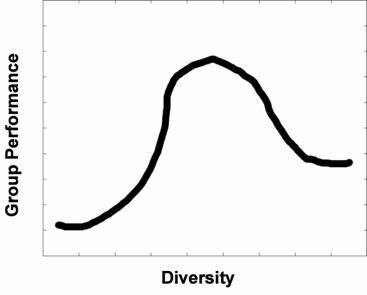
|
| Figure 1. The CEM predicts a curvilinear relationship between diversity and group performance like the one sketched above. Starting from the minimal-diversity point, increasing diversity should increase group performance … but eventually these performance increases will taper off, and performance may even decrease as diversity is increased to higher and higher levels |
| Pi(E) = < R(Ek) > Si(Ek)=Si(E) | (1) |
Where <> refers to expectation in the above equation. That is, to determine its predicted reward for an event, an agent searches through its experience vector, finds all events with identical sensory outputs, and then averages the true reward of those events. A particularly interesting measure for us will be an agent's predicted reward vector Pi>, which will simply be a vector of predicted rewards for the events the agent was originally exposed to:
| Pi = { Pi(E1), Pi(E2),…, Pi(En) } | (2) |
| Ji = { | Pi(E1) - R(E1) |, | Pi(E2) - R(E2) |, … ,| Pi(En) - R(En) | } | (3) |
| Table 1 | ||||||
| Events | Descriptions of events (for us) | Sensor Names (all possible sensors) | (TRUE) REWARD R | |||
| VISIBILITY | ENEMIES | WAS I HUNGRY? | TEMPERATURE | |||
| Event 1 | fighting many enemies | excellent | many | no | hot | -300 |
| Event 2 | on vacation | excellent | none | no | hot | 100 |
| Event 3 | stranded in Antarctica | poor | none | yes | cold | -25 |
| Event 4 | cooking dinner | excellent | none | yes | hot | 100 |
| Table 2 | ||||
| Events | Descriptions of events (for us) | Sensor Names (for X) | TRUE REWARD R | PREDICTED REWARD PX |
| TEMPERATURE | ||||
| Event 1 | fighting many enemies | hot | -300 | -33.3 |
| Event 2 | on vacation | hot | 100 | -33.3 |
| Event 3 | stranded in Antarctica | cold | -25 | -25 |
| Event 4 | cooking dinner | hot | 100 | -33.3 |
| Table 3 | ||||
| Events | Descriptions of events (for us) | Sensor Names (for Y) | TRUE REWARD R | PRED. REWARD PY |
| ENEMIES | ||||
| Event 1 | fighting many enemies | Many | -300 | -300 |
| Event 2 | on vacation | None | 100 | 58.3 |
| Event 3 | stranded in Antarctica | None | -25 | 58.3 |
| Event 4 | cooking dinner | None | 100 | 58.3 |
| Table 4: | |||||
| Events | Descriptions of events (for us) | Sensor Names (for G = X & Y) | TRUE REWARD R | PRED. REWARD PG | |
| ENEMIES | TEMPERATURE | ||||
| Event 1 | fighting many enemies | many | hot | -300 | -300 |
| Event 2 | on vacation | none | hot | 100 | 100 |
| Event 3 | stranded in Antarctica | none | cold | -25 | -25 |
| Event 4 | cooking dinner | none | hot | 100 | 100 |
| Fi = f Pi + ( 1 - f ) PG | (4) |
| Ji = { | Fi(E1) - R(E1) |, | Fi(E2) - R(E2) |, … ,| Fi(En) - R(En) |} | (5) |
which of course reduces to our earlier expression in the absence of bias effects (f = 0).
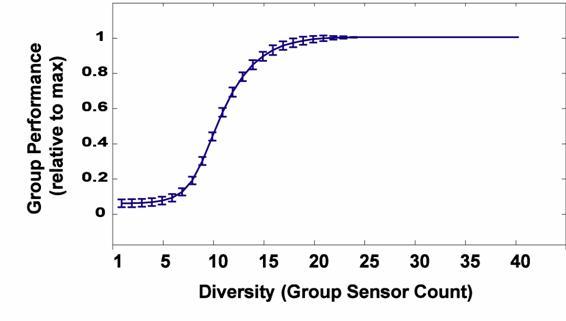
|
| Figure 2. Relative group performance (1 - group predicted reward error / max error) as a function of diversity (no categorization effects considered) |
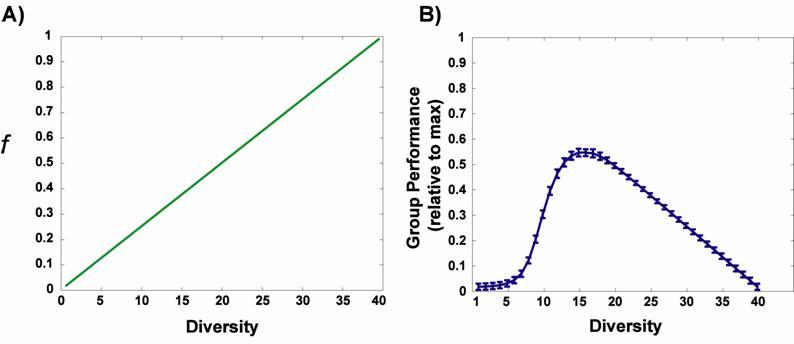
|
| Figure 3. Average, per-agent predicted reward error for the linear diversity/bias model. (A) shows the assumed relationship between diversity and the bias parameter f (which represents a group's negative reaction to diversity), and (B) plots group performance (1 - average error / max possible error) as a function of diversity |
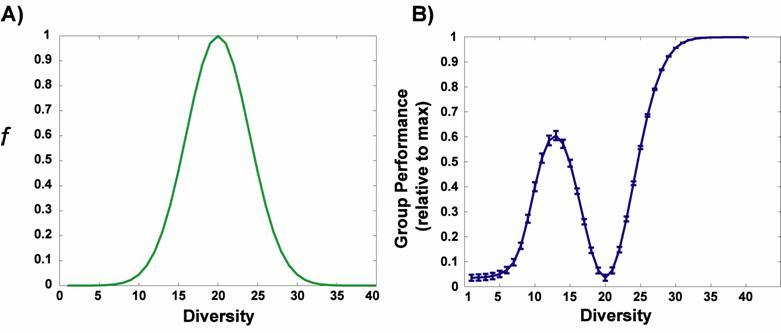
|
| Figure 4. Average, per-agent predicted reward error for the comparative fit diversity/bias model. (A) represents the relationship between diversity and the bias parameter f (which represents a group's negative reaction to diversity), and (B) plots group performance (1 - average error / max possible error) as a function of diversity |
BANTEL, K., & Jackson, S. (1989). Top management and innovations in banking: does the composition of the team make a difference? Strategic Management Journal (10) 107-124.
BECKER, G. S. (1968). Discrimination, Economic, in Sills, D.L. (ed.), International Encyclopedia of the Social Sciences, vol. 4, New York, Macmillan and Free Press, 208-210.
BECKER, Gary S. (1971). The Economics of Discrimination, Second Edition (Chicago: University of Chicago Press).
BREWER, M.B. (1979). In-group bias in the minimal inter-group situation: A cognitive-motivational analysis. Psychological Bulletin, 86, 307-324.
BRODBECK, F. (2003). Contradiction as an inhibitor and facilitator of group performance. Paper presented at the 11th European Congress of Work and Organizational Psychology, Libson, Portugal.
CANNON-BOWERS, J.A., & Salas, E. (2001). Reflections on shared cognition. Journal of Organizational Behavior (22), 195-202.
COX, T. H., Lobel, S. A., & McLeod, P. L. (1991). Effects of ethnic group cultural differences on cooperative and competitive behavior on a group task. Academy of Management Journal (34) 827-847.
DE DRUE, C. K., & Weingart, L. r. (2003). Task and relationship conflict, team performance, and team member satisfaction: a meta-analysis. Journal of Applied Psychology (88), 741-749.
DONOHUE, J. (2005). The Law and Economics of Antidiscrimination Law. Yale Law School John M. Olin Center for Studies in Law, Economics, and Public Policy Working Paper Series. Paper 290.
EARLEY, P. C., & Mosakowski, E. (2000). Creating hybrid teams cultures: An empirical test of transnational team functioning. Academy of Management Journal (43), 26-49.
FUCHS, Victor R. (1998). Women's Quest for Economic Equality (Cambridge, MA: Harvard University Press).
GONZALEZ-ROMA, V., West, M. A., Borrill, C.S. (2003). Demographic diversity and team innovation: Testing a curvilinear relationship model. Unplished manuscript, University of Valencia.
GUZZO, R. & Dickson, M. (1996). Teams in organizations: Recent research on performance and effectiveness. Annual Review of Psychology, 47, 307-338.
HELLERSTEIN, J.K., Neumark, D., Troske, K.R. (1998). Market Forces and Sex Discrimination, Labor and Demography 9807002, Economics Working Paper Archive at WUSTL.
HORNSEY, M. J., & Hogg, M. A. (2000). Assimilation and diversity: an integrative model of subgroup relations. Personality and Social Psychology Review (4) 447-472.
JACKSON, S. E. (1992). Team composition in organizational settings: Issues in managing an increasingly diverse workforce. In S. Worchel, W. Wood, & J.A. Simpson (Eds.), Group processes and productivity (pp. 136-180). Newbury Park, CA: Sage.
JEHN, K.A., Northcraft, G.B., & Neale, M.A. (1999). Why differences make a difference: A field study of diversity, conflict, and performance in workgroups. Administrative Science Quarterly, 44, 741-763.
MILLIKEN, F., & Martins, L. (1996). Searching for common threads: Understanding the multiple effects of diversity in organizational groups. Academy of Management Review, 21, 402-433.
MURNINGHAN, J. K., & Conlon, D. E. (1991). The dynamics of intense work groups: A study of British string quartets. Administrative Science Quarterly (36), 165-186.
OAKES, P. J., Haslam, S. A., & Turner, J. C. (1994). Stereotyping and social reality. Malden, MA: Blackwell.
O'NEILL, J. (1994). Discrimination and Income Differences. In Susan F. Feiner, ed. Race and Gender in the American Economy. (Englewood Cliffs, NJ: Prentice-Hall, Inc.), pp. 13-17.
O'REILY, C. A., Caldwell, D. F., & Barnett, W. P. (1989). Work group demography, social integration, and turnover. Administrative Science Quarterly (34), 21-37.
PELLED, L. H., Eisenhardt, K. M., & Xin, K. R. (1999). Exploring the black box: An analysis of work group diversity, conflict, and performance. Administrative Science Quarterly (44), 1-28.
POSNER, R.A. (1987). The Efficiency and the Efficacy of Title VII, University of Pennsylvania Law Review, (136) 513-521.
RIORDAN, C., & Shore, L. (1997). Demographic diversity and employee attitudes: Examination of relational demography within work units. Journal of Applied Psychology, 82, 342-358.
SIMONS, T., Pelled, L. H., & Smith, K. A. (1999). Making use of difference: Diversity, debate, and decision comprehensiveness in top management teams. Academy of Management Journal (42) 662-674.
TAJFEL, T., & Turner, J. (1986). The social identity of intergroup behavior. In W.A.S. Worchel (Ed.), Psychology and intergroup relations. Chicago: Nelson-Hall.
TRIANDIS, H.C., Kurowski, L. L., & Gelfand, M. J. (1994). Workplace diversity. In H.C. Triandis, M. P. Dunnette, & L. M. Hough (Eds.), Handbook of Industrial and Organizational Psychology (2nd ed., Vol. 4, pp. 769-827). Palo Alto, CA: Consulting Psychologists Press.
TSUI, A.S., Egan, T.D., & O'Reilly, C.A. (1992). Being different: Relational demography and organizational attachment. Administrative Science Quarterly, 37, 549-579.
TURNER, J.C., Hogg, M.A., Oakes, P.J., Rieicher, S.D., & Wetherell, M.S. (1987). Rediscovering the social group: A self-categorization theory. Oxford, United Kingdom: Blackwell.
VAN KNIPPENBERG, D., De Dreu, C., Homan, A.C. (2004). Work Group Diversity and Group Performance: an Integrative Model and Research Agenda. Journal of Applied Psychology, 89(6), 1008-1022.
WAGNER, W., Pfeffer, J., & O'Reilly, C. (1984). Organizational demography and turnover in top management groups. Administrative Science Quarterly (29), 74-92.
WILLIAMS, K.Y., & O'Reilly, C.A. (1998). Demography and diversity in organizations: A review of 40 years of research. Research in Organizational Behavior, 20, 77-140.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]