Anthony Dekker (2007)
Studying Organisational Topology with Simple Computational Models
Journal of Artificial Societies and Social Simulation
vol. 10, no. 4 6
<https://www.jasss.org/10/4/6.html>
For information about citing this article, click here
Received: 28-Feb-2007 Accepted: 25-Jun-2007 Published: 31-Oct-2007
 Abstract
Abstract
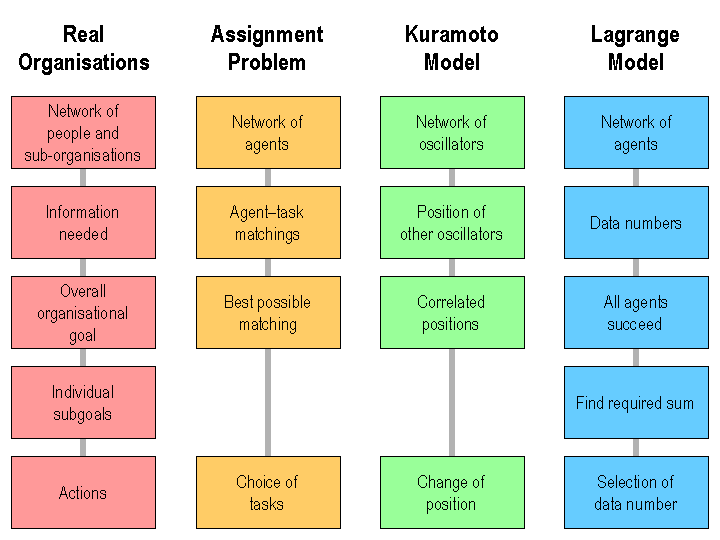
|
| Figure 1. Characteristic of the three simple simulation models discussed in this paper, compared to real organisations |
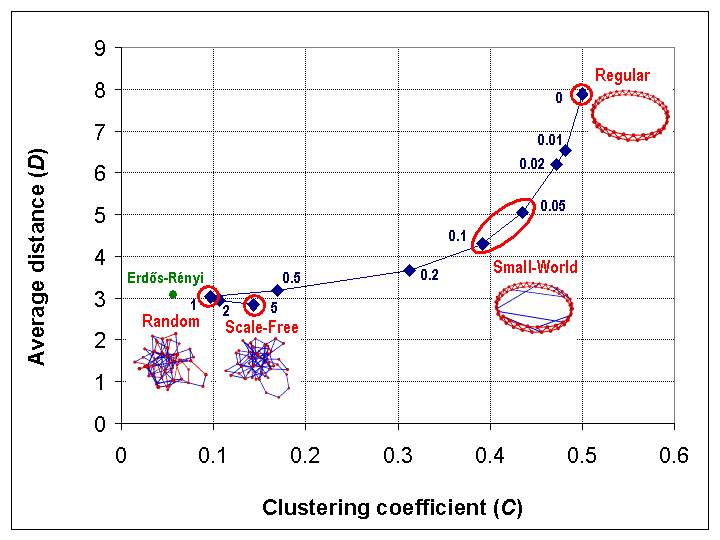
|
| Figure 2. Illustration of the Kawachi process, starting with a 60-node antiprism (top right) |
| D = 2.04 + 1.07 p-0.32 | (1) |
Mathematically, the Kawachi process defines a continuous mapping from the interval [0,5] to the set of probability distributions on networks, and hence induces continuous mappings from the interval [0,5] to various network metrics. Figure 2 can be viewed as illustrating the mappings from the interval [0,5] to the metrics C and D.
| Q = 12.5 + 85.8/D2 | (2) |
This regression equation, illustrated in Figure 3, explained 57% of the variance in the data (a correlation of 0.76, statistically significant at better than the 10-100 level, by analysis of variance). Since the average network distances D ranged from 2.6 to 7.9, this regression equation corresponds to the average quality percentages ranging from 14% to 25%. Extrapolating, it suggests that if every agent were directly connected to every other (i.e. D = 1), then the quality percentage would average about 98%.
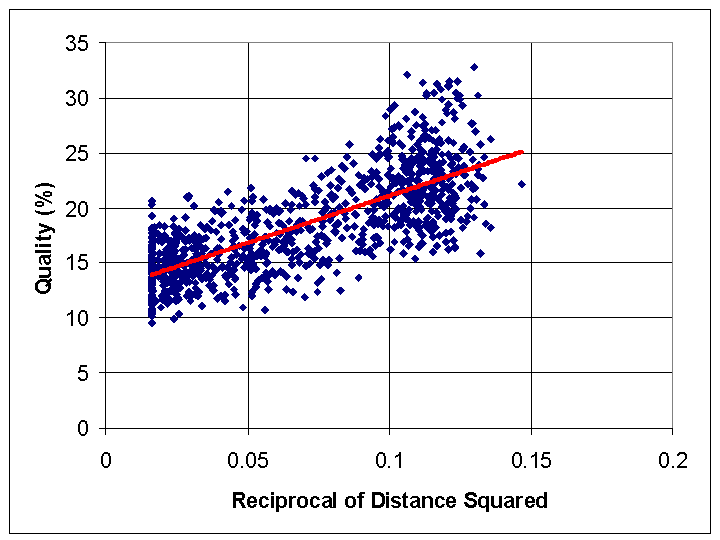
|
| Figure 3. Results for Assignment Problem simulation, showing fit of data to the regression equation |
|
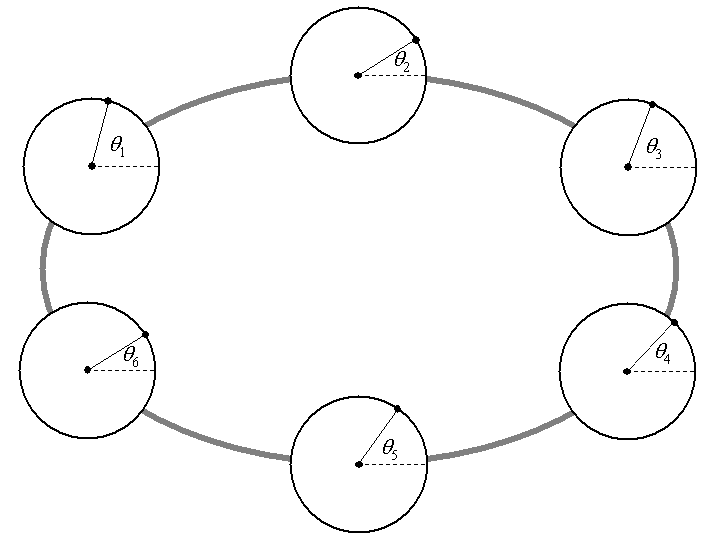
| Figure 4. Six Kuramoto oscillators connected in a ring network, showing the position (phase) of each oscillator |
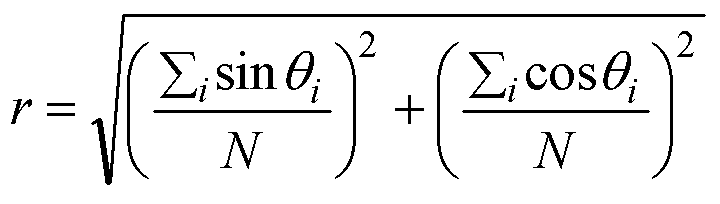
|
(3) |
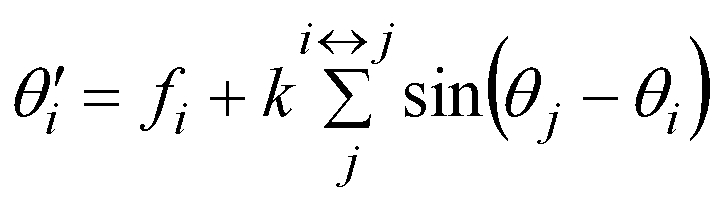
|
(4) |
Here the summation is over all agents j directly connected to agent i, and the multiplier k is 0.001 (substantially greater values than this result in chaotic behaviour when discretized). This differential equation can be approximated as a difference equation, specifying the changing phase over one timestep. We iterated this for 100,000 time steps to see if self-synchronization would occur, with the average frequency fi being sufficiently low (around 0.02) to ensure that the timestep behaviour would be a good approximation to the continuous behaviour specified by the differential equation.
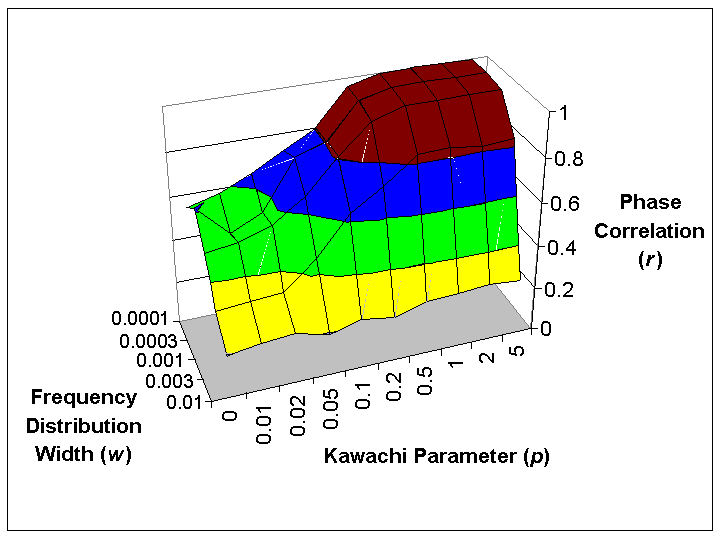
|
| Figure 5. Average values of the correlation r between oscillator phases, for different values of the Kawachi parameter used to generate networks and for different frequency distribution widths |
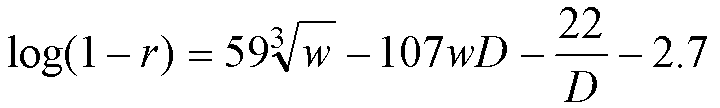
|
(5) |
This equation explained 74% of the variance in the data (a correlation of 0.86, with all components statistically significant at better than the 10-100 level). Using a square root rather than a cube root explained only 73% of the variance, and other network characteristics (such as the clustering coefficient, or even polynomials in the Kawachi parameter) did not provide additional explanatory power.
|
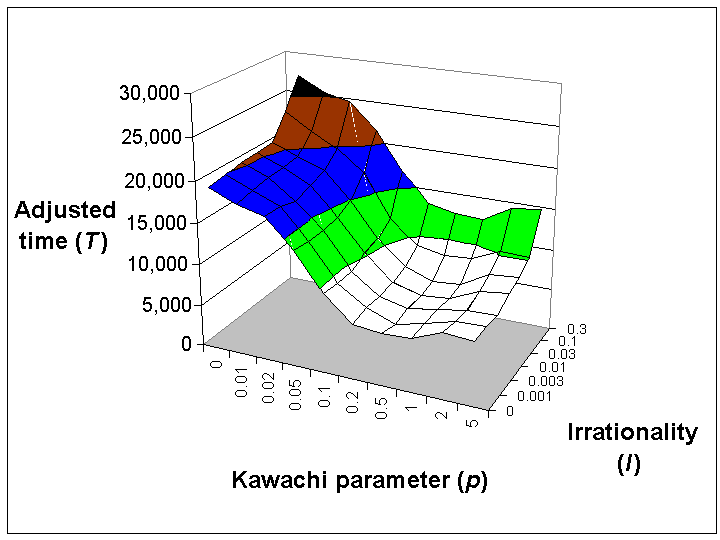
| Figure 6. Mean adjusted completion time (T) for the Lagrange Model, for different values of the Kawachi parameter p and the irrationality factor I. Networks with p = 0.5 performed best |
| T = 22,200 I - 58.9 D3 - 15,700 K + 2,600 K D + 30,500 | (6) |
This predicts 76% of the variance in the data (a correlation of 0.87). All components of this polynomial are statistically significant at the 10-30 level or better, with the choice of the cubic power for D significant at the 10-5 level, and no other cubic or quartic terms significant.
|
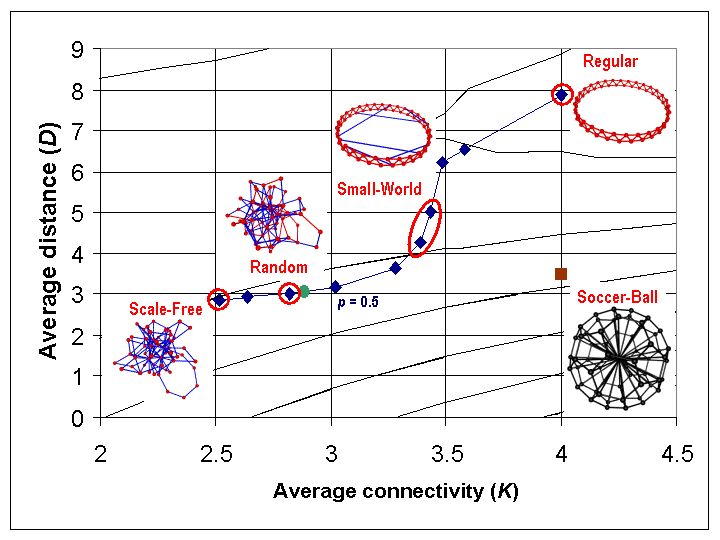
| Figure 7. Change in average network distance (D) and average connectivity (K) for Kawachi process, overlaid on contour lines for polynomial predictor of the adjusted completion time (T) |
BARABÁSI, A-L (2002), Linked: The New Science of Networks. Cambridge, MA: Perseus Publishing.
BOLLOBÁS, B (2001), Random Graphs, 2nd edition. Cambridge: Cambridge University Press.
CHRISTOFIDES, N (1975), Graph Theory: An Algorithmic Approach. London: Academic Press.
CHUNG, F and LU, L (2001), "The diameter of sparse random graphs." Advances in Applied Math, Vol. 26, pp 257-279.
DEKKER, AH (2005), "Network Topology and Military Performance." In Zerger, A. and Argent, R.M. (eds), MODSIM 2005 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand, December, pp 2174-2180, ISBN: 0-9758400-2-9. http://www.mssanz.org.au/modsim05/proceedings/papers/dekker.pdf
DEKKER, AH (2006), "Collaborative Problem-Solving and Network Structure." Presentation to Complex Adaptive Systems and Interacting Agents Workshop, Oxford, September.
DEKKER, AH (2007), "Using Tree Rewiring to Study 'Edge' Organisations for C2." Proceedings of SimTecT 2007, Simulation Industry Association of Australia, June, pp 83-88, ISBN: 0-9775257-2-4.
DOROGOVTSEV SN, GOLTSEV AV, and MENDES JFF (2007), "Critical phenomena in complex networks." arXiv:0705.0010v2 [cond-mat.stat-mech], 1 May.
GIBBONS, A (1985), Algorithmic Graph Theory. Cambridge: Cambridge University Press.
HECHT-NIELSEN, R (1990), Neurocomputing. Reading, MA: Addison Wesley.
KALLONIATIS, AC (2007), "Self-synchronisation and stability in the Network Kuramoto model," to appear.
KAWACHI Y, MURATA K, YOSHII S and KAKAZU Y (2004), "The structural phase transition among fixed cardinal networks." Proc. 7th Asia-Pacific Conf. on Complex Systems, pp 247-255. Australia: Central Queensland University.
MOFFAT, J (2003), Complexity Theory and Network Centric Warfare. Washington, DC: CCRP Publications. http://www.dodccrp.org/files/Moffat_Complexity.pdf
NEWMAN, MEJ (2001), "The structure of scientific collaboration networks." Proc. Nat. Acad. Sci., Vol. 98, No. 2, pp 404-409.
NEWMAN, MEJ (2003), "The structure and function of complex networks." SIAM Review, Vol. 45, No. 2, pp 167-256.
PEREZ, P and BATTEN, D (2006), Complex Science for a Complex World: Exploring Human Ecosystems with Agents. Canberra: ANU E Press, http://epress.anu.edu.au
PUJOL JM, FLACHE A, DELGADO J and SANGÜESA R (2005), "How Can Social Networks Ever Become Complex? Modelling the Emergence of Complex Networks from Local Social Exchanges." Journal of Artificial Societies and Social Simulation, 8(4)12 https://www.jasss.org/8/4/12.html
SRBLJINOVIC A, PENZAR D, RODIK P and KARDOV K (2003), "An Agent-Based Model of Ethnic Mobilisation." Journal of Artificial Societies and Social Simulation, 6(1)1 https://www.jasss.org/6/1/1.html
STOCKER R, CORNFORTH D and BOSSOMAIER T R J (2002), "Network structures and agreement in social network simulations." Journal of Artificial Societies and Social Simulation, 5(4)3 https://www.jasss.org/5/4/3.html
STROGATZ, SH (2000), "From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators." Physica D: Nonlinear Phenomena, Vol. 143, pp 1-20.
WARNE L, BOPPING D, ALI I, HART D and PASCOE C (2005), "The challenge of the seamless force: the role of informal networks in the battlespace." Proc. 10th International Command and Control Research and Technology Symposium. Washington, DC: CCRP Publications. http://www.dodccrp.org/events/10th_ICCRTS/CD/papers/215.pdf
WATTS, D J (2003), Six Degrees: The Science of a Connected Age. London: William Heinemann.
WATTS, D J and STROGATZ, S H (1998), "Collective dynamics of 'small world' networks." Nature, Vol. 393, pp 440-442. http://www.tam.cornell.edu/SS_nature_smallworld.pdf
WEISSTEIN, E (2006), "Lagrange's Four-Square Theorem." http://mathworld.wolfram.com/LagrangesFour-SquareTheorem.html
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]