Rob Stocker, David Cornforth and T. R. J. Bossomaier (2002)
Network Structures and Agreement in Social Network Simulations
Journal of Artificial Societies and Social Simulation
vol. 5, no. 4
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/5/4/3.html>
Received: 31-Jul-2002 Accepted: 28-Sep-2002 Published: 31-Oct-2002
 Abstract
Abstract
|
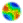
| Figure 1. Representation of network structures: (a) random, (b) scale-free and, (c) hierarchical (Stocker et al. 2001) |
|
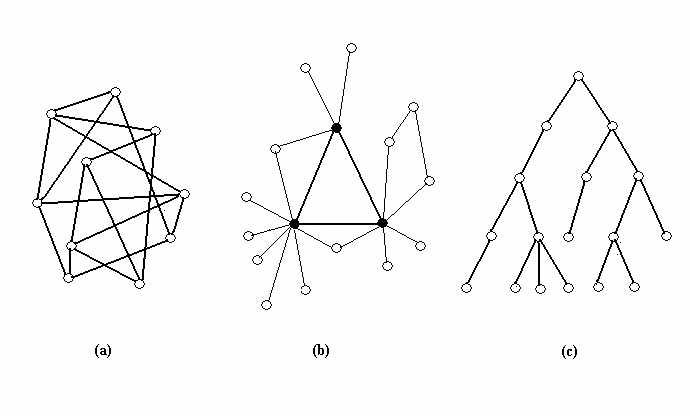
| Figure 2. Patterns of connections to each node in the constrained hierarchical network structure, number of layers = 3, number of nodes in first layer = 1, connections to second layer = 4 and connections to the final layer = 24. This is designated Hierarchy 3λ1λ4λ24. |
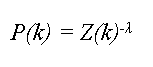
|
|
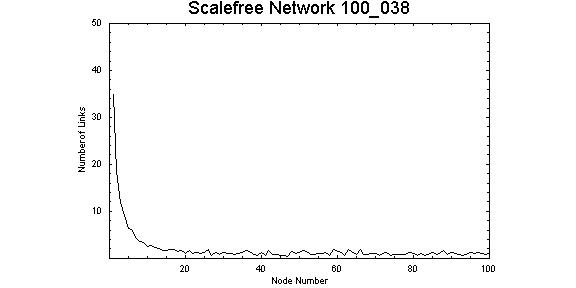
| Figure 3. Connectivity pattern for values Z = 0.38 and λ = 1.00. Node 1 has 35 connections and node 5 has 6 connections, the majority of nodes have only 1 or 2 connections. |
|
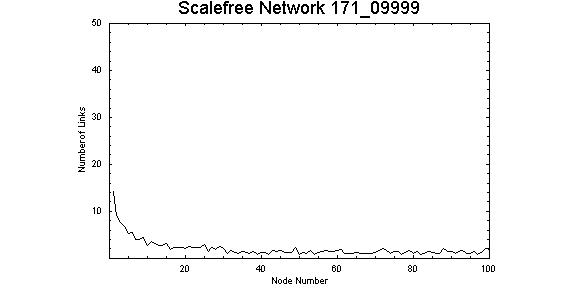
| Figure 4. Connectivity pattern for values Z = 0.9999 and λ = 1.71. Node 1 has 14 connections and node 5 has 5 connections, the majority of nodes have only 1 or 2 connections. |
// initialise each node
for each node
set opinion 0 or 1
set influence between 0 and 1
set susceptibility between 0 and 1
next node
// initialise node connectivity for hierarchy OR scale-free
if hierarchy
for each node i in current layer
select different node j in next layer
create link between i and j
next node i
if scale-free
for each node i
k = number of connections for node i
for each node j from 1 to k
create link between i and j
next node j
next node i
// execute interaction between connected nodes
for time step (1000)
for node i (1 to population)
for node j (1 to population)
if node i connected to node j
if influence of node (i > j) AND susceptibility of node (i < j)
state of j = state of i
else if influence of node (i < j) AND susceptibility of node (i > j)
state of i = state of j
next node j
next node i
record state of each node for each time step
next time step
|
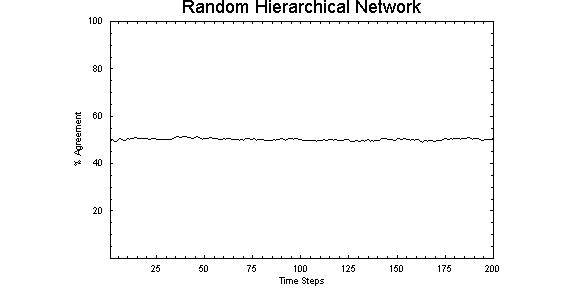
| Figure 5. Agreement patterns through time for the random general tree hierarchical network structure, demonstrating stability through all time steps |
|
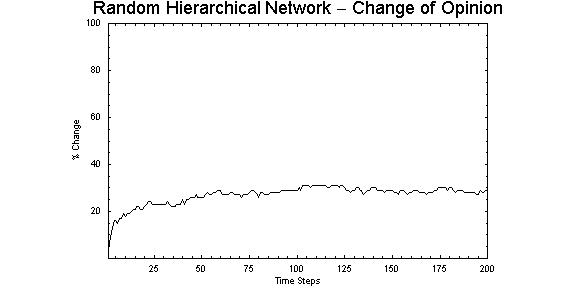
| Figure 6. The percentage of nodes that changed state settling to stability through 0 to 100 time steps, indicating a possible chaotic attractor |
.
|
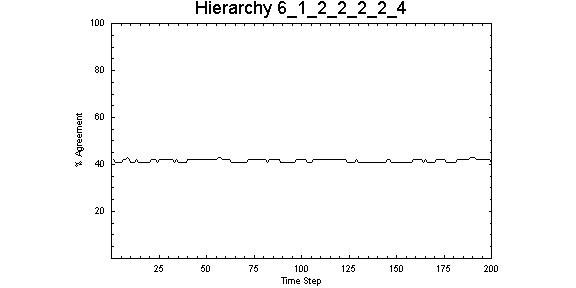
| Figure 7. Representative of the consistent and stable patterns of opinions in hierarchical structures, this system comprised six layers with one node in the top layer. For subsequent layers, there are two links from the previous layer and four links to the final layer resulting in a population of 95 for this structure |
|
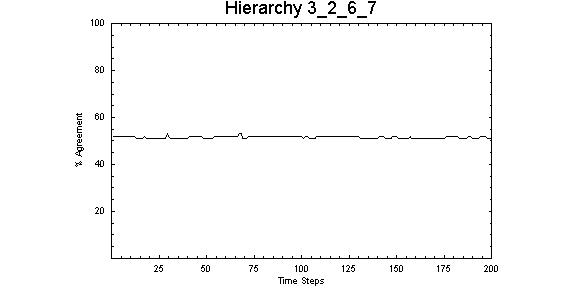
| Figure 8. Relatively narrow3-layer hierarchical structure with 2 nodes in the top layer, 6 links to the second layer and 7 links to the final layer, demonstrates stable opinion patterns (compare Fig 7) suggesting a point of attraction |
.
|
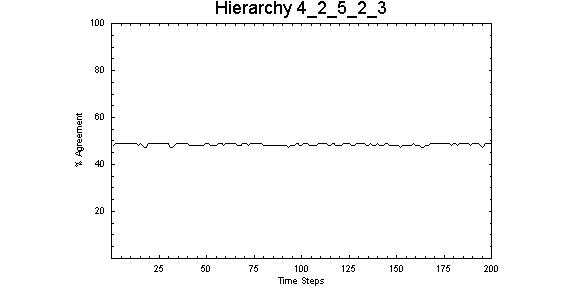
| Figure 9. For this 4-layer structure, the number of links from the first layer to the second exceeds the number of links to subsequent layers. Note the stable patterns of opinion. |
|
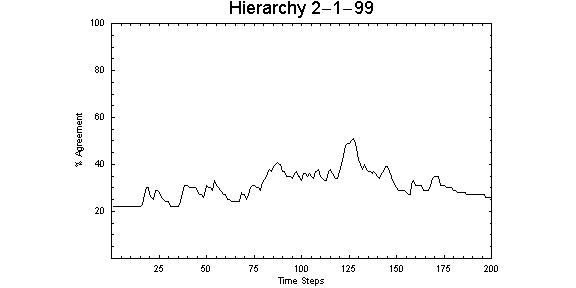
| Figure 10. Representative of broad hierarchical structures, this 2-layer hierarchical network with one node in the top layer and links to ninety-nine nodes in the lowest layer, demonstrates complex behaviour and instability over time, where opinion patterns fluctuate from 20 per cent to 50 per cent. |
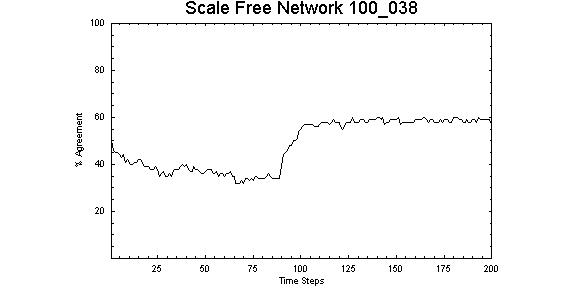
|
| Figure 11. Scale-free network with Z = 0.38, λ = 1.00 showing significant change in number of "yes" around 100 time steps. |
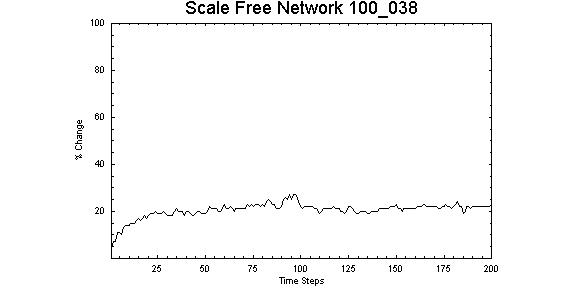
|
| Figure 12. Scale-free network with Z = 0.38, λ = 1.00 showing corresponding the protuberance or increase in the number of nodes changing state at around 100 time steps |
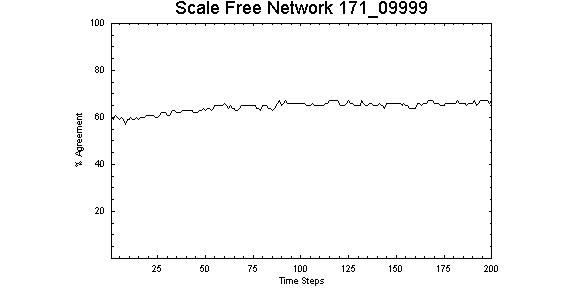
|
| Figure 13. Scale-free network with Z = 0.9999, λ = 1.71 showing gradual move to stable opinion patterns over the first 100 time steps |
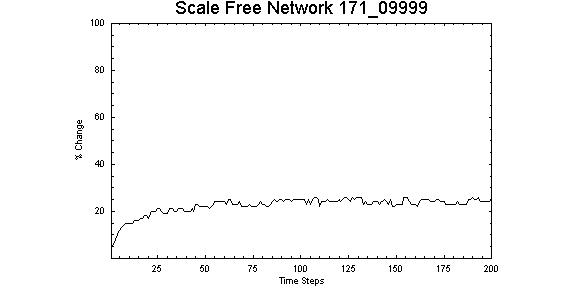
|
| Figure 14. Scale-free network with Z = 0.9999, λ = 1.71 showing an increase in the number of nodes changing state at around 100 time steps that is similar to Z = 0.38, λ = 1.00. |
ALBERT R and Barabási A-L (2001), Statistical mechanics of complex networks. arXiv:cond-mat/0106096, 1: 6 Jun, 1-54.
ALLEN Peter M (1998), Evolving complexity in social science. In Systems: New paradigms for the human sciences, (3-38). Berlin: Walter de Gruyter GmbH & Co.
AXELROD Robert (1997), The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution, 41: 203-226.
AXTELL Robert L (2000), Effects of interaction topology and activation regime in several multi-agent systems. Working Paper 12, Center on Social and Economic Dynamics, Ann Arbor: University of Michigan.
BOSSOMAIER T R J and Harvey I (1997), Time out of joint: Attractors in asynchronous boolean networks. In P Husbands and I Harvey (Eds) Proc. Fourth European Conference on Artificial Life, 67-75
BURA S GuérinλPace F Mathian H Pumain D and Sanders L (1995), Cities can be agents too: A model for the evolution of settlement systems. In Gilbert, Nigel and Conte, Rosaria. Artificial societies: The computer simulation of social life, 86-102. London: University College London Press.
BURT R S (1987), Social contagion and innovation: Cohesion versus structural equivalence. American Journal of Sociology, 88: 1287-1335.
CORNFORTH D Green D G Newth D Kirley M (2001), Ordered asynchronous processes in natural and artificial systems. In Peter Whigham, Mitsuo Gen et al. (Eds) Proceedings of the Fifth Japan-Australia Joint Workshop on Intelligent and Evolutionary Systems, 105 - 112. Dept of Information Science, University of Otago, Dunedin, NZ.
DOREIAN P and Stokman F N (1997), The dynamics and evolution of social networks, NewYork: Gordon and Breach.
DUNBAR R I M Duncan N D C and Nettle D (1995), Size and structure of freely forming conversational groups. Human Nature, 6: 1, 67-78.
DUNBAR R I M and Duncan N D C (1997), Human conversational behaviour. Human Nature, 8: 3, 241-246.
ERICKSON B H (1988), The relational basis of attitudes. In Barry Wellman and S. D. Berkowitz, Social structures: A network approach, 99 - 121. New York: Cambridge University Press.
GILBERT N and Conte R (1995), Introduction. In Nigel Gilbertand Rosaria Conte Artificial societies: The computer simulation of social life, 1-15. London: University College London (UCL) Press.
GILBERT N and Troitzsch K G (1999), Simulation for the social scientist, Buckingham, UK: Open University Press.
GRANOVETTER Mark (1978), Threshold models of collective behaviour. American Journal of Sociology, 83 (6): 1420-1443.
GREEN D G (1993), Emergent behaviour in biological systems. In Complex Systems - From Biology to Computation. (ed. Green, D G and Bossomaier, T R J), 25-36. Amsterdam: IOS Press.
HALES D (1998), An open mind is not and empty mind: Experiments in the meta-noosphere. Artificial Societies and Social Simulations, 1(4), 1-26.
HANNEMAN R A (1995), Simulation modelling and theoretical analysis in sociology. Sociological Perspectives, 38 (4): 457-462.
HOLLAND J (1995), Hidden order: How adaptation builds complexity, Reading, MA: Perseus Books.
JEONG H Tombor B Albert R Oltavi Z N and Barabási A-L (2000), The large-scale organisation of metabolic networks. Nature, 407: 651-654
KLÜVER J and Schmidt J (1999), Topology, metric and dynamics of social systems. Journal of Artificial Societies and Social Simulation, 2: 3.
LIEBRAND Wim B G (1998), Computer modelling and the analysis of complex human behaviour: Retrospect and prospect. In Liebrand, et al. (Eds) Computer Modelling of Social Processes: New Technologies for Social Research, London: Sage Publications: 1-19.
NOWAK A and Lewenstein M (1996), Modelling social change with cellular automata. In R. Hegselmann, et al., Modelling and simulation in the social sciences from the philosophy of science point of view, (249-285). Netherlands: Kluwer Academic Publishers.
NOWAK A Szamrej J and Latané B (1990), From private attitude to public opinion: A dynamic theory of social impact. Psychological Review, 97(3), 362-376.
PASTOR-SATORRAS R and Vespignani A (2001), Epidemic spreading in scale-free networks. Phys. Rev. Lett, 86(14), 3200-3203.
SCOTT J (1991), Social network analysis: A handbook, London: Sage Publications.
STOCKER R Green D G and Newth D (2000), Connectivity, cohesion and communication in simulated social networks. In Akira Namatame Yasuhiro Tsujimura Mitsuo Gen Bob McKay Ruhul Sarker Xin Yao(Eds) Proceedings of the Fourth Japan-Australia Joint Workshop on Intelligent and Evolutionary Systems, 156 - 163. National Defence Academy, Japan; Ashikaga Institute of Technology, Japan; University of New South Wales, Australia.
STOCKER Rob Green David G and Newth David (2001), Consensus and cohesion in simulated social networks. Journal of Artificial Societies and Social Simulations, Volume 4 Issue 4. (https://www.jasss.org/4/4/5.html).
TROITZSCH Klaus G (1997), Social science simulation - Origins, prospects, purposes. In Conte, R et al. (Eds) Simulating social phenomena, Heidelberg: Springer-Verlag: 40-54.
TROITZSCH Klaus G (1998), Multilevel process in the social sciences: Mathematical analysis and computer simulation. In Liebrand, et al. (Eds) Computer Modelling of Social Processes: New Technologies for Social Research, London: Sage Publications: 20-36.
VALENTE Thomas W (1996), Social network thresholds in the diffusion of innovations. Social Networks, 18: 69-89.
WELLMAN B (1988), Structural analysis: From method and metaphor to theory and substance. In Wellman B and Berkowitz S D (Eds), Social structures: A network approach, Cambridge: Cambridge University Press: 19-61.
WELLMAN B and Berkowitz S D (1988), Introduction: studying social structures. In Wellman B and Berkowitz S D (Eds), Social structures: A network approach, Cambridge: Cambridge University Press: 1-18.
WELLMAN B Carrington P J and Hall A (1988), Networks as personal communities. In Wellman, B and Berkowitz S D (Eds), Social structures: A network approach, Cambridge: Cambridge University Press: 130-184.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2002]