Ugo Merlone, Michele Sonnessa and Pietro Terna (2008)

Horizontal and Vertical Multiple Implementations in a Model of Industrial Districts

Journal of Artificial Societies and Social Simulation vol. 11, no. 2 5
<https://www.jasss.org/11/2/5.html>

For information about citing this article, click here

Received: 04-Aug-2007    Accepted: 06-Jan-2008    Published: 31-Mar-2008

Abstract

In this paper we discuss strategies concerning the implementation of an agent-based simulation of complex phenomena. The model we consider accounts for population decomposition and interaction in industrial districts. The approach we follow is twofold: on one hand, we implement progressively more complex models using different approaches (vertical multiple implementations); on the other hand, we replicate the agent-based simulation with different implementations using jESOF, JAS and plain C++ (horizontal multiple implementations). By using both different implementation approaches and a multiple implementation strategy, we highlight the benefits that arise when the same model is implemented on radically different simulation environments, comparing the advantages of multiple modeling implementations. Our findings provide some important suggestions in terms of model validation, showing how models of complex systems tend to be extremely sensitive to implementation details. Finally we point out how statistical techniques may be necessary when comparing different platform implementations of a single model.

Keywords:

Replication of Models; Model Validation; Agent-Based Simulation

Introduction

1.1

In this paper we consider a model of industrial districts where different populations interact symbiotically. According to Becattini (2003) the industrial district "first and fundamental decomposition is to be the one between the productive apparatus and the human community in which it is, so to speak, "embedded"." In our approach, the two populations considered allow for this decomposition: the first one represents the productive apparatus, while the second one can be considered as the human community. Several aspects about industrial districts have been examined in the literature; for an introduction the reader can refer to Garofoli (1981, 1991, 1992), Becattini et al. (1992) or Belussi and Gottardi (2000). Carbonara (2005) analyzes some common key features in the literature on geographical clusters, and in particular, on industrial districts^[1]. She identifies, among the others, both "a dense network of inter-firm relationships, in which the firms cooperate and compete at the same time" and "a dense network of social relationships, based mainly on face to face contact, which is strictly inter-connected with the system of economic relationships." The first aspect is one we consider in our approach. In fact, starting from the definition given by Squazzoni and Boero (2002) where "industrial districts can be conceived as complex systems characterized by a network of interactions amongst heterogeneous, localized, functionally integrated and complementary firms," we introduce and model the role of workers interacting with firms.

1.2

The model of industrial district we therefore obtain consists of two populations that have different peculiarities and interact in the same environment. In the literature, the representation of districts as communities of populations is not a new idea (see for instance Lazzeretti and Storai 1999; 2003). Nevertheless, to the best of our knowledge, studies devoted to the dynamical evolution of these populations are still limited.

1.3

Ecological models of population dynamics for different species can be found both in mathematical ecology and in computer science literature. Ecology of populations examines the dynamics of a number of organisms. In this field the use of mathematical models is quite common in explaining the growth and behavior of population; for a first introduction the reader may refer to Hastings (1997). The most famous model is probably the well known Lotka-Volterra prey predator model (Lotka 1925; Volterra 1926); in this model, which is the simplest prey predator system, two species coexist with one preying on the other (for a concise mathematical discussion of the model the reader may refer to Hofbauer and Sigmund 1998). For more recent contributions about mathematical models of population the reader may refer to Royama (1992). When considering different populations , cooperation has been an other examined thoroughly in the literature has been cooperation, and specifically the evolution of cooperation (see for instance Axelrod 1984). Most of the contributions stem out from the well known prisoner's dilemma game; for example, Flake (1998) discusses an ecological model where only a limited number of organisms can be supported and the population adopting a given of each strategy is some fractional part of the entire ecosystem; other approaches consider both cooperation and the geometry of the interaction network (see Gaylord and D'Andria 1998, for some examples).

1.4

In the model of industrial districts we consider, cooperation is in some sense more implicit, since the structure of the model assumes that workers and firms cooperate; obviously this does not assume that different agents have the same goal. In fact, each of the two species (namely, the workers and the firms), is necessary to the other. In this sense our model exhibits a sort of necessary symbiotic evolution of the two species. In Frank (1997) three different models of symbiosis are considered: the first one is the interaction between kin selection and patterns of transmission; the second is the origin and the subsequent evolution of the interactions between two species; finally, the third considers symbiosis as asymmetrical interaction between species, in which one partner can dominate the other. Our model describes a symbiotic interaction that is similar to the second case, even if, when some parameters of the model are chosen appropriately, we may have a slight dominance of one species.

1.5

In this sense, our model exhibits a sort of necessary symbiotic evolution of the two species. In order to emphasize this requisite our model may allow the analysis of the dynamics and, eventually, of both populations equilibria^[2], trying to isolate the effects each population produces upon the other. By fixing one population behavior we collect results to be compared with the outcomes generated by its co-evolving scenario. Such reference data can help in understanding complex phenomena behind the model, as well as the impact of relationships on its dynamics.

1.6

From this approach we consider the dynamics of the populations of firms and workers and their evolution. In particular, we are interested in shedding light on the emergence of industrial districts when the mentioned decomposition is considered, showing that this simple interaction is sufficient for firms to form clusters. While this cannot be an exhaustive explanation of districts' behavior, it is an interesting insight.

1.7

Since the system is highly complex, a valid mathematical model of it is itself complex, precluding any possibility of an analytical solution. As is common in these cases, the model must be studied by means of simulation; for further details on the role of simulation, the reader may refer to Law and Kelton (2000). The simulation approach for the analysis of districts is not new. For example, Zhang (2003) uses agent-based simulation to study the dynamics of high-tech industrial clusters, Squazzoni and Boero (2002) use computational techniques to focus on some evolutionary fundamentals of industrial districts modeling, and Brenner (2002) uses simulation to study some mechanisms of the evolution of industrial clusters.

1.8

While in the simulation of real systems several techniques are used in order to increase the model validity and credibility, not all of them can be used when implementing a theoretical model such as in our case. Software developers are well aware that computer programming is an intrinsically error-prone process; for example, Becker (2005) claims "As applications become more complex, their resource management requirements become more complex, and despite our best efforts, our designs often have holes in them, or we apply our designs incorrectly, or we make coding errors." This is well known in the simulation literature; for example, in Law and Kelton (2000), several techniques are suggested for the model verification, i.e., "determining whether the conceptual simulation model (model assumptions) has been correctly translated into a computer program." Nevertheless, only recently does the agent-based modeling literature seem to be aware of the potential pitfalls (see for example Polhill et al. 2005). For these reasons we decided to use an approach similar to the one of Cerruti et al. (2005), i.e. to consider and compare different model implementations. To obtain completely identical implementations, however, is not a straightforward process, given the complexity of the considered model. Nevertheless, we found that the whole process of comparing and discussing the different implementations is extremely beneficial. In this sense, while the results' replication is to be considered preliminary – at the moment we cannot obtain exactly the same results with the three implementations – the process of discussing and comparing different implementations details and results seems to be extremely beneficial and promising in terms of model verification. Finally, this approach looks promising in dealing with some important issues as those mentioned in Polhill et al. (2005).

THE MODEL

2.1

The model we consider simulates a small industrial district consisting of two interacting populations and four different components:

• the orders or productive tasks to be completed. The tasks come from the external world, and when completed, disappear from the model scope;
• the skills or abilities that are necessary to perform the different production phases of each order;
• the firms receiving the orders either from the market or from other firms and processing them;
• the workforce that, when hired by firms, allows them to process the orders.

In each time period, new workers and firms are, according to some parameters, generated and randomly located.

2.2

Here we describe each of the four components and discuss their mutual relationships.

2.3

Each order contains a recipe, i.e. the description of the sequence of activities to be done by the firms in order to complete a specific product. The different activities or phases to be done belong to the skill set S but are not necessarily of the same kind. In this sense, skills can be considered as technical abilities. This assumption is motivated by different studies of skill dynamics in manufacturing; for an empirical study on the Italian manufacturing firms, the reader may refer to Piva et al. (2003). To explain how skills are modeled consider a district with three skills 0,1,2. A feasible example of order is '00120': this is a five-phase order where the first two phases need skill 0, the third needs skill 1, the fourth skill 2, and the last skill 0. Each firm is specialized in a single skill and the same holds for workers. Obviously, other approaches in modeling production processes using recipes are possible; for example, the modeling of production operations as recipes is adopted by Auerswald et al. (1998). Or, for a complexity- and knowledge- based approach, the reader may refer to Sorenson et al. (2004).

2.4

In the current version of the model, specialization for firms and workers is randomly attributed and does not change. Firms can only process order phases denoted with their skill specialization, and workers are preferably hired by firms with the same skill. The orders consisting of non-homogeneous phases need to be sent to different firms to be completed. The mechanisms with which workers are hired and which firms pass each other the orders rely on the social structure of the district: the environment is a (social) space with (metaphorical) distances representing trustiness and cooperation among production units (the social capital). While firms have a social visibility that increases according to their longevity, workers' visibility is fixed. Only mutually visible agents can cooperate, i.e., firms may hire only workers that are in their social network and orders can be passed between mutually visible firms. This aspect refers to the other key feature which is mentioned by Carbonara (2004), i.e., the network of social relationships. In our model, to keep the analysis simple, we do model the network in terms of distance. With these assumptions an important aspect of the model arises: cooperation is not optional; rather, it is necessary for agents to survive.

2.5

At each turn of the simulation, both firms and workers bear some costs, and both hired workers and producing firms receive some revenue. In the current version, net profits and wages are modeled simply assuming that marginal costs are not greater than marginal revenues for firms, as well as a positive salary for workers. Consequently, if for prolonged time either a worker is not hired or a firm has no worker, their balance may become negative. Workers and firms with negative balance disappear. Negative balance is the only cause of default for workers.

2.6

By contrast, other reasons for a firm's default are prolonged inactivity and the impossibility of sending concluded orders to other firms to perform the successive steps. While the interpretation of the first two default causes for firms is straightforward, the third one requires some explanation. First, we assume that a totally completed order is absorbed by the market; the rationale for this is that since the market generated this order, there exists demand. Second, recalling that orders may consist of different phases, when a partially completed order cannot be sent to a firm with the needed skill, this means either that such a firm at the moment does not exist or that it is out of scope. The latter may be interpreted as a lack of knowledge and trust, i.e., gaps in the social capital. It is worthwhile to remark that all these aspects are consistent with the mentioned definition of industrial districts given by Squazzoni and Boero (2002). In all these cases the permanence of the agent on the market is economically unfeasible; for these reasons we summarize these situations with the broad term default.

2.7

All the firms and workers are located and operate on a two superimposed toroidal grids: one for the workers and one for the firms^[3].

2.8

From the populations perspective we can identify some specific distinctiveness. The workforce population is heterogeneous in terms of the skills each individual is specialized in. Incomes of workers depend on how much the skill they offer matches the firms' demand. Population dynamics is regulated by two coefficients, conveniently chosen: the birth frequency k of new workers and the probability r that a worker is hired by a firm. This factor is indirectly correlated with the death rate of workers. In fact, a worker is supposed to come out of the model in case her income balance is negative.

2.9

The dynamics of the firms' population depends on many factors. We are interested in identifying which parameter-combination can reproduce an equilibrium, without considering the workforce contribution. We take into account that firms' survival is pledged by the possibility of trading production phases with other skill-complementary firms, as well as by an adequate flow of orders in the system. The output we expect is an equilibrium shaped as an economic cycle, without explosions or district failures.

2.10

The separation of two population dynamics is obtained removing the element joining them: the workforce hiring process. This feature has been maintained throughout the modeling process.

2.11

In trying to summarize the enter/exit process, we can identify one cause of death for workers:

• when a worker is not employed for a long time;

and two causes for firms:

• when a firm does not receive orders for some time;
• when it has to shorten social visibility so that it cannot deliver orders to other firms.

2.12

Joining the two populations into a co-evolving model introduces another cause of death for firms:

• when the production stock, generated by hired workers, is negative, the firm cannot complete the production step.

The novelty of this model structure is the introduction of the interaction "within" a model layer (the one containing the productive structures) while the classical Lotka-Volterra structure exploits only the consequences of the interaction "between" two different layers.

2.13

In order to produce, firms have to interact with other firms, with the constraint of only considering the units sharing a portion of their visibility space as mutually visible, in a synthetic way of representing trust. The "within" interaction influences the dimension of the productive clusters, while the "between" interactions has the role of determining the spatial localization of the clusters. With this abstract but not unrealistic tool we can verify the emergence of well-known phenomena and, in a parallel way, of new ones, which appear as unobvious but plausible behaviors of the district structures.

Multiple Approaches To Model Implementations

3.1

When considering complex systems such as the one described in the previous section, it may be extremely useful to consider different approaches for implementation. In this section we do not refer to modeling tools, but to the different ways to study a system as mentioned in Law and Kelton (2000).

3.2

We implement the model described in the previous section using different methodologies. We call this vertical multiple implementation since it is different from the multiple implementation of the model which uses different tools based on the same modeling approach (such as Swarm, Repast and Netlogo for agent-based Simulation). This approach is extremely promising for at least two reasons. First, it allows the assessment of the potentialities and drawbacks of the different modeling philosophies. Second, the comparison of the results obtained via the different approaches may be extremely useful in the model validation. In the following, we illustrate why, after having first considered a mathematical approach and then system dynamics model, we decided finally to use an agent-based approach.

3.3

Our model can be formalized as a discrete time dynamic system. Consider two sets of variables, the first one describing the worker, w_i∈ W_i and the second one describing the firm f_i∈ F_i. Since workers and firms are located on two p× q superimposed toroidal grids, we can consider a single grid where each cell can: a) contain a worker and no firm, b) contain a firm and no worker, c) contain both a firm and a worker, d) be empty. In cases a), b) c) the cell state consists of the informative variable of its content, while in case d) all the informative variables are null. The state of cell at location i,j can be formalized as a vector x_ij =(w,f)∈W₁ ×···× W_m ×F₁ × ···× F_n with the convention that either w or f can be the null vector, when respectively either no worker or no firm are present. We define the time t state of the system as the vector of the states of cells at time t x:=(x^t₁₁, x^t₁₁,..., x^t_pq). Finally, consider the following stochastic processes:

(1)

describing respectively the orders generation, new workers entry, and new firms entry, then the evolution of the system can be formalized as follows:

(2)

3.4

The direct consequence of non-linearity and complexity is that the theoretical analysis of the formal model is not straightforward. This is well known in the literature and, according to many authors (e.g.Carley and Prietula 1994), many models are too complex to be analyzed completely by conventional techniques that lead to closed-form solutions. In order to obtain some results turning to simulation is natural and necessary.

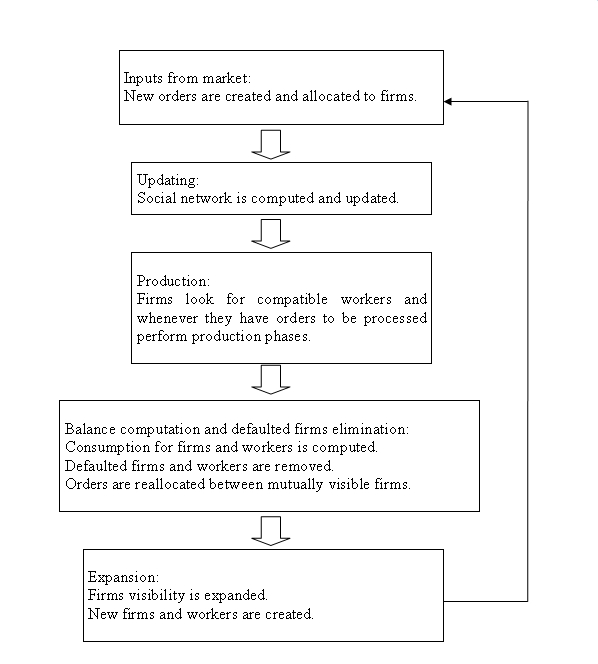
Scheme 1. Scheme of a simulation turn

3.5

Having described all the agents interaction in our model of industrial district, to introduce the structure of the simulation is immediate. For each turn, first new orders are created and allocated to firms, then, after updating the social network induced by the mutual visibility of firms and workers, the productive process begins. Successively compatible and visible workers are hired by firms, all the firms with orders perform productive phases, then costs and revenues are accounted for and balances are computed. Defaulted workers and firms are removed. Finally visibility for firms is updated and new workers and firms are created. At this point the state of the system is displayed both in terms of graphical output and in terms of relevant data.

3.6

The activities of one turn are displayed in Scheme 1.

A Simple Formal Model

3.7

When assuming one single skill and perfect visibility—that is, all workers are perfectly visible to the firms—it is immediate to formalize the dynamics of the two populations, workers and firms, as follows:

(3)

Where

• b: indicates the workers arrival rate
• d: indicates the firms arrival rate
• s: indicates the number of firms sustainable by the district

3.8

While in the first equation the max(W_t – F_t,0) term captures the fact that sustainable workers need to be employed, in the second equation, the max(F_t – W_t, F_t – s, 0) term captures the fact that firms need workers to hire and orders to be processed in order to remain in the district; in this sense these two terms model the symbiotic relation between firms and workers.

3.9

Simple algebra allows determining the several the fixed points of the system, they are

(4)

3.10

Finally, observe that either fixing F_t in the first equation or W_t in the second we can decompose the two population dynamics.

3.11

While this mathematical analysis is extremely simple, it allows a first understanding of the model dynamics. The main drawbacks are the homogeneous-agents assumption and the fact that revenue and wage modeling does not take into account accumulation effects over time.

A System Dynamics Approach

3.12

In terms of modeling, we need to take a further step towards the complex interactions that our model aims to describe. A first solution is the use of system dynamics; the reasons for this choice are that this approach allows, by the use of stocks and flows, the analysis of some threshold effects. According to Mass (1980), stocks are critical in system dynamics modeling since they characterize the state of the system, provide systems with the inertia and memory and are the sources of delays, as a consequence; since our system encompasses many of these aspects, system dynamics seems likely to provide interesting insights.

3.13

The approach we follow consists of three steps. First, we write the System Dynamics correspondent of the piecewise linear model we considered in the previous section. This model is represented in Figure 1, and perfectly replicates the analytical solution of the formal model in terms of results.

Figure 1. The System Dynamic version of the piecewise linear model

3.14

Second, we separate the two populations after introducing the wage and the revenue variables, as described in Section 2. The two single population models are similar, the role of wage for workers is the same as revenue for firms; in addition, the s term is replaced by the number of firms that is sustainable. They are represented in Figures 2 and 3. Finally, some balancing loops occur in both populations.

Figure 2. The System Dynamic model of workers population

Figure 3. The System Dynamic model of firms population

3.15

Finally, the two population models are linked considering the dependencies in the model we presented in Figure 4.

3.16

The main dependencies between the two populations occur by way of the number of firms increasing the w(age) accruing rate and the number of workers reducing the F(irms) default rate. These dependencies generate a self enforcing loop constrained by the number of orders.

3.17

The System Dynamics model allows us to highlight some of the aspects that the formal model described in Section 3 could not take into account; nevertheless, even this approach is not completely satisfactory since it cannot consider several important aspects of our model.

3.18

In fact, it is evident that the System Dynamics model is relative to one single skill and even in this case the network structure characterizing industrial districts is not considered. Furthermore, since all workers and firms are aggregated into single stocks, it cannot take into account the heterogeneity and geographical structure which are peculiar to the system we consider. Finally it should be mentioned that System Dynamics models —which can be converted into ordinary differential equations— presume a continuous world. For these reasons it will be pointless to further discuss the System Dynamics model output in depth, and will consider an agent-based model.

3.19

While we will not be able to compare the System Dynamics results to the full fledged agent-based model, the System Dynamics approach still constitutes an important step in terms of modeling process, as it links the mathematical formalization presented in the previous subsection and the agent-based model.

Figure 4. The System Dynamic model of the workers and firms population

The Agent-Based Approach

3.20

A first analysis of this model is presented in Merlone and Terna (2006), the direct consequence of non-linearity and complexity is that the theoretical analysis of such a formal model is not straightforward. This is well known in the literature, and, according to many authors (e.g.Carley and Prietula 1994), many models are too complex to be analyzed completely by conventional techniques that lead to closed-form solutions. In order to obtain results, turning to simulation is natural and necessary.

3.21

Having described all the agents' interaction in our model of industrial district, and having presented the System Dynamic model, it is immediate to introduce the structure of the simulation. For each turn: first, new orders are created and allocated to firms; then, after updating the social network induced by the mutual visibility of firms and workers, the productive process begins. Successively compatible and visible workers are hired^[4] by firms, and all the firms with orders perform productive phases. Costs and revenues are then accounted for, and balances are computed. Defaulted workers and firms are removed. Finally, visibility for firms is updated and new workers and firms are created. At this point, the state of the system is displayed both in terms of graphical output and in terms of relevant data.

3.22

Figures 5 and 6 show the parallel interacting process of order completion, production/stocking and workforce hiring. These processes are supposed not to be interconnected in Figure 5, which is the case of different unlinked populations. On the contrary, Figure 6 shows the case of a coevolving symbiotic scenario in which production depends on the availability of workers, whose absence can cause the firm to go out of stock (one more cause of death).

Figure 5. The dynamic process of independent populations

Figure 6. The dynamic process of the co-evolving model

The Agent Based Implementation

4.1

Different simulation tools are available to social scientists interested in agent-based simulations. Among the most widely used we recall Swarm, Repast, NetLogo, though other approaches are possible. For example, it is also possible to implement models through custom simulation platforms using high level languages. While the choice of the simulation platform should have no effects on the simulations results, this might not always be true (see for examplePolhill et al. 2005). Furthermore, in science, repetition is what allows results to be validated and accepted by the scientific community.

4.2

Considering computer simulations, repetition can be intended just like experiment replication by other scientists, or, more dramatically, as model reimplementation. While experiment replication can be easily achieved, reimplementation is a more rigorous process in which the model is deeply reexamined. Given the complexity of the models considered, and the fact that computer programming is an extremely error-prone process, reimplementation of the model may be extremely valuable in order to identify potential problems that may invalidate results. We call this kind of multiple implementation horizontal multiple implementation to contrast with the vertical multiple implementation which was discussed in Section 3. While the first kind of multiple implementation allows mainly a deeper understanding of the model, the second horizontal or parallel implementation is meant especially to replicate the models and to determine whether the conceptual simulation model has been correctly translated into a computer program.

Figure 7. Dependent multiple implementation

4.3

After the model has been implemented once, the successive implementation may either have the first implementation as a starting point (Figure 7) or may be originated by the model as independent implementations (Figure 8)^[5].

Figure 8. Independent multiple implementation

4.4

The first approach allows for assessing the internal consistency of the code and for a comparison of the different platforms. With the second approach it is additionally possible to have a comparison of the modeling choices alongside a more thoughtful discussion of the model assumptions.

4.5

Finally, while the first approach is relatively faster, its main drawback is that the modeling choices, as well as possible misinterpretations of the model, are less likely to be discovered since they may be inherited in the successive implementations.

4.6

We implement this model using jESOF, an enterprise simulator based on Swarm, JAS and a custom C++ implementation.

4.7

Our purpose is to compare the advantages of the three implementations and highlight the benefits that arise when the same model is implemented on radically different platforms.

4.8

For the different implementations, some relevant parts of the code are available upon request; for instance, as it concerns jESOF, code is included in the last distribution at http://web.econ.unito.it/terna/jes/; for the JAS, the model is available at http://jaslibrary.sourceforge.net/models/District-article.zip; finally, for the C++ implementation, the classes district, firm, order and worker are available at http://web.econ.unito.it/terna/jes/merlone/district-classes.zip.

The jESOF/Swarm Implementation

4.9

We use the original package jESOF (java Enterprise Simulation Open Foundation, described at http://web.econ.unito.it/terna/jes/). The package is built using the Swarm library for agent-based models (described at http://www.swarm.org).

4.10

The purpose of the jESOF structure is to develop a two-side multilayer world, considering both the actions to be done —in terms of orders to be accomplished (the "What to Do" side, WD)— and the structures able to execute them, in terms of production units (the "Which is Doing What" side, DW). WD and DW can be consistent or inconsistent, and the presence of social capital —expressed by the necessity of firms inter-visibility as a condition to exchange— introduces inconsistent situations reproducing real world occurrences.

4.11

The jESOF dictionary states the following:

• unit: a productive structure; a unit is able to perform one of the steps required to accomplish an order;
• order: the object representing a good to be produced; an order contains technical information (the recipe describing the production steps);
• recipe: a sequence of steps to be executed to produce a good.

4.12

The central tool in this simulation environment is a proprietary scripting language. This is used to describe units acting in the simulated world, and to define actions to be done within the simulation framework by the recipes contained in the orders. The recipes can call computational functions written in Java code to make complicated steps, such as creating new firms or workers, hiring workers, or accounting for income and consumptions of the different units.

4.13

In our case the scripting language uses two different sets of recipes included in orders.

• In the firm stratum we have recipes related to production, with sequences of steps describing the good to be produced.
• In the workers stratum, which is also the interaction place, recipes produce five kinds of effects: (i) new workers appear in the simulation context, either near to similar ones, or randomly distributed; (ii) firms hire workers and recipes modify workers and firms private matrices; this is done accounting for both the availability of the labor production factor (firm side) and household income (workers side); (iii) firms make use of available labor production factors; (iv) firms either short of orders to be processed, or lacking adequate workers on the market, or being unable to deliver produced goods disappear from the economic scenario; (v) workers also disappear if unable to find a firm for prolonged time.

4.14

Recipes are able to perform complex tasks, such as those described above, and are developed via computational steps. These steps can be interpreted as calls to code functions (methods of a Java class) invoked by a scripting language.

4.15

As an example, the sequence '1001 s 0 c 1220 2 0 0 1 s 0' is a recipe describing a task of type (ii) above, going from a unit of type 1001 (a firm) to a unit of type 1 (a worker) and invoking a computational step with id code # 1220.

4.16

An example of the Java code is given in figure 9; note that the method uses both internal parameters and matrix references.

Figure 9. Java Code implementation for a computational firm

The JAS Implementation

4.17

The next implementation we present is written using the JAS library (described at http://jaslibrary.sourceforge.net). It is compliant with the standard modeling approach often used in agent-based modeling: the model-observer paradigm. Everything related to the description of the model is put into a section (a set of classes) called 'model', while the code relative to data analysis, graphical representation and interaction with user is put into the 'observer' section.

4.18

While JAS is very similar to the Swarm architecture, the former implementation is very different from the one presented here, since the jESOF layer introduces a well-defined language and structure to model organizations. It allows a higher level of abstraction in the model description.

4.19

JAS is used here only as a basic platform, offering the modeler some well-tested libraries. The logic of the model has been designed from scratch, using object-oriented programming and Java formalism.

4.20

Figure 10 shows the dynamic structure of the model, representing the sequence of events which activates the agents. It is described using a modified UML sequence diagram, as described in Richiardi et al. (2006).

Figure 10. Time-sequence UML diagram of the model implemented with JAS

Figure 11. The method getPlayersInMyDomain() from DomainPlayer class

4.21

Thanks to the JAS built-in libraries, the implementation is rather standard. In fact, the toroidal space representation, as well as the random number-generators, is available in the package. The trickiest aspect of the model implementation has been represented by the management of intersections between firms and workers and among firms.

4.22

Taking advantage of the object-oriented programming, both the Firm and Worker classes have been implemented as subclasses of a generic class called DomainPlayer. Through its methods, all the domain players (firms and workers) are able to expand the domain visibility and computer intersection with other players. In particular, the intersection algorithm is shown in Figure 11.

The C++ Custom Implementation

4.23

The implementation we present here is written for C++; in particular, we use Borland C++ Builder 5.0. Our approach consists of two phases: first, the model is coded as a set of classes; second, we decide what sorts of information is displayed to the user. The first phase is independent from the C++ compiler used, while the second may rely more on the used compiler and will involve technical aspects irrelevant here. For these reasons, we shall focus our attention on the first phase.

4.24

The implementation we chose is hierarchical; we modeled a container class called district which contains pointers to objects belonging to classes order, worker and firm. The container class implements the methods performing each phase of a simulation turn, the graphical display methods and the interface with the main unit. The code for a turn of simulation is reported in Figure 12.

Figure 12. C++ implementation code for a simulation turn

Replicating complex systems: details matter

5.1

As we mentioned previously, the model of industrial district considered is rather complex, as it is composed of several tightly coupled components (for other aspects of dynamic complexity seeSterman 2000). As a consequence, we expect to observe in the model many of the properties that characterize complex systems. In fact, the sensitivity to apparently insignificant details seems to be a characteristic of our model implementation. This was particularly evident during a phase of the testing of the model; we report this example as evidence of how such small details may have dramatic consequences.

5.2

As previously discussed, one of the features of the industrial district model we consider is decomposition in different populations. This decomposability feature was kept during the vertical multiple implementation. As a consequence, in order to compare the different platform implementations, we compared their results when the firms order subsystem was considered.

5.3

Since the causes of the different behavior we observed in the different (horizontal) implementations could have been both different random generators we used and also some consequences of floating point rounding (see, for instance, Polhill et al. 2005 andCerruti et al. 2005), we decided to consider a deterministic environment where orders were distributed to firms according to a certain order. In particular, we considered a single skill district with fixed five-phase length orders assigned to firms according to a rotating list. The results when comparing the JAS and C++ version are remarkably different (see Figure 13).

Figure 13. Results in the deterministic order allocation for firm population

5.4

With the considered parameters configuration, it is immediately observable that, while the steady number of firms is 32 in the C++ implementation, the number of firms is only 22 with the JAS implementation. This stark difference can be explained when carefully considering how the list for order allocation is managed under the different implementation.

5.5

With the C++ implementation, the order of operations was:

1. top of the list firm gets the order
2. top of the list firm goes to the bottom
3. a new firm is added at bottom;

5.6

With the JAS implementation, the order is slightly different:

1. top of the list firm gets the order
2. bottom of the list firm goes to the top
3. a new firm is added at bottom.

5.7

The effects of the different rotation direction (named respectively top-bottom and bottom-top) are depicted respectively in Figures 14 and 15. When considering the same rotation in both implementations the results became identical.

Figure 14. Results in the deterministic order allocation for firm population (top-bottom)

Figure 15. Results in the deterministic order allocation for firm population (bottom-top)

5.8

Such a detailed analysis shows how different implementations of the same model may differ from one another. This is one reason why the choice of the simulation platform does not only have effects on the formal description of the system, but may also affect some of the behaviors. The impact that apparently insignificant details like management of collections, discrete time representation and sequences of events can have on the model outcomes is remarkable.

5.9

While C++ implementation allows the researcher to implement algorithm with the maximum flexibility, the choice of a framework like JAS or jESOF introduces some constraints that reduces the programmer's freedom in code implementation. As a matter of fact, we were able to replicate this exact behavior comparing C++ and JAS. The same exact implementation on the three platforms would have been very difficult.

5.10

While one would expect that introducing randomness would be sufficient to have these differences vanishing, this is not completely correct. In fact, while having 5-phase orders randomly attributed to firms the results is identical, when the order length is randomly generated and the orders are distributed according the list we described above, the results are remarkably different, as seen in Figures 16 and 17.

Figure 16. Number of firms over time, for random length order with top-bottom firm list rotation

Figure 17. Number of firms over time, for random length order with bottom-top firm list rotation

5.11

The different behavior can be explained by the prolonged inactivity default; in the stochastic length orders with top-bottom list rotation, the number of firms the district can support is independent of the length of orders, as always the same firms get orders and the others default for prolonged inactivity. This can be seen in Figure 18, where the list of firms together with their inactivity values is shown at two different consecutive times. Firm 2 gets the order and is moved at the bottom of the list, while firm 20 defaults and is removed; at the following period, inactivity for all firms but 2 is increased and a new firm is added to the list. Nevertheless, it is easy to observe that all firms in odd position will default while only those in even position will be assigned orders regardless of the order dimension. Vice-versa with the bottom-top list rotation the firm permanence in the district is determined by the order length, which can be observed in Figure 16.

Figure 18. Firm list evolution, for random length order with top-bottom firm list rotation

A Discussion on the Strengths and Weaknesses of the Different Implementations

6.1

While the first two approaches rely on well-tested libraries, and most of the implementation details are hidden from the programmer, the third approach requires almost everything to be built from "ground zero". As a result it is more time-consuming and certainly more error prone. On the other side, the definitive advantage of the second approach is flexibility, both in terms of graphical output and interactivity.

6.2

The three implementations follow an increasingly abstract approach. In fact, while the C++ implementation does not refer to any modeling framework, the JAS one is founded on a well-known and accepted implementation pattern. It is the so called model-observer paradigm, which is largely adopted in many platforms like Swarm, Repast and JAS.

6.3

Not only is a JAS-compliant model easier to debug and read by others, but it can get at a more elegant way to declare some modeling specific aspects, like the time event structure. The model definition is self-contained into a specific class (DistrictModel). The number, type and relationships of agents are declared at the model building procedure as well as the declaration of the events fired during the simulation execution.

6.4

The extreme abstraction is reached in the jESOF implementation. Even if it is based on Swarm, which is largely comparable with JAS, the jESOF layer provides a declarative approach in designing agent-based models. In fact, through the declaration of a set of unit capabilities and a sequence of recipes (the doing-what and what-to-do perspectives), the model is quite complete. The custom logic—differentiating the model from the basic jESOF model—is provided by some algorithms defined as computational steps.

6.5

Even if none of the three approaches provides an agent-based specific language, as exemplified by the Starlogo/Netlogo experience, some of them provide a protocol in design process. The Swarm-like platforms are based on the following principles:

• the use of object-oriented programming language, with different objects representing different agents (and agent types);
• a separate implementation of the model and the tools used for monitoring and controlling experiments on the model (the so called "Observer");
• an architecture that allows nesting models one into another, in order to build a hierarchy of "swarms". One swarm can thus contain lower-level swarms whose schedules are integrated into the higher-level schedule.

6.6

These three principles are followed in the three approaches with a lot of differences. Taking into account the multi-object (or multi-agents) approach, this is naturally present in both the C++ and JAS implementations, while the jESOF provides an abstraction which does not require an explicit model of an agent type. There is an implicit description of their capabilities. They are only logically modeled.

6.7

The separation of model and observer is naturally present in the jESOF and JAS implementation, since they are both based on platform providing a "model-observer" framework. The C++ one follows the principle, even if the separation is less rigorous.

6.8

The possibility of nesting swarms into swarms is possible in the three implementations, thanks to the flexibility of object-oriented programming languages. Obviously, the jESOF platform has an embedded multi-layered architecture, providing a natural way of nesting models and sub-models. The other two approaches would thus require a specific implementation of such model separation. JAS automatically manages schedule integration, while C++ would require its custom management.

6.9

Since the final goal of parallel implementation is the replication of results, the whole process is certainly beneficial for the theoretical validation of the model. In fact, the analysis and comparison of the implementation details resulted in the discussion of the assumptions of the entire model—even about some apparently insignificant details, such as those discussed in Section 5. Furthermore, while some economies of scale (in designing, at least, the "housekeeping" algorithms) are to be expected when working with parallel implementations, this did not occur in our case. The reason is that the C++ implementation could not benefit from the Swarm or JAS libraries. On the other hand, this may avoid the implementation of ill-designed algorithms.

6.10

When comparing the three implementations, the results we obtain are qualitatively the same, even if they are different in terms of exact replication. There are several reasons for these differences. Mainly, they come from minor modeling differences in the three implementations; secondarily, they come from more technical reasons, such as the error accumulation when floating-point arithmetic operations are performed; and the different random number generators routines used in the two different codes.

6.11

As for the first point, while in our case the consequences of floating point arithmetic are not as serious as those described in Polhill et al. (2005), the fact that we performed several branching comparing floating point variables may be one of the reasons leading to the different behaviors of our platforms. The other relevant aspect to be discussed concerns random numbers generators. jESOF code uses well-tested routines internal to the Swarm library and devoted to integer or double precision number, quoting Swarm documentation "The generator has a period close to 2¹⁹⁹³⁷, about 10⁶⁰⁰¹, so there is no danger of running a simulation long enough for the generator to repeat itself. At one microsecond per call, it would take about 3.2 10⁵⁹⁸⁷ years to exhaust this generator. For comparison, the age of the Universe is 'only' 2 10¹⁰ years! This generator can be asked either for a real number (a variable of type double) between [0,1) or for an integer, which will be uniformly distributed on the range [0,4294967295] = [0,2³²-1]". Even JAS uses a well tested and very fast algorithm for generation of random number^[6]: the Mersenne twister. As explained in Matsumoto and Nishimura (1998), it provides for fast generation of very high quality pseudorandom numbers, having been designed specifically to rectify many of the flaws found in older algorithms.

6.12

With the C++ implementation we felt we could not rely on the internal random numbers generator. The reasons for our decision can be found in Press et al. (2002), and we decided to use a Minimal Standard generator with a shuffling algorithm which is reported there as "ran1".

Conclusions

6.13

In this paper we examined and discussed the process of modeling a complex system through different models, compared in terms of vertical and horizontal multiple implementations.

6.14

The model represents an industrial district where social agents cooperate symbiotically. Its complex network of relationships, as well as the positive and negative feedbacks characterizing individual relationships, make its analysis very suitable to be carried on under different points of view. We first focused on comparing multiple model implementations in terms of level of details and of different description techniques. Therefore, the system is modeled using what we call vertical multiple implementations, i.e., different modeling paradigms. To obtain a reliable model, we first start considering the analytical solution of a simplified mathematical model, then move to a System Dynamics approach and, finally, to agent-based modeling.

6.15

The System Dynamics model allows us to highlight some of the aspects that the formal model is unable to take into account. Nevertheless, even this approach does not account for the heterogeneity of the agents we considered in our model. For this reason a third modeling approach was introduced. The agent-based modeling technique produces results which are more difficult to be interpreted, despite the better, more flexible description of details and relationships among individual entities.

6.16

While we could motivate the agent-based approach by way of the vertical multiple implementations, we considered horizontal multiple implementations in order to reduce the risk of introducing unattended phenomena due to computer implementation issues. The multiple implementation approach allows the results-comparison and a deeper discussion of the model assumptions; in particular, we provided a parallel implementation of the model with jESOF, JAS and C++. This choice is motivated by the suggestion by Edmonds and Hales (2003) to use different kinds of languages to re-implement simulations possibly programmed by different people.

6.17

Our interest was not only in results reliability, but in their replication; while the results we obtained were qualitatively the same, there were differences in terms of exact replication. The reasons for these differences can usually be found both in the error accumulation process involved in sequences of floating point operation and in the different random generators used, yet we have shown also how some apparently insignificant algorithm implementation aspects can be relevant in terms of aggregated results. A parallel implementation can stress the sensitivity of some details in the overall behavior of numeric outcomes.

6.18

With this concern in mind, the comparison of results was mainly conducted to understand which aspects of the model implementation become relevant in comparison with model design. In fact, even if the results are supposed to be qualitatively the same, it is important that the implementations are coherent with the theoretical model.

6.19

Having followed Edmonds and Hales' (2003) suggestion in terms of re-implementation, it seems evident, at least in our case, that pursuing a hard approach in terms of replication may be particularly onerous, especially when the model considers non-deterministic aspects. In fact, while the first step consists in the replication of the deterministic behavior of the model, the second step needs all the implementations to use the same random generator.

6.20

As in the deterministic comparison of our implementation, we showed how even small details can have dramatic effects, yielding a trade-off: the more different the implementation approach, the less easy it is to obtain full replication, as assumptions implicit in the modeling platforms interfere.

6.21

A possible solution comes from the statistical comparison of the models' output. In fact, according to Law and Kelton (2000), as "[…] simulations driven by random inputs will produce random output" appropriate statistical techniques applied to output data are imperative. One first technique could be adapting some of the time-series approaches for comparing model output data with system output data, to the comparison of output data coming from the different implementations, but this will be the topic of further research.

6.22

Finally, an important prescriptive lesson arises from our experience. To maximize effectiveness in agent-based modeling, the scientist should consider first to implement a prototype model by a fast development platform such as Netlogo or jESOF in order to assess its feasibility. After this phase the serious researcher should consider both someone else rewriting the model with a more customizable platform (either using a generalized ABM such as Swarm or using object oriented languages) and reengineering its structure avoiding the constraints which were imposed by the shell quoted above. These are important steps of modeling-discussion and are obviously the first ones necessary in order to encourage scientific repeatability, with important facts that even some partially successful attempts towards replicability are most beneficial for the discussion of the considered model and its assumptions.

6.23

Other suggestions coming from the experience of implementing the same model with different approaches consist in the important impact that tools have in turning a model description into a computer artifact. In fact, in order to obtain the same results, parameter sets, algorithm tuning and implementation architectures have to be carefully managed with a continuously improving testing process.

6.24

Researchers potentially need a wide range of techniques in their modeling toolkit to be effective. An important point is that depending on the exact nature of the model we are developing, a subset of those techniques and tools are required. Over time, the variety of problems requires the use of each tool at some point.

6.25

The time between an action and the feedback on that action is critical, mostly when working with other people on the same model. It is therefore necessary that the implementation technique allows a near-instant feedback on modeling ideas.

6.26

In further research, we plan to identify and use the appropriate techniques to make a statistical comparison of the output generated by the different implementations.

Acknowledgements

The authors are grateful to the organizers of M2M 2007, Third International Model-to-Model Workshop, Marseille, France, 15-16 March 2007, for providing a good opportunity to discuss their research and also to the participants of the workshop for their helpful suggestions.

Notes

¹ Carbonara (2004) points out how Italian geographical clusters are usually referred as Industrial Districts.

² In particular for firms, the equilibrium is expected to be similar to an economic cycle.

³ In the jES Open Foundation version of the model we have also instrumental layers showing separately the presence of workers for each type of skill, but, obviously, the two implementations are equivalent in terms of modeling.

⁴ We remark that the employee-employer relationship is negotiated at each simulation turn and therefore is not permanent.

⁵ The careful reader will notice that the graphical representation we provide is similar to the one proposed in Edmonds and Hales (2003); this is not a coincidence.

⁶ The generator is taken from the COLT library ( http://dsd.lbl.gov/~hoschek/colt-download/releases/) and more precisely is referred to the class cern.jet.random.engine.MersenneTwister.

References

AUERSWALD, P, Kauffman, S, Lobo, J, Shell, K (2005). "The Production Recipes Approach to Modeling Technological Innovation: An Application to Learning by Doing". CAE Working Paper, 98-10.

AXELROD, R (1984). The Evolution of Cooperation. New York: Basic Books.

BANKS, J, Carson II, J S, Nelson B L, and Nicol D M, (2005). Discrete-Event System Simulation. Fourth Edition, Upper Saddle River, NJ: Pearson Prentice Hall.

BECATTINI, G, Pyke, F, Sengenberger, W (Eds.) (1992). Industrial Districts and Inter-firm Co-operation in Italy. Geneva: International Institute for Labour Studies.

BECATTINI, G (2003). "From the industrial district to the districtualisation of production activity: some considerations". In F. Belussi, G. Gottardi, and E. Rullani (Eds.), The Technological Evolution of Industrial Districts . Dordrecht: Kluwer Academic Publisher.

BECKER, P (2005). "Bad Pointers". C/C++ Users Journal. 23(9), 37-41.

BELUSSI, F, Gottardi, G (Eds.) (2000). Evolutionary Patterns of Local Industrial Systems. Towards a Cognitive Approach to the Industrial District. Sydney: Ashgate.

BRENNER, T (2002). "Simulating the Evolution of Localised Industrial Clusters: An Identification of the Basic Mechanisms". Presented at IG2002, Sophia Antipolis, France, January 18-19, 2002.

CARBONARA, N (2004). "Innovation processes within geographical clusters: a cognitive approach". Technovation, 24, 17-28.

CARBONARA, N (2005). "Information and communication technology and geographical clusters: opportunities and spread". Technovation, 25, 213-222.

CARLEY, K M and Prietula, M J (1994). Computational Organization Theory. Hillsdale. N.J: Lawrence Erlbaum Associates.

CERRUTI, U, Giacobini, M, Merlone, U (2005). "A New Framework to Analyze Evolutionary 2×2 Symmetric Games". Proceedings of the IEEE 2005 Symposium on Computational Intelligence and Games, April 4-6 2005 Essex University, Colchester, Essex, UK.

EDMONDS, B and Hales, D (2003). "Replication, Replication and Replication: Some Hard Lessons from Model". Journal of Artificial Societies and Social Simulation, 5(4) 11 https://www.jasss.org/6/4/11.html

FLAKE, G W (1988). The Computational Beauty of Nature. Cambridge (MA): The MIT Press.

FRANK, S A (1997). Models of Symbiosis. The American Naturalist. 150(S), S80-S99.

GAROFOLI, G (1981). "Lo sviluppo delle aree "periferiche" nell'economia italiana degli anni '70". L'industria 3, 391- 404.

GAROFOLI, G (1991). "Local Networks, Innovation and Policy in Italian Industrial Districts". In E. Bergman, G. Mayer and F. Tödtling (Eds.), Regions Reconsidered. Economic Networks Innovation and Local Development in Industrialized Countries. London: Mansell.

GAROFOLI, G (1992). "Industrial Districts: Structure and Transformation". In G Garofoli (Ed.), Endogeneous Development and Southern Europe. Avebury: Aldershot, 49-60.

GAYLORD, R J , and D'Andria, L J (1998). Simulating Society. New York: Springer-Verlag.

HASTINGS, A (1997). Population Biology. Concepts and Models. New York: Springer-Verlag.

HOFBAUER, J, and Sigmund, K (1998). Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press.

LAW, A M and Kelton, W D (2000). Simulation modeling and analysis. Boston: Mc-Graw-Hill.

LOTKA, A J (1925). Elements of physical biology. Baltimore: Williams and Wilkins Co.

LAZZARETTI, L, and Storai, D (1999). "Il distretto come comunità di popolazioni organizzative. Il caso Prato". Prato: Quaderni IRIS n.6.

LAZZERETTI, L and Storai, D (2003). "An ecology based interpretation of district 'complexification': the Prato district evolution from 1946 to 1993". In F Belussi, G Gottardi, and E Rullani (Eds.), The Technological Evolution of Industrial Districts . Dordrecht: Kluwer Academic Publisher.

MASS, N (1980). "Stock and flow variables and the dynamics of supply and demand". In Randers, J (ed.), Elements of System Dynamics Method. Waltham, Ma: Pegasus Communications

MATSUMOTO, M and Nishimura, T (1998). "Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator". ACM Transactions on Modeling and Computer Simulation (TOMACS), Vol.8(1) p. 3-30.

MERLONE, U and Terna, P (2006). "Population Symbiotic Evolution in a Model of Industrial Districts", in Rennard J.P (ed.), Handbook of Research on Nature Inspired Computing for Economics and Management, Idea Group Inc.

PIVA, M, Santarelli, E, Vivarelli, M (2003). The Skill Bias Effect of Technological and Organizational Change: Evidence and Policy Implications. IZA Discussion Paper, 934.

POLHILL, J G, Izquieredo, L R, Gotts, N M (2005). "The Ghost in the Model (and other effects of the floating points arithmetic)". Journal of Artificial Societies and Social Simulation, 8(1) 5. https://www.jasss.org/8/1/5.html

PRESS, W H, Teulkolsky, S A, Vetterling, W T, Flannery, B P (2002). Numerical Recipes in C++. Cambridge: Cambridge University Press.

RICHIARDI, M, Leombruni, R, Sonnessa, M and Saam, N (2006). "A Common Protocol for Agent-Based Social Simulation". Journal of Artificial Societies and Social Simulation 9(1) 15 https://www.jasss.org/9/1/15.html

ROYAMA, T (1992). Analytical population dynamics. New York : Chapman and Hall.

SORENSON, O, Rivkin, J W and Fleming, L (2004). "Complexity, Networks and Knowledge Flow", Working Paper.

SQUAZZONI, F and Boero, R (2002). "Economic Performance, Inter-Firm Relations and Local Institutional Engineering in a Computational Prototype of Industrial Districts". Journal of Artificial Societies and Social Simulation, 5(1)1 https://www.jasss.org/5/1/1.html.

STERMAN, J D (2000). Business Dynamics: System Thinking and Modeling for a Complex World". Boston, MA: Irwin McGraw-Hill.

VOLTERRA, V (1926). Variazioni e fluttuazioni del numero d'individui in specie animali conviventi. Roma: Mem. R. Accad. Naz. dei Lincei. VI(2).

ZHANG, J (2003). "Growing Silicon Valley on a landscape: an agent-based approach to high-tech industrial clusters". Journal of Evolutionary Economics 13. 529-548.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2008]