Conrad Power (2009)

A Spatial Agent-Based Model of N-Person Prisoner's Dilemma Cooperation in a Socio-Geographic Community

Journal of Artificial Societies and Social Simulation vol. 12, no. 1 8
<https://www.jasss.org/12/1/8.html>

For information about citing this article, click here

Received: 28-May-2008    Accepted: 01-Dec-2008    Published: 31-Jan-2009

Abstract

The purpose of this paper is to present a spatial agent-based model of N-person prisoner's dilemma that is designed to simulate the collective communication and cooperation within a socio-geographic community. Based on a tight coupling of REPAST and a vector Geographic Information System, the model simulates the emergence of cooperation from the mobility behaviors and interaction strategies of citizen agents. To approximate human behavior, the agents are set as stochastic learning automata with Pavlovian personalities and attitudes. A review of the theory of the standard prisoner's dilemma, the iterated prisoner's dilemma, and the N-person prisoner's dilemma is given as well as an overview of the generic architecture of the agent-based model. The capabilities of the spatial N-person prisoner's dilemma component are demonstrated with several scenario simulation runs for varied initial cooperation percentages and mobility dynamics. Experimental results revealed that agent mobility and context preservation bring qualitatively different effects to the evolution of cooperative behavior in an analyzed spatial environment.

Keywords:

Agent Based Modeling, Cooperation, Prisoners Dilemma, Spatial Interaction Model, Spatially Structured Social Dilemma, Geographic Information Systems

Introduction

1.1

The evolutionary processes that are fundamental to cooperation in social situations have been an enduring theoretical problem in biological, sociological, and geographical research. Cooperation is behavior that may initially cost a person or group but ultimately benefits other individuals or social assemblages. While this may seem an uncomplicated concept, the derivation of satisfactory theoretical explanations for real-world altruistic behavior has been a challenge (Killingback and Doebeli 2002). However, the prisoner's dilemma has become one of the most widely adopted methodologies for studying the evolution of cooperation in simulated social environments.

1.2

Most of the published work about the prisoner's dilemma deals with the two-player iterated game. These articles show how the repeated interactions between pairs of players can result in the emergence of cooperation due to reciprocal altruism. Beginning with Axelrod (1984), iterated prisoner's dilemma tournaments have been run to compare and identify the evolutionary strategies that consistently produce the best cooperation results. The more successful strategies have demonstrated that spatial structure is an influential factor in building cooperation. Nowak and May (1992) presented the seminal work that showed how the spatial effects of the interactions between simple agents in a cellular automata (CA) model of the iterated prisoner's dilemma was sufficient enough for the evolution of cooperation. Alonso et al. (2006) devised a similar CA model that simulated cooperation through the behavioral adaptation of Pavlovian agents as they adjusted their cooperation by mimicking the most successful player in a neighbourhood.

1.3

N-person prisoner's dilemma (NPPD) has also been a research topic of spatial modelers who are interested in the emergence of collective cooperation in social groupings. Referred to as a social dilemma situation, a player has to choose between his own interests or exhibit cooperative behaviors that benefit the grouping of N players. Akimov and Soutchanski (1994) developed a spatial NPPD game to relate how collective cooperation depends on the behavioral patterns of simple automata within a CA. Szilagyi (Szilagyi 2003) presented a CA model of NPPD based on the interactions of irrational agents in a social unit and revealed how the chaos like actions of the agents was an important condition for decentralized group cooperation. Zhao et al. (Zhao 2005) expanded the work of Szilagyi (2003) and proposed an N-person model that establishes a continuous state of cooperation from the attitudes and personality types of agents in a CA. They found that the depth of the neighbourhood of the social groupings was the central factor that determined cooperation dynamics in the simulation runs. This point raises an important condition of a prisoner's dilemma CA in that the automata are usually fixed entities in a regular lattice of cells. Context preservation has been established as a key factor in the evolution of cooperation and is intuitively linked to the neighbourhood and mobility rules within the spatial model. However, there is minimal published research that deals with the spatial modeling of NPPD involving mobile agents.

1.4

In this paper, it is argued that a spatial agent-based model of N-person prisoner's dilemma can extend the study of collective communication and cooperation within a socio-geographic community. Based on a tight-coupling of REPAST and a vector Geographic Information System (GIS), the model is designed to simulate the emergence of communal cooperation relative to the mobility behaviors and interaction strategies of citizen automata. Support for the methodology is demonstrated with simulation runs for a real-world analyzed environment and a discussion of its use in simulating scenarios of social dynamics.

Agent-Based Models

2.1

Agent-based models (ABM) are comprised of a community of agents, an agent being an autonomous entity that is able to act locally in response to stimuli from the environment, to communicate with other agents, and to have goals that it aims to satisfy. Community relates to the relationship between individual agents in the system, and these could be either reactive or cooperative (Benenson and Torrens 2004).

2.2

The goal of agent-based models of social systems is to enrich the understanding of the fundamental processes that may appear in the environment. This requires the modeling of the essential characteristics and attributes of the agents, the simple rules of agent interaction, and the emergent patterns of automata communication and interactions. Communication is one of the most important characteristics necessary for agent interactions and is the basis for the emergence of negotiation, collective behaviors, and social cooperation.

Prisoner's Dilemma and Social Cooperation

3.1

Many studies in the social and computer sciences have utilized the prisoner's dilemma to analyze the emergence of cooperation among non-relatives in social environments (Brembs 1996; Trivers 1971; Axelrod 1984). The popularity of the prisoner's dilemma stems from it being a robust and fundamental method of modeling the emergent social structures from the reciprocity of cooperative actions from members of social and biological communities (Cohen et al. 1998). Furthermore, the game is appealing from its simplicity of statement and design and its applicability to agent-based simulations of leadership, cooperation, and social differentiation from the interactions between neighbouring agents.

Prisoner's Dilemma

3.2

Originating within the field of game theory, the prisoner's dilemma (PD) is a type of non-zero sum game played by two players who can choose between two moves, either to cooperate with or defect from the other player. The problem is called the prisoner's dilemma, because it is an abstraction of the situation felt by a prisoner who can either cut a deal with the police and tell on his partner (defect) or keep silent and therefore tell nothing of the crime (cooperate). The key tenet of this game is that the only concern of each individual player is to maximize his payoff during the interaction, which sets the players as naturally selfish individuals. The dilemma arises when a selfish player realizes that he can not make a good choice without knowing what the other one will do. Non-zero sum is a situation where the winnings of one player are not necessarily the losses of the other. As such, the best strategy for a given player is often the one that increases the payoff to the other player as well.

3.3

Table 1 highlights the structure of a canonical payoff matrix used in a PD game.

Table 1: Payoff Matrix for a General Prisoner's Dilemma Game
	Player A
Player B		Cooperate	Defect
	Cooperate	R, R	S, T
	Defect	T, S	P, P

R is the reward payoff that each player receives if they both cooperate, P is the punishment that each receives if both defect, T is the temptation to defect alone, and S is the sucker payoff that is assigned when a player cooperates alone. The payoff structure is such that T>R>P>S, which ensures that there's always the temptation to defect since the gain for mutual cooperation is less than the gain for one player defection.

3.4

McCain (2003) states that the premise of a PD game is the strict domination of cooperation by defection so that the only possible equilibrium is obtained when all players defect. However, the pursuit of selfish interests will not produce a collective order required for the functioning of a social system. Some form of prisoners dilemma is therefore needed for the modeling the dynamics of a social community.

3.5

While it has been extensively modeled, researchers have dismissed the basic PD as an unrealistic abstraction of individual interactions. Firstly, PD is intended to study finite two person interactions, but real-world social communities can consist of long-term many-person interactions. Secondly, it is assumed that there is no communication between the two players and no history of past exchanges. Prior knowledge of past interactions may commit the players to coordinated strategies of cooperation. Lastly, the players are assumed to be rational, which implies that both will continually decide to defect to maximize their individual payoffs and never cooperate.

3.6

Nevertheless, researchers have expanded the standard PD game to enable participants to play the game multiple times and to have knowledge of previous moves. The iterated prisoner's dilemma has demonstrated that the players' decision to cooperate or defect accumulates over time as each player develops a reputation that affects the incentive of others to cooperate.

Iterated Prisoner's Dilemma

3.7

Axelrod (1984) presents an extension to the classical prisoner's dilemma scenario that permits players to repeatedly choose mutual strategies and have memories of their previous encounters. A strategy in a repeated game is a decision rule that specifies the probability of cooperation or defection for a player given some history of interactions against a particular opponent. For example, an agent that adopts the strategy ALLC (all cooperate) will always cooperate with the opponent, regardless of past interactions and expected payoffs.

3.8

During iterative prisoner's dilemma (IPD) play, two participants will play several consecutive iterations of the game using a payoff matrix (see Table 2) to accumulate a total score. The player with the larger cumulative score is deemed the winner and influences the cooperation strategy of the opponent.

Table 2: Payoff Matrix for an Example Iterated Prisoner's Dilemma Game
	Player A
Player B		Cooperate	Defect
	Cooperate	3, 3	0, 5
	Defect	5, 0	1, 1

3.9

Through iterative play, cooperative and non-cooperative behavior will typically be reciprocated to a certain extent. Trivers (1971) describes how reciprocal altruism usually occurs through repeated interactions with the same individuals where a player returns the loyalty to an opponent who has previously cooperated.

3.10

Several researchers (Axelrod 1984;Boyd and Lorderbaum 1987;Nowak and Sigmund 1992) organized computer tournaments to detect strategies that would favor cooperation among individuals engaged in IPD. The goal of these contests is to pit different computer strategies against each other to identify ones that had the highest scores or instances of cooperation. Axelrod (1984) was one of the first to coordinate an IPD tournament, a round robin competition between fifteen deterministic strategies. The simplest strategy, Tit-For-Tat (TFT), was determined the best; cooperate on the first move and mimic the opponent's move for all subsequent moves. Altruistic strategies tended to outperform the greedy methods over the long-term.

3.11

An important finding of the competitions is that context preservation was determined to be a crucial factor for sustaining cooperation for interaction processes (Cohen et al. 1998). The emergence and maintenance of cooperation often depend on conditions that preserve the neighborhood of the interacting players. In addition, context preservation increases the likelihood of local influencing (the tendency of players who interact frequently to become more similar over time) and homophily (the tendency to interact more frequently with the same individuals).

3.12

Stochastic strategies have also been used in IPD tournaments. Nowak and Sigmund (1992,1993) revised the simulations of Axelrod (1984) to model cooperation in noisy environments. They argue that it is possible that the actions of a player may be misinterpretations due to random errors, thus leading to a sequence of unwarranted punishment or cooperation. Running the competition with a variety of stochastic strategies, such as Pavlov, it was shown that cooperation could emerge as long as a stochastic version of TFT is included. This highlights the importance of a minimal social structure required for evolution of cooperation (Eckert et al. 2005).

3.13

Critics have questioned the ability of IPD to simulate real world problems because of its structure as a two-person game (Yao and Darwen 1994). Many social and economic problems require analysis of group dynamics, and the strategies that work well for individuals in the IPD fail in large groups. For example, a two-person strategy that is predicated on the self interest of a single individual is not designed to model the emergence of cooperation from collective behaviors. The n-person prisoner's dilemma is a more realistic and general game to model real-life social problems.

N-Person Prisoner's Dilemma

3.14

N-person prisoner's dilemma (NPPD) models have been referred to as social dilemma games, because they are focused on the simulation of the collective actions and behaviors in social groups (Schelling 1973). Harden (1968) describes NPPD as a "tragedy of the commons" game in which the players are worse acting according to their self interests than if they were cooperating and coordinating their actions. During play, individual players may cooperate with each other for the collective good of their social environment, or they may prefer to pursue their selfish interests. The incentives to cooperate may depend on how many players are contributing to the group and the effect of their actions. In multi-player interactions, cooperation and social cohesion emerge from the consensus behaviors and actions of the social unit even though the preferred course of action for an individual player is still defection.

3.15

A typical social dilemma can be considered an n-person game (n ≥ 2), in which each player has the same preferred option that does not change regardless of the actions of the other players. Every player has the same payoff structure and can choose to either cooperate, C, or defect, D. The payoff of each player that defects is represented as D(m), where m is the number of players in a social grouping that cooperate (0 ≤ m ≤ n-1). The payoff for each cooperating player is donated as C(m). The social dilemma game is then defined by the following conditions (Akimov and Soutchanski 1994):

1. D(m) > C(m + 1): each player is better off choosing to defect rather than cooperate, regardless of how many players choose to cooperate on a particular play of the game.
2. C(n) > D(0); if everyone cooperates, each player is better off if everyone defects.
3. D(m + 1) > D(m) and C(m + 1) > C(m); the more players cooperate, the better off each player is, regardless of whether he chooses to cooperate or defect.
4. (m + 1)C(m + 1) + (n - m - 1)D(m + 1) > mc(m) + (n - m)D(m); society as a whole is better off the more players cooperate.

3.16

Figure 1 is a graphical representation of an example situation that shows the payoff functions for a player that chooses the preferred defection option (P) or the un-preferred cooperation (U) alternative, depending on the number of other players (0 to n) that choose U.

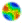
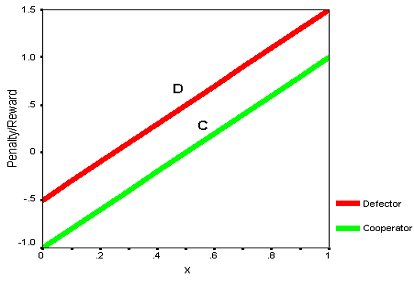
Figure 1. N-Person Prisoner's Dilemma Payoff Functions for Preferred Defection and Un-Preferred Cooperation, Relative to the Number of Other Players that Decide to Cooperate: (from Akimov and Southchanski 1994)

3.17

To illustrate, at x = n/3, a third of the players choose to cooperate and two thirds defect: P_x and U_x are the payoffs to the player that chooses the defection (preferred) or cooperation (un-preferred) alternatives, respectively. The payoff functions in the NPPD are structured so that each player receives a higher payoff for defection than for cooperation (the P curve must always be above the U curve).

3.18

It is important to note that an NPPD game is not an expanded version of the iterated pairwise interaction game. It is a true multiplayer game where each player simultaneously interacts with all of the other players in a social grouping and decides to either cooperate or defect according to the rewards or punishments derived from the collective. A player's decision to cooperate or defect is therefore dependent on the number of cooperators and defectors in his neighbourhood and the utility of the payoff functions at each time step of the play sequence.

3.19

While not as numerous in the literature as the two-person IPD, NPPD simulations have been presented as agent based models. The sequencing of these simulations depends on the components and parameters of the ABM. First of all, the initial probabilities of cooperation and actions of each individual in the social environment are assigned, often randomly, according to user-defined instance parameters. Secondly, the neighbourhood configuration of the social grouping is determined. This can range from a grouping of socially similar players, a spatially defined interaction region, such as a Moore neighbourhood in a cellular automata, or the entire social environment itself. Next, the interaction strategies and the payoff and updating schemes dictate the course of the game play. Many different types of strategies have been tested in NPPD games, but most are deterministic strategies based on the probability distribution for the two possible actions and the history of player interactions among the social group (Kehagias 1994). Payoff functions similar to figure 1 determine the reward/penalty assigned to each player dependent on the number of cooperators and defectors within the neighbourhood. The appeal of this type of model for simulating cooperation for real-world applications is the capability of setting the players as probabilistic learning automata so that their behaviors are learned and adjusted throughout the simulation. In this manner, behavior refers to how an agent decides to act based on his current state, the reward/penalty from previous actions, and the actions and states of the neighbours. Szilagyi (2003) makes the compelling argument that human behavior is best described as stochastic but influenced by personality characteristics. His work investigates the role of personalities in stochastic learning automata in the multiplayer PD game. Stochastic learning automata are agents whose behavior is influenced by random perturbances to simulate noise or stochastic responses from the environment. Assigning personalities to the agents imitates human decision-making and presents a method of specifying the updating schemes from certain attitude states and personal influences (Zhao et al. 2005). Therefore, agents with different personalities can be assigned different updating schemes and allowed to interact with each other, resulting in observations of how the various personality types respond to one another in the same social environment. A variety of personalities, such as Pavlov, conformist, and greedy (Brembs 1996), have been applied in NPPD games, the specifics of each will be discussed later. Some of the updating schemes of the agents used in NPPD games have been implemented as utility functions, probabilistic equations, and choice heuristic decision rules (Axelrod 1997). The updating schemes adjust the probabilities of the agent's actions by the reward/penalty received from the environment based on his and the other players' behaviors and attitudes. The actions of the participating agents as they make repeated decisions and interactions will determine the degree of cooperation that occurs within a social unit.

3.20

The N-person prisoner's dilemma game seems well suited for realistic albeit simple investigations of collective behaviors within a social system and can be the foundation for a spatial agent based model of cooperation within a socio-geographic community.

Spatial Agent Based Modeling of N-Person Prisoner's Dilemma Cooperation

4.1

The development of a spatial agent-based model of NPPD is contingent on the processes that define a socio-geographic community. From a research perspective, a socio-geographic community is both a geographical object and a sociological subject. Firstly, it is an integrated geographic network of social units defined by the interaction patterns and citizen flows throughout a dynamic area of collective social, economic, and emotional actions. Flow refers to labour market dynamics, individual flows to access goods and services, daily commuting activities, etc. As a sociological subject, a community codifies norms and behaviors to control the processes of social and institutional interactions (Loomis 1996). The community becomes a social system of local communication and actions involving a collective identity, solidarity, and collaborative efforts. As a cohesive object and subject, the simulation of a real world community involves agents with personalities and attitudes that communicate and move throughout the environment as part of their daily activities. Formally, the model must specify the social unit as an analyzed environment and the citizen agents as analyzed automata. Analyzed agents are automata that mimic real world entities based on empirical data, and the analyzed environment is a real world location (Couclelis 2001).

4.2

This section of the paper presents the development of a conceptual spatial agent-based model of citizen cooperation within a socio-geographic community. Each citizen agent is designed with reference to the spatial structure of the analyzed environment, states variables relevant to the application, state transition rules, movement rules, neighbourhood calculation, and the NPPD game play. Before these components are discussed, an overview of the basic architecture of the generic model is given.

The Architecture of the Generic Model

4.3

The generic model is developed as an exploratory approach for simulating the trends and patterns of citizen automata in social groupings. Generic infers that the model is applicable to multiple socio-geographic environments and contains functionality that is fundamental for any given social system. Also, the parameters of the model are set with user-defined variables that characterize the simulation scenario.

4.4

The model is designed as a modeling-centric system with embedded vector Geographic Information System (GIS) capabilities (see figure 2). Formally, the tight coupling of agent-based modeling and GIS functionality create an identity relationship between an agent and its spatial feature (Brown et al. 2005). The agent-based modeling platform was developed with REPAST (Recursive Porous Agent Simulation Toolbox 2007) Java to simulate agent interactions, movements, and the NPPD game play.

4.5

Within this component, agents are object-oriented entities that use their states and definitions to simulate behaviors. The agent based methods model the behavior of the agents and alter their states, which are stored as geographic features within the GIS as polygons and points. GIS operations are implemented with a number of software libraries that are imported into the simulation toolbox. Specifically, Java Topology Suite (2007) is utilized to calculate topology and neighbourhood configurations, GeoTools (2008) provides data importation and exportation, and OpenMap GIS (2007) is used for attribute querying and map visualization. As a further enhancement, the sequential line graphing and movie creation methods within Repast are used to record changes during simulation runs.

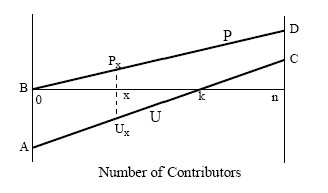
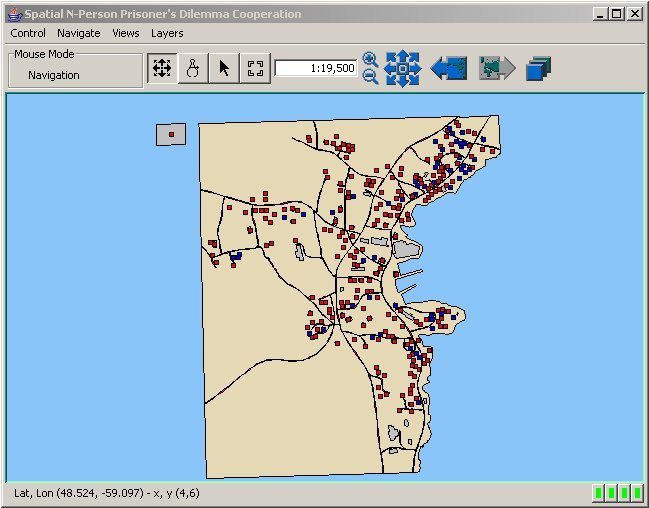
Figure 2. Interface of the Spatial Agent-Based Model of NPPD Cooperation

Spatial Structure of Agent Locations in an Analyzed Environment

4.6

An analyzed environment is a real world study area that is set as the spatial confluence region for the simulation runs. The entities required for the simulation of cooperation in a socio-geographic community are fixed non-mobile building automata, specifically resident households, businesses, community services, and schools, and non-fixed mobile citizen agents. The modeling configuration is set to the town of Catalina, Newfoundland and Labrador, Canada (figure 3) because of the availability of satellite imagery and, more importantly, individual level socio-economic statistics to microsynthesize and assign state variables to each citizen agent. Locations of both types of agents follow a vector GIS geo-referencing convention. The building entities are first derived from an imported ESRI^© shapefile that was digitized from the satellite imagery. Since they are fixed automata, the buildings are directly registered as two dimensional polygon objects with coordinate lists and topology within the GIS component. The citizen agents are also directly registered during initialization, but are locationally pointed during movement events. At initialization, the household locations of a user-defined number of citizens are assigned as the coordinates of the computed centroids of randomly selected building polygons. This produced a set of citizen point objects that are directly geo-referenced to their assigned household locations. The relationship between both types of entities is hierarchical such that the point citizen agents are spatially nested within the building automata. As a citizen moves, the destination location is geo-referenced by pointing to a specific building object. For example, the destination for citizen agent A at time t+1 could be a school, whose locational coordinates are stored and easily accessible from the GIS database. Locational pointing is convenient for mobile agents because their locations can be constantly varied and reset as the simulation proceeds.

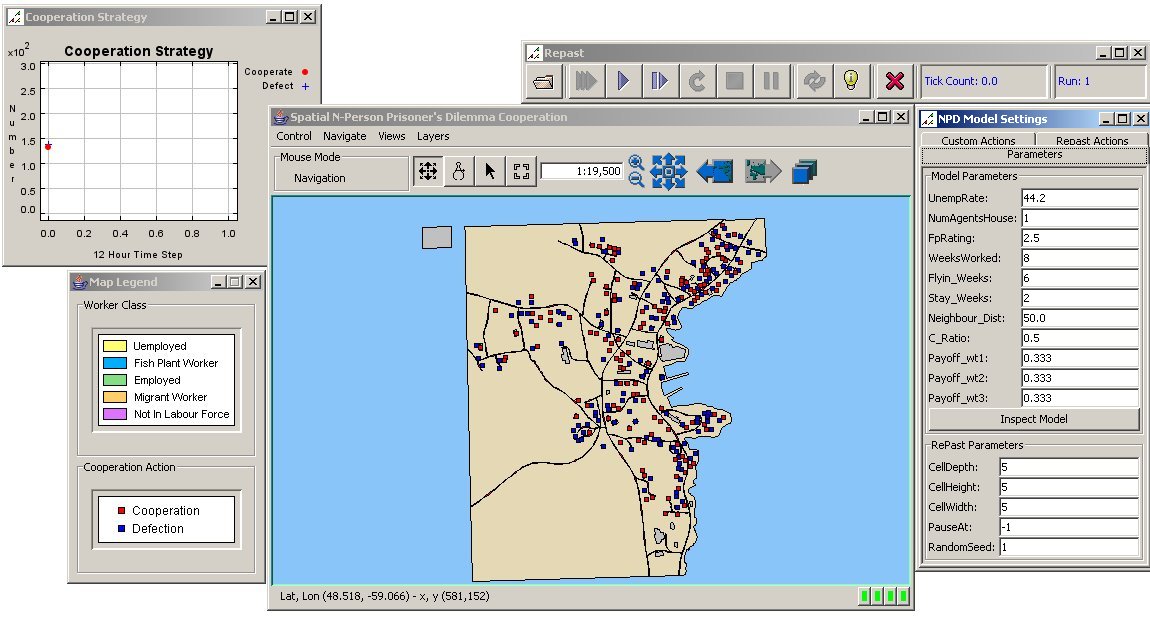
Figure 3. Analyzed Environment of Central Catalina, Newfoundland and Labrador, Canada

State Variables and State Transition Rules

4.7

State variables are the characteristics of the fixed and mobile entities that are inputted into the transition rules to determine their behaviors. The buildings have a single state variable according to their previously determined type: household, business, public service, or school.

4.8

The citizen agents are specified with state variables that determine their mobility behavior and their initial action choice for the NPPD game play. Each point agent is initialized with an age, gender, education level, and worker type (unemployed, fish plant worker, migrant worker, other, or not in labour force). These variables were microsynthesized from selected population and occupation tables from the 2006 general census release from Statistics Canada (Statistics 2006). During the setup sequence of a simulation run, the population and occupation data is entered into a set of initialization equations to randomly compute or assign the states to each citizen agent.

4.9

State transition rules are currently only applicable to the citizen agents and consist of two sets of heuristics: those relating to the probability of cooperative action and rules that are relevant to the simple demographic profile of the citizens. The demographic rules are concerned with increasing the age of each citizen by a factor of 1 for each yearly equivalent of time steps and altering the worker type according to a random updating event. Throughout the simulation run, the model can implement a worker turnover ratio to randomly change the worker type attribute of citizen agents between the ages of 15 to 65. A change in the worker type of an agent can affect its mobility behavior.

Movement Rules

4.10

The object-oriented framework of REPAST coordinates movement as discrete event simulations, in which a scheduling mechanism directs the sequencing of agents' mobility behaviors (Zeigler et al. 2000). In this model, movement rules manage both short-term migration (fly-in/fly-out employment) events and daily commuting activities of the citizen agents. Both types of mobility are scheduled in a asynchronous manner, where the agents' move between a pair of origin and destination locations at a specified time step. Each time step represents a 12-hour interval and two consecutive time steps a typical day. The destination for a movement event is based on the worker type of each agent, where it is assumed that he is most likely to travel to and from his household to the site of his particular occupation. For example, a school is the most probable destination for a teacher and children aged 5 to 18 during the weekday period. P_exp is the probability that a citizen moves to the expected site and is arbitrarily set at 0.9. However, a stochastic perturbance value is computed for each destination choice to model the nonlinearities of human decision-making, where a person often fails to make the obvious choice. A random number generator class in REPAST computes a perturbance value, P_stoc, between 0 and 1 to determine whether an agent moves to another business or service location or whether he stays at his residence for that particular time step. When P_stoc > P_exp, a destination option is randomly selected from all relevant buildings, except the usual place of work and other agent households, and a motion rule relocates the citizen to this new position for this sequence.

4.11

The fly-in/fly-out workers are an increasing familiar subcommunity of individuals in communities throughout Newfoundland and Labrador. These are workers who are employed for weeks in locations outside of the community of residence. Even though these workers are frequently detached from their home communities, they are still an important and influential socio-economic unit within the broader community network. Fly-in/fly-out employment is a work pattern consisting of both an outmigration and immigration event. During model setup, each migrant worker is randomly assigned a start date of his first migration event, and a pair of scheduled basic action rules are initialized to implement the outmigration and immigration events. Outmigration is a scheduled action of placing a migrant worker agent in a virtual migration container for a user-defined period of time (see Flyin_Weeks variable on right side of figure 2) and immigration is a scheduled action that returns a migrant worker to his household for a user-defined stay period (Stay_Weeks variable on figure 2). This sequential movement continues throughout the entire simulation.

4.12

Mobility behavior is an important element in the spatial agent-based simulation of cooperation in a social environment, because it sets the neighbourhood configuration for the prisoner's dilemma game play.

Interaction Neighbourhoods

4.13

The depth of an interaction neighbourhood defines the extents of the spatial association of a social grouping within the environment. The rule set for neighbourhood delineation is based on the proximity of citizen agents on a geometric network, where agents within a specified straight-line distance of each other are considered neighbours. At each time step, the topology and automata composition of the neighbourhood for each citizen agent is estimated with a GIS buffer operation. Formally, a buffer, or enclosing circle, of a user-defined radius is drawn around the point location of each agent, and a point-in-polygon method identifies those agents that fall within the buffered area and classifies them as neighbours. The radius of each neighbourhood is a constant value for all agents that is set as a parameter during initialization (see figure 2) according to a user's perceived average neighbourhood size. For example, the citizen points symbolized in yellow in figure 4 are the neighbours situated within a 50 meter radius of agent A. With the neighbourhood defined, an arraylist of agent objects including the identified neighbours and the citizen of interest is passed to the agent-based model to begin the NPPD game.

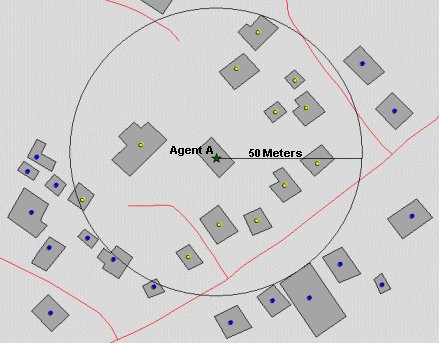
Figure 4. Configuration of a 50 Meter Neighbourhood Buffer of Agent A

4.14

An interesting consideration for the simulation of agent cooperation is the effect that movement has on the calculation of neighbourhoods. Each time an agent moves, it necessitates the generation of a new neighbourhood configuration and produces a different listing of neighbours. Recall that for the two-person IPD, context preservation was a crucial element for the emergence of cooperation. It is assumed that context preservation will be a factor for the worker agents while they are at their place of work, because the calculated neighbourhood will be a compact grouping of social agents with a shared interaction history and similar state variable values. It is possible that a degree of social cohesion will arise amongst these agents and that they will be more inclined to cooperate with each other during the social dilemma simulation.

Spatial N-Person Prisoner's Dilemma

4.15

The aim of a spatial NPPD game is to investigate social interaction behaviors and communication between people situated in a stochastic environment. As Szilagyi (2003) corrects surmises, human behavior can not be accurately simulated with rational agents, because biological objects rarely act rationally. As a result, several researchers (Boone et al. 1999; Szilagyi and Szilagyi 2002; Zhao et al. 2005) have stressed the need to investigate the role of personalities in the prisoner's dilemma and to set the agents in the model as stochastic learning automata. These considerations were central to the development of the NPPD component in this model.

Basic Definition

4.16

Each citizen agent is a stochastic learning three-step memory entity with a predetermined personality type and cooperation action. In a neighbourhood of N agents, the state of each citizen at time t is characterized by 0 (defection) or 1 (cooperation). During an interaction event, agents take actions according to the probabilities updated on the basis of the reward/penalty received for previous actions, their neighbours' actions, and their personalities. The updating sequence occurs synchronously for all of the agents in the neighbourhood.

Components and Parameters of the N-Person Prisoner's Dilemma

As a generic game, constraint parameters are set by the user to facilitate the NPPD simulation and to initialize the agents' states. First, the percentage of the total number of agents, C _x, that begin the simulation as cooperators is included. Next, a set of initialization rules in the setup methods of REPAST uses C_x to randomly set each agent as either a cooperator or defector and initialize both its individual probability of cooperation and defection.

4.17

At each time step, the model calculates the neighbourhood of each agent and determines the total number of cooperators and defectors in that grouping. The interaction proceeds as the reward/penalty for each agent is computed from a set of payoff functions. Lastly, each agent updates their cooperation action according to a weighted reward/penalty estimation derived from three-step memory payoff values and the influence of its personality. In modeling terms, personalities are the interaction strategies that agents employ during game play. Zhao et al. (2005) lists several of the personality profiles and strategies that have been used in NPPD simulations:

• Pavlovian: an agent with a coefficient of learning whose probability of cooperation changes by an amount proportional to the reward/penalty it receives from the environment
• Stochastically predictable: an agent whose probability of cooperation is constant but fluctuates with periodic random perturbances. For example, an angry agent (p=0) always defects.
• Accountant: an agent whose probability of cooperation depends on the average reward for the social grouping for a previous action.
• Conformist: an agent who imitates the action of the majority in the social unit.
• Greedy: an agent who imitates the neighbour with the highest reward.

4.18

These personality types represent certain simple aspects of actual human behavior. Szilagyi and Szilagyi (2002) state that Pavlovian agents are the most realistic automata for the investigation of the evolution of cooperation, because they are simple enough to know nothing about their rational choices but intelligent enough to follow Thorndike's (1911) Law of Conditioning. Specifically, an action that produces a satisfactory state of affairs tends to reinforce the repetition of that particular action. Therefore, the citizen agents in this model are set as Pavlovian automata, and the interaction functions are specified to support this condition.

4.19

Figure 5 shows the payoff curves for the cooperators and defectors, and, as required, the D curve is above the C curve so it is always best for an agent to choose to defect. Note that the payoff of an agent depends on its previous action (C or D), the ratio of cooperators to the total agents, and a stochastic factor added to the environment. The payoff curves for both the defectors and cooperators are straight lines functions expressed as (Szilagyi 2003):

D = -0.5 + 2x

(1)

C = -1 + 2x

(2)

where x represents the ratio of the number of cooperators to the total number of neighbours. The stochastic factor is a parameter that accounts for any uncertainty in the agent interactions and noise in the environment. When dealing with linear payoff functions, stochasticity is applied by thickening the width of each line relative to the y axis to produce a range of payoffs for a cooperation ratio. For example, an agent with previous action C in a neighbourhood with 0.60 cooperation receives a payoff reward of 0.207 ± 0.033. A line drawn from the bottom of the C function intersects the payoff axis at 0.174 while a line from the top of C hits the axis at 0.24. The derived cooperation value will be a random value chosen within the range of 0.174 to 0.24. In a deterministic environment where the stochastic factor is zero, the width of the payoff function would be and the payoff reward would equal 0.207.

Figure 5. Reward/Penalty Payoff Functions for Pavlovian Defectors and Cooperators (from Szilagyi 2003)

4.20

Several researchers (Hauert and Schuster 1997; Milinski and Wedekind 1998; Zhao-Han et al. 2008) have determined that memory capabilities enhance the success of the Pavlov strategy in PD simulations. When memories are incorporated, agents have the ability to remember defectors from previous iterations, and these defectors are tempted to change state to avoid reprisals from vengeful cooperators. Shao-Meng et. al (2008) also found that a memory effect enhances the density of cooperation in IPD games regardless of agent strategy. For this research, it is logical that a bias towards cooperation for mobile agents that continually move between static origin-destination locations requires some sort of memory capacity. Repetitively interacting agents become true neighbours in the sociological sense, because a degree of familiarity causes the payoff rewards for the individuals to be superceded for the benefits of the collective thus leading to the emergence and growth in cooperation.

4.21

The practice of three-step memory Pavlovian strategies is adopted from Zhao-Han et al. (2008) where the interaction histories of agents are formulated as a weighted payoff, an average production function, and a three-step memory coefficient of learning. Given a citizen agent, the weighted payoff is defined as

(3)

,where Wi is a weighting parameter such that all weights sum to one, and Mc_i is the history payoff (i.e. Mc₁ stores the current payoff). Assuming that the effects of memory decrease with time, W₁ ≥ W₂ ≥W₃.

4.22

The updating scheme is a set of functions that assign an action to a citizen agent probabilistically based on his behavior and the behaviors of the collective from the memory events. Let p_i (t) be the probability of cooperation for agent i at time t, and q_i (t) the probability of defection for agent i at time t. At each iteration, agent i changes p_i (t) and q_i (t) according to the reward/penalty received from the environment's responses. For instance, at time t, the agent chooses C and the payoff functions reward it, then the probability of choosing C is increased for subsequent time steps. Each agent is also assigned a coefficient of learning α _i, where 0 < α _i < 1, to adjust the probability according the neighbourhood responses and past cooperation states. α _i increases if an agent makes repeated actions within the environment but decreases as the actions become varied. For agent state S(t) for time t, there are three possible adjustments to the learning coefficient with α _i restricted to the range 0.1 to 1:

1. α _i (t+1) = α _i (t) + 0.15, if (S(t) = S(t-1)) and (S(t-1) = S(t-2))
2. α _i (t+1) = α _i (t) + 0.10, if (S(t) = S(t-1)) and (S(t-1) ≠ S(t-2))
3. α _i (t+1) = α _i (t) - 0.10, if (S(t) ≠ S(t-1))

Consequently, the probability of cooperation for agent i at time t+1 is:

p( t+1) = p( t) + (1-p( t)) * α i, if at time t, S(t) = C and RPwt > 0

(4)

p( t+1) = (1-α i) * p( t), if at time t, S(t) = C and RPwt ≤ 0

(5)

Note that for every t there must be q( t) = 1 - p( t). The same set of equations are also used for updating the action probabilities when the previous action is D:

q( t+1) = q( t) + (1-q( t)) * α i, if at time t, S(t) = D and RPwt > 0

(6)

q( t+1) = (1-α i) * q(t), if at time t, S(t) = D, and RP wt ≤ 0

(7)

4.23

The state of agent i is updated contingent on its previous state, the average neighbourhood production function, and the probabilities for both C and D. The neighbourhood production function for time t is the cooperation payoff for the group computed as:

(8)

where C_j is the payoff value for agent j and N is the total number of agents in the neighbourhood. The average neighbourhood function for three memory events is formulated as:

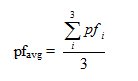
(9)

Thus, the state of agent i at time t+1 with S( t):

For S(t) = C: S( t+1) =

(10)

For S(t) = D: S( t+1) =

(11)

,where R_u∈ [0,1] is a uniform random value.

Results

5.1

The goal of the simulation scenarios is to test the ability of the system to model social cooperation in a spatial environment considering a number of fundamental considerations and questions. First of all, the emergence of cooperation in social groupings can depend on the context preservation and depth of neighbourhoods so it is imperative to consider the effects of the mobility of the citizens on agent interactions. Szilagyi (2002) found that cooperation decreases as the depth of the neighbourhood for agents increases so it is important to investigate if the same condition applies to both fixed and mobile citizens. Secondly, a qualitative visual analysis of the resultant cooperation maps will identify any localized patterns of cooperation or defection and whether their emergence is due to agents' worker type and mobility status. For these purposes, simulations with initial settings of 50% cooperators were run for neighbourhood depths of 50 and 150 meters, and were repeated with both fixed and mobile citizen agents. To simulate the interaction of fixed citizen agents, their mobility rules are disabled, and they are restricted to their place of residence. The social community involves 271 citizen objects in an analyzed geographic environment that interacted and communicated for a full calendar year.

5.2

Figure 6 and 7 are the map and graph of the cooperation patterns for mobile agents in a 50 meter neighbourhood respectively. The graph in figure 7 shows the proportion of cooperating agents in social environment as a function of the number of iterations. Throughout this simulation scenario, there is a slightly unstable equilibrium with a large number of cooperators rewarded marginally and a small number of defectors rewarded greatly. While the total numbers of cooperators and defectors remain relatively constant, the locations of the mobile agents change, which produced varying aggregate patterns of cooperation. The map in figure 6 has large clusters of cooperators throughout the environment and several smaller groupings of defectors in the more densely populated sections (see northeast corner of map). As Zhao et. al. (2005) have reported, cooperation emerges as the dominant action in small neighbourhood depth environments but the effect of agent mobility on context preservation for cooperation in this scenario is difficult to gauge. However, the effect of context preservation is evident in figure 8 and 9; the map and graph of the cooperation patterns for fixed agents in a 50 meter neighbourhood. Firstly, there is a similar majority of cooperators throughout the simulation event, but there are fractionally more total cooperators at each iteration for the fixed agents in figure 9 as compared to the mobile agents in figure 7. Secondly, there is a slight increasing trend in the total number of fixed agent cooperators after 300 iterations and a reciprocal decrease in defectors. At this time step, many cooperating agents throughout the environment continue to cooperate due to their high cooperation probabilities and never again defect. This was characteristic of the agents in the western and southern section of the map in figure 8 where the agents are geographically dispersed and the number of total agents in the individual neighbourhoods is low. An interesting result of the simulation is the emergence of small segregated clusters of defectors (northeast corner and central section) nested within the large grouping of cooperators that covers most of the study area. Since the agents in the sparsely populated sections have reached an equilibrium, state changes only occur in the more densely populated regions where each agent interacts with a higher than average number of neighbours during NPPD play.

Figure 6. Map of Cooperation Pattern for Mobile Agents in a 50 Meter Neighbourhood

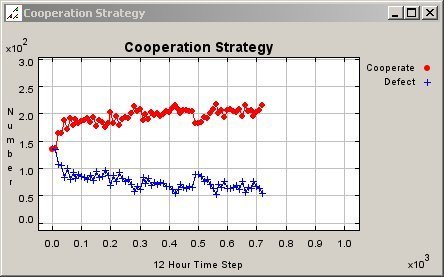
Figure 7. Graph of Cooperation Pattern for Mobile Agents in a 50 Meter Neighbourhood

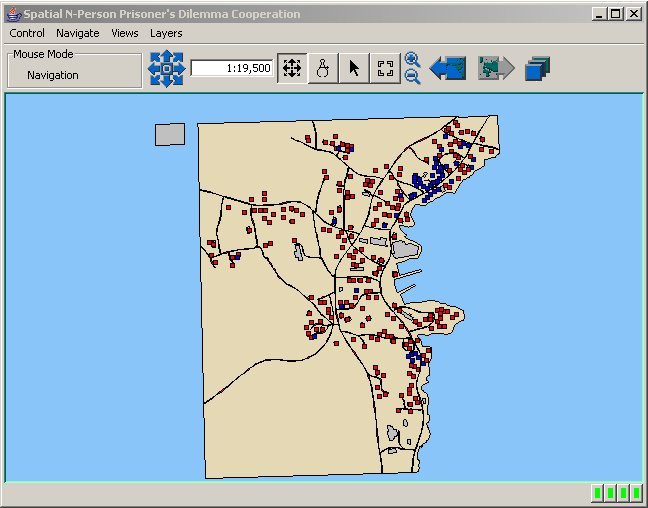
Figure 8. Map of Cooperation Pattern for Fixed Agents in a 50 Meter Neighbourhood

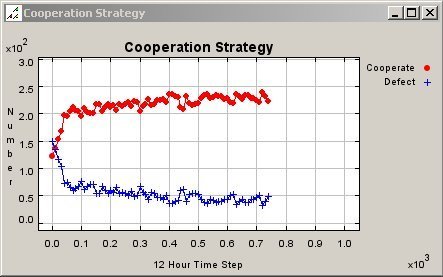
Figure 9. Graph of Cooperation Pattern for Fixed Agents in a 50 Meter Neighbourhood

5.3

This implies that geographic distribution in conjunction with context preservation plays a role in cooperation. Consequently, the reason for the difference in the emergence and maintenance of cooperation among the purposely fixed and mobile citizens can be attributed to context preservation in the modeling environment. The fixed citizens are homophily agents that interact with the same neighbours at each time step, and this creates a degree of relational stability, trust, and familiarity amongst them. This can result in an increase for each fixed agent in their average learning rate and probabilities of choosing the action of the majority of their social grouping. Conversely, mobile agents experience fluctuations in learning rate and the probability of cooperation as their neighbourhoods change during their daily activities, and this can result in frequent changes in cooperation action.

5.4

The following two sets of simulation results are for mobile (figure 10 and 11) and fixed (figure 12 and 13) citizen agents in a 150 meter neighbourhood investigate the effect of neighbourhood depth on the emergence of cooperation. Referring to Szilagyi (2002), it is expected that increasing the neighbourhood depth will produce fewer incidences of cooperation at each iteration, and the simulation results substantiate this fact. Figure 11 shows that the number of agents that choose C and D tend to oscillate, but the overall counts are generally equal during the experiment runs. The spatial patterns changed constantly as a consequence of the transition rules even though the fraction of cooperators remained constant. Small clusters of cooperation and defection are visible on figure 10, but it was found that these groupings are highly susceptible to change. An important factor to remember is that these simulation runs contain mobile agents together with fixed workers, such as the people not in the labour force and the unemployed. The small clusters of C and D that emerge are situated around the places of residence of these fixed agents, which further substantiates the importance of context preservation in spatial NPPD modeling.

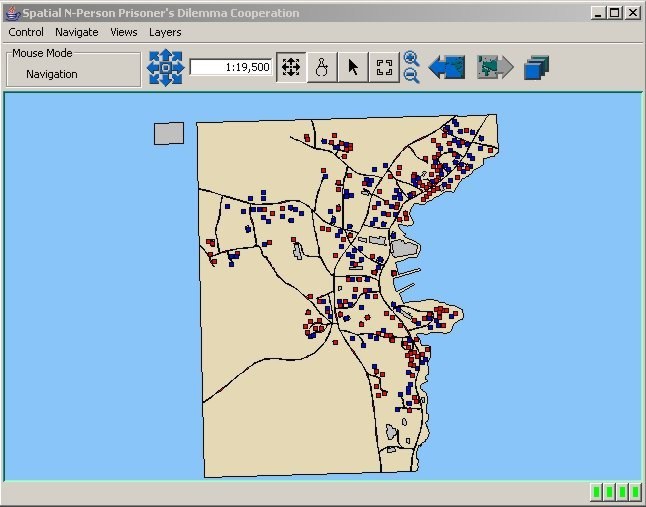
Figure 10. Map of Cooperation Pattern for Mobile Agents in a 150 Meter Neighbourhood

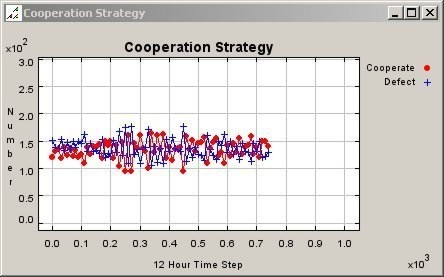
Figure 11. Graph of Cooperation Pattern for Mobile Agents in a 150 Meter Neighbourhood

5.5

The map and graphing results (figure 12 and 13) for the fixed citizen agents show that, from the start of the simulation, there is a pattern of more defectors than cooperators for all but a small number of iterations. The sequential linear graphs of the cooperators and defectors are generally constant with periodic minor readjustments at specific time steps. The map in figure 12 has a large cluster of cooperators in the west, a cluster of defectors in the south, several smaller but clearly segregated clusters of both C and D in the northeast, and an intermingling of both strategy states in the rest of the study area.

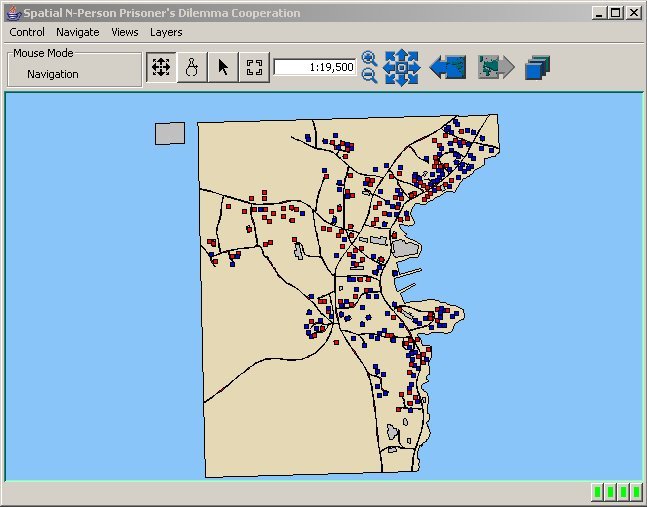
Figure 12. Map of Cooperation Pattern for Fixed Agents in a 150 Meter Neighbourhood

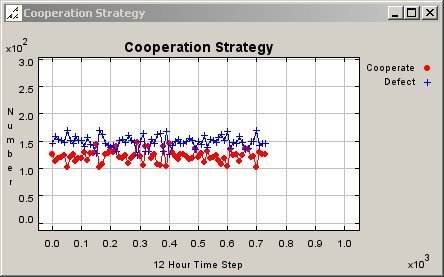
Figure 13. Graph of Cooperation Pattern for Fixed Agents in a 150 Meter Neighbourhood

5.6

An agent that has many citizens within its neighbourhood will have multiple interactions with them during its own NPPD and the others' game play. In other words, the same agents can be grouped many times if they live close to each other, and could start to adopt similar actions over time. The emergent clusters of C and D are due to context preservation, but equally important is the proximity and number of citizens in each agents' neighbourhood.

5.7

Widening the neighbourhood buffer to 150 meters increases the number of citizens in each agent's neighbourhood, and this can decrease the probability of cooperation due to the form of the payoff and production functions. Equations 8 and 9 show that state changes occur when the average payoff value is less than the average production function, and, from the results, this happens when there is either a considerable majority of cooperators or defectors in the NPPD interaction. For a scenario with 50% C and a large value of N, a single agent could choose defection at time t+1 with minimal change to the production function value from time t. However, a change in state of an agent in a small neighbourhood (e.g. 4 agents) could produce a considerable change in payoff and production function from time t to t+1. A state change by a single agent results in situation where the average production function is less than the payoff value so this increases the possibly of corresponding changes in its neighbours in subsequent play events.

5.8

A research issue that arises from these results is can a quantitative index of cooperation be derived according to neighbourhood depth and mobility. To realistically model a socio-geographic community, agents have to be able to move throughout the environment. A simplistic cooperation measurement could be based on the neighbourhood depth up to a limit where the total number of C approaches the same number of D. Depending on the geographic distribution of agents, initial cooperation ratio, and spatial configuration of the study area, the user could provide a predefined buffer size that provides the accepted number of cooperators throughout the simulation. From these above results, that distance is within the 50-150 meter range, and is probably closer to the 50 meter threshold. This is a topic that will be thoroughly investigated in future versions of the model.

Conclusion

6.1

The purpose of this paper is to present a spatial agent-based approach for modeling the processes of communication and cooperation within a socio-geographic community. As a generic modeling-centric system with a tight coupling of REPAST and a vector GIS, the model is designed to simulate the mobility and daily interactions of citizen agents in an analyzed spatial environment. The postulate of the system is that competition and cooperation will emerge from the behaviors of the citizens as they engage in N-Person prisoner's dilemma play. These citizen agents are set as stochastic learning automata that take actions according to probabilities updated on the basis of the reward/penalty received for previous actions, their neighbours' actions, and their Pavlovian personalities.

6.2

The value of the model for simulating cooperation in a social-geographic environment was evaluated from the results of two sets of experimental runs. It was determined that the initial percentage of cooperators in a simulation had little bearing on the emergence of cooperation, but the mobility of the citizen automata was the central factor. The preservation of neighbourhood context in fixed citizen agent environments produced larger clusters of cooperators and defectors than the mobile agent environments. As the fixed citizen agents continuously interact with the same neighbours, they become homophily automata with increasing learning rates and probabilities of copying the action of the majority of their social grouping. Conversely, the environments of mobile citizen agents produced small clusters of C and D, but they were susceptible to variations in size and location as the agent neighbourhoods changed. Even though the proportion of cooperators remained constant, the spatial patterns changed repeatedly as a consequence of the movement and action updating rules.

6.3

The work presented in this paper is a very simplistic model of cooperation-agent interaction situations and should not be considered a complete analysis of the processes within a socio-geographic community. Future revisions of the model are necessary for it to be applicable to more realistic problems of human interactions in analyzed environments.

6.4

The first step towards expanding the model is to investigate the performance of other learning rules, payoff functions, and updating schemes. This version of the model is developed as a linear reward/penalty probabilistic learning automaton system, but it is possible that the learning rules and updating scheme are inappropriate for nonfixed spatial agents and may have to be reconsidered.

6.5

Secondly, the classical definition of N-Person prisoner's dilemma is an essentially unrealistic analogy for cooperation, because it only allows a boolean assignment to two cooperation classes. In reality, cooperation should be measured on a continuous state space that varies at each time step according to the attitudes of the agents. Research in this regard has been undertaken by Killingback and Doebeli (2002), who discuss a continuous iterated prisoner's dilemma model of cooperation from reciprocal altruism. A further expansion to the model is to develop a methodology of assigning fuzzy memberships to an agent for both cooperation and defection. Using a set of fuzzy membership functions similar to figure 14, each agent is assigned a degree of membership in both classes to produce a continuum of cooperation in the modeling environment. See Power et al. (2001) for a detailed explanation of fuzzy set theory. The advantage of utilizing fuzzy logic in the design of the transition rules and updating schemes is that possibility theory permits memberships values that do not have to sum to 1 (a condition of probability theory). This flexibility could be implemented to account for noise and random errors known to exist in implementing a choice during real-world interactions. Support for this augmentation is provided by Fort and Perez (2005) who present an IPD model that incorporates fuzzy set theory into Pavlovian strategies to investigate 5 measures of success used by agents in gauging game performance. In the form of asynchronous cellular automata, fuzzy membership functions are used to account for the stochastic component in the adaptive behaviors of the players during the IPD interchange, which provides a means of including uncertainty in the analysis.

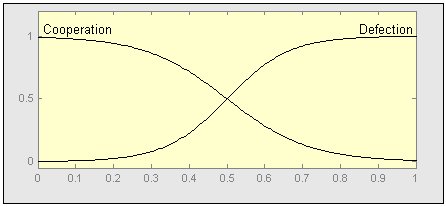
Figure 14. Fuzzy Membership Functions of Cooperation and Defection

6.6

As a further model revision, a fuzzy inference system can provide a flexible base for developing a modeling component that permits agents to have multiple personality types. Through the combination of fuzzy membership functions for a number of personality types and a compositional rule of inference, a fuzzy transitional rulebase will assign varying degrees of personalities to an agent. The overall personality of an agent then becomes a combination of the degrees of membership in the personality strategies, with the membership values varying at each social dilemma game play. Agents with mixed personalities and interaction strategies are intuitively appealing for a spatial agent-based model of cooperation in a socio-geographic environment.

References

AKIMOV, Vladimir, and Mikhail Soutchanski (1994). Automata Simulation of N-Person Social Dilemma Games. Journal of Conflict Resolution, 38(1), pp. 138-148.

ALONSO, J., A. Fernandez, and H. Fort (2006). Prisoner's Dilemma Cellular Automata Revisited: Evolution of Cooperation Under Environmental Pressure. Journal of Statistical Mechanics: Theory and Experiment, 13, pp. 1-15.

AXELROD, Robert (1984). The Evolution of Cooperation. New York: Basic Books Publishing.

AXELROD, Robert (1997). The Complexity of Cooperation: Agent-Based Models of Competition and Cooperation. Princeton, New Jersey: Princeton University Press.

BENENSON, Itzhak, and Paul Torrens (2004). Geosimulation: Automata-Based Modeling of Urban Phenomena. West Sussex, England: John Wiley and Sons Ltd.

BOONE, C., B. De Brabander, and A. van Witteloosluijn (1999). The Impact of Personality on Behavior in Five Prisoner's Dilemma Games. Journal of Economic Psychology, 28, pp. 343-377.

BOYD, R., and J. Lorderbaum (1987). No Pure Strategy is Evolutionary Stable in the Repeated Prisoner's Dilemma Game. Nature, 32(6117), pp. 58-59.

BREMBS, Bjorn (1996). Chaos, Cheating, and Cooperation: Potential Solutions to the Prisoner's Dilemma. OIKOS 76, 1, pp. 14-24.

BROWN, D. G., R. Riolo, D.T. Robinson, M. North, and W. Rand (2005). Spatial Process and Data Models: Toward Integration of Agent-Based Models and GIS. Journal of Geographical Systems, Special Issue on Space-Time Information Systems, 7(1), pp. 25-47.

COHEN, Michael D., Rick L. Riolo, and Robert Axelrod (1998). The Emergence of Social Organization in the Prisoner's Dilemma: How Context Preservation and Other Factors Promote Cooperation. Santa Fe Institute Working Paper 99-01-002.

COUCLELIS, Helen (2001). Why I No Longer Work with Agents: A Challenge for ABMs of Human-Environment Interactions. In Parker, D.C., Berger, T. and Manson, S.M. (Eds.) Meeting the Challenge of Complexity: Proceedings of a Special Workshop on Land-Use/Land-Cover Change, Irvine, California.

ECKERT, Daniel, Stefan Koch, and Johann Mit_hner (2005). Using the Iterated Prisoner's Dilemma for Explaining the Evolution of Cooperation in Open Source Communities. Proceedings of the First International Conference on Open Source Systems, Genova, July 11-15.

FORT, Hugo, and Nicolás Pérez (2005) The Fate of Spatial Dilemmas with Different Fuzzy Measures of Success, Journal of Artificial Societies and Social Simulation, 8(3)1, https://www.jasss.org/8/3/1.html

GEOTools 2.4.4 (2008). Open Source Java GIS Toolkit. http://geotools.codehaus.org/.

HARDEN, Garett (1968). The Tragedy of the Commons. Science, 162, pp. 1243-1248.

HAUERT, C. and H.G. Schuster (1997) Effects of Increasing the Number of Players and Memory Size in The Iterated Prisoner's Dilemma: A Numerical Approach. Proceedings of the Royal Society of London B, 264, pp. 513-519.

JAVA Topology Suite 1.8 (2007). Vivid Solutions. http://www.vividsolutions.com/jts/jtshome.htm.

KEHAGIAS, A (1994). Probabilistic Learning Automata and the Prisoner's Dilemma. http://users.auth.gr/~kehagiat/KehPub/other/1994JLA1.pdf.

KILLINGBACK, Timothy, and Michael Doebeli (2002). The Continuous Prisoner's Dilemma and the Evolution of Cooperation through Reciprocal Altruism with Variable Investment. The American Naturalist, 160(4), pp. 421-438.

LOOMIS, Charles P. (1996). Social Systems: Essays on Their Perspective and Change. Toronto, Canada: D. Van Nostrand Company Inc.

MCCAIN, Roger (2003). Specifying Agents: Probabilistic Equilibrium with Reciprocity. Computing in Economics and Finance, 9, pp. 1-34.

MILINSKI, Manfred, and Claus Wedekind (1998) Working Memory Constrains Human Cooperation in the Prisoner's Dilemma. Proceedings of the National Academy of Science USA, 95, pp. 13755-13758.

NOWAK, Martin A., and Robert M. May (1992). Evolutionary Games and Spatial Chaos. Nature, 359, pp. 826-829.

NOWAK, Martin A., and Karl Sigmund (1992). Tit for Tat in Heterogeneous Population. Nature, 355, pp. 250-253.

NOWAK, Martin A., and Karl Sigmund (1993). A Strategy of Win-Stay, Lose-Shift that Outperforms Tit-For-Tat in the Prisoner's Dilemma Game. Nature, 364, pp. 56-58.

OPENMAP 4.6.3 (2007). BBN Technologies. http://openmap.bbn.com

POWER, Conrad, Alvin Simms, and Roger White (2001). Hierarchical Fuzzy pattern Matching for the Regional Comparison of Landuse Maps. International Journal of Geographical Information Systems, 15(1), pp. 77-100.

RECURSIVE Porous Agent Simulation Toolbox (2007). Java Version 3.0, University of Chicago and Argonne National Laboratory. http://repast.sourceforge.net.

SCHELLING, T.C. (1973). Hockey Helmets, Concealed Weapons, and Daylights Savings. Journal of Conflict Resolution, 13(3), pp. 381-428.

SHAO-MENG Qin, Yong Chen, Xiao-Ying Zhao, and Jian Shi (2008) Memory Effect on Prisoner's Dilemma Game in a Square Lattice. http://arxiv.org/PS_cache/arxiv/pdf/0801/0801.2827v2.pdf

STATISTICS Canada (2006). General Census Release. http://www12.statcan.ca/english/census/index.cfm.

SZILAGYI, Miklos, and Zoltan Szilagyi (2002). Non-Trivial Solutions to the N-Person Prisoner's Dilemma. Systems Research and Behavioral Science, 19(3), pp. 281-290.

SZILAGYI, Miklos (2003). Simulation of Multi-Agent Prisoner's Dilemma. Systems Analysis and Modeling Simulation, 43(6), pp. 829-846.

THORNDIKE, E.L. (1911). Animal Intelligence. Darien, Connecticut: Hafner Press.

TRIVERS, R.L. (1971). The Evolution of Reciprocal Altruism. Quantitative Reviews in Biology, 46, pp. 35-57.

YAO, Xin, and P.J. Darwen (1994). An Experimental Study of N-Person Iterated Prisoner's Dilemma. Informatica, 18, pp. 435-450.

ZEIGLER, B.P., H. Praehofer, and T.G. Kim (2000). Theory of Modeling and Simulation: Integrating Discrete Events and Continuous Complex Dynamic Systems. New York: Academic Press, 2nd Edition.

ZHAO, Jijun, Miklos Szilagyi, and Ferenc Szidarovszky (2007). A Continuous Model of N-Person Prisoner's Dilemma. Game Theory and Applications, 12, pp.207-242.

ZHAO-HAN Sheng, Yun-Zhang Hou, Xiao-Ling Wang, and Jian-Guo Du (2008) The Evolution of Cooperation with Memory, Learning, and Dynamic Preferential Selection in Spatial Prisoner's Dilemma Game. 2007 International Symposium on Nonlinear Dynamics, Journal of Physics: Conference Series 96, pp. 1-6

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2009]