Patrick Groeber, Frank Schweitzer and Kerstin Press (2009)

How Groups Can Foster Consensus: The Case of Local Cultures

Journal of Artificial Societies and Social Simulation vol. 12, no. 2 4
<https://www.jasss.org/12/2/4.html>

For information about citing this article, click here

Received: 17-Aug-2008    Accepted: 23-Jan-2009    Published: 31-Mar-2009

Abstract

A local culture denotes a set of rules on business behaviour among firms in a cluster. Similar to social norms or conventions, it is an emergent feature of interaction in an economic network. To model its emergence, we consider a distributed agent population, representing cluster firms. Further, we build on a continuous opinion dynamics model with bounded confidence (ε), which assumes that two agents only interact if differences in their behaviour are less than ε. Interaction results in more similarity of behaviour, i.e. convergence towards a common mean. Two aspects extend this framework: (i) The agent's in-group consisting of acquainted interaction partners is explicitly taken into account, leading to an effective agent behaviour as agents try to continue to interact with past partners and thus seek to stay sufficiently close to them. (ii) The in-group network structure changes over time, as agents form new links to other agents with sufficiently close effective behaviour or delete links to agents no longer close in behaviour. Thus, the model introduces a feedback mechanism of agent behaviour and in-group structure. Studying its consequences by means of agent-based computer simulations, we find that for narrow-minded agents (low ε) the feedback mechanism helps find consensus more often, whereas for open-minded agents (high ε) this does not necessarily hold. Overall, the dynamics of agent interaction in clusters as modelled here, are conducive to consensus among all or a majority of agents.

Keywords:

Social Norms, Conventions, Bounded Confidence, Dynamic Networks

Introduction

1.1

Since the early 1990s, economic theory and policy has dedicated a lot of attention to the causes and effects of clusters, i.e. spatial concentrations of firms in one or a few related industries (Ellison and Glaeser 1997). Driven by their impressive prosperity, the factors underlying cluster success were extensively studied in the hope of replicating areas like the Silicon Valley or London. Locating in a cluster provides several benefits for firms.^[1] However, the existence of these benefits hinges on a set of rules on acceptable business practice - the cluster's ' local culture'. For instance, there is a rule among banks located in Frankfurt that they should not hire personnel away from competitors. In the Silicon Valley, the local culture is such that firms openly exchange ideas even with direct competitors. In order to do business within the cluster, firms need to know and respect these rules. This has made it difficult for outside companies (e.g. multinational enterprises) to successfully enter the cluster through subsidiaries (Heiduk and Pohl 2002). While some work has been conducted to determine the nature and enforcement of such local cultures, their emergence remains far from understood. So far, anecdotal evidence suggests that it depends on agreement about the nature of desirable business practice.

1.2

To shed light on the emergence of local cultures, the present paper studies the emergence of the initial consensus. It argues that cluster firms have to interact with each other. As these interactions are not cost-free, they give rise to changes in firm behaviour and different inter-firm networks that affect the future behaviour of constituent firms. Both mechanisms can lead to convergent or divergent behaviour. Those cases finding converging behaviour among all or a majority of cluster firms constitute situations in which the basis for a local culture emerges. This is also important for the emergence of clustering benefits and therefore the economic viability of the cluster. To study the emergence of converging behaviour (i.e. the first step towards a local culture), this paper develops an opinion dynamics model with bounded confidence and group-influence as both aspects are required to mimic the dynamics of inter-firm interaction in clusters.

1.3

In doing so, the paper proceeds as follows. The next section describes the case under study. The emergence and effect of local cultures is found to be similar to that of norms and conventions as both are means to solve co-ordination and cooperation problems. However, the costliness of inter-firm interactions requires some amendments to existing models (see Local cultures as norms or conventions). In particular, it justifies the application of a bounded confidence model thereafter (Modelling the emergence of consensual behaviour): Agents (=firms) will only interact if they are sufficiently close in behaviour as the risk of a costly transaction going wrong are too high otherwise. Moreover, ties stemming from previous interactions link agents. Thanks to costly interaction, agents try to maintain these 'in-groups' and modify their behaviour accordingly. The results are discussed in light of the conditions for consensual behaviour among all or a majority of agents. It is found that the existence and influence of in-groups fosters consensus, especially if agents would only interact with behaviourally similar actors. As a result, the nature of inter-firm interactions in clusters is conducive to consensus and thereby the emergence of a local culture.

Defining local cultures

2.1

In economic geography, local cultures with rules like "do not hire from competitors, exchange ideas freely or deliver only the highest quality" are a phenomenon characterising clusters like Silicon Valley (IT), London (financial services) or Prato, Italy (textiles). Adherence to these local cultures - once established - is key to successfully doing business with its constituent firms. Moreover clusters require local cultures as the benefits are subject to various co-ordination and co-operation issues solved by the rules in the local culture.

2.2

Cluster benefits relate to scale and specialisation effects as well as positive externalities. The former (scale and specialisation) emerge since companies in a cluster usually divide the production process. Rather than having all firms manufacture shoes, one specialises in soles while another provides laces, tops, linings and so on (Pyke et al 1990). This division of labour leads to scale and specialisation benefits: Firms can achieve a greater output with a limited budget and become more efficient in their activities (Smith 2003). Moreover, companies conduct competing and complementary activities under identical local conditions in the cluster. This leads to positive externalities in the diffusion of ideas and the availability of skilled labour.^[2]

2.3

To generate these benefits, cluster firms have to overcome several dilemmas. For a division of labour to emerge, suppliers need a fair price and a sufficient market (Smith 2003, p. 27). Moreover, the quantities provided by different firms have to be aligned. Positive externalities in knowledge and personnel are tied to respective investments in research and training. This is only viable if defection (free-riding) is limited.^[3] Akin to famous cooperation problems like the Kula Ring (Ziegler 2007) or the Chicago diamond market (Coleman 1990), the cluster literature argues, that these dilemmas are solved by rules on acceptable business practice that make up the local culture. While some work has determined what local cultures look like (e.g. Porter 1990; Pyke et al. 1990; Saxenian 1994) and how enforcement can be ensured (Holländer 1990; Kandel and Lazear 1992) their emergence is far less understood.

2.4

It is usually suggested local cultures emerge as firms learn about successful behaviour in interacting with others. Successful past behaviour is then repeated and possibly copied among firms in the cluster, which implies that it gradually spreads in the population. Once established, such consensual "good" behaviour creates expectation about others' future behaviour, thereby reducing frictions in interaction. Specific rules making up a local culture can finally emerge to foster and enforce this consensual behaviour by monitoring and punishment of defecting agents (Maskell 2001, p. 926). The first step towards a local culture is thus a behaviour that is viewed as desirable enough to become the basis of rule making. We argue that a good candidate for viable rules is behaviour already prevalent in the cluster, i.e. a behaviour that is shared by (a majority of) local firms. As a result, consensus on certain behaviour constitutes the necessary condition for rule making, rule enforcing and the emergence of local cultures. This paper investigates how consensus on a specific behaviour emerges in a cluster. In doing so, the paper argues that the division of labour in clusters requires interaction between firms to manufacture the product. As interactions are not cost free (Coase 1937; Williamson 1975), two mechanisms come into play.

2.5

First, interaction costs increase with the difference in firm behaviour. Firms with similar behaviour are likely to respond similarly to future developments. This makes it unnecessary to specify all possible scenarios in a contract thereby reducing the cost of interaction. If all interactions are equally beneficial, the increasing cost of interaction implies that (a) firms will not interact with all possible partners and (b) the partners to an interaction modify their behaviour to become more similar. Second, costly interactions make it beneficial to maintain links with existing partners. Firms therefore become more embedded in networks emerging from their interaction history. Moreover, the desire to maintain these networks may constrain their behaviour as firms seek to remain sufficiently similar to existing partners.

2.6

The consensus resulting from these mechanisms (if any) can take very different forms. It can reside with a behaviour that is very co-operative, i.e. each firm invests in activities subject to externalities and supplier-buyer relations are characterised by fairness. This provides high incentives for free riding, implying that this behaviour is not self-enforcing. In other instances, consensus can reside with very defective behaviour where all firms try to exploit one another as much as possible and do not invest in activities with externalities. This situation would provide no incentive for deviation (at least not to an individual firm), i.e. the local culture is self-enforcing.

Local cultures as norms or conventions

3.1

Once established, local cultures fulfil the function of social norms or conventions insofar as they solve co-operation or co-ordination problems. As a result, their emergence mimics that of norms and conventions, which unfolds as follows: The first stage is build on consensus formation, where agents reach consensus on a certain behaviour through different mechanisms like optimising behaviour (Opp 1982; Weber 1999), imitating or replicating successful strategies (Asch 1956; Sherif 1973) or through trial and error search (Demsetz 1967). Once consensual behaviour spreads and remains in the population, it creates expectations about everyone's future behaviour, thus reducing friction in interactions (Axelrod 1986; Koford and Miller 1991; Sugden 1989). Depending on whether the behaviour is self-enforcing (convention) or not (norm), the second stage of the process differs. For conventions, the emergence of consensus is sufficient. In case of norms behavioural regularities have to result in a sense of "oughtness" (Opp 2001) that may eventually lead to an enforceable norm prescribing this behaviour: "Thus, patterns of action emerge that then become normative […]. Individuals comply with the new norm both for the original reason that the behaviour was appealing, and also because it is now socially enforced" (Horne 2001, p. 6).

3.2

Depending on the nature of consensual behaviour (self-enforcing or not), local cultures correspond to conventions or social norms. In either case, the first stage of their emergence process (consensus building) is identical. This makes models on the emergence of norms or conventions applicable to our case. In the literature, most work on norms and conventions is based on game-theory with a smaller subset of research studying consensus formation (through voter models or bounded confidence approaches). The game-theoretic approach to norms and conventions (Fehr and Fischbacher 2004; Holländer 1990; Kandel and Lazear 1992; Pujol et al. 2005; Ullmann-Margalit 1977; Voss 2001) is not applicable to our case for several reasons. By focussing on the nature of the game (e.g. payoff structure, repetition) and underlying agent interaction, incentives and efficient outcomes are derived. Conventions correspond to situations where the optimal outcome is a non-unique Nash equilibrium. Depending on the underlying mechanisms, different equilibria may be selected (e.g. Pujol et al. 2005; Shoham and Tennenholtz 1992). Norms instead emerge in situations where the optimal solution is not an equilibrium outcome. The norm then constitutes a solution to those problems that otherwise prevent a better outcome to the game.^[4]

3.3

The focus on payoffs and incentives implies that there is a known optimal behaviour. In other words, agents know the consequences of their actions, anticipate the choices of others and are thereby able to determine, what kind of behaviour leads to efficient outcomes. In the Prisoner's Dilemma situation, cooperation is the ex ante optimal behaviour when jointly maximising the outcome. Moreover, game theory is less concerned with the emergence of a particular norm or convention than with its effect for the game's equilibrium outcome. Since we cannot determine ex-ante payoff values for business strategy and our concern is with the emergence of local cultures, game-theoretic models are not suited for our research question. We therefore focus on an approach that does not assume an 'optimal' behaviour but where the value of an agent's behaviour only depends on the number of agents adhering to it and on that behaviour's compliance with the predominant behaviour in the agent's personal network. In this sense, any consensus among all agents is 'good' - regardless of the nature of consensual behaviour.

3.4

There are several models studying the emergence of consensus from agent interaction (e.g. Axelrod 1997, Deffuant et al. 2000; DeGroot 1974; Hegselmann and Krause 2002; Lehrer and Wagner 1981). They fall into two main classes: Voter models and bounded confidence models. In voter models, agents are characterised by a discrete opinion (a binary variable in most cases) and are embedded in a network of given topology. They may adopt other opinions according to their frequency in the agent's neighbourhood. In linear voter models, the transition towards a given opinion is directly proportional its local frequency. In non-linear voter models other types of frequency dependent behaviour are possible (Schweitzer 2007). While consensus is always reached in linear voter models, non-linear responses to the local frequency of an opinion may prevent (Schweitzer and Behera 2009) or accelerate (Stark et al. 2008a,b) consensus.^[5]

3.5

Another class of consensus models deals with continuous opinions x_i represented as a real number between 0 and 1 (Deffuant et al 2000). Two agents i and j, randomly chosen at each time step, can only interact if the difference in their opinions does not exceed a threshold value ε. Rather than occurring on a predefined network, agent interactions are randomised and conditional. Hegselmann and Krause 2002 apply this mechanism of 'bounded confidence' with all possible interactions happening simultaneously. As investigated by means of several approaches (e.g. Ben-Naim et al 2003; Lorenz 2006) consensus then largely depends on the value of the key parameter ε.^[6]

3.6

Our model, formalized in the following section, builds on the bounded confidence approach, but combines it with the consideration of the dynamics in an agent's social network. Dependent on the relationship between i and j, we distinguish between an in-group (members of a social network seen as friends) and an out-group (members with adversary relations, enemies; see Fent et al 2007).^[7] In addition to in-group relations, we include dynamics of the agents' social network. This is based on a feedback mechanism between an agent's behaviour and her personal network: Past interactions with partners from the agent's in-group affect her individual behaviour which in turn influences the structure of the in-group, iteratively. Hence, as the novel element, our model combines both opinion dynamics and network dynamics at the level of individual agents.

3.7

Both aspects relate to the fact that interaction between agents is not cost-free. First, we argued that costs increase with differences in agent behaviour since many actions are beneficial as long as both agents behave in the same way.^[8] As a consequence, interactions are conditional on sufficient behavioural similarity. Moreover, interacting agents approach each other's behaviour to lower interaction cost. Second, costly interactions make keeping past partners very beneficial. Agents will thus want to keep past partners (their in-group) and modify their behaviour accordingly. The behaviour of the group will therefore determine the range of agent behaviour. Conversely, agent behaviour feeds back on her in-group and therefore allows for changes in-group structure as a function of interaction and behavioural dynamics. The following section provides more detail on the formal treatment of these mechanisms.

Modelling the emergence of consensual behaviour

4.1

We argued before that costly interactions result in two effects, (i) consensus formation, i.e. optimising behaviour within a group to avoid friction, and (ii) network formation, i.e. optimising the agents' social network structure by deleting links with agents whose behaviour largely deviates from one's own, thus making interaction more costly (or creating links with agents whose behaviour is more similar). The two interlinked dynamics are specified as follows.

4.2

Consensus formation. In order to reflect the first consequence of costly interactions, we need a model that makes interaction conditional on agent behaviour. Following Deffuant et al 2000, agent i's behaviour x_i is represented as a real number between 0 and 1. Thus, we are able to measure the distance of behaviours and to model a gradual approach if these agents interact. This is different to the cultural dissemination framework of Axelrod 1997 where cultures constitute a finite, discrete and in general non-metric set. There, interaction between two agents can only lead to complete assimilation of behaviour for one of them, whereas agents approach each other's behaviour in our model. We further define the behaviour profile x=(x₁…,x_n).

4.3

In our model, in accordance with Deffuant et al. 2000, two agents i and j are randomly chosen at each time step. They can only interact if the difference in their behaviour does not exceed a threshold value ε, which can be regarded as a measure of openness. Regarding agent interaction, we can also interpret ε as the difference in behaviour where the costs and benefits break even: With greater behavioural differences, interaction costs would increase while the benefits are assumed to be constant. Such an interaction would lead to a net cost to the agents involved and will therefore not occur.^[9] As the benefits and costs are identical for all agents, the necessary condition for an interaction of i and j becomes:

|xi (t)-xj (t)|< ε

(1)

4.4

If two agents interact, they try to maximise the benefits of this exchange. As benefits are constant and costs decrease with behavioural differences, the behaviour of interacting agents becomes more similar as both approach each other by identical amounts:

xi (t+1)=xi (t)+μ(xi (t)-xj (t)) xj (t+1)=xj (t)+μ(xj (t)-xi (t))

(2)

The speed of approach in behaviour depends on the parameter μ. It reflects the well-established phenomenon that interacting parties become more similar (e.g. Axelrod 1997; Macy and Skvoretz 1998; McPherson et al. 2001; Strang and Soule 1998).

4.5

The dynamics specified by Eqs. (1) and (2) are referred to as the baseline model in the following, as they result in the known behaviour already discussed by Deffuant et al. 2000. We now extend this model by introducing the second aspect: Costly interactions imply benefits to keeping past partners. This is modelled by aggregating each agent's past interaction partners. Each agent i thus has a set I_i of other agents constituting her in-group, i.e. the agent's acquainted partners. As the agent would like to interact with these partners later, she tries to keep her behaviour sufficiently similar to them. As agent behaviour changes with her interactions, we argue that the in-group exerts an influence on the agent's future interactions. This is achieved by combining an agent's behaviour x_i and the mean behaviour of her in-group x_i ^I to determine the effective behaviour

xi eff (t)=(1-ai (t)) xi (t) + ai (t) xi I

(3)

at time t. The use of the mean behaviour is chosen to mirror that the agent is equally interested in interacting with any of her past partners.^[10]

4.6

In Eq. (3), a_i ∈ [0,1] determines the influence of agent i's in-group on her effective behaviour. We use this parameter to mirror the strength of group influence. Based on the aforementioned notion that agents like to keep past partners, the influence of the group would increase with its size. In this model, we define a_i endogenously by

ai (t)=|Ii (t)| (|Ii (t)|+1)-1

(4)

Hence, we assume that each agent puts equal weight on her own and each in-group member's behaviour. If i has never interacted with another agent, her in-group is empty (|I_i (t)|=0) implying a_i=0. Hence, the effective behaviour of agent i is identical to her behaviour (x_i ^eff =x_i). Further, a_i approaches 1 with growing in-group size |I_i|. If the in-group is large, i 's effective behaviour will therefore tend towards the average in-group behaviour.

4.7

In our model, two agents wanting to interact now have to compare the distance between their effective behaviour (influenced by their respective in-groups) instead of that of their own behaviour. As a result, the necessary condition for interaction between agents becomes

|xi eff (t)-xj eff (t)| < ε

(5)

If two agents with empty in-groups interact, this is identical to Eq. (1) as x_i ^eff =x_i and x_j ^eff =x_j for I_i=I_j=[].

4.8

Network formation. In addition to maintaining their in-group, agents also seek to expand it with suitable new partners. To specify this, we assume that in-groups are initially empty for all agents. Later, they evolve according to the agents' interactions as follows: In each simulation step, two agents i and j are randomly selected. If Eq. (5) holds for them, they interact and are added to each other's in-group (if they are not already contained). Over time, agents i and j may interact with different agents. Therefore, their effective behaviour can be altered either directly due to a change of x_i and x_j resulting from interaction with other agents, or indirectly by interactions of agents in their in-group affecting the average behaviour of the respective in-group. Thus, we may encounter a situation where agents i and j interacted at time t and were added to each other's in-group while later at t' > t, their effective behaviour may be modified such that |x_i ^eff (t')-x_j ^eff (t')| ≥ ε. In this case, agents i and j could no longer interact when selected and would be removed from each other's in-group. Thus, if i and j are selected at time t, we have

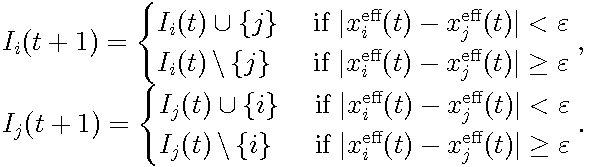
(6)

Note that the in-group relation is symmetric but may not be transitive, i.e. agent i being contained in agent j 's in-group and agent j being contained in agent k 's in-groups does not require k being in j 's in-group.

4.9

As indicated before, the behaviour of interacting agents becomes more similar. This means that interaction at time t alters the agents' behaviour according to Eq. (2). For t+1, this feeds back on the effective behaviour of i and j (Eq. 3), as well as on the effective behaviour of agents whose in-group contains i or j. The effect of modifying i's behaviour for her effective behaviour will decrease with larger I_i. Over time, the agent can interact with others in and outside her in-group if Eq. (5) is satisfied. This influences her behaviour as well as the evolution of her in-group over time. Agents previously outside i's in-group are added to the set I_i once i successfully interacts with them. The addition of new agents to I_i influences her effective behaviour and thereby her potential for future interaction.^[11] Thus this model provides a feedback mechanism between the agents' behaviour and their in-group's structure.

4.10

In the context of local cultures, we are mainly interested in whether the dynamics lead to consensus or in quantifying the degree of heterogeneity in agent behaviour. We therefore investigate how the results for the baseline model are affected by the two extensions proposed here, namely the evolving agent network and its feedback on agent behaviour. As known, equilibrium outcomes depend on the key parameter ε, which distinguishes between open-mindedness and narrow-mindedness of agents. Similar to the baseline model, high values of ε favour the emergence of consensus or of a small number of unrelated population subgroups (=components).^[12] Note that in equilibrium, the dynamics always partition the agent population into a certain number of network components, with all agents in a component sharing the same behaviour. Obviously, the difference between the behaviour in any two components is at least the threshold ε as interaction between agents from different components would still be possible otherwise. Further, each agent's in-group coincides with her respective network component: Agents within a component are fully connected but have no links to outside agents.

Findings

5.1

As explained before, agents need to agree on desirable business behaviour to allow for a local culture and cluster benefits to emerge. This consensus results from past interactions and the successful behaviour therein. The strength of any local culture thus relates to the spread of a specific behaviour in the population. Therefore one quantity measured in our simulations is the frequency of consensus among all agents, i.e. how often all agents exhibit the same behaviour in equilibrium. As the behaviour profile does not converge within a finite number of time steps, we call a behaviour profile x consensus profile if the maximum distance between two agents' respective behaviours is at most ε. In this case, all agents' behaviour will finally converge to the mean behaviour in the population.

5.2

Similarly, we can define a sufficient condition for non-convergence. First, there must be two components whose distance is at least ε, i.e. if there exist agents i and j with |x_i-x_j|≥ ε, there is no other agent whose behaviour is between x_i and x_j. Second, we require that there are no links between these ε-separated components. In this case, the respective limit behaviours for i and j even for large t cannot coincide. However, we should also take into account to what extent there is a shared behaviour among the agents in case of no consensus. We measure this by the size of the largest component of agents with identical behaviour. For example, a situation where 95% of the agents share the same behaviour is much closer to consensus than one where the population of agents splits into three equally sized components with different behaviour.

Figure 1a	Figure 1b
Figure 1c	Figure 1d
Figure 1e	Figure 1f
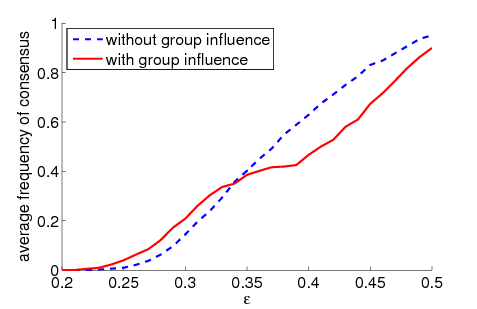
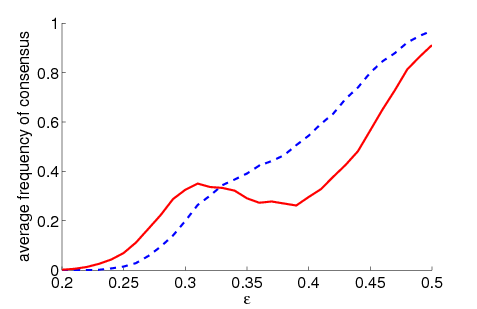
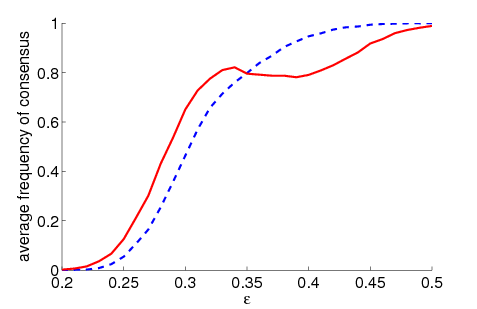
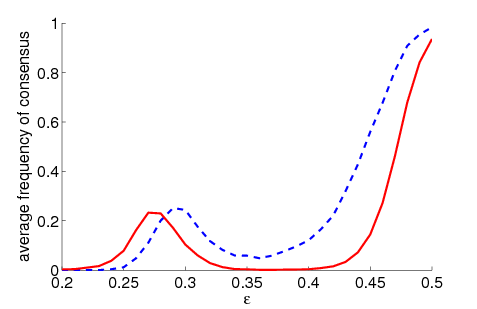
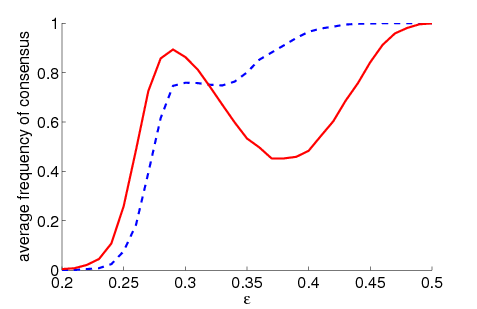
Figure 1. Average frequency of consensus dependent on ε for 5000 runs and different values of n and μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty. For narrow-minded agents (small ε), the group influence fosters consensus while for open-minded agents (high ε), the probability of identical behaviour is lower than in the baseline model

5.3

We analyse the local cultures model with respect to these quantities by means of computer simulations and compare the results to the baseline model that has no feedback between behaviour and network. The key parameter varied is ε, with high values characterising the open-mindedness of agents. The main result relates to the question whether the feedback mechanism between the agents' behaviour and their network structure (group influence) is beneficial in the sense that a common behaviour is fostered. Our simulations (see Figure 1 and 2) show that for more narrow-minded agents, i.e. small thresholds ε, the group influence results in both a higher average frequency of consensus and a larger maximum component size as compared to the baseline model. Hence, the mechanism introduced in our model increases the likelihood of consensus formation.

Figure 2a	Figure 2b
Figure 2c	Figure 2d
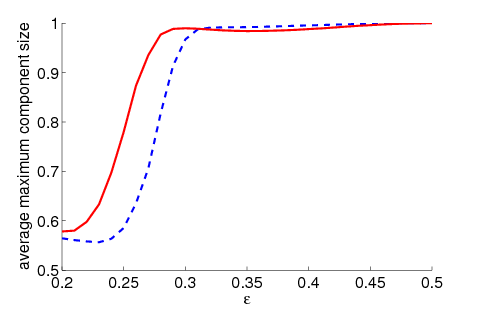
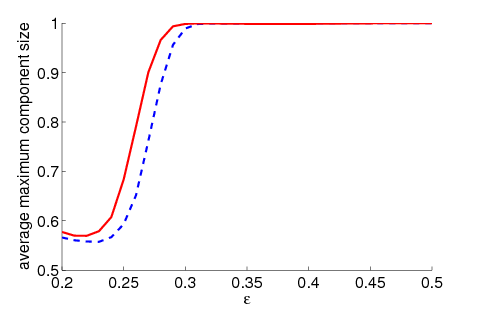
Figure 2e	Figure 2f
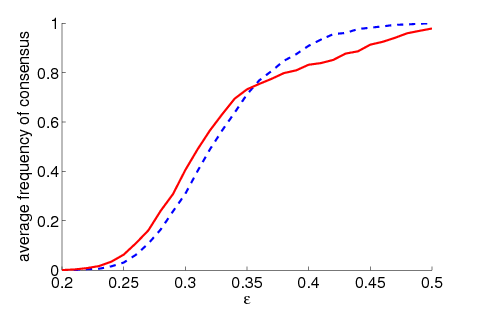
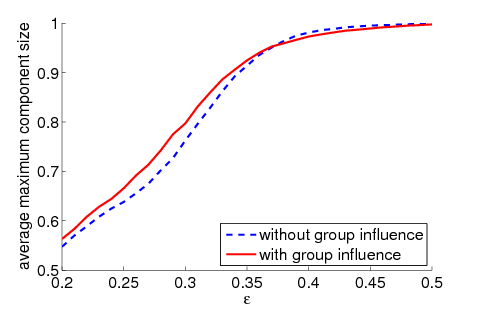
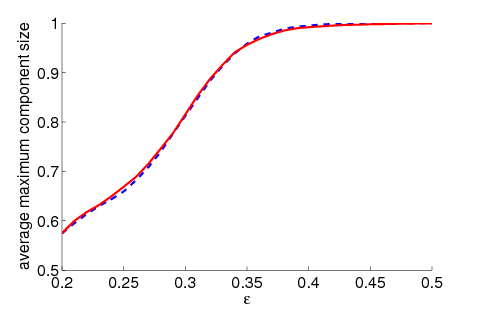
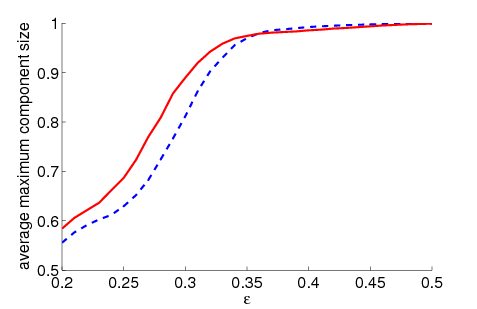
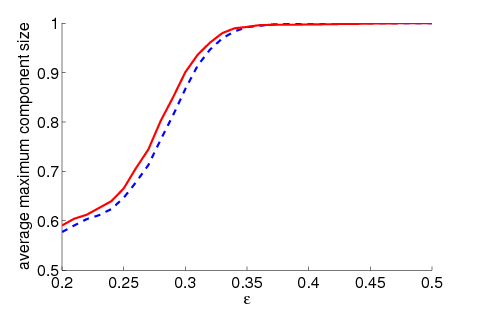
Figure 2. Average maximum relative component size dependent on ε for 5000 runs and different values of n and μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty. For narrow-minded agents (small ε), our model increases the average maximum component size compared to the baseline model without group influence. For open-minded agents (high ε), there is almost no difference between the models with respect to the average maximum component size

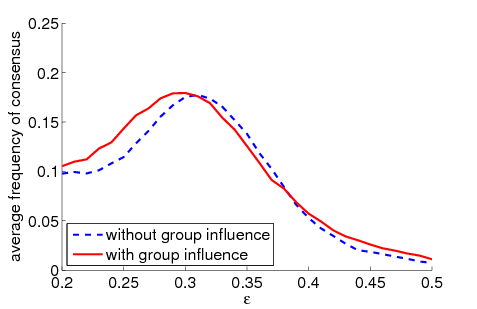
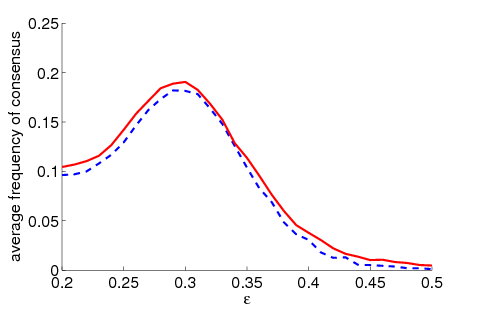
Figure 3a	Figure 3b
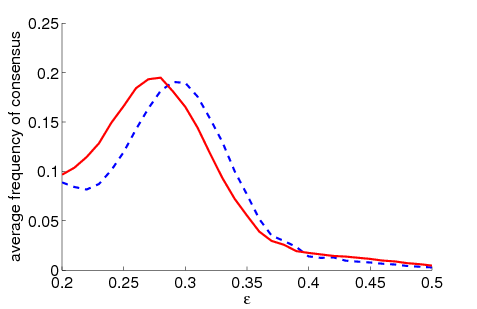
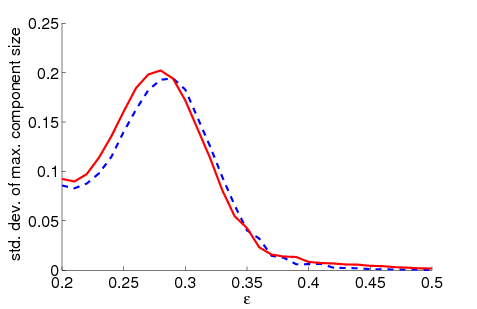
Figure 3c	Figure 3d
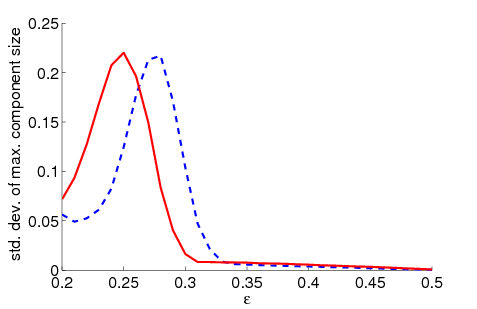
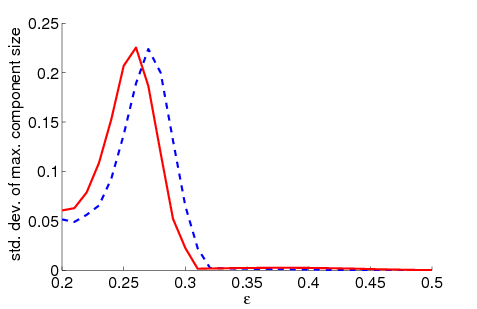
Figure 3e	Figure 3f
Figure 3. Standard deviation of the maximum relative group size dependent on ε for 5000 runs and different values of n and μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty

5.4

This result, interestingly and counter-intuitively, changes for larger thresholds and therefore more open-minded agents. Here, the feedback mechanism weakens the emergence of a local culture in general. Agents subject to group influence reach less consensus on average than in the baseline model. We note, however, that the mechanism's effect differs between the two measures: While the frequency of consensus is significantly decreased (Figure 1), the effect on the maximum component size is much smaller (Figure 2).

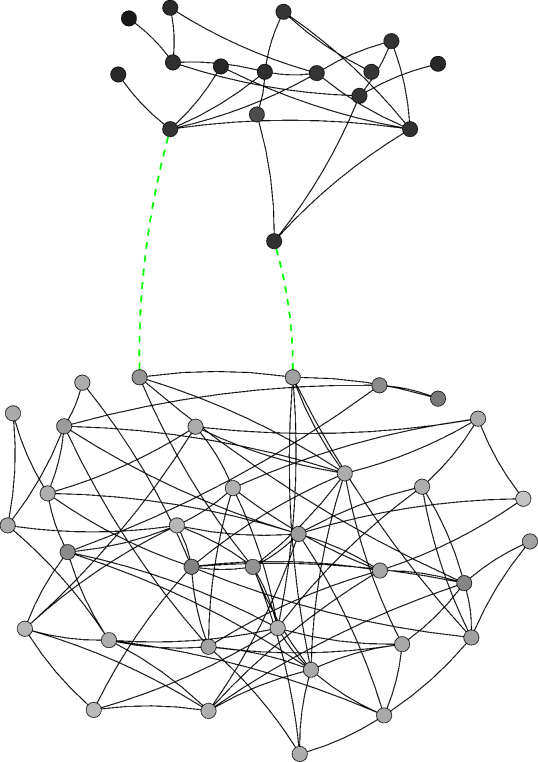
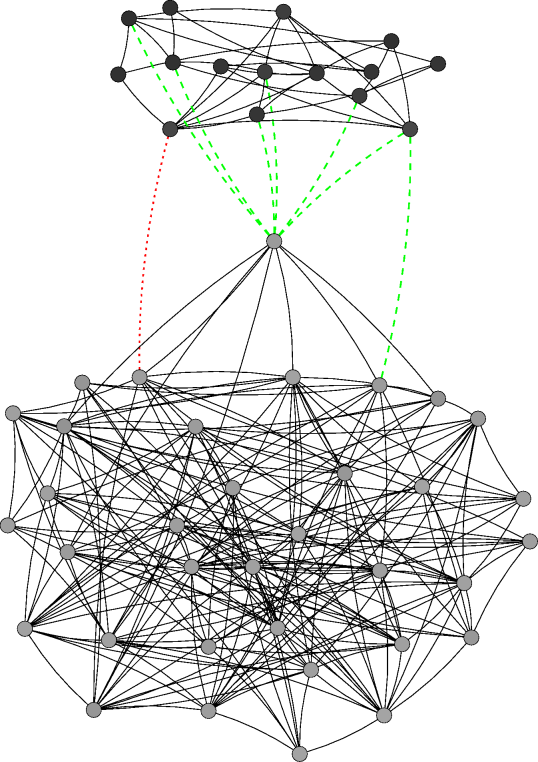
Figure 4a	Figure 4b
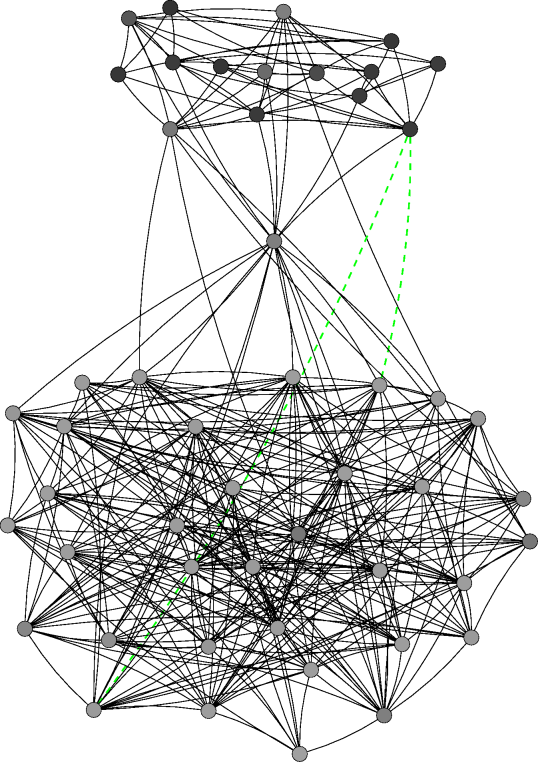
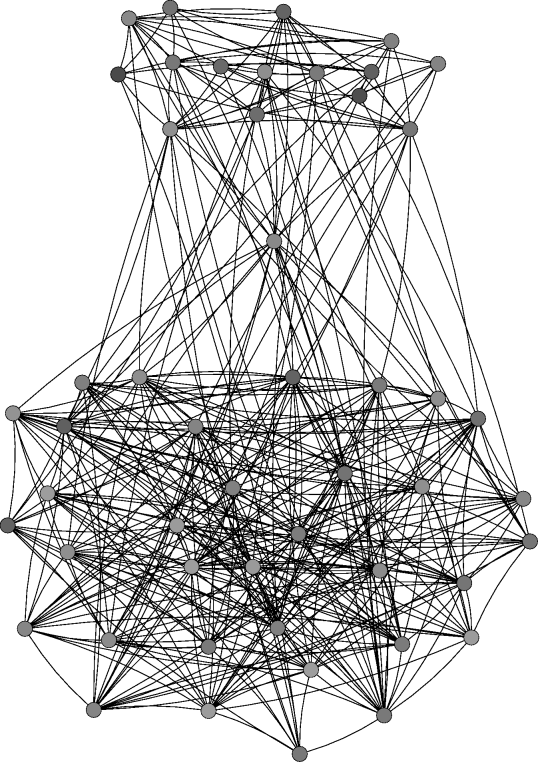
Figure 4c	Figure 4d
Figure 4. Network evolution for a simulation with 50 agents and ε=0.3 at different time steps. Note: The agents' initial behaviour is determined randomly according to a uniform distribution the initial network is empty. A node's colour indicates the respective agent's behaviour (white=0, black=1). A green dashed link denotes that the respective agents' difference in effective behaviour is below the threshold while their respective own behaviours differ more than ε. Thus, such a link persists in the local cultures model but would be deleted in the baseline model. A red dotted link indicates that the respective agents' difference in effective behaviour is above the threshold, i.e. the link would be deleted if the respective agents were chosen at that time step

5.5

To explain the influence of agents open-mindedness, we argue that the feedback mechanism in the local cultures model implies two opposed effects compared to the baseline model. On the one hand, agents with "extreme" initial behaviour (i.e. an initial behaviour close to zero or one) are less likely to interact with other agents and are therefore more likely to stay in that border area. The longer these agents remain in isolation (i.e. without interacting), the denser the network of other agents becomes, implying more averaging of behaviour in determining the effective behaviour of these networked agents. As more averaging leads to values closer to the mean, there are fewer and fewer agents within the interaction range of any isolated agent (as compared to the baseline model), and full consensus becomes more unlikely.

5.6

On the other hand, the feedback mechanism fosters consensus by increasing the coalescence of subpopulations with different behaviour, i.e. components within the network. To illustrate this, consider the simulation depicted in Figure 4.^[13] In Figure 4a, there are two nearly separated components, the upper, smaller one with a higher average behaviour, and the lower, larger one with a lower average behaviour. The two links that connect these components would not persist in the baseline model as the respective nodes' difference in terms of their own behaviour is above the threshold. However, as this is not the case for their effective behaviour, the involved agents can still interact in our model. Hence, the two agents from the upper component still influence agents in the lower component by increasing their effective behaviour (compared to their other neighbours whose behaviour is lower). For the same reason, the neighbours from the lower component decrease the two upper agents' effective behaviour. Thus, they could establish further connections to the lower component. Nevertheless, interaction with agents from the upper component would increase their behaviour and hence increase the distance to their neighbours from the lower component.^[14]

5.7

Therefore, whether the two components stay connected and finally evolve to a complete graph or become separated depends on which nodes are chosen in the near future, i.e. is a path dependent process. Any interaction between the different components increases the probability of their coalescence; any interaction within the same component decreases that probability. In our example, one agent can establish further connections to the lower component (Figure 4b) and in return enable her neighbours from different components to interact (Figure 4c). Very quickly, more and more agents from the different components interact, become more similar and finally make the components coalesce (Figure 4d). This effect of coalescing components is also apparent in a higher variance of the maximum component size for narrow-minded agents as compared to the baseline model (cf. Figure 3).

5.8

Which of these effects decides over the strength of a local culture depends on the threshold ε: For narrow-minded agents, the baseline model is generally more likely to obtain several components instead of consensus. Thus, in the local cultures model, the increased probability of the coalescence of components increases both the frequency of consensus and the maximum component size. For open-minded agents, this effect vanishes because of the greater ex-ante likelihood of consensus in the baseline model. In this situation, the effect of isolation of agents with extreme behaviour comes into play: While both models favour consensus in general, it is more likely for the local cultures model to find agents at the spectrum's borders being separated from the other agents because of the faster dynamics towards the centre. Therefore, the frequency of consensus is lower in this model. On the other hand there are only few agents separated from the majority, so the maximum component size is only slightly decreased by the feedback mechanism in the local cultures model. Hence, if we only consider this quantity to measure a local culture's magnitude, the feedback mechanism significantly strengthens a local culture for narrow-minded agents and only slightly weakens it for open-minded agents.

5.9

What is the effect of variations to the population size n and the convergence speed μ on our findings? To explain this we consider how both parameters affect the consensus frequency in our model and the baseline model. In both cases, an increase in the population size usually leads to a decreased consensus probability as it becomes more likely that a single agent with extreme initial behaviour is separated from the rest of the population. For open-minded agents, this effect is amplified by the faster dynamics towards the centre in the local cultures model. Thus, we observe that the reduction in frequency of consensus is greater than in the baseline model (cf. Figure 1).

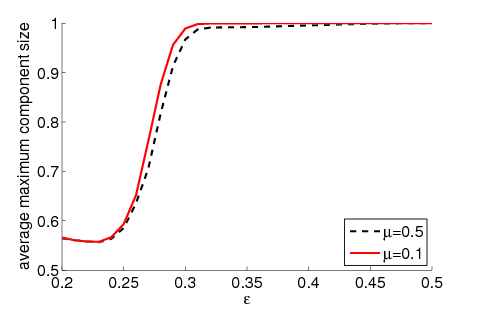
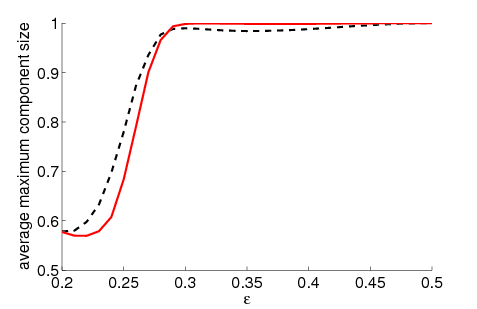
Figure 5a	Figure 5b
Figure 5. Average maximum relative component size dependent on ε for 5000 runs, 500 agents and different values of μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty. For the baseline model without group influence (5a), a decrease of the convergence speed μ leads to an increase of the maximum component size for all ε. This holds only for open-minded agents (high ε) in case of our model (5b).

5.10

With respect to the average maximum component size, an increase in the population size increases the advantage of the local cultures model compared to the baseline model for narrow-minded agents (cf. Figure 2). In this case, the increased number of agents leads to a higher probability for bridging links between two almost separated components. Hence, these components more often coalesce and thereby increase the difference between the maximum component size in our model and that in the baseline model as n grows. The increased distance of the variance peaks between both models (cf. Figure 3) also indicates this. If we decrease the convergence speed μ, we observe an increase in the consensus frequency for both models for all thresholds ε as the agents' behaviour moves slower towards the centre. With respect to the maximum component size, this only holds for the baseline model. Figure 5 shows that this quantity decreases for narrow-minded agents, i.e. if ε is small. The reason is that the coalescence of components becomes less likely for smaller values of μ as interaction with a bridge link between two almost separated components becomes less effective in this case.

Discussion

6.1

The present paper set out to study the emergence of local cultures. To do so, it focused on the first stage of the process where agents need to obtain consensus on acceptable business practice. Within a bounded-confidence model of opinion dynamics, we added a feedback mechanism between an agent's behaviour and the evolving agent network. The effect of this mechanism depends on the value of the interaction threshold ε. In comparison with the baseline model (Deffuant et al. 2000), our feedback increased the likelihood of consensus for narrow-minded agents (small ε) as the group effect may foster a coalescence of otherwise separated components. For open-minded agents (large ε), the likelihood of consensus decreased because the group effect worked to speed up convergence as compared to the baseline case. In some instances, this convergence was too fast for all agents to reach consensus. However, this constellation still had a substantial proportion of component agents finding consensus (the maximum component size was almost as large as in the baseline case). The fact that all component agents want to maintain their networks thus leads to behavioural constraints that may impede full consensus for very open-minded agents but increases it for narrow-minded ones. As local cultures can also emerge within a sub-population, the aforementioned results suggest that the desire to maintain interaction networks has a positive effect on the emergence of (full or partial) consensus, which would then form the basis of a local culture.

6.2

A next step in advancing the model would consist in a benchmark against data. Unfortunately, the key model parameters (especially open-mindedness of agents) are very difficult to operationalise and thereby measure. As a result, any data investigation would probably have to rely on qualitative, case-study evidence investigating how component agents choose to interact with each other and whether a concern for one's past partners does exist. Such findings would give an inclination of whether the mechanisms proxied in the model are actually at work. Beyond a data benchmark, the link between open-mindedness and group effects on consensus could be investigated experimentally. Participants could be surveyed on open-mindedness and would be allocated to two groups accordingly. The experiment could then study in how far the consensus dynamics differ between both groups.

6.3

A second avenue for expanding the present paper consists in model extensions. Two aspects spring to mind. First, one could investigate the effect of heterogeneity among agents regarding their open-mindedness (ε). Recent contributions (Lorenz 2008) suggest that heterogeneity plays a substantial role for the likelihood of consensus in the baseline model. Second, one could introduce non-empty initial networks (in-groups) to proxy that entrepreneurs in components often have an initial set of acquaintances from living in the area or studying in the same university. Given the contrasting effect of groups on consensus, it would be interesting to investigate in how far non-empty initial in-groups affect it. In a more general theoretic context, it would pay to apply this model to the emergence of norms and conventions in general. Given the more expansive body of research in this field, opportunities for benchmarking the model's results against other existing studies will probably arise. It would be particularly interesting to see whether our counterintuitive result on group-effects and consensus is applicable to other constellations.

Acknowledgements

The authors would like to thank Andreas Flache, Wander Jager and Jan Lorenz for fruitful discussions and comments on early versions of the paper. At a later stage, two anonymous referees provided helpful suggestions for improvement. Any remaining errors are the responsibility of the authors.

Notes

¹ Neatly summarised by HJ.U.Nieminen, CEO Nokia: "When an inventor in Silicon Valley opens his garage door to show off his latest idea, he has 50 per cent of the world market in front of him. When an inventor in Finland lifts his garage door, he faces 3 feet of snow." (quoted in van Tulder 1988, p. 169).

² Competitors experiment with different strategies under identical conditions. This allows for direct comparisons of performance and selection of best practice. In addition, firms tackling the same or related problems may exchange knowledge through various mechanisms (Allen 1983). Both aspects contribute to knowledge spillovers. Finally, many firms in a cluster increase the quality of the local labour pool by training activity and immigration of skilled people.

³ Investment research and training requires an understanding that allows firms to capitalise on it, i.e. no exploitation of others' efforts or hiring away of personnel trained elsewhere.

⁴ Candidate mechanisms are repeated games, reputation formation, signalling or punishment (Nowak 2006). To be effective, consensus about the behaviour that ought to be adopted is needed (e.g. cooperation). To some, this would already constitute a norm (Opp 2001). In addition to strong information requirements, game-theoretic approaches thus need a general co-operation 'norm' to identify defectors.

⁵ Stark et al 2008a, b have discussed a modification to the linear voter model, where agents become more reluctant to change their current opinion the longer they have it. It was shown that this deceleration of individual dynamics may, for certain growth rates of reluctance, even accelerate the formation of consensus at the system level. This counterintuitive result is partly due to agent heterogeneity, i.e. differences in their individual behaviour.

⁶ Deffuant et al. 2005 extend the mechanism to study innovation diffusion. For a survey of results in bounded confidence models see Lorenz 2007.

⁷ Fent et al 2007 have investigated the role of in- and out-group interaction (in a fixed network) for the emergence of social norms. Under certain conditions, convergence towards a single norm, coexistence of two opposing norms, and coexistence of a multitude of norms can be found. The key element was a local utility maximization, where agent i seeks to maximise similarities with her in-group, while minimising the disutilities from the out-group in her social network.

⁸ The greatest losses often result from diverging strategies (e.g. prisoner's dilemma).

⁹ As in Moscovici and Doise 1992, where opinions too far from the majority don't enter group discussion.

¹⁰ This treatment of group influence by averaging has a long tradition. Formal models of group decision-making (French 1956; Harary 1959; Hegselmann and Krause 2002; Lehrer 1975; Lehrer and Wagner 1981; Wagner 1978) account for group influence by weighted averages. Social impact theory (Latané 1981; Latané and Nowak 1997) also constructs group influence by averaging. Similar to social impact theory, our model features a decreasing marginal group influence with in-group size.

¹¹ Many models in sociology build upon a reciprocal link of behaviour and interaction. See Carley 1991; Coleman 1961; Coleman 1980; Ennett and Baumann 1994; Friedkin and Johnsen 1990; Marsden and Friedkin 1993 or Nowak et al. 1990 among others.

¹² For both models, this does not hold in general as the probability of consensus and the average maximum component size as a function of ε are not monotonically increasing (see Ben-Naim et al. 2003 for the baseline model).

¹³ A video of the simulation is available online. It uses the arf algorithm for dynamic network layout (Geipel 2007). For viewing the video, go to http://web.sg.ethz.ch/publications/local_cultures/web-cultures.html

¹⁴ This increase would have two reasons: first the increase of their own behaviour, second the decrease of their lower component's neighbours' influence on their effective behaviour as the share of lower component agents of the neighbourhood also decreases.

References

ALLEN, R.C. (1983). Collective invention. Journal of Economic Behavior & Organization 4(1), 1-24.

ASCH, S.E. (1956). Studies of independence and conformity: I, a minority of one against a unanimous majority. Psychological Monographs 70(9), 1-70.

AXELROD, R. (1986). An evolutionary approach to norms. The American Political Science Review 80(4), 1095-1111.

AXELROD, R. (1997). The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution 41, 203-226.

BEN-NAIM, E.; Redner, S.; Kaprivsky, P.L. (2003). Bifurcation and Patterns in Compromise Processes. Physica D 183, 190-204.

CARLEY, K. (1991). A Theory of Group Stability. American Sociological Review 56(3), 331-354.

COASE, R.H. (1937). The nature of the firm. Economica 4(16), 386-405.

COLEMAN, J.S. (1961). The adolescent society: the social life of the teenager and its impact on education. New York: Free Press.

COLEMAN, J.S. (1980). Friendship and the peer group in adolescence. In: J. Adelson (ed.), Handbook of adolescent psychology, New York: Wiley. pp. 408-431.

COLEMAN, J.S. (1990). Foundations of Social Theory. Cambridge MA: Harvard University Press.

DEFFUANT, G.; Huet, S.; Amblard, F. (2005). An individual-based model of innovation diffusion mixing social value and individual benefit. American Journal of Sociology 110(4).

DEFFUANT, G.; Neau, D.; Amblard, F.; Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems 3, 87-98.

DEGROOT, M.H. (1974). Reaching a Consensus. Journal of the American Statistical Association 69(345), 118-121.

DEMSETZ, H. (1967). Towards a theory of property rights. American Economic Review 57(2), 347-359.

ELLISON, G.; Glaeser, E. (1997). Geographic Concentration in U.S. Manufacturing Industries: A Dartboard Approach. Journal of Political Economy 105(5), 889-927.

ENNETT, S.T.; Baumann, K.E. (1994). The contribution of influence and selection to adolescent peer group homogeneity: The case of adolescent cigarette smoking. Journal of Personality and Social Psychology 67(4), 653-663.

FEHR, E.; Fischbacher, U. (2004). Third-party punishment and social norms. Evolution and Human Behaviour 25, 63-87.

FENT, T.; Groeber, P.; Schweitzer, F. (2007). Coexistence of Social Norms based on In- and Out-group Interactions. Advances of Complex Systems 10, 271-286 .

FRENCH, J. (1956). A formal theory of social power. Psychological Review 63, 181-194.

FRIEDKIN, N.; Johnsen, J. (1990). Social influence and opinions. Journal of Mathematical Sociology 15, 193-205.

GEIPEL, M. (2007). Self-Organization applied to Dynamic Network Layout. International Journal of Modern Physics C 18(10).

HARARY, F. (1959). A criterion for unanimity in French's theory of social power. In: D. Cartwright (ed.), Studies in Social Power, Ann Arbour: Institute for Social Research.

HEGSELMANN, R.; Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis, and simulation. Journal of Artificial Societies and Social Simulation 5(3).

HEIDUK, G.; Pohl, N. (2002). Silicon Valley's Innovative Milieu: A Cultural Mix of Entrprepreneurs or an Entrepreneurial Mix of Cultures?, Erkunde, 56(3), 241-252.

HOLLÄNDER, H. (1990). A Social Exchange Approach to Voluntary Cooperation. American Economic Review 80(December), 1157-1167.

HORNE, C. (2001). Sociological perspectives on the emergence of norms. In: M. Hechter; K. Opp (eds.), Social Norms, Russell Sage Foundation. pp. 3-34.

KANDEL, E.; Lazear, E.P. (1992). Peer Pressure and Partnership. Journal of Political Economy 100(4), 801-817.

KOFORD, K.J.; Miller, J.B. (1991). Social Norms and Economic Institutions. Ann Arbour, MI: University of Michigan Press.

LATANÉ, B. (1981). The psychology of social impact. American Psychologist 36, 343-356.

LATANÉ, B.; Nowak, A. (1997). Self-organizing social systems: Necessary and sufficient conditions for the emergence of clustering, consolidation and continuing diversity. In: G.A. Barnett; F.J. Boster (eds.), Progress in Communication Sciences: Advances in Persuasion, London: Ablex Publishing Corporation. pp. 43-74.

LEHRER, K. (1975). Social consensus and rational agnoiology. Synthese 31, 141-160.

LEHRER, K.; Wagner, C.G. (1981). Rational Consensus in Science and Society. Dordrecht: D. Reidl Publishing Co.

LORENZ, J. (2006). Consensus Strikes Back in the Hegselmann-Krause Model of Continuous Opinion Dynamics under Bounded Confidence. Journal of Artificial Societies and Social Simulation 9(1).

LORENZ, J. (2007). Continuous Opinion Dynamics Under Bounded Confidence: A Survey. International Journal of Modern Physics C 18(12), 1819-1838.

LORENZ, J. (2008). Heterogeneous bounds of confidence: Meet, Discuss and Find Consensus! http://arxiv.org/abs/0801.1399v1

MACY, M.W.; Skvoretz, J. (1998). The Evolution of trust and cooperation between strangers: A computational model. American Sociological Review 63(5), 638-660.

MARSDEN, P.; Friedkin, N. (1993). Network studies of social influence. Sociological Methods and Research 22, 127-151.

MASKELL, P. (2001). Towards a Knowledge-based Theory of the Geographical Cluster. Industrial and Corporate Change 10(4), 921-943.

MCPHERSON, M.; Smith-Lovin, L.; Cook, J.M. (2001). Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology 27, 415-444.

MOSCOVICI, S.; Doise, W. (1992). Dissension et consensus: Une théorie générale des décisions collectives. Paris: Presses Universitaires de France.

NOWAK, A.; Jacek, S.; Latané, B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychological Review 97, 362-376.

NOWAK, M.A. (2006). Five rules for the evolution of cooperation. Science 314(5805), 1560-1563.

OPP, K. (1982). The evolutionary emergence of norms. British Journal of Social Psychology 21, 139-149.

OPP, K. (2001). How Do Social Norms Emerge? An Outline of a Theory. Mind and Society 2, 101-128.

PORTER, M.E. (1990). The Competitive Advantage of Nations. London: Macmillan.

PUJOL, J.; Delgado, J.; Sangüesa, R.; Flache, A. (2005). The Role of Clustering on the Emergence of Efficient Social Conventions. In: Proceedings of the 19th International Joint Conference on Artificial Intelligence IJCAI-05. Edinburgh, Scotland, pp. 965-970.

PYKE, F.; Beccattini, G.; Sengenberger, W. (1990). Industrial districts and inter-firm co-operation in Italy. Geneva: International Institute for Labour Studies.

SAXENIAN, A. (1994). Regional Advantage: Culture and Competition in Silicon Valley and Route 128. Cambridge, Mass.: Harvard University Press.

SCHWEITZER, F. (2007). Collective Decisions in Multi-Agent Systems. In: S. Takahashi; D. Sallach; J. Rouchier (eds.), Advancing Social Simulation: The First World Congress, Tokyo: Springer. pp. 7-12.

SCHWEITZER, F.; Behera, L. (2009). Nonlinear voter models: The transition from invasion to coexistence. European Physical Journal B 67.

SHERIF, M. (1973). The Psychology of Social Norms. New York: Octagon Books.

SHOHAM, Y.; Tennenholtz, M. (1992). Emergent Conventions in Multi-Agent Systems: Initial Experimental Results and Observations. In: Proceedings of Knowledge Representation and Reasoning. pp. 225-231.

SMITH, A. (2003). The Wealth of Nations (1776). Bantam Classic, New York: Bantam Dell.

STARK, H.-U.; Tessone, C.J.; Schweitzer, F. (2008a). Decelerating microdynamics can accelerate macrodynamics in the voter model. Physical Review Letters 101(1), 018701(4).

STARK, H.-U.; Tessone, C.J.; Schweitzer, F. (2008b). Slower is Faster: Fostering Consensus Formation by Heterogeneous Inertia. Advances in Complex Systems 11(4).

STRANG, D.; Soule, S.A. (1998). Diffusion in organizations and social movements: From hybrid corn to poison pills. Annual Review of Sociology 24, 265-290.

SUGDEN, R. (1989). Spontaneous Order. The Journal of Economic Perspectives 3(4), 85-97.

ULLMANN-MARGALIT, E. (1977). The Emergence of Norms. Clarendon Press.

VAN Tulder, R. (1988). Small European countries in the International Telecommunications Struggle. In: C. Freeman; B.-A. Lundvall (eds.), Small Countries Facing the Technological Revolution, London, Pinter Publishers, pp. 169-183.

VOSS, T. (2001). Game theoretical perspectives on the emergence of social norms. In: M. Hechter; K.-D. Opp (eds.), Social Norms, New York: Russell Sage Foundation. pp. 105-136.

WAGNER, C.G. (1978). Consensus through respect: A model of rational group decision-making. Philosophical Studies 34, 335-349.

WEBER, M. (1999). Essays in economic sociology. Princeton NJ: Princeton University Press.

WILLIAMSON, O.E. (1975). Markets and Hierarchies - Analysis and Anti-Trust Implications. New York: Free Press.

ZIEGLER, R. (2007). The Kula Ring of Bronislaw Malinowski. Bayerische Akademie der Wissenschaften.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2009]