Abstract

Auction mechanisms have attracted a great deal of interest and have been used in diverse e-marketplaces. In particular, combinatorial auctions have the potential to play an important role in electronic transactions. Therefore, diverse combinatorial auction market types have been proposed to satisfy market needs. These combinatorial auction types have diverse market characteristics, which require an effective market design approach. This study proposes a comprehensive and systematic market design methodology for combinatorial auctions based on three phases: market architecture design, auction rule design, and winner determination design. A market architecture design is for designing market architecture types by Backward Chain Reasoning. Auction rules design is to design transaction rules for auctions. The specific auction process type is identified by the Backward Chain Reasoning process. Winner determination design is about determining the decision model for selecting optimal bids and auctioneers. Optimization models are identified by Forward Chain Reasoning. Also, we propose an agent based combinatorial auction market design system using Backward and Forward Chain Reasoning. Then we illustrate a design process for the general n-bilateral combinatorial auction market. This study serves as a guideline for practical implementation of combinatorial auction markets design.

Keywords:

Combinatorial Auction, Market Design Methodology, Market Architecture Design, Auction Rule Design, Winner Determination Design, Agent-Based System

Introduction

1.1

In the explosive growth of electronic commerce, electronic auctions have received a great deal of interest in recent years. Especially, auctions have become one of the most highly-promoted forms for resource and task allocation in B2B trading. More recently, the popularity of auctions in B2B marketplaces has yielded diverse auction market types.

1.2

Traditional auctions that trade single items take several forms including the English auction, the Dutch auction, the First Price, and the Vickrey's Second Price auction (Wolfstetter 1996). In a traditional auction format where the items are auctioned separately, a bidder needs to estimate which other items he/she will receive in other auctions. This requires an intractable look ahead in a series of auctions. Even after looking ahead, residual uncertainty exists due to incomplete information on the other participants' bids.

1.3

The combinatorial auction can be used to overcome these deficiencies stemming from the problems of uncertainties (Abrache et al. 2004; Holzman et al. 2004;Sandholm and Suri 2003; Wurman et al. 1998). The combinatorial auction, also called the multi-item auction or bundle auction, refers to an auction involving multiple items at the same time, as opposed to auctions for single items. Compared to single item auction types, it keeps bidders from the risk of receiving only parts of combinations that they desire. Combinatorial auctions have received much attention because they give more expressive power to bidders through complementary or substitute bids.

1.4

There have been many combinatorial auction studies in Operations Research focused on optimization models (Park and Rothkopf 2005; Rothkopf et al. 1998), efficient algorithms for winner determination (Leyton-Brown et al. 2000; Nisan 2000;Sandholm 2000;Zurel and Nisan 2001), and in economics research mainly based on the proof of the existence of equilibrium status and economic efficiency (McAfee and McMillan 1996; Xia et al. 2005). Also, there have been many studies on pricing issues including valuation (Elmaghraby and Keskinocak 2003), bundling strategy (Song and Regan 2002), or pricing strategy (Ba et al. 2001; Bikhchandani and Ostroy 2002; Parkes 2001). Valuation covers issues like the valuation of combined items that are auctioned off. Bundling strategy is about how to select combinatorial items for bidding. And pricing strategy focuses on what is the best bidding price for combinatorial items or on how the bidding strategy should be changed if the auction is proceeded through multi-rounds.

1.5

Meanwhile, given the diversities of combinatorial auction mechanisms, it is timely to discuss the issues of mechanism design because the design of new market mechanisms is an emerging field (Bichler et al. 2002; Lim et al. 2005). Although there have been several studies covering some factors or partial dimensions of combinatorial auction design, they don't suggest systematic design guidelines for the combinatorial auction. It means that it is difficult to suggest market design methodology for supporting a comprehensive range of combinatorial auction models and we need a scientific market design approach.

1.6

Thus, we propose an agent-based combinatorial auction market design methodology with a systematic framework on market architecture, auction rules, and winner determination. A market architecture design is for designing market architecture types based on Backward Chain Reasoning. Auction rules design is to design transaction rules for auctions. The specific auction process type is identified by Backward Chain Reasoning. Winner determination design is about determining the decision model for selecting optimal bids and auctioneers. Optimization models are identified by Forward Chain Reasoning. This approach gives systemic guidelines for the combinatorial auction market design through in-depth analysis on the relationship among design factors.

1.7

This research is organized as follows. In Section 2, we review the previous literature on combinatorial auction and market design related areas. In Section 3, we propose a combinatorial auction design model composed of three phases - market architecture design, auction rules design, and winner determination design. In Section 4, we propose a system architecture for the combinatorial auction market design agent (CAMDA) and illustrate a design process of the simultaneous general n-bilateral combinatorial auction market. Finally, the contributions of this paper and future research issues are discussed.

A review of related research

2.1

The combinatorial auction is used to describe any auction mechanism that simultaneously sells multiple items, and allows all-or-nothing bids on combinations of these items (Pekec and Rothkopf 2003). Generally, it is necessary to solve combinatorial optimization problems, such as set packing and partitioning problems (Bichler et al. 2006).

2.2

There are several applications of combinatorial auctions. Examples in real-world situations are the FCC (Federal Communications Commission) spectrum auction (McAfee and McMillan 1996), auctions for airport landing slots (Sandholm 2000), railroad segments (Brewer and Plott 1996), shipping (Gomber et al. 1999), and scheduling (Wellman et al. 2001; Kaihara et al. 2008). de Vries and Vohra (de Vries and Vohra 2003) surveyed diverse combinatorial auction applications including the logistics service and the eProcurement area. Combinatorial auction models are becoming popular among the next generation of B2B marketplaces operated by combinatorial auction specialists such as Net Exchange ( www.nex.com), CombineNet ( www.combine.net) and Trade Extensions ( www.tradeextensions.com). Na et al. (2005) describe the use of combinatorial auctions by Home Depot and Sears Logistics Services (SLS) for procuring logistics services.

2.3

As combinatorial auction mechanisms have diversified, several studies have covered combinatorial auction design issues. Bichler et al. (2002) suggested several design factors for resource allocation problems in the combinatorial auction market. In this research, the primary criteria for characterizing the allocation problems are the number of participants, and the types of traded goods. The allocation problems change in different settings in terms of the number of participants: bilateral allocation problems, n-bilateral allocation problems (e.g., single-sided and double auctions), and multilateral allocation problems. Also, the auction formats can be categorized by several different dimensions of the goods in negotiation: the number of different items in the negotiation (e.g., a single item or multiple items), the negotiable qualitative attributes (e.g., a single item or multiple attributes), and the quantity for each item (e.g., a single item or multiple units). Abrache et al. (2004) and Mu'alem and Nisan (2008) discussed several design issues that are encountered in the design of combinatorial auctions. These issues are related to the formulation of the winner determination problem, the expression of combined bids, and the design of progressive combinatorial auctions. Pekec and Rothkopf (2003) described the single-round, first-price sealed bidding, Vickrey-Clarke-Groves (VCG) mechanisms, uniform and market-clearing price auctions, and iterative combinatorial auctions as standard combinatorial auction types. In a similar study, Sandholm et al. (2002) proposed a wider range of combinatorial market designs: combinatorial auctions, combinatorial reverse auctions, and combinatorial exchanges, with one or multiple units of each item, with and without free disposal. Porter et al. (2003) described several combinatorial auction designs such as continuous auctions, multi-round auctions, and hybrid auctions that combine continuous bidding and multi-round auctions. Vinyals et al. (2008) suggested a combinatorial algorithm to generate artificial data that is representative of the sort of scenarios a winner determination algorithm is likely to encounter. Bichler et al. (2009) compared different iterative combinatorial auction formats, and then designed and analyzed new auction rules for auctions with pseudo-dual linear prices.

2.4

On the other hand, studies on optimized allocation reflecting the strategy of the seller or buyer have been proposed. The optimal allocation problem in combinatorial auctions is commonly formalized as an integer programming (IP) problem (Xia et al. 2005). Given a set of bids on subsets of the items in a combinatorial auction, the objective of the auctioneer is to assign items to the bidders such that the auction objective is maximized or minimized according to the characteristics of the objective. In case of optimization problems underlying the combinatorial auction, several studies present the constraint factors that impact optimization model formulation. Bichler et al. (2006) proposed the allocation constraints such as the maximum or minimum number of winning sellers, and the maximum or minimum amount procured from each seller for the reverse combinatorial auction. In addition, Giovannucci et al. (2004) suggested the constraint factors such as the maximum or minimum number of winning sellers, supply capacity, maximum or minimum supply volume, maximum or minimum demand volume, and reserve price. Also, he (Giovannucci et al. 2008) proposed a new integer program for mixed multi-unit combinatorial auctions that simplifies the winner determination problem by taking advantage of the topological characteristics.

2.5

Abrache et al. (2004) proposed the bidding operator, which is a two-level representation of a combined bid. At the inner level, bidding operators impose conditions on the executed proportions of packages of atomic single-item bids. The inner-level bidding operators include the composition operators such as the proportion ordering operator, the equal operator, the SIMPLEX operator, the selection operators such as the maximum or minimum number of atomic bids, and the hybrid operators that combine functions of the selection operator and composition operators. In contrast, the outer-level bidding operators include logical operators AND, OR, and XOR. Similarly, Nisan (2000) introduced several logical bidding operators for the combinatorial auction: OR bids, XOR bids, OR-of-XOR bids, and so on.

2.6

Although several studies have proposed the design issues of the combinatorial auction market and covered a few design factors or partial dimensions of combinatorial auction design, these analyzed parts of the entire characteristics that make up combinatorial auction markets. This requires comprehensive and systematic approaches for designing the combinatorial auction markets.

Combinatorial auction design model

3.1

In the combinatorial auction market, there are five elements as depicted in Figure 1: marketplace, participants, auction items, auction rules, and winner determination. The first two elements determine the architecture of the auction market. The auction rules specify rules for trading. The auction items mean products or services for transaction. The last element, winner determination, is related to the selection of the most competitive partners, which includes bid selection and auctioneer selection. These lead to an approach involving the three-phased combinatorial auction market design: market architecture design, auction rule design, and winner determination design. This framework enables market owners to design more effective combinatorial auction markets.

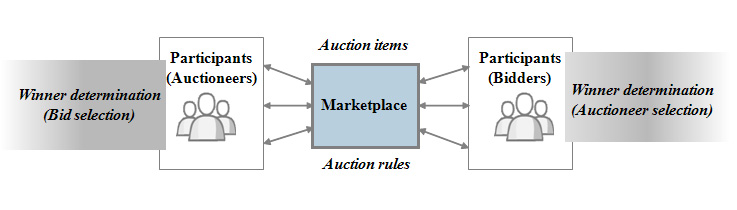
Figure 1. Five elements of the combinatorial auction market

3.2

Especially, winner determination is necessary for awarding and acknowledging. Awarding is the process of bid selection and acknowledging is the process of auctioneer selection. In a general or reverse combinatorial auction, winner determination means only bid selection. However when the number of auctioneers is more than one, namely in case of a general or reverse n-bilateral combinatorial auction, an auctioneer selection process is necessary.

3.3

Figure 2 describes the combinatorial auction market design process with this three-phased framework. To design an auction market, a market architecture and auction rules should be specified. According to the auction rules, the auction process proceeds step by step. Another important thing in designing an auction market is winner determination for bid selection and auctioneer selection. A specific combinatorial auction market model is determined through these three market design phases.

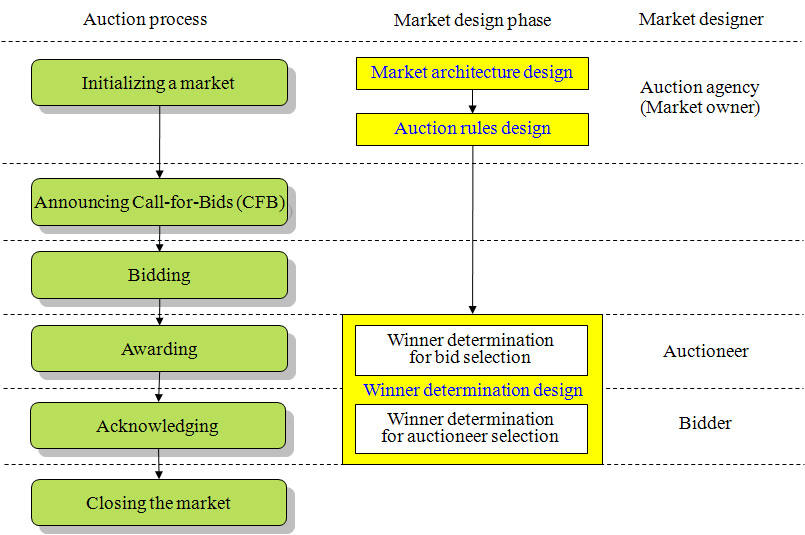
Figure 2. The combinatorial auction market design process with the three-phased framework

3.4

In the market architecture design phase, the auctioneer or intermediary designs the logical market architecture and opens the combinatorial auction market. Generally, an intermediary is not necessary in the e-marketplace of the seller-side or buyer-side auction. On the other hand, in the auction agency's e-marketplace, the roles of the auctioneer and intermediary are different. The auction agency plays the role of the intermediary. In the auction rule design phase, bidding, bid selection, and auction stopping rules are defined. These rules that govern the activities of market participants are determined by the auctioneer or intermediary. After the above two design phases, the buyers and sellers make their decision strategies for the winner determination. In the winner determination design phase, the strategies for bidding, bid selection, and auctioneer selection are determined by auctioneers or bidders. The bidding strategy of the bidders is composed of bids and bid requirements for the bids. The bid selection strategies and auctioneer selection strategies are composed of a single objective and multiple constraints.

Market architecture design

3.5

In the market architecture design phase, a specific market architecture type is defined. The factors that determine the market architecture are marketplace, cardinality of participants, and role of participants.

3.6

The marketplace is an e-marketplace where a real transaction among participants occurs. There are the seller's e-marketplace, auction agency's e-marketplace, and buyer's e-marketplace. The seller's e-marketplace is the most common type among B2B marketplaces. The auction agency's e-marketplace is usually operated by the auction agency who is an intermediary. The buyer's e-marketplace using the auction mechanism is generally a reverse auction market.

3.7

The cardinality of participants means the numeric relationship between sellers and buyers. The sellers and buyers meet in the marketplace with three types of numeric relationship: one seller-to-many buyers, many sellers-to-one buyer, many sellers-to-many buyers. In the seller's e-marketplace, in general, one seller participates as the auctioneer. In the buyer's e-marketplace, on the contrary, the buyer participates as the auctioneer. In case of the auction agency's e-marketplace, many sellers and many buyers participate in the auction process.

3.8

The roles of participants are determined by the relationships between market participants. There are three alternatives for the roles of participants: seller (auctioneer) vs. buyer (bidder), seller (bidder) vs. buyer (auctioneer), and seller (bidder) vs. buyer (bidder). Among the roles of participants, seller (auctioneer) vs. buyer (bidder) is the general combinatorial auction, and seller (bidder) vs. buyer (auctioneer) means the reverse combinatorial auction. The seller (bidder) vs. buyer (bidder) role means the combinatorial exchange where sellers and buyers participate as bidders at the same time in the e-marketplace of the auction agency that plays the role of intermediary. Figure 3 depicts the AND/OR graph for identifying market architecture types. A market architecture type can be identified by Backward Chain Reasoning (Luger and Stubblefield 1993).

3.9

The alternatives of three market architecture design factors can logically make 27 combinations, which is the result from 3 (marketplace) × 3 (cardinality of participants) × 3 (role of participants). Through the analysis, however, we define seven market architecture types with reasonable relationships as shown in Figure 3.

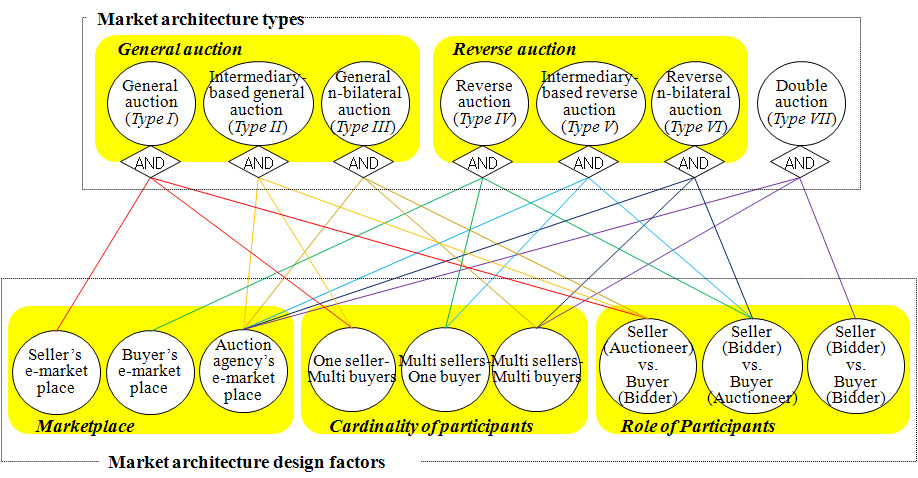
Figure 3. AND/OR graph for identifying market architecture types

3.10

Market Architecture Type I is a general combinatorial auction market operated in the seller's e-marketplace. In this architecture, the buyers (bidders) visit the seller's e-marketplace. Based on the bids submitted by buyers, each seller (auctioneer) selects optimal bids. FCC spectrum allocation (McAfee and McMillan 1996) and airport landing slot allocation (Rassenti et al. 1982) are included in this market architecture type. Market Architecture Type II is basically the same as Type I, but the main difference is that the auction is processed via the auction agency. The sales problem of TV advertising airtime (Jones and Koehler 2002) can be classified into Type II. Type III is a general n-bilateral combinatorial auction, which is a newly-proposed market type in our research. In the general n-bilateral combinatorial auction, operated by the intermediary, multi-sellers participate as auctioneers and multi-buyers as bidders. Market Architecture Type IV is a typical reverse combinatorial auction in the buyer's e-marketplace. Transportation service procurement (Hoesel and Müller 2001) are classified into this market architecture type. Market architecture Type V is a reverse combinatorial auction opened in the auction agency's e-marketplace. Transportation procurement (Gomber et al. 1999) and commodities procurement (Sandholm 2000) are examples of this type. Market Architecture Type VI, also newly-suggested in our study, is a buyers' driven reverse n-bilateral combinatorial auction, in which multi-buyers participate as auctioneers and multi-sellers as bidders. Market Architecture Type VII is a typical combinatorial exchange (Fan et al. 1999;Sandholm 2000;Sandholm et al. 2002) where a combinatorial double auction is done by matching sellers and buyers so as to maximize market surplus. Multi-sellers and multi-buyers participate in the combinatorial exchange as bidders. They are allowed both to buy and to sell items simultaneously, or just to buy, or just to sell (Sandholm et al. 2002).

Auction rule design

3.11

In the auction rule design phase, the rules for bidding, bid selection point, and the closing condition for the entire process are defined. Auction rule design factors and their relationships are depicted in Figure 4. The factors can be classified into base factors and dependent factors. The base factors are independent factors, while the dependent factors are dependent on the base factors or upper dependent factors. The base factors include bidding type, bidding rounds, and bid requirements. Max. total bids per bidder, bid selection point, Max. bidding rounds per bidder, and closing condition are dependent on the bidding type or bidding rounds. We call them the first dependent factors because they are directly dependent on the base factors. On the other hand Max. bids in each round per bidder is the second dependent factor. This is dependent on the Max. total bids per bidder - the first dependent factors, and bidding type - the base factor.

3.12

In order to bid, participants must be concerned with bidding type, bidding rounds, Max. bidding rounds per bidder, Max. total bids per bidder, Max. bids in each round per bidder, and bid requirements. The alternatives for bidding type are simultaneous or continuous bids. A Simultaneous bid means a simultaneous sealed bid. A continuous bid means a continuous open cry or a continuous sealed bid. In the continuous bid, each bidder can submit a bid at any point within the specified time. New bids can be tendered in real time and can either be placed on a standby list to be combined with others, or used immediately to directly replace tentatively winning bids.

3.13

The bidding rounds, Max. bidding rounds per bidder, Max. total bids per bidder, and Max. bids in each round per bidder are determined according to the specified number of rounds or bids. In particular, iterative auctions occur when bidding rounds are two or more. Sealed bids are submitted in each round. Integer programming (IP) is used to find the highest valued combination of winning bids at the end of each round. The winners are posted and a new round is started. New bids can be submitted and the IP is run again to see if there is a new solution. Since the Internet enables enhanced communications capabilities, iterative auctions can be effectively implemented. The iterative auction over multiple rounds, generally, is coordinated by the intermediary. Iterative auctions are attractive because bidders can learn about their rivals' valuation through the bidding process, which could help them adjust their own bids. Also, the iterative auction provides enough opportunities for the participants to correct any bidding or trading strategy they might submit in earlier rounds.

3.14

The bid requirements define the permittable bid selection operators that are submitted by each bidder. Namely, bid requirements of each bidder can be expressed using bid selection operators such as AND, OR, XOR, and IF-THEN. AND means all bids in a bid set should be executed. OR means at least one bid in a bid set should be executed. XOR means just one bid in a bid set should be executed. This allows the bidders to express general preferences that are both complementary and substitutable, namely the bidder can express any bid set. IF-THEN means one subset of a bid set should be executed when the other subset of the bid set is executed. As more concise representation, there are composite operators such as OR-of-XOR, by which XOR disjuncts can be combined with the non-exclusive OR to represent independence. In Figure 4, b_ij means the jth unit bid of bidder i and it is composed of items, quantity and unit bid price. B_i means a set of all unit bids by bidder i.

3.15

The bid selection point is about the timing of bid selection. The alternatives of bid selection point are round or bid, which means that bid selection occurs once per round or whenever a new bid is entered.

3.16

Closing condition specifies the conditions for the closing of the auction. For the closing conditions, there are four alternatives; when there are no bids within a round, a predetermined number of rounds, and a predetermined auctioneer's goal. The predetermined auctioneer's goal can be applied to the general or reverse combinatorial auction because it can be applied when there is only one seller or buyer.

3.17

The alternatives of auction rule design factors can make 48 combinations by 2 (bidding type) × 2 (bid selection point) × 3 (closing condition) × 4 (bid requirements). But we define 36 reasonable alternatives by 3 (combinations of the bidding type and bid selection point) × 3 (closing condition) × 4 (bid requirements) as shown in Figure 4.

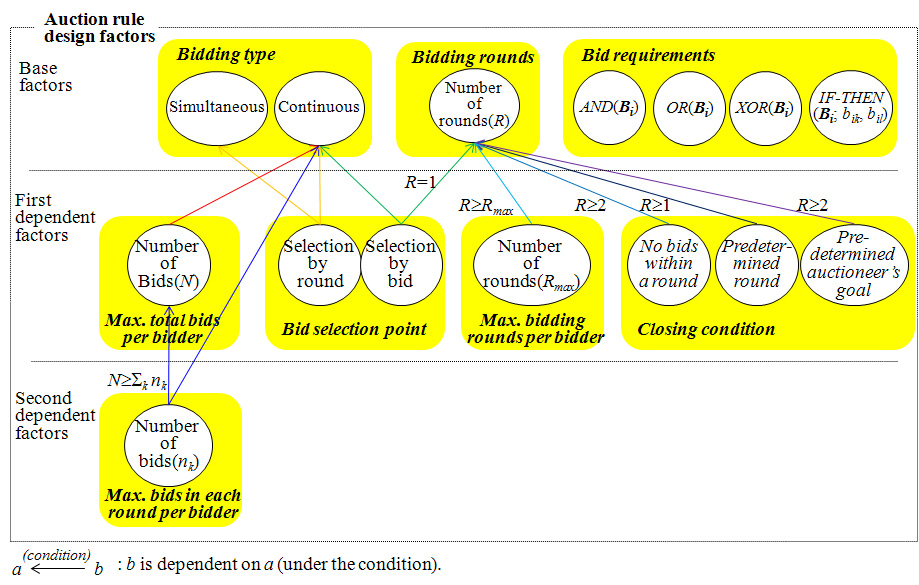
Figure 4. Auction rule design factors

3.18

Bidding type and bid selection point in the auction rule design factors and cardinality of participants in the market architecture design factor affect the auction process. The alternatives of participant cardinality, bidding type, and bid selection point can logically make 12 combinations, which are the result from 3 (participant cardinality) × 2 (bidding type) × 2 (bid selection point). Through the analysis, however, we define three auction process types with a reasonable relationship as shown in Figure 5. Figure 5 depicts the AND/OR graph for identifying auction process types. An auction process type can be identified by Backward Chain Reasoning (Luger and Stubblefield 1993).

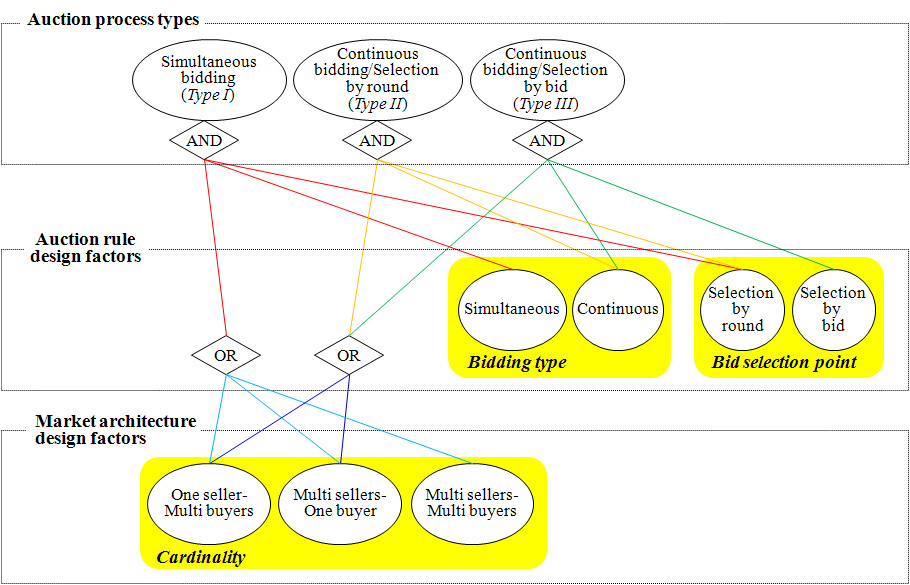
Figure 5. AND/OR graph for identifying auction processes

3.20

An illustration of each basic process type is depicted in Figure 6. Process Type I in Figure 6 (a) is the simultaneous auction during just one round or iterative multiple rounds. Bids are submitted simultaneously in each round, and optimal bids are selected in each round. In Process Type II, the bidders submit open or sealed bids continuously within one round, and the optimal bids are selected at the end of the round. In case of Process Type III, the overall process is the same as Process Type II except that optimal bids are selected whenever a new bid is submitted within the round. On the other hand, the number of auctioneers who participate in an auction can be one or multiple. Thus, the auctioneer selection process is necessary when there is more than one auctioneer.

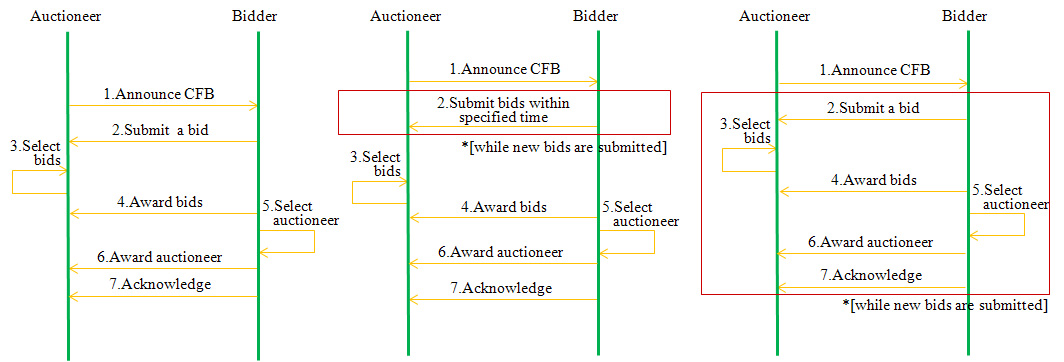
(a) Simultaneous bidding (Process type I)	(b) Continuous bidding/selection by round (Process type II)	(c) Continuous bidding/selection by bid (Process type III)
Figure 6. Combinatorial auction process types

Winner determination design

Bidding strategy

3.21

In the winner determination design phase, the bidding, bid selection, and auctioneer selection strategy are defined. As the first process for the combinatorial auction, when the call for bids is announced in the bidding stage, the bidders specify their bidding strategies. The bidding strategy is to define the bid requirements. The bid requirements, based on an endogenous bidding strategy, are composed of bids on items, quantity, and unit bid price, and bid selection operators such as AND, OR, XOR and IF-THEN etc. The equation below depicts the bid requirements of bidder i.

Bid Requirementsi= (AND(Bi) |OR(Bi) |XOR(Bi) | IF-THEN(Bi; bik, bil)),

where bij = (items, quantity, unit bid price).

Bid selection

3.22

Each auctioneer sets up a bid selection strategy as the second process. The purpose of bid selection strategy is to obtain the best bids from the bidders.

3.23

The bid selection strategy is composed of endogenous and exogenous factors as presented in Figure 7. The operator NOR/OR means OR condition of NOR and OR. That is, it is true if all components are not selected, or more than one is selected. The endogenous factors are composed of a single objective and multiple constraints. The objective is determined by the auctioneer's trade objective. Therefore we call it an endogenous objective. The possible objectives of the auctioneers may be maximizing total sales, profit, or market surplus. Maximizing total sales or profit is possible when one or more sellers are auctioneers. Maximizing market surplus is generally applied to a combinatorial exchange.

3.24

The constraints are classified into two categories. One is exogenous constraints by the auctioneer's winner determination and the other is exogenous constraints by the bid requirements from the bidders. The allocation, price, and resource constraints are endogenous constraints derived from the endogenous factors. The maximum or minimum number of winning bidders, the maximum or minimum number of accepted bids, and the maximum or minimum allocation volume per bidder comprise the allocation constraints. The auctioneers may want to restrict the number of bidders for each item, either for security or strategic reasons. The constraints on the maximum or minimum number of accepted bids and the maximum or minimum allocation volume per bidder mean that the number of accepted bids or allocation volume that a single bidder may gain per item is restricted. There also are price-related constraints like reserved price (Holzman et al. 2004; Wolfstetter 1996). In many situations, sellers reserve the right not to sell the item if the price determined in the auction is lower than some threshold amount. Such a price is called the reserved price. This means a specific item should be submitted above the minimum unit price. There are resource-related constraints such as supply capacity. Finally, bid selection constraints, derived from bid requirements by each bidder, affect the bid selection model as the exogenous constraints.

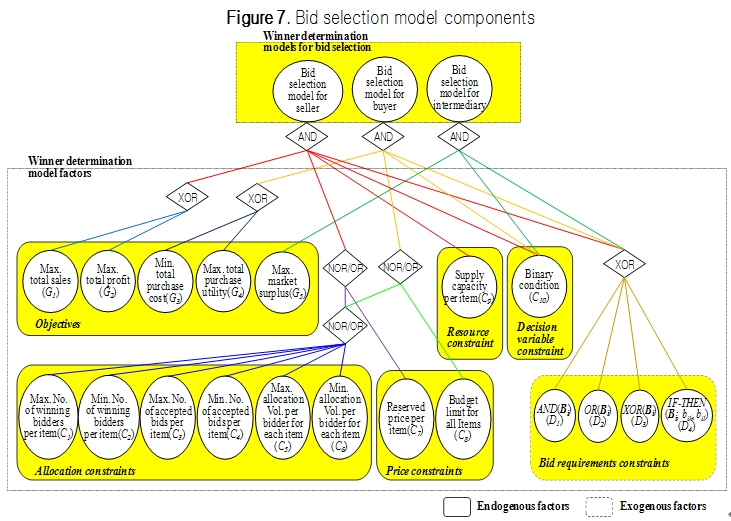
Figure 7. Bid selection model components

3.25

The bid selection model has a single objective and multiple constraints as follows.

Bid Selection Model = (Model_Objective(G_i); Model_Constraints{ C_j, C₉, C₁₀, D_k}).

If there are no conflicts among the objective and constraints, and each combination of the alternatives of the objective and constraints makes a valid model, the number of possible models is l × (Σ_{i m}C_i + 1), in which l is the number of possible objective, m is the number of selective constraints, and i =1, 2, …, m. By the combination of alternatives, we can define diverse bid selection models for participants; 2 (objectives) × (Σ _{i 7}C_i + 1)(6 allocation constraints and one price constraint) × 4 (bid requirements) cases of bid selection models for the seller and buyer, and 4 (bid requirements) cases for the intermediary.

3.26

Each model can be identified through Forward Chain Reasoning (Luger and Stubblefield 1993) using the model identification rules as follows.

IF Endogenous_Strategy(Gi) THEN Model_Objective(Gi),

IF Endogenous_Strategy(C_j) THEN Model_Constraint(Cj),

IF Exogenous_Strategy(Bid_Selection_Requirements(d_k)) THEN Model_Constraint(D_k).

3.27

For example, in the general n-bilateral combinatorial auction where multiple sellers are auctioneers, if we assume that a seller selects the objective of maximizing total sales (G₁), and constraints including maximum number of winning buyers (bidders) (C₁), minimum allocation volume per bidder for each item (C₆), reserved unit price (C₇), supply capacity per item (C₈),and XOR(bid) (D3), then the bid selection model is as below. The corresponding model components are in Table 1.

Bid Selection Model = (Model_Objective(maximizing total sales (G₁));
Model_ Constraints{maximum number of winning bidders C₁),
minimum allocation volume per bidder for each item (C₆),
reserved unit price (C₇),
supply capacity per item (C₉),
binary condition (C₁₀),
XOR(B_i) (D₃)}).

Table 1: Bid selection model components
Model component type	Model components	Mathematical representation
Objective	maximizing total sales (G1))	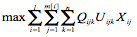	(1)
Allocation constraints	maximum number of winning bidders(buyers) (C1)	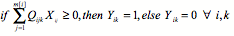	(2)
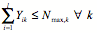
			(3)
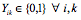
			(4)
	minimum allocation volume per bidder for each item (C6)	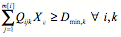	(5)
Price constraint	reserved unit price (C7)	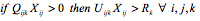	(6)
Resource constraint	supply capacity per item (C9)	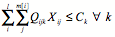	(7)
Decision variable constraint	binary condition (C10)	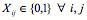	(8)
Bid requirement constraint	XOR(Bi) (D3)	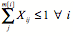	(9)

3.28

The notation is as follows: i is the index of buyers, {1, 2, …, l }; j is the index of bids, {1, 2, m [ i]}; k is the index of items, {1, 2, … n }; U_ijk is the bid unit price for item k in bid j of buyer i; R_k is the reserve price for item k of the seller; Q_ijk is the bid item quantity of buyer i for item k in bid j; N _max,k is the maximum number of selected buyers for item k; D_min,k is the minimum allocation volume per buyer for item k; C_k is the supply capacity per item of the seller for item k; and X_ij is the decision variable. X_ij is 1 if bid j is allocated to buyer i, or 0; Y _ik is 1 if item k is sold to buyer i, or 0.

3.29

When a bid requirement using the operator OR(B_i), AND(B_i), or IF-THEN(B_i; b_ik, b_il) is submitted, the corresponding bid requirement constraints are Eq. (10), (11), or (12), (13) in Table 2. n(B_i) is the number of unit bids of bidder i.

Table 2: Bid requirements constraints for bid selection
Model component type	Model component	Mathematical representation
Bid requirement constraints	OR(Bi)	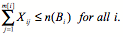	(10)
	AND(Bi)	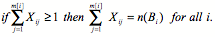	(11)
	IF-THEN(Bi; bik, bil).	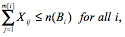	(12)
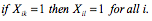
			(13)

Auctioneer selection

3.30

The third process in the combinatorial auction is to select the optimal auctioneers. The optimal auctioneer selection process occurs only in the general or reverse n-bilateral combinatorial auction market in which multi-auctioneers participate. The auctioneer selection strategy of the bidders refers to the strategy of selecting optimal bids among the bids awarded by the auctioneers. The bidder's objective is to select the optimal bids among awarded bids to maximize the value of the bids. The auctioneer selection model is composed of a single objective and multiple constraints. The objective and constraints are all endogenous for bidders.

3.31

For instance, in the general n-bilateral combinational auction where multiple sellers are auctioneers and multiple buyers are bidders, the objective of a buyer can be minimizing total purchase price. There are several constraints related to allocation, cost, and bid selection as shown in Figure 8. They include the maximum or minimum number of winning auctioneers. This means that the bidders want to restrict the number of auctioneers to whom each item is awarded. Other allocation constraints are the maximum or minimum number of accepted bids, and the maximum or minimum allocation volume per auctioneer. Finally, the alternatives for the cost constraints are the maximum unit item price and budget limit. These constraints are useful for selecting the optimal auctioneers when the bidder submit bids composed of diverse bid selection operators such as AND, OR and IF-THEN. In addition, the preference information on the auctioneers may be used to select the optimal alternatives.

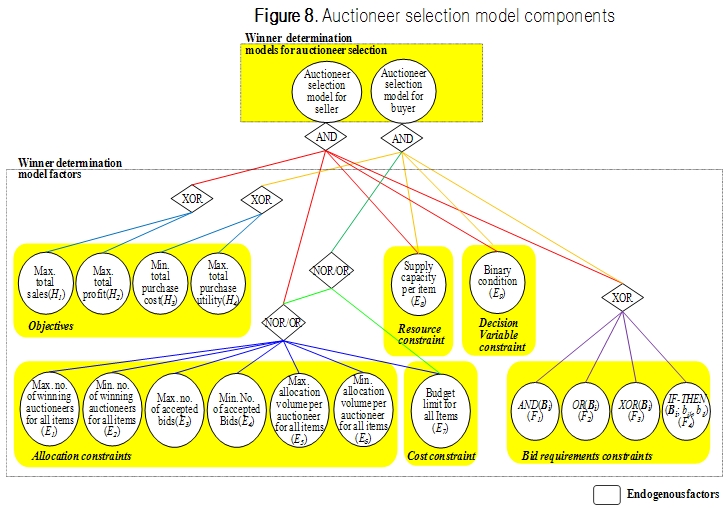
Figure 8. Auctioneer selection model components

3.32

The auctioneer selection model has basically the same form as the bid selection model. The auctioneer selection model has a single objective and multiple constraints as depicted in the following semantic representation.

Auctioneer selection model = ((Model_Objective(H_i); Model_Constraints{E_j, E₉, F_k}).

3.33

Like the bid selection model each bidder can define diverse auctioneer selection models by the combination of 2 (objectives) × (Σ _{i 6}C_i + 1)(6 allocation constraints) × 4 (bid requirements) for sellers and 2(objectives) × (Σ _{i 7}C_i + 1)(6 allocation constraints and 1 cost constraint) × 4(bid requirements) for buyers.

3.34

The auctioneer selection model is converted to a semantic model using the model identification rules below.

IF Endogenous_Strategy(H_i) THEN Model_Objective(H_i),

IF Endogenous_Strategy(E_j) THEN Model_Constraint(E_j),

IF Endogenous_Strategy(Bid_Selection_Requirements(d_k)) THEN Model_Constraint(F_k).

3.35

For example, in a general n-bilateral combinational auction, if one buyer selects the objective of maximizing total purchase utility (H₄), and constraints such as XOR(B_i) (F₃), then the auctioneer selection model is as follows.

Auctioneer Selection Model =
(Model_Objective(maximizing total purchase utility (H₄));
Model_Constraints{binary condition (E₉),
XOR(B_i) (F₃)}).

The combinatorial auction market design agent

4.1

In this section, we propose the system architecture for the combinatorial auction market design agent (CAMDA) based on intermediary, and illustrate the agent based design process using Forward and Backward Chain Reasoning for the simultaneous general n-bilateral combinatorial auction market.

The architecture for the CAMDA system

4.2

The CADMA system is composed of two main agents: market architecture and auction rule design agent (MAARDA) and winner determination model design agent (WDMDA) as shown in Figure 9. The auction agency defines market architecture, auction rules, and auction process communicating with MAARDA. MAARDA has three main components, market architecture manager, auction process manager, and auction rule manager, and their corresponding knowledge - market architecture design rules (Figure 3), auction rule design rules (Figure 4), and auction process design rules (Figure 5). WDMDA has two main components, bid selection model manager and auctioneer selection model manager, for auctioneers and bidders. Auctioneers and bidders identify their winner determination models, bid selection model and auction selection model, using winner determination modeling rules with the help of WDMDA.

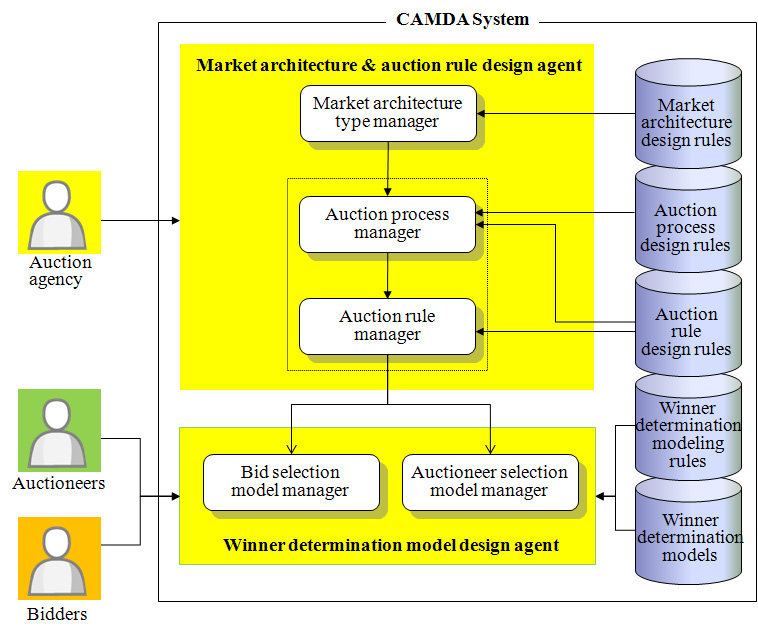
Figure 9. The overall architecture of the CAMDA systems

4.3

The function of each component of MAARDA and WDMDA for implementing the CADMA system is described in Table 3.

Table 3: Components for the CADMA system
Components	Description
Market architecture and auction rule design agent	Market architecture manager	Defines the combinational auction market architecture for trading
	Auction rule manger	Controls defined combinatorial auction rules
	Auction process manager	Manages the auction process among participants
Winner determination model design agent	Bid selection model manager	Selects optimal bids among bids submitted by bidders
	Auctioneer selection model manager	Selects optimal auctioneers from awarded bids

The design process for the general n-bilateral combinatorial auction

The design of market architecture and auction rules

4.4

The reasoning for market architecture type in design phase I involves three questions by CAMDA on the marketplace, cardinality of participants, and roles of participants. After completing the three questions through Backward Chain Reasoning a specific market architecture type is determined.

4.5

In design phase II, the auction agency designs auction rules. After specifying base factors including bidding type, bidding round, and bid requirements as shown in Figure 10(a), the auction agency determines the first dependent factors including maximum total bids per bidder, bid selection point, maximum bidding rounds per bidder, closing condition and the second dependent factors including maximum bids in each round per bidder. We assume that bidding type is simultaneous. Thus, second dependent factors are not necessary according to the rules for auction rule design. As mentioned before, the auction process type is identified by two design factors, bidding type and bid selection point using auction process design rules. The inferred auction process type is simultaneous bidding.

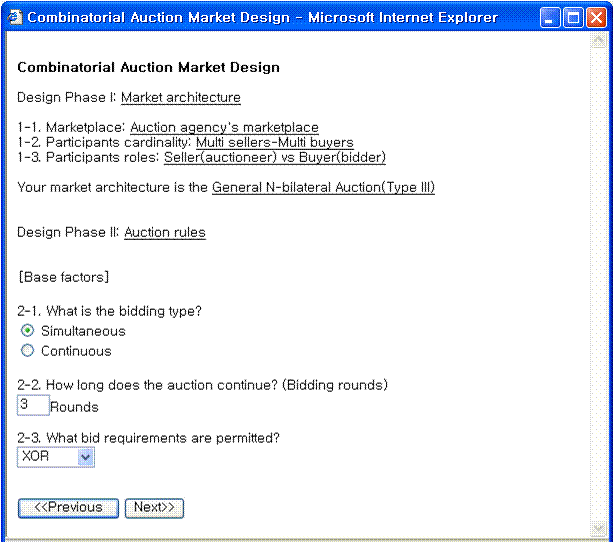
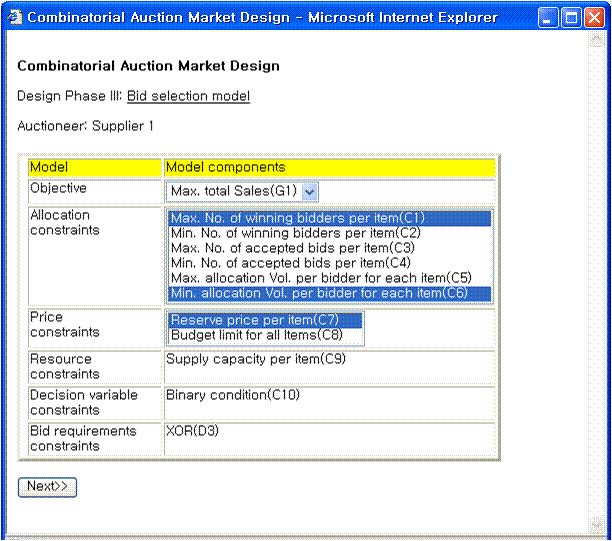
(a) The auction rule design	(b) An Auctioneer's bid selection model design
Figure 10. The design of auction rules and bid selection models

The design of winner determination models

4.6

For the selection of optimal bids, auctioneers build bid selection models according to their decision strategies. Here, the resource constraint supply capacity per item, the decision variable constraint binary condition, and the bid requirement constraint XOR are automatically determined because the resource and decision variable constraints are mandatory and the bid requirement constraint was already specified as XOR by the auction agency as shown in Figure 10(a). Each auctioneer determines an objective function and one or more constraints on the allocation or price as shown in Figure 10(b). The model components of the bid selection model are identified by Forward Chain Reasoning with winner determination modeling rules.

Conclusions

5.1

Auction mechanisms have attracted a great deal of interest and have been used in diverse e-marketplaces. In particular, the combinatorial auction provides a useful trading mechanism when several items are complementary or substitutes. Some of the previous studies on combinatorial auctions have resolved design issues of the combinatorial auction market. However, these studies only cover some of the factors or partial dimensions of combinatorial auction design. Given the potential practical value of combinatorial auctions, it is necessary to approach the design with an integrated and systematic design framework for supporting a comprehensive range of combinatorial auction models. Thus we proposed an agent-based scientific market design approach on a more effective combinatorial auction. It is based on three phases: market architecture design, auction rule design and winner determination design.

5.2

Through this study, we analyzed the relationships between diverse design factors for market design and identified market architecture types and auction process types using Backward Chain Reasoning based on market architecture design rules and auction process design rules. Also, we analyzed the model components reflecting winner determination, refined the model components in mathematical expressions, and showed that our winner determination design methodology can cope with diverse user requirements for bid selection and auctioneer selection by Forward Chain Reasoning. In addition, we proposed the model components for winner determination and identified them using Forward Chain Reasoning based on the winner determination modeling rules. Also, we implemented the prototype of the CADMA system and illustrated a design process for the n-bilateral combinatorial auction market. The proposed design methodology serves as a framework that characterizes the diverse combinatorial auction models and leads to a useful taxonomy of the combinatorial auction design factors. Furthermore, through the systematic framework, we can discover new market architecture types that have never existed before by providing a guide for making a new market model.

5.3

Although we proposed a comprehensive framework for supporting most of the combinatorial auction models, much research is needed to extend the results to make a more rigorous and practical methodology for market design. One of the research areas is the winner determination design.

5.4

The important research issue in the winner determination design is the bidding support mechanism by which each bidder can get a decision guide on whether he/she should submit bids or not, what combinations of items are most effective and what prices he or she should submit. Thus, a flexible and effective decision support system should be incorporated in the future to our frameworks to strategically guide the participating players' complex combinational trading strategies for a given auctioning problem.

Acknowledgements

This research was supported by WCU(World Class University) program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (Grant No. R31-2008-000-10062-0).

References

ABRACHE, J, Bourbeau, B, Crainic, T G and Gendreau, M (2004) A new bidding framework for combinatorial e-auctions. Computers & Operations Research, 31(8), 1177-1203. [doi:10.1016/S0305-0548(03)00071-6]

ABRACHE, J, Crainic, T G, and Gendreau, M (2004) Design issues for combinatorial auctions. 4OR, 2(1), 1-33.

BA, S, Stallaert, J and Whinston, A B (2001) Optimal investment in knowledge within a firm using a market mechanism. Management Science, 47 (9), 1203-1219. [doi:10.1287/mnsc.47.9.1203.9781]

BICHLER, M, Davenport, A, Hohner, G and Kalagnanam, J (2006) Industrial procurement auctions, In Cramton P, Shoham Y R and Steinberd R (Eds). Combinatorial Auctions, MIT Press, Cambridge, MA.

BICHLER, M, Kalagnanam, J, Lee, H S and Lee, J (2002) Winner determination algorithms for electronic auctions: A Framework design. Lecture Notes in Computer Science, 2455, 37-46. [doi:10.1007/3-540-45705-4_5]

BICHLER, M and Segev, A (2001) Methodologies for the design of negotiation protocols on E-markets. Computer Networks, 37 (2), 137-152. [doi:10.1016/S1389-1286(01)00212-2]

BICHLER, M, Shabalin, P and Pikovsky. A (2009) A computational analysis of linear-price iterative combinatorial auctions. Information Systems Research, 20 (1). 33-59. [doi:10.1287/isre.1070.0151]

BIKHCHANDANI, S, and Ostroy, J M (2002) The Package Assignment Model. Journal of Economic, 107 (2), 377-406. [doi:10.1006/jeth.2001.2957]

BREWER, P J and Plott, C R (1996) A binary conflict ascending price (BICAP) mechanism for the decentralized allocation of the right to use railroad tracks. International Journal of Industrial Organization, 14 (6), 857-886. [doi:10.1016/0167-7187(96)01014-4]

DE VRIES, S and Vohra, R V (2003) Combinatorial auctions: A survey. INFORMS Journal on Computing, 15 (3), 284-309. [doi:10.1287/ijoc.15.3.284.16077]

ELMAGHRABY, W and Keskinocak, P (2003) Dynamic pricing in the presence of inventory considerations: Research overview, Current practices and future directions. Management Science, 49 (10), 1287-1309. [doi:10.1287/mnsc.49.10.1287.17315]

FAN, M, Stallaert, J and Whinston, A B (1999) A web-based financial trading system. Computer, 32 (4), 64-70. [doi:10.1109/2.755007]

GIOVANNUCCI, A, Rodriguez-Aguilar, J A, Reyes, A, Noria, F X and Cerquides, J (2004) Towards automated procurement via agent-aware negotiation support.. In: Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems, 244-251.

GIOVANNUCCI, A, Vinyals, M and Rodríguez-Aguilar J A (2008) Computationally-efficient Winner Determination for Mixed Multi-Unit Combinatorial Auctions. In: Proceedings of the Seventh International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS 08), 1071-1078.

GOMBER, P, Schmidt, C and Weinhardt, C (1999) Efficiency, incentives and computational tractability in MAS-coordination. International Journal of Cooperative Information Systems, 8 (1), 1-14. [doi:10.1142/S0218843099000022]

HOESEL, S V and Müller, R (2001). Optimization in electronic markets: examples in combinatorial auctions. Netnomics: Economic Research and Electronic Networking, 3 (1), 23-33. [doi:10.1023/A:1009940607600]

HOLZMAN, R, Kfir-Dahav, N, Monderer, D and Tennenholtz, M (2004) Bundling equilibrium in combinatorial auctions. Games and Economic Behavior, 47 (1), 104-123. [doi:10.1016/S0899-8256(03)00184-2]

JONES, J L and Koehler, G J (2002) Combinatorial auctions using rule-based bids. Decision Support Systems, 34 (1), 59-74. [doi:10.1016/S0167-9236(02)00004-0]

KAIHARAL, T, Sashio1, K and Miura, K (2008) Social contract based manufacturing scheduling with combinatorial. In: Proceeding the 41st CIRP Conference on Manufacturing Systems, 265-268.

LEYTON-BROWN, K, Pearson, M and Shoham, Y (2000) Towards a Universal Test Suite for Combinatorial Auction Algorithms. In: Proceedings of the Second ACM Conference on Electronic Commerce, 66-76. [doi:10.1145/352871.352879]

LIM, G G, Park, S H and Kim, J (2005) Modeling of the b-Cart based Agent System in B2B EC. Lecture Notes in Artificial Intelligence, 3398, 279-288. [doi:10.1007/978-3-540-30585-9_31]

LUGER, G F and Stubblefield, W A (1993) Artificial Intelligence. 2nd Ed. The Benjamin/Cummings Publishing Company, Inc.

MCAFEE, R P and McMillan, J (1996) Analyzing the airwaves auction. The Journal of Economic Perspectives, 10 (1), 159-176. [doi:10.1257/jep.10.1.159]

MU'ALEM, A and NISAN, N (2008) Truthful approximation mechanisms for restricted combinatorial auctions. Games and Economic Behavior, 64 (2), 612-631, [doi:10.1016/j.geb.2007.12.009]

NA, A, Wedad, E and Pinar, K (2005) Bidding Strategies and their Impact on Revenues in Combinatorial Auctions. Journal of Revenue and Pricing Management, 3 (4), 337-357. [doi:10.1057/palgrave.rpm.5170119]

NISAN, N (2000) Bidding and Allocation in Combinatorial Auctions. ACM Conference on Electronic Commerce, 1-12. [doi:10.1145/352871.352872]

PARK, S J and Rothkopf, M H (2005) Auctions with bidder-determined allowable combinations. European Journal of Operational Research, 161, 399-415. [doi:10.1016/j.ejor.2003.08.057]

PARKES, D (2001) An iterative generalized Vickrey auction: strategy-proofness without complete Revelation. In: Proceedings of AAAI Spring Symposium on Game Theoretic and Decision Theoretic Agent, 78-87

PEKEC, A and Rothkopf, M H (2003) Combinatorial auction design, Management Science, 49 (11), 1485-1503. [doi:10.1287/mnsc.49.11.1485.20585]

PORTER, D, Rassenti, S, Smith, V and Roopnarine, A (2003) Combinatorial auction design. In: Proceedings of the National Academy of Sciences of the United States of America (PNAS), 100 (19), 11153-11157. [doi:10.1073/pnas.1633736100]

RASSENTI, S J, Simth, V L and Bulfin, R L (1982) A combinatorial auction mechanism for airport item slot allocation. Bell Journal of Economics, 12 (2), 402-417. [doi:10.2307/3003463]

ROTHKOPF, M H, Pekec, A and Harstad, R M (1998) Computationally manageable combinational auctions. Management Science, 44 (8), 1131-1147. [doi:10.1287/mnsc.44.8.1131]

SANDHOLM, T (2000) Approaches to winner determination in combinatorial auctions. Decision Support Systems, 28 (1/2), 165-176. [doi:10.1016/S0167-9236(99)00066-4]

SANDHOLM, T (2002) eMediator: A next generation electronic commerce server. Computational Intelligence, 18 (4), 656-676. [doi:10.1111/1467-8640.t01-1-00209]

SANDHOLM, T and Suri, S (2003) BOB: Improved winner determination in combinatorial auctions and generalizations. Artificial Intelligence, 145 (1/2), 33-58. [doi:10.1016/S0004-3702(03)00015-8]

SANDHOLM, T, Suri, S, Gilpin, A and Levine, D (2002) Winner determination in combinatorial auction generalizations. In: Proceedings of the First International Joint Conference on Autonomous Agents and Multi-Agent Systems, 69-76. [doi:10.1145/544741.544760]

SONG, J, and Regan, A C (2002) Combinatorial auctions for transportation service procurement: The carrier perspective. Transportation Research Record, 1833, 40-46. [doi:10.3141/1833-06]

WELLMAN, M P, Walsh, W E, Wurman, P R and MacKie-Mason, J K (2001) Auction protocols for decentralized scheduling. Games and Economic Behavior, 35 (1/2), 271-303. [doi:10.1006/game.2000.0822]

WOLFSTETTER, E (1996). Auctions: An introduction, Journal of Economic Surveys, 10 (4), 367-420. [doi:10.1111/j.1467-6419.1996.tb00018.x]

WURMAN, P R, Wellman, M P and Walsh, W E (1998) The Michigan Internet AuctionBot: A Configurable Auction Server for Human and Software Agents. In: Proceedings of the Second International Autonomous Agents, 301-308. [doi:10.1145/280765.280847]

XIA, M, Stallaert, J and Whinston, A B (2005) Solving the combinatorial double auction problem. European Journal of Operational Research, 164 (1), 239-251. [doi:10.1016/j.ejor.2003.11.018]

VINYALS, M, Giovannucci, A, Cerquides, J, Meseguer, P and Rodriguez-Aguilar, J A (2008) A test suite for the evaluation of mixed multi-unit combinatorial auctions. Journal of Algorithms, 63 (1-3), 130-150. [doi:10.1016/j.jalgor.2008.02.008]

ZUREL, E and Nisan, N (2001) An Efficient Approximate Allocation Algorithm for Combinatorial Auctions. In: Proceedings of the ACM Conference on Electronic Commerce, 125-136. [doi:10.1145/501158.501172]