Abstract

Researchers from many disciplines have been interested in the maintenance of cooperation in animal and human societies using the Prisoner's Dilemma game. Recent studies highlight the roles of cognitively simple agents in the evolution of cooperation who read tags to interact either discriminately or selectively with tolerably similar partners. In our study on a one-shot Prisoner's Dilemma game, artificial agents with tags and tolerance perceive dissimilarities to local neighbors to cooperate with in-group and otherwise defect. They imitate tags and learn tolerance from more successful neighbors. In terms of efficiency, society-wide cooperation can evolve even when the benefits of cooperation are relatively low. Meanwhile, tolerance however decreases as agents become homogenized. In terms of stability, parochial cooperators are gullible to the deviants - defectors displaying tolerably similar tags. We find that as the benefits of cooperation increase and the dimensions of tag space become larger, emergent societies can be more tolerant towards heterogeneous others. We also identify the effects of clustering and small-world-ness on the dynamics of tag-based parochial cooperation in spite of its fundamental vulnerability to those deviants regardless of network topology. We discuss the issue of tag mutability in search for alternative societies in which tag-based parochial cooperation is not only efficient but also robust.

Keywords:

Prisoner's Dilemma Game, Tags, Parochial Cooperation, Clustering, Small-World-Ness, NetLogo

Introduction

1.1

If people have the highest levels of trust, they always cooperate towards others. However, such societies are not only idealistic but also vulnerable to defectors. Human agents have various levels of trust toward diverse others in differentiated societies. "In-group favoritism" (Hammond and Axelrod 2006; Efferson et al. 2008) or "parochialism" (Bowles and Gintis 2004) is a nearly universal human predisposition.

1.2

How can society-wide cooperation at the global level emerge from local interactions of people who read observable markers and have limited tolerance for cooperating with others who they see as different from themselves, then? Such parochial cooperation stops at group boundaries. Within-group cooperation and between-group non-cooperation do not result in globalized cooperation. High levels of cooperation in parochial societies are possible either when their members look very alike in spite of low levels of tolerance or when more tolerant agents constitute a vast majority of the population. Which societies will emerge under selection pressure - if human agents learn tolerance and imitate makers from more successful others?

1.3

Parochial cooperators can recognize each other by "secret handshaking" (Robson 1990) to share the disproportionate benefits of in-group favoritism. But, emergent cooperative societies may be no longer stable in the presence of defectors who learn signals among cooperators. The failure of secret handshaking may lead to serious downward spirals of cooperation. Societies in which less parochial residents trust heterogeneous others are desirable concerning the diversity of tolerance and markers. However, more tolerant societies are more easily vulnerable to immigrated deviants displaying similar markers without providing any help. How can cooperation on the basis of similarity be stable in spite of repeated attacks by defectors with tolerably similar markers?

Mechanisms of Cooperation

2.1

Imagine the very simple situation that if Person A helps Person B at a cost c, Person B receives a benefit b. This helping game is the same as the Prisoner's Dilemma game if the benefit-to-cost ratio is bigger than 1, where mutual cooperation is Pareto optimal, but both individuals are worse off. Several mechanisms have been proposed to explain the evolution of cooperation in human societies.

2.2

According to the theory of kin selection (Hamilton 1964), altruism can be preferred if its benefit-to-cost ratio is higher than the probability of sharing a gene (Nowak 2006). This cannot be extended to cooperative behavior among genetically unrelated people, however.

2.3

Direct reciprocity (Axelrod 1984) leads to cooperation if the benefit-to-cost ratio is higher than the possibility of another encounter between the same two individuals (Nowak 2006). It is not applicable to sizeable populations consisting of those who rarely interact with the same partners. It is a theoretical and empirical puzzle to explain the emergence of cooperation and its maintenance in the setting of one-shot interaction without reciprocity.

2.4

Local interaction alone can facilitate society-wide cooperation in a one-shot Prisoner's Dilemma game among multiple agents (Nowak and May 1992). Agents play the game with adjacent neighbors, and then parents produce offspring in the neighborhood in proportion to their fitnesses. As long as small clusters of cooperators form and they can benefit from interactions with their own kind while avoiding interactions with defectors, global cooperation will continue. This idea of "network reciprocity" (Nowak 2006) reasonably considers "territoriality" (Axelrod 1984), unlike models on the basis of dyadic interactions between randomly matched players. However, agents use the same single strategy, either to always cooperate with all neighbors or always defect toward them, which means that they assume to have either the highest or lowest level of trust per generation (or round). Also, cooperation cannot survive under a more mundane condition that the benefit-to-cost ratio is lower relative to the number of neighbors in such a population purely composed of unconditional cooperators and defectors (Ohtsuki et al. 2006).

2.5

Recent studies have scrutinized another mechanism through which altruists interact with each other so preferentially that they can receive a disproportionate share of the benefit of altruism. 'Cues' such as reputation (Nowak and Sigmund 1998; Suzuki and Akiyama 2005; Janssen 2006) and communication tokens (Miller et al. 2002) can increase the likelihood of assortative interactions among cooperative agents. These models are concerned with partner identification, but agents should be able to have relatively high cognitive capacities.

2.6

Another related approach highlighting tag-based partner identification has contributed to a better understanding of the evolution of cooperation among minimally cognitive agents (Riolo 1997; Riolo et al. 2001; Hales 2000; Hales 2004a; Hales 2004b; Hales and Edmonds 2003; Edmonds and Hales 2005; Choi et al. 2006). Human agents have observable markers called 'tags' as the phenotype of "memes" (Dawkins 1976) to form "memetic kin" (Heylighen and Campbell 1995). In other words, human agents, albeit genetically unrelated, have perceived social distances to others reading tags to distinguish 'us' from 'them.'

Two Approaches to Tag-based Societies

3.1

There are two distinctive approaches in tag-based models. It is useful to differentiate what actions to choose (i.e. the action strategy) from how to select partners (i.e. the selection strategy) following Yamagishi et al. (1994). In one usage of tags, agent has tag-mediated perception of dissimilarity to interaction partners. Tolerance serves as a proxy strategy. Agent can use different strategies to different partners depending on whether or not her perceived distances to her partners are less than her tolerance level (Riolo et al. 2001; Choi et al. 2006). Agents globally interact with a few randomly selected others (e.g.Riolo et al. 2001) or locally with adjacent neighbors on the lattice (e.g.Choi et al. 2006). Either global or local interaction is forced without so-called the "exit option" (Orbell and Dawes 1993).

3.2

In the other convention, it is the chance of interactions that is affected by 'tagging' (Riolo 1997; Hales 2000; Hales 2004a; Hales and Edmonds 2003; Edmonds and Hales 2005). This usage is closer to the original meaning of tagging as a pervasive mechanism which facilitates selective interactions through aggregation and boundary formation in complex adaptive systems (Holland 1993; Holland 1995). For instance, agents move around to search the population for identical partners (e.g.Hales 2000; Hales 2004a; Hales and Edmonds 2003; Edmonds and Hales 2005). Either no interaction (i.e. 'unforced play') or interaction with any of others randomly selected (i.e. 'forced play') is implemented if there is not any identical partner (Edmonds and Hales 2005). In Riolo (1997)^[1], the chance of interaction between agent A and B is 1 - | t _A -t _B | ^p given that agents have real-number tags t ∈ [0, 1]. A single fixed value of "pickiness," p = 0.2, is used, instead of endogenous tolerance. It should be noted here that agent's strategy is not driven by tag-mediated perception of dissimilarity and tolerance. For example, unconditional cooperation and unconditional defection are taken in Hales and Edmonds (2003) and Hales (2004a). Riolo (1997) employs stochastic strategies represented by triple real numbers.

Problems in Tag-based Parochial Cooperation

4.1

Riolo et al. (2001) is a classical example in the first approach we follow. In their model, each agent interacts with p others ("pairings") randomly drawn from the population. Agents have real-number tags and tolerances. Agent cooperates only if her perceived dissimilarity to her partner is less than or equal to her tolerance level, and otherwise defect. After all agents participate in all pairings in a generation, each agent adopts the other's tolerance and tags if the other's payoff is higher than or equal to her own. This cultural imitation (i.e. learning from more successful others) is equivalent to genetic reproduction under selection pressure. A small amount of mutation occurs in the copying process.

4.2

Riolo et al. (2001) find that tag-based in-group favoritism significantly facilitates global cooperation. However, it is primarily due to the following four assumptions. First, tags t and tolerance T are assigned randomly to agents from U [0, 1] in their model. Given two agents A and B, if | t _A -t _B | <= T _A, then agent A cooperates; otherwise, defect. As Roberts and Sherratt (2002: 500) and Edmonds and Hales (2003) point it out, Riolo et al. (2001) would have had lower levels of cooperation if a 'strict tolerance' rule | t _A -t _B | < T_A had been used. The next related issue is whether to cooperate or not when agents A and B have exactly the same tags and T _A is 0. Agent A will cooperate in Riolo et al. (2001), but not any longer if | t _A -t _B | < T _A. In other words, not only agents with T > 0 but also agents with the minimum tolerance (i.e. T = 0) always cooperate with identical others in their model. Third, Edmonds and Hales (2003) mention that the 'selected bias' method for reproduction (i.e. 'higher than or equal to') is another factor to explain high donation rates in Riolo et al. (2001). The 'no bias' method (i.e. 'higher than') would make fundamentally different results. Lastly, Edmonds and Hales (2003) observe that tags mutate faster than tolerance in Riolo et al. (2001), which is also problematic provided that "tags must mutate faster than strategies" for high levels of cooperation in tag-based systems (Hales 2004a).

4.3

The level of cooperation is the primary concern in the critiques by Roberts and Sherratt (2002) and Edmonds and Hales (2003). Our study underlines not only the efficiency of tag-based parochial cooperation but also its stability in the presence of mutation in relation to Riolo et al.'s discussion about "tides of tolerance" (Sigmund and Nowak 2001). First, Riolo et al. (2001) observe that tolerance decreases drastically as the average donate rate increases rapidly during the first few generations (See Figure 1). After this transient period, "the agents in the resulting 'dominant tag cluster' have an advantage as there are more of them to help each other" (Riolo et al. 2001: 442). Riolo et al. (2001: 442) report that "about 75-80% of the agents have tags that are so similar that they are within each other's tolerance range," but "the simulation quickly becomes dominated by a single group of individuals, all of whom have exactly the same tag" (Edmonds and Hales 2003: 9.4). Second, altruists in the dominant tag cluster are, however, vulnerable to invasion by relatively intolerant mutants with tags within the range of tolerance of the typical members of the dominant cluster. Once these mutants have higher payoffs, a transition to a new tag cluster occurs. The average tolerance drops significantly once again, but the average donation rate returns to its previous level (Riolo et al. 2001: 441. See Figure 1). A significant erosion of tolerance is a major trend, but if more tolerant agents benefit from each other to spread across the population, the average tolerance can increase temporarily. They conclude: "in our model, the cycle of increasing and decreasing tolerance could reflect, for example, a loss of sensory discrimination in a population when there is little selection pressure to retain it, followed by a recovery when a more discriminating individual succeeds (Riolo et al. 2001: 442)."

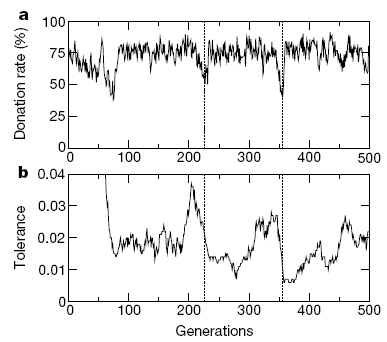
Figure 1. Dynamics of Tag-based Cooperation and Tolerance Change in Riolo et al. (2001: 441)

4.4

In sum, there are two issues in societies of tag-based parochial cooperation. First, both tolerance and tag diversity decrease more drastically as selection pressure becomes stronger. In other words, agents adapt themselves to increasingly homogenized environments by learning intolerance from more successful others. Second, global cooperation can disintegrate temporarily if a mutant agent is introduced who is indistinguishably similar to the majority of cooperators, but who is less tolerant than them. Another shift is possible along with an increase in the average tolerance if more tolerant mutant agents benefit and learn from each other to become the majority.

4.5

However, what Riolo et al. (2001) can explore are small-scale fluctuations between cooperative regimes. Since agents with the minimum tolerance ( T = 0) still cooperate with identical partners, there is no possibility in their model that mutant unconditional defectors may cause a great transformation of cooperative societies into betrayal ones.

In Search for Solutions

5.1

There seem to be a couple of solutions for alternative tag-based societies without significant loss of tolerance and tag diversity which achieve robust parochial cooperation against mutant defectors. First, higher rates of mutation in both tags and tolerance could supply more heterogeneity to societies. Particularly, less parochial mutants are frequently generated to reciprocate each other's help before cooperation is monopolized by agents displaying stronger parochialism or cooperation is wiped out by defectors. However, too high and arbitrary mutation rates are not acceptable in evolutionary dynamics. A small amount of mutation (1%) is thus implemented in the present study.

5.2

Second, the population size is definitely a critical factor in the dynamics of tag-based parochial cooperation. In larger societies, there would remain a greater number of less parochial agents who accept a broader range of heterogeneous partners as in-group members. Either universal cooperation driven by the strongest parochial cooperators or universal defection by unconditional defectors is less likely to happen because assimilative influence through learning could hardly overcome an increased amount of heterogeneity in large populations. Our study therefore intends to examine the dynamics of tag-based parochial cooperation in a small-sized population.

5.3

Agents in our study do local playing and learning in structured populations, instead of global playing and learning in unstructured populations. The findings in Riolo et al.'s study are predicated on agents' interacting with partners randomly drawn from the population and parents' leaving offspring globally. If agents had been spatially connected to interact and learn locally, it should have been that the local emergence of tag-based cooperation, its global diffusion, and its downfall due to cascades of non-cooperation triggered by mutant defectors occur more quickly.

5.4

We note that Riolo et al. (2001) implicitly consider the average number of interaction partners (i.e. "pairings" defined by the number of times per generation each agent has an opportunity to interact with a randomly encountered other), but how agents are locally clustered cannot be explored in Riolo et al.'s model. We also notice that large-sized societies have, on average, longer path lengths than small-sized ones. This factor is related to the effects of population size on the variation in tags and tolerance mentioned above. This is why the present study pays particular attention to the effects of both clustering (i.e. agents are linked to form transitive triads) and small-world-ness (i.e. agents at greater distances are connected through cross-cutting ties) on the dynamics of tag-based parochial cooperation, given a population of the same size.

5.5

Lastly but not least, some studies use real-number tags (e.g. Riolo 1997; Riolo et al. 2001) while others use binary tags (e.g. Hales 2004a; Edmonds and Hales 2005; Choi et al. 2006) or integer tags (e.g. Hales and Edmonds 2003). We prefer binary tags^[2] assuming that agents are more likely to perceive dissimilarity in a dichotomized way. Tagging helps agents confirm their group membership as social identities (Hogg 2007) through "categorization" (Tajfel 1974). The Hamming Distance indicates that agents count the presence or absence of attributes across a certain number of dimensions available. The average of Hamming Distance across the whole population (or all local neighbors) can be regarded as the mean perceived social distances^[3].

5.6

In sum, agents in the present study play a one-shot Prisoner's Dilemma game with local neighbors. They use binary tags across multiple dimensions to make distinctions between in-group and out-group. Tolerance serves a yardstick for agents to decide a course of their discriminating actions to neighbors. They learn tolerance and imitate tags from neighbors scoring higher payoffs, but with 1% of copying errors. We take only the last one out of aforementioned four assumptions in Riolo et al. (2001). Therefore, tolerance is stricter; reproduction is non-biased; tags and tolerance mutate at the same rate; and unconditional defectors - those who do not even cooperate with culturally identical partners - are introduced into the population. Agents play the game not only on the torus but also on static networks with different topologies such as regular networks, small-world networks, and random networks. We examine not only the likelihood of the emergence of universal cooperation but also the characteristic levels of tolerance and tag diversity in the absence of mutation under varying conditions of the payoffs and the tag length; and the evolutionary stability of tag-based parochial cooperation in the face of mutant defectors.

The Model^[4]

6.1

The model, with reference to Choi et al. (2006), consists of the steps in Table 1. Agents are selected in a random order without particular schedules. Updating is synchronous. The simulated longitudinal data are stored in Excel files through 'NetLogo Behavior-Space' (Wilensky 1999).

Table 1: Stages of Simulation

Initialization For each round, For each agent, Similarity perception End For each agent, Local interactions End For each agent, Payoff calculation End For each agent, Learning from successful neighbors with 1% of its error. End End

6.2

Initialization: agents have both binary tags (t _i ∈{0, 1} ^L ) and tolerance (T _i ∈{0, 1, …, L + 1}) randomly selected from the uniform distribution. Here, L stands for the tag length. N = 49 agents are located on a torus (TO hereafter in Figures and Tables) with the Moore Neighborhood, and 50 on a regular network (RG hereafter), a small-world network (SW hereafter), or a random network (RN hereafter). The regular network has exactly eight adjacent neighbors since each agent is connected to her four neighbors on either side. The average degree < k > is controlled as eight in both the random network and the small-world network. The Erdös-Rényi probability of the random network is 0.16. A small-world network is a graph with n vertices and average degree k that exhibits the average path length APL ≈ APL _random ( n, k), but the average clustering coefficient ACC >> ACC _random ≈ k/n (Watts, 1999). A small-world network can be generated from its equivalent regular network when the following two tests are satisfied at a significant level (α = 0.05)^[5]: the average clustering coefficient of a graph after a certain number of rewiring should be significantly bigger than that of the initial regular graph; and there should be no significant difference in the average path lengths between the two graphs. Therefore, the first test is one-tailed, but the second test is two-tailed. Table 2 summarizes the descriptive statistics of these two properties of three network topologies. The results of the Post-hoc Test (Scheffé) are also presented.

Table 2: ACC and APL of Regular, Small-world, and Random Networks
ACC	N	Mean	Std. Deviation	Min	Max	Post-hoc Test
RG SW RN	400 400 400	.64286 .19221 .16221	.000000 .014459 .022050	.643 .163 .105	.643 .235 .231	RG vs. SW *** RG vs. RN *** SW vs. RN ***
APL	N	Mean	Std. Deviation	Min	Max	Post-hoc Test
RG SW RN	400 400 400	3.57143 2.07872 2.08434	.000000 .001155 .060568	3.571 2.077 1.904	3.571 2.080 2.342	RG vs. SW *** RG vs. RN *** SW vs. RN

Note: ** p < .05; *** p < .01. p = .076 for the APL difference between SW and RN.

6.3

Similarity perception: if L = 0, agents cannot have social distances to their local neighbors since agents do not have tags. Otherwise, they do 'tagging' based on the Hamming distance HD. Min( HD) = 0 and max( HD) = L. If HD _ij < T _i, agent i accepts j as in-group; otherwise, out-group.

6.4

Local interactions: agent i cooperates with j if j is perceived in-group; otherwise, defects. In our model, agent i will defect in spite of no difference between two tags as long as T _i is 0 (i.e. 'always defect'). In the same way, agent i will cooperate as long as T _i is L + 1 (i.e. 'always cooperate') because the maximum tag difference is L. If L = 0, there are only two types of agents in the population since min( T) = L = 0 and max( T) = L + 1 = 1. Since all agents without tags in the population are identical, agents with T = 0 always defect toward others, while agents with T = 1 always cooperate. In this way, our model at L = 0 represents a conventional model of unconditional defection and unconditional cooperation without discriminators. Only if L ≥ 1, then agents with T = i ( i ∈{1, 2, …, L }) are able to employ conditional strategies. Agents with min( T) = 0 are always unconditional defectors, while agents with max( T) = L + 1 are always unconditional cooperators. Agents with T ≥ 1 cooperate with culturally identical partners, but all agents in Riolo et al. (2001) cooperate with them.

6.5

Payoff calculation: if an ego cooperates, she pays cost c to produce benefit b. If the benefit-to-cost ratio b/c is greater than 1 (i.e. b > c > 0), the payoff matrix in Table 3 satisfies the conditions for the Prisoner's Dilemma game. The payoff matrix in our study is the same as that in Riolo et al. (2001). For example, b/c = 2 in our model is equivalent to the cost-to-benefit ratio = 0.5 in Riolo et al. (2001) because b = 1 is fixed in their model.

Table 3: Payoff Matrix in Prisoner's Dilemma Game
	Cooperate	Defect
Cooperate	b - c, b - c	- c, b
Defect	b, - c	0, 0

6.6

Payoff-based local learning: given one randomly chosen neighbor, if her score is higher than an ego, the ego copies both her tags and tolerance. Unlike Riolo et al. (2001), we use the 'no bias' method (i.e. 'higher than' instead of 'higher than or equal to'). In the presence of mutation, agent errs in copying traits: her tags and tolerance are replaced by a new set of traits randomly.

6.7

Each replication is run for 1,000 time steps. Only in the absence of mutation, it can stop in the middle if either universal cooperation or universal defection emerges, whichever comes first.

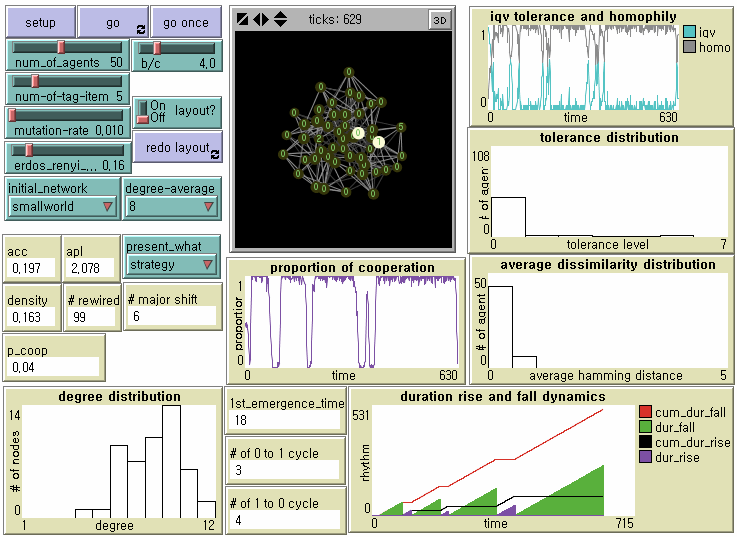
Figure 2. NetLogo Interface

Notes: From the upper left, N = 50, b/c = 4, L = 5, < k > = 8, and μ = .01. The small-world network with ACC = .197 and APL = 2.078 was generated after 99 random rewirings. Its degree distribution is displayed at the bottom left plot. Number in each node represents the level of tolerance. The node size is proportional to its degree. Its brightness is proportional to how many of neighbors with whom she cooperates out of the total number of neighbors.

6.8

We record the proportion of cooperation (0.04 from p_coop in Figure 2), the average tolerance (0.16), the average perceived dissimilarity operationally defined by the averaged Hamming Distance in the population (0.1757), the measure of homophily defined by the total number of links with the same level of tolerance over the total number of links (0.8871), the first emergence time of universal cooperation (18 from 1st_emergence_time in Figure 2), the total duration of the half downward cycle from universal cooperation to universal defection (512), the total duration of the half upward cycle from universal defection to universal cooperation (94), the number of the half downward cycle (4 from # of 1 to 0 cycle in Figure 2), the number of the half upward cycle (3 from # of 0 to 1 cycle in Figure 2), and the number of the dominance of defectors (6 from # major shift in Figure 2) which indicates how many times agents with the minimum tolerance (i.e. indiscriminate defectors) become the majority of the population.

Experimental Design

7.1

In a factorial design, the ratio of benefit to cost ( b/c) and the length of tag ( L ) are expressed in columns and rows, respectively. In the absence of mutation, 100 repetitions for each group G _ij. 2,500 cases per network topology - Torus, Regular Network, Small-world Network, and Random Network. The number of cases is 10,000 in total (Table 4).

Table 4: Experimental Design I (No Mutation)
	b/c
L	2	4	6	8	10
0	G11	G12	G13	G14	G15
1	G21	G22	G23	G24	G25
5	G31	G32	G33	G34	G35
10	G41	G42	G43	G44	G45
20	G51	G52	G53	G54	G55

7.2

The experiment continues at the mutation rate μ = 0.01 given an intermediate tag length L = 5 (See 8.2) to examine the evolutionary dynamics of tag-based cooperation on networks with different topologies at varying benefit-to-cost ratios. We drop b/c = 10 which is higher than the average degree = 8. The torus (i.e. ACC = 0.429 and APL = 2.333) is not included in this experiment since it is as homogeneous as the regular network. There are noticeable differences in both ACC and APL between the two, but both topologies have higher ACCs and longer APLs than those of the other two topologies (i.e. SW and RN). The regular network is thus sufficient for the sake of comparison with the small-world network and the random network. 100 replications are done at each experimental condition. The total number of cases comes up to 1,200 (Table 5).

Table 5: Experimental Design II (Mutation)
	b/c
L	2	4	6	8
5	G61	G62	G63	G64

Results

8.1

Local interaction and learning alone without 'tagging' is not sufficient for cooperation to survive when b/c <= 8 regardless of network topologies. Since L = 0, the population consists purely of those who always cooperate others and those who always exploit others. Recall that we use the Moore neighborhood. Therefore, the results at L = 0 indicate that unconditional cooperators cannot beat unconditional defectors when agents locally interact with neighbors and learn from them unless the benefit-to-cost ratio is higher than the average number of interaction partners. This is consistent with the rule that cooperation can survive if the benefit-to-cost ratio exceeds the average number of neighbors (i.e. the average degree of the network) in structured populations of unconditional cooperators and defectors (Ohtsuki et al. 2006)^[6].

Table 6: The Likelihood of Universal Cooperation [7]
	b/c
L	2	4	6	8	10
0	0/0/0/0	0/0/0/0	0/0/0/0	0/0/0/0	0/1/0/4
1	0/1/0/1	3/6/0/2	2/8/7/10	8/4/7/9	13/49/14/21
5	93/100/98/92	97/96/91/91	94/97/90/88	96/99/86/92	94/99/89/85
10	100/100/100/100	97/100/99/98	100/100/100/96	100/99/98/99	99/99/96/97
20	100/100/100/100	100/100/100/100	99/100/100/99	99/100/100/99	100/100/100/100

Notes: The number at each cell represents how many times out of 100 trials societies arrive at the equilibrium of universal cooperation in the absence of mutation. A torus, a regular network, a small-world network, and a random network from the left to the right. For examples, when L = 1 and b/c = 4, the chance of universal cooperation is 3% on TO, 6% on RG, 0% on SW, and 2% on a RN.

8.2

Tag-based local interaction and learning significantly increases the likelihood of the survival of cooperation. When agents use a single dimension to make distinctions between 'us' and 'them,' cooperation is more likely to evolve even at the b/c ratios lower than the average degree of the network. This likelihood increases as the b/c ratio becomes high, regardless of network topologies. Once agents make a more fine-grained distinction with five dimensions^[8], tag-based local interaction and learning facilitates universal cooperation up to about 90% within a whole range of the b/c ratios. When the tag length is long enough ( L ≥ 10)^[9], tag-based societies almost always arrive at the state of universal cooperation - there are no significant differences in its likelihood among four network topologies.

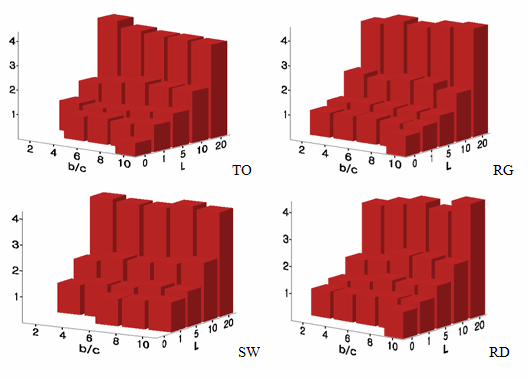
Figure 3. Means of Final Tolerance

8.3

The modes of final tolerance are not shown here, but tolerance dramatically decreases up to 1 during the first few generations especially when L = 1 and L = 5 in all of four topologies. This implies that agents learn intolerance quickly from more successful neighbors; and a single group finally evolves after a transient period of non-cooperation between tag clusters and cooperation within them. The reason why they learn intolerance is that agents with the most discriminating cooperative strategy, those who want to cooperate only with identical neighbors, are most likely to be successful under selection pressure. In other words, agents with T = 1 can beat unconditional defectors, and they are also always at least as good as agents with any other higher tolerance levels. This finding is in parallel to Nowak and Sigmund (1998) on the evolution of indirect reciprocity by image scoring. They find from the baseline model^[10] that agents become more intolerant to members with negative reputation scores. The population at the equilibrium consists almost entirely of the most discriminating strategy among all possible cooperative strategies.

8.4

In the absence of mutation, societies in the long run reach one of two absorbing states at the equilibrium^[11]: universal cooperation led by agents with T ≥ 1 or universal defection by agents with T = 0. As is illustrated in Figure 3, agents with higher levels of tolerance can remain if the b/c ratio is sufficiently high. Figure 3 also indicates that societies can preserve more tolerance on average when L is long enough to generate more tag diversity.

Table 7: Robust Regression on Average Tolerance[12]
Variable	b	SE	Variable	b	SE
b/c = 4 (dummy)	.05899	.05251	b/c = 4 (dummy)	.05899	.05251
b/c = 6 (dummy)	.07818	.05252	b/c = 6 (dummy)	.07818	.05252
b/c = 8 (dummy)	.07617	.05249	b/c = 8 (dummy)	.07617	.05249
b/c = 10 (dummy)	.08978*	.05242	b/c = 10 (dummy)	.08978*	.05242
L = 1 (dummy)	.07033	.50356	L = 1 (dummy)	.07033	.50356
L = 5 (dummy)	.23813	.49480	L = 5 (dummy)	.23813	.49480
L = 10 (dummy)	.89673*	.49576	L = 10 (dummy)	.89673*	.49576
L = 20 (dummy)	2.56723***	.49574	L = 20 (dummy)	2.56723***	.49574
Tag diversity	2.33304***	.06623	Tag diversity	2.33304***	.06623
SW (dummy)	-.16515***	.04057	Ranking in ACC	.05127**	.02341
RN (dummy)	-.15948***	.04049	Ranking in APL	.05694**	.02346
Intercept	1.0378		Intercept	.9183
Probability > F	0.0000		Probability > F	0.0000
N	4484		N	4484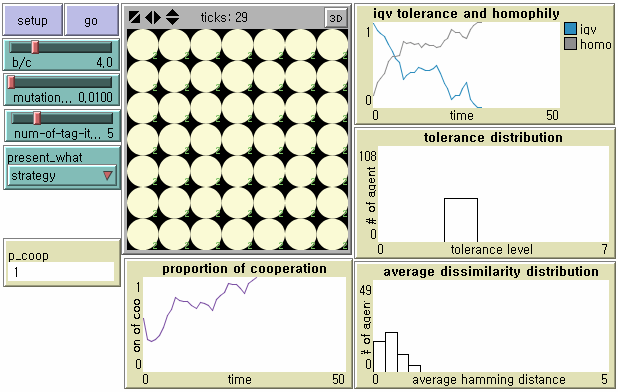

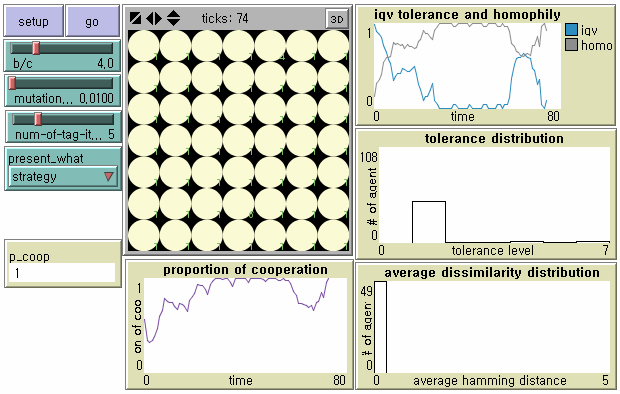
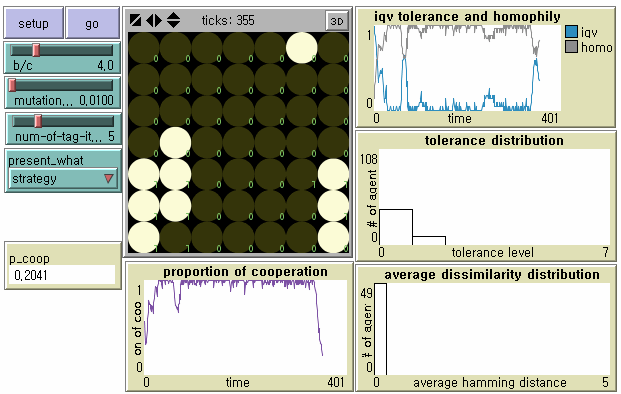
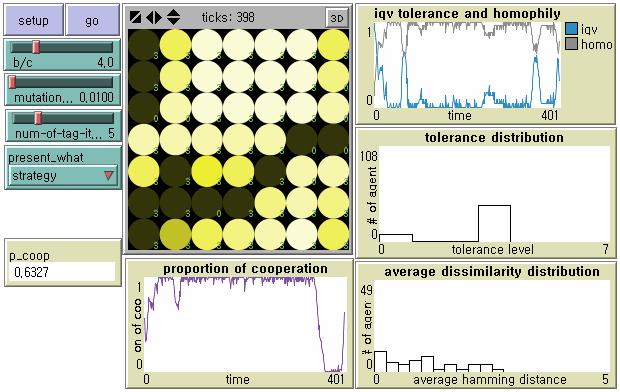
Note: * p < .10; ** p < .05; *** p < .01. The cases of universal cooperation in RG, SW, and RN are selected. From Table 2, the average clustering coefficient is highest in RG (3), the second in SW (2), and the lowest in RN (1), and the average path length is longest in RG (3), the second in RN (2), and the shortest in SW (1). Here, the numbers in six parentheses are their ranks in ascending order.

Figure 4. Evolutionary Dynamics of Tag-based Cooperation under Mutation Note: N = 49, b/c = 4, L = 5, < k > = 8, and μ = .01.

8.5

We take a robust regression of the average tolerance at the state of universal cooperation on the b/c ratio, the tag length, the degree of tag heterogeneity measured by the averaged Hamming Distance, and two dummy variables of SW and RN given that the omitted variable is Regular Network (Left Panel in Table 7). The effects of the b/c ratio are significant when b/c = 10 ( p < .10). The longer L ( p < .10 for L = 10; p < .01 for L = 20), the more tag diversity ( p < .01), and then the higher tolerance. Controlling for the effects of the b/c ratio, the tag length, and the degree of tag heterogeneity, the average tolerance at the equilibrium of universal cooperation is significantly lower in SW and RN than that in RG ( p <. 01 for both). This result seems to suggest that agents with higher levels of tolerance are more likely to survive in networks with higher degrees of local clustering and longer path lengths, but it is hard to evaluate their effects at this moment. The effects of averaged clustering and averaged small-world-ness are therefore tested in another model (Right Panel in Table 7). Controlling for all other variables, the average tolerance at the state of universal cooperation significantly depends on both network properties ( p < .05 for both): the higher clustering, the longer path length, and then the weaker parochialism. Figure 4. Evolutionary Dynamics of Tag-based Cooperation under Mutation Note: N = 49, b/c = 4, L = 5, < k > = 8, and μ = .01.

8.6

We capture snapshots of the dynamics of tag-based parochial cooperation in the presence of mutation in Figure 4. At the beginning, an equal number of agents (i.e. 7) have each level of tolerance, from 0 through 6, given the tag length L = 5. For the first few generations, there is a transient state in which within-group cooperation co-exists with between-group discrimination. However, agents become less tolerant in increasingly homogeneous environments. In other words, dominant cultural groups displaying stronger parochialism emerge as the number of clusters with different tags decreases over time. The level of global cooperation goes up in spite of a significant loss of the average tolerance because cooperation occurs among more homogeneous agents. Finally, a single tag cluster evolves. Agents with T = 2 are dominant in the population. Note that agents with T = 2 regard as in-group not only identical neighbors but also very similar neighbors with the same tags except one dimension as their own. This is why although the society reaches the state of universal cooperation there still remains a significant degree of tag diversity (Upper Left in Figure 4).

8.7

Existing cooperators are vulnerable to agents with T < 2, however. as mutants displaying stronger parochialism (i.e. T = 1) win against agents with T = 2, a new tag cluster begins to replace the old one. Meanwhile, the society becomes more homogenized. This is why the level of global cooperation can be restored to its previous one although the society is based on the strongest parochial cooperation (Upper Right in Figure 4): T = 1 is the minimum level for cooperation because agents with T = 1 cooperate only with culturally identical neighbors, and otherwise defect. In this way, our model shows small-scaled perturbations between cooperative regimes in Riolo et al. (2001).

8.8

Even the strongest discriminating cooperators fail to maintain their parochial cooperative society in the face of mutant defectors who display exactly the same tags as their own (Lower Left in Figure 4). This invasion by indistinguishable mutant defectors followed by cascades of non-cooperation is what Riolo et al. (2001) do not consider. In our model, there are not only minor shifts between cooperative societies with different levels of tolerance ( T ≥ 1), but also qualitative changes from cooperative societies to betrayal societies.

8.9

While defectors do not benefit from each other, cooperation can emerge locally once cooperators happen to cluster together through 'network reciprocity' (Lower Right in Figure 4). The emerging group in a new cooperative society consists of moderate discriminators with T = 3. One can predict that although they temporarily cooperate with heterogeneous neighbors they will be disturbed by more parochial agents in the near future with a serious loss of cultural diversity. Otherwise, since they regard a broader range of neighbors as in-group, the society will be destroyed by identical mutant defectors or defectors with the same tags except either one or two dimensions.

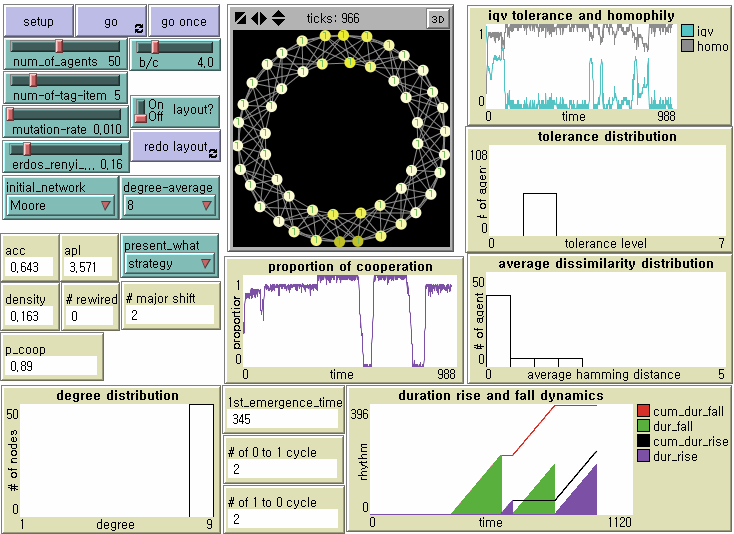
Figure 5. Local Emergence, Global Diffusion, and Invasion by Mutants on Regular Network

Note: N = 50, b/c = 4, L = 5, < k > = 8, and μ = .01.

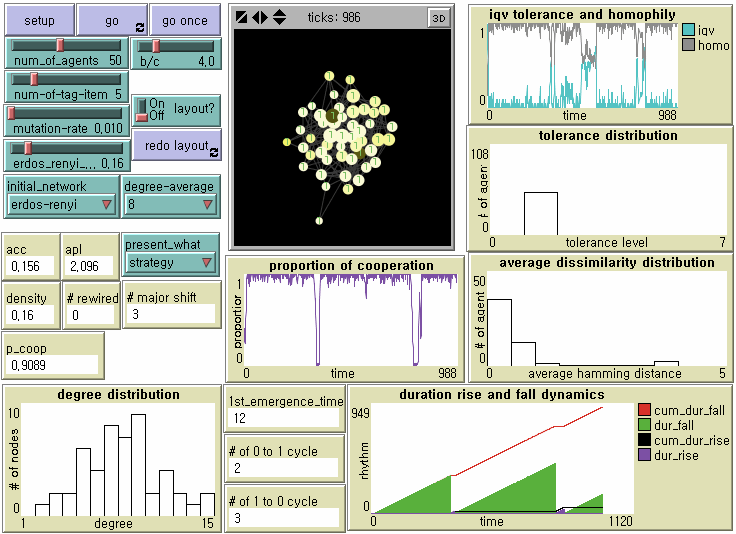
Figure 6. Local Emergence, Global Diffusion, and Invasion by Mutants on Random Network

Note: N = 50, b/c = 4, L = 5, < k > = 8, and μ = .01.

8.10

Unfortunately, tag-based parochial cooperation is not evolutionarily robust against indistinguishable mutant defectors in all three small-sized networks. However, we find that the dynamics of the local emergence of cooperation, its spatial diffusion, and invasion by mutant defectors differ from one network topology to another. Since we statistically analyze them later, let us now check what happens on a regular network (Figure 5) and a random network (Figure 6). (See Figure 2 for a small-world network). Obviously, high clustering on average contributes to the rapid formation of cooperative clusters. Small-world-ness is a double-edged sword, as Cassar (2007) and Hanaki et al. (2007) address it. In a regular network, a long path length should contribute to the stable evolution of cooperation by slowing down the speed at which defectors traverse. On the other side, it delays the accomplishment of society-wide cooperation, however. In a random network with a shorter path, mutant defectors can invade cooperative clusters more efficiently through cross-cutting ties. Meanwhile, it takes shorter for locally emerged parochial cooperation to penetrate other regions. We now examine whether there are significant differences in the first emergence time of universal cooperation, the duration from universal defection to universal cooperation, and the number of transitions from universal cooperation to universal defection across regular networks, small-world networks, and random networks when controlling for all other parameters at b/c = 4 and L = 5.

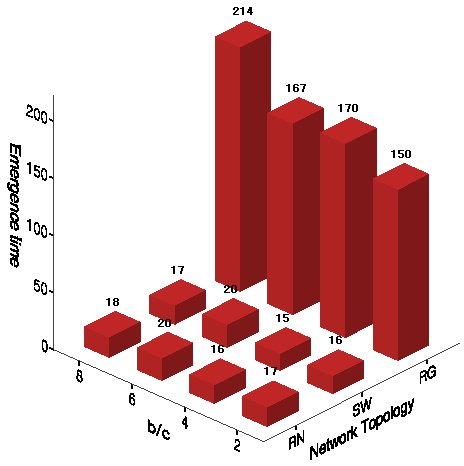
Figure 7. First Emergence Time of Universal Cooperation

8.11

We first measure the average time step of societies reaching the state of universal cooperation in the main experiments (Figure 7). On the regular networks with longer path lengths, it takes much longer for local cooperation to be globalized for the first time when controlling for the benefit-to-cost ratio. On the regular networks, universal cooperation is delayed at higher b/c ratios because both tolerance and cultural diversity are most likely to be preserved. These effects of small-world-ness and the b/c ratio are consistent with the results in the absence of mutation (See Table 7).

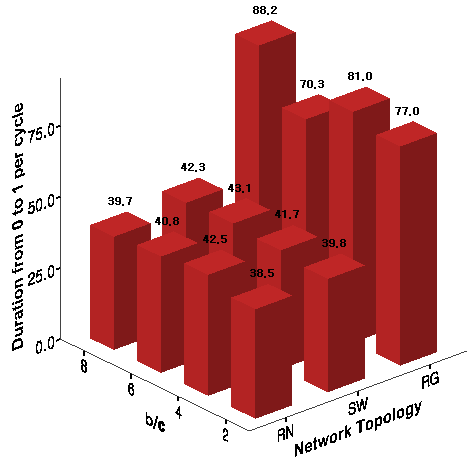
Figure 8. Duration from Universal Defection to Universal Cooperation

8.12

The average duration of the half upward cycle from universal defection to universal cooperation after the first emergence of universal cooperation and its downfall is presented in Figure 8. This measure indicates how fast localized cooperation globally diffuses through cross-cutting links after its first emergence. Although local cooperation is reinforced quickly on the regular networks with higher degrees of clustering, it takes much longer until betrayal societies are completely repaired. In contrast, locally emerged cooperation is transformed into a global institutional order much faster both on the small-world networks and the random networks with shorter path lengths.

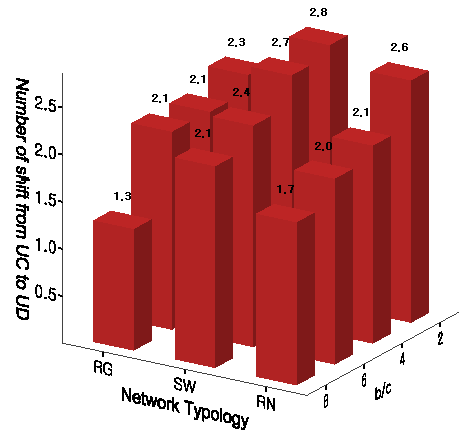
Figure 9. Frequency of Transition from Universal Cooperation to Universal Defection

8.13

We finally focus on how often there are the half downward cycles from universal cooperation to universal defection after the first emergence of universal cooperation. For its comparison, we first want to check differences in how many times defection becomes the orientation in the majority of population^[13]. This frequency is significantly higher on the random networks than the frequency on the other two networks with relatively high degrees of clustering. In other words, local clusters of parochial cooperators quickly emerge in the middle of invasion by mutant defectors on the regular networks and the small-world networks. However, the transitions from universal cooperation to universal defection occur on the small-world networks more frequently than on the regular networks^[14]. This is because mutant defectors can penetrate across the population more rapidly on small-world networks with shorter path lengths.

Conclusions and Discussions

9.1

The present study first demonstrates that 'network reciprocity' in structured populations of indiscriminating agents can promote global cooperation if the benefit-to-cost ratio of the Prisoner's Dilemma game is higher than the average number of interaction partners. However, it is otherwise impossible for altruists to survive in the face of defectors in the non-iterated Prisoner's Dilemma game. Recent studies spotlight the roles of parochial agents who read tags and conditionally cooperate only with in-group and otherwise defect in the evolution of cooperation. In tag-based societies where tolerance is not observable, agents sharing a common belief that 'in-group members will help each other' cooperate toward perceived similar players. Our study also shows that agents in such societies learn intolerance to adapt themselves to increasingly homogenized environments under selection pressure. As less tolerant agents are more successful than more tolerant ones, the strongest parochial cooperators are the most dominant in the population.

9.2

We discover that tolerance in emergent cooperative societies is more likely to be preserved on the regular network with higher clustering and longer paths. Most of time, however, emergent tag-based societies can maintain society-wide cooperation only when tolerance and cultural diversity erode significantly. Another problem in tag-based societies is that parochial cooperators are vulnerable to free-riders with tolerably similar tags. Parochial cooperation on the regular network is more robust in the presence of mutation, but endless cycles between cooperative societies and betrayal societies are inevitable in small-sized populations regardless of network topologies.

9.3

In search for an alternative tag-based society to establish robust parochial cooperation without huge loss of tolerance and cultural diversity, we pay due attention to the relationship between the speed of tag change and the speed of tolerance change. Hales (2004a), although his work on tag-based 'selection' is not inherently related to tag-based 'cooperation' and its evolutionary stability in our study, provides two necessary conditions for tag-based systems to support high levels of cooperation: tags must mutate faster than strategies; and cooperative tag groups need to spread by mutation of tags before free-riders by mutation on strategies invade the group (See also Edmonds and Hales (2005)). Hales (2004a) applies different rates of mutation μf and μ to the tag change and the strategy change respectively to demonstrate that high levels of cooperation continue when the mutation factor f > 5. We first apply his suggestion to our model - in which tolerance is a proxy strategy - at the mutation rate μ = 0.01 and f = 10. Tag-based cooperation becomes more robust, but emergent societies very often experience cascades of non-cooperation (Figure 10). If tags mutate 30 times faster than tolerance, tag-based cooperation becomes highly stable. However, the level of global cooperation decreases too much in terms of efficiency due to increased tag diversity (Figure 11).

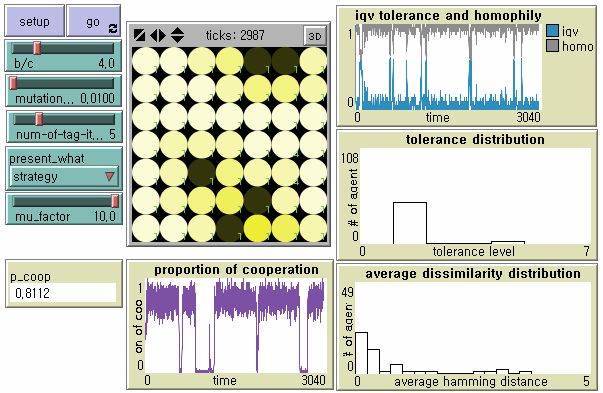
Figure 10. Dynamics of Tag-based Cooperation When Tag Mutates Faster than Tolerance ( f = 10)

Note: N = 49, b/c = 4, L = 5, < k > = 8, and μ = .01.

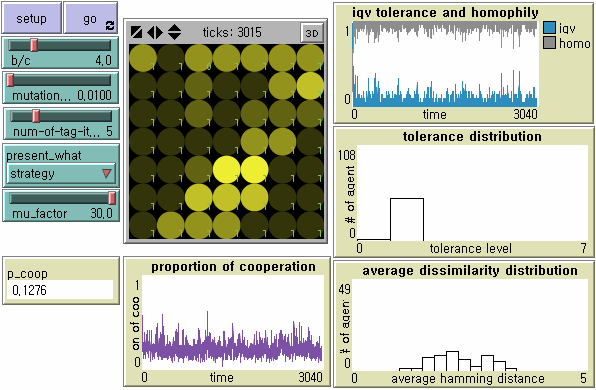
Figure 11. Dynamics of Tag-based Cooperation When Tag Mutates Faster than Tolerance ( f = 30)

Note: N = 49, b/c = 4, L = 5, < k > = 8, and μ = .01.

9.4

It should be noticed here that Riolo et al. (2001) are basically concerned with genetic evolution of cooperation to assume tags are completely mutable. This is the same case with societies where tags mutate much faster than strategies (Hales 2004a). Robust cooperation is achievable in spite of completely mutable tags because parochial cooperators change tags rapidly before mutant defectors attack cooperative clusters: the more frequently they alter their signals (e.g. passwords), the possibility of invasion by defectors decreases (e.g. password hackers download files without any contribution). From a viewpoint of cultural transmission, the instability of tag-based parochial cooperation is due to the fact that mistakes in learning culture often produce agents who display tolerably similar tags, but have a predisposition to defection.

9.5

The evolutionary instability of tag-based cooperation in the presence of mutation can be regarded as a common phenomenon in cooperation based on 'cues' such as communication tokens and linguistic codes (Miller et al. 2002; Nettle and Dunbar 1997). For instance, cooperation can evolve through signaling among altruists, but it fails to continue immediately after the emergence of those who use the same communication token but defect (Miller et al. 2002). We notice that cues are completely changeable in their model. The consequence is that defectors have little difficulties to mimic cues once exclusively shared among existing cooperators (cf.Robson 1990; Skyrms 2004). As Nettle and Dunbar (1997: 98) discuss it, "the free-rider... could not possibly survive in populations where each local group had its own language or dialect. Each group would be able to tell by his speech that he was an outsider and where he came from. This is not to imply, of course, that social identity is an unchanging, clear-cut matter." In this sense, we point out that some tags (e.g. linguistic codes, attitudes, and opinions) are more changeable and negotiable than others (e.g. ethnic markers).

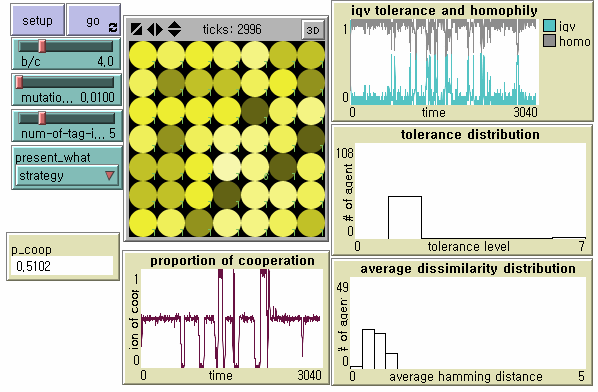
Figure 12. Dynamics of Tag-based Cooperation in a Caste Society (Model I)

Note: N = 49, b/c = 4, L = 5, < k > = 8, and μ = .01.

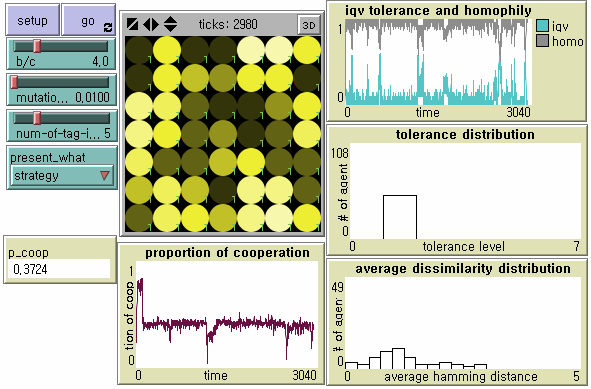
Figure 13. Dynamics of Tag-based Cooperation in a Modern Society (Model II)

Note: N = 49, b/c = 4, L = 5, < k > = 8, and μ = .01.

9.6

For future studies, instead of applying differential mutation rates to tags and tolerance, we propose alternative models in which tags as cultural markers rather than as genetically inheritable ones have different levels of mutability in the multidimensional tag-space. As with the baseline model in the present study, agents learn tolerance and imitate tags from more successful neighbors, but each agent has one core marker which is not subject to both learning and its error. In a 'caste' society (Model I in Figure 12), each agent has such a core marker at the same dimension, and therefore the society as a whole has one unchangeable master culture. In a 'modern' society (Model II in Figure 13), each agent has such a core marker at different dimensions, and the society as a whole does not have any master culture. We preliminarily find that the strongest parochial cooperators are mostly dominant in spite of increased cultural diversity in both models. However, a moderate level of cooperation stably continues only in 'modern' societies consisting of multiple emerging groups with different cultures. Parochial cooperators do not need to develop new signals. Members in some cooperative clusters may accept mutant defectors displaying tolerably similar markers as in-group, but it is less likely to happen to their neighboring clusters.

Acknowledgements

The author is very thankful to Robert Hanneman, Jeong-Kyu Choi, Vincent Buskens, and three anonymous reviewers for valuable comments on earlier versions of this paper. Insightful feedback from Jeong-Kyu Choi and Peter Burke on future directions should be gratefully acknowledged.

Notes

¹ As Riolo (1997: 6-7) points it out, "however, there is a cost of searching which reduces A's fitness in proportion to the number of searches it does." This search cost increases for individuals who are far in tag-space from the rest of the population. "Also, an individual must play a minimum number of IPD games each generation, so if after some number of meetings A still has not found an acceptable partner, then A gives up being picky and plays the next individual it meets." In this way, Riolo (1997) does not choose either 'forced play' or 'unforced play' (or 'exit') without payoff change (i.e. fitness change). He also does not allow a sufficient number of trials for search (e.g. 5 in Riolo (1997), whereas 1,000 in Hales (2000).) Recall that if the chance of interaction is simply proportional to the degree of cultural similarity between agents, then they do not interact when it is zero. This is the way Axelrod (1997) explains how cultural diversity can be sustained in spite of social influence. For this reason, local convergence and global divergence in his model is a predictable consequence. Riolo (1997) does not entail the pitfalls of 'selective play' or 'distance-biased interaction.'

² Real-number tags are not realistic in the sense that human agents cannot make such a fine-grained distinction. Either integer tags with a single bit (e.g. t ∈ [1, 2,… , 500] in Hales and Edmonds (2003)) or long-winded binary tags (e.g. L ≥ 32 in Hales (2000), Hales (2004a), and Edmonds and Hales (2005)) is also somewhat problematic, given the experimental result that human agents use a small number of dimensions on average to construct their identities, for instance, 5.4 in the context of international relations (Rousseau and van der Veen 2005).

³'1 - Standardized Hamming Distance' is the same with the 'Simple Matching Index' (Hanneman and Riddle 2005) which is a common measure of similarity in social network analysis.

⁴ The NetLogo (Version 4.0.2) is used (Wilensky 1999). Our model applets are available at http://student.ucr.edu/~jkim081/simulation.htm.

⁵ Another strategy is to begin with regular networks and create fixed networks along different levels of the rewiring probability rp. For example, a regular network ( rp = 0) and a random network ( rp = 1). This approach has some limitations, however. First, although small-world networks exist within a broad range of rps, there is still no guarantee that small-world networks can be obtained even at middle levels of rp since ACC always decreases as rp decreases, but APL not always. Moreover, APL in a graph at higher rp is not necessarily shorter than APL in another graph at lower rp. Second, in statistical models including a single independent variable rp, the effects of both ACC and APL are absorbed in its effects. We want to distinguish the effects of APL from the effects of ACC, as is in Table 7 (Right Panel).

⁶ Ohtsuki et al. (2006) introduce three different rules of strategy updating: 'death-birth updating'; 'birth-death updating'; and 'imitation updating.' For death-birth updating, at each time step a random individual is selected to die, and then her neighbors compete for the empty site proportional to their fitness. For birth-death updating, at each time step an individual is chosen for reproduction proportional to fitness, and then the offspring replaces a randomly selected neighbor. For imitation updating, at each time step a random individual is chosen to update her strategy; she will stay with her own strategy or imitate one of her neighbors proportional to fitness. They verify that cooperation can survive if the benefit-to-cost ratio exceeds the average number of neighbors in structured populations of altruists and defectors when the death-birth updating rule is applied: b/c > k. The birth-death rule does not favor cooperation. It holds true that b/c > k + 2 under the imitation updating rule. Our finding is that b/c > k, but we should point out that the imitation rule in Ohtsuki et al. (2006) is not the same with the updating rule in the present paper (See 6.6).

⁷ This likelihood is not influenced by the population size. Given N = 400 on the torus, for an instance, [(0, 0, 0, 0, 0) at L = 0; (0, 0, 18, 42, 37) at L = 1; (88, 87, 89, 94, 92) at L = 5; (80, 86, 88, 88, 88) at L = 10; (85, 87, 74, 89, 88) at L = 20]. Numbers in parentheses are in the same order of b/c as Table 7. The population size is not a problem in the absence of mutation. It is a critical issue in the presence of mutation (See 5.2).

⁸ For example, the possibilities of universal cooperation at L = 4 are: 88/99/88/90 at b/c = 2; 92/95/85/84 at b/c = 4; 87/96/84/92 at b/c = 6; 88/95/86/84 at b/c = 8; and 87/98/81/85 at b/c = 10. All cannot be shown, but since there is a leap between L = 2 and L = 3, and between L = 3 and L = 4, L = 5 can be regarded as the minimal tag length for universal cooperation within a broad range of the b/c ratios.

⁹ A reviewer addressed that the initial proportion of unconditional defectors should influence the overall results in Table 6 when controlling for b/c. For examples, the initial proportion of agents with T = 0 is 1/( L + 2) = 1/2 given L = 0, whereas it is 1/22 at L = 20. Because agents with T ≥ 1 cooperate with identical partners in our model, it is expected that: the longer tag length L, the higher proportion of agents with T ≥ 1 from the beginning, and therefore the higher possibility of universal cooperation. We tested the sensitivity of the likelihood at b/c = 4 and L = 5. Each of 10 experiments is composed of 50 independent trials. The test results are: ( i = 12, j = 24.5, k = 88); (13, 26.5, 87); (14, 28.6, 89); (15, 30.6, 82); (16, 32.7, 86); (17, 34.7, 77); (18, 36.7, 90); and (19, 38.8, 76). Here, i = Number of agents of T = 0 at the initial setting, j = Percent of agents of T = 0 at the initial setting, and k = the likelihood of universal cooperation in parentheses. Once i is set, T = 1 through T = 6 are distributed uniformly and randomly to agents. The likelihood is sufficiently robust within a broad range of the initial percentages of unconditional defectors, approximately between 25% and 40%. Another sensitivity test is aimed at checking whether or not it is the tag length that affects the likelihood of universal cooperation when controlling for the initial distribution of the experimental population. It was executed at the same level of b/c = 4 and L = 3, but we allowed agents to have L = 10 before playing the game. Out of 150 independent runs, the likelihood is 100%. This is significantly different from the likelihood of 72% at b/c = 4 and L = 3 under which the initial number of unconditional defectors is 9.8 (= 0.2 × 49). In this experiment, the average number of unconditional defectors in the initial setting is 9.77 and its standard deviation is 2.774. Given these two results, we confirm the tag length effects in Table 6. I thank Jeong-Kyu Choi for calling my attention to the second approach.

¹⁰ In the baseline model, each agent has an image score s from -5 to +5 known to every other player. All agents have image score 0 at the beginning, and it increases (or decreases) by one unit every time they cooperate (or defect). The range of strategy k is from -5 to +6. Unconditional cooperation through conditional cooperation to unconditional defection are available to agents, given the rule that a donor i cooperates with a recipient j only if s_j ≥ k_i.

¹¹ Societies tend to reach another equilibrium, neither universal cooperation nor universal defection, when agents on the torus and the regular network have relatively long lists of tags. For example, 56.3% cases at L ≥ 5 show that different tag clusters are aligned with each other in parallel so that group boundaries can be preserved along straight lines. In other words, tags act as "self-enforcing stereotypes" (Sigmund and Nowak 2001) to make it difficult for tolerance to cross structurally segregated enclaves with different markers. This case is not observed in any other two heterogeneous networks in spite of synchronous updating in our model. In Table 6 and 7, we drop these cases.

¹² Neither the effect of b/c = 4 nor the effect of L = 5 is statistically significant at the significance level of α = .05. In other words, agent's inclination to learn intolerance does not significantly lessen at these two levels. This is the reason why we employ b/c = 4 and L = 5 in the second experiment under mutation.

¹³ According to the Post-hoc Test (Scheffé), there are significant differences in how many times defectors become the majority of the population between RG and RN and between SW and RN ( p < .01 for both), but not between RG and SW. Mean = 2.21 and Standard Deviation = 1.950 in RG; Mean = 2.12 and Standard Deviation = 1.692 in SW; and Mean = 1.65 and Standard Deviation = 1.497 in RN.

¹⁴ In the Post-hoc Test (Scheffé) on the number of the shifts from universal cooperation to universal defection, p = .000 between SW and RG, and between SW and RN, but p = .129 for RG and RN. Mean = 1.94 and Standard Deviation = .966 in RG; Mean = 2.48 and Standard Deviation = 1.228 in SW; and Mean = 2.09 and Standard Deviation = 1.092 in RN.

References

AXELROD, R (1984) The Evolution of Cooperation. New York: Basic Books.

AXELROD, R (1997) The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution 41, pp. 203-226. [doi:10.1177/0022002797041002001]

BOWLES, S and Gintis H (2004) Persistent Parochialism: Trust and Exclusion in Ethnic Networks. Journal of Economic Behavior and Organization 55, pp. 1-23. [doi:10.1016/j.jebo.2003.06.005]

CASSAR, A (2007) Coordination and Cooperation in Local, Random, and Small World Networks: Experimental Evidence. Games and Economic Behavior 58, pp. 209-230. [doi:10.1016/j.geb.2006.03.008]

CHOI, J-K, Yang, J-S and Jo H-H (2006) The Co-evolution of Cooperation and Trait Distinction. Proceedings of the First Complexity Conference, The Complexity Network and Complexity Sciences Center, Samsung Economic Research Institute. Seoul, South Korea. 2006-12-06. (In Korean with an English abstract).

DAWKINS, R (1976) The Selfish Gene. Oxford: Oxford University Press.

EDMONDS, B and Hales D (2003) Replication, Replication, and Replication: Some Hard Lessons from Model Alignment. Journal of Artificial Societies and Social Simulation 6(4)11 https://www.jasss.org/6/4/11.html.

EDMONDS, B and Hales D (2005) Computational Simulation as Theoretical Experiment. Journal of Mathematical Sociology 29, pp. 209-232. [doi:10.1080/00222500590921283]

EFFERSON, C, Lalive, R and Fehr E (2008) The Coevolution of Cultural Groups and Ingroup Favoritism. Science 321, pp. 1844-1849. [doi:10.1126/science.1155805]

HALES, D (2000) Cooperation without Space or Memory: Tags, Groups and the Prisoner's Dilemma. In Moss S and Davidson P (Eds.) Multi-Agent-Based Simulation - Lecture Notes in Artificial Intelligence 1979/ 2000, Springer-Verlag. pp. 157-166. [doi:10.1007/3-540-44561-7_12]

HALES, D (2004a) Understanding Tag Systems by Comparing Tag Models. Second Model-to-Model Workshop (M2M2) at the Second European Social Simulation Association Conference (ESSA'04), Valladolid, Spain. 16-19th September 2004.

HALES, D (2004b) From Selfish Nodes to Cooperative Networks. Proceedings of the Fourth IEEE International Conference on Peer-to-Peer Computing, IEEE Computer Society Press.

HALES, D and Edmonds B. (2003) Evolving Social Rationality for MAS using 'Tags.' Proceedings of the Second International Joint Conference on Autonomous Agents and Multiagent Systems, ACM Press. pp. 497-503. [doi:10.1145/860575.860655]

HAMILTON, W D (1964) The Genetical Evolution of Social Behavior. Journal of Theoretical Biology 7, pp. 17-52. [doi:10.1016/0022-5193(64)90039-6]

HAMMOND, R A and Axelrod R (2006) The Evolution of Ethnocentrism. Journal of Conflict Resolution 50(6), pp. 926-36. [doi:10.1177/0022002706293470]

HANAKI, N, Peterhansl, A, Dodds P S and Watts D J (2007) Cooperation in Evolving Social Networks. Management Science 53, pp. 1036-1050. [doi:10.1287/mnsc.1060.0625]

HANNEMAN, R A and Riddle M. (2005) Introduction to Social Network Methods. University of California, Riverside. http://faculty.ucr.edu/~hanneman/nettext/.

HEYLIGHEN, F and Campbell D T. (1995) Selection of Organization at the Social Level: Obstacles and Facilitators of Metasystem Transitions. World Futures: the Journal of General Evolution 45, pp. 181-212. [doi:10.1080/02604027.1995.9972560]

HOGG, M A (2006) Social Identity Theory. In Burke P J (Ed.) Contemporary Social Psychological Theories, Palo Alto, CA: Stanford University Press. pp. 111-136.

HOLLAND, J H (1993) The Effect of Labels (Tags) on Social Interactions. SFI Working Paper 93-10-064. Santa Fe Institute. Santa Fe, NM.

HOLLAND, J H (1995) Hidden Order: How Adaptation Builds Complexity. Reading, MA: Addison-Wesley Publishing Company, Inc.

JANSSEN, M (2006) Evolution of Cooperation when Feedback to Reputation Scores is Voluntary. Journal of Artificial Societies and Social Simulation 6(4)17 https://www.jasss.org/9/1/17.html.

MILLER, J H, Butts C T and Rode D (2002) Communication and Cooperation. Journal of Economic Behavior and Organization 47, pp. 179-195. [doi:10.1016/S0167-2681(01)00159-7]

NETTLE D and Dunbar R I M (1997) Social Markers and the Evolution of Reciprocal Exchange. Current Anthropology 38, pp. 93-99. [doi:10.1086/204588]

NOWAK, M A (2006) Five Rules for the Evolution of Cooperation. Science 314, pp. 1560-1563. [doi:10.1126/science.1133755]

NOWAK, M A and May R M (1992) Evolutionary Games and Spatial Chaos. Nature 359, pp. 826-9. [doi:10.1038/359826a0]

NOWAK, M A and Sigmund K (1998) The Dynamics of Indirect Reciprocity. Journal of Theoretical Biology 194(4), pp. 561-74. [doi:10.1006/jtbi.1998.0775]

OHTSUKI, H, Hauert C, Lieberman E and Nowak M A (2006) A Simple Rule for Evolution of Cooperation on Graphs and Social Networks. Nature 441, pp. 502-505. [doi:10.1038/nature04605]

ORBELL, J and Dawes R M (1993) Social Welfare, Cooperator's Advantage, and the Option of not Playing the Game. American Sociological Review 58, pp. 787-800. [doi:10.2307/2095951]

RIOLO, R L (1997) The Effects of Tag-mediated Selection of Partners in Evolving Populations Playing the Iterated Prisoner's Dilemma. SFI Working Paper 97-02-016. Santa Fe Institute. Santa Fe, NM.

RIOLO, R L, Cohen M D and Axelrod R (2001) Evolution of Cooperation without Reciprocity. Nature 414, pp. 441-443. [doi:10.1038/35106555]

ROBSON, A J (1990) Efficiency in Evolutionary Games: Darwin, Nash and the Secret Handshake. Journal of Theoretical Biology 144, pp. 379-96. [doi:10.1016/S0022-5193(05)80082-7]

ROBERTS, G and Sherratt T N (2002) Does Similarity Breed Cooperation? Nature 418, pp. 499-500. [doi:10.1038/418499b]

ROUSSEAU, D and van der Veen A M (2005) The Emergence of a Shared Identity. Journal of Conflict Resolution 49(5), pp. 686-712. [doi:10.1177/0022002705279336]

SIGMUND, K and Nowak M A (2001) Tides of Tolerance. Nature 414, pp. 403-404. [doi:10.1038/35106672]

SKYRMS, B (2004) The Stag Hunt and the Evolution of Social Structure. Cambridge: Cambridge University Press.

SUZUKI, S and Akiyama E (2005) Reputation and the Evolution of Cooperation in Sizable Groups. Proceedings of the Royal Society B 272, pp. 1373-1377. [doi:10.1098/rspb.2005.3072]

TAJFEL, H (1974) Social Identity and Intergroup Behavior. Social Science Information 13, pp. 65-93. [doi:10.1177/053901847401300204]

TRIVERS, R L (1971) The Evolution of Reciprocal Altruism. The Quarterly Review of Biology 46(1), pp. 35-57. [doi:10.1086/406755]

WATTS, D J (1999) Small Worlds: The Dynamics of Networks Between Order and Randomness. Princeton, NJ: Princeton University Press.

WILENSKY, U (1999) NetLogo. Evanston, IL. http://ccl.northwestern.edu/netlogo/.

WILENSKY, U and Rand W (2007) Making Models Match: Replicating an Agent-Based Model. Journal of Artificial Societies and Social Simulation 10(4)2. https://www.jasss.org/10/4/2.html.

YAMAGISHI, T, Hayashi N and Jin N (1994) Prisoner's Dilemma Networks: Selection Strategy versus Action Strategy. In Schulz U, Albers W and Mueller U (Eds.) Social Dilemmas and Cooperation. Berlin: Springer-Verlag. pp. 233-250.