Abstract

In the interactions of a social group, people usually update and express their opinions through the observational learning behaviors. The formed directed networks are adaptive which are influenced by the evolution of opinions; while in turn modify the dynamic process of opinions. We extend the Hegselmann-Krause (HK) model to investigate the coevolution of opinions and observational networks (directed Erdös-Rényi network). Directed links can be broken with a probability if the difference of two opinions exceeds a certain confidence level ε, but new links can form randomly. Simulation results reveal that both the static networks and adaptive networks have three types: more than one cluster (fragmented) with small ε, consensus with a certain probability with moderate ε, always consensus with large ε. Also, on both networks, the tendencies of average of opinion clusters, consensus probability and average of convergence rounds are similar, and the fewest of average of opinion clusters satisfies the rough 1/(2 ε)-rule. On static networks, final opinions are influenced by percolation properties of networks; but on directed adaptive networks, it is basically determined by the rewiring probability, which increases the average degree of networks. When rewired probability is larger than zero, the results of adaptive networks are getting better than static networks. However, after the final average in- and out-degree of both networks exceeds a threshold, there is little improvement on the results.

Keywords:

Opinion Dynamics, Directed Adaptive Networks, Social Group, Coevolving Networks

Introduction

1.1

In recent years, statistical physical models and computational tools, especially the agent-based computational modeling tools, have been applied to investigate how global complex properties can emerge from purely local rules in various social phenomena, such as the opinion formation in a population of human beings, culture dissemination, the spreading of linguistic conventions and so on (Xia et al. 2011). For opinion dynamics, statistical physics tries to define the opinion states of a population and the elementary processes that determine transitions between such states (Castellano et al. 2009). The studies on opinion dynamics can explain a wide range of social phenomena, e.g. minority opinion survival, collective decision making and consensus building.

1.2

The opinion dynamics models can be classified into discrete (including binary) models and continuous models depending on the representation of opinions. Discrete models represent an opinion as a discrete variable. The typical discrete models include Ising model (Galam et al. 1982; Galam & Moscovici 1991), voter model (Holley & Liggett 1975; Slanina and Lavička 2003), majority rule model (Galam 2002), models based on social impact theory (Nowak et al. 1990; Lewenstein et al. 1992) and Sznajd-Weron model (Sznajd-Weron & Sznajd 2000; Sznajd-Weron 2005), etc. The discrete models have been extensively studied and a lot of useful results have been obtained. Continuous models mainly include the Deffuant-Weisbuch (DW) model (Deffuant et al. 2000; Fortunato 2004; Lorenz & Urbig 2007), the Hegselmann-Krause (HK) model (Hegselmann & Krause 2002; Fortunato 2005) and a plenty of their variants and extensions (Deffuant et al. 2002; Hegselmann & Krause 2002; Fortunato et al. 2005; Hendrickx 2008; Urbig et al.2008; Pan 2010; Kurmyshev et al. 2011; Lorenz 2010). On the early stage, most opinion dynamics studies focus on the influence of model parameters on a linear chain, grid or regular lattices, and then the focus turns to the influence of topological features of (adaptive) complex networks, such as small-world networks and scale-free networks (Gandica et al. 2010; Li et al. 2006; Wang et al. 2008; Feng et al.2010; Xiong & Hu 2012).

1.3

Recently, more studies have considered the network of social interactions coevolveing with the agents' opinions. However, only few of them are based on the framework of directed networks. Many social networks are adaptive. The dynamics of their nodes influence the network topologies, while the network topologies in turn modify the dynamics of the nodes. The time scale on opinions and links of nodes evolve can be different: either fast, slow or the same order. The dynamic evolution of node states is very fast with respect to the network topological evolution (Ehrhardt et al. 2006a; Ehrhardt et al. 2006b). Links can be broken more easily if two interacting agents differ in their opinions, but new contacts do generally appear owing to the random events in the social life of the agents (Zanette & Gil 2006; Iñiguez et al. 2009; Kozma & Barrat 2008a, 2008b; Zimmermann et al. 2004; Fu & Wang 2008). Gil and Zanette (2006) assume that interaction links can be broken when agents fail to reach agreement of their opinions. Gross et al. (2006) study the epidemic dynamics on an adaptive network, where the susceptible agents can avoid contacting with infected ones by rewiring their network connections. Gross and Blasius (2008) attempt to classify generic patterns of the dynamics of adaptive networks. Holme and Newman (2006) consider that the new connection is established towards an agent with a similar opinion for a model of agents with continuous opinions and bounded confidence. The effects of a mixed population with distinctive relinking preferences on both the convergence time and the network structures have been investigated (Zhong et al. 2010). Singh et al. (2012) have studied how a small fraction of committed agents can dramatically influence the scaling of consensus times on structurally evolving networks through a variant of the Axelrod model with homophily-driven rewiring. Frequently pairs of agents are allowed to change their locations to improve the homogeneity of opinion with respect to their short-range environment in a one-dimensional ring (Iñiguez et al. 2011). Gargiulo and Huet (2010) analyze the reciprocal feedback between the opinions of the individuals and the structure of the interpersonal relationships at the group level. Fu and Wang (2008) investigate the co-evolutionary dynamics of opinions and networks based upon majority-preference and minority-avoidance rules.

1.4

While many social links are undirected, there are also a significant number of them that are directed and must also be modeled. In this study, we investigate the coevolution of the agents' opinions and a directed adaptive network of interacting agents in a social group, and analyze how to foster all agents to form fewer opinion clusters even to reach a consensus more efficiently. We extend the HK model to the directed adaptive network, in which opinions and links of nodes evolve in the same order. The directed network is more realistic than the undirected networks in the cases of most social networks, such as a meeting of a group of people, a bulletin board system (BBS) community on internet, social circles from Twitter, LiveJournal online social network, and social circles from Google+ and so on. The contact between agents can be modeled as a directed link more naturally than an undirected link which is used in many other studies of evolving networks, especially the DW-based models. Directed links may be broken with a probability if the difference of two opinions exceeds a certain threshold. New links will appear randomly without requiring prior knowledge of the opinions of agents. The threshold ε and rewired probability of the model have important consequences on the final opinions and on the structure of the interaction network.

1.5

The remainder of this paper is organized as follows. Firstly, the model and directed adaptive networks are explained. Next, we compare the cases of static networks with adaptive networks, and show the results of opinion formation with the structure of the network and the effects of the rewiring probability. Finally, we discuss all results and describe the potential for future work.

Extended HK (EHK) Model

2.1

In the HK model, opinions take continuous real values in an interval, and an agent i interacts with neighboring agents whose opinions lie in the range of its confidence level. The difference between the HK and the DW model is the update rule: in the HK model, agent i does not interact with any of its compatible neighbors that is used in the DW model, but with all neighbors who lie in its confidence level simultaneously, then update its opinion to the average of these opinions. The HK model is intended to describe small or medium formal meetings, where there is an effective interaction involving all people at the same time. In contrast, the DW model is suitable to describe the opinion dynamics of large populations where people meet in random pairs (Castellano et al. 2009).

2.2

We extend the HK model to the directed adaptive networks and note it as EHK model. In the EHK model, every agent in a social group pay attention to a finite number of neighbors and cannot get a priori communicate with all the other agents. For example, in a BBS community, everyone can express his opinion on some issue after reading many others' opinions. This is a typical observational learning process, in which agent obtains opinions of its interested others, and then form its new opinion. The directed interaction means an agent who receives influence from a provider may not affect the provider, being different from the DW model in which the influence is bidirectional. The representative network structure is taken as a directed random graph in which agents pay attention to <k> acquaintances on average, i.e. the initial network corresponds to a directed Erdös-Rényi (ER) network with average in- and out- degree <k>.

Directed Networks

3.1

The agents in set A={1, 2,…,n} form a directed social network. A neighborhood matrix G^t is used to represent the social relationships on A at time t. For all i, j ∈ A, 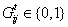indicates whether there is a directed link from agent i to j at time t. So the n × n matrix G^t is defined as

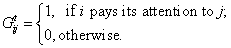
(1)

where 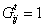denotes agent i can receive an opinion from a provider agent j. Technically, we assume that each agent is always connected with itself, i.e. 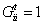, for all i ∈ A, all t. G^t is asymmetric to describe a directed network, so that 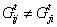, for some i, j. An agent i ∈ A only observes itself and its neighbors, including the agents in set of 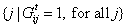, at time t.

Updating Opinions

3.2

The opinions of n agents at time t are represented by an 1 × n vector 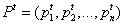, where 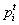is the agent i's opinion at time t, .

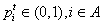3.3

Define 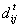as the difference between 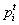and 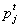at time t:

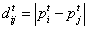
(2)

where | | denotes the absolute value of a real number. Obviously, we have 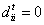and 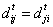for all i, j, all t.

3.4

Defines 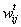as the weight of influence from j to i:

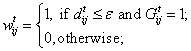
(3)

where ε is the confidence level (CL) and 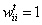, for ε ≥ 0, all i, all t.

3.5

Agent i updates its opinion by taking average of all opinions which lie in its CL including its opinion at each time step t. The element 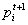of new opinion vector P^t+1 is calculated by formula (4):

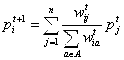, for all t.

(4)

When P^t+1 satisfies formula (5), it is convergent and the process of evolution is end.

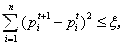
(5)

where ξ is a very small positive number, and here it is 10^-4.

Updating Networks

4.1

Directed links may be broken if difference between two opinions exceeds a certain CL. But new contacts do generally appear owing to random events in interactions of agents. Some models consider that new connections are established between agents with similar opinions (Holme & Newman 2006), but this requires a priori information of the agents' opinions. In fact the agent cannot get the other agents' opinions if the connections between them are broken. Thus, here we stick to the hypothesis of a randomly established new link (Kozma and Barrat 2008a; 2008b).

4.2

There are two situations where network connections are updated:

Situation 1: A directed link from i to j exists at time t, i.e. 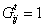, which means the agent i pays attention to agent j's opinion. If 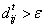, the directed link decays spontaneously with a certain probability of 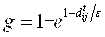at time t+1; otherwise the directed link are naturally maintained.

4.3

Now we check the decay probability 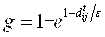for different d and ε, as shown in Figure 1. Obviously, as d increases, the probability of g increases. The growth of g gets faster with a smaller ε. As ε increases, the maximum of probability g (at the point of d=1) is reduced from 1 to 0. This means that with the same d, the links are more likely to be broken under a smaller ε.

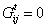Situation 2: There is no directed link from i to j at time t, i.e. , and a new directed link from i to j is rewired with a certain probability q at time t+1, q ∈ [0,1].

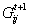Then it gets the adaptive networks at the next time step t+1.

4.4

When networks are complete and static, i.e. 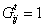, for all i , j and all t, the EHK model would degenerate to the original HK model.

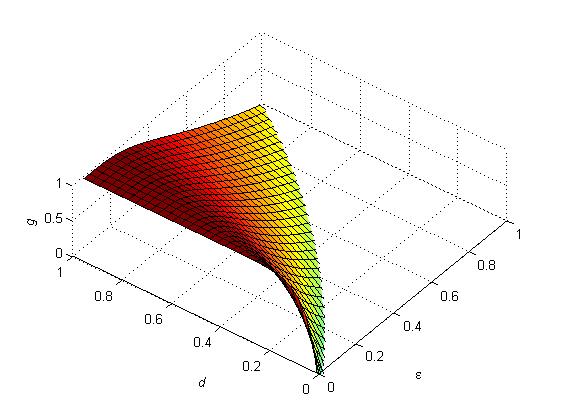
Figure 1. The decay probability g for different d and ε (d > ε).

4.5

The initial states are usually a population of n agents in a social group, forming a complex networks, such as ER random networks, small world networks or scale-free networks, with randomly assigned opinions represented by real numbers within interval (0, 1) and homogeneous or heterogeneous CL and q.

Simulation

5.1

The EHK model under bounded confidence is nonlinear and analytically unsolvable. Therefore, agent-based computational modeling and simulation has been widely used to study the influence on opinion formation with various parameters of the model and the networks.

5.2

Here, we consider a small or medium network with n nodes representing agents and K randomly directed links representing social attentions. The average in- and out-degree of the nodes are 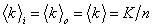. The opinions are initially randomly distributed in the open interval (0, 1). The maximum number of rounds is set to 50. Simulation results are averaged over 100 different networks.

5.3

Then, the following statistical indicators are defined, from which we can draw interesting summaries about the behaviors of the coevolution with macroscopic scale:

• AOC (Average of Opinion Clusters): the average number of opinion clusters at the end of the simulation. Since in the final state, many agents have very close but not identical opinions. Opinion clusters are formed by repeating the following rule, until there is no more new formed cluster: if the minimum of the furthest distance between opinions in any two clusters is smaller than δ (here δ=0.01), a new cluster will be formed by them. The agents in an opinion cluster may be not existed in the same network topology in which they may have no directed links between each other.
• CP (Consensus Probability): CP is defined as the relative frequency of runs that finally lead to a consensus. A larger probability of CP is more likely to reach a consensus.
• ACR(Average of Convergence Rounds): all agents update their opinions simultaneously at each discrete time t (t=1,2,3…), which is called "a round". So, discrete time t is used to denote "rounds". "Convergence rounds" is the maximum time t (the number of rounds) until all opinions are almost stable (P^t+1 satisfies formula (5)). ACR is the average number of rounds over large numbers of simulations. A smaller ACR requires fewer rounds to make all opinions get convergent.

HK model on Static Networks

6.1

Let us first consider the HK model on a static directed ER random network. Figure 2 depicts the average of opinion clusters as a function of the parameter ε, with various networks sizes and average degrees. As the CL ε increases from 0.1 to 0.6, the AOC decrease to a low level of 1, which means all opinions reach a consensus. All initial networks can always converge to the same opinion cluster over a certain level of ε, which is influenced by the size and average degree of network. With the increase of <k> or decrease of the network size n, AOC will decrease, which enlarges the range of ε leading to global consensus. This is also conformed in the CP of Figure 2. AOC is getting closer to the value of 1/(2ε) when increasing <k> or decreasing n. The rough 1/(2ε)-rule notes that the number of final opinion clusters is roughly equivalent to the value of 1/(2ε), which is reported in the DW model and the HK model (Deffuant et al. 2000; Weisbuch et al. 2002; Hegselmann & Krause 2002).

(a)                                                                                                                         (b)

Figure 2. AOC as a function of ε on different static networks. The blue dashed line corresponds to the value of 1/(2ε). (a) <k>=10, 20, 30 with the same n=1000. (b) n=100,500,1000 with the same <k>=10.

6.2

The probability of consensus CP sheds more light on the behavior of evolution, as shown in Figure 3. A small ε leads to a lot of opinion clusters as shown in Figure 2, which makes it impossible to reach a global consensus. Moderate parameter ε leads to the same opinion cluster with a certain probability, although the AOC is much larger than 1. In this moderate range of CL ε, smaller size and higher average degree of networks have a strongly effect on the increase of CP. A large ε always leads to a global consensus. The CL ε has different ranges of small, moderate and large with various networks. Increasing <k> with the same n, will enlarge the range of large ε and reduce the range of moderate ε. But Increasing <n> with the same <k>, will enlarge the range of small ε and reduce the range of large ε.

(a)                                                                                                                         (b)

Figure 3. CP as a function of ε on different static networks. (a) <k>=10, 20, 30 with the same n=1000. (b) n=100,500,1000 with the same <k>=10.

6.3

Figure 4 indicates that as ε increases, ACR decreases to a stable level of about 10 or fewer. In the meantime, increasing <k> with constant n requires fewer rounds of updating the opinions to reach a convergent state as shown in Figure 4(a). Figure 4(b) illustrates that with n increasing from 100 to 1000, ACR is distinctly increased in the range of 0.1 ≤ ε < 0.25, but there is no much increase in the range of 0.25 ≤ ε ≤ 0.6.

(a)                                                                                                                         (b)

Figure 4. ACR as a function of ε on different static networks. (a) <k>=10, 20, 30 with the same n=1000. (b) n=100,500,1000 with the same <k>=10.

6.4

When the agents are linked through a static directed ER network, increasing <k> or decreasing the number of network nodes requires fewer rounds to converge, forms fewer opinion clusters, enlarges the range of parameter ε leading to global consensus and increases consensus probability.

EHK model on adaptive networks

7.1

Let us turn to the case of directed adaptive network in which agents with far apart opinions over a certain CL can break their links. The probability of rewiring links is given by q: the larger q, the more rewiring events are likely to occur. The curves of HK in Figure 5, 6, 7 and 8 are the results of HK model on static networks for N=1000, <k>=10, as described in former section.

7.2

The tendency of AOC, CP and ACR in EHK model on adaptive networks is similar to the HK model on static networks with increasing parameter ε, as shown in Figure 5, 6, 7. But their quantities are quite different.

7.3

With q=0, the directed link can be broken, but the broken links cannot be reconnected. With the same ε as the HK model, this model gets more opinion clusters, lower probability to reach a global consensus and more rounds before convergence. But it should be noted that the difference of AOC between them is getting smaller as ε increases, because the broken probability g is decreased with the same d, as shown in Figure 1.

7.4

With very small q:0.001~0.01, all aforementioned indicators have an improvement over q=0, and much better than the ones of the HK model. AOC is very close to the value of 1/(2ε). Increasing q enlarges the range of ε leading to a global consensus. With q:0.01~0.05, there is only a little improvement on these aforementioned indicators.

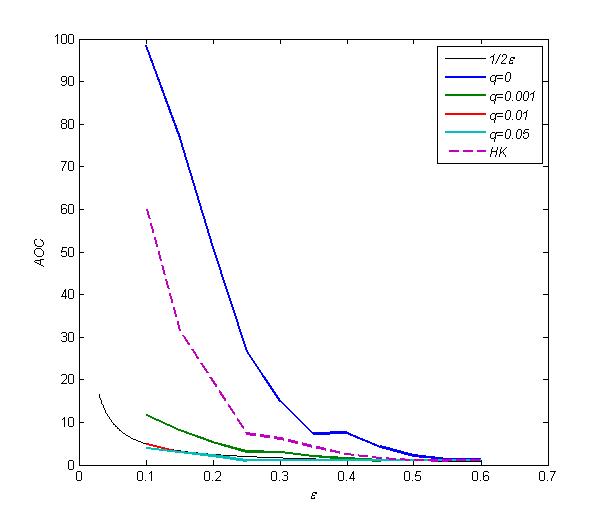
Figure 5. AOC as a function of ε for different q with n=1000, <k>=10. The black curve corresponds to the value of 1/(2ε). The dashed curve is AOC of the HK model on static networks with n=1000, <k>=10.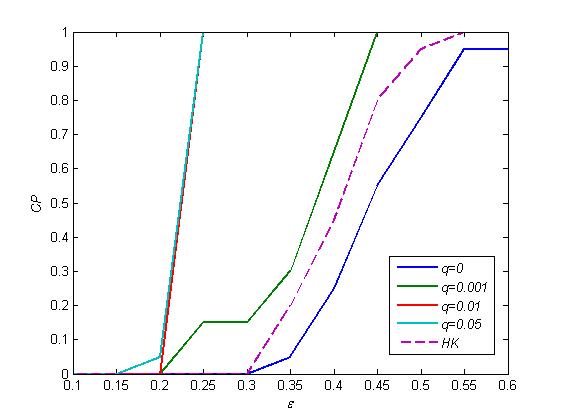

Figure 6. CP as a function of ε for different q with n=1000, <k>=10. The dashed curve is CP of the HK model on static networks with n=1000, <k>=10.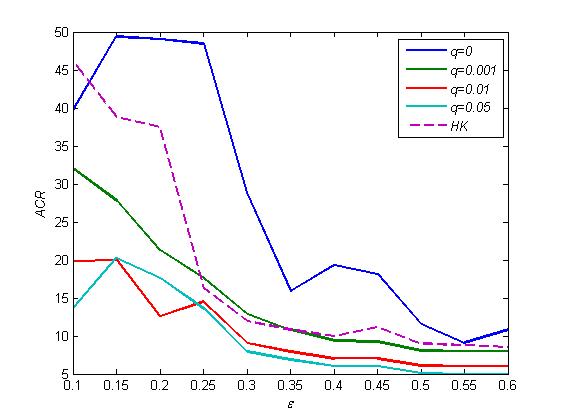

Figure 7. ACR as a function of ε for different q with n=1000, <k>=10. The dashed curve is ACR of the HK model on static networks for n=1000, <k>=10.

7.5

Figure 8 shows the average degree of final state of adaptive networks for the initial networks of n=1000, <k>=10. With q=0 and small ε, the links cannot be rewired, which makes the average degree to be decreased and the interactions of agents to be fewer than static networks. As ε increases, the average degree of adaptive networks gets closer to <k> of static networks, which makes the difference of statistical results between two networks smaller. As q increases from 0.001 to 0.05, the average degree of final networks increases and becomes larger than that of the HK model.

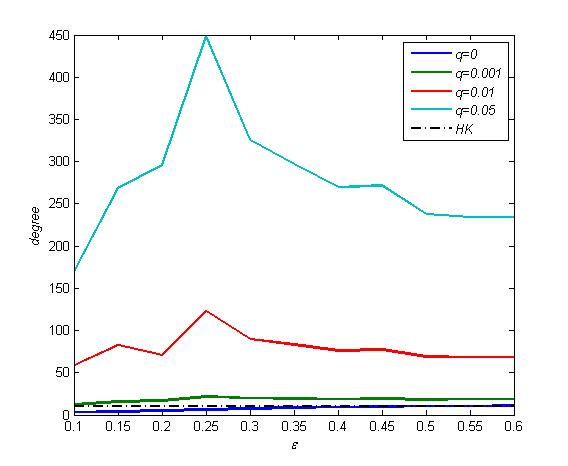
Figure 8. Final average degree as a function of ε for different q with n=1000, <k>=10. The dashed curve is the degree <k>=10 of HK model on static networks with n=1000.

7.6

We have indeed checked (not shown) that for a certain q=0.01, the increase of n or initial <k> of networks does not make much improvements on the aforementioned statistical indicators, because the average degree of final networks has exceeded a certain level of degree, as shown in Figure 9.

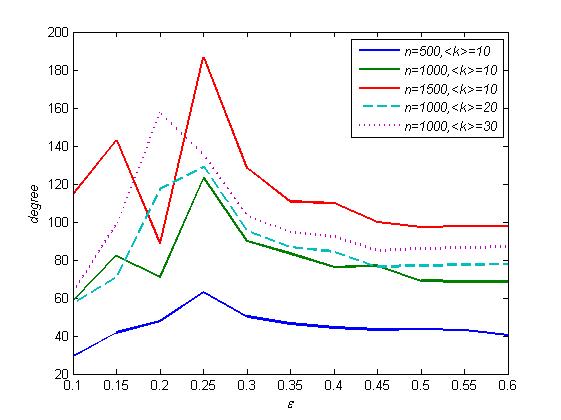
Figure 9. Final average degree as a function of ε for different networks with q=0.01.

(a) ε=0.1                                                                                                                                                         (b) ε=0.2

(c) ε=0.3                                                                                                                                                        (d) ε=0.4

Figure 10. The distribution of final opinions with ε=0.1,0.2,0.3,0.4, n=1000, <k>=10 and q=0.01.

7.7

The distribution of final opinions on adaptive directed ER networks does not maintain the typically symmetric results of the HK model with small ε as shown in Figure 10(a) and (b). The distribution of final opinions between the HK and the DW model is different, because the random order of paired interaction in the DW model often leads to a single extreme convergence; while the group interactions and simultaneous updates of the HK model lead to symmetric results. The EHK model on adaptive networks extends the HK model. The number and opinions of an agent's neighbors in EHK model vary dynamically over time, which makes the final opinions difficult to predict with small ε. But the final opinion clusters are going to converge at the opinion of about 0.5 with an increasing ε, and finally reach a consensus at the point of about 0.5, which is the same as the result of HK model, as shown in Figure 10 (c) and (d).

7.8

The adaptive case shows that the rewired rate of the EHK model has important consequences on the evolution of opinions and on the structures of interaction networks. When new links could not be rewired (q=0), the situation becomes worse than static networks, which forms more opinion clusters and lower probability of consensus and needs more rounds to converge. But just for a small rewired probability, all indicators are better than the static network. The average degree of final networks will rise with the increasing of q, which leads to form fewer opinion clusters and reaches a consensus more likely with fewer rounds of interactions. In the meantime, increasing q can enlarge the range of ε leading to a global consensus. But when q ≥ 0.01, the increase of n or the initial <k> of networks has little effect to the improvements on AOC, CP and ACR, although the average degree of networks has a huge rise.

Discussion

8.1

In this paper, we have studied the opinion dynamics on adaptive networks through the investigation of the extended HK model: directed links may be broken with a probability when difference between two opinions exceeds the confidence level ε, but new links do generally appear randomly. On static networks, the evolution of opinion is basically determined by the initial configuration of networks which includes the size of nodes and the average degree of networks. However, it is determined by the rewired probability of EHK model on adaptive networks.

8.2

The main results of the static and adaptive networks can be summarized as follows:

1. As parameter ε increases, the tendencies of AOC, CR and ACR in the EHK model on adaptive networks are similar to that of the HK model on static networks. The large confidence level ε of both models leads to influence each other more easily, and reduce the decay probability of EHK model. So the difference of AOC between two models is getting smaller as ε increases. The fewest AOC satisfies the rough 1/(2ε)-rule. Increasing <k> or decreasing n in the HK model leads AOC to get closer to the value of 1/(2ε), but increasing q in the EHK model leads to the same results.
    
   However, on the same initial networks, when q=0, aforementioned indicators of the HK model are better than that of the EHK model; when q>0, the results are opposite. Because for q=0, new links cannot be rewired, which makes the average degree of networks to be decreased and the interactions of agents to be fewer than static networks. The rewired probability of q>0 increases the <k> of network, which enhances communications between agents and fosters opinion formations.
2. Final opinion clusters have three types: 1) more than one cluster (fragmented) with small ε; 2) consensus with a certain probability with moderate ε; 3) always consensus with large ε. With the increase of ε, opinion clusters of original HK model step from plurality to polarisation and finally to consensus. So type 2 is special for the directed ER networks. The ranges of small, moderate and large are determined by n and <k> of networks in the HK model, but by q in the EHK model. The final opinions of the EHK model are not symmetric with small ε, because the number and opinions of neighbors are dynamic over time. But with an increasing ε, it will finally converge at the opinion of about 0.5, which is the same as the result of original HK model.
3. There is a certain average degree of networks which is called "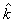" for both networks. Here, 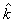is about 40, as shown in Figures 1 and 9. When the <k> is larger than 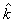, the influence of <k> on opinion formation is getting less, which means there are a little improvements on AOC, CP and ACR. When <k>=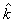, AOC, CP and ACR have almost reached their limits. That explains the results in Figure 9: when <k> have exceeded 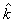, there are very close results of aforementioned indicators. But when <k> is in the range of (0, 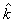), a larger <k> or fewer n leads to better results.

8.3

These findings can be used for many applications, such as decision making or opinion formation in a social group of people. Here we suppose that individuals in group are homogeneous, which means that they have the same confidence level, number of neighbors, rewired probability and randomly distributed opinions. In the process of opinion formation, the results show that it only needs to ask individuals to pay attention to a small part of people, which is also possible to lead to a few opinion clusters, even a consensus. And adding new attentions to others or the rewired probability of broken links would produce better results. The previous hypothesis about homogeneous people may be unrealistic on some real social phenomena. So in the future, we will try to validate and improve the model with the real data sets on the internet, which include the dynamic structure of real social networks, opinions about some issue and heterogeneous individuals. This is a very challenging task, but it is important and meaningful.

Appendix

Source code for the EHK model on directed adaptive networks (used as a matlab R2010a mfile)

n=1000; %node size of directed networks
t=1; %round number
epsilon=0.5; %confidence level
q=0.01; %rewired probability
%set ER networks with n nodes and K directed links
G(1:n,1:n)=0;
for i=1:n
      G(i,i)=1; %link to itself
end
degree=10; %average degree of networks
K= degree*n;
countk=0;
while countk < K
      ni=randi([1,n],1);
      nj=randi([1,n],1);
      if G(ni,nj)==0 && ni~=nj
              G(ni,nj)=1;
              countk = countk +1;
      end
end
P(t,:)=rand(1,n); %random opinion vector on interval (0,1) at time t
tMax=50; %maximum rounds
xi=0.0001;
for t=1:tMax
      I(1:n,1:n)=0;
      for i=1:n
              countop=0;
              for j=1:n
                       d(i,j)=abs(P(t,i)-P(t,j)) ;
                       if d(i,j)<= epsilon && G(i,j)==1
                                countop=countop+1;
                                w(i,j)=1;
                       else
                                w(i,j)=0;
                       end
              end
 
              %update I
              for k=1:n
                       I(i,k)=w(i,k)/countop;
              end
 
              %update G
              for j=1:n
                  if G(i,j)==1
                      dt=abs(P(t,i)-P(t,j));
                       if dt> epsilon
                               randomg=rand(1,1);
                                if randomg <=(1-exp(1-dt/epsilon))
                                        G(i,j)=0;
                                end
                       end
                  else if G(i,j)==0
                                randomq=rand(1,1);
                                if randomq <=q
                                   G(i,j)=1;
                               end
                       end
                  end
              end
         end
 
         %update P
        P(t+1,:)=I*P(t,:)';
        sumerr=0;
         for cc=1:n
                sumerr = sumerr +(P(t+1,cc)-P(t,cc))^2;
         end
         if sumerr <=xi
                  break;
         end
end
plot(P);

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 61374185). We would like to thank the JASSS reviewers who provided valuable suggestions to enhance the content of the paper.

References

CASTELLANO C., Fortunato S., & Loreto V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81, 591–646. [doi:10.1103/RevModPhys.81.591]

DEFFUANT G., Neau D., Amblard F., & Weisbuch G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(1–4), 87–98. [doi:10.1142/S0219525900000078]

DEFFUANT G., Amblard F., Weisbuch G., & Faure T. (2002). How can extremism prevail ? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation. 5, 4 <https://www.jasss.org/5/4/1.html>

EHRHARDT G. C. M. A., Marsili M., & Redondo F. V. (2006a). Diffusion and growth in an evolving networks, Int. J. Game Theory. 34, 282. [doi:10.1007/s00182-006-0025-6]

EHRHARDT G. C. M. A., Marsili M., & Vega-RedondoF. (2006b). Phenomenological models of socio-economic net-work dynamics. Phys. Rev. E, 74, 036106, [doi:10.1103/PhysRevE.74.036106]

FENG C F et al (2010). Effects of average degree of network on an order disorder transition in opinion dynamics, Chin. Phys. B, 19(4), 060203. [doi:10.1088/1674-1056/19/6/060203]

FORTUNATO S. (2004). Universality of the Threshold for Complete Consensus for the Opinion Dynamics of Deffuant et al. Int. J. Mod. Phys. C, 15, 1301–1307. [doi:10.1142/S0129183104006728]

FORTUNATO S. (2005). On the Consensus Threshold for the Opinion Dynamics of Krause Hegselmann. International Journal of Modern Physics C, 16(2), 259–270. [doi:10.1142/S0129183105007078]

FORTUNATO S., Latora V., Pluchino A., & Rapisarda A. (2005). Vector Opinion Dynamics in a Bounded Confidence Consensus Model, International Journal of Modern Physics C, 16(10), 1535–1551. [doi:10.1142/S0129183105008126]

FU F., & Wang L. (2008). Coevolutionary dynamics of opinions and networks: From diversity to uniformity, Phys. Rev. E, 78, 016104. [doi:10.1103/PhysRevE.78.016104]

GALAM S., Gefen Y., & Shapir Y. (1982). Sociophysics: a new approach of sociological collective behavior. J. Math. Sociol., 9, 1–3. [doi:10.1080/0022250X.1982.9989929]

GALAM S. & Moscovici S. (1991). Towards a Theory of Collective Phenomena: Consensus and Attitude Changes in Groups. Eur. J. Soc. Psychol., 21, 49–74. [doi:10.1002/ejsp.2420210105]

GALAM S. (2002). Minority opinion spreading in random geometry. Eur. Phys. J. B., 25(4), 403–406. [doi:10.1140/epjb/e20020045]

GANDICA Y et al (2010). Continuous opinion model in small-world directed networks. Physica A, 389, 5864–5870. [doi:10.1016/j.physa.2010.08.025]

GARGIULO F., & Huet S. (2010). Opinion dynamics on a group structured adaptive network. EPL, 91, 58004. [doi:10.1209/0295-5075/91/58004]

GIL S., & Zanette D. H. (2006). Coevolution of agents and networks: Opinion spreading and community disconnection, arXiv:cond-mat/0603295v.

GROSS T., Dommar D'Lima C. J., & Blasius B., (2006). Epidemic dynamics on an adaptive network. Phys. Rev. Lett., 96, 208701–4. [doi:10.1103/PhysRevLett.96.208701]

GROSS T., & Blasius B. (2008). Adaptive Coevolutionary Networks–A Review. J. R. Soc., Interface 5, 259. [doi:10.1098/rsif.2007.1229]

HEGSELMANN R., & Krause U. (2004). Opinion Dynamics Driven by Various Ways of Averaging. Comput. Econ., 25(4), 381–405. [doi:10.1007/s10614-005-6296-3]

HENDRICKX J. M. (2008). A generalized version of Krause's opinion dynamics model. Physica A, 387, 5255–5262. [doi:10.1016/j.physa.2008.05.018]

HEGSELMANN R., & Krause U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5 (3), 8. <https://www.jasss.org/5/3/2.html>

HOLLEY R., & Liggett T. (1975). Ergodic theorems for weakly interacting infinite systems and the voter model. Ann. Probab., 3(4), 643–663. [doi:10.1214/aop/1176996306]

HOLME P., & Newman M. E. J. (2006). Nonequilibrium phase transition in the coevolution of networks and opinions. Phys. Rev. E, 74, 056108. [doi:10.1103/physreve.74.056108]

IÑIGUEZ G, Kertész J, Kaski K K, & Barrio R A (2009). Opinion and community formation in coevolving networks. Phys. Rev. E, 80, 066119. [doi:10.1103/physreve.80.066119]

IÑIGUEZ G. et al (2011). Phase change in an opinion-dynamics model with separation of time scales. Phys. Rev. E, 83, 016111. [doi:10.1103/physreve.83.016111]

LEWENSTEIN M., Nowak A., & Latané B. (1992). Statistical mechanics of social impact, Phys. Rev. A, 45, 763–776. [doi:10.1103/PhysRevA.45.763]

KOZMA B, & Barrat A (2008a). Consensus formation on adaptive networks. Phys. Rev. E, 77, 016102. [doi:10.1103/PhysRevE.77.016102]

KOZMA B, & Barrat A (2008b). Consensus formation on coevolving networks: groups' formation and structure. J. Phys. A, 41, 2240201. [doi:10.1088/1751-8113/41/22/224020]

KURMYSHEV E., Juárez H. A., & González-Silva R. A. (2011). Dynamics of bounded confidence opinion in heterogeneous social networks: Concord against partial antagonism. Physica A, 390, 2945–2955. [doi:10.1016/j.physa.2011.03.037]

LI P. P., Zheng D. F., & Hui P. M. (2006). Dynamics of opinion formation in a small-world network. Phys. Rev. E, 73, 056128. [doi:10.1103/PhysRevE.73.056128]

LORENZ J. & Urbig D. (2007). About the Power to Enforce and Prevent Consensus. Adv. Complex Syst. 10, 251–269. [doi:10.1142/S0219525907000982]

LORENZ J. (2010) Heterogeneous bounds of confidence: meet, discuss and find consensus!. Complexity, 15(4), 43–52.

NOWAK A., Szamrej J., & Latané B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychol. Rev., 97, 362. [doi:10.1037/0033-295x.97.3.362]

PAN Z. Z. (2010). Trust, influence, and convergence of behavior in social networks. Mathematical Social Sciences, 60, 69–78. [doi:10.1016/j.mathsocsci.2010.03.007]

SINGH P., Sreenivasan S., Szymanski B. K., & Korniss G. (2012). Accelerating consensus on coevolving networks: The effect of committed individuals. Phys. Rev. E, 85, 046104. [doi:10.1103/physreve.85.046104]

SLANINA F. & Lavička H. (2003). Analytical results for the Sznajd model of opinion formation. Eur. Phys. J. B, 35, 279–288. [doi:10.1140/epjb/e2003-00278-0]

SZNAJD-WERON K., & Sznajd J. (2000). Opinion evolution in closed community. International Journal of Modern Physics C, 11(6), 1157–1165. [doi:10.1142/S0129183100000936]

SZNAJD-WERON K. (2005). Sznajd model and its application, Acta Phys. Pol. B, 36, 2537.

URBIG D., Lorenz J., & Herzberg H. (2008). Opinion Dynamics: The Effect of the Number of Peers Met at Once. Journal of Artificial Societies and Social Simulation, 11(2), 4 https://www.jasss.org/11/2/4.html.

WANG R., Chi L. P., & Cai X. (2008). Opinion Dynamics on Complex Networks with Communities. Chinese Phys. Lett., 25, 1502. [doi:10.1088/0256-307X/25/4/091]

WEISBUCH G, Deffuant G, Amblard F, et al (2002). Meet, Discuss, and Segregate!. Complexity, 7(3), 55-63. [doi:10.1002/cplx.10031]

XIA H., Wang H., Xuan Z. (2011). Opinion Dynamics: A Multidisciplinary Review and Perspective on Future Research. International Journal of Knowledge and Systems Science, 2(4), 72-91. [doi:10.4018/jkss.2011100106]

XIONG X. & Hu Y. (2012). Research on the dynamics of opinion spread based on social network services, Acta Phys. Sin., 61(15), 150509.

ZANETTE D., & Gil S. (2006). Opinion spreading and agent segregation on evolving networks. Physica D, 224, 156. [doi:10.1016/j.physd.2006.09.010]

ZHONG L. X., Ren F., Qiu T., Xu J. R., Chen B. H., & Liu C. F. (2010). Effects of attachment preferences on coevolution of opinions and networks. Physica A, 389, 2557. [doi:10.1016/j.physa.2010.02.019]

ZIMMERMANN M. G., Eguíluz V. M., & San Miguel M. (2004). Coevolution of dynamical states and interactions in dynamic networks, Phys. Rev. E, 69, 65102. [doi:10.1103/PhysRevE.69.065102]