 Abstract
Abstract
- Artificial society simulations may provide unprecedented insight into the intricate dynamics of economic markets. Such an insight may help solve the well-known black-box dilemma of business simulations, where designers prefer model concealment over model transparency. The core contribution of this work is an agent-based business simulation that models the marketplace as an artificial society of consumers. In the simulation, users assume the role of a store owner playing against an artificial intelligence competitor. The simulation can be accessed via a graphical user interface that animates the decision behavior of consumers. Consumers are modeled as agents with concrete beliefs, intentions and desires that act to maximize their utility and accomplish their purchase plans. We claim that unlike the classical equation-based approach, the visualization of market dynamics facilitated by our agent-based approach can provide important information to the user. We hypothesize that such information is key to understanding several economic concepts. To validate our hypothesis, we conducted an experiment with 30 users, where we compared the effects of the graphical animation of the market. Our results indicate that the agent-based approach has better learning outcomes both at the level of users' subjective self-assessment and at the level of objective performance metrics and knowledge acquisition tests. As a secondary contribution, we demonstrate by example how simple codification rules at the level of the utility functions of agents allow the emergence of diverse macroeconomic behavior of a two-product duopoly.
- Keywords:
- Agent-Based Modeling, Business Simulation, Consumer Behavior, Learning Processes
 Introduction
Introduction
- 1.1
-
Business simulations were created to serve as virtual environments where the learning of concepts, theories and practices from economics and management could occur in a systematic experimental way. These simulations usually consist of business games where the participant takes the role of a firm manager in a competitive market, most often against other human players (Summers 2004).
- 1.2
-
Since the 1980s much debate has been held on the black-box nature of traditional business simulations. In black-box simulations, the internal structure of the model supporting the simulation is not disclosed to the participants. Participants operate by trial and error and base their decisions on the static results that conventional equation-based models provide.
- 1.3
-
Authors such as Machuca (2000) and Größler et al. (2000) propose that business simulations should be made transparent to promote more effective learning. They argue that users should have access to information regarding the underlying model structure and be able to relate this information to the observed results. The authors claim that the additional provision of information may improve users' performance and learning acquisition.
- 1.4
-
Despite the ongoing discussion, empirical studies such as Kopainsky et al. (2011) show only a weak to moderate relation between simulation transparency and learning of users. This can be explained by the limited explanatory capabilities of the equation-based models used in the studies.
- 1.5
-
A paradigm not yet extensively applied to business simulations is the agent-based approach, whose explanatory potential has been subject to much debate (Grüne-Yanoff 2009; Waldherr & Wijermans 2013).
With the agent-based approach, the underlying operation of the simulation can be disclosed without diminishing its strategic value, as this technique can provide a natural description of an economic environment and capture its macro behavior as an emergent phenomena.
- 1.6
-
In this work, we present an agent-based business simulation and conduct an empirical study on the impact of the information provided by the agent-based approach. We start in Section 2 with a review of demand models in business simulations. Section 3 and 4 detail our agent-based simulation and underlying model of consumer behavior. In Section 5, we describe our empirical study and demonstrate that information exclusively provided by the agent-based approach can promote effective learning. In Section 6 we conclude with a discussion of our results and a reflection on our work.
 Background
Background
- 2.1
-
The problem of modeling the marketplace is perhaps the most fundamental challenge of a business simulation. In fact, the algorithms responsible for calculating market and firm level demand have been considered the most complex and demanding algorithms of a business simulation (Goosen et al. 2001).
Such algorithms are core as firms' ability to capture market share forms the essence of a business simulation.
- 2.2
-
Since Goosen (1981) first proposed a formal algorithm for business simulations, several demand models have been presented, with much effort being devoted to enhance their flexibility and validity. These models typically fall into the following four major categories, which we describe in detail in the sections below:
- Equation-based: mathematical functions model market demand and firm demand.
- Interpolation-based: an interpolation method derives the graphics of market and firm demand functions.
- Statistical-based: purchase probability distributions measure the proportion of consumers who consume a given product.
- Agent-based: the complexity of the marketplace is captured using a bottom-up approach that models the behavioral rules of each consumer. In this way, the macro behavior of the system emerges from the interaction between consumers and firms.
Equation-based models
- 2.3
-
An equation-based demand model usually consists of two functions:
- A function of market demand (Q) calculated from the average values of demand determinants such as price (P), advertising and promotion variables (M) and product quality variables (R):
- A function of firm level demand (qi) used to calculate the weight of each firm (wi) when allocating market share:
Interpolation approach
- A function of market demand (Q) calculated from the average values of demand determinants such as price (P), advertising and promotion variables (M) and product quality variables (R):
- 2.4
-
Goosen & Kusel (1993) recognized that to find general flexible mathematical functions to model market and firm demand was an intricate task. Hence, the authors proposed the interpolation approach as a method of implementing self-designed functions.
The method is a graphical approach where the simulation designer has to sketch the function desired between two variables such as price and quantity, choose a number of important points (inflection, minimum and maximum points), program an interpolation function and finally, using that function, generate the remaining points.
- 2.5
-
The interpolation method was criticized (Gold 1993) for its difficulties to model interactive effects between demand variables and for being rather time-consuming. This might explain why its adoption never became as widespread as the equation-based approach.
Statistical approach
- 2.6
-
Carvalho (1995) proposed another approach to model market demand. The author considered that previous work did not explicitly model the crucial element of a marketplace: the consumer. Hence, Carvalho proposed a model based on the so-called 'equimarginal principle' using a gamma probability distribution to simulate the preferences of consumers.
- 2.7
-
Carvalho's model received negative critics regarding the instability of its demand function, the lack of the self-claimed independence of consumers and suppliers, and the difficulties to control the distribution parameter values defining the marketplace (Gold & Pray 1995). Similarly to the interpolation approach, this type of model never became as popular as equation-based models.
Agent-based approach
- 2.8
-
Agent-based modeling can be defined as an approach to simulate complex adaptive systems comprised of several autonomous and interacting entities (Bandini et al. 2009). Parunak et al. (1998) provide an extensive discussion of the similarities and differences between the agent-based approach and traditional equation-based modeling.
- 2.9
-
Several authors (Yilmaz et al. 2006; Arai et al. 2005) have argued in favor of using the agent-based approach to generate behavior in business simulations. Industry games such as SimCity 2013 have started to adopt multi-agent systems as their main approach to economic environment modeling. In academia also, a number of agent-based games have been presented, such as the work of Umeda et al. (2009).
- 2.10
-
Extensive work has been done in the general area of agent-based models of consumer behavior. Among the most important contributions is the work of Said et al. (2002) and Delre et al. (2010). These models simulate the marketplace as a multi-agent system where consumers are agents that perform complex interactions such as imitation and social comparison. Such models have a considerable degree of complexity since they are devised to explain particular market phenomena such as lock-in and innovation diffusion.
 Business Simulation
Business Simulation
-
Figure 1: Interface of simulation including the (I.A) decisions panel, (I.B) agent-based panel and (I.C) panel with information of firms. ![\includegraphics[width=15.5cm]{richinformationinterfacec.png}](7/img1.png)
- 3.1
-
We developed an agent-based business simulation where the user plays against an artificial intelligence (AI) competitor in a two-product duopoly. The simulation is a round-based game, as it is typical in most business simulations (Kenworthy & Wong 2005). The simulation game consists of the following elements:
Firm represents the human player. The user acts as a firm and manages a bakery store where he or she can sell two distinct products (bread, cookies) to the final (artificial) consumer.
Competitor Firm represents the AI competitor to the user. The AI competitor manages a bakery store that competes with the human player to sell two products. The final consumer is agnostic regarding the type of seller (human player or artificial player).
Consumers represent the autonomous (artificial) agents of the simulation. In each round, the consumer has a given budget (I) to spend on products from the bakeries. The game considers a population of 100 consumers with an income distribution according to a Poisson distribution (λ=300). To decide on which products to purchase, the consumer uses information about the products for sale and maximizes an utility function. Consumers attempt to accomplish their intentions sequentially in a random order.
Products represent the goods sold by the firms to consumers. In the simulation , we consider two products: bread and cookies. We assume that marginal costs are constant and equal for both firms (USD 10). The two products have equal marginal utilities as the utility function of consumers is the following:
where x1, x2 represent the quantities of products 1 (bread), 2 (cookies) that the consumer can purchase at prices p1, p2 with a budget I. - 3.2
- Fig. 1 depicts the simulation interface and its three fundamental elements: (I.A) decisions panel, (I.B) agent-based simulation panel and (I.C) panel with information about the firms.
- 3.3
- In each round, the human player has to decide on two issues using the decisions panel I.A: (1) quantity for sale and (2) selling price of products. After the user submits his/her decisions in panel I.A, the AI competitor submits its decisions. The human player and the AI competitor decide simultaneously without knowing each other decisions for that round.
- 3.4
- The reasoning algorithm of the AI competitor is based on Cournot's adjustment model, first proposed in the context
of a duopoly model by Cournot (1838). The AI competitor assumes that the human player (1) will set the prices of products equal to the market prices of the last market quantities sold and (2) set the same quantities for sale as in the previous round. The AI competitor sets the price of products equal to the prices it predicts the human player is going to set and chooses quantities for sale as best responses to the quantities it assumes the human player is going to chose.
- 3.5
- The performance of the human player (and AI competitor) is evaluated according to their cumulative profits. The user wins the game if s/he either (i) has more cumulative profits than his or her AI competitor at the end of the game (determined by a pre-set number turns) or (ii) is able to bankrupt his or her AI competitor. Both firms start with an initial capital of USD 10,000.
Figure 2: Interface of CAPSTONE simulation (http://www.capsim.com/business-simulations/products/capstone.html). ![\includegraphics[width=10cm]{capstone.jpg}](7/img5.png)
- 3.6
-
Note that existing equation-based simulations usually do not present results to participants with real-time animations, as they can only display the final output of a demand equation at the end of each round. Hence, results are presented statically through the use of spreadsheets. Fig. 2 shows an example of a traditional equation-based business simulation interface.
Figure 3: Participants can analyze performance indicators changing in virtual time as the simulation runs (Panel I.C - Information of firms). ![\begin{subfigure}
% latex2html id marker 110
[b]{0.305\textwidth}
\includegraph...
...idth]{consumers01a.png}
\caption{At start of round simulation}
\end{subfigure}](7/img6.png)
![\begin{subfigure}
% latex2html id marker 116
[b]{0.3\textwidth}
\includegraphic...
...twidth]{consumers02a.png}
\caption{Middle of round simulation}
\end{subfigure}](7/img7.png)
(a) Start of round (b) Middle of round - 3.7
-
In contrast, in our simulation, the results of a round are not the outcome of an equation. Instead, results emerge from the complex interaction of several consumer agents during a period of time. Consequently, in each round, participants can analyze in virtual time the change of several indicators of firms' performance, such as quantities sold, stock and profit (see Fig. 3).
- 3.8
-
Importantly, our agent-based approach can show how performance indicators change in response to the behavior of consumer agents. The intention of a consumer to purchase a product is shown by an animation where an icon representing a customer moves from a house icon to a store icon (see Fig. 4). If consumers change their purchase plans, they may visit the same bakery several times during the same round.
Figure 4: The agent-based simulation allows analysing the behavior of consumers in virtual time. ![\begin{subfigure}
% latex2html id marker 110
[b]{0.305\textwidth}
\includegraph...
...idth]{consumers01a.png}
\caption{At start of round simulation}
\end{subfigure}](7/img8.png)
![\begin{subfigure}
% latex2html id marker 116
[b]{0.3\textwidth}
\includegraphic...
...twidth]{consumers02a.png}
\caption{Middle of round simulation}
\end{subfigure}](7/img9.png)
(a) Consumers try to accomplish their purchase plans (b) Consumers return home and reformulate their purchase plans - 3.9
-
When elaborating their purchase plans, consumers are aware of product prices but not of product availability at stores. Accordingly, consumers may fail to accomplish their intentions if a product is not available at a particular store. In such case, they may go to other stores or give up on their purchase intentions. Consumers display the level of accomplishment of their intentions by a graphical change of their state. Satisfied consumers, i.e., consumers who are able to purchase all the products they intended to get at a given store, are represented with green color while dissatisfied consumers are represented with red color (see Fig. 4b).
 Consumer Model
Consumer Model
- 4.1
-
While several models of consumer behavior have been presented (Delre et al. 2010; Lee et al. 2013; Sengupta & Glavin 2013), these usually are not suited for business simulations. They aim to explain particular phenomena and are rather complex. Teach & Murff (2008) argue that the trend to develop more and more complex models may in fact hinder the educational effectiveness of business simulations. Among other arguments, the authors challenge the pre-established view that the amount of cognitive processing of users relates to complexity of simulation model. We agreed to this assessment and thus created a simple agent-based model for our business simulation.
A simple agent-based model
- 4.2
-
In our simulation, consumer behavior is based on the deliberative Beliefs, Desires and Intentions (BDI) architecture (Bratman 1987), perhaps the best known and most studied model of practical reasoning agents.
In our architecture, the internal state of the (artificial) consumer consists of the following elements illustrated in Fig. 5:
Beliefs represent the information the consumer has about the current state of the world, i.e., the marketplace, and its own internal state. Two types of beliefs are considered:
- Belief in the availability of a particular product at a store.
- Belief that given its available budget (I), the consumer is able to purchase products.
Intentions represent the possible courses of action of the consumer. Purchase intentions are generated during the reasoning process of the consumer, each for a possible bundle of products given the agent's budget restriction. A purchase intention is characterized by a tuple (x11, x12, x21, x22) with xij representing the quantity of product i from firm j desired by the agent.
- 4.3
-
The reasoning process of a consumer consists in the following steps:
- Step 1
- The consumer verifies three conditions: (1) if the desire to consume goods is a current goal, (2) the agent holds the belief in its economic capability and (3) at least one belief in the availability of products at stores. If all these three conditions hold, the reasoning process proceeds to Step 2. Otherwise, the reasoning process ends.
- Step 2
- For each affordable combination of goods the consumer generates a purchase intention. The generation of intentions is grounded in the beliefs regarding the availability of a product on the market and its economic capability.
For illustration purposes, consider a scenario where the human player (Player 1) sets prices p1=200 and p2=200 and the AI competitor (Player 2) sets p1=400 and p2=400. A consumer with a budget of 400 believing that stores have all products available generates five consumption intentions at this step. The generated intentions correspond to all possible combinations of products it can afford given its current budget: (1,1,0,0), (2,0,0,0), (0,2,0,0), (0,0,1,0) and (0,0,0,1).
- Step 3
- The consumer selects a preferred intention from the list of purchase intentions according to the maximization of an utility function. In case of identical utility values, a random factor is used. Utility function (1) is used to simulate the preferences of the consumer.
- Step 4
- The consumer attempts to accomplish its preferred purchase intention as an effective purchase plan. At this point, all the simulated consumers attempt to purchase their desired products in sequence in a random assortment. The accomplishment of an agent's purchase plan thus depends on its indirect interaction with its peers.
- Step 5
- The consumer updates its beliefs and desires as follows:
- Economic capability belief: according to the amount spent on successful purchases, the agent updates its available budget and the belief in its economic capability if it still has money left to buy another unit of an available product
- Product availability belief: the agent abandons its belief in the availability of a product at a store if its attempt to purchase a given product at a store was unsuccessful
- Desire to consume: if the list of intentions generated in Step 2 is empty the agent drops its desire to consume
- 4.4
-
While our business simulation simulates a two-product duopoly with singular market dynamics, our model of consumer behavior was designed to be able to accommodate the simulation of diverse market structures. The use of distinct utility functions in Step 3 can lead to a myriad of emergent economic phenomena. On this diversity lies much of the potential of the agent-based approach as opposed to the equation-based approach. For illustrative purpose, we provide specific examples of utility functions that can cover the major economic phenomena addressed in introductory microeconomics textbooks such as Frank & Glass (1997).
Simulation of independent goods
- 4.5
-
Independent goods can be simulated in our model by introducing different budget restrictions for each good. The following equations illustrate a market of two independent goods.
Simulation of effects of changes in price and income
It is possible to simulate ordinary as well as inferior and normal goods using our model and the following construction. This construction also implements the concept of diminishing marginal utility by the use of a decreasing preference function (bi(j)) (7). With this set of equations we can also simulate Veblen goods by introducing the price of the good in the definition of the preference function (bi(j, pi)). As the price increases, the consumer can perceive this increase as an evidence of high quality. A similar preference function (bi(j, ai)), varying with the exposure of the consumer to advertising (ai), can model advertising effects.
Simulation of substitute and complementary goods
It is possible to simulate substitution effects in our model. For instance, Equation 9 allows simulating perfect substitute goods while equation 10 allows simulating substitute goods with different marginal utility rates.
Complementary goods can be simulated by introducing a virtual complementary product to the consumer's utility function with r1 and r2 representing the ratio of products 1 and 2 which compose the ''virtual'' complementary product 12:
 Experiment
Experiment
- 5.1
-
We conducted an experiment with users to investigate how the information provided by the agent-based approach influences learning with business simulations. To assess learning we used the classical four-level framework of Kirkpatrick (1959). To apply this framework we followed the guidelines of Schumann et al. (2001) on how to adapt Kirkpatrick's model to business simulations.
- 5.2
-
We decided to assess two of the four levels of Kirkpatrick's model: reaction and learning. The reaction level assesses how the learner perceives the simulation experience. At this level, we were interested in how human players perceive their learning. The learning level evaluates the extent to which participants change their attitudes, improve their knowledge or increase their skill within the context of a simulation session. At this level we were interested in the improvement of performance in playing the business simulation and the acquisition of basic concepts related with behavior of firms and markets. Based on these two levels we formulated three main hypotheses:
- Reaction Hypothesis (Reaction Level): Human players subjectively perceive that they learn more when agent-based information is present.
- Economic Concept Acquisition Hypothesis (Learning Level): Human players' performance on tests about economic concepts is better when agent-based information is present.
- In-Simulation Performance Hypothesis (Learning Level): Human players' performance in the simulation is better when agent-based information is present.
- 5.3
-
Before proceeding, we briefly explain why we did not consider the other two levels of Kirckpatrick's framework. The behavior level requires assessing how participants are able to apply the newly acquired knowledge and skills to new settings. Given the difficulties associated with such assessment, this level was not considered. We also did not evaluate the results level which consists of the evaluation of the return on investment of the learning experience. This level was not applicable in the context of our experiment.
Method
Subjects and Design
- 5.4
-
Thirty subjects from the National Institute of Informatics participated in the study. There were 6 females and 24 males between 22 and 39 years of age (average 27 years). All subjects were students or staff at the institute, recruited through flyers. 25 subjects (83%) had previous experience with computer simulations, 7 subjects (23%) had previous experience with business simulations and 6 subjects (20%) were acquainted with concepts from economics. Subjects were paid an equivalent of USD 10 for participation. To provide a further incentive for good performance, an extra amount, equivalent to USD 5, was awarded to each winning participant.
Figure 6: Interface of simulation without the information tools provided by the agent-based approach. ![\includegraphics[width=0.8\textwidth]{sparseinformationinterfacec.png}](7/img15.png)
- 5.5
-
We prepared two conditions as independent variables:
- Rich information (RI) condition: here subjects play the simulation with the complete set of information tools provided by the agent-based approach. Accordingly, subjects use the graphical interface shown in Fig. 1.
- Sparse information (SI) condition: subjects play the simulation without the set of information tools provided by the agent-based approach. Subjects use the graphical interface shown in Fig. 6.
- 5.6
-
The dependent variable of our study was the learning outcome of the participants. We assessed this variable using the reaction and learning levels of Kirckpatrick's framework with the following metrics:
reaction was measured by analyzing subjects' answers to a post-experiment questionnaire;
learning was measured by using two approaches:
- Pre-experiment test and post-experiment test: These tests aimed to measure the knowledge of participants on a range of economic topics related with the behavior of firms and markets.
- Behavior logging: The behavior of participants was logged during the simulation sessions. To assess subjects' performance we used the following three metrics: (1) number of rounds to win game, (2) profit per round, and (3) cumulative profits.
- 5.7
-
In the study, a between-subject design was used to compare the RI and SI conditions. Subjects were assigned to the conditions randomly. During the experiment, subjects were seated in front of a laptop computer and used a mouse to interact with the simulation.
Materials
- 5.8
-
In this section, we briefly review the materials used in the experiment.
Instructions
The instructions provided to the subjects consisted of (i) a description of the purpose of the experiment, (ii) instructions on how to play the game, and (iii) the equation of market demand. Participants were told that the experiment was intended to investigate people's decision process in a business simulation.Tests
The pre-experiment test and post-experiment test consisted of the same set of five multiple-choice questions. Each question was devised to assess the subject's knowledge about a particular economic concept. Table 1 presents the list of questions used.Questionnaire
The post-questionnaire is concerned with the reaction level of the subjects. We used a 7-point Likert scale. Table 2 presents the two statements that aimed to investigate subjects' subjective perception of their knowledge acquisition.Table 1: Questions of knowledge acquisition tests. Economic Concept ID Question Law of demand E-Q1 If a firm increases the price of a product (with everything else constant) what happens? Substitute Products E-Q2 Consider a market with two firms A and B competing to sell the same product. If firm A increases its price (with everything else constant) what happens? E-Q3 Consider a market with two firms A and B competing to sell the same product. If firm A decreases its price (with everything else constant) what happens? Behavior of firms E-Q4 Consider a market with two firms competing to sell the same product. The goal of each firm is to increase its working capital. Each firm can decide on the price and quantity for sale of its product. In this scenario, what is the best strategy of a firm? Market Behavior E-Q5 Consider a market with two firms competing to sell two products A and B. The goal of each firm is to increase its working capital. Each firm can decide on the price and quantity for sale of its product. Assume each firm has a limited warehouse capacity and a fixed cost per unit. In this scenario, what do we predict that happens after some time?
Procedure
- 5.9
-
The study was conducted by an experimenter and a non-technical assistant, and was divided into five main parts:
- Welcome (5 min): subjects are welcomed to the study and read the instructions
- Profiling and pre-experiment test (10 min): subjects fill in a profiling form and answer the knowledge acquisition test shown in Table 1
- Training (5 min): subjects play the simulation for two rounds as a training session
- Simulation (40 min): subjects play the business simulation for 15 rounds
- Reaction questionnaire and post-experiment test (10 min): subjects answer the questionnaire shown in Table 2 and the knowledge acquisition test shown in Table 1
- 5.10
-
Finally, the subjects receive the reward. Each experiment lasted up to 1 hour and 10 minutes.
Results
Reaction Hypothesis
- 5.11
-
In this section we analyze the results of the reaction questionnaire in Table 2 to compare the subjective perception of subjects on how much they learned between the RI condition and the SI condition. Results from the the questionnaires suggest that subjects in the RI condition felt more strongly they learned about markets (Mean = 5.71, STD = 0.73) and behavior of firms (Mean = 5.93, STD = 0.73) than students in the SI condition (Mean = 4.93, STD = 1.53 and Mean = 4.60, STD = 1.30).1 In particular, Student t-tests (unequal variances) showed that the agreement levels of subjects on questions R-Q1 and R-Q2 were statistically different between the RI and SI conditions (p < 0.05). Figure 8 summarizes the mentioned findings. Based on these findings, we claim that the Reaction Hypothesis is confirmed.
Figure 8: Agreement levels on questions R-Q1 and R-Q2 for RI and SI conditions. 1: "strongly disagree"; 2: "disagree"; 3: "weakly disagree"; 4: "neutral"; 5: "weakly agree"; 6: "agree"; 7: "strongly agree". ![\includegraphics[width=0.8\textwidth]{reactionresults.png}](7/img17.png)
Economic Concept Acquisition Hypothesis
- 5.12
-
In this section we analyze the results of the pre-experiment and post-experiment knowledge tests to compare the knowledge acquisition of subjects between the RI condition and the SI condition. Here, knowledge acquisition or improvement means that subjects, who gave wrong answers in the pre-experiment test, were able to give the correct answer in the post-experiment test.
- 5.13
-
Results from our pre-experiment and post-experiment knowledge tests (Table 1) suggest that a high percentage of students already knew the concept of the law of demand (60%) and substitute goods (70%) – even though only 20% of the subjects reported having previous knowledge in economics. Our results suggest that the subjects unacquainted with these concepts were better able to learn them in condition RI than in condition SI. As shown in Fig. 9, in comparison to condition SI, condition RI had a higher proportion of subjects showing signs of knowledge improvement for questions E-Q1 (law of demand) and E-Q2 (substitute products).
- 5.14
-
In contrast with the law of demand and substitute products, the results of our pre-experiment tests indicate that only 27% of students had prior knowledge on strategic behavior of firms (E-Q4) and only 30% of students had prior knowledge on the expected outcome of the simulated market (E-Q5).
Results of our post-experiment tests on those questions suggest that the subjects unacquainted with the topics of firm and market behavior were better able to learn them in condition RI rather than in condition SI. As shown in Fig. 9, condition RI had a higher proportion of subjects showing signs of knowledge improvement in questions E-Q4 and E-Q5, than condition SI. Differences in learning between the two conditions were particularly pronounced when testing the knowledge of participants on the predicted outcome of the simulated market (difference of 26% on E-Q5). These results confirm the Economic Concept Acquisition Hypothesis.
In-Simulation Performance Hypothesis
- 5.15
-
Here we want to compare subjects' actual in-simulation behavior between the RI condition and the SI condition. As metrics we used (1) the number of rounds to defeat the AI competitor, (2) the profits per round (USD) and (3) cumulative profits (USD).
- 5.16
-
Among the 19 subjects who were able to defeat the AI competitor, 10 were under the RI condition and 9 under the SI condition. Interestingly, the subjects in the RI condition were able to win in less rounds (Mean = 9.3, STD = 1.16) than subjects in the SI condition (Mean = 13.1, STD = 2.93). This difference was statistically significant according to a Student t-test (p<0.01).
- 5.17
-
We compared the average profit per round of subjects under RI condition and under SI condition. In line with the previous results, we found that subjects had higher profits per round in RI condition (Mean = 4,172, STD = 2,772) than in SI condition (Mean = 2,045, STD=2,273)2. This difference was statistically significant according to a Student t-test (p<0.05).
Figure 10 depicts the evolution of average profit per round in condition RI and SI. As shown, for the majority of the rounds (73.3%), subjects were able to achieve higher profits per round under the RI condition.
- 5.18
-
Finally, we also compared RI and SI conditions according to cumulative profits of subjects at the end of the seventh round (the minimum set of rounds played by subjects). An analysis of our results showed that, as expected, subjects had higher cumulative profits in the RI condition (Mean = 23,167, STD = 16,628) than in the SI condition (Mean = 10,508, STD=13,478)3. This difference was statistically significant according to a Student t-test (p<0.05).
 Discussion and Conclusions
Discussion and Conclusions
- 6.1
-
We described a business simulation where the marketplace is modeled as a complex system composed of several interacting consumer agents. The unique feature of our simulation is an interface that animates the operation of the agents (consumers) and thus allows the user to visualize the dynamics of the marketplace.
- 6.2
-
The core question of our work is whether users actually learn better when provided with information facilitated by an agent-based simulation of an economic environment. To answer this question we set out to investigate learning at two fundamental levels: the reaction and learning levels of Kirckpatrick's classical framework.
- 6.3
-
The first level, reaction, consisted on the self-assessment of learning by subjects. Our results support the hypothesis that subjects perceive better learning with the agent-based information. Of course, this subjective finding is not sufficient to support the claim of improved actual learning. As has been shown (Sitzmann et al. 2010), the correlation between self-assessment and actual learning is only moderate. However, this is an important result since it suggests that participants of business simulations are more engaged in their learning processes when having access to agent-based information.
- 6.4
-
The second level, learning, allowed us to objectively assess learning based on factual evidence. Supported by the outcome of pre-experiment and post-experiment knowledge acquisition tests, we concluded that subjects are better able to learn concepts from economics, such as the law of demand, substitute products, strategic behavior and dynamics of markets, when agent-based information is present. We also observed that subjects demonstrate better in-simulation performance in the presence of agent-based information.
- 6.5
-
Designing a convincing real-time interface for an agent-based system is not an easy task. The difficulty of such endeavor tends to increase with the complexity of the agent-based model. In our work, we were able to create an interface that had a proven positive influence on the learning processes of users, as evidenced by the results of our study. This is a significant achievement of our design.
Nonetheless, novel techniques from the field of intelligent user interfaces could be applied to further improve the current implementation. It seems to us, that this topic is quite unexplored and can be of great interest both for the community of business simulations and for the general community of artificial societies and social simulation.
- 6.6
-
Regarding the future improvement of our agent-based model we face two of the traditional challenges of designers of agent-based models (Knoeri et al. 2011). The first challenge is how to ensure model validation, and the second challenge is how to create a simulation with behaviorally realistic agents.
Our implementation of rational choice theory is based on the BDI architecture, in line with with classical microeconomics. Proper validation of the proposed model can be achieved using one or more of the validation approaches proposed by Moss (2008).
- 6.7
-
Sun & Naveh (2004) raised the interesting question whether agent-based models might benefit from having agents with more cognitive realism. As stated before, it is not clear if learning, the primary purpose of business simulations, depends on realism and complexity. Accordingly, we must carefully study this topic in the future and try to balance the need for increased realism with effective learning processes.
- 6.8
- To summarize, we have outlined the three main research directions to further our study: (1) intelligent agent-based interfaces, (2) extending and validating the present agent-based model, and (3) increasing its realism and complexity.
 Notes
Notes
- 1
- Prior to statistical analysis, an outlier was removed from the data of the reaction questionnaire. This subject was under condition RI and showed strong disagreement when asked if he had learned about the behavior of firms (R-Q1) and markets (R-Q2) with the simulation. When asked about the reasons for his strong disagreement the subject reported that he felt that the simulation did not portray a real-life market. Surprisingly, the subject was able to win the simulation in few number of rounds (8 compared to the mean of 9.3 of condition RI), answered all the knowledge acquisition questions correctly and showed a deep knowledge of the simulated market when questioned. His assessment (1: strongly disagree) of sentences R-Q1 and R-Q2 largely deviated from the average classification (Mean = 5.71 and Mean = 5.93) of the remaining subjects under the same condition. In summary, our experiment was not designed for experts in economics.
- 2
- Prior to this statistical analysis, an outlier was removed from the data. This subject was under RI condition and exhibited a very low profit per round (16.8) largely deviating from the average (Mean = 4,172) of the remaining data.
- 3
- Prior to this statistical analysis, three outliers were removed from the data. One was in condition RI reporting a cumulative profit of 298, comparably lower than the average (Mean=23,167) while the other two were in condition SI, reporting cumulative profits of 36,573 and 38,620, three times higher than the average of the set (Mean=10,508).
 References
References
-
ARAI, K., DEGUCHI, H. & MATSUI, H. (2005).
Agent-Based Modeling Meets Gaming Simulation. Springer. [doi:10.1007/4-431-29427-9]
BANDINI, S., MANZONI, S. & VIZZARI, G. (2009). Agent based modeling and simulation: An informatics perspective. Journal of Artificial Societies and Social Simulation 12(4), 4. https://www.jasss.org/12/4/4.html. [doi:10.1007/978-0-387-30440-3_12]
BRATMAN, M. (1987). Intentions, Plans, and Practical Reason. Harvard University Press.
CANNON, J. N., CANNON, H. M. & SCHWAIGER, M. (2012). Modeling the 'profitable-product death spiral': Accounting for strategic product-mix interactions in marketing simulation games. Simulation & Gaming 43(6), 761-777. [doi:10.1177/1046878111434474]
CARVALHO, G. (1995). Modeling the law of demand in business simulators. Simulation & Gaming 26(1), 60-79. [doi:10.1177/1046878195261006]
COURNOT, A.-A. (1838). Recherches sur les principes mathématiques de la théorie des richesses. Hachette.
DELRE, S., JAGER, W., BIJMOLT, T. & JANSSEN, M. (2010). Will it spread or not? The effects of social influences and network topology on innovation diffusion. Journal of Product Innovation Management 27(2), 267-282. [doi:10.1111/j.1540-5885.2010.00714.x]
FRANK, R. H. & GLASS, A. J. (1997). Microeconomics and behavior. McGraw-Hill.
GOLD, S. (1993). Modeling interactive effects in mathematical functions for business simulations: A critique of Goosen and Kusel's interpolation approach. Simulation & Gaming 24(1), 90-94. [doi:10.1177/1046878193241010]
GOLD, S. & PRAY, T. (1995). The use of the gamma probability distribution: A critique of Carvalho's demand simulator. Simulation & Gaming 26(1), 80-87. [doi:10.1177/1046878195261007]
GOLD, S. C. & PRAY, T. F. (1997). Modeling attributes in demand functions of computerized business simulations: An extension of Teach's gravity flow algorithm. Developments in Business Simulation and Experiential Exercises 24, 132-141.
GOOSEN, K., JENSEN, R. & WELLS, R. (2001). Purpose and learning benefits of simulations: A design and development perspective. Simulation & Gaming 32(1), 21-39. [doi:10.1177/104687810103200104]
GOOSEN, K. & KUSEL, J. (1993). An interpolation approach to developing mathematical functions for business simulations. Simulation & Gaming 24(1), 76-89. [doi:10.1177/1046878193241009]
GOOSEN, K. R. (1981). A generalized algorithm for designing and developing business simulations. Developments in Business Simulation and Experiential Learning 8, 41-47.
GRößLER, A., MAIER, F. H. & MILLING, P. M. (2000). Enhancing learning capabilities by providing transparency in business simulators. Simulation & Gaming 31(2), 257-278. [doi:10.1177/104687810003100209]
GRüNE-YANOFF, T. (2009). The explanatory potential of artificial societies. Synthese 169(3), 539-555. [doi:10.1007/s11229-008-9429-0]
KENWORTHY, J. & WONG, A. (2005). Developing managerial effectiveness: Assessing and comparing the impact of development programmes using a management simulation or a management game. Developments in Business Simulations and Experiential Learning 32, 164-75.
KIRKPATRICK, D. (1959). Techniques for evaluating training programs (a four-part series beginning in the november issue). Journal of American Society of Training Directors 13(11), 3-9.
KNOERI, C., BINDER, C. R. & ALTHAUS, H.-J. (2011). An agent operationalization approach for context specific agent-based modeling. Journal of Artificial Societies and Social Simulation 14(2), 4. https://www.jasss.org/14/2/4.html.
KOPAINSKY, B., ALESSI, S. M. & PIRNAY-DUMMER, P. (2011). Providing structural transparency when exploring a model's behavior: Effects on performance and knowledge acquisition. In: 29th International Conference of the System Dynamics Society.
LEE, K., KIM, S., KIM, C. O. & PARK, T. (2013). An agent-based competitive product diffusion model for the estimation and sensitivity analysis of social network structure and purchase time distribution. Journal of Artificial Societies and Social Simulation 16(1), 3. https://www.jasss.org/16/1/3.html.
MACHUCA, J. A. (2000). Transparent-box business simulators: An aid to manage the complexity of organizations. Simulation & Gaming 31(2), 230-239. [doi:10.1177/104687810003100207]
MOSS, S. (2008). Alternative approaches to the empirical validation of agent-based models. Journal of Artificial Societies and Social Simulation 11(1), 5. https://www.jasss.org/11/1/5.html.
PARUNAK, H. V. D., SAVIT, R. & RIOLO, R. L. (1998). Agent-based modeling vs. equation-based modeling: A case study and users' guide. In: Multi-Agent Systems and Agent-Based Simulation. Springer.
SAID, L., BOURON, T. & DROGOUL, A. (2002). Agent-based interaction analysis of consumer behavior. In: 1st International Conference on Autonomous Agents and Multiagent Systems. ACM.
SCHUMANN, P. L., ANDERSON, P. H., SCOTT, T. W. & LAWTON, L. (2001). A framework for evaluating simulations as educational tools. Developments in Business Simulation and Experiential Learning 28, 215-220.
SENGUPTA, A. & GLAVIN, S. E. (2013). Predicting volatile consumer markets using multi-agent methods: Theory and validation. In: Simulation in Computational Finance and Economics: Tools and Emerging Applications (ALEXANDROVA-KABADJOVA, B., MARTINEZ-JARAMILLO, S., GARCIA-ALMANZA, A. L. & TSANG, E., eds.). IGI Global, Hershey, pp. 339-358.
SITZMANN, T., ELY, K., BROWN, K. G. & BAUER, K. N. (2010). Self-assessment of knowledge: A cognitive learning or affective measure? Academy of Management Learning & Education 9(2), 169-191.
SUMMERS, G. J. (2004). Today's business simulation industry. Simulation & Gaming 35(2), 208-241. [doi:10.1177/1046878104263546]
SUN, R. & NAVEH, I. (2004). Simulating organizational decision-making using a cognitively realistic agent model. Journal of Artificial Societies and Social Simulation 7(3) 5. https://www.jasss.org/7/3/5.html.
TEACH, R. D. (1990). Demand equations which include product attributes. Developments in Business Simulation and Experiential Learning 17, 161-166.
TEACH, R. D. & MURFF, E. J. (2008). Are the business simulations we play too complex? Developments in Business Simulation & Experiential Exercises 35, 205-211.
UMEDA, T., ICHIKAWA, M., KOYAMA, Y. & DEGUCHI, H. (2009). Evaluation of collaborative filtering by agent-based simulation considering market environment. Developments in Business Simulation and Experiential Learning 36, 214-222.
WALDHERR, A. & WIJERMANS, N. (2013). Communicating social simulation models to sceptical minds. Journal of Artificial Societies and Social Simulation 16(4), 13. https://www.jasss.org/16/4/13.html.
YILMAZ, L., ÖREN, T. & AGHAEE, N.-G. (2006). Intelligent agents, simulation, and gaming. Simulation & Gaming 37(3), 339-349. [doi:10.1177/1046878106289089]
![\includegraphics[width=12cm]{bdia.png}](7/img10.png)
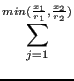 b12(j)
b12(j)![\includegraphics[width=0.8\textwidth]{economiconcept.png}](7/img18.png)
![\includegraphics[width=1\textwidth]{averageprofitperround.png}](7/img19.png)