Abstract

To maintain stability yet retain the flexibility to adapt to changing circumstances, social systems must strike a balance between the maintenance of a shared reality and the survival of minority opinion. A computational model is presented that investigates the interplay of two basic, oppositional social processes—conformity and anticonformity—in promoting the emergence of this balance. Computer simulations employing a cellular automata platform tested hypotheses concerning the survival of minority opinion and the maintenance of system stability for different proportions of anticonformity. Results revealed that a relatively small proportion of anticonformists facilitated the survival of a minority opinion held by a larger number of conformists who would otherwise succumb to pressures for social consensus. Beyond a critical threshold, however, increased proportions of anticonformists undermined social stability. Understanding the adaptive benefits of balanced oppositional forces has implications for optimal functioning in psychological and social processes in general.

Keywords:

Cellular Automata, Social Influence, Opinion Dynamics

Introduction

1.1

What basic social processes are necessary for a social system to maintain stability, yet retain the flexibility to adapt to changing circumstances? A shared reality reflecting the convergence of values, opinions, norms, and knowledge is clearly essential for social harmony and coordinated collective action (Festinger 1950; Steiner 1972). Such uniformity, however, can hinder long-term adaptation. Diversity of opinion among members of a social system—whether an ad hoc group or a society—is essential to correct collective decisions that prove counter-productive (Janis 1972), to decrease collective error (Page 2007), and to generate new courses of action in response to changing circumstances and information (Page 2008).

1.2

Research relevant to this issue has typically stressed the importance of a confident and consistent minority group (e.g., Moscovici & Nemeth 1974). Nowak, Szamrej, and Latané (1990) developed a computational model that demonstrated how a minority group gains such strength and can resist the influence of the majority. In their model, a small number of highly influential agents act as anchors for minority opinion clusters, enabling neighboring conformists to hold the minority opinion they would otherwise relinquish. Minorities survive, in other words, because of the same conformity pressures that promote convergence on a majority position. The present research investigated whether there is another viable mechanism by which minority opinion can survive, and do so without the support of highly influential agents. In particular, rather than assuming that all individuals display conformity, we investigated the fate of minority opinion when some individuals without above-average influence behave in opposition to group pressure.

1.3

Despite the propensity for groups to converge on a shared reality (Asch 1956; Deutsch & Gerard 1955; Festinger et al. 1950; Latané 1981; Myers & Lamm 1976; Schachter 1951), people sometimes display an opposing tendency to act against prevailing group norms and sentiments for the sake of being different (Imhoff & Erb 2009; Leonardelli et al. 2010; Maslach et al. 1985; Nail et al. 2000; Nowak et al. 2013a). To be sure, the anticonformity tendency is suppressed in certain group contexts such as groupthink (Janis 1972) and deindividuation (Zimbardo 1969). But even in settings stacked in favor of conformity tendencies, some individuals resist pressures for uniformity and instead express judgments and opinions that conflict with the prevailing group position (Imhoff & Erb 2009). This tendency, moreover, is often judged to be socially desirable despite its potentially disruptive effects (Dar-Nimrod et al. 2012).

1.4

Individuals who consistently oppose group norms on all matters are no doubt rare, but one can envision individuals who are not satisfied with being like everyone else on a particular issue. Such individuals may seem like inconsequential outliers in a sea of conformity, but a dynamical framework reminds us that even a small subset of individuals can have a disproportionately large effect on group processes (Nowak & Vallacher 1998b). Although the benefits of anticonformity for group decision making (e.g., playing the devil's advocate) are sometimes recognized and encouraged (Nemeth et al. 2001), the role of anticonformity in global minority opinion dynamics has yet to be established. The present research thus explored whether individuals engaging in an oppositional behavior strategy (i.e., anticonformity), but with average amounts of social power, could serve an anchoring function similar to influential individuals.

1.5

The inclusion of both conformity and anticonformity tendencies in a social system may bring optimal distinctiveness theory (ODT) to mind for some readers (Brewer 1991; Leonardelli et al. 2010). ODT proposes that people have competing needs for belonging and uniqueness that can both be met by identifying with a social group that is optimally distinct. An optimally distinct group is one that is large enough to be inclusive, but small enough that it stands apart from others and thus creates a between-group distinctiveness. Though this theory is applicable to the means through which individuals satisfy competing internal needs through their identification with social groups, it does not address the dynamics of opinion diversity within groups. ODT, moreover, was not developed to capture the disproportionately large group-level effects of a small amount of individual-level oppositional dynamics. This difference between the two approaches can also be seen in how they are computationally implemented (Smaldino et al. 2012). Thus, the present article is applicable to within-group opinion dynamics that are complementary to, but distinct from, the social identity processes described by ODT.

Computational Modeling

1.6

In psychological experiments, researchers attempt to establish causality by controlling as much of the situation as possible and demonstrating that manipulations of specific variables result in a given behavior (e.g., an individual conforming to a group norm). In a computational model, agents are programmed with different configurations of these tendencies (e.g., conformity or anticonformity) to explore the unpredictable group dynamics that emerge from their interactions. Psychological experiments are important for establishing causality in understanding the behavior of individuals, but computational models are often necessary to explore the nonlinear, group-level implications of such behaviors among interdependent social actors exerting reciprocal influence on one another (acting simultaneously as both social influence sources and targets). Computational modeling offers levels of precision, control, and replicability in studying such emergent group phenomena that are not possible in experimental research (Epstein 2006; Nowak et al. 1990; Nowak & Vallacher 1998b; Tanford & Penrod 1984). Moreover, without the aid of computational models, the human mind is poor at predicting the nonlinear group-level dynamics that emerge from interactions between individuals (Nowak et al. 2013b).

1.7

Models are necessarily simplifications of the target system. This can be misunderstood as a weakness of computational modeling to be rectified by designing the model in as realistic a manner as is possible. Such desires are compounded by the allure of big data that promises to capture everything down to the minutiae of human behavior. But one of the key insights in complexity science is that complex, realistic group-level phenomena that emerge from interdependent agents can be generated by simple individual-level behavioral rules. Thus, the goal of much computational modeling is not to reproduce a system in its messy entirety, but to develop minimalistic theoretical accounts of the core individual-level mechanisms that drive the complex group phenomena of interest (Nowak 2004). Just as psychological experiments often sacrifice realism for experimental control, so do computational models sacrifice realism for theory development.

Computational Models of Social Influence

1.8

Computational models of social influence are primarily found in the statistical physics literature (Nyczka & Sznajd-Weron 2013; see, also, models of opinion dynamics, e.g., Hegselmann & Krause 2002), and most focus either on conformity-like behavior to the exclusion of anticonformity (e.g., voter, majority, and Sznajd models), or on anticonformity to the exclusion of conformity (Regnault et al. 2009). A few models do include both conformity and anticonformity (e.g., Galam 2004; Lama et al. 2005; Nyczka et al. 2012), but they differ from the present model in their objective and computational implementation. In terms of research aims, none of the models focus on the potential of a small number of anticonformists to enable opinion diversity among a larger number of conformists.

1.9

In terms of computational design, all of the models lack a spatial dimension (i.e., each agent had an equal probability of interacting with any other agent in a given step). Social influence, however, is embedded in a spatial environment (Marsh et al. 2009) in which social space limits interactions to proximal neighbors in the social structure. Overlapping neighborhoods of social interaction then collectively generate macro-level social patterns (Hegselmann & Flache 1998). Without a spatial structure, the potential for local and macro phenomena is lost, thus changing the potential dynamics of the model itself (see, e.g., Smaldino et al. 2012). This constitutes a rather strong barrier to the integration of past models with social psychological research and it stands as our computational model's point of departure.

1.10

Using a spatial cellular automata platform, the aim of the research was to investigate the fate of a spatially situated minority opinion as a function of the proportion of anticonformists in the population and the initial distribution of minority opinion. Of particular interest were the emergent effects that a small number of anticonformists had on the social system as a whole, above and beyond the changes in their own opinions. The simulations tested whether there was an optimal level of anticonformity in a social system: too little anticonformity was hypothesized to leave minority opinion vulnerable to collapse, whereas too much anticonformity was hypothesized to promote heightened and disruptive volatility, undermining the stability necessary to achieve a shared reality and act in a coordinated collective fashion. In the model, anticonformity is independent of opinion content when operationalized at a local level. Anticonformists, in other words, will gravitate towards the minority opinion among neighboring agents even if it is not the global minority opinion. As such, this research does not explore the effects of a particular group of global minority opinion holders, but rather the effects on opinion diversity of an opinion-independent oppositional process.

Research Design

2.1

Cellular automata are widely used in modeling dynamical systems of interacting elements or agents, and they are especially well suited to describe the spatial patterns and reciprocal forces of social influence (see, e.g., MacCoun 2012). In such models, individuals are represented as cells in a two-dimensional lattice representing a social space. The agents remain stationary in the two-dimensional social space during the model, but can change their state from one model step to the next. Each agent can be in one of a finite number of states (e.g., a small number of possible opinions) at each moment in time. Agents are programmed to act according to specific updating rules that dictate the conditions under which they will or will not change their state in the next unit of time (e.g., agents change states when a minimum number of neighboring cells are in a state different from their own). Because updating rules apply to the individual agents as opposed to the group as a whole, the group-level patterns of behavior that emerge from the local iterative interactions between agents are unpredictable and not predetermined by the behavioral rules themselves. In other words, a small change in one model parameter may have disproportionately large and unforeseeable changes on the global system via the nonlinear feedback loops linking agents. Thus, such models can offer insight into complex group-level phenomena such as evolutionary processes and interpersonal dynamics (Conway 1970; Nowak & Vallacher 1998a; Wolfram 1986).

2.2

The present OppForces (oppositional forces) model of social influence processes was designed using the freely available programming language Processing (https://processing.org/). The raw data from Experiments One and Two, R code for reproducing the figures and results, an animation of the models, and computer code for the models are publicly available online (https://osf.io/nf4q9/). The model portrayed a two-opinion system in which agents display either dispositional conformist or anticonformist tendencies. Because a binary opinion was modeled, these dispositional tendencies only describe agents' responses to social influence in relation to the binary opinion over the course of a single simulation run. Thus, these dispositional tendencies pertain to a finite period of time and are not intended to describe consistent behavioral patterns for an agent across other hypothetical opinions. Dispositional conformity and anticonformity rules were used to provide a baseline of the simplest model possible, in order to explore any complex group phenomena that emerge from it.

2.3

Cellular automata represent a class of formal models that are typically studied with a synchronous update rule (e.g., Wolfram 1986), where all cells update at the same time. Such synchronous update rules produce fully deterministic results (i.e., the same initial conditions generate the same results at every repetition of the simulation). This is useful if the simulations are used to study the properties of a formal model (e.g., the Game of Life; Conway 1970) and to study exact dynamical patterns produced by various simulation rules (e.g., Wolfram 1986). Social systems, however, are never fully deterministic. When social influence from interpersonal interaction leads to change in the individuals, such changes rarely occur in the exact same moment for all individuals. Instead, some changes occur earlier, and others later.

2.4

The present model, therefore, uses a Monte Carlo updating procedure in which agents are updated sequentially in a random order (see, e.g., Binder 1986). Such an approach is used in other computational models of related social phenomena (see, e.g., Stauffer 2003) and yields results more representative of partially asynchronous social interactions. In addition, a practical benefit of the random updating procedure is that, when combined with multiple simulation runs, it produces robust results that do not depend on the order in which agents update. Thus, although cellular automata do not traditionally use a Monte Carlo updating procedure, it was considered important for the social processes presently under study.

2.5

The OppForces model allowed us to examine the dynamics of opinion change as a function of the local interactions between agents with different dispositional tendencies and varying initial proportions of minority opinion. Social influence was modeled using a square grid with 75 agents on a side for a total of 5,625 agents, each representing an individual fixed in space. Agents could have two states (0 or 1), representing any number of binary opinions. Such a simple setup can capture a wide range of scenarios, given that important attitudes tend to take a binary "either-or" form (Latané & Nowak 1994; Nowak & Vallacher 1998b; van der Maas et al. 2003). Agent influence was defined by a Moore neighborhood whereby each agent influenced and was influenced by the eight neighbors surrounding it. A torus topology was used in which the lattice's edges wrapped so that agents on one edge were neighbors to agents on the opposite edge. Such representations of a basic social space have been shown to be sufficient for producing rich and complex social phenomena (e.g., MacCoun 2012; Nowak et al. 1990).

2.6

The percentage of anticonformists and the initial proportion of minority opinion served as the two primary control parameters that were systematically varied to generate different initial model configurations. Both opinions and spatial positions of anticonformists and conformists were randomly distributed upon initialization of the model. Once the values of these parameters were set for a given run, the percentage and locations of anticonformists in the model remained stable across all subsequent steps. The opinion distribution could change, however, according to agents' conformist or anticonformist updating rules, which specified how neighboring agents mutually influenced one another's opinion. Conformists followed a local majority rule by adopting the opinion held by the majority of cells around them (i.e., the opinion held by five or more neighboring cells, including their own opinion). Conversely, anticonformists followed an oppositional influence function, adopting the opinion contrary to the local neighboring majority. When neighboring cells were equally split between the two opinions (i.e., four neighboring cells holding each opinion), conformists retained their current state because the inclusion of their own state would put them in the local numerical majority. Anticonformists, however, changed their opinion when surrounded by four neighbors of the same opinion because, including themselves, this amounted to being in a local majority of five individuals.

Experiment One

Method

3.1

This computational experiment examined the survival of a minority opinion in the presence of different percentages of anticonformists and different levels of initial minority opinion support. Simulations were run with 0%, 5%, 10%, and 15% anticonformists present. The initial opinion distribution varied from 100:0, representing a single opinion shared by everyone, to a 70:30 majority-minority initial distribution amongst all agents. The model was run 100 times at each control parameter configuration in order to observe stable effects suitable for analysis. Each of these individual replications entailed running the model through 100 Monte Carlo steps in order to allow the social influence effects to play out, although with these parameters the minority opinion clusters typically stabilized or died out within 10 to 20 steps. During each step in this Monte Carlo updating procedure, agents were chosen at random, and the agents' updating rules were applied (either conformity or anticonformity). For each Monte Carlo step, 5,625 agents (the number of agents in the simulation) were chosen at random and updated. Given the random selection of agents, it was possible for the same agent to be selected multiple times for updating, leading to only a subset of the agent population having the chance to update in a given step. The steps in the model represent the passing of time, but the timeframe represented by this model is purposefully nonspecific (i.e., an entire simulation may represent the course of hours, days, etc.), given that the social processes under examination can unfold at different rates but are qualitatively similar in nature.

3.2

Diversity of opinion was measured in terms of conformist minority opinion survival. This was calculated as the percentage of the 100 replications at a given set of starting parameters in which the minority opinion was held by some number of conformists in the last Monte Carlo step.

Results

3.3

Figure 1 shows the survival rates of conformist minority opinion as a function of initial opinion distributions and the percentage of anticonformists. The influence of anticonformists should be measured against the model containing all conformists (0% anticonformists) because this is essentially a traditional majority influence model of conformity. In the presence of all conformists, the simulations showed that it takes a substantial minority population to withstand the majority influence. Simulations beginning with 20% or fewer individuals initially holding minority opinions resulted in survival of conformist minority opinion less than 5% of the time when no anticonformists were present. A 25% initial minority opinion or more was necessary for conformist opinion diversity to persist more than 5% of the time (e.g., with a 25% initial minority opinion, the minority opinion survived in 40% of the simulations).

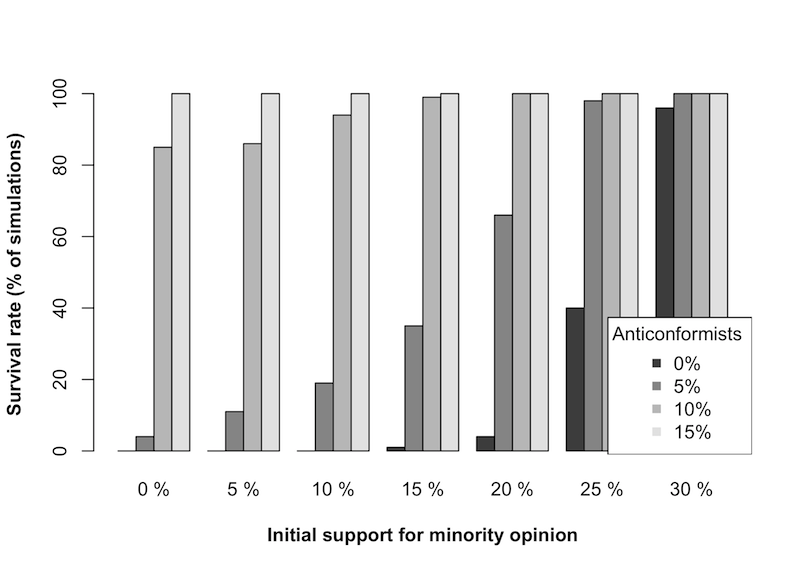
Figure 1. Survival of conformist minority opinion.

3.4

The addition of anticonformists yielded two important results. First, when the initial minority opinion was less than 30%, a conformist minority opinion was more likely to survive with anticonformists than without (see Figure 1). For example, with a 20% initial minority opinion, the minority had only a 4% chance of survival with only conformists present but a 66% chance of survival when just 5% of the population was anticonformists. Second, an increased percentage of anticonformists in the population decreased the minimum threshold of initial minority opinion at which a diversity of opinion would survive. For example, although a conformist minority opinion never persisted with an initial minority opinion of 10% in the absence of anticonformists, it persisted 19% of the time when 5% of the population consisted of anticonformists.

3.5

Experiment One demonstrated that a small number of anticonformists can have a disproportionately large effect on group dynamics. Experiment Two introduced additional realism to the model to test the robustness of this effect and its implications for group stability.

Experiment Two

4.1

The simulations in Experiment One reached stable equilibria at which all agents were content to retain their current opinion (i.e., all conformists were in the local majority, and all anticonformists were in the local minority). These equilibria were attained because all agents followed their conformity/anticonformity rules precisely. Behavior in real-world settings, however, is influenced by numerous factors, some known (e.g., individual differences in personality) and others unknown (subtle situational forces). The influence of these factors is addressed in experimental research through random participant selection and group assignment, wherein the noise from other factors affects participants' behavior, but in a similar way for all experimental groups. In computational models, the analogue of controlling for random effects is the introduction of noise. Noise causes agents to err slightly in the implementation of their rules, thus introducing random influence that is independent of whether or not the agent is a conformist or anticonformist. Such random influence makes it possible to test the stability of a model equilibrium, assessing whether minority opinion clusters are strong enough to withstand the sorts of random factors found in the real world.

Method

4.2

Random influence, as controlled by a noise parameter, caused agents to err in their count of the neighboring majority opinion by adding a positive or negative value from a uniform random distribution bounded by [-2, 2] to their counts of the neighboring opinions. Otherwise, Experiment Two employed the same grid size (75 × 75) and the same conformist and anticonformist updating rules as employed in the first experiment. The percentage of anticonformists were varied at smaller intervals than in the first experiment—from 0 to 50%, increasing in 1% intervals—in order to explore changes that might occur in system-wide patterns due to small changes in the percentage of anticonformists in the context of noise. Instead of varying the initial opinion distribution, as was done in Experiment One, it was set to a 45:55 initial opinion distribution. This distribution maximized the minority opinion's likelihood of survival in the unfavorable noise conditions, while still maintaining a clear minority and majority opinion from the start. This level of initial support was kept constant in order to focus on the effects of the different anticonformist-to-conformist ratios on group dynamics. At every anticonformist-to-conformist ratio, 100 repetitions were again run in order to observe stable effects. Within each of these repetitions, a given simulation was run through 2000 Monte Carlo steps because the added noise increased the amount of time needed for stabilization to occur. This contrasts with the 100 steps used in Experiment One, when stabilization occurred more quickly in the absence of noise.

4.3

The same conformist minority opinion survival rate used in Experiment One was again used to calculate the percentage of the time that some number of conformists remained holding the minority opinion. Two additional dependent measures were used in Experiment Two. The amount of opinion diversity was measured by the amount of conformist minority opinion, which was computed as the percentage of conformists holding the minority opinion at the final step of each simulation. Anticonformists were not included in this calculation because this research focused on the effects of anticonformists on minority groups made up primarily of conformists. Moreover, anticonformists will always hold the minority opinion when surrounded by the majority opinion, thus making them a poor indicator of the general system-wide diversity of opinion. In addition, system volatility was measured as an indicator of general system dynamics and was operationalized as the percentage of agents (of those updated in the Monte Carlo procedure) that changed their opinion in the final step of the model. Anticonformists were included in this calculation because their changes in opinion would contribute to the overall volatility of the social system at a given point in time.

Results

4.4

As in Experiment One, the model containing all conformists offered an appropriate baseline against which to compare the effects of anticonformists. Figure 2 shows the probability of a conformist minority opinion surviving when between 0 and 10% anticonformists were present. When only conformists were present, this model converged to a single opinion in every simulation. However, with the addition of even 1% anticonformists, the conformist minority opinion survived 5% of the time. When the proportion of anticonformists exceeded 5%, conformist minority opinion survived in every simulation.

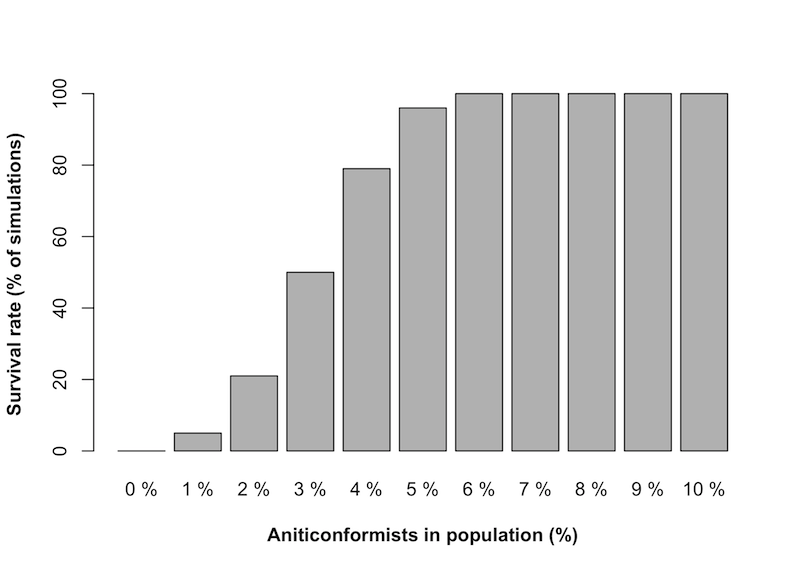
Figure 2. Survival of conformist minority opinion in the presence of noise.

4.5

Next, the relationship between the number of anticonformists present and the amount of conformist minority opinion was examined. As illustrated in Figure 3, minority opinion held by conformists increased as the percentage of anticonformists increased. Figure 3 also shows the system volatility at different anticonformist-to-conformist ratios. There is a clear trend toward instability as the number of anticonformists increases. At 30% anticonformists, for example, an average of 15% of the agents changed their opinions in the final step, compared with an average of .5% of the agents changing their opinion in the final step when only 5% anticonformists were present.

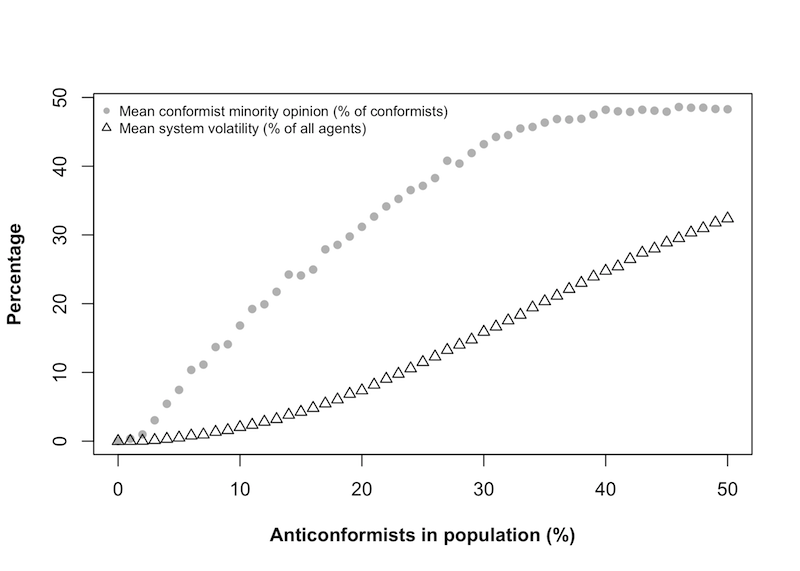
Figure 3. Conformist minority opinion and system volatility in the presence of noise.

4.6

The visualization in Figure 4 provides an example of the opinion clusters that emerged from these oppositional dynamics. This is a typical social space resulting from a population with 5% anticonformists at the last (2000^th) step in a simulation. Blue circles represent conformists and green circles represent anticonformists. The red and white cell colors represent the two possible opinions. Note that although minority clusters are made up primarily of conformists, several anticonformists often occupy the edges of the clusters. These anticonformists were observed to serve as anchors over the life of the simulation, protecting the borders from inward collapse due to influence from the surrounding majority (Experiments One and Two) and from the disruptive effects of random variation due to noise (Experiment Two).

Figure 4. Typical opinion cluster at 5% anticonformists with noise.

General Discussion

5.1

In the context of a disruptive noise, even the addition of 1% anticonformists increased the likelihood that a conformist minority opinion would survive, while more than 5% anticonformists virtually guaranteed that the minority opinion would survive until the last step of the simulation. The findings thus support the hypothesis that oppositional dynamics produced by a small number of anticonformists increase the resilience of a minority opinion held by a larger number of conformists, thereby facilitating a system's long-term diversity of opinion. This suggests that anticonformists may prevent the shrinking of minority cluster edges in a manner similar to that provided by socially influential agents (Nowak et al. 1990). Thus, this research offers a route to opinion diversity that is obtainable without highly influential minority opinion holders. A subset of agents engaged in oppositional anticonformity behavior appears to enable conformists to hold a minority opinion amidst the pressures of social influence that would otherwise make them untenable.

5.2

In the context of this finding, it should be noted that the OppForces model differs from recent analytic studies of opinion dynamics amidst conformity and anticonformity (e.g., Altafini 2013; Büchel et al. 2013; Cao et al. 2012; Eger 2013; see also Degroot 1974). These studies take different approaches (e.g., operationalizing conformity/anticonformity and opinions as continuous variables; e.g., Eger 2013) that sometimes yield different results (e.g., convergence on a single consensus opinion in the presence of both conformists and anticonformists; Cao et al. 2012). An important distinction between these and the present OppForces model is the implementation of conformity and anticonformity behaviors. While the conformists/anticonformists in the OppForces model adopted the local majority/minority opinion, the conformists/anticonformists in the analytic approaches move towards or away from the arithmetic average of the relevant local agents. These different conformity/anticonformity rules, in addition to differences from using a continuous opinion parameter (see Hegselmann & Flache 1998), may account for many of the divergent findings.

5.3

The use of an arithmetic average also implicitly tests a different theory of behavior. The calculation of an average opinion would be cognitively demanding and even impossible in some circumstances (e.g., with opinions that cannot be quantified). The OppForces model, however, intentionally uses a simple conformity/anticonformity strategy because noticing a local majority/minority opinion and adopting it can be done quickly, and even outside of conscious awareness (see Cialdini & Goldstein 2004). Thus, these different approaches and findings likely generalize to different types of behaviors and opinion dynamics. This emphasizes the sensitivity of these methods to their computational or analytic implementations, while also highlighting the flexibility of such methods for testing different theory-driven operationalizations of processes under study.

5.4

Returning to general findings from the OppForces model, although a low percentage of anticonformists enhanced the resilience of the conformist minority opinion, Experiment Two also demonstrated the destabilizing effects that can result from a high percentage of anticonformists. Figure 3 suggests that between 5 and 10% anticonformists was an optimal range in the present research—it allowed for the emergence of a resilient conformist-held minority opinion without leading to the increased volatility from frequent opinion changes that was observed with higher anticonformist percentages. Although diversity of opinion is desirable for purposes of long-term adaptation, system stability is also important for a system to thrive. Thus, a system might become undesirable by virtue of instability if the amount of oppositional dynamics exceeds a threshold.

5.5

Accordingly, an important goal for future research is to explore the optimal range of oppositional dynamics in real social systems. The specific values observed in this research—such as the 5% threshold of anticonformists beyond which the survival of a conformist minority opinion was virtually guaranteed and the 5-10% range of anticonformists that created optimal levels of both diversity and stability—offer initial estimates for the corresponding real-world values, but it remains for archival and experimental research to determine what these numbers, thresholds, and ranges are in actual social systems.

Limitations and Future Directions

5.6

The OppForces model is heuristic in its intentionally simplistic use of dichotomous opinions, constant conformist or anticonformist updating rules, and artificial grid-like social structure. And yet, the model was integrative in that it married the two competing social processes of conformity and anticonformity, producing complex group dynamics in hypothetical social systems. Thus, although the model's simple structure is a limitation in terms of its direct comparability with real-world social processes, the results from this model exemplify the strengths of a dynamical minimalism approach in which a small number of simple behaviors are able to generate a complex, informative, and theoretically meaningful pattern of group phenomena (Nowak 2004).

5.7

Future research employing the OppForces model should increase the correspondence between system parameters and the relevant individual and social factors discussed in social psychological research. It might, for example, increase the complexity of the agents' updating rules (e.g., incorporate behavior independent of social influence; Nail et al. 2000; Nyczka & Sznajd-Weron 2013; Packer et al. 2014) and introduce more dynamic rules for whether or not an agent engages in conformist or anticonformist behavior (e.g., set thresholds at which agents switch from one behavior pattern to another).

5.8

Future models could also use social network structures that are more realistic than nearest neighbor interactions (Sobkowicz 2009; Westaby et al. 2014). In addition, the present model allowed for only two possible opinions, thus constricting the operationalization of diversity to its most basic form: the survival of both opinions. Future computational models should be designed in a way that allows for the existence of a wider array of possible opinions and the potential for new opinions to emerge through social interactions. Finally, all of these models can and should be designed in conjunction with other empirical methods so that insights from each can inform the other.

Implications

5.9

Oppositional behavioral processes introduce interesting phenomena into the discussion of social adaptation and stability. Anticonformity is a unique social mechanism in its ability to affect group dynamics without requiring high social power or capital. A moderate amount of oppositional dynamics (via anticonformity) introduces the potential for a resilient diversity and the adaptive potential that such diversity affords. In excess, however, oppositional dynamics can promote heightened volatility that can destabilize a social system and undermine its shared reality. The issue, then, is not whether or not oppositional dynamics are adaptive for a social system, but rather what is their optimal level. More specifically, where is the point of balance at which the tradeoff between flexibility and stability is optimal for a group? In the often unstable world in which we find ourselves, this question merits additional computational and empirical attention.

5.10

Beyond its implications for the functioning of social systems, the present research highlights the importance of process over content. It was not only individuals with different opinions who made social dynamics more adaptive, but individuals with a particular orientation (anticonformity) that acted in opposition to the prevailing strategy (conformity). The underlying notion that oppositional convergent and divergent dynamics facilitate adaptive functioning scales to different levels of social reality. It can be seen, for example, in cognition (Förster & Dannenberg 2010; Guilford 1950; Piaget 1952; Schroder & Harvey 1963), self-concept (Csikszentmihalyi 1993), self-development (Imamoğlu 1998), and group membership (Brewer 1991)—not to mention its importance in systems studied in the natural sciences (Camazine et al. 2001). The goal of the present research is not simply to add social dynamics to this list, but to encourage empirical consideration of the ways in which this convergent-divergent oppositional framework might capture important aspects of dynamics in and across different levels of human experience.

Acknowledgements

The authors wish to thank Wiesław Bartkowski for his input into the model design and Paul Smaldino for his feedback on a draft of the paper. The authors disclosed receipt of the following financial support for the research and authorship of this article: Andrzej Nowak and Wojciech Borkowski received funding through a grant from the Polish Committee for Scientific Research [DEC-2011/02/A/HS6/00231].

References

ALTAFINI, C. (2013). Consensus problems on networks with antagonistic interactions. Automatic Control, IEEE Transactions on, 58(4), 935–946. [doi:10.1109/TAC.2012.2224251]

ASCH, S. E. (1956). Studies of independence and conformity: I. A minority of one against a unanimous majority. Psychological Monographs: General and Applied, 70(9), 1–70. [doi:10.1037/h0093718]

BINDER, K. (Ed.). (1986). Monte Carlo methods in statistical physics (2nd ed.). Berlin: Springer-Verlag. [doi:10.1007/978-3-642-82803-4]

BREWER, M. B. (1991). The social self: On being the same and different at the same time. Personality and Social Psychology Bulletin, 17(5), 475–482. [doi:10.1177/0146167291175001]

BÜCHEL, B., Hellmann, T., & Klößner, S. (2013). Opinion dynamics and wisdom under conformity. Presented at the Contributions to the Annual Meeting of the Association for Social Policy 2013: Competition Policy and Regulation in a Global Economic Order, German Economic Association. Retrieved from <http://www.econstor.eu/bitstream/10419/79770/1/VfS_2013_pid_443.pdf>

CAMAZINE, C., Deneubourg, J., Franks, N. R., Sneyd, J., Theraula, G., & Bonabeau, E. (2001). Self-Organization in Biological Systems. Princeton, NJ: Princeton University Press.

CAO, Z., Yang, M., Qu, X., & Yang, X. (2012). Rebels lead to the doctrine of the mean: opinion dynamic in a heterogeneous DeGroot model. <http://arxiv.org/abs/1204.0161>

CIALDINI, R. B., & Goldstein, N. J. (2004). Social influence: Compliance and conformity. Annual Review of Psychology, 55(1), 591–621. [doi:10.1146/annurev.psych.55.090902.142015]

CONWAY, J. (1970). The game of life. Scientific American, 223(4), 4.

CSIKSZENTMIHALYI, M. (1993). The evolving self: A psychology for the third millennium. New York, NY: Harper Collins.

DAR-NIMROD, I., Hansen, I. G., Proulx, T., Lehman, D. R., Chapman, B. P., & Duberstein, P. R. (2012). Coolness: An empirical investigation. Journal of Individual Differences, 33(3), 175–185. [doi:10.1027/1614-0001/a000088]

DEGROOT, M. H. (1974). Reaching a Consensus. Journal of the American Statistical Association, 69(345), 118–121. [doi:10.1080/01621459.1974.10480137]

DEUTSCH, M., & Gerard, H. B. (1955). A study of normative and informational social influences upon individual judgment. The Journal of Abnormal and Social Psychology, 51(3), 629–636. [doi:10.1037/h0046408]

EGER, S. (2013). Opinion dynamics under opposition. http://arxiv.org/abs/1306.3134 [doi:10.2139/ssrn.2352555]

EPSTEIN, J. M. (2006). Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton University Press.

FESTINGER, L. (1950). Informal social communication. Psychological Review, 57(5), 271–282. [doi:10.1037/h0056932]

FESTINGER, L., Schachter, S., & Back, K. W. (1950). Social pressures in informal groups: A study of human factors in housing. New York, NY: Harper & Brothers.

FÖRSTER, J., & Dannenberg, L. (2010). GLOMO^sys: A systems account of global versus local processing. Psychological Inquiry, 21(3), 175–197. [doi:10.1080/1047840X.2010.487849]

GALAM, S. (2004). Contrarian deterministic effects on opinion dynamics: "The hung elections scenario." Physica A: Statistical Mechanics and Its Applications, 333, 453–460. [doi:10.1016/j.physa.2003.10.041]

GUILFORD, J. P. (1950). Creativity. American Psychologist, 5(9), 444–454. [doi:10.1037/h0063487]

HEGSELMANN, R., & Flache, A. (1998). Understanding complex social dynamics: A plea for cellular automata based modelling. Journal of Artificial Societies and Social Simulation, 1(3). <https://www.jasss.org/1/3/1.html>

HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3). <https://www.jasss.org/5/3/2.html>

IMAMOĞLU, E. O. (1998). Individualism and collectivism in a model and scale of balanced differentiation and integration. The Journal of Psychology, 132(1), 95–105. [doi:10.1080/00223989809599268]

IMHOFF, R., & Erb, H.-P. (2009). What motivates nonconformity? Uniqueness seeking blocks majority influence. Personality and Social Psychology Bulletin, 35(3), 309–320. [doi:10.1177/0146167208328166]

JANIS, I. L. (1972). Victims of Groupthink. Boston, MA: Houghton Mifflin.

LAMA, M. S. de la, López, J. M., & Wio, H. S. (2005). Spontaneous emergence of contrarian-like behaviour in an opinion spreading model. Europhysics Letters (EPL), 72(5), 851–857. [doi:10.1209/epl/i2005-10299-3]

LATANÉ, B. (1981). The psychology of social impact. American Psychologist, 36(4), 343–356. [doi:10.1037/0003-066X.36.4.343]

LATANÉ, B., & Nowak, A. (1994). Attitudes as catastrophes: From dimensions to categories with increasing involvement. In R. R. Vallacher & A. Nowak (Eds.), Dynamical systems in social psychology. (pp. 219–249). San Diego, CA: Academic Press.

LEONARDELLI, G. J., Pickett, C. L., & Brewer, M. B. (2010). Optimal distinctiveness theory: A framework for social identity, social cognition, and intergroup relations. Advances in Experimental Social Psychology, 43, 63–113. [doi:10.1016/S0065-2601(10)43002-6]

MACCOUN, R. J. (2012). The burden of social proof: Shared thresholds and social influence. Psychological Review, 119(2), 345–372. [doi:10.1037/a0027121]

MARSH, K. L., Johnston, L., Richardson, M. J., & Schmidt, R. C. (2009). Toward a radically embodied, embedded social psychology. European Journal of Social Psychology, 39(7), 1217–1225. [doi:10.1002/ejsp.666]

MASLACH, C., Stapp, J., & Santee, R. T. (1985). Individuation: Conceptual analysis and assessment. Journal of Personality and Social Psychology, 49(3), 729. [doi:10.1037/0022-3514.49.3.729]

MOSCOVICI, S., & Nemeth, C. (1974). Social influence II: Minority influence. In C. Nemeth (Ed.), Social psychology: Classic and contemporary integrations (pp. 217–249). Chicago, IL: Rand McNally.

MYERS, D. G., & Lamm, H. (1976). The group polarization phenomenon. Psychological Bulletin, 83(4), 602–627. [doi:10.1037/0033-2909.83.4.602]

NAIL, P. R., MacDonald, G., & Levy, D. A. (2000). Proposal of a four-dimensional model of social response. Psychological Bulletin, 126(3), 454. [doi:10.1037/0033-2909.126.3.454]

NEMETH, C., Brown, K., & Rogers, J. (2001). Devil's advocate versus authentic dissent: Stimulating quantity and quality. European Journal of Social Psychology, 31(6), 707–720. [doi:10.1002/ejsp.58]

NOWAK, A. (2004). Dynamical minimalism: Why less is more in psychology. Personality and Social Psychology Review, 8(2), 183–192. [doi:10.1207/s15327957pspr0802_12]

NOWAK, A., Bartkowski, W., Samson, K., Rychwalska, A., Kacprzyk, M., Roszczynska-Kurasinska, M., & Jagielska, M. (2013a). No need for speed: Modeling trend adoption in a heterogeneous population. Advances in Complex Systems, 16(04n05), 1350025.

NOWAK, A., Rychwalska, A., & Borkowski, W. (2013b). Why Simulate? To Develop a Mental Model. Journal of Artificial Societies and Social Simulation, 16(3), 12. <https://www.jasss.org/16/3/12.html>

NOWAK, A., Szamrej, J., & Latané, B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychological Review, 97, 362–376. [doi:10.1037/0033-295X.97.3.362]

p>NOWAK A. & Vallacher, R. (1998a). Toward computational social psychology: Cellular automata and neural network models of interpersonal dynamics. In S. J. Read & L. C. Miller (Eds.), Connectionist models of social reasoning and social behavior. Mahwah, NJ: Lawrence Erlbaum Associates, Inc.

NOWAK, A., & Vallacher, R. R. (1998b). Dynamical social psychology. New York, NY: The Guilford Press.

NYCZKA, P., & Sznajd-Weron, K. (2013). Anticonformity or independence? Insights from statistical physics. Journal of Statistical Physics, 151(1-2), 174–202. [doi:10.1007/s10955-013-0701-4]

NYCZKA, P., Sznajd-Weron, K., & Cisło, J. (2012). Phase transitions in the q-voter model with two types of stochastic driving. Physical Review E, 86(1). [doi:10.1103/PhysRevE.86.011105]

PACKER, D. J., Fujita, K., & Chasteen, A. L. (2014). The motivational dynamics of dissent decisions: A goal-conflict approach. Social Psychological and Personality Science, 5(1), 27–34. [doi:10.1177/1948550613486676]

PAGE, S. E. (2007). Making the difference: Applying a logic of diversity. The Academy of Management Perspectives, 21(4), 6–20. [doi:10.5465/AMP.2007.27895335]

PAGE, S. E. (2008). The difference: How the power of diversity creates better groups, firms, schools, and societies. Princeton, NJ: Princeton University Press.

PIAGET, J. (1952). The origins of intelligence in children. New York, NY: International Universities Press. [doi:10.1037/11494-000]

REGNAULT, D., Schabanel, N., & Thierry, É. (2009). Progresses in the analysis of stochastic 2D cellular automata: A study of asynchronous 2D minority. Theoretical Computer Science, 410(47-49), 4844–4855. [doi:10.1016/j.tcs.2009.06.024]

SCHACHTER, S. (1951). Deviation, rejection, and communication. The Journal of Abnormal and Social Psychology, 46(2), 190–207. [doi:10.1037/h0062326]

SCHRODER, H. M., & Harvey, O. J. (1963). Conceptual organization and group structure. In O. J. Harvey (Ed.), Motivation and Social Interaction: Cognitive Determinants (pp. 134–166). New York, NY: Ronald.

SMALDINO, P., Pickett, C., Sherman, J., & Schank, J. (2012). An agent-based model of social identity dynamics. Journal of Artificial Societies and Social Simulation, 15(4), 7. <https://www.jasss.org/15/4/7.html>

SOBKOWICZ, P. (2009). Modelling opinion formation with physics tools: Call for closer link with reality. Journal of Artificial Societies and Social Simulation, 12(1), 11. <https://www.jasss.org/12/1/11.html>

STAUFFER, D. (2003). How to convince others? Monte Carlo simulations of the Sznajd model. In J. E. Gubernatis (Ed.), AIP Conference Proceedings (Vol. 690, pp. 147–155). Los Alamos, NM: AIP Publishing. [doi:10.1063/1.1632125]

STEINER, I. D. (1972). Group process and productivity. New York, NY: Academic Press.

TANFORD, S., & Penrod, S. (1984). Social influence model: A formal integration of research on majority and minority influence processes. Psychological Bulletin, 95(2), 189–225. [doi:10.1037/0033-2909.95.2.189]

VAN DER MAAS, H. L. J., Kolstein, R., & van der Pligt, J. (2003). Sudden transitions in attitudes. Sociological Methods & Research, 32(2), 125–152. [doi:10.1177/0049124103253773]

WESTABY, J. D., Pfaff, D. L., & Redding, N. (2014). Psychology and social networks: A dynamic network theory perspective. American Psychologist, 69(3), 269–284. [doi:10.1037/a0036106]

WOLFRAM, S. (1986). Theory and applications of cellular automata: Including selected papers, 1983-1986. Singapore: World Scientific Publishing Company, Inc.

ZIMBARDO, P. G. (1969). The human choice: Individuation, reason, and order versus deindividuation, impulse, and chaos. Nebraska Symposium on Motivation, 17, 237–307.