 Abstract
Abstract
- College drinking is a problem with severe academic, health,
and safety consequences. The underlying social processes that lead to
increased drinking activity are not well understood. Social Norms
Theory is an approach to analysis and intervention based on the notion
that students' misperceptions about the drinking culture on campus lead
to increases in alcohol use. In this paper we develop an agent-based
simulation model, implemented in MATLAB, to examine college drinking.
Students' drinking behaviors are governed by their identity (and how
others perceive it) as well as peer influences, as they interact in
small groups over the course of a drinking event. Our simulation
results provide some insight into the potential effectiveness of
interventions such as social norms marketing campaigns.
- Keywords:
- Group Formation, Peer Influence, Identity Control Theory, Social Norms, College Drinking
 Introduction
Introduction
- 1.1
- College drinking in the United States is a problem with
severe academic, health, and safety consequences. Around 25 percent of
US college students cite alcohol as a reason for missing classes and
falling behind or reduced performance in their coursework. Some 599,000
US students receive accidental injuries during alcohol use, with
approximately 1825 US students dying from such events. Around 690,000
US students are assaulted by a student who had been drinking, and over
97,000 sexual assaults are alcohol-involved. These statistics, as
reported by the US National Institute on Alcohol Abuse and Alcoholism
(NIAAA) ("College Drinking" 2014),
illustrate some of the challenges of alcohol use on US college
campuses.
- 1.2
- Heavy episodic or "binge" drinking, which has been defined (Wechsler & Nelson 2001)
as five or more drinks "in a row" for men and four or more drinks in a
row for women, is a particularly difficult aspect of college drinking
in the US. Drink is meant as the US "Standard Drink:," which contains
10 grams of ethanol, approximating the rule of thumb that one (12oz)
beer equals one (5oz) glass of wine equals one (1.25oz) shot of
distilled spirits. The Harvard College Alcohol Survey (Wechsler et al.
2002), a nationally representative sample of over 54,000 students at
120 US four-year colleges and universities in four different years,
shows that students who drank in this manner once or twice in a
two-week period were nearly five times more likely to have missed
class, 3 times more likely to have engaged in unprotected sex, and more
than 2.5 times more likely to have suffered an injury than are students
who do not engage in heavy episodic drinking. Students engaging in
heavy episodic drinking three or more times in a two-week period were
more than 16 times more likely to have missed class, 6 times more
likely to have engaged in unprotected sex, and more than 8 times more
likely to have suffered an injury. This style of drinking is much more
common in college students than in their non-college peers (Slutske 2004). These are among
the reasons that many US college presidents view drinking as an
important problem on their campuses (Wechsler
et al. 2004; CSPI 2008;
Biden 2000) and that so
much effort is focused on intervention.
- 1.3
- Intervention, however, has proved to be a challenging
process, and attempts to change the culture of college drinking have
mixed results. A number of strategies have been applied, including
intensive, multiple session face-to-face interventions (Carey et al. 2007), brief
motivational interventions (Borsari
& Carey 2000), computer-based electronic
interventions (Elliott et al. 2008),
and social norms marketing campaigns (Perkins
& Wesley 2002; Neighbors
et al. 2006; Perkins et
al. 2005; DeJong et al.
2006; Schulenberg et
al. 2001). Each of these has its advantages and
disadvantages, and some show significant promise. Understanding the
circumstances under which these strategies will be effective is quite a
challenging task.
- 1.4
- In fact, intervention has become such a difficult issue in
recent years that some in the United States have advocated for the
reduction of the minimum legal drinking age (MLDA), repealing federal
legislation passed in 1984 that effectively raised the MLDA to 21
nationally. Over 120 college presidents across the US have signed the
Amethyst Initiative statement ("Amethyst
Initiative Statement" 2014) that "twenty-one is not working."
A primary reason given by the Amethyst Initiate group is that, since
drinking is illegal for them, college students are unable to model
drinking behavior on more healthy behaviors. Forced to hide their
drinking, students instead adopt dangerous drinking styles, with heavy
episodic or binge drinking becoming a cultural rite of passage.
European drinking laws are used as an argument as well, but research
demonstrates that young people in Europe are not more responsible than
their American counterparts (Friese
& Grube 2010). A reduction of the minimum legal
drinking age in the US would be a very large-scale social experiment
with major political, economic and public health consequences that are
extremely difficult to forecast.
- 1.5
- To gain some insight into the problem of college drinking
on US college campuses, we have embarked on an agent-based modeling
effort to examine the impact of social interactions on alcohol
consumption. Distinct from compartmental models (Scribner et al. 2009; Ackleh, et al. 2009; Rasul et al. 2011; Fitzpatrick et al. 2012)
and other agent-based models (Garrison
& Babcock 2009; Gorman
et al. 2006; Giabbanelli
& Crutzen 2013), the model we have developed is a
simple model of a single drinking event that incorporates Identity
Control Theory and Peer Influence as social mechanisms affecting
drinking rates. The deterministic compartmental models of Scribner and
colleagues partition the college population into four drinking styles
(abstainer, social, problem, and binger) and use contact transitions to
model the dynamics of the population as in an epidemic model. The
result is a drinking structure of the population evolving over multiple
academic years (Scribner et al.
2009; Ackleh et al. 2009;
Rasul et al. 2011; Fitzpatrick et al. 2012).
Garrison and Babcock (2009)
model an academic year but treat the motivation to drink based on the
agent's "use rate," the agent's attitude toward drinking, and peer
pressure. Garrison and Babcock (2008) observed that drinker behaviors
evolved into cyclical events, with periods of lots of drinking followed
by periods with little to no drinking. Our work also differs from the
work of Gorman et al. (2006)
where they had modeled drinking status (susceptible, current drinker,
or former drinker) as a function of contacts with current drinkers and
internal tendencies to resist drinking or to engage in drinking
behavior. The researchers had found that contacts rates can affect the
rate at which agents convert from susceptible drinkers to current
drinkers. The model of Giabbanelli and Crutzen (2013) is an interesting
social network model relying on a peer influence model much like the
one presented herein and on a selective interaction model of network
ties, in which agents with similar drinking styles are potentially more
likely to interact. The peer influence portion of that model involves a
construct that binge drinkers have a stronger influence than non-binge
drinkers. The simulation operates like a game-theoretic model of
repeated play in which agents are selected from a large population and
paired with drinking confederates for a single interaction. In our
current model, we are modeling a single drinking event with a limited
number of participants that interact multiple times with several other
agents over a relatively short time period. This has allowed us to
build a fine-grained model that integrates some intriguing and
important social theories.
- 1.6
- A central issue distinguishing college drinking, especially
underage drinking, is that students interact in an unsupervised manner
in the absence of responsible role models. Indeed, this is the primary
argument for reducing the minimum legal drinking age in the US. To gain
some understanding into what might be happening within such drinking
events, we have developed a simple mathematical and computer model of
some key social theories that lead from social interactions to
immediate changes in drinking behavior at an event. Computational
models of human behavior are of course fraught with challenges, and any
simulation such as the one we discuss in this paper distills human
agency into a small set of actions, in an attempt to balance accuracy
and feasibility with coarse approximations. Our model does include a
number of interesting features, however, most notably computational
implementations of Identity Control Theory (Burke
1991; Stets &
Burke 2000) and peer influence (PI) as a form of Social
Influence (Friedkin &
Johnsen 2011; Mason et al.
2007), which we have put into action as simple feedback
loops. As students congregate at an event, they mingle, giving out and
receiving information from their interaction partners. We supplement
these models with mechanisms to investigate misperceptions and
overestimations that students may have about peer drinking, finding
that both of these models can lead to increased drinking. While we
envision this one-day, one-party model as a component of a larger-scale
simulation with consequences and learning, even with this simple model
we can look, at least partially, into the inverse problem of reducing
misperceptions and the corresponding levels of reductions in drinking.
- 1.7
- The remainder of this article is organized as follows. In Section 2, we provide an overview of the single-event model, describing the relevant social theories, the agent attributes, and the basic functional units of the simulation. In Section 3, we discuss the details and operation of the group formation unit. In Section 4, we describe the experimental design of the study, and we present the results. We close in Section 5 with some observations pertaining to policy, interventions, and potential for survey and observational research, as well as some thoughts about the larger project of simulating many events with additional longer term considerations.
 Social
Norms Theory, Identity Control Theory, and Peer Influence
Social
Norms Theory, Identity Control Theory, and Peer Influence
- 2.1
- Alcohol use on college campuses is a very complex problem,
involving a number of demographic and environmental factors. The
College Alcohol Survey (CAS) (Wechsler
et al. 2002) observes the importance of gender, ethnicity,
parental educational attainment, economic status, residential status,
physical availability, and other variables as significantly related to
student drinking behavior. Social factors are also thought to be key:
college drinking is seen as fundamentally a social phenomenon. In fact
a majority of students reported in the CAS that celebrating and that
having good times with friends were either important or very important
reasons for drinking. An interesting question is the extent to which
students modify their drinking behavior as part of a social experience.
Here we consider three social theories, how they might be modeled
computationally, and what their implications are for a drinking event.
Social Norms Theory
- 2.2
- Social Norms Theory (SNT) has earned a prominent position
in the research literature on college drinking. Simply put, social
norms theory states that individual behavior is influenced by
misperception of peer behavior (Berkowitz
2005). Misperceptions among college students about college
drinking are quite pervasive (Borsari
& Carey 2003; Wechsler
et al. 2002; Baer et al.
1991; Perkins et al. 2005;
Scribner et al. 2011).
- 2.3
- Data from the Social Norms Marketing Research Project
(SNMRP) (DeJong et al. 2006;
Scribner et al. 2011)
shows that students' perceptions are nearly across the board higher
than the actual drinking reported. In the study, 32 college campuses
were invited to participate in a study. At each university, 300
students were randomly sampled to participate in the study.
Approximately 150 students responded to the survey from each campus.
Over a four year period, 19,838 student surveys were collected in
total. Figure 1 shows the empirical cumulative distribution function
(ECDF) of the responses to two questions from this survey. In this
figure, we contrast students' actual drinking
behavior ("When you party, how many drinks do you usually have"), with
the perceived drinking behavior of their peers
("How many alcoholic drinks do you think students at this school have
when they party (Males)?"). For simplicity, we have only included males
in the subset of this figure.
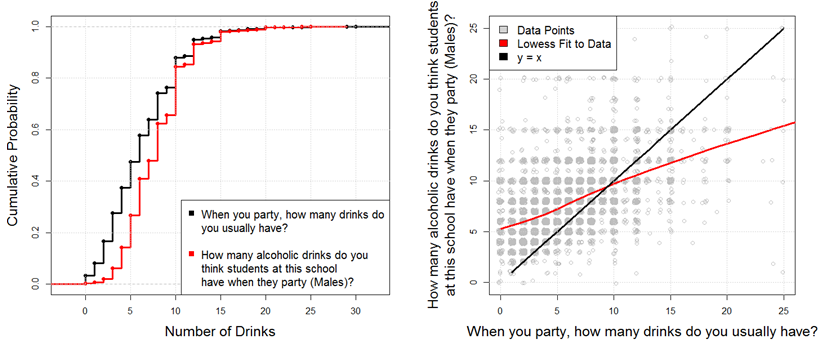
Figure 1. ECDF (left) and scatterplot (right) of the "number of drinks when you party" and "How many drinks do you think students at this school have when they party?" - 2.4
- As we can see from Figure 1,
on the left, a comparison of the two distributions indicates that the
distribution "How many alcoholic drinks do you think students at this
school have when they party" is uniformly shifted to the right of the
actual drinks students tend to consume. While not shown on the figure,
this shift in distributions is observed among 31 of the 32 universities
in the SNMRP sample. On the right, we plot perception of drinking
versus actual drinking: each of the gray circle data points represents
individual student drinking and opinion of the drinking of others. In
the right panel, the reader should note that the actual survey data is
ordered pairs of integers. Were we to plot integral values, the data
points would obscure each other, so we have added a small amount of
random noise to ("jittered") each data point so that the density can be
more easily seen. In the right panel, we see that students that drink
less than 10 drinks (approximately 85% of the population) tend to
overestimate the level of drinking that occurs. While the variables are
moderately correlated (Spearman rho=0.5260), it is clear that most of
the data points are above the line y=x, indicating that most students
have a tendency to over-perceive, with the exception of the heaviest
drinkers in the population.
- 2.5
- As mentioned previously, social norms theory suggests that
perception of drinking behavior leads students to approximate that
behavior (Berkowitz 2005).
The scatterplot (right) of Figure 1
indicates a positive correlation between actual and perceived drinking
levels, leading us to this question: "why is the perceived behavior not
eventually attained?" If we consider a simple dynamical system in which
drinking rates change in accordance with the discrepancy between the
actual drinking level and the perceived norm, we might expect the
actual drinking level to tend toward the perceived norm (Lapinski & Rimal 2005).
Since the perceived norm remains higher, we are left wondering about
the nature of the dynamics.
- 2.6
- SNT in this form does not address the issue of dynamics.
How individuals choose reference systems or groups to moderate
individual behavior and how reference systems change remain to be
resolved. In order to elaborate on the SNT model, we integrate some key
insights from Identity Control Theory, a dynamic
model of social interaction. Identity Control Theory provides a
foundation that naturally allows the incorporation of misperception and
the wa
- 2.9
- y in which it enters drinking behavior dynamics.
Identity Control Theory
- 2.7
- Identity Control Theory (ICT) states that identities are
formed by a set of meanings that serve as a reference or standard for
defining who one is (Burke 1991;
Stets & Burke 2000;
Burke & Stets 2009).
An individual's self comprises a number of identities, any of which may
be salient in a given context or situation (Stryker
& Burke 2000). When an identity becomes salient in a
social situation, the individual or agent perceives appraisals from
others. If the appraisals are not in line with the agent's meanings,
the agent experiences distress. This distress may lead to behavioral
changes in the agent. Burke and Stets (2009)
use the analogy of engineering feedback control systems that monitor
inputs from their environments and apply control signals to bring the
system outputs into agreement with a reference or tracking signal.
Inputs are generally meant as direct or indirect social cues that are
referred to as appraisals from agents in the social environment (Burke 1991), and the controls
are an agent's behavior. A conceptual diagram of ICT (slightly adapted
from Burke 1991) is
provided in Figure 2.
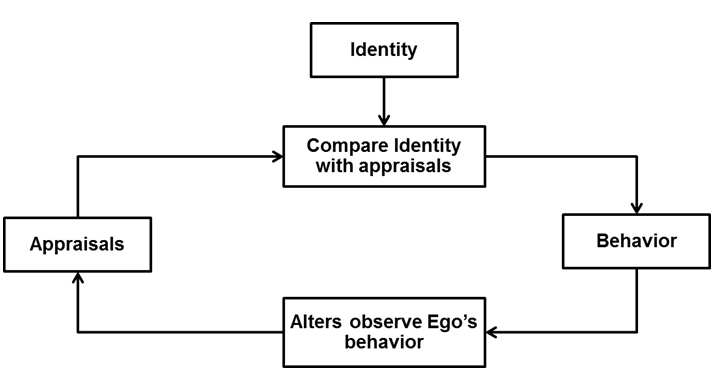
Figure 2. Block diagram of ICT appraisal processing and behavior adaptation. - 2.8
- All this is certainly not to say that humans operate
exactly as an aircraft's flight control system or chemical plant's
mixing reactor. As noted by Burke and Stets (2009),
the control system is but one component of Identity Theory. Cognitive
and emotional processes are also involved in identities, and conscious
thought and action play vital roles in how we act and what we do.
Humans also have multiple identities (e.g., father, student, activist,
soccer enthusiast, waitress) with complex salience and prominence
hierarchies suggesting which identities may become activated and which
identities are preferred by the agent (Stryker
1968, 1980; McCall & Simmons 1966).
The control system analogy serves here as a simple basis for
constructing a small-scale computational society in which agents
interact and modify their behaviors in response to interactions.
- 2.10
- A brief illustration of the identity control process may
serve to show how the model works. Consider "Joe," an 18 year old
freshman in college. Joe wants to join the most exclusive fraternity on
campus. This fraternity has the reputation of being hard drinkers. In
order to join the fraternity, Joe develops a set of meanings of what it
means to be a fraternity member. These meanings may define how he
dresses, how he acts, who he socializes with, among other things. In
addition, he also incorporates meanings that define what kind of
drinker he should become. This drinker identity serves as a standard
for his drinking behavior.
- 2.11
- As Joe interacts with his friends, while consciously or
not, he monitors the appraisals from his peers about his own drinking
behavior. If the appraisals that he receives suggest that he is not
drinking enough, then he consumes more alcohol. If those appraisals
suggest that he is drinking too much, then he slows down his rate of
consumption. The key notion here is that individuals monitor appraisals
and adjust behavior so that the appraisals that he receives from his
peers are consistent with how he sees himself. In essence, individuals
modify their behaviors so that their identities are verified in their
interaction encounters. We refer to this form of feedback control as
Identity Verification (IV).
- 2.12
- The "tracking error" in this control model is referred to
as distress. Distress is a central concept in Identity Control Theory,
since it is believed that individuals will modify their behaviors in
order to reduce the distress, or the discrepancy between their identity
standard (their set of meanings for that identity) and the inputs that
they receive from their interaction partners.
- 2.13
- We also note that, while modifying behavior to reduce
distress is the simple control model we adopt here, other ways of
coping with distress are possible. Another way is to change identity (Burke 2006; McFarland & Pals 2005),
so that behavior and appraisals are consistent with the new identity
standard. Alternatively, one can engage in selective interaction
strategies by finding interaction partners that are more likely to
verify an identity (Robinson
& Smith-Lovin 1992). In the present model, we make
the simplifying assumption that agents only reduce distress by
modifying behavior.
- 2.14
- Experimental evidence for this model includes the teamwork
exercise to explore a "dominant person" identity (Swann & Hill 1982) and
other laboratory and survey research (see, Burke
and Stets 2009, and the references therein). Recent results
of Stets and Burke (2014)
suggest that distress reduction may contain some nonlinearities. The
simplest computational interpretation of behavioral change to bring
appraisals into agreement with identity meanings is a linear feedback
of the distress, as measured by "appraisals minus meanings." Stets and
Burke observed in experimental settings that when an identity implies
positive and negative connotations (such as, being a good employee or
being an "honest" person) appraisals that are more positive may lead to
an enhancement effect of good feelings as well as the expected
consistent effect of distress over unmatched feedback. What this
experimental result suggests is that appraisals that "overshoot" an
identity meaning may not lead to the same level of distress as
appraisals that "undershoot." That is, an agent may work harder or
faster on behavior to alleviate negative appraisal discrepancies than
s/he would to reduce positive ones. In this regard we are most
certainly simplifying the identity control process. Emotional and
cognitive thought processes thus impact the control loop in ways we do
not fully understand. With these caveats in mind, we take this first
step in implementing ICT into a computer simulation of a college
drinking event.
Peer Influence
- 2.15
- ICT provides an important complementary process to
classical Social Influence Theory (Abelson
1964; Friedkin
& Johnsen 2011; Isenberg
1986; Mason et al. 2007).
We consider in this work a peer influence (PI) model of social
influence as a second form of feedback control of drinking behavior.
The distinction from IV is that PI models a behavioral change in which
individuals seek approval by adopting the behavior of others. Peer
influence can encompass a number of control actions (Borsari & Carey 2001).
Within the college drinking context, peer influence can range from
direct offers of drinks to indirect modeling of others' behaviors to
that of identity control. Indeed, ICT involves an element of peer
influence, as peers provide appraisals that an individual processes to
examine identity. Our PI model is the indirect sense of an individual
attempting to model the behavior of peers, much like attitude and
opinion dynamics of Abelson (1964).
Indeed the simple feedback model we define below closely follows the
dynamics of Abelson's attitude model. As noted in Borsari and Carey (2001), this indirect sense
involves an individual matching the concurrent drinking of peers within
the drinking event: past observations do not tend to enter into the
control model. Moreover, this control behavior appears to be
independent of the individual's awareness of the peer influence.
Experiments (DeRicco &
Garlington 1977; DeRicco
1978) have tended to corroborate the notion that agents are
influenced by indirect PI within a drinking context. Osgood and
colleagues (2013) also
observe not only significant relationships between individual and peer
behavior in alcohol use but also strong tendencies for friendship
selection based on similar drinking behavior.
- 2.16
- Together, the PI and IV models form our social influence
model of drinking behavior, which is illustrated in Figure 3. It is interesting to note that IV
and PI have different impacts on group, and hence aggregate, behavior.
Both PI and IV affect the individual agent's behavior, but the agent's
behavior becomes a component of the group behavior, which creates a
loop back to the individual through the PI model.
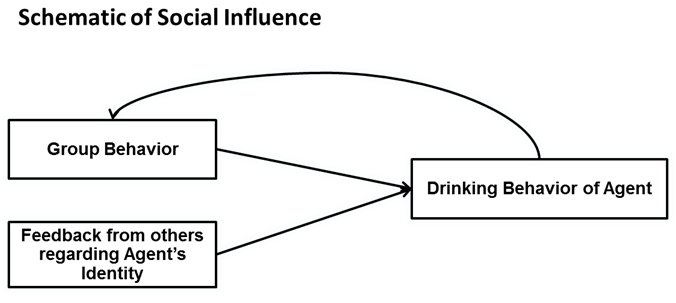
Figure 3. Drinking behavior adaptation from ICT appraisal feedback and peer influence. - 2.17
- Together the IV process and the PI process can be applied
to explain the drinking rate of the individuals. Figure 4 is a conceptual representation of
how these two processes intermingle. Since individuals may weigh
identity appraisals and the group influence differently, we suggest
weighting factors (a and ß) that
are used to define an agent's commitment to his/her
drinker identity; that is, those agents that are highly committed to
their drinker identity will weigh the appraisals that they receive more
heavily than those that have a low commitment to their identity. The
concept of commitment is an important component in the identity control
process (Burke & Reitzes 1991).
While the impact of social influence in the PI model is the act of
modifying behavior to match the drinking rate of a person's peers, the
form of influence that results from an interaction encounter results
from a person's desire to meet verification needs.
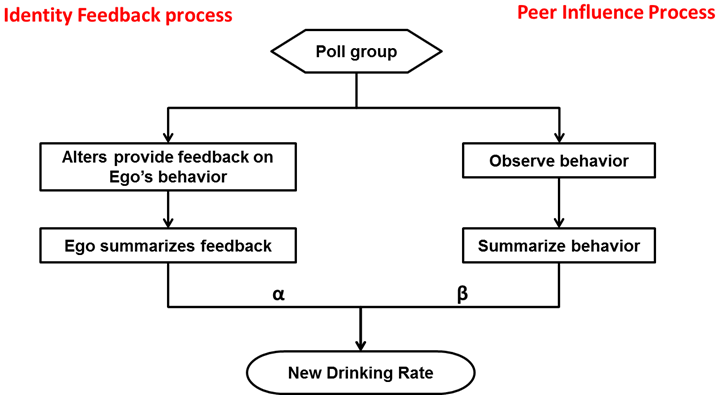
Figure 4. Adaptation of Identity Verification needs and Peer influence. - 2.18
- By focusing on drinking identities, we are of course
abstracting the problem down from the many complex issues that make up
a population of college students. Gender, ethnicity, socio-economic
status (including parental educational attainment as well as income),
and other identities all have impacts on a student's drinking behavior (Wechsler et al. 2002).
Interacting Groups at the Party
- 2.19
- Generally speaking, party events do not involve a single
large group of individuals who are simultaneously interacting with
everyone else, nor do they involve singletons behaving as if alone.
Rather, parties and social events tend to involve smaller clusters of
interaction partners within the larger event (Bakeman
& Beck 1974; Ingram
& Morris 2007). One of the primary challenges with
this particular aspect of the model is that little empirical research
exists on how small groups form and break up at short-time social
events such as parties. Interesting technical innovations (see, e.g., Cattuto et al. 2010; Setti et al. 2013) including
Radio Frequency Identification (RFID) chips and computer vision systems
offer new means of tracking groups and clustering at parties and other
events, but empirical studies using these for social sciences purposes
are quite few. A number of more mathematical approaches (Kelly 2011; Wilenski 1997) have also been
developed.
- 2.20
- There is, on the other hand, a great deal of empirical
research on many aspects of the evolution of groups and of social
networks and their dynamics. Much of this work is focused on a longer
time-scale than is at issue for a single party or drinking event, but
the network structure and dynamics provide some insight into friendship
networks. The Framingham Heart Study Social Network (see Christakis & Fowler 2007;
Rosenquist et al. 2010)
shows the importance of friendship ties in health behaviors over a long
time period, wherein a "three degree of separation" emerges as a strong
indicator of related behaviors. Rosenquist et al. (2010) note that both social
network and interpersonal effects are important in alcohol consumption
behaviors and observe that social network effects may have both
positive and negative impacts on drinking behavior, a result in line
with the IV and PI components of our model.
- 2.21
- We should note that there are interesting longer term effects of the interplay between drinking behavior, friendships, and groups, which are not modeled in the present work. Our short-time model of an individual drinking event involves a group formation dynamic based on a friendship network and trait similarity (homophily) which is not correlated with drinking rates. Osgood et al (2013) demonstrates correlations between drinking rates and interaction partners. Over time, we might expect a learning process to engage, in which agents modify their friendship networks based on similar drinking behavior as well as trait similarity. Modeling this more complex longer term process may be rather challenging: Shalizi and Thomas (2011) note teasing out the causality of events arising from homophily and social influence is quite difficult.
 A
Simulation Model of a Drinking Event
A
Simulation Model of a Drinking Event
- 3.1
- A single college drinking event ("party" hereafter) can
range from a few friends meeting up in a dorm room to a large party
hosted by a Greek organization (fraternities or sororities, which are
social organizations common to US universities) to a pre- or post-game
gathering around a large sporting event. The basic properties we take
for a party include a number of participants (agents), access to
alcohol, and a limited duration for the party. During the party, agents
form groups dynamically, and individuals may depart to join other
groups or split along with others to form new groups. Friendships and
trait similarities govern the manner in which groups form and break
apart. Also during the party, individuals consume alcohol based on the
feedback models of ICT and PI.
- 3.2
- The party operates with a pre-determined number of agents, N,
and for a pre-determined number of hours, H. We run
a discrete time simulation with a fixed clock ticking every ?t
hours. A drink is the so-called "standard drink," which contains 10
grams of ethanol, approximating the rule of thumb that one beer equals
one glass of wine equals one shot of liquor. During the party, as noted
above, the agents consider their groups and their drinking rates.
- 3.3
- A few primary processes are needed to instantiate the
agents and implement their behaviors in a simulation.
- Agents assort themselves into interacting groups. For this simple model, a friendship network and a trait attribute are used to simulate the dynamics of grouping together and breaking apart. Agents assess their similarity in terms of friendships and traits with members of groups to decide whether to remain in a group or move on to another. The grouping governs the interaction partnerships, which in turn govern the drinking signals.
- Agents observe the drinking in the group. This indirect PI process contributes to the agent's decisions on how much to drink.
- Agents give to and receive from members of their group appraisals about drinking behavior. Drinking behavior is an identity, instantiated as a categorical drinker type. Each agent attaches a quantitative drinking rate "meaning" to each drinking identity type, and the appraisals an individual receives are coded as these drinking rate meanings. These IV appraisals also contribute to an agent's decisions on how much to drink.
- 3.4
- Three key parameterizations are involved in the drinking
processes (B) and (C):
- Each agent weights the IV (C) and PI (B) drinking rate information to make a decision concerning her/his drinking rate. We denote these weights by a and ß respectively.
- Each agent has an identity, which is a qualitative categorical symbol of her/his drinker type. Associated with this identity, the agent has a meaning that denotes an actual numerical drinking rate that the agent connects to her/his identity.
- Each agent has a set of meanings that s/he attaches to each the identity types as s/he perceives them to apply to others. These meanings are actual numerical drinking rates for each identity type. In view of SNT's ideas related to misperception, these identity meanings (which form the basis of appraisals the agent will provide to others) may be positively biased away from "truth" (which we infer from SNMRP survey responses).
- 3.5
- Before drilling down into the group and drinking blocks, we
describe the agent attributes needed to model the dynamics.
Agent Attributes and Model Parameters
- 3.6
- Agents in the model are relatively simple actors with a
small number of attributes. We delineate them below. A number of
attributes are random quantities whose distribution models require some
flexibility. We will discuss those details when we specify parameter
values and provide simulation examples in Section 4. Modeling the
dynamic process also requires the selection of functional forms for a
number of decision computations. As is often the case in agent-based
modeling of social systems, we have little in the way of hard data to
choose these forms, and here we make selections based on directionality
(do the relationships go in the right direction?) and simplicity.
- Agent ID number: we assign each agent a unique number IDi from 1 to N, where N is the number of agents attending the party.
- Agent trait: each agent is assigned a random trait Ti from a uniform distribution on the interval [0,1]. This quantity is an abstract trait meant to provide a means of agents finding other agents with similar interests for the grouping process (A).
- Agent drinking identity: each agent is randomly assigned a category Di, one of the five drinking types. The likelihoods of the five types are specified as a simple probability mass function, and this distribution is flexible. This attribute determines the agent's identity as in (C).
- Agent identity definitions: for an agent to define his/her identity and to provide appraisals to others, the agent must have an idea of what level of drinking is compatible with each type. Each agent is assigned five drinking level perceptions, R1i, R2i, R3i, R4i, R5i, one for each category. These levels are drawn from lognormal distributions (this distribution is discussed more below) whose parameters are flexible. The agent sets as R*i the drinking level from these five levels that corresponds to his/her identity. This attribute provides the meaning an agent attaches to her/his identity (and in the absence of SNT misperception to the identities of others). These numbers provide simple, specific meanings to the identities as in (C).
- Agent identity misperception: the parameter eji = 0, j=1,2, …, 5 is added to the identity definitions Rij as a means to model SNT misperception. This parameter may be set to 0 or sampled from one of a choice of distributions. The use of a non-negative misperception derives from empirical research (see, e.g., Borsari & Carey 2003).
- Agent appraisal feedback: the parameter Fji = Rji + eji is the appraisal agent i provides to group members of the 5 drinking identity types. These quantities are not independent attributes: rather they are determined directly from attributes 4 and 5. It is an important feature of the model that an agent may provide higher appraisal feedback to others than s/he might expect for him/herself. These feedback appraisal drinking rates are the meanings an agent attaches to the identities of other agents.
- Agent commitment to identity: a number ai between 0 and 1 is assigned to each agent, governing (as described in Subsection 3.3 below) how strongly the agent responds to appraisal feedback on identity, relating to (C) above. How much of an agent's drinking rate is based on IV is governed by this parameter. The assigning distribution is flexible.
- Agent responsiveness to peer pressure: a number ßi between 0 and 1 is assigned to each agent, governing (as described in Subsection 3.3 below) how strongly the agent responds to peer pressure to conform to the group drinking rate, relating to (B) above. We require ai + ßi = 1 for each agent. How much of an agent's drinking rate is based on IV is governed by this parameter.
- Friendship network: encoded as an array (called an adjacency matrix), Cij with indices denoting two agent ID numbers, the friendship network is defined by Cij = 1 when agents i and j are friends and 0 if they are not. This matrix is undirected. This may be initialized as 0 for a freshman mixer model or any other network construct. The friendship network impacts the dynamics of groups as in (A) above.
- 3.7
- With the individual agent attributes in hand, we define
parameters and model functions that are fixed for all the agents for
the party simulation.
10. Size of party: N is the number of agents attending the party.
11. Duration: H is the party duration in hours.
12. Time step: ?t is the time step in hours at which simulated actions are taken.
13. Group similarity model parameters: to determine an agent's "fit" within a group, Agent i computes the dynamic quantity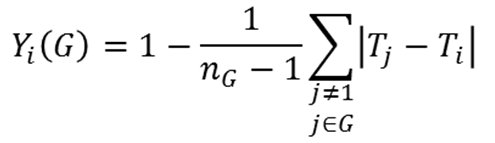
(1) for each group G (with i added to G if i is not a member). This quantity is the trait similarity score for Agent i, which in turn becomes the overall similarity score
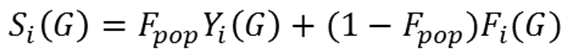
(2) In Equations (1) and (2), we use the following notation: Tk denotes the trait of Agent k; n is the number of individuals in the group; Fpop is the fraction of the population that the agents have identified as friends (this is a vector); and Fi = Fi (G) is the fraction of the group that the agents have identified as friends (also a vector). Equation (1) provides a simple trait-discrepancy based score for how well the agent fits into a group. The similarity score of Equation (2) allows the agent to weight friendships and trait similarity. If the agent has few friends at the party as a whole, then the agent is more attracted to a group containing friends. If the agent has many friends at the party, the agent becomes more likely to seek groups of individuals with similar traits.
14. The probability of departing a group due to dissimilarity is the dynamic quantity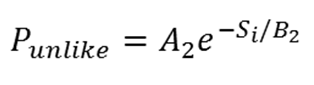
(3) For the purposes of the simulation, we set A2 = 0.6, B2 = 0.15. Equation (3) provides a simple functional form to the idea that as the similarity score increases, the individual becomes more likely to leave the group in search of another.
15. Group entropy model parameters: groups may split up from "entropy" as well as dissimilarity. The model is a probability of departing that depends on group size: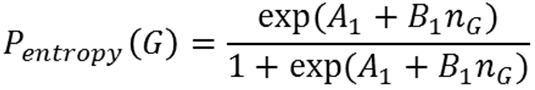
(4) in which the dynamic quantity ng denotes the number of individuals in the group, and the constants are set as A1 = -7.00, B1 = 0.50. Equation (4) provides a simple functional form that increases and saturates with the number of individuals in the group.
16. Identity appraisal statistic: each individual receives appraisals from group members concerning the drinking rate deemed appropriate for the individual's identity. The agent forms a statistic SIV, which may be set as the median, the mean, or a weighted average of the feedback appraisals the agent receives from the other members of the group. The statistic can be flexibly selected but takes the same functional form for all agents.
17. Peer influence statistic: each individual observes the drinking rates of the group members. The agent forms a statistic SPI, which may be set as the median, the mean, a weighted average, or the maximum, of the rates of the other group members. The statistic can be flexibly selected but takes the same functional form for all agents.
18. Blood Alcohol Content (BAC) statistic: as a simple means of introducing a reasonable upper bound on consumption, we use Widmark's function (Snyder 1992) for BAC in terms of drinks (D) and the elapsed time in hours since consumption (h):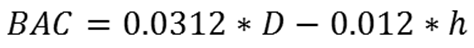
(5) The constants are empirically determined (and in general depend on body mass and gender, Snyder 1992). Individuals pass out at a BAC of 0.30 and die at a BAC of 0.40.
The Group Formation Model
- 3.8
- As agents enter the party, they form into groups. The
process of grouping is illustrated in the flow diagram of Figure 5.
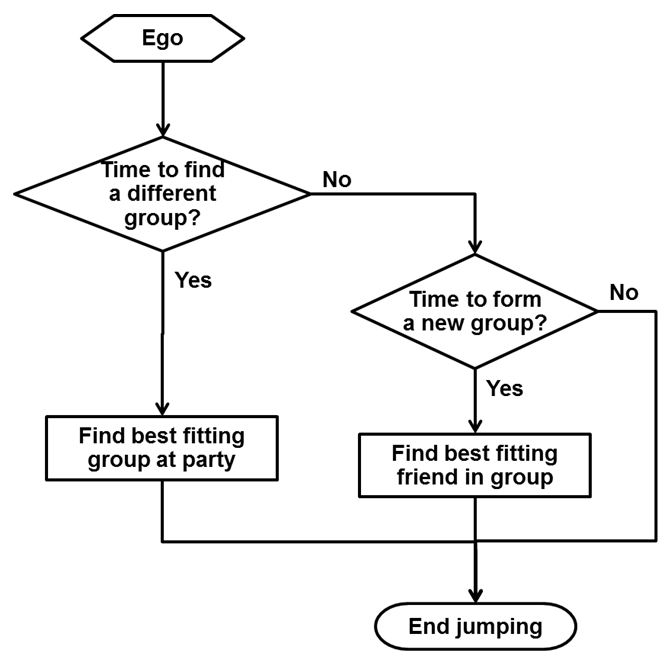
Figure 5. Block diagram of group formation. - 3.9
- We outline the process as follows. At a given simulation
time step, we perform the following operations.
- Loop through the agents in randomized order to select the "ego" agent.
- Compute trait similarity score for the current group and other groups.
- If there is a better group, jump to that one with probability Punlike.
- Compute the entropy probability and depart with closest trait similarity scoring group member to form a new two person group with that probability.
The Drinking Model
- 3.10
- The drinking model has agents consuming alcohol in terms of
standard drinks over the party duration. The rate at which agents
consume will impact their BAC and hence their basic state of being
active, passed out, or deceased. In the end, the model's primary output
is the number of standard drinks each student has consumed. The process
of drinking is illustrated with a block diagram in Figure 6.
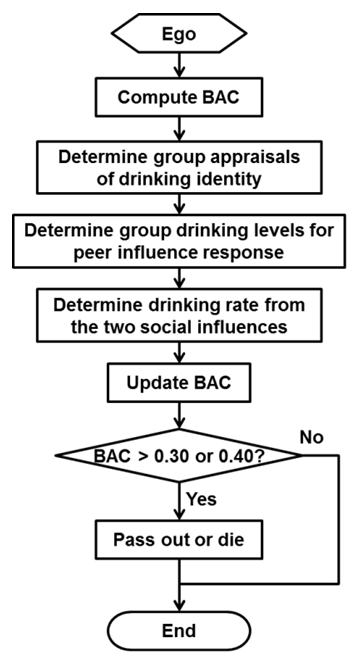
Figure 6. Drinking Component - 3.11
- We outline the process as follows. At a given simulation
time step, we perform the following operations.
- Loop through the agents in randomized order to select the "ego" agent.
- Compute the statistic SPI for the members of ego's group.
- Compute the statistic SIV from the members of ego's group.
- Compute ego's new drinking rate:
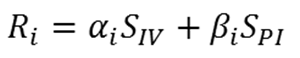
(6)
The Friendship Formation Model
- 3.12
- As agents participate in groups, they may encounter other
agents they do not directly know either entering a new group or staying
with a group that gains new participants. In this module, agents that
were selected to consider jumping will loop through the members in
their group for the possibility of gaining new friends. In our simple
model, we use the trait attribute to model similarity for the purposes
of friendship. If two individuals i and j
are not friends, then the agent will compute how similar the two agents
are with respect to their traits values: pairwise trait similarity
between agents i and j is Ui,j
= 1- |Ti - Tj|,
where Ti and Tj
correspond to the trait values of agents Ego and Alter. The probability
that these two agents would become friends is given by the following
logistic function:
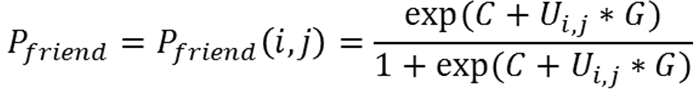
(7) where C and G are numeric constants set to -5 and 2. We choose the logistic as a model for the "befriending" decision due to its simple functional form, increasing with horizontal asymptotes at 0 to the left and 1to the right.
- 3.13
- We note that, in this simple model of a dynamic friendship
network, friendships form but do not break. We also note that the
formation of new friendships will have an impact on group assessments
and dynamics. That is, when an agent considers a decision to remain in
her/his current group or move to another group, that agent's friendship
network plays an important role.
The Simulation Model "At A Glance"
- 3.14
- We close this section by summarizing the model in a list of
computational steps, integrating the attribute and dynamic blocks into
a single procedural outline.
1. Initialize the event, by choosing the time duration and the number of agents.
2. Initialize the agent population:
- Assign each agent a trait variable from a uniform distribution.
- Assign each agent an identity from a discrete distribution of identity types, namely abstainer, infrequent, light, moderate, or heavy.
- Assign each agent an identity meaning, which is a drinking rate, from a lognormal distribution associated with the agent's identity type.
- Assign each agent five identity meanings to be used when providing feedback appraisals to other agents.
- Assign each agent commitment levels (a and ß) to IV and PI processes, from uniform distributions (and normalized to sum to 1).
- Build an initial friendship network as a random graph.
- Check the grouping. Agents will decide (with probability from Equation 3) to consider moving to another group. If a "considering" agent finds a group that has higher similarity (as determined by Equation 2), then the agent may join that group. If a considering agent does not find a higher similarity group, that agent may (with probability determined by Equation 4) decide to take a friend in the current group and split off into a new group.
- Check friendships. Agents who have considered moving to a new group will also examine individuals with whom they are not currently friends. The "considering" agent will add not-current-friends to their friendship network with a probability that depends on trait similarity, from Equation (7).
- Check the drinking. Agents will decide (at a random rate) to consider drinking more. The "considering" agent will obtain appraisals from group members and observe the drinking rates of group members, forming a new drinking rate according to Equation (6). The agent will then check BAC from Equation (5).
- 3.15
- We move now to running the simulation to investigate the effects of misperception, social influence, and identity control on aggregate drinking outcomes.
 Simulation
Analysis
Simulation
Analysis
- 4.1
- Having discussed the model's design and parameterization,
we conduct a suite of simulation studies to investigate the collective
behavior of students drinking at a party. As noted above, there are a
number of parameters relating to the IV and PI modeling. The impact of
these model specifications on the system is of great interest, both for
the design of surveys and other data collection efforts and the
development of policy actions that may mitigate problem outcomes.
Parameter Specification
- 4.2
- For the purposes of this exposition, we simulate the
behavior of N = 20 students at a party of duration H
= 4 hours under a number of parametric configurations. A number of
parameters defined in the Agent Attributes and Model Parameters section
as "flexible" need to be specified.
- 4.3
- First, the proportions of agents in each identity type are
given in Table 1. The
identity labels are taken from Wechsler et al. (2002), and the proportion
values are loosely based on the CAS results described therein.
Respondents to the CAS were asked to self-identify as one of seven
types (these five plus Abstainer-in-Recovery and Problem Drinker). It
is important to note that students were not given definitions of these
terms: rather, the respondents chose the term felt to be most
self-descriptive.
Table 1: Probabilities of agents being assigned to each drinking identity Drinking Type Proportion Abstainer ~ D1
Infrequent ~ D2
Light ~ D3
Moderate ~ D4
Heavy ~ D50.1697
0.3138
0.2255
0.2477
0.0433 - 4.4
- Second, the drinking levels for each of these five types
are specified in Table 2. In order to assign a level of drinking to
each of these identities, we examined the number of drinks consumed at
a drinking event by individuals who self-identified in each of the five
types in the CAS survey. From these data we obtain five probability
distributions to model the individual drinking levels. Thus, we tie
these self-selected identity terms to the amount the individual is
likely to consume at a drinking event. The lognormal distributional
form we use to fit these data is commonly used for modeling drinking
rates (see, e.g., Ledermann 1956;
Skog 1985; Nahas et al. 1999). The choice
of the lognormal relates to the nonnegative, left skew, relatively long
tail behavior it exhibits that is typically seen in observations of
drinking rates across a population. Figure 7
shows the lognormal densities having these parameter specifications.
Table 2: Parameters for drinking rates for each of the five identities Drinking Type Lognormal Mean Lognormal Standard Deviation Mean Drinks/Event Standard Deviation Drinks/Event Abstainer
Infrequent
Light
Moderate
Heavy-4.6874
0.1830
0.9770
1.4895
1.90352.0224
0.9031
0.5213
0.4067
0.25360.0712
1.8054
3.0431
4.8172
6.92860.5457
2.0270
1.7005
2.0431
1.7857 - 4.5
- For the IV agent identity misperception, we consider three
cases: e = 0 (no misperception), e
lognormally distributed with mean 0.5 and variance 1.0, and e
lognormally distributed with mean 1.0 and variance 1.0.
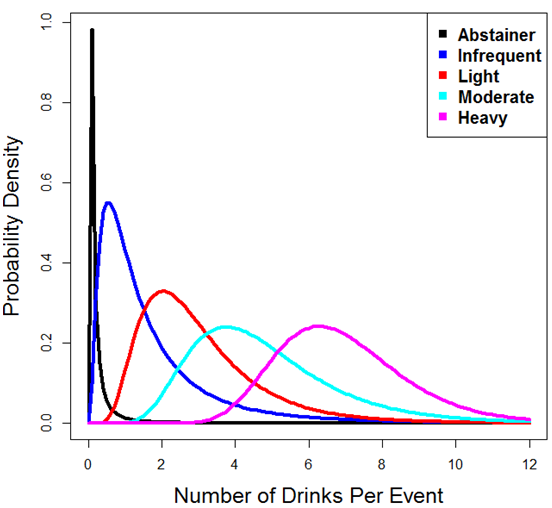
Figure 7. Modeled drinking level likelihoods for the five drinking types - 4.6
- We note here that a heavy episodic or binge identity is not
specifically part of the model. With the standard definition of heavy
episodic drinking being five or more drinks in a single event period
for men, we see that even self-identified abstainers have some chance
of becoming bingers, while moderate and heavy drinking identities are
quite likely to undertake binging behavior.
- 4.7
- For agent commitment to identity (a) and
responsiveness to peer influence (ß), we consider
three cases. We set a0 =
0.20, 0.50, or 0.80 and ß0 =1-
a0, and for each agent
we generate a pair of uniform random numbers (a', ß')
on (0, a0), (0, ß0)
respectively. Finally these pairs must be normalized to sum to one, so
we set a = a'/(a'+ ß'),
ß = ß'/( a'+ ß'). Figure 8 illustrates the resulting
distribution for a based on this process, for a0
= 0.20, 0.50, or 0.80, as well as the expected value of a
(after the normalization). A simpler modeling choice would be to model a
with a uniform on [0, a0] and
take ß=1-
a. The slightly unusual choice we have made
still allows the population of agents to have a full spectrum of (a,
ß) pairs between 0 and 1 but with bias in one direction or
the other depending on a0.
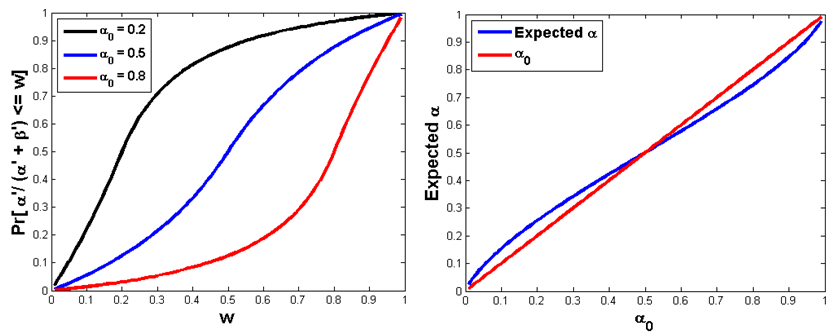
Figure 8. ECDF of a (left panel) and expected a (right panel) - 4.8
- We have now fully specified the model's functional forms
and parameters so that simulations can be executed. Table 3 summarizes the 3×4 factorial
design of this study. As previously mentioned, we have 3 levels of the a0
conditions (0.20, 0.50, 0.80), and we have four levels of the
misperception condition. Table 3
summarizes the structure of the model, and follows our inquiry into
investigating sources of influence on agent behaviors. The a0
conditions define the distributions of agents' commitment levels to
their drinking identities and of their responsiveness to peer pressure.
As can be seen in Figure 8, the
low choice of a0 =0.20 leads
to a population of agents that are highly susceptible to peer
influence, while the higher choice of a0
=0.80 leads to a population of agents that drink at a rate that matches
their identity verification needs. The second factor in the analysis
involves the different forms of misperceptions (either biased
appraisals or different group conditions) and their effect on drinking
behavior.
Table 3: Experimental conditions for our simulation study High a0=0.8 Medium a0=0.5 Low a0=0.2 e = 0, group median
e = 0, group max
e ~ LogNorm(0.5,1), group median
e ~ LogNorm(1.0,1), group mediane = 0, group median
e = 0, group max
e ~ LogNorm(0.5,1), group median
e ~ LogNorm(1.0,1), group mediane = 0, group median
e = 0, group max
e ~ LogNorm(0.5,1), group median
e ~ LogNorm(1.0,1), group median - 4.9
- For each of these 12 conditions, we simulate 10,000 Monte
Carlo realizations. In the following subsections, we discuss different
aspects of the model output.
Illustration of Simulation Dynamics
- 4.10
- For illustration purposes, we have selected our baseline
model of a0 = ß0
= 0.50, with e=0/group median for the
feedback statistics agents use to adjust their drinking rates. In the
following figures, we present the network dynamics of group jumping,
group sizes, the drinking behavior of agents over time.
- 4.11
- Figures 9–12 provide a glimpse into the
behavior of agents at the parties, for two realizations of the model
simulation. In Figure 9, the
left panel contains the initial simulation state. The panel on the
right contains the final state at the end of the simulation. The
circles denote the agents, with the line segments denoting the
friendship network. Numbers on the agents denote the drinks consumed,
and colors denote the group membership. Figure 10
provides an animated GIF of the 20 partiers as they group together,
separate, and drink, starting from the left graph illustration of
Figure 9 and ending at the
right. Figures 11 and 12 are identical in concept to 9 and 10
but illustrate a different realization.
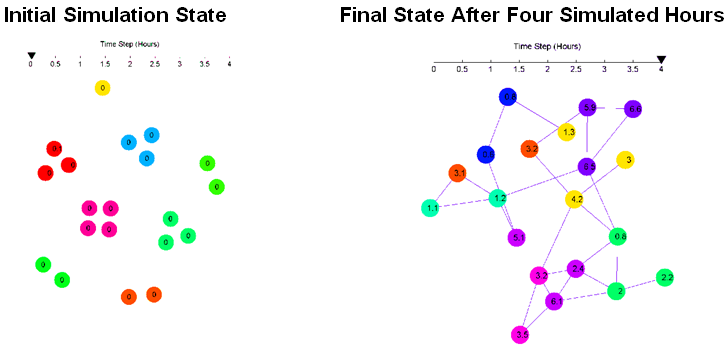
Figure 9. Initial State and Final State of one Realization. Example 1. 
Figure 10. Animation of Network evolving #1 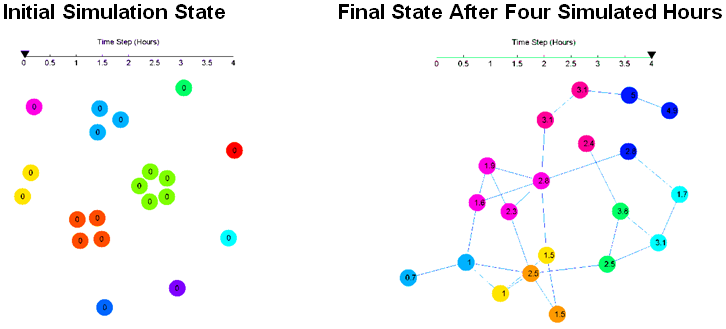
Figure 11. Initial State and Final State of one Realization 
Figure 12. Animation of Network evolving #2 - 4.12
- Statistics of the grouping process are recorded in Figure 13 and 14,
for 1,000 realizations of the model simulation. In Figure 13, we present an image plot of the
group size for all time steps in the model. At the bottom of the figure
(along the x-axis), we present time in units of hours (for a 4 hour
party). Along the y-axis, we observe the size of the group. The colors
in the figure denote the fraction of each group size in the population.
The black line in the figure denotes the median group size for those
realizations. Moving from left to right in the figure, we observe that
group size starts out fairly small (around 4), increases dramatically
(up to 6), but decreases to a median of size 3. We also notice that the
variance of group size also decreases. At the fourth hour, the
distribution is positively skewed as noted by the dramatic change in
color intensity between group sizes 2 and 3 along the y-axis, and the
gradual change in color values from group sizes 3 to 7. In Figure 14, we present animation of these
processes over the course of the party.
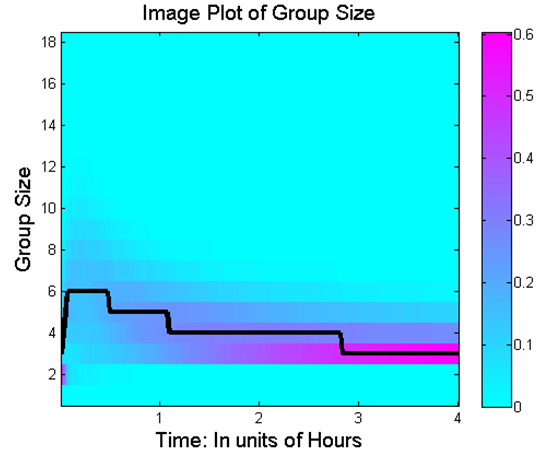
Figure 13. Distribution of group size as a function of time. Black line in the figure denotes the median group size for each time step. The cyan and magenta color intensities denote the proportion of the population for each group size. 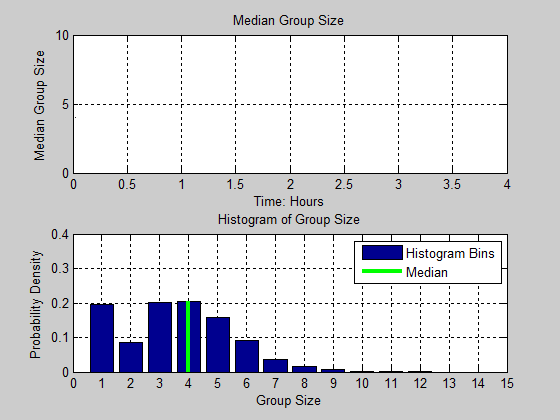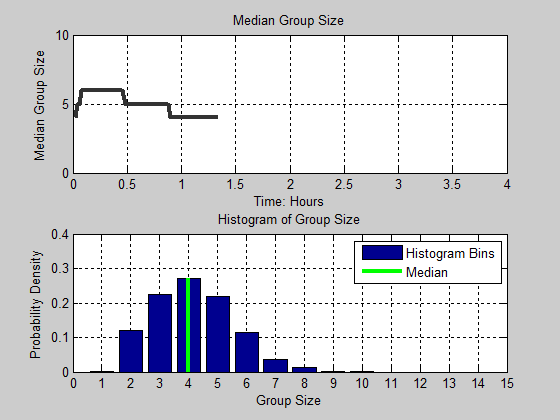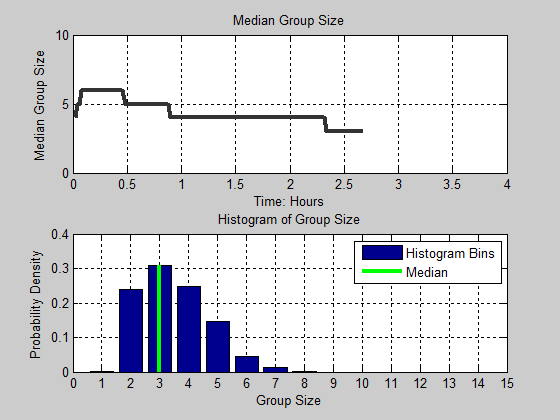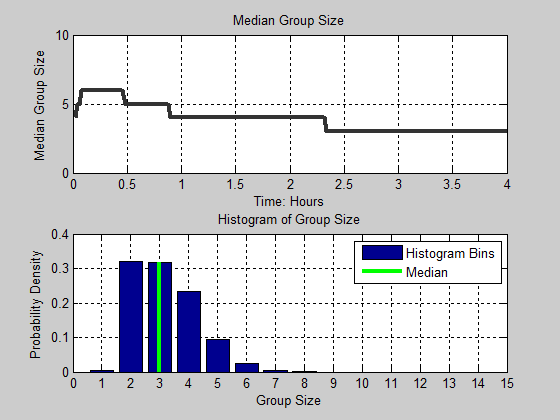
Figure 14. Animation of Median Group Size and Histogram of Group Size as a function of time - 4.13
- In Figure 15, we
observe an animation of the proportion of group departures for one
thousand independent simulations. That is, how many times do agents
jump to new groups or form new groups during the course of a party? In
the top panel of the figure, we see the median number of departures for
all 1000 simulations. The bottom panel of the figure provides a
histogram of the jumping behavior as it changes through the course of
the simulation. The animation illustrates that initially agents make
many departures quickly; however, after a while they have a tendency to
find individuals in groups that they get along with. Also, in the
bottom panel of the figure, we observe a histogram of the jumping
frequencies. The variance of the distribution appears to increase as
'outliers' (i.e., agents with no friends) make last ditch efforts to
find suitable interaction partners at the party.
Figure 15. Animation of Median Group Departures and Histogram of Group Departures as a function of time - 4.14
- Figure 16 contains
an animation of the kernel density estimate of the number of drinks
consumed, computed for 1000 realizations. The top portion of the figure
contains the drinking rates of those agents at the
first, second, and third quartiles of the drinks distribution, as it
varies over time. As observed in the animation, agents ramp up their
drinking behavior to catch up with the appraisals and peer influence
models. However, after an hour of drinking their drinking rates slow
down. It is also important to note that this time period is the most
active time period in the model. This is where most of the group
departures occur and where the variation in group size tends to be the
largest.
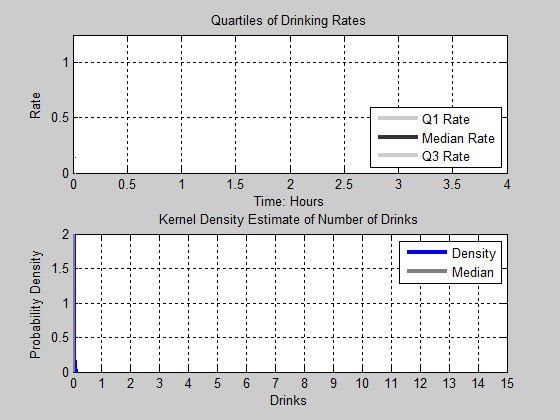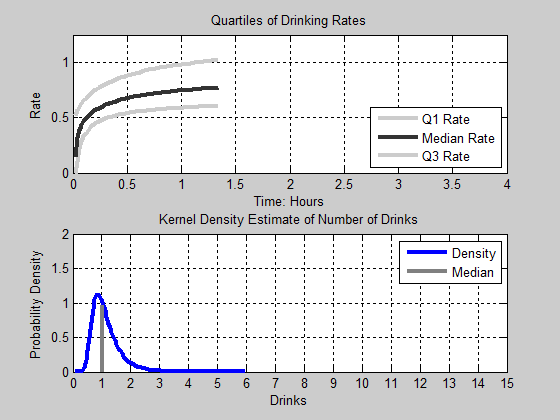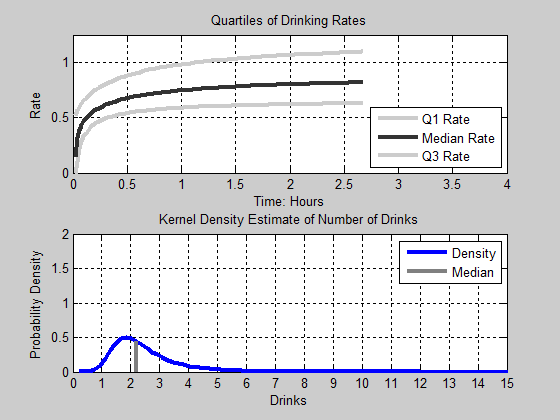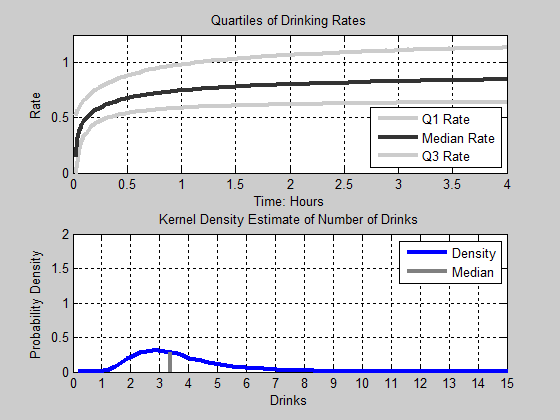
Figure 16. Animation of Drinks. Top Panel: The first, Second, and Third Quartile of Drinking Rates as a function of time. Bottom Panel: The Kernel Density Estimate of the Number of Drinks consumed - 4.15
- Those agents that are at the first quartile appear to
settle into an equilibrium after three hours, while those agents at the
second and third quartiles appear to continue to slightly increase
their rate of consumption.
- 4.16
- These images and animations provide a nice visual sense of
the simulation's operation. Using the model for scientific and policy
inquiry is the topic of the next subsection, wherein we examine the
full 10,000 realizations for each of the 12 experimental conditions of
Table 3.
- 4.17
- Again we note that a paucity of quantitative empirical data
on dynamic grouping in a social environment makes it difficult to
validate the model. However, qualitatively this data appears to match
observed video data of mixing at parties (Setti
et al. 2013), and quantitatively the group size data compares
well to related observational data (Bakeman
& Beck 1974). Figure 17
compares the cumulative distributions of our simulation with two sets
of data presented in Bakeman and Beck (1974).
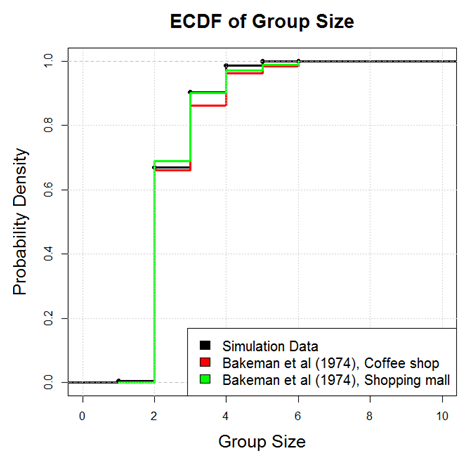
Figure 17. Comparison of simulated group sizes with observed grouping behavior from Bakeman & Beck (1974). Analysis of the Simulated Drinking Data
- 4.18
- We begin our analysis with the aggregate drinking behavior
of the population at the end of the party. In Figure 18, we see the ECDFs of all 12
experimental conditions. Each of the four panels in the figure is
conditioned on the misperception settings, while the data contained
within each panel compares the a0,
ß0 settings. The black
line on all figures called "identity" is how much the agents would
consume in the absence of any influence whatsoever. One can view this
curve as the drinking behavior that would arise from agents drinking
alone for 4 hours according to their drinking identities.
Mathematically, this curve is the mixture distribution of the
lognormals of Figure 7 with
mixing proportions from Table 1.
As observed from these data, we notice that alpha has a large effect on
drinking behavior when e=0 and PI equals the max (top right of the
figure). However, for the remaining models, the effect of the a0,ß0
settings are small but consistently ordered from less drinking when a0
is high to more drinking when a0
is low. Further, we observe a slight reduction in variance of each
distribution as a0
decreases.
- 4.19
- We also note that the e=0/group median condition, our
baseline model without misperception, is uniformly shifted to the right
of the identity distribution. This curious result is explainable:
agents' movements among groups have consequences for drinking behavior.
In short, as agents seek to have their identities verified, they are
faced with one of two choices. If their appraisals cause them to drink
more, then the agents will consume more alcohol. However, when they are
given appraisals that tell them they are drinking too much, they may
only refrain from drinking. Since it is not possible to undrink,
agents must wait for time to pass for their identities to be verified
in those interaction encounters that suggest the agents have had too
much. Therefore, modifying behavior in order to achieve identity
verification (by multiple group members) leads to an effect comparable
to a running max of appraisals. A running max of n+1
independent lognormals for different values of n is
illustrated in Figure 19. If
agents were to drink alone, then their drinking behavior would match
the identity distribution. As we can see, taking the max of 2
appraisals leads to a median 1 additional drink over the four hour
period, and the max of 8 appraisals will bring about 3 additional
drinks at the median.
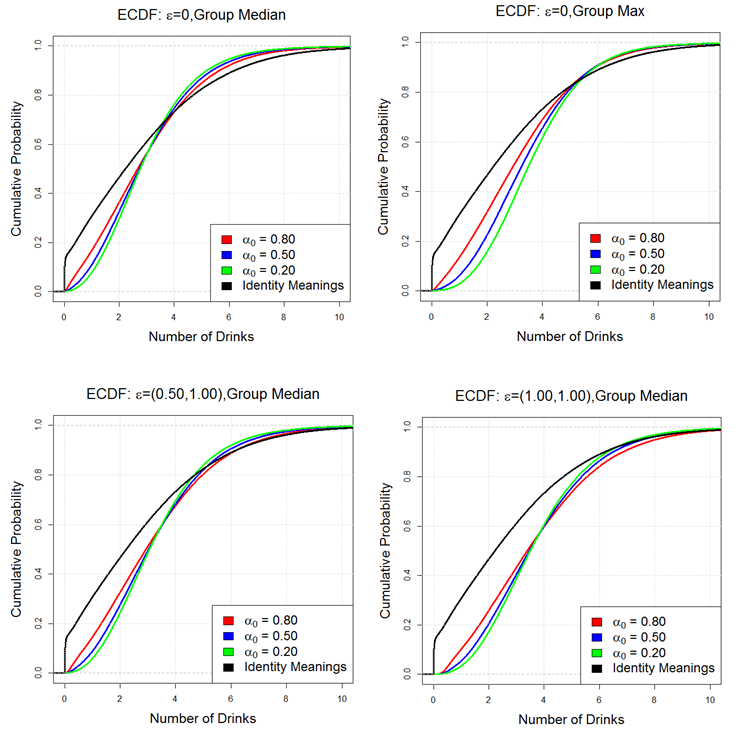
Figure 18. Comparison of ECDFs for each Influence Condition: No Misperception, e=0, Group Medium (top left); Group Misperception e=0,Group Max (top right); Moderate Identity Misperception e=(0.50,1.00), group Median (bottom left); High Identity Misperception e=(1.00,1.00), group Median (bottom right) 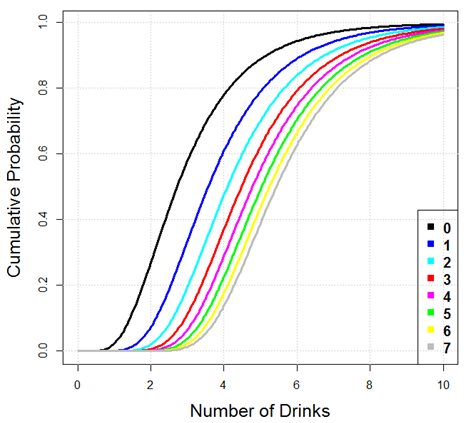
Figure 19. Running max of n+1 lognormals, n=0,1,…,7. - 4.20
- In Figure 20, we
reorient the graphs in terms of the experimental conditions, organizing
the plots by the a0, ß0
settings. In these figures, we can see how
each misperception condition varies as a function of a0,
ß0. Also particularly
noteworthy, is that when a0=
0.80, the e = 0/group max condition and the e = (0.50,1.00)/group
median condition behave similarly. However, when a0
=0.50 the effect of the group max condition
is just as influential as the e = (1.00,1.00)/group median condition.
And when a0 = 0.20, the
drinking behavior of the agents under the e = 0/group max condition
exceeds the identity misperception condition e = (1.00,1.00)/group
median.
- 4.21
- As an additional parametric sensitivity study, we
considered the impact of the initial friendship network. All of the
simulations to this point were conducted as if at a freshman mixer,
with no friendship ties at the onset of the event. We consider two
straightforward modifications of this parameter setting. In one, we
initialize the friendship network by setting all agents with trait
differences less than 0.05 to be friends ("some friends initially"). In
a second perturbation, we initialize the friendship network to be fully
connected ("all friends initially"). In Figure 21,
we see that knowing more people at the onset of the event reduces
drinking slightly, a result nearly entirely due to the reduced movement
from group to group that results from knowing more people.
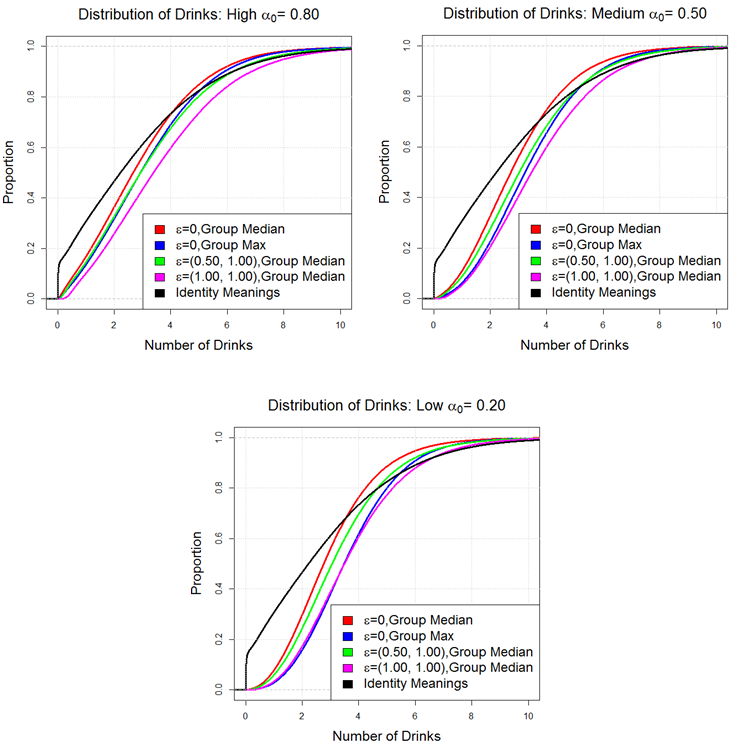
Figure 20. Comparison of ECDFs for each alpha condition: High (top left), Medium (top right), Low (bottom) 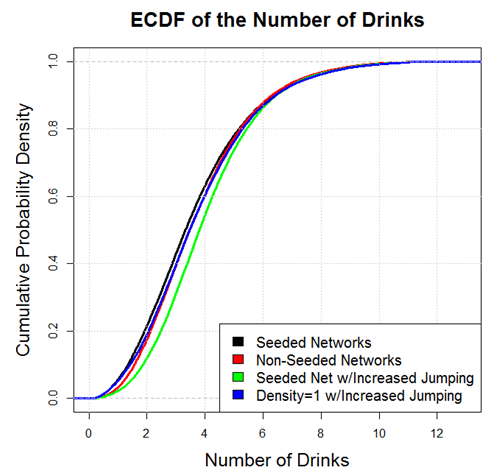
Figure 21. Dependence of drinking activity on initial friendship network. - 4.22
- The ECDFs in Figures 18
and 20 show a slight variance
reduction at the macro level due to the decrease in a0
and resulting increase in the impact of peer influence. In order to
understand better the impact of the group on drinking behavior, we
consider the intraclass correlation coefficient (ICC), a measure of the
extent to which observations of units in the same group match (Sokal & Roholf 1995).
In the large sample limit, the ICC can be viewed as the
proportion of variance attributable to variation between groups. Thus,
small values of the ICC indicate that variability within a group is
comparable to variability between groups, whereas large ICC suggests
that within group variability is small relative to the population's
variability as a whole.
- 4.23
- In Table 4, we
examine the drinking data in terms of grouping. We present ICCs for the
12 simulation settings. The ICC allows us to assess how similar the
drinking behavior is within the small groups that form during the
party. As observed in Table 4,
the ICC increases as a0
decreases. The trend is to be expected, in that smaller a0
means agents emphasize peer behavior matching in their drinking rates
(see Equation 6), but the strength of the effect is quite remarkable
for low a0, corresponding to
stronger peer influence, which pulls quite hard on the individuals to
drink similarly to their group members.
Table 4: Intraclass correlation coefficient of Log Drinks within groups a0 e = 0,
Group Mediane = 0,
Group Maxe ~ lN(0.50, 1.00),
Group Mediane ~ lN(1.00, 1.00),
Group Median0.80 0.35 0.30 0.35 0.37 0.50 0.61 0.54 0.63 0.65 0.20 0.83 0.77 0.84 0.86 - 4.24
- To investigate the results of our 12 simulation studies
more deeply, we apply a hierarchical linear statistical model (HLM),
using the number of drinks as the dependent variable, with individual
identity, number of jumps from groups, individual a,
and an identity*a interaction term as the
independents. The hierarchy in the model arises from the formation of
small groups, essentially a random effect that impacts the individual
behavior. Membership in groups is an important effect for the
inference, as the group members provide appraisal feedback and offer
peer influence, and these dynamics create a within-group effect as is
seen in Table 4. To integrate
group membership into the inference, we note that while agents are
joining groups at all times during the simulation, the agents have a
tendency to settle into relatively stable social structures towards the
end of the four hour period. Therefore, we use the group that the agent
was in at the last time step to define a random effect term in the
hierarchical linear model.
- 4.25
- Our regression model takes the form
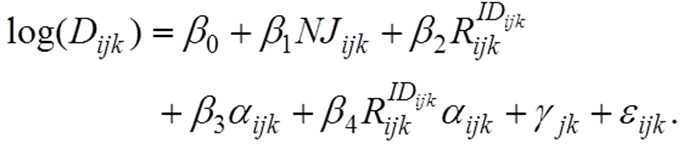
(8) In Equation 8, the five regression coefficients, ß0, ß1, ß2, ß3, ß4, relating the dependent log-drink variable to the independents, are given in Table 5 for each of the 12 different simulation settings. We use Dijk, NJijk, IDijk, R IDijk ijk, aijk, to denote the number of drinks, number of jumps, identity type, identity meaning, and a value (respectively) for the ith member of the jth group in Monte Carlo realization k. The mixed-effects hierarchical variable ?jk is a zero-mean random quantity modeling dependence of the log-drink variable on group membership in group j in Monte Carlo realization k. Finally, eijk denotes independent identically distributed zero-mean random errors. The number of groups and the number of agents in each group vary randomly within each Monte Carlo realization. Even though the indexing may suggest a three-level model, we are really modeling only two levels of hierarchy, with agents embedded in groups at a party, and Monte Carlo realizations provide replicate samples.
- 4.26
- In order to compare the resulting coefficients across the
12 simulation settings, we have scaled the independent variables to
standard normal units prior to conducting the regression analysis. We
have also removed those agents that passed out or died. Table 5 contains results from this
inference, indicating the five estimated regression coefficients (and
their standard errors in parentheses) for the 12 distinct simulation
experimental conditions. All coefficients are significant at the p
< 0.001 level of significance. The extremely small p-values
are due in part to the number of Monte Carlo simulations that we
conducted.
Table 5: HLM Results for log drinks: standardized coefficients a0 e = 0,
Group Mediane = 0,
Group Maxe ~ lN(0.50, 1.00),
Group Mediane ~ lN(1.00, 1.00),
Group Median0.20 Intercept 0.9215 (0.0020) 1.1474 (0.0017) 1.0281 (0.0019) 1.1754 (0.0018) # jumps 0.0199 (0.0006) 0.0115 (0.0005) 0.0178 (0.0006) 0.0155 (0.0005) Identity Meanings 0.1345 (0.0005) 0.1093 (0.0005) 0.1276 (0.0005) 0.1126 (0.0004) a -0.0749 (0.0005) -0.1225 (0.0005) -0.0691 (0.0005) -0.0539 (0.0004) Identity meanings*a 0.1314 (0.0005) 0.1291 (0.0005) 0.1190 (0.0005) 0.0953 (0.0004) 0.50 Intercept 0.8712 (0.0018) 1.0447 (0.0016) 0.9826 (0.0018) 1.1421 (0.0016) # jumps 0.0278 (0.0010) 0.0236 (0.0009) 0.0260 (0.0009) 0.0191 (0.0008) Identity Meanings 0.3230 (0.0009) 0.2709 (0.0008) 0.3021 (0.0008) 0.2618 (0.0007) a -0.1116 (0.0009) -0.1681 (0.0008) -0.1027 (0.0008) -0.0781 (0.0007) Identity meanings*a 0.2020 (0.0009) 0.1909 (0.0008) 0.1780 (0.0008) 0.1376 (0.0007) 0.80 Intercept 0.7573 (0.0016) 0.8692 (0.0015) 0.8788 (0.0015) 1.0706 (0.0013) # jumps 0.0354 (0.0013) 0.0369 (0.0012) 0.0311 (0.0012) 0.0242 (0.0011) Identity Meanings 0.6431 (0.0013) 0.5696 (0.0012) 0.5937 (0.0012) 0.4965 (0.0010) a -0.1308 (0.0013) -0.1872 (0.0012) -0.1137 (0.0012) -0.0819 (0.0010) Identity meanings*a 0.2465 (0.0013) 0.2418 (0.0012) 0.2116 (0.0012) 0.1561 (0.0010) * all coefficients are significant at p <0.001. ** Independent variables are in standard normal units. *** Standard Errors are in parentheses. **** Agents that passed out or died are removed from the regression results. - 4.27
- In these linear models, we observe that the number of jumps
is positively associated with more drinking. This appears to be the
result of the 'running max' phenomenon that is observed when agents
interact with new interaction partners in the course of a drinking
event. We also observe an interaction between "identity meanings" and
an agent's a (i.e., commitment to their identity). When his identity
meaning is a high drinking rate (high rate identity) and when he has a
strong commitment to his identity, then the agent will consume more (on
average) than someone with a lower commitment to his identity.
Similarly, an agent with an identity meaning with a lower drinking rate
and a high commitment to this identity will drink less (on average)
than an agent that has a low commitment to their identity. We also note
that as a0 increases, the
identity meanings variable becomes the strongest predictor variable,
due to the increase in size of the identity coefficient.
- 4.28
- Looking across the different experimental conditions for
perception and influence, we see that the coefficient for the a
independent variable has the greatest magnitude in the Group Max
condition (in which peer influence acts to draw drinking toward the
maximum rate within the group). Since the coefficient's sign is
negative, we interpret this result to mean that the a
variable is a stronger moderator of drinking under this condition. This
pattern persists as a0
decreases.
- 4.29
- We also see that the coefficient for the identity meanings independent variable is positive, a result one would expect: those whose identities are associated with higher levels of drinking should in fact drink more. What is interesting is that this coefficient decreases in the presence of the misperception condition: as interaction partners provide appraisals based on misperception, the correlation between drinking rate and personal identity meaning deteriorates. This pattern also persists as a0 decreases.
 Conclusions
and Future Work
Conclusions
and Future Work
- 5.1
- College drinking is a significant public health problem
with many negative consequences. The design of effective interventions
requires careful study of the environmental and social aspects of
alcohol consumption on campuses. Simulation models force us to examine
our assumptions in quantitative detail and allow us to explore their
consequences; thus, agent-based simulations offer an important tool for
investigating this public health challenge. We have developed the first
module of an agent-based simulation to gain insights into the social
processes that influence drinking behavior.
- 5.2
- Generally speaking, data on college drinking arises from
surveys that capture a single snapshot in time, with multiple year
surveys capturing different groups of students. Higher frequency
longitudinal data is much less common. This state of affairs puts us in
a difficult position of comparing the results to data. Perhaps a more
difficult problem is that the current model is a high-rate control loop
embedded in a larger, multiscale problem of the drinking distribution
evolution over an academic year (and a student's college career).
Slower rate adaptations based on rewards for surviving (and even
thriving through) heavy drinking episodes – and on regret and negative
consequences for those episodes – requires an additional level of
modeling that forms the target of our future efforts.
- 5.3
- However, this simple model of a single drinking event
demonstrates that social science theory can be applied to college
drinking in a quantitative simulation and provides a number of
insights. For example, the relative weight that a person may assign to
his identity verification needs in comparison with his susceptibility
to peer pressure has an interesting impact on alcohol consumption: at
the macro level, drinking tends to increase when peer pressure is the
stronger influencing factor. This result is partially countered at the
individual level when an identity is taken into account: drinking
increases for heavier drinking individuals that have a greater need for
identity verification.
- 5.4
- In the presence of misperceptions about drinking behavior,
Identity Verification and Peer Influence can lead to higher rates of
drinking. The structure of the misperceptions, their effects, and the
possible interventions, however are quite different.
- 5.5
- The converse of these observations is potentially more
important to public health interventions. That is, social norms
marketing campaigns that are effective at reducing misperceptions may
lead to significant reductions in drinking rates. Moreover, bystander
interventions, in which specially trained participants provide light or
abstaining drinking models in groups, may also moderate overall
drinking.
- 5.6
- Specifically, the primary intervention action of social
norms marketing campaigns is to reduce misperceptions that students
have about the normative drinking on campus. These campaigns educate
students by providing accurate data on the actual campus drinking
environment. If most students erroneously believe that others drink
more than themselves, they may provide appraisals that overestimate the
normative drinking, encouraging others to drink more. A well-designed
social norms intervention would have a tendency to correct these
appraisals. This particular aspect of social norms marketing
interventions compares directly to the e
misperception model in our simulation, and we can envision a reduction
in e's mean as an effect of this intervention. Our
simulations suggest that this effect can be quite large when a's
are large, as Figure 20
illustrates, leading us to suggest that social norms campaigns may be
particularly effective when commitment to identity verification is
strong.
- 5.7
- A second, more indirect impact of social norms campaigns is
the notion that the education about actual drinking levels empowers
students to withstand pressures to drink more. That is, in addition to
correcting misperception about peer drinking rates across campus, the
intervention also attempts to make students conscious of peer
influences and to encourage students to resist peer influences. Within
the present model, this intervention component corresponds to lowering ß
(and hence increasing a). Our model shows that
reducing ß leads to reduced drinking , but the size
of this effect is small (as we see in Figure 18) except for the
situation in which the group max is used to assess peer behavior. This
reduction, even if it is small, may lead to a synergistic effect of
increasing commitment to identity verification, which improves overall
effectiveness of misperception reduction at the population level.
- 5.8
- One difficulty with peer pressure is that PI misperception
is modeled as an on-the-spot inaccurate observation of group activity,
while IV misperception is a more global, longer-time-scale
misconception of drinking rates that are associated with identity
labels. The educational message of social norms campaigns appears aimed
at misperception that we have associated with appraisal feedback (and
therefore IV). The potential effect of these campaigns on PI
misperception appears to be subtle. Interventions for PI misperception
may be more difficult to construct: more effective actions appear to be
required within the party/group structure. An approach noted in the
qualitative study of Vander Ven (2001)
is that of bystander intervention, where "control" actors at a party
work to correct perceptions during the event, one on one, nudging group
estimates to more accurate observations and mitigating riskier
behaviors. We also suggest that a by-stander intervention in which
actors who drink at lower rates will, through the peer influence
mechanism, have a tendency to reduce drinking rates in aggregate.
- 5.9
- We further note that a number of interventions of interest
involve enforcement of laws and campus regulations, such as driving
under influence (DUI) checkpoints, improved identification/age
verification, and other community-campus partnership programs. The
current model, focusing on the drinking outcomes of a single drinking
event, is not designed to consider these interventions. By developing a
model that creates a sequence of parties over a longer time period and
includes environmental variables such as consequences, accessibility,
and enforcement, we hope to address important policy implementation
questions. Another important future consideration is the evolution of
social networks, especially as friendship formation takes into account
drinking similarity in addition to trait similarity, which will
certainly impact aggregate drinking rates.
- 5.10
- The model we have developed in this work, however, does provide some interesting insights into college drinking and the potential for social norms and bystander interventions to mitigate extremes of drinking behavior. The micro-level structure of the model, built on small groups of students interacting in a single event, permits the implementation of the social theories of Identity Control and Social Influence at a fine level of detail, which in turn gives us a way of investigating the misperception issue at the heart of Social Norms Theory. We remind ourselves and the reader, however, that many longer term processes must be considered before making strong conclusions about the effectiveness of intervention strategies.
 Acknowledgements
Acknowledgements
- Research presented in this paper was supported by the National Institute on Alcohol Abuse and Alcoholism (NIAAA) of the National Institutes of Health (NIH) under Award Number R01AA019785-01A1 to BGF entitled "Agent-Based Mathematical and Computational Modeling of Social Norms in College Drinking." We would also like to thank the reviewers for their very helpful comments on earlier drafts of this manuscript.
 References
References
- ABELSON, R. P. (1964).
Mathematical models of the distribution of attitudes under controversy.
In N. Frederiksen & H. Gulliksen (Eds.), Contributions
to mathematical psychology (pp. 142–160). New York: Rinehart
Winston.
ACKLEH, A. S., Fitzpatrick B. G., Scribner R., Simonsen N., & Thibodeaux J. J. (2009). Ecosystem models of college drinking: Parameter estimation and comparing models to data. Math and Computer Modeling, 50(3–4), 481–497. [doi:10.1016/j.mcm.2009.03.012]
AMETHYST INITIATIVE STATEMENT. (2014). http://www.theamethystinitiative.org/statement/ Archived at: http://www.webcitation.org/6P5BOOHDr
BAER, J. S., Stacy A., & Larimer M. (1991). Biases in the perception of drinking norms among college students. Journal of Studies on Alcohol, 52(6), 580–586. [doi:10.15288/jsa.1991.52.580]
BAKEMAN, R., and Beck, S. (1974). The size of informal groups in public. Environment and Behavior (6), 378–390.
BERKOWITZ, A. D. (2005). An overview of the social norms approach. In L. C. Lederman & L. P. Stewart (Eds.), Changing the culture of college drinking: A socially situated health communication campaign. New York: Hampton Press, Inc.
BIDEN, J. R. (2000) Excessive drinking on America's college campuses. Washington, DC: the Office of Senator Joseph R. Biden, Jr.
BORSARI, B., & Carey K. B. (2000). Effects of a brief motivational intervention with college student drinkers. Journal of Consulting & Clinical Psychology, 68(4), 728–733. [doi:10.1037/0022-006X.68.4.728]
BORSARI, B., & K. Carey (2001). Peer influences on college drinking: A review of the research, Journal of Substance Abuse, 13(4), 391–424.
BORSARI, B., & K. Carey (2003). Descriptive and injunctive norms in college drinking: A meta-analytic integration, Journal of Studies on Alcohol, 64(3), 331–341.
BURKE, P. J. (1991). Identity processes and social stress. American Sociological Review, 56(6), 836-849. [doi:10.2307/2096259]
BURKE, P. J. (2006). Identity change. Social Psychology Quarterly, 69(1), 81–96. [doi:10.1177/019027250606900106]
BURKE, P. J., & D. C. Reitzes. (1991). An identity theory approach to commitment. Social Psychological Quarterly, 54(3), 239–251. [doi:10.2307/2786653]
BURKE, P.J. & Stets J.E. (2009). Identity Theory, New York: Oxford University Press.
CAREY, K. B., Scott-Sheldon L. A. J., Carey M. P., & DeMartini K. S. (2007). Individual-level interventions to reduce college student drinking: A meta-analytic review. Addictive Behaviors, 32(11), 2469–2494. [doi:10.1016/j.addbeh.2007.05.004]
CATTUTO, C., Van den Broeck, W., Barrat, A., Colizza, V., and Pinton, J-F. (2010) Dynamics of person-to-person interactions from distributed RFID sensor networks, PLoS One, 5(7), 1–9.
CENTER FOR SCIENCE IN THE PUBLIC INTEREST (CSPI) (2008). Binge drinking on college campuses, http://www.cspinet.org/booze/collfact1.htm. Archived at: http://www.webcitation.org/6TOqGhDME.
CHRISTAKIS, N. A. and Fowler, J. H. (2007). The spread of obesity in a large social network over 32 years. The New England Journal of Medicine 357(4), 370–379. [doi:10.1056/NEJMsa066082]
DEJONG, W., Schneider, S. K., Towvim, L. G., Murphy, M. J., Doerr, E. E., Simonsen, N. R., Mason, K. E., & Scribner, R. A. (2006). A multisite randomized trial of social norms marketing campaigns to reduce college student drinking. Journal of Studies on Alcohol, 67(6), 868–879. [doi:10.15288/jsa.2006.67.868]
DERICCO, D. A. (1978). Effects of peer majority on drinking rate. Addictive Behaviors (3), 29–34. [doi:10.1016/0306-4603(78)90007-2]
DERICCO, D. A., and Garlington W. K. (1977) The effect of modeling and disclosure of experimenter's intent on drinking rate of college students. Addictive Behaviors (2), 135–139. [doi:10.1016/0306-4603(77)90031-4]
ELLIOTT, J. C., Carey, K. B., & Bolles, J. R. (2008). Computer-based interventions for college drinking: a qualitative review. Addictive Behaviors, 33(8), 994–1005. [doi:10.1016/j.addbeh.2008.03.006]
FITZPATRICK B., Scribner, R., Ackleh, A., & Simonsen, N. (2012). Forecasting the effect of the Amethyst Initiative on college drinking. ACER, 36(9), 1608–1613. [doi:10.1111/j.1530-0277.2012.01765.x]
FRIEDKIN, N. E., & Johnsen, E. C. (2011). Social influence network theory. New York: Cambridge University Press
FRIESE, B., & Grube, J. W. (2010). Youth drinking rates and problems: A comparison of European countries and the United States. Pacific Institute for Research and Evaluation. http://resources.prev.org/documents/ESPAD.pdf. Archived at http://www.webcitation.org/6PQU5m4Pj.
GARRISON, L., & Babcock, D. (2009). Alcohol consumption among college students: An agent-based computational simulation. Complexity, 14(6), 35–44. [doi:10.1002/cplx.20259]
GIABBANELLI, P., & Crutzen, R. (2013). An agent-based social network model of binge drinking among Dutch adults. Journal of Artificial Societies and Social Simulation, 16(2), 10 <https://www.jasss.org/16/2/10.html>. Access at http://www.webcitation.org/6PQUXWYcJ.
GORMAN, D. M., Mezic, J., Mezic, I., & Gruenewald P. J. (2006). Agent-based modeling of drinking behavior: a preliminary model and potential applications to theory and practice. American Journal of Public Health, 96(11), 2055–2060. [doi:10.2105/AJPH.2005.063289]
INGRAM, P., and Morris, M. W. (2007) Do people mix at mixers? Structure, homophily, and the "life of the party," Administrative Science Quarterly (52), 558–585.
ISENBERG, D. J. (1986). Group polarization: A critical review and meta-analysis. Journal of Personality and Social Psychology, 50(6), 1141–1151. [doi:10.1037/0022-3514.50.6.1141]
KELLY, F. P. (2011). Reversibility and stochastic networks, Cambridge: Cambridge University Press.
LAPINSKI, M., & Rimal, R. N. (2005). An explication of social norms. Communication Theory, 15(2), 127–147. [doi:10.1111/j.1468-2885.2005.tb00329.x]
LEDERMANN, S. (1956). Alcoolisme et alcoolisation. (Vol. 2). Paris: Presses Universitaires de France.
MASON, W. A., Conrey, F. R., & Smith, E. R. (2007). Situating social influence processes: Dynamic, multidirectional flows of influence within social networks. Personality and Social Psychology Review, 11(3), 279–300. [doi:10.1177/1088868307301032]
MCCALL, George J. and J.L. Simmons. (1966). Identities and interactions. New York: Free Press.
MCFARLAND, D., & Pals, H. (2005). Motives and contexts of identity change: A case for network effects. Social Psychology Quarterly, 68(4), 289–315. [doi:10.1177/019027250506800401]
NAHAS, G., Trouve, R., & Latour, C. (1999). The distribution of consumption of alcohol and marihuana," in G. Nahas, K. Sutin, D. Harvey, S. Agurell, N. Pace, & R. Cancro (Eds.), Marihuana and medicine (pp. 731–736). Totowa: Humana Press.
NEIGHBORS, C, Dillard, A. J., Lewis, M. A., Bergstrom, R. L., & Neil, T. A. (2006). Normative misperceptions and temporal precedence of perceived norms and drinking. Journal of Studies on Alcohol, 67(2), 290–299. [doi:10.15288/jsa.2006.67.290]
NIAAA. (2014). College drinking. National Institute on Alcohol Abuse and Alcoholism. http://www.niaaa.nih.gov/alcohol-health/special-populations-co-occurring-disorders/college-drinking. Archived at: http://www.webcitation.org/6P5B5qSXv
OSGOOD, D. W., Ragan, D. T., Wallace, L., Gest, S. D., Feinberg, M. E., & Moody,
J. (2013). Peers and the emergence of alcohol use: Influence and selection processes in adolescent friendship networks. Journal of Research on Adolescence 23(3), 500–512. [doi:10.1111/jora.12059]
PERKINS, H. W., Haines, M. P., & Rice, R. (2005). Misperceiving the college drinking norm and related problems: a nationwide study of exposure to prevention information, perceived norms and student alcohol misuse. Journal of Studies on Alcohol, 66(4), 470–478. [doi:10.15288/jsa.2005.66.470]
PERKINS, H. W., & Wesley, H. (2002). Social norms and the prevention of alcohol misuse in collegiate contexts. Journal of Studies on Alcohol Supplement, (14), 164–172. [doi:10.15288/jsas.2002.s14.164]
RASUL, J., Rommel, R., Jacquez, G. M., Fitzpatrick, B., Ackleh, A. S., Simonson, N., & Scribner, R. (2011). Heavy episodic drinking on college campuses: Does changing the legal drinking age make a difference? Journal of Studies on Alcohol and Drugs, 72(1), 2011, 15–23.
ROBINSON, D. T., & Smith-Lovin, L. (1992). Selective interaction as a strategy for identity maintenance: An affect control model. Social Psychology Quarterly. 55(1), 12–28. [doi:10.2307/2786683]
ROSENQUIST, N.J., Murabit, J., Fowler, J.H., Christakis, N.A. (2010). The spread of alcohol consumption behavior in a large social network, Annals of Internal Medicine, 152(7), 426–433
SCHULENBERG, J., Maggs, J. L., Long, S. W., Sher, K. J., Gotham, H. J., Baer, J. S., Kivlahan, D. R., Marlatt, G. A., & Zucker, R. A. (2001). The problem of college drinking: insights from a developmental perspective. Alcoholism, Clinical and Experimental Research, 25(3), 473–477. [doi:10.1111/j.1530-0277.2001.tb02237.x]
SCRIBNER, R., Ackleh, A., Fitzpatrick, B., Jacquez, G., Thibodeaux, J., Rommel, R., & Simonsen, N. (2009). A systems approach to college drinking: Development of a deterministic model of testing alcohol control policies. Journal of Studies on Alcohol and Drugs, 70(5), 805–821. [doi:10.15288/jsad.2009.70.805]
SCRIBNER, R. A., Theall, K. P., Mason, K., Simonsen, N., Schneider, S. K., Towvim, L. G., & DeJong, W. (2011). Alcohol prevention on college campuses: The moderating effect of the alcohol environment on the effectiveness of social norms marketing campaigns. Journal of Studies on Alcohol and Drugs, 72(2), 232–239. [doi:10.15288/jsad.2011.72.232]
SETTI, F. , Lanz, O., Ferrario, R., Murino, V., and Cristani, M. (2013) Multiscale f-formation discovery for group detection, Proceedings of the 20th IEEE International Conference on Image Processing, Povo, Italy, 15–18 September.
SHALIZI, C. R., & Thomas, A. C. (2011). Homophily and contagion are generically confounded in observational social network studies. Sociological Methods & Research, 40, 211–239. [doi:10.1177/0049124111404820]
SKOG, O.-J. (1985). The collectivity of drinking cultures: A theory of the distribution of alcohol consumption. British Journal of Addiction, 80(1), 83–99. [doi:10.1111/j.1360-0443.1985.tb05294.x]
SLUTSKE, W. S. (2004). Alcohol use disorders among US college students and their non-college peers. Archives of General Psychiatry, 62(3), 321–327. [doi:10.1001/archpsyc.62.3.321]
SOKAL, R. R. & Rohlf, F. J. (1995). Bioemetry (3rd ed.). New York: Freeman.
STETS, J. E., & Burke, P. J. (2000). Identity theory and social identity theory. Social Psychology Quarterly, 63(3), 224–237. [doi:10.2307/2695870]
STETS, J. E., and Burke, P. J. (2014). Emotions and identity non-verification, Social Psychology Quarterly (77).
STRYKER, Sheldon. (1968). Identity salience and role performance. Journal of Marriage and the Family, (4), 558–64. [doi:10.2307/349494]
STRYKER, Sheldon. (1980). Symbolic interactionism: A social structural version. Menlo Park, CA: Benjamin Cummings.
STRYKER, Sheldon., & Burke, P. J. (2000). The past, present, and future of an identity theory. Social Psychology Quarterly, 63(4), 284–297. [doi:10.2307/2695840]
SWANN, W. B., and Hill, C. A. (1982). When our identities are mistaken: Reaffirming self-conceptions through social interaction, Journal of Personality and Social Psychology, (52), 881–889.
SNYDER, M. B. (1992). Driving under the influence: A report to Congress on alcohol limits. Department of Transportation, National Highway Traffic Safety Administration. Archived at: http://www.webcitation.org/6P0hDKCSJ.
VANDER VEN, T., (2011). Getting wasted: Why college students drink too much and party so hard. New York: New York University Press.
WECHSLER, H., Lee, J. E., Kuo, M., Seibring, M., Nelson, T. F., & Lee, H. (2002). Trends in college binge drinking during a period of increased prevention efforts. Findings from 4 Harvard School of Public Health College Alcohol Study surveys: 1993-2001. Journal of American College Health, 50(5), 203–217.
WECHSLER, H., and T. F. Nelson (2001). Binge drinking and the American college student: What's five drinks? Psychology of Addictive Behaviors, 15(4), 287–291.
WECHSLER, H., Seibring, M., Liu, I. C., and Ahl, M. (2004). Colleges respond to student binge drinking: reducing student demand or limiting access. Journal of American College Health; 52(4), 159–168. [doi:10.3200/JACH.52.4.159-168]
WILENSKI, U. (1997). NetLogo party model. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL. http://ccl.northwestern.edu/netlogo/models/Party. Archived at: http://www.webcitation.org/6TOqll6kk.