Abstract

The different ways individuals socialize with others affect the conditions under which social norms are able to emerge. In this work an agent-based model of cooperation in a population of adaptive agents is presented. The model has the ability to implement a multitude of network topologies. The agents possess strategies represented by boldness and vengefulness values in the spirit of Axelrod's (1986) norms game. However, unlike in the norms game, the simulations abandon the evolutionary approach and only follow a single-generation of agents who are nevertheless able to adapt their strategies based on changes in their environment. The model is analyzed for potential emergence or collapse of norms under different network and neighborhood configurations as well as different vigilance levels in the agent population. In doing so the model is found able to exhibit interesting emergent behavior suggesting potential for norm establishment even without the use of so-called metanorms. Although the model shows that the success of the norm is dependent on the neighborhood size and the vigilance of the agent population, the likelihood of norm collapse is not monotonically related to decreases in vigilance.

Keywords:

Social Norms, Agent-Based Modeling, Social Networks, Neighborhood Structure, Cooperation

Introduction

1.1

The role of the structure of personal social networks in the process of diffusion of specific social facts has been now long acknowledged. Research in social network analysis subscribes to the structuralist hypothesis which claims that the adoption of social facts such as norms is not the cause but rather the effect of an individual's structural location in the complex web of social interactions. That is, people acquire norms as they acquire information – through ties structured in the network – and their spread is the direct consequence of the resources available to each and every individual in the network (Wellman 1983). Granovetter (1973) has famously validated this point of view in his classic study on the strength of weak ties. Other studies of diffusion dynamics have since shown that social network topologies can have important consequences for emergent patterns of collective behavior (see Newman et al. 2006). Moreover, most social contagion is complex, in the sense that multiple channels of communication and exposure are being exploited concurrently, yet possibly at varying spatial and temporal scales (Centola & Macy 2007). Individual-level decision-making thus plays an ever more important role as social contagion is dependent on strategic behavior as well as the percieved credibility and legitimacy of the social fact being diffused.

1.2

In this article special attention is therefore given to spatial agent-based modeling as a means of providing a powerful framework for exploring the mechanisms which lie at the foundations of the norm establishment process. In fact the use of computational simulation in the form of agent-based models to study social norms is nothing new. Axelrod (1986) used a game-theoretical foundation combined with an evolutionary approach; Axtell et al. (2001) observed the mechanics of transitions from social inequality to an equitable state by employing a model of individual action grounded in behavioral game theory; Epstein (2001) also explored the role of bounded rationality and thoughtless conformity on the adoption of norms with an ABM; just to name a few examples. This work draws heavily from Axelrod's norms game, however it modifies the original framework to fit the purposes of simulating a population of a single-generation of adaptive agents in a spatial environment rather than using an evolutionary approach.

1.3

Thirty years later, the norms game, as Axelrod had dubbed it, is still a very valuable model because it attempts to account for the amorphous and opaque, yet much discussed concept of norm emergence through the lens of individual actions. Moreover, it does so using only a very simple and clearly understandable framework. However, the trouble with such abstract models is that they can often fall into the trap of theoretical instrumentalism, where choice of assumptions is subject to predictive power or plausible results (Hedström 2005). One can argue that research in the social sciences should always be led under the maxim of grounding its explanatory mechanisms in empirical findings (De Marchi 2005). In this article, the aim is to introduce a modified set of assumptions which draws from Axelrod's ideas, but at the same time avoids fictionalist temptations regarding parts of the model design. Moreover the focus is shifted to simulating agent adaptation in spatial structures within a single generation.

1.4

In doing this, the hope is to answer the following question: how does the changing nature of individuals' social network structures affect the emergence and internalization of certain social norms? This paper will focus on cooperation-based norms with defections beneficial to individuals yet detrimental to society. Even more specifically, the focus will be on such norms with defection rewards independent of the population size (one example of this type of norm is tax-paying and the issue of tax evasion, where the total sum of money evaded by any individual actor is certainly independent of the size of the population). The goal is to elucidate the answer with the help of a computational model extending and modifying the original norms game in order to study agent adaptation in a multitude of environmental configurations. A background review of sociological theory on communities and social networks is presented first, before demonstrating the re-implementation of the norms game in the MASON package. Most importantly, a full description and specification of the new model follows. Finally, some simulation results are discussed.

Background

2.1

Bicchieri (2006) defines a social norm as a behavioral rule such that a sufficiently large part of the population is aware of its existence and its application to relevant situations. Moreover, individuals must prefer to conform to this rule on the condition that others are believed to conform to it as well, and that others are believed to expect the individual to conform to it and may sanction behavior. The question of emergence of social norms is an age-old conundrum of the social sciences. Sociologists as far back as Durkheim ([1893] 1997) in the 19th century have hypothesized on the nature of how norms "come to life" and how they are propagated throughout society and sustained in an emergent bottom-up manner (see Sawyer 2002). Later in the second half of the 20th century, Parsons (1964) built his entire theory around the mechanisms responsible for the adoption of norms and their spread in modern societies.

2.2

It should be no surprise then, that ever since agent-based modeling established itself as a specific research domain in the social sciences, there have been attempts at using such computational simulation methods to explore the emergence of social norms. Today, there exists a large amount of research where agent-based models are used to help answer these questions.

2.3

Savarimuthu and Cranefield (2009) categorize simulation models of social norms with respect to the ways they represent a) norm creation, b) norm spreading, and c) norm enforcement. In different models norms can be designed off-line (Castelfranchi & Conte 1995), created by leader agents (Kittock 1993), or in other instances they can be cognitively deduced from the behavior of other agents (Andrighetto et al. 2008). Similarly the spread of norms can be fueled by leadership (Kittock 1993), imitation (Epstein 2001), as well as evolution (Axelrod 1986). The enforcement of social norms has been modeled using sanctioning mechanisms (Axelrod 1986) as well as reputation of agents (Hales 2002), among other approaches.

2.4

Such models have been recently used to model a variety of real-world applications, ranging from the international diffusion of political norms (Ring 2014), through the prediction of smoking cessation trends (Beheshti & Sukthankar 2014), to the mapping of diffusion of safe teenage driving (Roberts & Lee 2012). These represent only a small fraction of the entiry body of social norms research utilizing agent-based models. However, perhaps the first agent-based model concerned with the emergence of norms, and certainly the most classic one, is Axelrod's (1986) evolutionary model.

Axelrod's Norms Game

2.5

In his seminal 1986 paper "An Evolutionary Approach to Norms" (Axelrod 1986), Axelrod presents a simple agent-based model which seeks to explain the mechanisms which eventually lead to establishing a norm in a society. To achieve this goal Axelrod used the game-theoretical concept of the prisoner's dilemma and extended it to n players (see Manhart & Diekmann 1989). In the model, agents have a simple choice to either cooperate with other agents or to defect.

2.6

The agents possess two attributes which govern their behavior. These attributes are defined as boldness and vengefulness. Both of these can take on values between 0/7 and 7/7 (to constrain them to 3 bits). Agents also have a numerical score assigned to them, which represents how well they are doing in the "norms game". Finally each agent gets assigned a probability of being seen during the defection. This probability is a random number sampled each round from a uniform distribution on the interval \((0,1)\). An agent will then defect, if its boldness is higher than the probability of being seen in the given round. Every time an agent defects it receives a temptation payoff of \(T = 3\); at the same time all of the other agents get a negative payoff of \(H = -1\), because they are hurt by the defection.

2.7

On the other hand, if an agent sees a defection, it will have to decide whether to punish it or not. This happens with a probability equal to its vengefulness value. After the punishment the original defector is hurt by \(P = -9\) points, however the punisher's score is also negatively adjusted by \(E = -2\), the assumption being that the enforcement of the punishment comes at a certain cost.

2.8

On top of this game-theoretic design, Axelrod (1986) superimposed an evolutionary mechanism responsible for selection and reproduction of high-scoring individuals. Every four rounds of the game, the agents are evaluated and ranked by their score. Players who are at most one standard deviation below the population average, but under one standard deviation above the average are given one offspring, and players who are at least one standard deviation above the mean are given two offspring to seed the next generation of agents (the next 4 rounds of the simulation). The offspring are then mutated, by introducing a small probability of flipping the bits of their boldness and vengefulness values.

2.9

Upon analyzing the model, Axelrod discovered that under the given conditions the norm rarely emerges. Thus, he revised the original model and introduced "metanorms" — that is, norms which dictate to not only punish defectors, but to also punish those who are seen not punishing defectors. Just as in the norms game, meta-punishment decreases the punished agent's score (\(\mathrm{MP} = -9\)) and it comes at an enforcement cost to the meta-punisher (\(\mathrm{ME}= -2\)). The agent's decision to punish as well as meta-punish is tied to the same vengefulness value. Only after the introduction of this new mechanism was Axelrod able to have norms emerge in the model.

2.10

The model has quickly become a staple of the agent-based modeling community and a classic in the modeling of norms. As such, it has also been heavily scrutinized and replicated (e.g. Galán & Izquierdo 2005; Galán et al. 2011; Mahmoud et al. 2012) as well as criticized. Authors have noted Axelrod's unclear and potentially weak experimental design, and the nature of model constraints and conditions, which seems to be arbitrary in certain cases (Galán & Izquierdo 2005). Another often cited shortcoming (Mahmoud et al. 2012) is the perfect knowledge which Axelrod's agents had possessed – in short, the players in the game always knew about the strategies and defections of all of the remaining players. For example in Mahmoud et al.'s (2012) paper the authors used a learning algorithm to overcome this aspect of the model. Another way of imposing some imperfection onto the agents' knowledge of their environment is to introduce a topology, or a spatial concept into the model.

2.11

There have in fact been studies on the norms game played between agents located on networks. Galán et al. (2011) have studied the effects of playing the metanorms game on random, small-world and scale-free networks. Other studies have also demonstrated the ability to establish norms on different network topologies through meta-enforcement and meta-punishment (Mahmoud et al. 2012b, 2012c, 2013). However, such extensions to networks have been singularly focused on the replication of the metanorms game and have not taken into account the effects of network topology on the original norms game. And so the possibility of norm emergence in populations of networked agents without the help of metanorms has been left as an open question. Moreover, these efforts have maintained the evolutionary approach first used by Axelrod. This study seeks to explore the effects of network topology and the ability of agents to adapt within a single generation in a modified version of the original norms game. But to understand how norms can emerge in a social environment where the agents' knowledge is constrained by the people they know, their culture and the social networks they are associated with, we must first study the patterns of social network structure in modern society.

Community Structure

2.12

Social research has concerned itself with the concept of community in modern society ever since its inception. The terms community and community structure are here understood in their sociological context as functional and cohesive groups of people, and the shape and quality of the interaction networks within them, as opposed to the more technical definitions employed in network analysis. Ferdinand Tönnies (1957 [1887]) was one of the first sociologists to address the issue of community. Others followed suit in the following century (e.g. Wirth 1938; Fischer 1975, 1984)

2.13

A modern sociological theory on community life, which will be of interest to the modeling effort presented in this paper, is due to Wellman (2002). Wellman establishes a tripartite typology of contemporary patterns of social aggregation. He calls these types little boxes, glocalization and networked individualism respectively. His claim is that there is a general teleological shift in modern society from the first, to the second and finally to the third type. He argues that originally people were living in little boxes: a handful of tightly bounded, densely knit communities, each of them tied to a specific locality: the family, the workplace, a club, or an organization. Even in large cities, people were bound to the neighborhood and visited each other door-to-door. The place was an essential part of what glued the communities together. But with the proliferation of expressways, affordable air transportation and the increasing ease of long-distance communication, whether it was the home telephone, later on cell-phones and most recently the Internet, a shift to glocalized networks occurred. Suddenly, people were not bound by their locale anymore. Thanks to the above mentioned technologies, individuals can now obtain the same form of support, solidarity and companionship from physically distant people, that they would earlier be able to enjoy only from people living in their neighborhood. The result is a network of multiple communities, some tightly knit, some more loosely, with sparse interactions across these communities, but most importantly the relationships of people across different communities and those even within their limits are not tied to a specific location.

2.14

Finally, the move away from glocalization to networked individualism is propelled by the rise of the Internet and mobile phones. Interactions in little boxes were door-to-door, glocalized interactions were place-to-place, but now we are experiencing a shift to person-to-person interactions. Networks become even sparser, communities less tightly bounded, linkages are more ad hoc.

2.15

What could this mean for the emergence of norms in societies differentiated by these three types of community life? Perhaps in societies where the glocalization or networked individualism community structure is dominant, one would see norms struggling to emerge due to the fragmentary and diversified nature of the society. Or perhaps, conversely, these societies could be more conducive to the diffusion of norms because the social cross-linking could allow for a richer sampling of the cultural landscape.

Methodology

3.1

To explore the concept of norm emergence in different spatial topologies, two different versions of an agent-based model implementing some basic concepts from Axelrod's (1986) original norms game have been developed. The first version of the model, which from here on will be referred to as "the network model" incorporates different network topologies on which the individual agents are allowed to interact. The second version, referred to as "the grid model" implements a grid-based environment for the agents' interaction. Naturally, a grid with some notion of neighborhood is by definition a network. The distinction between networks per se and grids is made because the "network model" can serve as a test of viability and of the general effects of playing the game in space by studying some well-known types of networks, whereas the grids provide a convenient way to represent a specific social theory (due to Wellman 2002). Both versions also simulate only a single generation of agents, who are however able to change their strategies throughout a simulation run in an attempt to adapt to changing environments.

3.2

The original model designed by Axelrod was also recreated for the purposes of comparison and verifying the correct implementation of the basic model assumptions. Replication and re-implementation computational models proves to be a very important tool for verifying the results of experiments (Axelrod 1997; Edmonds & Hales 2003). Although the technique is not yet wide-spread in the ABM community, replication is perhaps even more important in the field of simulation than in others (Wilensky & Rand 2007). The re-implementation done here serves as confirmation that the new models arise from the same basic framework as Axelrod intended it.

3.3

Both of the new models introduced here provide a simulation environment which for the purpose of this study is instantiated and ran a large number of times under different model parameter settings and, importantly, using different topologies. During these runs important model variables are tracked and recorded. Finally a sensitivity analysis of the model variables to parameters and topologies is performed.

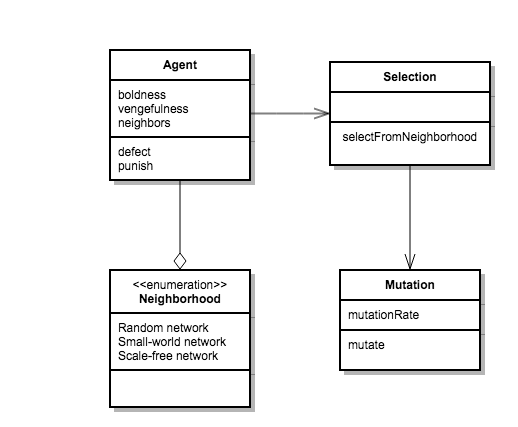
Figure 1. Class diagram of the model.

3.4

For the first version of the model three different network topologies are considered. Apart from random networks, small-world networks and scale-free networks are also utilized. Every time a random network is instantiated in the model, it is generated using the Erdös–Renyi algorithm (Erdös & Rényi 1959). In a similar vein, small-world networks are grown using the Watts–Strogatz algorithm (Watts & Strogatz 1998), and finally scale-free networks in the model are created via the Barabasi–Albert algorithm (Albert & Barabasi 2002). For random and small-world networks we focus solely on graphs with mean node degree \(k = 100\). This number was chosen somewhat arbitrarily, with the hopes of staying true to some of the theories on the average number of meaningful social connections of humans (Dunbar 1992), while also keeping computational efficiency in mind. The degree distribution of the scale-free network follows a power law, in which case the mean and standard deviation are not always well defined.

3.5

As hinted above, the networks' nodes represent the social actors in the model, in this case, individual people, while links between nodes represent meaningful social connections, such as friendship, kinship, professional acquaintances, colleagues, supervisors, etc. It is assumed, that any time two nodes are connected via a link, their relationship is such so that any behavior perceived as non-conforming to the actors' beliefs could potentially be met with a substantial reaction.

3.6

The model consists of a set number of agents connected via links in a network, an adaptive mechanism (strategy selection) which is used to re-seed the network with agents' new behavioral information at evenly spaced time intervals based on the attributes of the selected agents, and a mutation mechanism (Figure 1). The model includes a single global parameter \(W\) – the mean probability of an agent witnessing a defection. An agent \(i\) is then assigned its own probability \(W_i\) of witnessing a defection from the normal distribution centered at \(W\) with a standard deviation \(\sigma = 0.2W\). This attribute represents an agent's vigilance.

3.7

As in the original norms game each agent possesses a boldness value \(B\) ranging from 0/7 to 7/7 and a vengefulness value \(V\) also ranging from 0/7 to 7/7. Moreover every agent is assigned a numerical score which at the beginning of each simulation run is set at 0. However, because the motivation for this model is to model adaptation of behaviors in a network of actors rather than to simulate the evolution of agents, the payoffs are not reset at the beginning of each period. Because the model simulates a single generation of agents, the payoffs continue to accumulate throughout the entirety of a simulation run. Thus an agent's payoffs do not necessarily reflect how good its current strategy is. This is done because one of the aspects of the agents' bounded rationality is their inability to clearly discern the effects of individual strategies. The agents will simply emulate the behaviors of successful agents in their neighborhood. They do not, however, have the ability to discern which strategies contributed to which portion of the payoffs.

Agent Decision-Making

3.8

The first decision an agent has to make each round is whether to defect or not. To determine whether agent \(i\) defects we first need to know its boldness value \(B_i\) and \(S\), the probability it will be seen, should it decide to defect. The probability of being seen is directly tied to the number of an agent's neighbors and their witnessing probabilities. Naturally, the larger an agent's social network is, the bigger the chance of being caught by at least some of its neighbors. However, to avoid for the defection decision to become completely determined by the size of one's neighborhood, and to account for the diversity of conditions which are variedly favorable to defection, a certain amount of noise is added to the equation. Thus:

$$ S = 1- \prod_{i\in N} (1- W_i + R) $$

Here \(N\) is the set of the agent's neighbors, \(W_i\) is the witnessing probability of neighbor \(i\), and \(R\) is the normally distributed random variable with \(\mu = W\), \(\sigma = W\). Apart from this modification it is also assumed that agents only possess bounded rationality and thus will always gauge the probability of being seen with some degree of error. Therefore the perceived probability of being seen must be also calculated for each agent:

$$ S_p = 1- (1- W+R)^n $$

Here \(n\) is the number of agent's neighbors. Finally, an agent will defect only if \(B_i > S_p\), that is, if its boldness value is greater than the perceived probability of being seen by at least one of its neighbors. As the mechanism stands, the boldness label might not be appropriate anymore, opportunity being perhaps a better choice, however for the sake of clarity and continuity the original nomenclature is preserved.

3.9

The second decision an agent has to make, is whether to punish a defection. This is done for all of the agent's neighbors in the same way as in the original Axelrod model. That is, if an agent's neighbor defects, the model first checks whether the agent \(j\) sees the defection, which happens with probability \(W_j\). If the agent indeed sees the defection it then punishes the neighbor with probability equal to its vengefulness value \(V_j\). See Figure 2 for a flow diagram of agent activity.

3.10

Since \(W\) is an exogenous parameter, in model configurations with a high value of \(W\), some agents, while being very vigilant, will never follow through with any sort of punishment, because of their low vengefulness value. However, the notion behind vigilance is that it may potentially act as a deterrent even if the agents do not follow through, because the defecting agents cannot know with certainty whether the punishment will come or not.^[1] The vigilance parameter also represents the tightness of links between agents. Tightly-knit communities of agents, such as traditional family structures, are vigilant "by default" because their members interact with each other frequently. Thus, vigilance is also a proxy for frequency and intensity of other interactions which are not directly modeled.

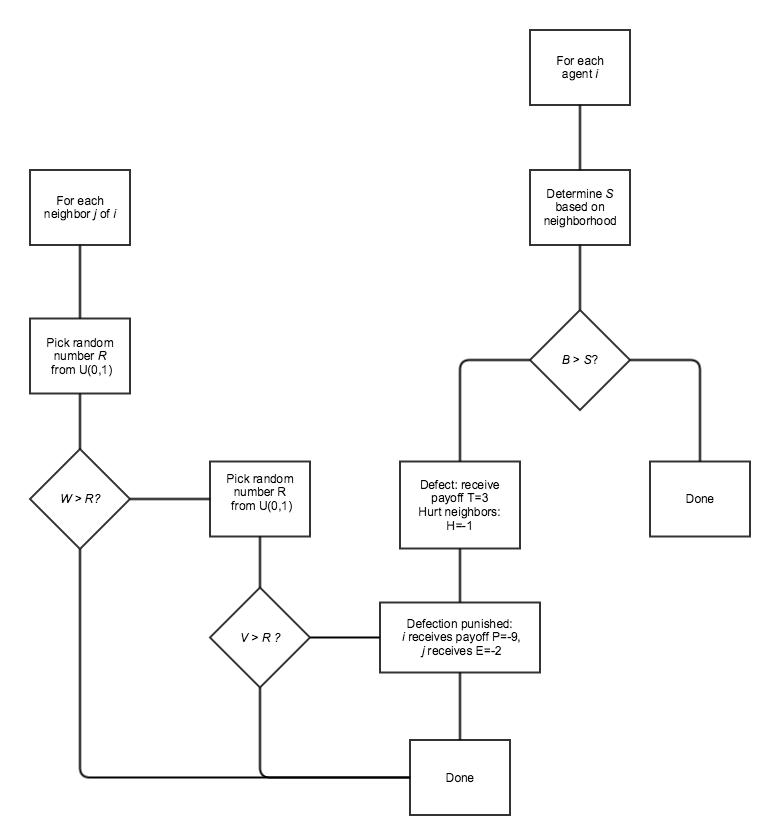
Figure 2. Agent activity in the modified norms game model.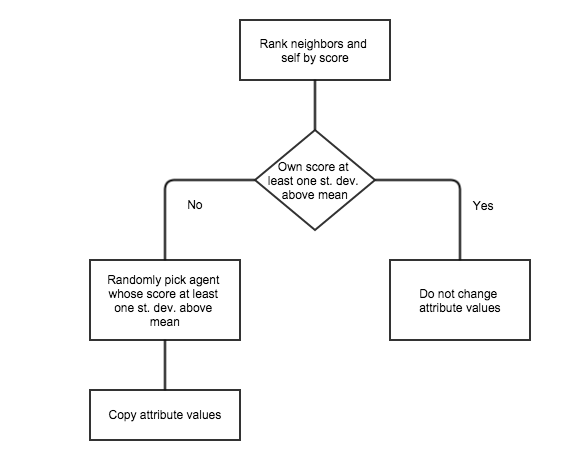

Figure 3. Adaptive mechanism.

3.11

All actions undertaken by the agents in the model result in payoffs distributed according to the same payoff matrix used in the original norms game.

3.12

After every four rounds each agent is evaluated together with all of its neighbors. The adaptive process is illustrated in Figure 3. At the beginning, the neighborhood is ranked by their payoffs. If the agent itself falls at least one standard deviation above the neighborhood's mean payoff value then the agent simply retains its current behavior and does not consider any further options. If it does not, then it randomly chooses any neighbor which lies at least one standard deviation above the neighborhood mean and copies that agent's behavior for its own. The reasoning behind this choice is simple: the agents have a rough idea of who in their neighborhood is doing pretty well and who is not. If they are doing well, then they are content with their current strategy. Otherwise they attempt to imitate a strategy of some well-off agent in their neighborhood.

3.13

After the adaptive process is done each agent's behavior has a small probability of being randomly modified. This represents imperfect imitation of behaviors. The modification is done as mutation in the original norms game where each bit has a 1% chance of being flipped.

3.14

The norm is said to emerge in the model if the average boldness of the agent population is low and the average vengefulness of the agent population is high. This represents the agents' internalization of cooperation-enabling behavior. It should be noted that cooperative behavior can be present even in agents who do not internalize the norm. For example an agent might decide not to defect, even though it has a high boldness value, simply because it thinks that the probability of getting caught is too high. Thus, it is important to distinguish between cooperative behavior and the internalization of cooperation-enabling dispositions.

Grid Model Design

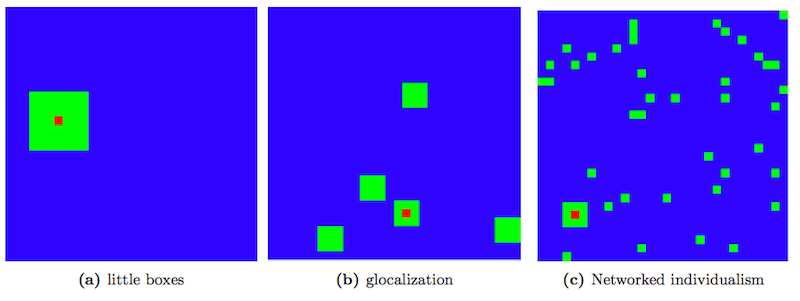
Figure 4. Neighborhood types in the grid model. Red cell is the inspected agent, green cells represent neighborhood cells.

3.15

In the second implementation of the model, the network topology is replaced by a spatial environment based on a rectangular grid. Each cell in the grid is occupied by a single agent. The most important way in which the two different models presented here differ is the way agents' neighborhoods are defined. The grid-based model makes use of the neighborhood typology introduced by Wellman (2002). Thus, three different types of neighborhoods were implemented into the model, to reflect the little boxes, glocalization, and networked individualism neighborhood patterns.

3.16

The little boxes mode is represented simply as a Moore neighborhood of radius 3 surrounding the agent's cell. This gives each agent precisely 48 neighbors. To represent the glocalization pattern each agent has a "core" neighborhood of the 8 surrounding cells as well as a number of "satellite" communities composed of \(3\times3\) cell squares of agents, randomly dispersed throughout the grid. The total number of communities (including the core) is taken from a normal distribution with mean \(\mu = 5.5\) and standard deviation \(\sigma = 0.5\). This gives every agent a mean number of 48.5 neighbors. Finally, networked individualism was implemented in two different ways. In the first approach the agent retains its core neighborhood of the 8 surrounding cells, with another 40 agents chosen randomly on the grid. In the second approach all 48 neighbors were selected randomly from the grid. Figure 4 provides a visual overview of the different neighborhood types.

3.17

The agent-decision making process as well as the strategy adaptation and modification processes work in precisely the same way as described in the network model design, with agents' neighborhoods based on the definitions of the three types described above.

3.18

All of the model versions described here were developed in the Java-based MASON package (Luke et al. 2005) which is specifically tailored for agent-based model programming. All of the model version were verified for proper functionality with code walkthroughs using the Java debugger and unit tests, and with the help of supporting print statements as well as visual neighborhood displays for neighborhood testing. The source code for all model versions is available at www.openabm.org/model/4714/.

Experimental Design

3.19

Experimentation consisted of multiple batches of a large number of simulation runs in both model cases. For the network version 100 simulation runs consisting of 1000 agents were executed for 5,000 time steps for each of the three network topologies (random, small-world and scale-free) and for four mean witnessing probability values \(W = 0.2\), \(0.1\), \(0.01\), \(0.001\), for a total of 1200 simulation runs. In the case of the grid version 100 simulation runs consisting of 10,000 agents (laid out on a \(100\times100\) square grid) were executed for 5,000 time steps for each of the four neighborhood types (little boxes, glocalization, and the two versions of networked individualism) and for each of four mean witnessing probability values \(W = 0.2\), 0.1, 0.01, 0.001, giving a total of 1600 runs. For all the results collected for a single parameter setting (neighborhood type/witnessing probability pair) the averages across all such executed simulation runs were recorded and stored. The re-implemented model originally designed by Axelrod was run 100 times for 10,000 time steps. The run lengths for each of the different model versions were chosen so as to allow the system to reach a state of (dynamic) equilibrium.

Results

4.1

The first test amounted to checking whether running the re-implementation of the original model, results in behaviors which resemble those described in Axelrod's paper (that is, almost ubiquitous collapse of the norm and very rare establishment on the other hand). Following in the footsteps of others who have re-implemented this model (Galán & Izquierdo 2005), the norm was defined to have collapsed at a given time step whenever the average boldness in the agent population was at least 6, while at the same time the average vengefulness was at most 1. Similarly, the norm was defined to have been established at a given time step whenever the average boldness was at most 2, and the average vengefulness was at least 5. Axelrod (1986) arrives at the correct conclusion that the norm collapses most of the time, although his results were in fact inconclusive. In their re-implementation Galán and Izquierdo (2005) observed that this variability in simulation runs was due to rather short run times in the original experiments. However, they demonstrated that in the long run, the norm does indeed collapse a vast majority of the time. The results obtained from the implementation developed for the purposes of this study visually match those of Galán & Izquierdo (2005). Figure 5 shows the proportion of runs resulting in either norm collapse or establishment over time.

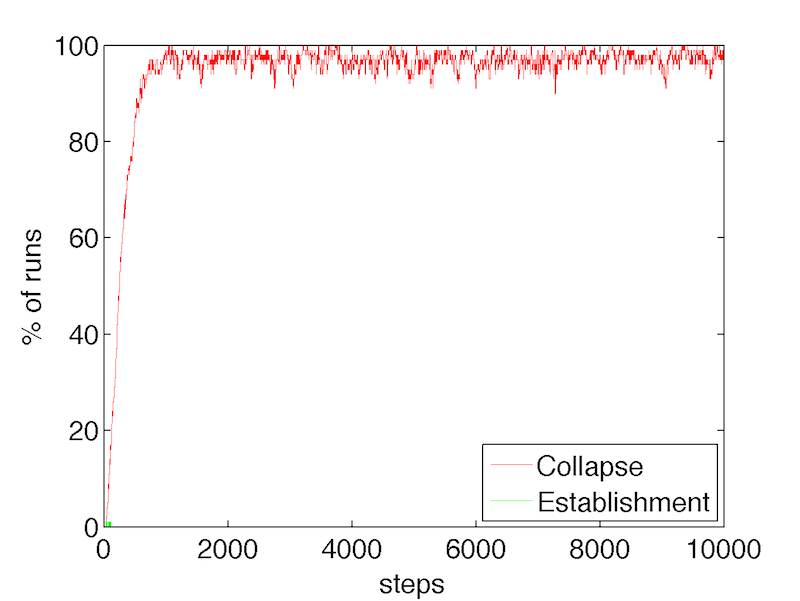
Figure 5. Proportions of runs that result in norm establishment vs. norm collapse in the re-implementation of the original Axelrod model.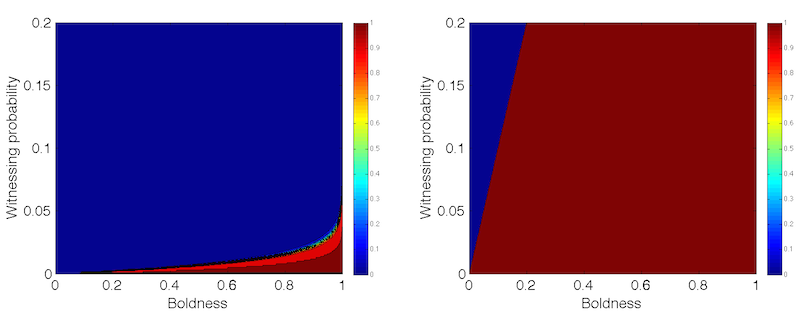

Figure 6. Contour plots of defection probability in small-world/random networks (left) with mean degree 100 and \(\sigma =10\), and scale-free networks (right).

4.2

An analysis of the modified network model is provided next. To begin with, the expected payoffs associated with defection and the expected costs associated with enforcement are tied to the size of agents' neighborhoods. Ignoring the effect of noise, the probability of defection of a random agent with boldness \(b\), assuming a fixed witnessing probability \(W\) can be calculated as follows:

$$ P(S < b) = P(1-W)^n < b) = P \left( n < \frac{\ln(1-b)}{\ln(1-W)} \right) $$

Here \(n\) is the number of neighbors to which the agent is connected in the network. Thus, for random and small-world networks where node degree is normally distributed the following is true:

$$ P(S < b) = \frac{1}{2} \left[ 1 + \mathrm{erf} \left( \frac{\frac{\ln(1-b)}{\ln(1-W)}-\mu}{\sigma\sqrt2} \right) \right] $$

Here, the right-hand side is obtained by simply substituting into the cumulative distribution function for the generalized normal distribution with mean \(\mu\) and standard deviation \(\sigma\). Similarly, the same expression can be evaluated for scale-free networks where the complementary cumulative degree distribution scales with \(n^{-2}\). Thus, the probability of defection for scale-free networks follows:

$$ P(S < b) = 1- \left( \frac{\ln(1-b)}{\ln(1-W)} \right)^{-2}$$

4.3

The contour plots for both probabilities as functions of boldness and witnessing probability are shown in Figure 6. Having expressed the defection probabilities, the expected cost of enforcing punishment, \(E(C_P)\), can be calculated. Specifically, for an agent with vengefulness \(v_i\), and assuming \(E=-2\) as enforcement cost, the following equality holds:

$$ E(C_P) = 2 \cdot W \cdot v_i \cdot \sum^n_{j=1} P(S < b_j) $$

Here \(n\) is the number of neighbors and \(W\) is the mean witnessing probability. Hence, the cost per unit of vengefulness:

$$ c_{UV} = 2 \cdot W \cdot \sum^n_{j=1} P(S < b_j) $$

4.4

Based on the previous analysis of the defection probability the cost can be derived explicitly. Thus, for random and small-world networks the cost at the beginning of a simulation run when the expected boldness is equal to 0.5 approaches zero for \(W > 0.01\). If \(W < 0.01\), the system undergoes a phase transition and \(C_{UV}\) scales with \(nW\). As the average boldness of an agent's neighborhood changes, so does the value of \(W\) at which the described transition occurs. For scale-free networks the costs scale with \(nW\) if and only if \(b > W\). The costs approach zero only when average boldness is lower than or equal to the witnessing probability. (see Figure 6).

4.5

Similarly the expected payoffs associated with defection, \(E(P_D)\) can also be derived. For any given agent with boldness \(b\) and mean witnessing probability \(W\), the following holds:

$$ E(P_D) = 3\cdot P(S < b)-9 \cdot P(S < b) \cdot W \cdot n \cdot \langle v \rangle $$

Here, \(\langle v \rangle\) is the average vengefulness in the agent's neighborhood. Obviously the payoffs are zero in the regions where the probability of defection is zero. However, in regions where \(P(S < b) \rightarrow 1\), the following is true:

$$ E(P_D) = 3- 9 \cdot W \cdot n \cdot \langle v \rangle \qquad \mathrm{if~}P(S < b) \rightarrow 1 $$

And so, payoffs from defection are positive whenever \(Wn\langle v \rangle < 1/3\). This is trivially true whenever \(Wn < 1/3\). One important observation to be made here is that while the temptation payoff remains the same (as it was established that it is in fact independent of the population size) the punishment component grows linearly with the number of neighbors.

4.6

This analysis shows that the agents' propensity to punish defectors depends heavily on the mean witnessing probability in the system and the size of the agents' neighborhoods. The larger the social network of an agent, the more costly it is to be vengeful. On the other hand, smaller individual probabilities of witnessing defections result in decreased enforcement costs in the long run. Unlike the original norms game where population and the expected probability of being seen remained fixed, these dependencies can have important effects on the simulation results. It remains to be seen how the addition of noise and the different spatial topologies affect the behavior of the system.

4.7

Figures 7–8 show that especially in the cases of random and small-world networks the system results into a state with low levels of boldness and defections and tolerable levels of vengefulness (the figures have semi-logarithmic axes – this was done to illustrate temporal trends in a more visible manner). Note that in these types of networks agents have on average 100 neighbors, whereas in the scale-free networks the typical number of neighbors would be very low (due to the power law nature of its node degree distribution). It is precisely the way in which the probability of being seen is implemented in the network model which dramatically affects the probability of norm emergence. Figure 9 shows the relationship between neighborhood size (degree) and average agent attributes. The analysis shows that neighborhood size becomes a factor when witnessing probability is neither too low nor too high. When \(W = 0.2\) vengefulness becomes costly. Conversely, when \(W = 0.001\), the impact of witnessing probability on the expected payoffs begins to exceed that of neighborhood size by far. This is in line with the previous mathematical analysis.

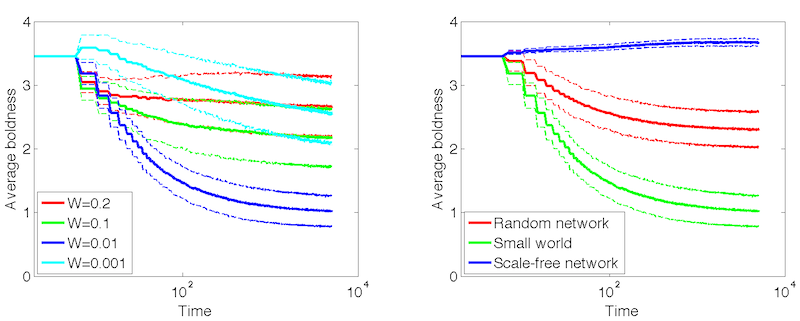
Figure 7. Average boldness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\).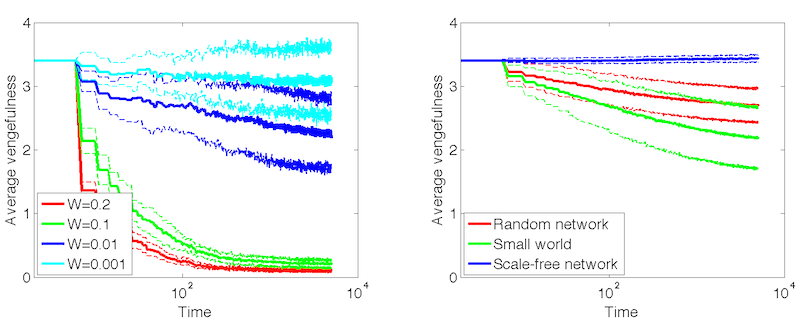

Figure 8. Average vengefulness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\).

4.8

It is also worth noticing the different dynamics of the population boldness with regard to the witnessing probability (see Figure 7). When \(W \geq 0.1\), boldness levels decrease only slightly. This is because with perfect information, the agents' probability of defection would have been zero for the most part (see Figure 6). However agents who still defect due to imperfectly estimating probabilities of being seen or because they represent outliers in terms of their neighborhood size receive negative payoffs for their action since \(Wn > 1/3\). This creates adaptive pressure towards lower boldness levels in this sub-population of agents. When \(W = 0.01\) boldness decreases because the expected defection payoffs are negative for most agents. When \(W = 0.001\) there is a small uptick in boldness followed by a slow decrease even though the payoffs are now positive. However, once a big enough fraction of agents' neighbors become defectors, the agents are hurt more than they can receive from their own defections, due to their large number of neighbors. Thus, small clusters of cooperators which can appear by chance will have the opportunity to spread throughout the population.

4.9

Figure 8 shows that vengefulness decreases only for high values of \(W\). When \(W \leq 0.01\) enforcement is fairly cheap, and since boldness is self-regulated, there is little adaptive pressure on vengefulness. Although, the actual cost of punishment is always non-zero, vengefulness levels of most agents will be allowed to remain fairly high, since defection ceases to occur due to decreasing levels of boldness. Moreover, the actual probability of enforcing punishment for any given agent is low, due to the low likelihood of seeing defections. In this way, there is no adaptive pressure^[2] exerted on the vengefulness attribute. The effect of added noise is most noticeable when \(W \geq 0.1\). The expected costs of enforcement are null, because no one is expected to defect. However, occasional misguided defectors (those affected by the added noise) still incur unnecessary costs on enforcers. Thus, for such large values of \(W\), the population vengefulness will converge to a quiescent state. Finally, the simulation results show that network topology does play some role in the rate at which boldness and vengefulness decrease.

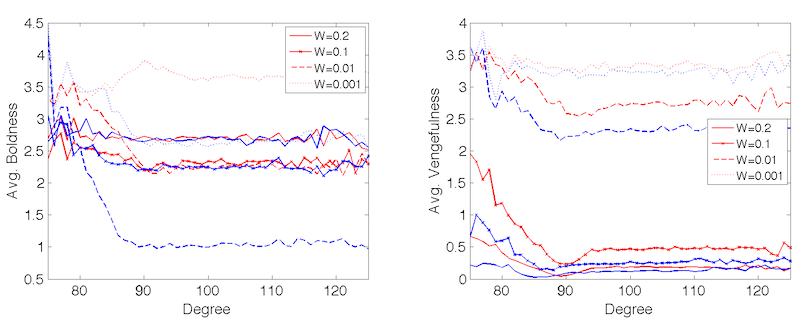
Figure 9. Relationship between neighborhood size (degree) and agent attributes for different values of \(W\). Red lines show values for small-world networks, blue lines show values for random networks.

4.10

To examine how the agents' strategy adaptation heuristic affects the resulting system behavior, the same runs were performed, but with the payoff mechanism implemented as in Axelrod's norms game, i.e. letting the payoffs reset after every four rounds. Figures 10–11 shows the results of these runs. It is clear that especially in cases of low vigilance the system reverts to the state described by Axelrod (1986) with prevailing high values of boldness and low levels of vengefulness essentially representing norm collapse. Thus, the heuristic is actually responsible for a large part of the interesting dynamics that can be seen in the new version of the model. This suggests that initial small advantages or disadvantages of certain agents in the beginning of the runs with accumulating payoffs can have potentially large effects on the resulting population average. This in turn depends on the initial conditions of the system – the exact topology of the network and the initial strategies of agents in specific locations within the network. To test the sensitivity of the system towards changing these initial conditions, additional runs were executed. First, For each of the model configurations described in the Experimental Design section a single, fixed network was used in 100 runs, randomly perturbing only the initial strategies of the agents in specific nodes. Figure 12 shows the dispersion of the resulting population averages at the end of each run. Next, extreme initial conditions were tested as well. Each of the configurations was run from four different initial population settings:

• Avg. Boldness: 1/7. Avg. Vengefulness: 1/7.
• Avg. Boldnes: 1/7. Avg. Vengefulness: 6/7.
• Avg. Boldness: 6/7. Avg. Vengefulness: 1/7.
• Avg. Boldness: 6/7. Avg. Vengefulness: 6/7.

4.11

The changes in the average population strategy from these initial conditions are shown in Figure 13. The resulting dynamics reveal that the system is in fact fairly "stiff" in that the initial conditions determine much of the resulting location of the population average in the strategy state space. Some cases show less dependence, such as runs with low levels of \(W\), or populations with low initial vengefulness levels. On the other hand, populations on scale-free networks are much "stiffer" than the other network topologies.

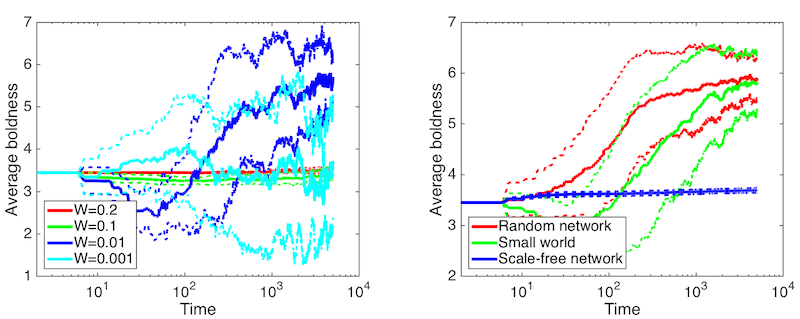
Figure 10. Runs with payoffs resetting every 4 rounds. Average vengefulness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\).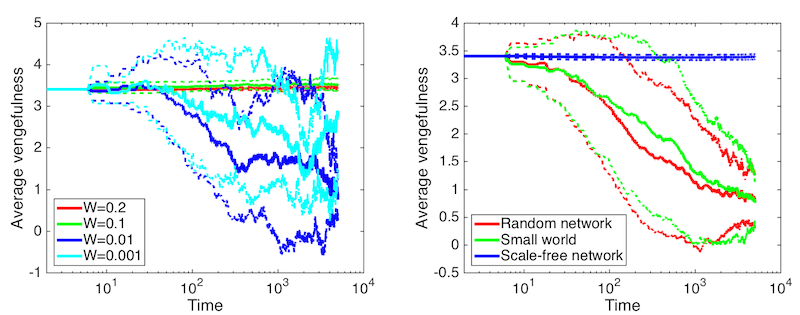

Figure 11. Runs with payoffs resetting every 4 rounds. Average vengefulness over time (error lines showing one standard deviation). LEFT: Small-world networks at different witnessing probabilities. RIGHT: Different network topologies at witnessing probability \(p = 0.01\).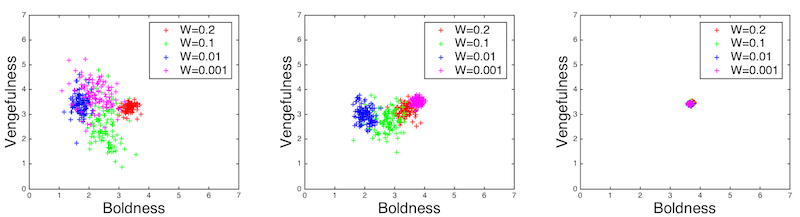

Figure 12. Average population boldness and vengefulness levels at ends of individual runs. LEFT: Small-world network. CENTER: Random network. RIGHT: Scale-free network.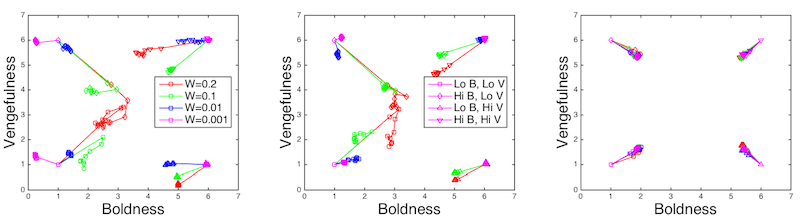

Figure 13. Change of average population boldness and vengefulness levels during runs from extreme initial conditions. Each point represents 1000 steps. LEFT: Small-world network. CENTER: Random network. RIGHT: Scale-free network.

4.12

When we turn our attention to the grid-based model the situation remains similar (see Figures 14–15). It is necessary to keep in mind that the dynamics are somewhat affected by the smaller average neighborhood size. However, the decrease in boldness as well as vengefulness for large witnessing probabilities is still noticeable. The forces driving the decrease are the same as in the case of the network model. The main difference lies in the behavior of the system under low levels of witnessing probability. When \(W = 0.01\) the expected costs of defection are now positive due to the smaller neighborhoods. However, just as in the network model, the hurtfulness of neighbors' defections still quickly exceeds the advantages of one's own defections, and yet again any clusters of cooperators will be allowed to spread. Once boldness falls to a certain level, the fraction of "free" enforcements increases and thus some agents with higher vengefulness levels will be allowed to survive. This explains the eventual slight increase in the average vengefulness as well as the growing variance when \(W = 0.01\). The same arguments hold for population boldness dynamics when \(W = 0.001\). However, what is most intriguing are the initial decreases in vengefulness under the lower levels of \(W\), which eventually taper off to zero in the case when \(W = 0.001\). Although the rates of defection in the systems are higher, now that neighborhood sizes are smaller which naturally results in higher costs of vengefulness, this alone cannot explain the observed dynamics. Indeed, the qualitative difference between the temporal trends of vengefulness of the little boxes neighborhoods and the other neighborhood types are obvious. Hence, some of the dynamics can only be explained by the chosen neighborhood topology.

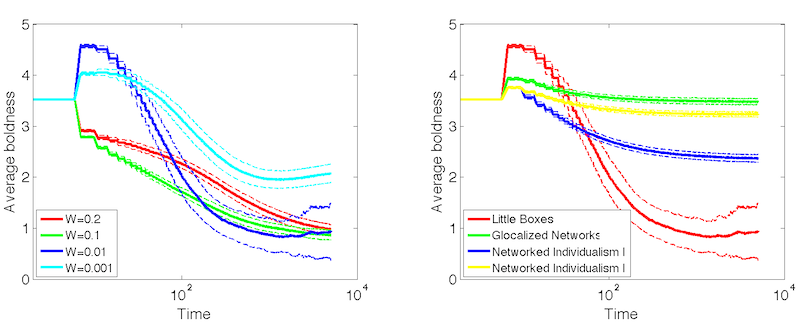
Figure 14. Average boldness over time. LEFT: Little boxes at different witnessing probabilities. RIGHT: Different neighborhood types at witnessing probability \(p = 0.01\).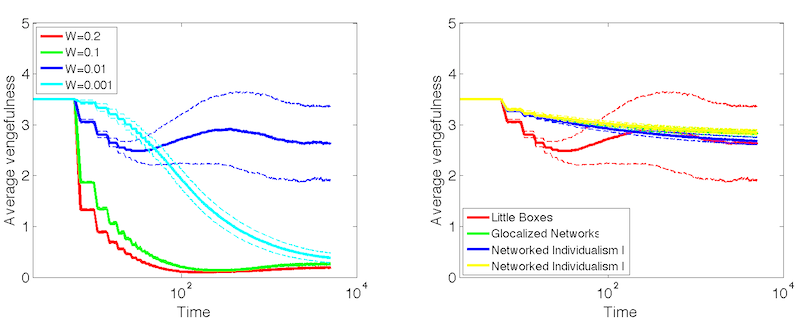

Figure 15. Average vengefulness over time. LEFT: Little boxes at different witnessing probabilities. RIGHT: Different neighborhood types at witnessing probability \(p = 0.01\).

4.13

Tracking average population values alone on its own cannot provide full insight into the dynamics of the model. To this end, visualizations of a large number of simulation runs were tracked, to elucidate the system's state over different periods of time. Figures 16–17 show the changes in the spatial distribution of population vengefulness over a long period of time for two different neighborhood types. One can notice that under certain configurations, and barring mutation, the system can reach a state close to a true equilibrium (see Figure 16). On the other hand, when employing the glocalized neighborhood, the model reaches a dynamic equilibrium, where the attributes of individual agents are in flux, yet on average the system retains the same aggregate state from a qualitative point of view. The same types of dynamics were witnessed in simulation runs employing the networked individualism neighborhood types.

Figure 16. Vengefulness in the population after 1,000 steps (left) and 10,000 steps (right) with little boxes neighborhoods and \(W = 0.01\). Showing a single representative run.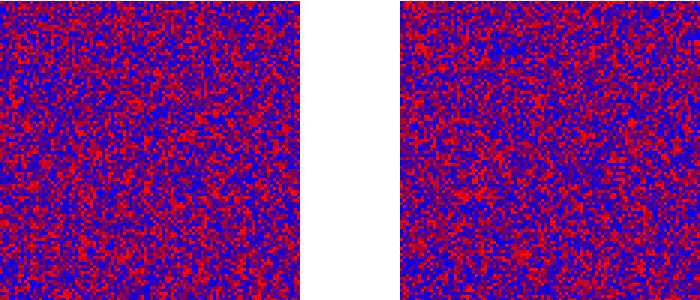

Figure 17. Vengefulness in the population after 1,000 steps (left) and 10,000 steps (right) with glocalized neighborhoods and \(W = 0.01\). Showing a single representative run.

Discussion

5.1

The model results show a number of interesting behaviors. Firstly, the probability of an individual witnessing a defection plays an important role in the global behavior of the system, and as the results have shown even very small probabilities on the individual level can discourage agents from their defection if they have enough neighbors. Using the mechanism for witnessing defections (and, perhaps more importantly, the expectations for witnessing defections) has prevented cases of norm collapse in the system even without the use of metanorms. This is achieved by a sort of "distributed vigilance" mechanism – agents as individuals will rarely witness a defection, but because of the effect of sheer neighborhood size and the relatively low costs and low adaptive pressure on enforcement, defectors are still being continuously policed. Moreover, due to the effect of neighborhood size and the variation in the spatial distribution of traits, boldness is effectively self-regulated – pockets of defectors hurt each other more than they can gain from their individual defections, which allows pockets of cooperators to fortuitously expand throughout the environment. On the other hand, a higher probability of seeing an individual's defection does not necessarily ensure a lower global rate of boldness, mostly due to low adaptive pressure. However, the emergence of the norm is not guaranteed. Specifically, in cases of low vigilance, the average vengefulness level in the population is a result of random drift. Furthermore, the heuristic which led agents to adopt other agents' strategies based on their aggregate performance over the course of the entire run has proved to be a major contributor to the resulting system states. If agents are unable to clearly judge the effects of strategies and just blindly copy agents who have had success in the past, norm collapse actually ceases to be the norm.

5.2

The model also demonstrated sensitivity to the different neighborhood types. The results showed qualitative differences in the overall trends in agents' adaptation across different neighborhood structures. The little boxes neighborhood mode also showed promising population dynamics in terms of boldness and vengefulness with certain levels of vigilance. The first hypothesis of this paper stated that the glocalization and networked individualism types would lead norm instability due to the fragmented and pluralistic nature of communities, while the alternate hypothesis suggested that it is precisely because of this diversity that individuals will be able to better "sample" the fitness landscape and find their way to an optimal solution faster. From the analysis of the simulation runs it would seem that there is more evidence for the first hypothesis. However, it is important to note that this comes at a price: there is always a trade-off between stability (norm emergence) and diversity as shown in Figure 16.

Conclusion

6.1

Previous modeling efforts have elicited conditions for norm emergence on networks either with the use of Axelrod's metanorms mechanisms (Galán et al. 2011; Mahmoud et al. 2012b, 2012c, 2013), or with entirely different mechanisms for norm spreading (Anghel et al. 2004). Conversely, some simulation models have shown the ability to establish norms with the use of imtitation-based norm adoption mechanisms, yet without any network structure (Andrighetto et al. 2008) or for different categories of norms (Epstein 2001). The model analyzed here has shown the dynamics of norm emergence on network topologies for single-generation populations of adaptive agents.

6.2

Moreover, the agent-based model presented here showed that neighborhood structure and social network topology do in fact have an effect on the emergence of norms. Furthermore, by representing vigilance as a social phenomenon and by focusing on behavior adaptation rather than evolution the simulation results showed the significance of neighborhood size, vigilance itself and most importantly of the interplay of these two factors.

6.3

The model was intended to be left simple and abstract in order to provide a first glimpse into the effect of social topologies on the emergence of norms. There is certainly ample room for modification. For instance, it might be even more realistic to introduce and calibrate a dynamic probability of witnessing defections for individuals rather than use a static one throughout the entire simulation run. Then there is the question of how many witnesses does it usually take to prevent a defection? In the model it sufficed to have just one witness, but this number might be different under certain circumstances. Perhaps if the model employed a weighted social network, then agents could possess a weight threshold for witnesses that would discourage them from defecting. The resulting dynamics would also most certainly change had the payoffs been calibrated differently. Moreover, further modifications to the agents' scope of knowledge would certainly yield new interesting results. For example, how would the outcome change if agents knew of their neighbors vengefulness levels and would be able to incorporate this knowledge into their defection decision? In the model described here the agents will not defect if they think they will be seen, regardless of the likelihood of actually being punished upon being caught. One could make the claim that more intelligent agents will learn from past experiences and tend to defect even in highly exposed situations, if their neighbors are continually reluctant to enforce punishment. However, these modifications are beyond the scope of the current work, which simply sought to extend the original norms game on networks with defection decisions based on the witnessing abilities of the agents' direct neighbors.

6.4

Most importantly, it is necessary to constantly test how realistic are the topologies used as a representation for social communities. The faithfulness of the small-world network and scale-free network representations has been recently questioned (Shekatkar & Ambika 2014). The accuracy of Wellman's neighborhood typology is also in question as it has never been thoroughly validated. Thus, it is important to further explore and re-evaluate our view and understanding of community structures in contemporary society, and validate these claims with well-designed studies before we can start to fully consider the validity of models regarding the emergence of norms, such as the one presented in this paper.

Acknowledgements

I would like to thank Claudio Cioffi-Revilla for his support and guidance. I would also like to thank Andrew Crooks for helpful advice and valuable feedback on drafts of the paper.

Notes

¹ This is similar to the police strategy of frequent motor patrolling of crime hot-spots. Studies have shown that just having enough police presence on its own leads to decreased crime rates in the affected areas (Sherman & Weisburd 1995).

² The term adaptive pressure is used in a sense similar to "selection pressure" in evolutionary algorithms when changes in the agents' strategies result in a change in the distribution of payoffs.

References

ALBERT, R., & Barabási, A.-L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics, 74, 47–97. [doi:10.1103/RevModPhys.74.47]

ANDRIGHETTO, G., Campenni, M., Cecconi, F. & Conte, R. (2008). How agents find out norms: A simulation based model of norm innovation. NORMAS, Volume 8, 16–30.

ANGHEL, M., Toroczkai, Z., Bassler, K.E. & Korniss, G. (2004). Competition-driven network dynamics: Emergence of a scale-free leadership structure and collective efficiency. Physical Review Letters, 92(5), 0587011–0587014. [doi:10.1103/PhysRevLett.92.058701]

AXELROD, R. (1986). An Evolutionary Approach to Norms. The American Political Science Review, 80(4), 1095–1111. [doi:10.2307/1960858]

AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. In Conte R, Hegselmann R, Terna P, editors. Simulating Social Phenomena (Lecture Notes in Economics and Mathematical Systems 456). Berlin: Springer-Verlag. [doi:10.1007/978-3-662-03366-1_2]

AXTELL, R., Epstein, J., & Young, P. (2001). The emergence of classes in a multi-agent bargaining model. In S. Darlauf & P. Young (Eds.), Social Dynamics. Cambridge, MA: MIT Press.

BEHESHTI, R., & Sukthankar, G. (2014). A normative agent-based model for predicting smoking cessation trends. In Proceedings of the 2014 international conference on Autonomous agents and multi-agent systems (pp. 557–564). International Foundation for Autonomous Agents and Multiagent Systems.

BICCHIERI, C. (2006). The Grammar of Society. New York, NY: Cambridge University Press.

CASTELFRANCHI, C. & Conte, R. (1995). Cognitive and social action. London: UCL Press

CENTOLA, D., & Macy, M. (2007). Complex Contagions and the Weakness of Long Ties. American Journal of Sociology, Vol. 113, No. 3, 702–734. [doi:10.1086/521848]

DE MARCHI, S. (2005). Computational and mathematical modeling in the social sciences. Cambridge, UK: Cambridge University Press. [doi:10.1017/CBO9780511510588]

DUNBAR, R. (1992). Neocortex size as a constraint on group size in primates. Journal of Human Evolution, 22(6), 469–493. [doi:10.1016/0047-2484(92)90081-J]

DURKHEIM, E. ([1893] 1997). Division of Labour in Society. New York, NY: Free Press.

EDMONDS, B. & HALES D. (2003). Replication, replication and replication: Some hard lessons from model alignment. Journal of Artificial Societies and Social Simulation, 6 (4) 11 <https://www.jasss.org/6/4/11.html>.

EPSTEIN, J. M. (2001). Learning to Be Thoughtless: Social Norms and Individual Computation. Computational Economics, 18(1), 9–24. [doi:10.1023/A:1013810410243]

ERDÖS, P., & Rényi, A. (1959). On random graphs I. Publicationes Mathematicae, 6 (pp. 17–61).

FISCHER, C. S. (1975). Toward a Subcultural Theory of Urbanism. American Journal of Sociology, 80(6), 1319–1341. [doi:10.1086/225993]

FISCHER, C. S. (1984). The Urban Experience. New York: Harcourt.

GALÁN, J. M. & Izquierdo, L. R. (2005). Appearances can be deceiving: Lessons learned reimplementing Axelrod's Evolutionary Approach to Norms. Journal of Artificial Societies and Social Simulation, 8 (3) 2 <https://www.jasss.org/8/3/2.html>.

GALÁN, J. M., Łatek, M. M., & Rizi, S. M. M. (2011). Axelrod's Metanorm Games on Networks. PLoS ONE, 6(5), e20474. [doi:10.1371/journal.pone.0020474]

GRANOVETTER, M. S. (1973). The Strength of Weak Ties. The American Journal of Sociology, 78(6): 1360–1380. [doi:10.1086/225469]

HALES, D. (2002). Group Reputation Supports Beneficent Norms. Journal of Artificial Societies and Social Simulation, 5 (4) 4 <https://www.jasss.org/5/4/4.html>.

HEDSTRÖM, P. (2005). Dissecting the social: On the principles of analytical sociology. Cambridge, UK: Cambridge University Press. [doi:10.1017/CBO9780511488801]

KITTOCK, J.E. (1995). Emergent conventions and the structure of multi-agent systems. In: Nadel, L. & Stein, D.L. (Eds.), 1993 Lectures in Complex Systems. Boston, MA: Addison-Wesley.

LUKE, S., Cioffi-Revilla, C., Panait, L., Sullivan, K., & Balan, G. (2005). Mason: A multiagent simulation environment. Simulation, 81, 517–527. [doi:10.1177/0037549705058073]

MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2012). Overcoming Omniscience for Norm Emergence in Axelrod's Metanorm Model. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VII (pp. 186–202). Springer Berlin Heidelberg. [doi:10.1007/978-3-642-35545-5_11]

MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2012b). Norm emergence: Overcoming hub effects in scale free networks. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VII (pp. 136–150). Springer Berlin Heidelberg.

MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2012c). Establishing norms for network topologies. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VII (pp. 203–220). Springer Berlin Heidelberg. [doi:10.1007/978-3-642-35545-5_12]

MAHMOUD, S., Griffiths, N., Keppens, J., & Luck, M. (2013). Norm Emergence through Dynamic Policy Adaptation in Scale Free Networks. In S. Cranefield, M. B. van Riemsdijk, J. Vázquez-Salceda, & P. Noriega (Eds.), Coordination, Organizations, Institutions, and Norms in Agent System VIII (pp. 123–140). Springer Berlin Heidelberg. [doi:10.1007/978-3-642-37756-3_8]

MANHART, K., & & Diekmann, A. (1989). Cooperation in 2-and N-Person Prisoner's Dilemma Games: A Simulation Study. Analyse and Kritik, 11(2), 134–153.

NEWMAN, N, Barabasi, A.-L., & Watts, D. (2006). The Structure and Dynamics of Networks. Princeton, NJ: Princeton University Press.

PARSONS, T. (1964). The Social System. New York, NY: The Free Press/Macmillan.

RING, J. (2014). An Agent-Based Model of International Norm Diffusion. Retrieved from http://myweb.uiowa.edu/fboehmke/shambaugh2014/papers/Ring_Diffusion_of_Norms__ABM_Approach.pdf. Archived at http://www.webcitation.org/6WmguxHgN.

ROBERTS, S. C., & Lee, J. D. (2012). Using Agent-Based Modeling to Predict the Diffusion of Safe Teenage Driving Behavior Through an Online Social Network. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 56(1), 2271–2275. [doi:10.1177/1071181312561478]

SAVARIMUTHU, B. T. R. & Cranefield, S. (2009). A categorization of simulation works on norms. In G. Boella, P. Noriega, G. Pigozzi & H. Verhagen (eds.), Normative Multi-Agent Systems , Dagstuhl, Germany: Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Germany.

SAWYER, R. K. (2002). Durkheim's Dilemma: Toward a Sociology of Emergence. Sociological Theory, 20(2), 227–247. [doi:10.1111/1467-9558.00160]

SHEKATKAR, S. M., & Ambika, G. (2014). Mediated attachment as a mechanism for growth of complex networks. ArXiv: 1410.1870 [cond-mat, physics:physics].

SHERMAN, L. W., & Weisburd, D. (1995). General deterrent effects of police patrol in crime 'hot spots': A randomized, controlled trial. Justice Quarterly, 12(4), 625–648. [doi:10.1080/07418829500096221]

TÖNNIES, F. (1957). Community and Society. New York, NY: Courier Dover Publications.

WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of "small-world" networks. Nature, 393(6684), 440–442. [doi:10.1038/30918]

WELLMAN, B. (1983). Network Analysis: Some Basic Principles. Sociological Theory 1:155–200. [doi:10.2307/202050]

WELLMAN, B. (2002). Little Boxes, Glocalization, and Networked Individualism. In M. Tanabe, P. van den Besselaar, & T. Ishida (Eds.), Digital Cities II: Computational and Sociological Approaches (pp. 10–25). Springer Berlin Heidelberg. [doi:10.1007/3-540-45636-8_2]

WILENSKY, U., & Rand, W. (2007). Making models match: replicating an agent-based model. Journal of Artificial Societies and Social Simulation, 10 (4) 2 <https://www.jasss.org/10/4/2.html>.

WIRTH, L. (1938). Urbanism as a Way of Life. American Journal of Sociology, 44(1), 1–24. [doi:10.1086/217913]