Introduction
Dunbar (1996) conjectures that many of the features of human cognition and neuro-anatomy that are unique compared to other species, for example large brain size and linguistic capabilities, can be explained by selection pressure for larger group sizes in the ancestral environment (the social brain hypothesis (Dunbar, 1998)). Although larger group sizes have many benefits, for example increased protection from predators, there are also many costs and unique challenges for species that attempt to exploit a niche by cooperating with other individuals.
Cooperation occurs when an individual takes an action which benefits another but at a cost to itself. Cooperators can be successful when their help is reciprocated. Reciprocation occurs when cooperators receive benefits in turn from the actions of others. When others do not reciprocate, we say that they defect or free-ride. The benefits to a cooperator may accrue directly from those who have been helped by the individual, in which case it is called direct reciprocity.
The classical example of cooperation via direct reciprocity is illustrated by the tit-for-tat strategy in the repeated Prisoner's Dilemma game (Axelrod & Hamilton, 1981; Axelrod, 1997). In this game, pairs of agents repeatedly interact over many rounds of play. In each round, both players simultaneously choose whether to cooperate (C), or to defect (D). The resulting payoffs are given in Table 1 where \(R\) is the reward for cooperation, \(P\) is the penalty for defection, \(T\) is the payoff that results in a temptation to defect, and \(S\) is the so-called "sucker's payoff". If these values satisfy \( T > R > P > S \) then the game qualifies as a prisoner's dilemma.
| C | D | |
|---|---|---|
| C | R,R | S,T |
| D | T,S | P,P |
Play then proceeds over many rounds with random stopping, and players are able to change their choice of cooperation or defection contingent on the history of play. Axelrod (1997) held a computerised Prisoner's Dilemma tournament and famously a strategy called ''tit-for-tat'' won the competition. This strategy cooperates conditionally based on the action chosen by its partner in the previous round of play; if the opponent cooperates then tit-for-tat reciprocates with cooperation. On the other hand it defects if, and only if, the opposing player defected in the previous round. If tit-for-tat encounters unconditional cooperators or other tit-for-tat players, then this results in direct reciprocity. Direct reciprocity occurs when cooperation is directly reciprocated by the partner who received the benefits of the cooperative act.
On the other hand, indirect reciprocity occurs when a cooperative action is not reciprocated directly, but rather via a third-party who did not receive the original benefits. Indirect reciprocity can occur when agents make use of the reputation, or ''image score'', of other agents in conditioning their strategy, in contrast to the personal history of interactions which typically bootstraps direct reciprocity. Nowak & Sigmund (1998a) model indirect reciprocity using a variant of the prisoner's dilemma called a donation game. As with the prisoner's dilemma, pairs of agents interact over many rounds of plays and the resulting payoffs are given in Table 1. The payoffs are chosen such that \(R = \gamma(k-1)\), \(S = -\gamma\), \(T = \gamma k\) and \(P = 0\), where \(\gamma > 0\) is a constant representing the cost of cooperation, and \(k > 1\) is a constant which determines the cost/benefit ratio. Here the act of cooperation can be interpreted as a donation from one agent to another, where the recipient receives some multiple greater than one of the original investment.
Provided that the cost/benefit ratio is greater than one, then a social surplus can be generated through reciprocation. This allows us to model cooperation in group settings which closely resemble social dilemmas that occur in nature. For example, intuitively, in an ecological context, we might interpret the interaction between agents as an allo-grooming activity in which the positive fitness payoff γk represents the fitness gains from parasite elimination, whereas the fitness cost - γ represents the opportunity cost of foregoing other activities, such as foraging, during the time γ allocated for grooming (Russell & Phelps, 2013).
Nowak & Sigmund (2005) start with the donation game, and introduce an ''image score'', which is an integer counter which is incremented every time an agent cooperates, and decremented every time an agent defects. They show that strategies which cooperate conditional on whether their partner's image-score is positive — which they call discriminators — are able to survive in equilibrium under various models of natural selection.
Note that both direct and indirect reciprocity make use of information about the other players in the game. Direct-reciprocity, as embodied by tit-for-tat, makes use of direct observations of others' behaviour, and requires the player to personally remember the choices made by the other players they have interacted with. On the other hand, indirect reciprocity, as embodied by discriminatory cooperation, uses information that is shared with all players. We might expect the success of each form of reciprocity to be contingent on the reliability and availability of the underlying information used by each strategy. Moreover, we should expect the availability and quality of this information to vary between settings.
Many theoretical models of the evolution of cooperation via reciprocity start with the assumption that agents interact in groups that are large relative to the expected number of pairwise interactions. These simple models are analytically tractable. However, in small or intermediate sized groups, the analysis is complicated by the fact that strategies based on both direct and indirect reciprocity can interact.
This is of utmost importance if we are to take these models seriously as explanations of actual cooperative behaviour in the real-world since many collective-action problems, in both human and non-human societies, occur between small groups of agents. For example, in human societies collective-action problems can occur between small numbers of nation states in the context of trade and climate negotiations (Tietenberg, 1985). Moreover, although we sometimes think of human societies as vastly interconnected, this is a parochial perspective; until very recently most people did not live in cities in developed nations, but rather in small isolated agricultural communities in the least developed countries (Ostrom, 1990; Diamond, 2013; Ostrom, 2000). In nature, the representative group sizes of many non-human social animals are typically of the order of between 10 and 102 individuals (Packer et al., 1990; Baird & Dill 1996), and even single-celled organisms have demographic constraints limiting interactions to groups sizes of the order of 103 individuals (Cremer et al., 2012). Finally, in the context of artificial agents there are many scenarios which constrain interactions to smaller groups of agents; for example, geographic and spacial constraints can lead to coordination problems between small numbers of autonomous vehicles, e.g. at traffic intersections (Arsie et al. 2009).
In this paper we introduce a framework for studying the cooperation in groups of varying size and intimacy, which incorporates reputation in the form of indirect reciprocity (Nowak & Sigmund 2005) together with direct reciprocity in the form of tit-for-tat strategies (Axelrod & Hamilton 1981).
We begin with a review of existing studies of trust and reputation: in Section 2 we discuss one of the simplest models for studying trust and cooperation — the Prisoners' Dilemma — which has been extensively studied both theoretically and experimentally (with both human and computerised agents), and review various refinements and extensions to the basic game. We proceed to discuss some of the issues inherent in achieving stable cooperation in groups where more than two agents interact, and review more advanced models that attempt to incorporate reputation. In Section 3 we describe our model of cooperation in detail. In Section 4 we describe our methodology detailing how we solve the model numerically. Finally we present our results in Section 5 and conclude in Section 6.
Related Work
There have been a number of experimental studies of the Prisoner's Dilemma with human subjects in which tit-for-tat like strategies are commonly observed to be voluntarily used, e.g. (Wedekind & Milinski 1996).
However, Roberts & Sherratt (1998) noted that tit-for-tat like strategies are not always observed in ecological field studies, and postulate that this is because the original model cannot account for differential levels of cooperation. They studied a simulated evolutionary tournament of a variant of the game that allows for different levels of cooperation, and found that a strategy raise-the-stakes was an evolutionary stable outcome. In later work Roberts & Renwick (2003) studied human subjects and found that they used a strategy similar to raise-the-stakes. This strategy starts off with a small level of cooperation and then rises to maximal cooperation dependent on the other player's level of cooperation in previous rounds. The behaviour of this strategy is qualitatively consistent with the self-reported behaviour of human subjects in longitudinal studies of friendship development as reported by Hays (1985). However, the latter study was restricted to North American students in their first year of study, and the model of Roberts & Sherratt (1998) has been questioned due to its reliance on discrete increments (Killingback & Doebeli 1999).
These earlier studies focused on social dilemmas which involve only dyadic interactions. However, in reality many social dilemmas arise when many agents interact with each other. In many-agent interactions, two key additional considerations come into play, which we discuss in turn below.
Firstly, the social-structure in which a population of agents are embedded can have a significant effect on the outcome. For example, the topology of the social-network can have a significant effect; in particular, scale-free networks can promote cooperation without the need for conditional reciprocation (Santos et al. 2006b). This assumes that the social network is a given, which then constraints collective-action, but it may be more appropriate to view social-structure as arising from collective-action; Santos et al. (2006a) allow for the possibility that the social network can change as agents break connections with defectors, and form new links chosen at random from the neighbourhood of the severed node, and Phelps (2013) introduces a model which allows agents to choose new nodes with which to connect based on reputation information. Thus, it may be more appropriate to view social structure and strategies based on conditional reciprocation as being in co-evolution with each-other.
The second issue with many-player interactions is that as the group grows larger, information about previous encounters with particular individuals becomes less useful simply because the probability of re-encountering the same individual grows smaller. In this case strategies like tit-for-tat are not sufficient on their own to prevent free-riding in larger groups.
Tit-for-tat relies on private information that has been obtained directly from previous personal encounters with other agents. However, there are other potential sources of information about the propensity of agents to cooperate. Nowak and Sigmund (Nowak & Sigmund 1998b; Nowak & Sigmund 2005; Nowak & Sigmund 1998a) use an evolutionary game-thoeretic model to analyse the effect of reputation information which is globally available to all agents in a population, which they call ''image scoring''. The central idea is that defection and cooperation are globally tracked and made available in a public score; agents can increase their image score by cooperating, but when they defect their score is reduced. Thus, when deciding whether or not to cooperate with an agent, indirect information about that agent's propensity to cooperate is now available.
This information is indirect because it has not been obtained by personal experience, but rather by a third-party. In turn, if agents now cooperate conditional on a positive image score, the presence of such discriminators can lead to indirect reciprocity; cooperating with somebody not because they are expected to reciprocate directly, but because the reputation so gained will encourage cooperation from strangers. Nowak & Sigmund (1998a) showed that, under some restrictive assumptions, provided the population contains a sufficient fraction of discriminators at the outset, then natural selection will eventually eliminate all defectors from the population.
Although the framework of evolutionary game-theory used in these models was originally formulated to describe the process of natural selection operating on genes, the same mathematical formalism can be used to describe a process of cultural evolution in which agents learn, rather than evolve, by imitating the strategies of other agents who appear to be more successful (Weibull 1997; Phelps & Wooldridge 2013; Boyd & Richerson 1988; Kendal et al. 2009). Indeed, Nowak and Sigmund's theoretical models are supported by evidence from empirical studies in which human subjects are observed to make-use of image-scores in social dilemma games played in the laboratory (Wedekind & Milinski 2000; Seinen & Schram 2006).
Nowak and Sigmund analysed their original models under the assumption that the size of the population is very large. This assumption makes modelling more tractable since many terms in the model become zero in the limit as the number of agents tends to infinity, and moreover it is not necessary to consider interaction between strategies based on indirect versus direct reciprocity, since the probability of re-encounter is negligible.
However, given that in reality many interactions do occur within smaller groups or populations, it is surprising that relatively little attention has been given in the literature to understanding the quantitative relationship between the size of the group and the resulting level of cooperation, when the effects of different forms of reciprocity are considered.
It is a well known empirical observation that in a traditional public-goods setting, free-riding increases as the group size increases (Olson 1965; Nosenzo et al. 2015; Kollock 1998). Although there have been some attempts to explain such phenomena theoretically, typical models do not explicitly consider the quantitative relationship between the group size and the resulting form and reliability of information available to strategies which are based on trust and reputation. For example, Heckathorn (1996) provides a conceptual framework which formulates public-goods games in terms of an underlying evolutionary game played between pairs of players randomly chosen from a larger population. Their model assumes that reputation-based strategies can acquire perfect information about their opponent's propensity to cooperate simply by paying a fixed information cost, without considering how this information is actually acquired, and how its reliability might vary with the group size. Under this restrictive assumption, the size of the population has no bearing on the final level of contribution to the public-good.
However, it is interesting to ask whether similar results would be obtained if we drop this assumption, and explicitly consider how reputation information is obtained. This entails explicitly modelling direct and indirect reciprocity. A priori, we should expect the group size to have a significant effect on the outcome. For example, in a small population, it may pay for an individual to switch to between direct reciprocity and reputation depending on the make-up of the rest of the group: in a population dominated by direct reciprocity there is little incentive to build a reputation. Similarly if the rest of the population offer help conditional on reputation. This reasoning suggests that the dynamics of switching between these two types of strategy would play an important role in determining the steady-state outcome.
Agent-based models have been used to analyse asymptotic outcomes in small populations in which agents can use both direct and indirect reciprocity in order to condition their donations (Bravo & Tamburino 2008; Phelps 2013; Roberts 2008; Conte & Paolucci 2002; Boero et al. 2010). These simulation analyses demonstrate that both forms of reciprocity can persist in steady-state, either when agents use individual-learning to adjust their strategy (Phelps, 2013), or when strategies evolve through natural selection (Bravo & Tamburino 2008; Roberts 2008). Although these models are able to account for both forms of reciprocity in smaller groups, their reliance on simulation methods means that they are not able to provide a systematic exploration of the dynamics of learning which lead to asymptotically-cooperative outcomes.
For example, the model described in Roberts (2008) is able to deal with small populations and genetic drift, but the analysis is based on a restricted set of initial conditions in which the initial makeup of the population has equal propensity over all strategies. Similarly, Phelps (2013) provides a qualitative analysis of the dynamics of the learning, but lacks an account of static equilibria, and analyses only the average level of cooperation without differentiating the social-welfare of different attractors.
Bravo & Tamburino (2008) show that image-scoring in a simulated alternating trust game leads to cooperative outcomes under two distinct experimental treatments: one in which agents have a high probability of re-encountering one another, and another in which re-encounter is extremely improbable. Thus in the former treatment, the image-score is more likely to encapsulate information about direct experience, whereas in the latter it encapsulates information from others. However, in this model agents cannot explicitly switch between using one form of information over the other, and there is no systematic analysis of the strategic interaction between these two forms of reciprocity other than reporting the final level of cooperation in each separate experimental treatment.
Similarly Boero et al. (2010) introduce an agent-based model in which information about the returns of financial securities is communicated among a population of agents. Agents in this model can cheat by misreporting information. Two experimental treatments are analysed corresponding to trust and reputation: one in which agents can use their own private experience of previous interactions in order to judge the trustworthiness of other parties (analogous to direct reciprocity), and another in which the first-order accuracy of other agents' reports is itself shared and communicated (analogous to indirect reciprocity). However, again, as with the model of Bravo & Tamburino (2008), the interaction between these two behaviours is not considered, and agents do not have the ability to switch between them depending on how these strategies perform.
We address the issues in the aforementioned analyses by introducing a model of cooperation which incorporates both direct and indirect reciprocity, and analysing it using a methodology called empirical game-theory (Wellman 2006; Phelps et al. 2010; Walsh et al. 2002), which uses a combination of simulation and rigorous game-theoretic analysis. By so doing we are able to quantitatively analyse cooperation in smaller groups without making assumptions in the limit, and we are able to gain insights into the strategic interaction between different forms of reciprocal behaviour by analysing both static (Nash) equilibria and also the dynamics of evolution of each of these strategies.
In the following section we give a formal description of our model before describing the empirical game-theory methodology in Section 4.
The Model
The population consists of a set of agents \(A = \{ a_1, a_2, \ldots, a_n \}\). Interaction occurs over discrete time periods \(t \in \{ 1, 2, \ldots, N \}\). During each time period a randomly chosen pair of agents \((a_i, a_j)\) interact with each other. We refer to \(n\) as the group size and \(N\) as the expected number of interactions.
At each time period \(t\) agent \(a_i\) may choose to invest a certain amount of effort \(u_{(i,j,t)} \in [0, U] \subset \mathbb{R}\) in helping their partner \(a_j\), where \(U \in \mathbb{R}\) is a parameter determining the maximum investment. This results in a negative fitness payoff \(-u\) to the donor, and a positive fitness payoff \(ku\) to the recipient of help \(a_j\):
In the special case that \(N=2\) and \(n=2\), this model has the same payoff structure as the original one-shot prisoner's dilemma. However, the more general social dilemma modelled here allows for repeated interaction between different pairs of individuals in a larger group \(n > 2\), who can modify their state and remember the history of play over a number of repeated interactions \(N > 2\). Once these interactions have occurred, all the agents' state is discarded except their accrued fitness, and then evolution proceeds. When the total expected number of number of interactions, \(N\), is large relative to \(n\) then repeated encounters between the same pairs of individuals are less likely, and intuitively we should expect this to negatively influence the efficacy of direct-reciprocity versus indirect-reciprocity, since there is correspondingly less information relating to direct interactions.
Since we are interested in the evolution of cooperation, we analyse outcomes in which agents switch between values of \(u\) that maximise their own fitness \(\phi_i\). Provided that \( k>1 \), over many bouts of interaction it is possible for agents to enter into reciprocal relationships that are mutually-beneficial, since the donor's initial cost \(u\) may be reciprocated with \(k \times u\) yielding a net benefit \(ku - u = u(k - 1)\). Provided that agents reciprocate, they can increase their net benefit by investing larger values of \(u\). However, by increasing their investment they put themselves more at risk from exploitation, since just as in the alternating prisoner's dilemma , defection is the dominant strategy if the total number of bouts \(N\) is known: the optimal behaviour is to accept the help without any subsequent investment in others. In the case where \(N\) is unknown, and the number of agents is \(n = 2\), it is well known that conditional reciprocation is one of several equilibria in the form of the so-called tit-for-tat strategy which copies the action that the opposing agent chose in the preceding bout at \(t-1\) (Miller 1996). However, this result does not generalise to larger groups \(n > 2\) (Fader& Hauser 1988).
Nowak & Sigmund (1998b) demonstrate that indirect reciprocity can emerge in large groups, provided that information about each agent's history of actions is summarised and made publicly available in the form of a reputation or ''image-score'' \( r_{(i, t)} \in [r_{\operatorname{min}}, r_{\operatorname{max}}] \subset \mathbb{Z} \). As in the Nowak and Sigmund model, image scores in our model are initialised \( \forall_i \; r_{(i, 0)} = 0 \) and are bound at \( r_{\operatorname{min}} = -5 \) and \( r_{\operatorname{max}} = 5 \). An agent's image score is incremented at \( t + 1 \) if the agent invests a non-zero amount at time t, otherwise it is decremented:
| $$r_{(i, t+1)} = \operatorname{min}(r_{(i, t)} + 1, \; r_{\operatorname{max}}) \iff u_{(i, x, t)} > 0 \\ r_{(i, t+1)} = \operatorname{max}(r_{(i, t)} - 1 , \; r_{\operatorname{min}}) \iff u_{(i, x, t)} = 0$$ |
| $$u_{(i, j, t)} = \left\{ \begin{array} {r@{\quad:\quad}l} \gamma & r_{(j, t)} \geq \sigma_i \\ 0 & r_{(j, t)} < \sigma_i \\ \end{array} \right.$$ |
In general, it is the cost-benefit ratio \( \gamma / \gamma k = 1/k \) relative to the social viscosity of the group that determines whether or not cooperation persists in equilibrium (Nowak, 2006). Accordingly, in our analysis we hold the cost-benefit ratio constant by choosing fixed parameter values for \( \gamma \) and \( k \) while systematically varying the number of agents \( n \), and the expected number of rounds of play \( N \), as described in the next section. We also repeat the analysis with \( k = 3.5 \).
Nowak & Sigmund (1998a) demonstrate that the conditions under which cooperation is achieved depend on the presence of discriminators; that is, agents which use a threshold of \( \sigma_i = 0 \) and thus only cooperate with others if they have a good reputation. In their paper they show that if the initial fraction of discriminators in the population is above a critical value then the population converges to a mix of discriminators and cooperators, and defectors are completely eliminated. This implies that strategies based on indirect reciprocity via reputation are an essential prerequisite for the evolution of cooperation in large groups.
The above model contrasts with that of Roberts & Sherratt (1998) who study interactions in which agents make their investment decision solely on the basis of private information about the history of previous interactions. In their model an agent \( a_i \) decides on the level of investment to give \( a_j \) as a function \( \psi_i \) of the most recent encounter with \( a_j \):
| $$u_{(i, j, t)} = \psi_i( u_{(j, i, t')} )$$ | (1) |
We are particularly interested in the effect of group size \(n\) and the number of interactions \(N\) on the evolution of cooperation. The analytical model of Nowak & Sigmund (1998a) assumes: a) that the group size \(n\) is large enough relative to \(N\) that strategies based on private history, such as tit-for-tat, are irrelevant (since the probability of encountering previous partners is very small); and b) that the we do not need to take into account the fact that an agent cannot cooperate with itself when calculating the probability with which any given agent is likely to encounter a particular strategy.
However, in order to model changes in group size, and hence interaction in smaller groups, it is necessary to drop both of these assumptions. The resulting model is more complicated, and it is not possible to derive closed-form solutions for the equilibrium behaviour. Therefore we use simulation to estimate payoffs, and numerical methods to compute asymptotic outcomes, as described in the next section.
Methodology
In order to study the evolution of populations of agents using the above strategies, we use methods based on evolutionary game-theory. However, rather than considering pairs of agents chosen randomly from an idealised very large population, our analysis concerns interactions amongst smaller groups of size n > 2 assembled from a larger population of individuals. The resulting game-theoretic analysis is complicated by the fact that this results in a many-player game, which presents issues of tractability for the standard methods for computing the equilibria of normal-form games.
Heuristic approaches are often used when faced with tractability issues such as these. In particular, heuristic optimisation algorithms, such as genetic algorithms, are often used to model real adaptation in biological settings (Bullock 1997). The standard heuristic approach to modelling multi-agent interactions is to use a Co-evolutionary algorithm (Miller 1996; Hillis 1992). In a co-evolutionary optimisation, the fitness of individuals in the population is evaluated relative to one another in joint interactions (similarly to payoffs in a strategic game), and it is suggested that in certain circumstances the converged population is an approximate Nash solution to the underlying game; that is, the stable states, or equilibria, of the co-evolutionary process are related to the evolutionary stable strategies (ESS) of the corresponding game. However, there are many caveats to interpreting the equilibrium states of standard co-evolutionary algorithms as approximations of game-theoretic equilibria, as discussed in detail by Ficici & Pollack (1998); Ficici & Pollack (2000).
In order to address this issue, we adopt the empirical game-theory methodology (Phelps et al. 2010; Wellman 2006; Walsh et al., 2002), which uses a combination of simulation and rigorous game-theoretic analysis. The empirical game-theory method uses a heuristic payoff matrix which is computed by running very many simulations, as detailed below.
The payoff matrix is said to be heuristic because several simplifying assumptions are made in the interests of tractability. We can make one important simplification by assuming that the game is symmetric, and therefore that the payoff to a given strategy depends only on the number of agents within the group adopting each strategy. Thus for a game with \(j\) strategies, we represent the payoff matrix as a map \( f : \mathbf{Z}^j \rightarrow \mathbf{R}^j \).
For a given mapping \(f(\bar{p}) = \bar{q}\) in the payoff matrix, the vector \(\bar{p} = \left( p_1, \ldots, p_j \right) \) represents the group composition, where \( p_i \) specifies the number of agents who are playing the \(i^{th}\) strategy, and \( \bar{{q}} \) represents the outcome in the form
For a game with \(n\) agents, the number of entries in the payoff matrix is given by
For example, for \(n = 10\) agents and \(j = 5\) strategies, we have a payoff matrix with \(s = 1001\) entriesFor each entry in the payoff matrix we estimate the expected payoff to each strategy by running a total of \(10^5\) simulations and taking the mean1 fitness rounded according to the corresponding standard error.
For example, if we have an entry in the payoff matrix
| $${p} = \left( 5, 4, 1, 0, 0 \right)$$ |
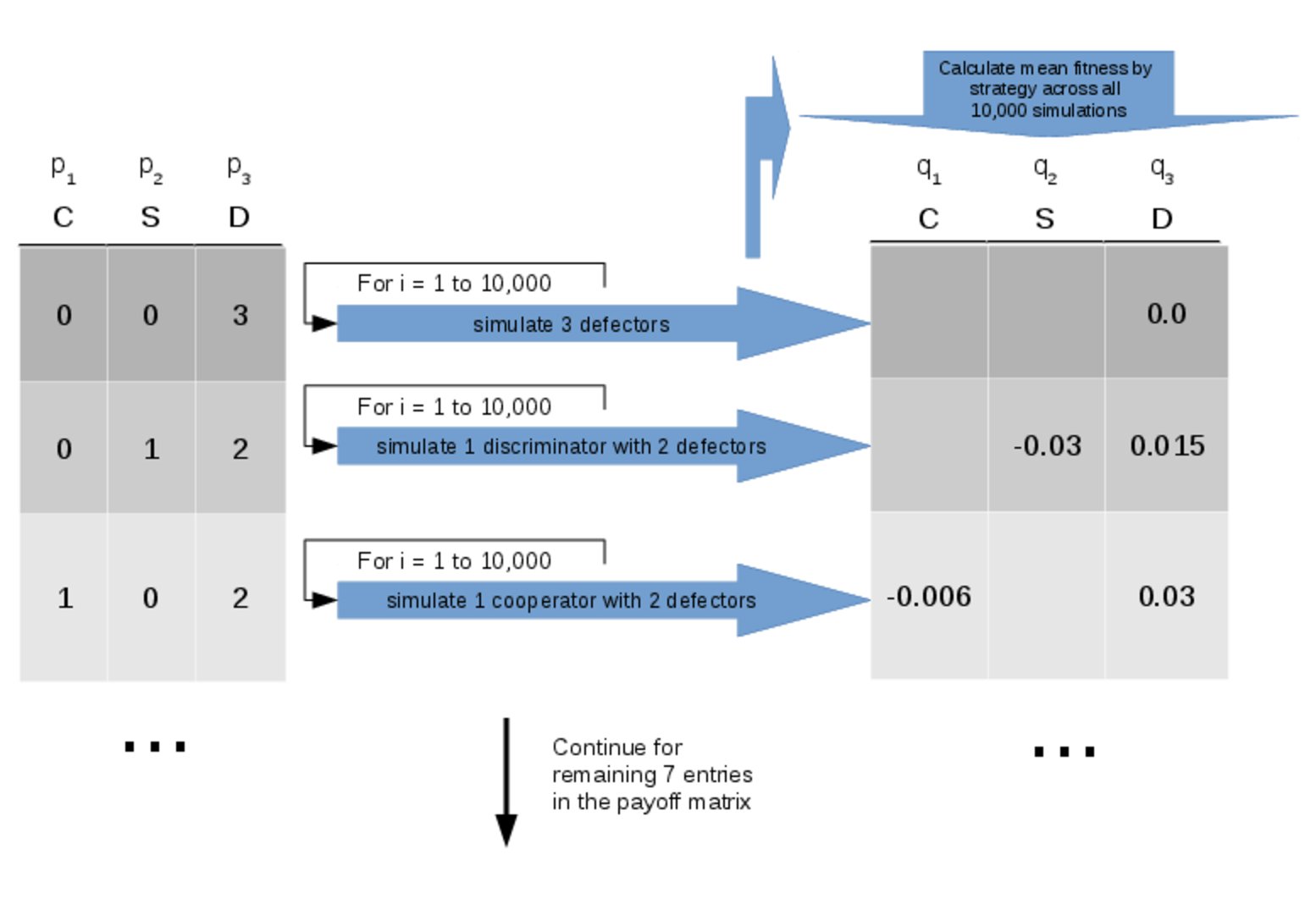
With estimates of the payoffs to each strategy in hand, we are in a position to model the evolution of populations of agents using these strategies. In our evolutionary model, we do not restrict reproduction to within-group mating; rather, we consider a larger population which temporarily forms groups of size \( n \) in order to perform some ecological task. Thus we use the standard replicator dynamics equation (Weibull, 1997) to model how the frequency of each strategy in the larger population changes over time in response to the within-group payoffs:
| $${m}_i = \left[u(e_i,\bar{m}) - u(\bar{m},\bar{m})\right]m_i $$ | (2) |
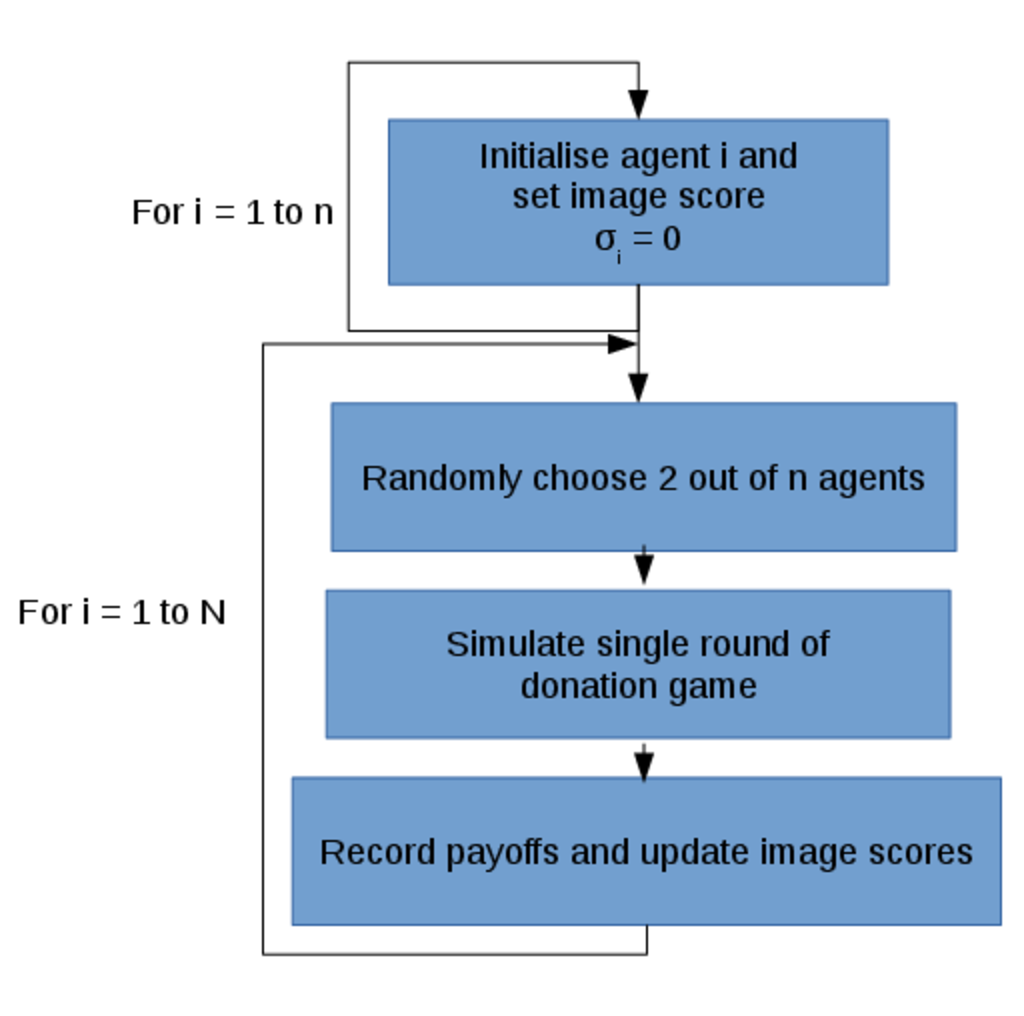
Each of the individual simulations consists of the iterative process illustrated below in Figure 2.
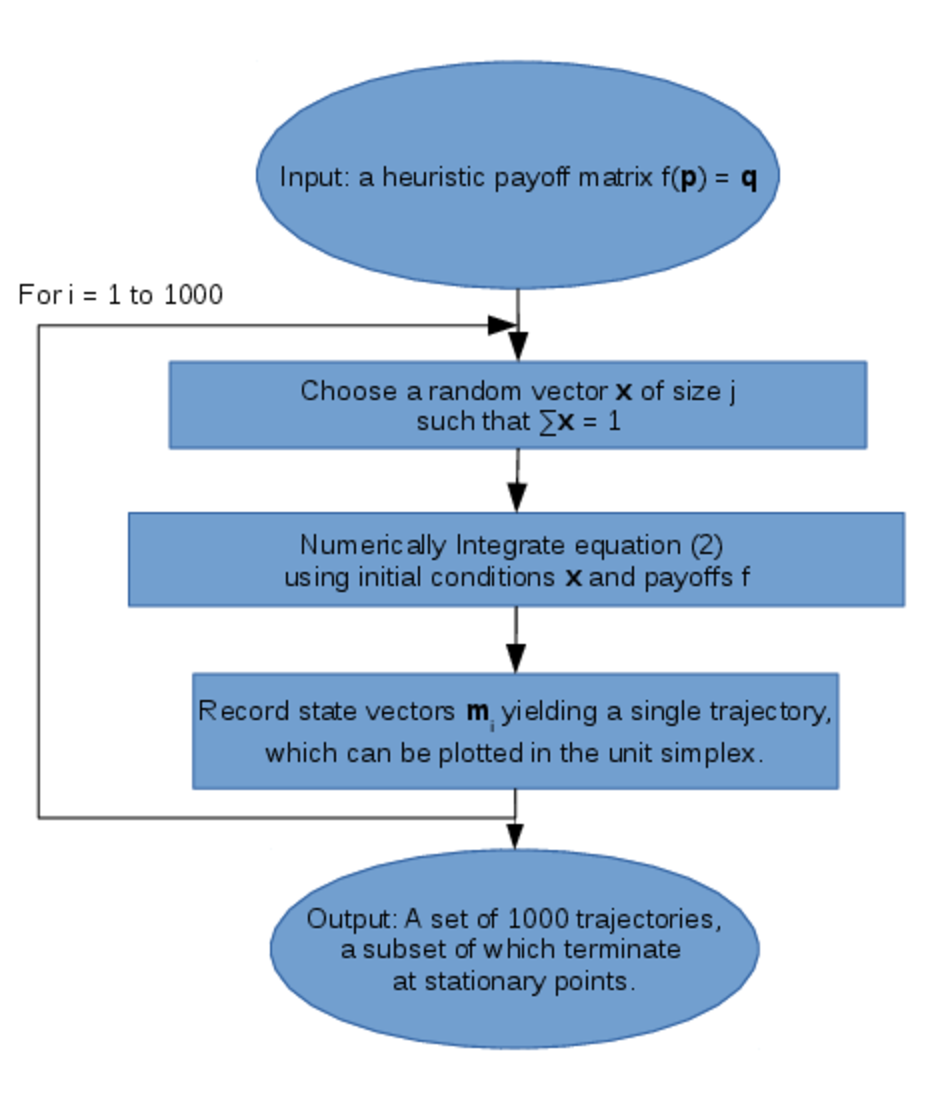
In our analysis we solve this system numerically: we choose \( 10^3 \) randomly sampled initial values which are chosen uniformly from the unit simplex by sampling from a Dirichlet distribution (Kotz et al., 2000), and for each of these initial mixed-strategies we solve Eq.2 as an initial value problem using R (Soetaert & Petzoldt, 2011; R Core Team, 2013). This results in \( 10^3 \) trajectories which either terminate at stationary points, or enter cycles. This process is illustrated in Figure 3 below.
We consider \( j = 4 \) strategies:
- \( C \) which cooperates unconditionally (\( \sigma_i = r_{min} \));
- \( D \) which defects unconditionally (\( \sigma_i = r_{max} + 1 \));
- \( S \) which cooperates conditionally with agents who have a good reputation (\( \sigma_i = 0 \)) but cooperates unconditionally when reputations have not yet been established;
- \( T \) which cooperates with agent \( a_j \) provided that \( a_j \) cooperated with \( a_i \) on the previous encounter, and cooperates unconditionally against unseen opponents.
Although this space of strategies is limited, and there are many variants of the discriminatory strategy which, for example, use different assessment rules for ascribing reputation depending on the reputation of both the donor and the recipient (Nowak & Sigmund, 2005), we restrict attention to the simplest strategies because of their simplicity and corresponding universality across species: direct reciprocity has been observed in primate grooming interactions (Barrett et al., 1999), and there is some empirical evidence to suggest that chimpanzees are capable of at least the simplest assessment rule for indirect reciprocity – ''scoring'' – as modelled here (Russell et al., 2008). The image scoring assessment rule is more plausible as a mechanism for understanding reciprocity in, e.g. primate allo-grooming, because it does not require language or other sophisticated cognitive resources: ''Scoring is the 'foolproof' concept of 'I believe what I see'. Scoring judges the action and ignores the stories.'' (Nowak & Sigmund, 2005, p. 1294).
A major advantage of our approach over other simulation studies is that there are very few free parameter settings, which are summarised in Table 2. The key values are the parameter settings for the multiplier and cost values, which determine the cost-benefit ratio. As discussed previously, theoretical considerations suggest that it is the social-viscosity relative to the cost-benefit ratio which determines the asymptotic outcome, and we systematically vary the former as described in the next section. The values \( \gamma = 10^{-1} \) and \(k = 10 \) were chosen to correspond to those of the original simulation study of Nowak & Sigmund (1998a)- see p. 569 therein, but we also analyse the model with a different multiplier of \(k = 3.5 \) to test the robustness of our results.
The remaining parameters effect numerical estimates and sample sizes. As can be seen we have chosen large sample sizes, and as shown in the next section the corresponding p-values and standard errors are very small throughout our study. All of the code used in our experiments is available in the public domain and can be downloaded under an open source license (Phelps, 2011).
| Parameter | Value(s) |
|---|---|
| Donation game multiplier\( k \) | \( \{10, 3.5\} \) |
| Donation game cost \( \gamma \) | \(10^{-1}\) |
| Number of agents \( n \) | \( \{3, 6, 10\} \) |
| Expected number of rounds \(N\) | \( \{5, 10, 15, \ldots, 50\} \) |
| Number of independent simulation runs per entry in the payoff matrix | \(10^5\) |
| Number of randomly sampled initial conditions for the replicator-dynamics integration | \(10^3\) |
| Time interval used to numerically integrate equation 2 | \(10^{-1}\) |
Results
Initially we restrict ourselves to a very simple scenario where we have \( n = 3 \) agents choosing between two strategies. Table 3 shows the heuristic payoff for three agents choosing between unconditional defection \(D\) or unconditional cooperation \(C\). The left-hand column shows the number of agents adopting each pure strategy, and the right-hand column shows the estimated expected payoff to each strategy. It is illuminating to compare this with the standard analytical 2-player normal-form payoff matrix for our model expressed in the same combinational form in Table 4. In the analytical two-player case the multiplier \(k\) determines the ranking of the four possible payoff combinations, which are denoted \(T\), \(R\), \(P\) and \(S\) representing the temptation to defect, the reward for cooperation, the punishment for defection, and the ''sucker's'' payoff respectively. For only two agents the ranking of these payoffs determines the structure of the social dilemma. In the case that \( k > 1 \) then \( T > R > P > S \) which is the classical prisoner's dilemma. However, when there are more than two agents, there are more payoff combinations. In Table 3 we see that when one cooperator interacts with two defectors, the temptation to defect is lessened since the two defectors interact with each other as well as the cooperator. On the other hand, the single cooperator in this case suffers the full sucker's payoff. This can be contrasted with next row in the table where we have two cooperators interacting with a single defector. Here the temptation to defect is strong since the defector can fully exploit the cooperators without suffering any defection, but the sucker's payoff is compensated by the reward from cooperation arising from the interaction of the two cooperators.
| n(C) | n(D) | u(C) | u(D) |
|---|---|---|---|
| 0 | 3 | 0 | |
| 1 | 2 | -0.1 | 0.5 |
| 2 | 1 | 0.4 | 1.0 |
| 3 | 0 | 0.9 |
| n(C) | n(D) | u(C) | u(D) |
|---|---|---|---|
| 0 | 2 | P = 0 | |
| 1 | 1 | S = - γ = -0.1 | T = γ k = 1 |
| 2 | 0 | R = γ (k-1) = 0.9 |
| n(T) | n(S) | n(D) | u(T) | u(S) | u(D) |
|---|---|---|---|---|---|
| 0 | 0 | 3 | 0.0 | ||
| 0 | 1 | 2 | -0.03 | 0.015 | |
| 1 | 0 | 2 | -0.006 | 0.03 | |
| 0 | 2 | 1 | 0.15 | 0.03 | |
| 1 | 1 | 1 | 0.26 | 0.28 | 0.04 |
| 2 | 0 | 1 | 0.45 | 0.06 | |
| 0 | 3 | 0 | 0.9 | ||
| 1 | 2 | 0 | 0.9 | 0.9 | |
| 2 | 1 | 0 | 0.9 | 0.9 | |
| 3 | 0 | 0 | 0.9 |
Although Table 3 could have been obtained analytically, the situation becomes much more subtle and complex when we introduce additional agents, and additional strategies representing reciprocity. We next extend our analysis to \( n = 10 \) agents, \(j = 3\) strategies, resulting in a payoff matrix with \(264\) rows. Rather than tabulate the numerically-obtained payoffs, we proceed directly to analysing this heuristic game by sampling \(10^2\) initial values and integrating the replicator dynamics specified by Eq. 2.
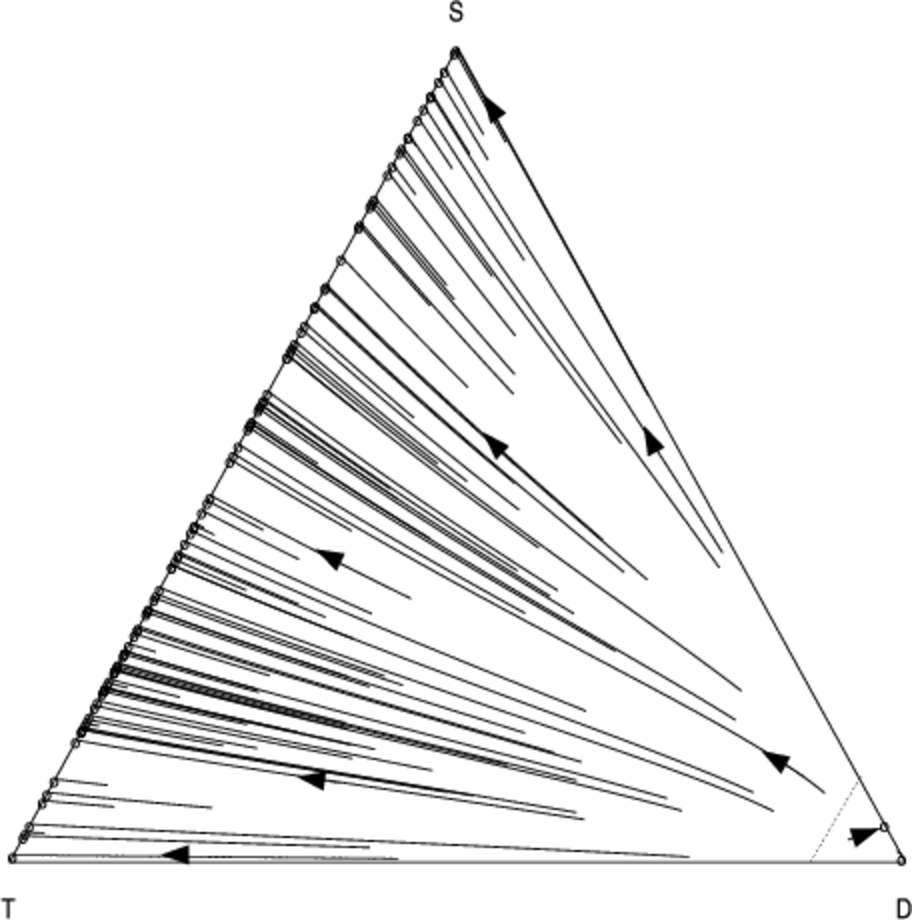
Since mixed strategies represent population frequencies, the components of \( \bar{{m}} \) sum to one. Therefore the vectors \( \bar{{m}} \) lie in the unit-simplex \( \bigtriangleup^{j-1} = \{ \bar{x} \in \mathbb{R}^j : \sum_{i=1}^{j} x_i = 1 \}\). In the case of \( j = 3 \) strategies the unit-simplex \( \bigtriangleup^2 \) is a two-dimensional triangle embedded in a three-dimensional space which passes through the coordinates corresponding to pure strategy mixes: \( (1, 0, 0) \), \( (0, 1, 0) \), and \( (0, 0, 1) \). We use a two dimensional projection of this triangle to visualise the population dynamics. Figures 4 and 5 show the phase diagram for the population frequencies when we analyse the interaction between cooperators (\(C\)), defectors (\(D\)) and discriminators (\(S\)) when we have a small group of \( n = 10 \) agents.
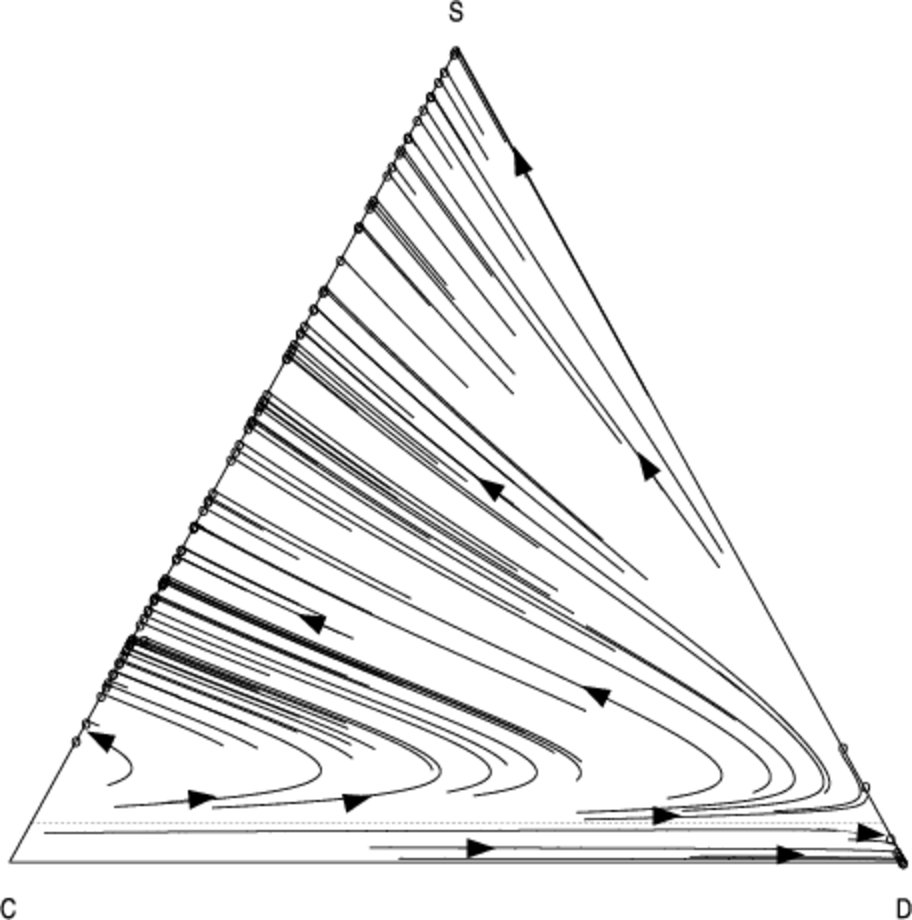

Each point in the above graphs represents the state of the population at a given moment in time. The triangle represents the unit simplex; i.e. it contains all vectors whose components sum to one. In the bottom-left corner \( (1, 0, 0) \), 100% of the population consists of cooperators (C); at the top of the simplex \( (0, 1, 0) \), 100% of the population consists of discriminators (S); in the bottom-right corner \( (0, 0, 1) \), 100% of the population consists of defectors; in the middle of the simplex \( (1/3, 1/3, 1/3) \) a third of the population is adopting each of the three strategies, and so-on for all the points in the simplex. The arrows show how the fraction of the population adopting each strategy changes over time as evolution progresses. The circles represent configurations of the population which are no longer changing; i.e. they are stationary points under the replicator dynamics.
As in Nowak & Sigmund (1998a) we find that a minimum initial frequency of discriminators is necessary to prevent widespread convergence to the defection strategy (the basin of attraction whose trajectories terminate in the bottom right of the simplex).
Using our analysis, we can quantify how the size of this basin changes in response to the number of pairwise interactions per generation \( N \). As \( N \) is increased from \(N = 13\) (Fig. 5) to \( N = 100 \) (Fig. 4), we see that the basin of attraction of the pure defection equilibrium is significantly decreased, and correspondingly the critical threshold of initial discriminators necessary to avoid widespread defection. Defection is less likely2 as we increase the number of interaction relative to the group size.
In smaller groups it is important to take into account the interaction between strategies representing both direct and indirect reciprocity, since there is a non-negligible probability that agents will repeatedly encounter previous partners; if we increase \(N\) relative to \(n\) we need to consider the effect of strategies that take into account private interaction history (direct reciprocity) as represented by the T strategy.
Figures 6 and 7 show the co-evolution between the \( T \), \(D\) and \(S\) strategies. For \(N = 13\), the results are virtually indistinguishable from the scenario in which we substitute \(T\) with unconditional cooperation \(C\) (Fig. 5). This is not surprising since the default behaviour of \(T\) is to cooperate in the absence of specific information about a particular partner. However as we increase \(N\) we see that \(T\) becomes more effective; for \(N = 100\) interactions, \(D\) remains a pure-strategy equilibrium, but with a significantly reduced basin-size compared to the scenario where \(S\) interacts with \(S\) and \(D\). Neither form of reciprocation is dominant over the other, suggesting that both forms of reciprocity could play an important role in smaller groups.
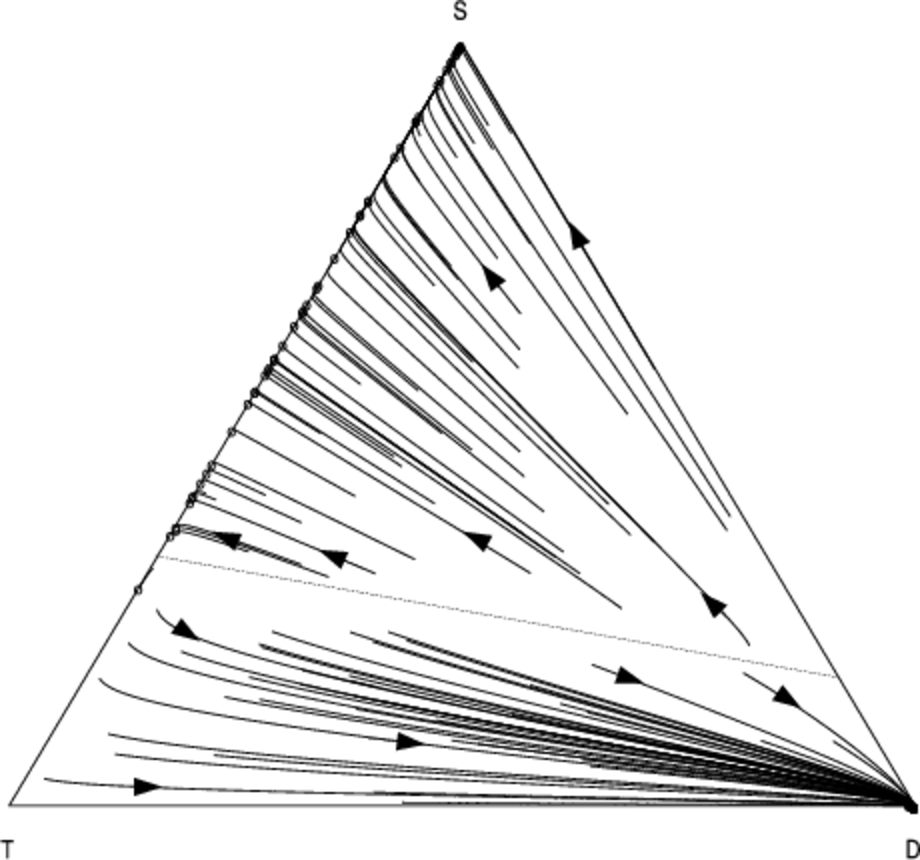
This is highlighted by an analysis of the heuristic payoffs for each strategy in a simplified setting where we have only three agents and three strategies. Table 5 shows the heuristic payoff matrix for this setting. Clearly both the \(S\) and \(T\) strategies are vulnerable to defectors. However, there is a quantifiable relative difference in how well they perform against defection: indirect reciprocity (\(S\)) gains a slightly higher payoff than direct reciprocity strategy (\(T\)) in the case where each agent adopts a different strategy (the fifth row of Table 5).
This is not surprising, since the agent using the discriminatory strategy S can gain valuable information by observing the interaction of the other two agents. The T strategy has no prior information about the behaviour of the defector, and so sacrifices a significant payoff by cooperating on the first move. On the other hand, the discriminatory strategy has a probability of observing this interaction, in which case it will consistently defect against the defector on subsequent encounter. Moreover the pure-strategy best-reply for the defecting player in this situation is to switch to either S or T (row eight or nine). On the other hand, the decision for a player adopting one of the reciprocating strategies is asymmetric: starting from row five, we can obtain a significantly higher payoff (0.45) by choosing direct reciprocity (T) in the next row down, as compared with a switch to indirect reciprocity in the previous row (0.15). Here the informational advantages to a passive S player are cancelled out by the fact that the scoring strategy S considered here is unable to distinguish between punishment and defection3 because a discriminator who fails to help a defector themselves incurs a reputation penalty.
In small groups, this effect can lead to an increase in the frequency of direct reciprocity. By analysing the mixed-strategy case using the replicator dynamics we can see that although neither \(S\) nor \(T\) dominate each other, direct reciprocity attracts a slightly higher following; that is, the distribution of mixed-strategy equilibria containing both \(T\) and \(S\) is skewed towards \(T\). This can be seen from the slight curvature of the trajectories towards the \(T\) direction in Fig. 8 (we will return to this discussion with greater statistical rigour below).
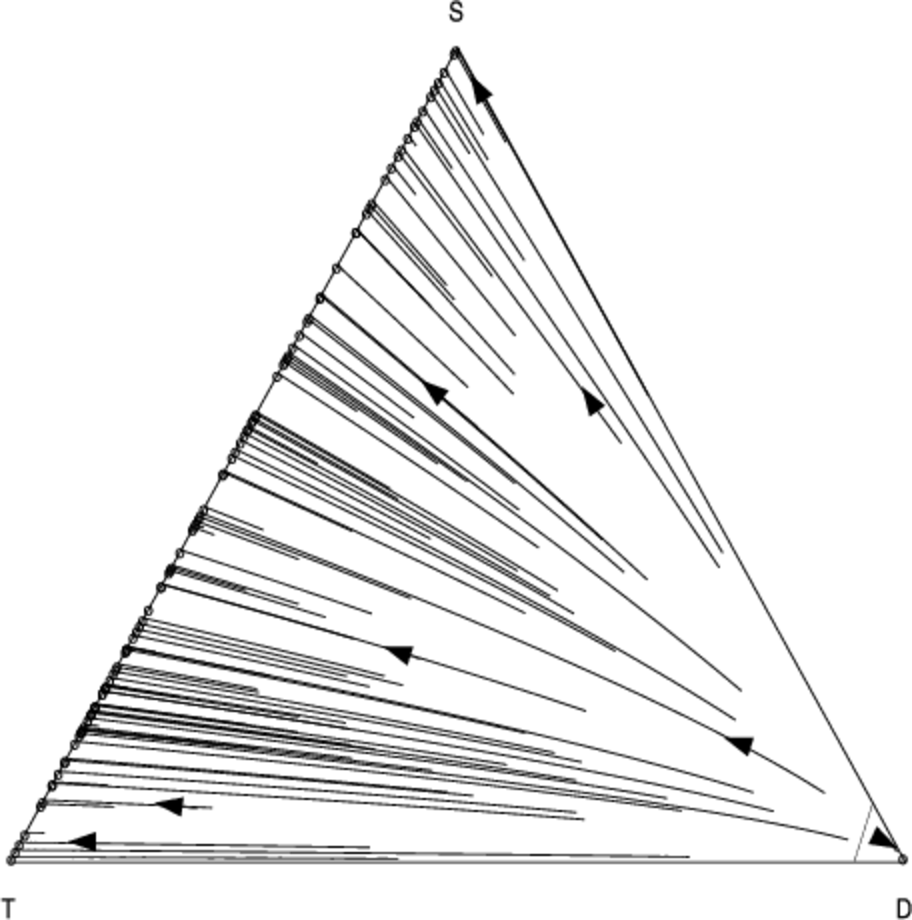
We obtain qualitatively similar results as we increase the number of agents to \(n = 10\) while holding \(N\) fixed — Figures 8 and 9 show how the direction field changes as we move from a smaller (Fig. 8) to a larger (Fig. 9) group. Here defection becomes slightly more stable, and the curvature of the trajectories in the \(T\) direction is slightly less pronounced.

We analyse the equilibrium frequencies of direct versus indirect reciprocity more systematically by including all four strategies in our analysis (\(T\), \(S\), \(C\) and \(D\)), and systematically varying \(N\). Fig. 10 shows our results when we hold the number of agents fixed at \(n = 6\) and systematically vary the number of interactions \(N\). In all cases, the expected frequency of direct reciprocity is intermediate between the level of cooperation and the level of indirect reciprocity.
In the figures below, we show the mean frequency of each strategy in equilibrium as \(N\) is varied from \([5, 50]\) in intervals of 5. This is estimated by randomly sampling \(10^3\) initial conditions and integrating the replicator dynamics equation numerically. The x-axis shows the number of pairwise interactions per generation \(N\) (normalised by \(n\) to allow for comparison between graphs). The error bars show the confidence interval for \(p = 0.05\). C denotes the proportion of unconditional altruists, \(D\) unconditional defectors, \(S\) discriminators and \(T\) the tit-for-tat strategy. The efficiency variable measures the ratio between the total payoff to all agents as compared with the hypothetical scenario where all agents cooperate. Although, the lower multiplier results in less efficient outcomes, both forms of reciprocity remain across all treatments.
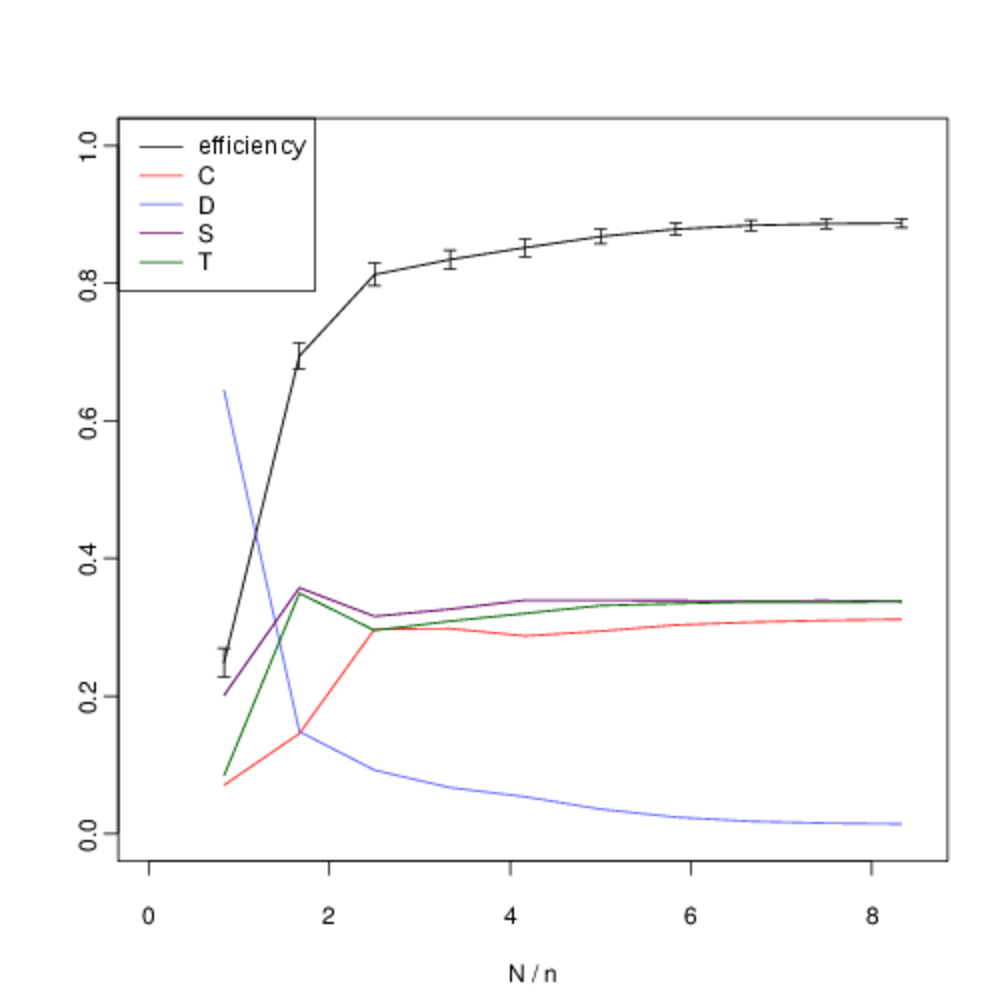
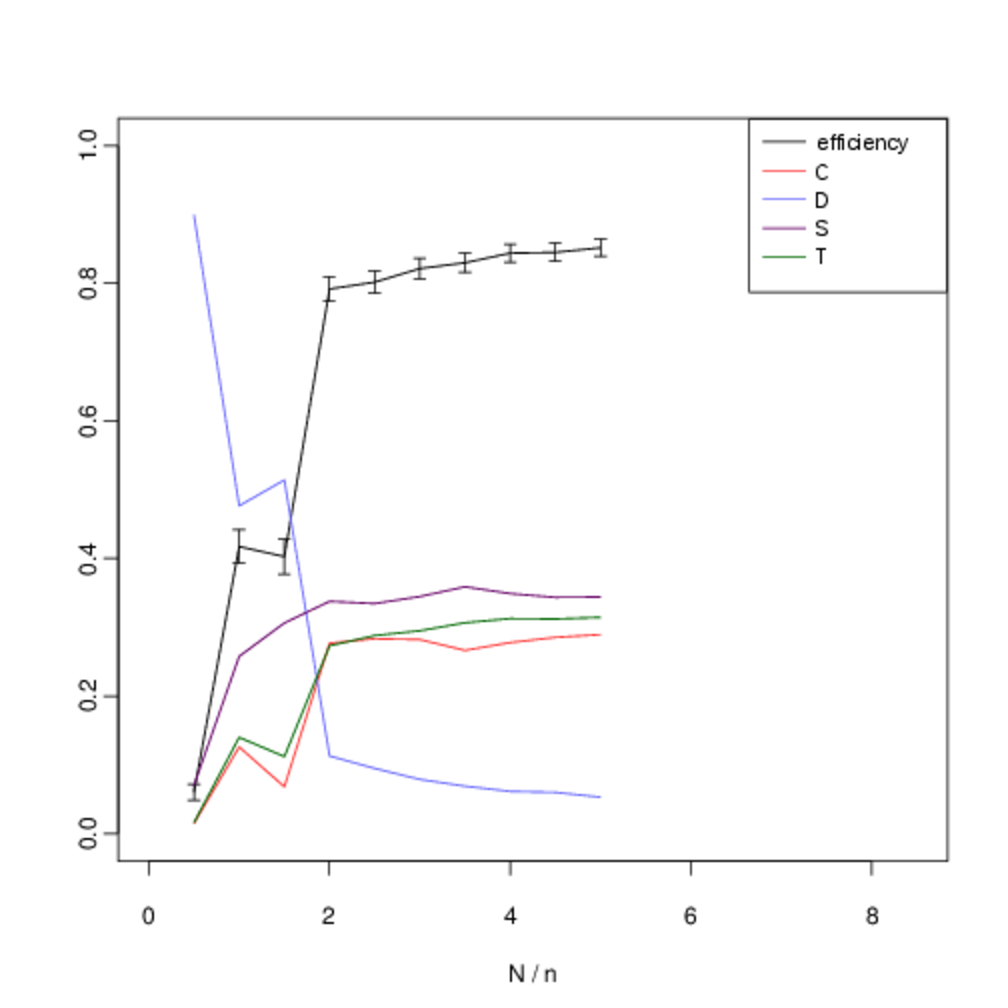
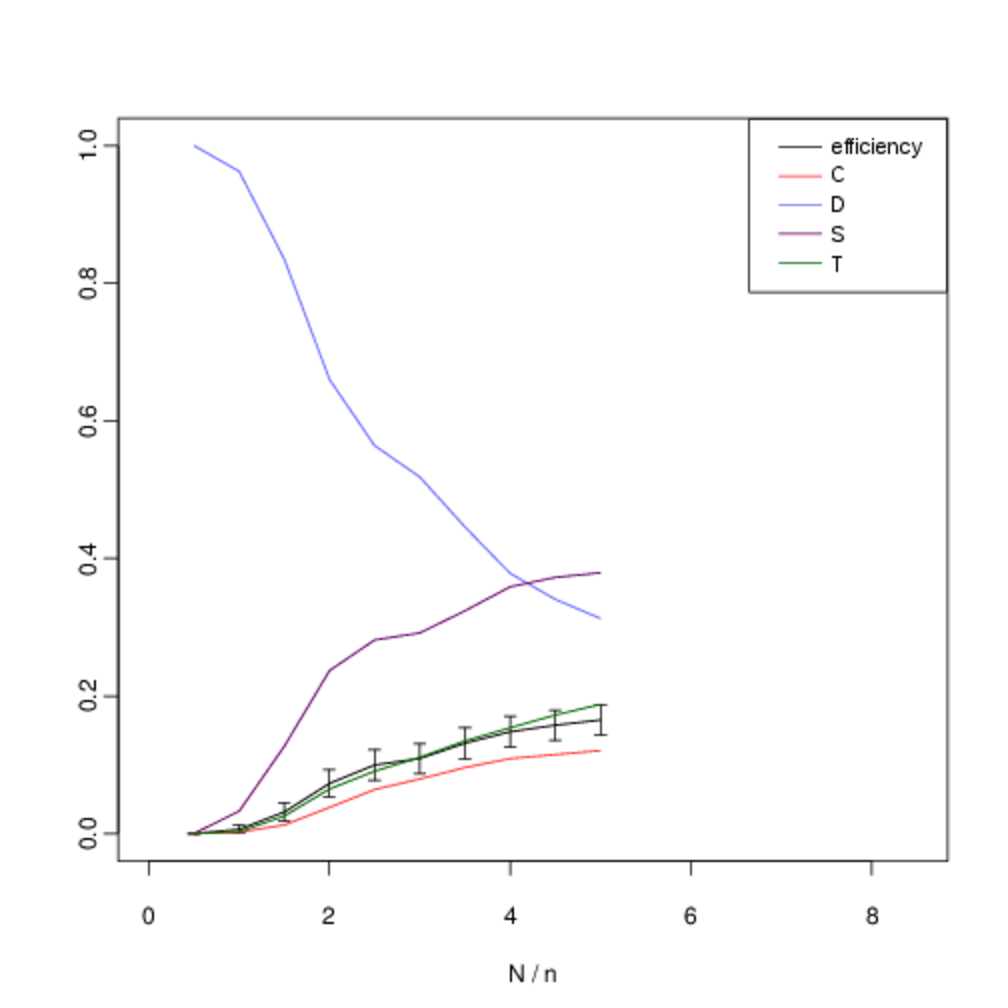
When repeated encounters are rare, \(T\) does not gain useful information and its behaviour, and corresponding frequency, is identical to \(C\). However, as the viscosity of the group increases and we move towards the right on the graph we see that the frequency of direct reciprocity increases as it gains more information. Asymptotically, its frequency approaches that of \(S\). In a well-mixed group both forms of reciprocity are effective in reducing the attractor for all-out defection. As defectors become less prominent, so do the strengths and weaknesses of each form of reciprocity in dealing with them, and their frequencies converge. Thus as the quality information available to direct reciprocity increases with increased interaction, we see direct reciprocity in intermediate frequencies between cooperation and discrimination.
Although there is some overlap in the standard error of the observed frequencies, we are able to reject the two null hypotheses that the frequencies of \(T\) versus \(C\), and T versus \(S\) are identically distributed. Table 6 shows the p-values for each hypothesis. We compare the observed frequency of the tit-for-tat strategy (\(T\)) with that of the cooperate strategy (\(C\)) and the discriminatory strategy (\(S\)) using a two-sample t-test. Intermediate values of \(N/n\) show statistically-significant difference in expected frequencies. For intermediate values of \(N\) there is a statistically-significant difference in the mean frequencies.
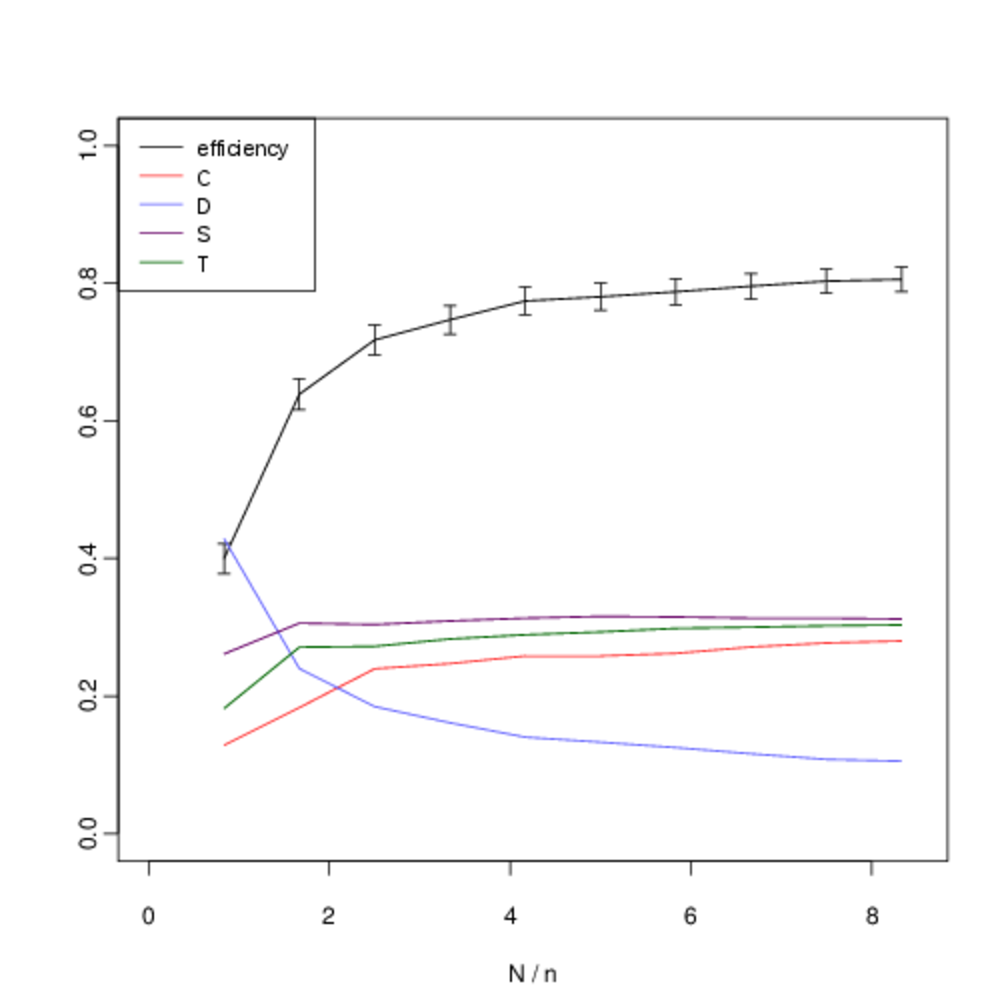
The inflexion in the graph for small values at \(N = 5\) and \(N = 10\) occurs because of noise in the payoffs introduced by the fact that with a small number of interactions not every agent is chosen to interact before reproduction or learning occurs. Nevertheless the persistence of indirect reciprocity at intermediate frequencies between cooperation and discrimination is still robust at this extremity. We obtain similar results when the number of agents is increased to \(n \geq 10\) (Fig. 11).
In the 2-player version of the game the outcome of the social dilemma is the same for all values of the multiplier \(k > 1\), since this defines the ranking in payoffs over the four possible strategy combinations. However, this does not necessarily hold in the extended version of the game, so we must take care to explore the effect of the multiplier. Fig. 13 shows the effect of keeping the number of agents at \(n = 10\), but reducing the multiplier to \(k = 3.5\). Although, as we would intuitively expect, this reduces the level cooperation, we see that both forms of reciprocity continue to persist, and that our central result still holds.
Returning to Figures 6 and 7 we see that each of the stationary points on the edge \( TS \), which represent mixed-strategy equilibria over direct and indirect reciprocity, are the terminations of trajectories which originate in the interior of the simplex, which implies that these are also Nash equilibria. This would suggest that mixed-strategies between direct and indirect reciprocity might be observed under alternative learning dynamics. As discussed in Section 2, the replicator dynamics was originally proposed as a model of genetic evolution but can also be interpreted as a model of social learning in which strategies replicate through imitation. However, when strategies are acquired through social learning it may be difficult for agents to accurately determine their utility (Boyd & Richerson, 1988). In such cases, a useful heuristic to determine the most useful strategies may be to copy the most frequently-occurring variant (Skyrms, 2005; Kendal et al., 2009). This conformist bias can be modelled by introducing a weighting \( \beta \) over the utility \( u(e_i) \) of a strategy \(i\) and its frequency \( x_i \):
| $$u'(e_i, x) = \beta \times x_i + (1 - \beta) \times u(e_i, \bar{x})$$ | (3) |
Conclusion
We have introduced a framework for analysing reciprocity within small groups of varying size. By using simulation and numerical methods we are able to avoid making assumptions contingent on values tending to infinity or zero, while simultaneously retaining the rigour of a game-theoretic analysis.
Our model incorporates both direct and indirect reciprocity, and we showed that for small groups both direct and indirect reciprocity persist in equilibrium, with neither strategy dominating the other. This finding is robust to an alternative model of agents' adaptation based on social learning with conformist bias, and also under low-viscosity conditions which induce noise. In contrast to previous studies, by using the empirical game-theory methodology, we have been able to provide a sound game-theoretic underpinning to our analysis, showing that the results obtained from analytical models are a special case under our analysis. In so doing we have been able to show that our results are not contingent on a restricted set of initial conditions. Moreover, by identifying the existence of mixed-strategy Nash equilibria over direct and indirect reciprocity in a symmetric game of cooperation, we have shown that in settings where interactions with previously-encountered agents are likely, it pays to to use trust in addition to reputation in the design of autonomous agents.
The persistence of both forms of reciprocity occurs as a direct consequence of trade-offs inherent in the type of information each strategy uses; indirect reciprocity can gain useful information about unseen partners, provided that the scoring information is sufficiently accurate to enable selective aid to potential cooperators. However, there is a negative feedback effect as increasing levels of discrimination coupled with the presence of defectors introduce unreliable scores due to the attribution issue. In such circumstances, the information provided by personal experience may be more reliable.
This is particularly relevant in a setting with bounds on rationality, which is representative of many real-world settings; there is much evidence to suggest that human strategic interaction is best explained from the perspective of bounded rationality (Erev & Roth, 1998), and this is even more important in non-human species (Russell et al., 2008; Russell & Phelps, 2013). Our findings are therefore also of relevance to biologists who seek to understand ecological interactions such as allo-grooming in terms of a social dilemma, or a ''biological market'' (Newton-Fisher & Lee, 2011; Henzi & Barrett, 2002; Barrett et al., 1999).
Although there is a great deal of research applying methods for detection of direct reciprocity to such interactions, in both non-human and human societies, our model suggests that both direct and indirect reciprocity may both interact, and thus it may be important to develop methods to additionally detect indirect reciprocity in field data. For example, it is a well-known empirical observation that in directed social-networks from human studies, a link from A to B tends to be reciprocated with a link from B to A; see e.g. Rivera et al. (2010). In certain contexts, this type of dyadic link reciprocation in a social-network might be interpreted as evidence for tit-for-tat-like behaviour, i.e. direct reciprocity in an underlying social-dilemma. However, our model suggests indirect reciprocity should play an equally important role, in which case we should look for triadic patterns, e.g. \(A\) helps \(B\) who helps \(C\) who helps \(A\), or more generally cycles in sub-graphs of size \(n > 2\). There is evidence that such triadic patterns do indeed existing in human social networks (Cross et al., 2001; Rank et al., 2010). In future work, we will use similar studies to quantitatively validate our model.
Acknowledgements
I am grateful to the editor, and the anonymous reviewers whose comments, suggestions and corrections led to a much improved version of this paper. I would also like to thank Andrew Howes, for many discussions and suggestions on these topics, and detailed corrections to earlier drafts of the paper.Notes
- We take the average fitness of every agent adopting the strategy for which we are calculating the payoff, and then also average across simulations.
- Assuming that all points in the simplex are equally likely as initial values.
- Note that in our previous discussion at the end of Section 4, we justified our choice of the scoring strategy on the grounds of its cognitive simplicity and universality in line with the arguments presented in Nowak & Sigmund (2005).
References
ARSIE, A., Savla, K., Member, S., Frazzoli, E.& Member, S. (2009). Efficient Routing Algorithms for Multiple Vehicles With no Explicit Communications. IEEE Transactions on Automatic Control, 54 (10), 2302-2317. [doi:10.1109/TAC.2009.2028954]
AXELROD, R. (1997). The Complexity of Cooperation: Agent-based Models of Competition and Collaboration. Princeton, NJ: Princeton University Press.
AXELROD, R.& Hamilton, >W. D. (1981). The evolution of cooperation. Science, 211 (4489), 1390-1396. [doi:10.1126/science.7466396]
BAIRD, R. W. & Dill, L. M. (1996). Ecological and social determinants of group size in transient killer whales. Behavorial Ecology, 7(4), 408-416. [doi:10.1093/beheco/7.4.408]
BARRETT, L., Henzi, S. P., Weingrill, T., Lycett, J. E.& Hill, R. A. (1999). Market forces predict grooming reciprocity in female baboons. Proceedings of the Royal Society B: Biological Sciences, 266 (1420), 665-665. [doi:10.1098/rspb.1999.0687]
BOERO, R., Bravo, G., Castellani, M.& Squazzoni, F. (2010). Why Bother with What Others Tell You? An Experimental Data-Driven Agent-Based Model. Journal of Artificial Societies and Social Simulation 13 (3), 6: https://www.jasss.org/13/3/6.html. [doi:10.18564/jasss.1620]
BOYD, R.& Richerson, P. J. (1988). Culture and the Evolutionary Process. Chicago: University Of Chicago Press.
BRAVO G. & Tamburino, L. (2008). The Evolution of Trust in Non-Simultaneous Exchange Situations. Rationality and Society, 20 (1), 85-113. [doi:10.1177/1043463107085441]
BULLOCK, S. (1997). Evolutionary Simulation Models: On Their Character, and Application to Problems Concerning the Evolution of Natural Signalling Systems. Thesis (phd), University of Sussex.
CONTE, R.& Paolucci, M. (2002). Reputation in Artificial Societies: Social Beliefs for Social Order. Heidelberg: Springer. [doi:10.1007/978-1-4615-1159-5]
CREMER, J., Melbinger, A. & Frey, E. (2012). Growth dynamics and the evolution of cooperation in microbial populations. Scientific reports 2, 281. [doi:10.1038/srep00281]
CROSS, R., Borgatti, S. P. & Parker, A. (2001). Beyond answers: Dimensions of the advice network. Social Networks, 23 (3), 215-235. [doi:10.1016/S0378-8733(01)00041-7]
DIAMOND, J. (2013). The World Until Yesterday: What Can We Learn from Traditional Societies? New York: Penguin.
DUNBAR, R. (1996). Grooming, Gossip and the Evolution of Language. Faber and Faber.
DUNBAR, R. (1998). The social brain hypothesis. Evolutionary Anthropology, 6, 178-190. [doi:10.1002/(SICI)1520-6505(1998)6:5<178::AID-EVAN5>3.0.CO;2-8]
EREV, I.& Roth, A. E. (1998). Predicting How People Play Games: Reinforcement Learning in Experimental Games with Unique, Mixed Strategy Equilibria. American Economic Review, 88 (4), 848-881.
FADER, P. S.& Hauser, J. R. (1988). Implicit Coalitions in a Generalized Prisoner's Dilemma. Journal of Conflict Resolution, 32 (3), 553-582. [doi:10.1177/0022002788032003008]
FICICI, S. G.& Pollack, J. B. (1998). Challenges in coevolutionary learning: Arms-race dynamics, open-endedness, and mediocre stable states. In: Proceedings of of ALIFE-6.
FICICI, S. G. & Pollack, J. B. (2000). A game-theoretic approach to the simple coevolutionary algorithm. In Schoenauer, et al. (Eds.), Parallel Problem Solving from Nature - PPSN VI 6th International Conference. Paris, France: Springer Verlag. [doi:10.1007/3-540-45356-3_46]
HAYS, R. B. (1985). A longitudinal study of friendship development. Journal of Personality and Social Psychology, 48 (4), 909-924. [doi:10.1037/0022-3514.48.4.909]
HECKATHORN, D. D. (1996). The Dynamics and Dilemmas of Collective Action. American Sociological Review, 61 (2), 250. [doi:10.2307/2096334]
HENZI, S. P.& Barrett, L. (2002). Infants as a commodity in a baboon market. Animal Behaviour, 63, 915-921. [doi:10.1006/anbe.2001.1986]
HILLIS, W. D. (1992). Co-evolving parasites improve simulated evolution as an optimization procedure. In Proceedings of ALIFE-2. Addison Wesley.
KENDAL, J., Giraldeau, L.-A. & Laland, K. (2009). The evolution of social learning rules: payoff-biased and frequency-dependent biased transmission. Journal of theoretical biology, 260 (2), 210-9. [doi:10.1016/j.jtbi.2009.05.029]
KILLINGBACK, T. & Doebeli, M. (1999). 'Raise the stakes' evolves into a defector. Nature, 400 (6744), 518. [doi:10.1038/22913]
KOLLOCK, P. (1998). Social Dilemmas: The Anatomy of Cooperation. Annual Review of Sociology, 24, 183-214. [doi:10.1146/annurev.soc.24.1.183]
KOTZ, S., Balakrishnan, N. & Johnson, N. L. (2000). Continuous Multivariate Distributions, Volume 1, Models and Applications. Hoboken: Wiley, 2nd ed. [doi:10.1002/0471722065]
MILLER, J. H. (1996). The coevolution of automata in the repeated Prisoner's Dilemma. Journal of Economic Behavior and Organization, 29 (1), 87-112. [doi:10.1016/0167-2681(95)00052-6]
NEWTON-FISHER, N. E. & Lee, P. C. (2011). Grooming reciprocity in wild male chimpanzees. Animal Behaviour, 81 (2), 439-446. [doi:10.1016/j.anbehav.2010.11.015]
NOSENZO, D., Quercia, S. & Ssefton, M. (2015). Cooperation in small groups: the effect of group size. Experimental Economics, 18 (1) 4-14. [doi:10.1007/s10683-013-9382-8]
NOWAK, M. A. (2006). Five rules for the evolution of cooperation. Science, 314 (5805), 1560-3. [doi:10.1126/science.1133755]
NOWAK, M. A.& Sigmund, K. (1994). The alternating prisoner's dilemma. Journal of theoretical Biology, 168, 219-226. [doi:10.1006/jtbi.1994.1101]
NOWAK, M. A. & Sigmund, K. (1998a). The dynamics of indirect reciprocity. Journal of Theoretical Biology, 194 (4), 561-574. [doi:10.1006/jtbi.1998.0775]
NOWAK, M. A. & Sigmund, K.(1998b). Evolution of indirect reciprocity by image scoring. Nature, 383, 537-577. [doi:10.1038/31225]
NOWAK, M. A.& Sigmund, K. (2005). Evolution of indirect reciprocity. Nature, 437, 1291-1298. [doi:10.1038/nature04131]
OLSON, M. J. (1965). The Logic of Collective Action: Public Goods and The Theory of Groups. Harvard University Press.
OSTROM, E. (1990). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge University Press. [doi:10.1017/cbo9780511807763]
OSTROM, E. (2000). Collective Action and the Evolution of Social Noms. The Journal of Economic Perspectives, 14 (3), 137-158. [doi:10.1257/jep.14.3.137]
PACKER, C., Scheel, D. & Pusey, A. E. (1990). Why lions form groups: food is not enough. American Naturalist, 136 (1), 1-19. [doi:10.1086/285079]
PHELPS, S. (2011). Source and binaries for image score experiments. http://sourceforge.net/projects/jabm/files/imagescore. Online; accessed 14/12/2011.
PHELPS, S. (2013). Emergence of social networks via direct and indirect reciprocity. Journal of Autonomous Agents and Multiagent Systems, 27 (3), 355-374.
PHELPS, S., Mcburney, P. & Parsons, S. (2010). A Novel Method for Strategy Acquisition and its application to a double-action market game. IEEE Transactions on Systems, Man, and Cybernetics: Part B, 40 (3), 668-674. [doi:10.1109/TSMCB.2009.2034731]
PHELPS, S. & Wooldridge, M. (2013). Game Theory and Evolution. IEEE Intelligent Systems, 28 (4), 76-81. [doi:10.1109/MIS.2013.110]
R CORE TEAM (2013). R: A Language and Environment for Statistical Computing R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org/.
RANK, O. N., Robins, G. L. & Pattison, P. E. (2010). Structural Logic of Intraorganizational Networks. Organization Science, 21 (3), 745-764. [doi:10.1287/orsc.1090.0450]
RIVERA, M. T.,Soderstrom, S. B. & Uzzi, B. (2010). Dynamics of Dyads in Social Networks: Assortative, Relational, and Proximity Mechanisms. Annual Review of Sociology, 36 (1), 91-115. [doi:10.1146/annurev.soc.34.040507.134743]
ROBERTS, G. (2008). Evolution of direct and indirect reciprocity. Proceedings. Biological sciences / The Royal Society, 275 (1631), 173-9. [doi:10.1098/rspb.2007.1134]
ROBERTS, G.& Renwick, J. S. (2003). The development of cooperative relationships: an experiment. Proceedings of the Royal Society, 270, 2279-2283. [doi:10.1098/rspb.2003.2491]
ROBERTS, G.& Sherratt, T. N. (1998). Development of cooperative relationships through increasing investment. Nature, 394, 175-179. [doi:10.1038/28160]
RUSSELL, Y. I., Call, J. & Dunbar, R. I. M. (2008). Image Scoring in Great Apes. Behavioural Processes, 78, 108-111. [doi:10.1016/j.beproc.2007.10.009]
RUSSELL, Y. I.& Phelps, S. (2013). How do you measure pleasure? A discussion about intrinsic costs and benefits in primate allogrooming. Biology and Philosophy, 28 (6), 1005-1020. [doi:10.1007/s10539-013-9372-4]
SANTOS, F. C., Pacheco, J. M. & Lenaerts, T. (2006a). Cooperation Prevails When Individuals Adjust Their Social Ties. PLoS Comput Biol, 2 (10), 1284-1291. [doi:10.1371/journal.pcbi.0020140]
SANTOS, F. C., Rodrigues, J. F. & Pacheco, J. M. (2006b). Graph topology plays a determinant role in the evolution of cooperation. Proceedings of the Royal Society B: Biological Sciences, 273 (1582), 51-55. [doi:10.1098/rspb.2005.3272]
SEINEN, I.& Schram, A. (2006). Social status and group norms: Indirect reciprocity in a repeated helping experiment. European Economic Review, 50 (3), 581-602. [doi:10.1016/j.euroecorev.2004.10.005]
SKYRMS, B. (2005). Dynamics of Conformist Bias. The Monist, 88 (2), 260-269. [doi:10.5840/monist200588213]
SOETAERT, K. & Petzoldt, T. (2011). Solving ODEs, DAEs, DDEs and PDEs in R. Journal of Numerical Analysis, Industrial and Applied Mathematics, 6 (1-2), 51-65: http://jnaiam.org/uploads/jnaiam_6_4.pdf.
TIETENBERG, T. H. (1985). Emissions trading, an exercise in reforming pollution policy. Resources for the Future.
WALSH, W. E., Das, R., Tesauro, G. & Kephart, J. O. (2002). Analyzing complex strategic interactions in multi-agent games. AAAI-02 Workshop on Game Theoretic and Decision Theoretic Agents.
WEDEKIND, C.& Milinski, M. (1996). Human cooperation in the simultaneous and alternating prisoner's dilemma: Pavlov versus generous tit-for-tat. Proceedings of the National Academy of Science USA, 93, 2686-2689. [doi:10.1073/pnas.93.7.2686]
WEDEKIND, C.& Milinski, M. (2000). Cooperation through Image Scoring in Humans. Science, 288 (5467), 850-852. [doi:10.1126/science.288.5467.850]
WEIBULL, J. W. (1997). Evolutionary Game Theory. MIT Press.
WELLMAN, M. P. (2006). Methods for Empirical Game-Theoretic Analysis. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.
