The Role of Homophily in the Emergence of Opinion Controversies

Introduction

In modern society, we observe the emergence of several controversial issues that can challenge the organization of the society. We have less severe issues, like the diffusion of conspiracy theories and more severe issues, like religious fundamentalisms, that can lead to violent attacks and terrorism.

In our society, where the communication patterns are so rapidly changing, understanding how these opinion niches are created and reinforced is a key issue: only a full comprehension of these phenomena can suggest the most suitable communication strategies to control or diffuse some ideas.

Several authors pointed out that a possible responsible of the strong opinion polarization in the society is the particular organization of online social networks (Mousavi & Gu 2014; Flache & Macy 2006), enormously enlarging the social pool where the social actors can look for peers (geographical and demographic barriers are broken down), allowing people to preferentially enter in contact with people sharing very similar ideas and socio-cultural traits. Moreover, the same filtering algorithms used by the social networks, in order to provide personalized information, amplify this effect favoring the membership in coherent groups and the connection between similar opinions. Online social networks amplify the homophily principle, a well-known tendency supported by several studies in social psychology (Lazarsfeld & Merton 1954), defined as the individual tendency to interact preferentially with people perceived as similar. The literature on homophily principle has rapidly developed in the last years, both with theoretical papers (McPherson et al. 2001; Rivera et al. 2010) and with experimental approaches (Munniksma et al. 2015; Stehlé et al. 2011; Stark & Flache 2012).

Several authors propose, therefore, that this mechanism of network formation based on homophily directly generates isolated echo chambers where the information flows remain trapped (Conover et al. 2011; Del Vicario et al. 2015). On the other side, all these papers mostly deal with the observation of the opinion flows at a quite initial stage of the opinion formation process: using microblogging data we can easily observe how an information spreads among the users, but it is difficult to track, on long time scales, if and how single users change their opinions.

In this paper, we investigate the process of opinion formation in an homophilous environment on the long term, using an ad-hoc simulation framework. Agent-based modeling approach is being broadly used in order to capture the emergent phenomena in opinion dynamics, when relevant individual mechanisms, postulated by social psychology theories, are applied to several agents (Castellano et al. 2009; Manzo 2014).

In the context of agent based simulations, several studies on rumor spreading (Apolloni & Gargiulo 2011) and controversies formation mechanisms (Delanoë & Galam 2014) have been published in the last decade, but none of these is focused on the social network structure. The basic research question we want to answer here is "is homophily in social network a possible origin of the strong opinion polarization observed in our society?". Opinion polarization, is defined, in our case, as the emergence of two cohesive opinion groups with radical opinions on a certain subject. Clearly this is not the only possible definition of a so articulated concept. Different definitions of polarization can be found in Bramson et al. (2016). Here, we develop our analysis on three levels, gradually extending the complexity of the model.

First, we focus on the network morphogenesis, where we describe a network generation model, simplifying the implementation proposed in Gargiulo & Mazzoni (2008), where the local rules for peer selection are based on homophily preferences. We show which are the basic topological properties of these network structures and, in particular, that these local rules, based on opinion, automatically generate the emergence of topological communities in the society. This first result is significant by itself since only few existing models are able to reproduce the emergence of the structural partitions that characterize real social networks, using few and essential ingredients.

Second, we investigate the opinion formation processes on networks displaying homophily. In particular, our interest is oriented to the bounded confidence models (Deffuant et al. 2000 and Hegselmann & Krause 2002), agent-based models, allowing to consider at the same time two central mechanisms of the social influence: the tendency toward conformity - explained by social comparison theory (Festinger 1954) and social balance theory (Heider 1946 and 1958) - and confirmation bias - the tendency to filter out informations that is too far from our points of view. In particular, we will consider the Deffuant BC model (DW), where the opinion evolution is based on peer interactions.

Fortunato (2004) has shown that the outcomes of the bounded confidence models are topology independent on static networks. On the contrary, Gargiulo & Huet (2010 and 2012), Apolloni & Gargiulo (2011) and Kozma & Barrat (2008) showed that results can strongly change on (co)-evolving networks. Here, we address the key question about the connection between homophily and opinion polarization (Neumann 2013): Is homophily promoting opinion controversies in the society as evoked, for example, in Conover et al. (2011) and Del Vicario et al. (2015)? We show that, on the stable final configurations, the contrary is true: networking based on homophily promotes consensus, due to the interplay of the dynamics inside and between the community structures.

Third, we add in the simulation framework a further ingredient represented by the traditional media, spreading with a more or less marked pressure, the opinion of the society’s empowerment. To model the media we extend the bounded confidence framework to an asymmetrical interaction between human agents and media, considering that the confirmation bias in the media exposure is a well-documented fact, usually called selective exposure (Iyengar & Hahn 2009). In every society, although the dominant tendencies usually follow the message promoted by dominant institutions (i.e. corporations for mass media, religion and educational institutions) some other less dominant tendencies/opinions always appear. A lot of effort has been devoted in trying to understand the mechanism leading to this evident opinion diversification. A counterintuitive effect, regarding the effect of mass media, has been observed in BC models. It has been shown in several papers (Carletti et al. 2006; Gargiulo et al. 2008 and Pineda & Buendía 2015) that, if the media pressure is low, media are able to attract all the opinions but, on the contrary, oppressive propaganda gives rise to the emergence of opposite extreme opinions both in the Deffuant model (DW) and in the Hegselmann and Krause (HK) model. A similar effect has been also observed in the Axelrod’s model for the dissemination of culture, in González-Avella et al. (2005), Gandica et al. (2011) and in particular more recently in Pulick et al. (2016) where, coherently to our case, the interplay between word-of-mouth and media is considered. This over-exposure phenomenon is well known in marketing studies (Groucutt et al. 2004).

Although all these studies address the research question of the formation of counter-message competing with the dominant mass media, in this work we explicitly focus on the structure of the non-aligned states. Carletti et al. (2006), Gargiulo et al. (2008) and Pineda & Buendía (2015) showed that, when the interaction is constrained by non-homophilous connectivity, the final outcome of the model, for high media pressure, is a strong cluster aligned with the media and a large number of unclustered opponent opinions. A second cohesive counter opinion cluster cannot be formed in BC models over regular complex networks. Here we show that, on the contrary, the presence of homophily in social networks over a media dominated system, plays a central role in the recomposition of a strong opponent cluster, leading to the final polarization of the opinions. At the same time, we show that homophilous system are more robust to media propaganda, allowing the formation of counter-clusters also for lower values of the media pressure.

Differently by the co-evolution frameworks (Gargiulo & Huet 2010 ; Gargiulo & Huet 2012; Apolloni & Gargiulo 2011; Kozma & Barrat 2008) where opinions are updated together with the network structure, in this paper we consider that network morphogenesis and opinion dynamics take place at different time scales. The formation of social network is a slow process and, in this case, the opinion on which we base the homophily choices is an abstract representation of a global vision of the world. Opinion dynamics processes represent the formation of a global opinion on a concrete subject (a new law, a referendum, a piece of news, etc). These processes have a fast dynamics that do not allow networks to coherently reshape. In this case, what we define opinion is the particular judgement that an individual, with a certain vision of the world, has on this subject. In this sense, the representation of the opinion in these processes is a sort of local characterization of the opinion on which network morphogenesis is based.

The paper is organized as follows: In Section 2, we present the network morphogenesis model and the topological properties of the obtained networks. In Section 3, we present the opinion evolution on homophily-based networks. In Section 4, we show the combined effect of media propaganda and homophily. Conclusions are presented in Section 5.

The network morphogenesis

The Model

We first propose a growing network model allowing to fine tune the homophily level. The growing network approach for network morphogenesis is a dynamical process where at each time step new nodes and new links enter the network and/or old links are canceled or rewired. We will consider the simplest case where at each time step a single node is added to the network with a set of associated links to the pre-existing nodes.

The probability that the new node \(N\) gets connected to the pre-existing node \(i\), \(\Pi_{N\rightarrow i}\sim \phi_N(i)\) contains the selected mechanism for network growth. The fitness function \(\varphi_N(i)\), associated to each pre-existing node, represents how attractive is a pre-existing node \(i\), for the new node \(N\), to establish a link.

It is well known that a fitness function based on the degree (\(k_i\)) of the pre-existing nodes \(\varphi_N(i)= k_i\), namely a situation where a node with a large connectivity (measured as its degree) has a larger chance to attract new links, gives the preferential attachment mechanism generating scale free networks with a power law degree distribution, hereby named BA-networks (Barabasi & Albert 2007).

Implementing a fitness function based on the degree is motivated by the larger visibility that highly connected nodes have: more friends I have, more probable is that I am present in different social circles and more probable is to meet new friends. Moreover, this is one of the mechanism on which friendship recommendations in online social networks are based.

To include homophily in the morphogenesis without forgetting the connectivity issue, in our setup, we construct the fitness function \(\varphi_N(i)\) so that the new node has a preference to get connected both to high degree nodes and with nodes with similar opinion:

$$\varphi_N(i)= k_i \exp (- \beta | \theta_N - \theta_i| )$$

(1)

where \(k_i\) is the degree of the ancient node \(i\), \(\theta_i\) its opinion, \(\theta_N\) the opinion of the new node and a coefficient tuning the homophily effect.

Let us note that when \(\beta\) = 0 the growing mechanism follows the classical preferential attachment, leading to the usual Barabasi-Albert network, with power-law degree distribution \(P(k)\sim k^{-3}\). When \(\beta \neq 0\) the homophily comes into play and a competition between the preferential degree attachment and the opinion similarity takes place. In the limit \(\beta \rightarrow \infty\) only homophily matters.

The model follows the following steps:

• Each node is initialized with an opinion randomly selected in a continuous interval between \(\theta_i\in [-1,1]\).
• The network generation process starts from an initial fully connected structure with \(N_{ini}\)=5.
• At each step a new agent, \(N\), enters in the network
• The new agent \(N\) gets connected to m pre-existing agents (\(m\) new links) using a roulette-wheel selection process (or fitness proportional selection), based on the probabilities:

  $$\Pi_{N\rightarrow i}=\frac{\varphi_N(i)}{\sum_{i=0}^N\varphi_N(i)}$$

  (2)

  Note that the parameter \(m\), namely the number of new links added to each new node has no influence on the global properties of the network (like degree distribution, clustering, mixing, etc.). This parameter defines the minimum degree of the network and the total number of edges.

In the appendix (Fig. 6), we report the the Python implementation of the algorithm for the network morphogenesis.

Results

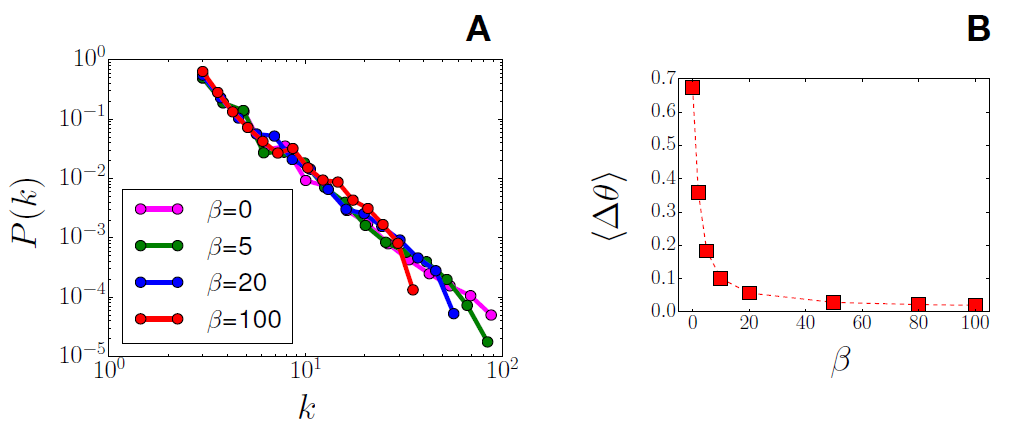
Due to the presence of the connectivity in the fitness function \(\varphi_N(i)\) (Eq.1), the final degrees of the network are distributed for a large range, as in the original BA model (\(\beta\) =0), on a power law distribution. Increasing, the homophily mechanism leads to a cutoff in the distribution, decreasing the maximum value of degree (Fig. 1-A).

In Fig. 1-B, we show the average opinion distance between connected nodes. The opinion similarity between connected nodes increases extremely fast as the homophily parameter \(\beta\) is switched on.

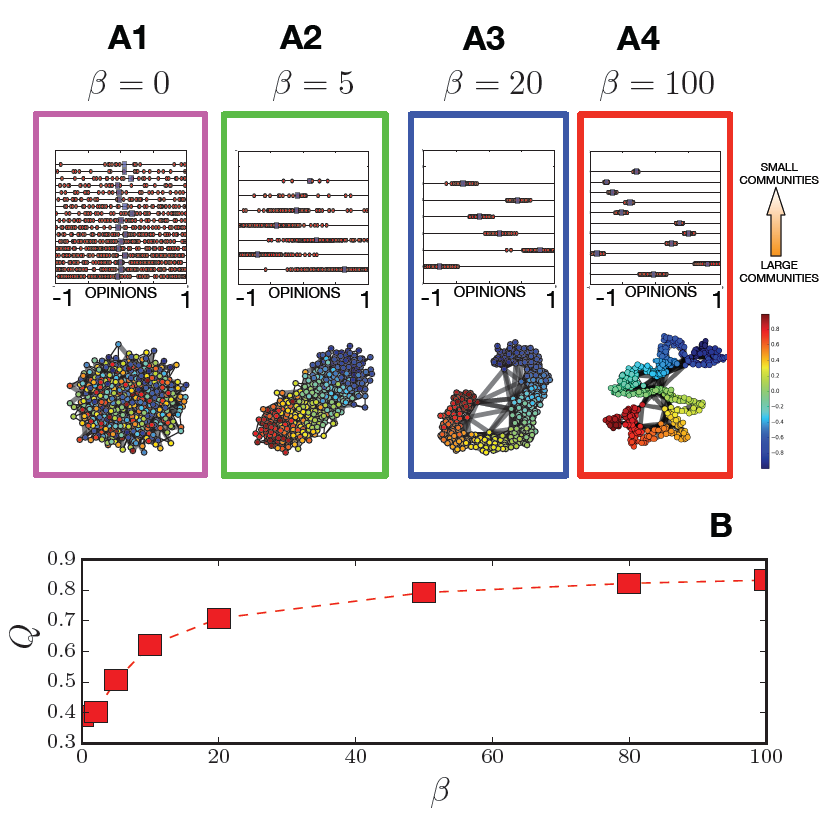
The results obtained in Fig. 1 are the direct consequence of the preference function structure. A more relevant emergent property can be observed in Fig. 2: networks with high homophily exhibit meaningful community structure. Topological communities are groups of nodes that are more strongly connected among them than with the rest of the network. Note, however, that there is a strong difference between community structures and network disconnected components: communities are largely connected among them but links exist also between the communities, connected components are totally disconnected among them. Several real network structures present signature of these properties - citation networks, mobility networks, social networks, semantic networks (Newman 2012). At the same time few network morphogenesis models are able to reproduce these patterns (Bianconi et al. 2014).

Several algorithms exist to identify community structures (for a review see for example Fortunato 2010). In the following, we used the Louvain algorithm (Blondel et al. 2008), http://perso.crans.org/aynaud/communities/.

The goodness of a partition is measured by the modularity (\(Q\)), a function comparing the concentration of edges within communities, in the network, with a rewired network with a random distribution of links (obtained with the configuration model). Large values of the modularity (\(Q\rightarrow 1\)) signify that the community structure is highly significant, namely the fraction of links within the community largely exceed the fraction of links between the same nodes in a random configuration. For a mathematical definition of the modularity see (Newman 2006).

The best partition is the configuration that maximize modularity. At the same time, if the community structure is not a significant marker of a network, modularity remains low also for the best partition. In Fig. 2 we display the modularity measure for the best partition of the network, as a function of the homophily parameter \(\beta\). Modularity monotonically increases with \(\beta\), implying that the presence of communities is a natural emergent effect of the homophily preference in network morphogenesis.

In the lower plots A1-4 of Fig. 2, we present a network visualization for different values of the homophily parameter. The used visualization layout (based on a force algorithm) has a repulsive force to push away disconnected nodes and a spring-like force attracting connected node. The result of this visualization algorithm is the spatial separation of the network communities: when the community structure is significant few connections (represented by the large black lines in the plot) exist between the communities that will be therefore pushed away among them, while the large number of links inside the communities will spatially group the nodes of the same community. We can observe that for the BA network (\(\beta=0\)) communities are not visible, while a more and more structured shape appear as homophily is switched on. Note that the communities are largely uniform in term of opinion. At the same time, links exist between all the communities. This factor is central for understanding the opinion propagation dynamics that will be described in the next section.

In the upper plots A1-4 of Fig. 2, we show the agents opinions inside each community. Each line in the plots represents a community, ranked from the largest (on the bottom) to the smaller (on the top). We observe that for the BA network the opinions are randomly distributed in all the communities and the average opinions of the communities coincide with the center of the opinion interval. When the homophily is present the communities specialize: their average opinion moves from the center. Largest it the value of \(\beta\) smaller is the dispersion of the opinions around the average opinion of the community.

In all our experiments, the initial opinion has been initialized according to a uniform distribution. We tested that the aggregated results we presented in Fig. 1 and Fig. 2B are robust to a changing in the simulation paradigm: before fixing the same opinion vector and after building different networks on these opinions. Note that using different distributions for the initialization (like i.e. a Gaussian) could change the final outcome of the process. Exploring this issue is out from the scopes of this paper (addressed mostly to understand the relationship between homophily and opinion propagation) and we leave this direction open for subsequent studies.

Central result:

Homophily as ingredient for network morphogenesis leads to networks where the community structure is a fundamental marker.

Opinion dynamics

The model

In the previous section, we described a morphogenesis algorithm to build network structures based on homophily. In this section, we will show how this network structure influences opinion dynamics processes.

Several different mechanisms can drive opinion formation. In peer interactions, two main factors have been observed as fundamental forces for mutual influence. The first one is conformity, a mechanism due to the psychological need to reduce conflict among peers that consists in the reduction of opinion distances after an opinion exchange. The second one is the confirmation bias, i.e., the selective filtering of opinions too far from ours. A well-known model taking into account both these mechanisms is the bounded confidence (BC) model (Deffuant et al. 2000). This model depends on a tolerance parameter \(\epsilon\) tuning the importance of confirmation bias. According to this model, once two agents (\(i; j\)) are selected as peers for an interactions, they will update their opinion using the following threshold rule:

$$if |\theta_i-\theta_j|<2\varepsilon\Rightarrow\begin{cases} \theta_i=\theta_i+\mu (\theta_j-\theta_i)\\ \theta_j=\theta_j+\mu (\theta_i-\theta_j) \end{cases}$$

(3)

If the velocity parameter is \(\mu\) = 1/2, as it is usually fixed, the two opinions will converge to their average. Note that we use the bound parameter 2\(\epsilon\) to be consistent with the previous works on BC. Indeed in Deffuant et al. (2000) and other papers (i.e., Fortunato 2004) on the BC model the opinion interval is in [0; 1] while in our case it is [-1; 1]. Therefore, to compare the threshold values with the ones found in the literature, we need to double the tolerance parameter.

The Python implementation of the function for a single interaction with the BC model is presented in the appendix in Fig. 7.

It is well known that, independently from the choice of the parameter the repeated application of this rule, on random pairs of peers in a fully connected population, drives to two possible scenarios: total consensus, where all the opinions converge to the initial opinion average, for \(\epsilon\) < 0.5 and opinion clustering, where two or more opinions coexist, for \(\epsilon\) < 0.5 (Lorenz 2007).

In the original description of the BC model (Deffuant et al. 2000), all the agents can interact with all the others. This complete mixing assumption can be quite unrealistic when we consider a large number of agents that cannot be in contact with anyone else in the society. People can interact and exchange opinions only with the peers that they meet in their everyday life (online or o line), namely with the neighbors in their social network. A second important step, after Deffuant et al. (2000), is therefore to constrain the peer selection only to couples of nodes connected by a link in a network structure.

Fortunato (2004) showed that the same scenarios and the same transition threshold to consensus \(\varepsilon_c\) = 0.5 is observed if the peers are selected only between the edges of a more static complex network structure (random graphs, small world networks, scale free networks). On the other side, Kozma & Barrat ( 2008), Gargiulo & Huet (2010) and Gargiulo & Huet (2012) showed that the consensus threshold can change on dynamical networks, once some rewiring based on nodes’ opinion can take place.

In the following, we will study how the parameter \(\beta\), tuning the homophily level in networks, can influence the outcome of the BC model. Namely we will address the question: Does a larger homophily in the network structure implies the formation of opinion bubbles?

The model evolves according to the following steps (see Fig. 8 in the appendix for a Python implementation):

• A random uniform opinion distribution and a network structure (with \(N\) nodes and with a \(\beta\) parameter) are created.
• At each time step \(N\), couples of neighboring nodes (connected by a link of the network) are selected and a pairwise interaction with BC model is performed (asynchronous update).
• The loop is halted when, on all the edges no more successful interactions are possible \(|\theta_i-\theta_j|>2\varepsilon\) or \(|\theta_i-\theta_j|=0\).

Results

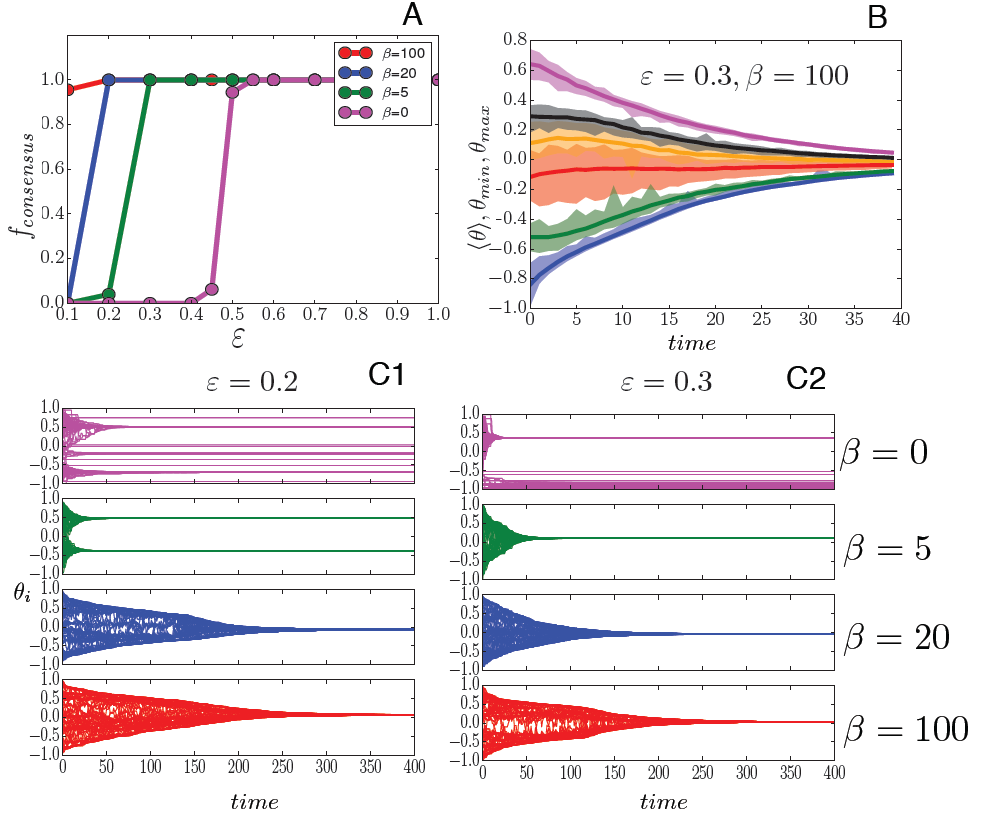
In Fig. 3, we show that the answer to the question "Does a larger homophily in the network structure implies the formation of opinion bubbles?", is clearly negative and that, on the opposite, a large homophily reduce the existence of radical issues.

In Fig. 3A, we plot the fraction of replicas ending up to consensus for different values of the homophily parameter. For = 0 (Barabasi-Albert network), we observe the transition at \(\varepsilon_c\)= 0.5 predicted in Fortunato (2004). However, for higher values of \(\beta\) we observe that the transition threshold becomes smaller and smaller (\(\lim_{\beta\rightarrow\infty}\varepsilon_c(\beta)=0\)), meaning that the system will always end up at consensus.

Fig. 3C shows how it happens. Remember that the system can evolve until on some links of the social network the agents connected by the link have two different opinions at a distance smaller than the tolerance. Now when on all the links, agents have the same opinion or their opinion difference is larger than 2, whatever pair is selected for the opinion dynamics, opinions will not change anymore.

For low values of \(\beta\), the system gets frozen at a very initial phase. After few iterations, agents cannot find in their neighborhood any peers with whom having "positive exchanges" (for all the couples \(|\theta_i-\theta_j|\geq 2\varepsilon\)). The agents with a moderate opinion rapidly converge forming a major cluster (located around the average opinion of the system \(\langle\theta\rangle=0\)). Larger is \(\epsilon\), larger is the central cluster size. Since the link construction is independent by the opinion, there is therefore a large probability that the radical agents are connected with agents in the majoritarian cluster (positioned at an opinion distance larger than 2\(\epsilon\) from their actual opinion) and not among them. The radical agents remain therefore isolated, keeping their initial opinion.

For larger values of the homophily, the dynamics is slower, but much more "inclusive". Since radicals agents are now mostly connected with similar, they do not remain isolated. Agents always find peers with an opinion sufficiently near to interact, and therefore their opinions change gradually at each interaction.

As we can observe in Fig. 3B (where each color represents the opinion span in each community), the dynamics happens at two levels: a rapid convergence inside the communities and a slower one between the communities. The large number of links inside the communities allow the fast convergence to the average opinion of the communities, at the same time the links between the communities (in their turn connecting communities with similar average opinions) allow a slow dynamics of the average opinions of the communities, toward consensus. To use a visual conceptualization, the homophily structure, provides a sort of continuous path allowing the radical opinions to join the central ones.

Central result:

In a situation where opinions evolve in time, homophily in social networks favors consensus formation. Therefore, contrarily to the common idea that online social networks are directly responsible for the installation of sever opinion wars in the society, we can argue that, on larger time scales, homophily acts stopping the propagation of radical issues. This process happens through the grouping of radical opinions in substantial clusters allowing the dialogue between extreme radicals and more moderates ones. This issue allows the creation of a community sense around the radicals that prevents the dangerous situation of single individuals remaining isolated and exposed to the tendency toward solipsistic radical actions. At the same time, looking to this result from another perspective, a possible consequence of homophily is the reduction of opinion diversity in the society (opinion convergence to consensus).

Opinion dynamics in the presence of dominant media

In this section, we add a further ingredient in the system: the presence of an external media, diffusing with a certain pressure \(p_m\) a constant opinion \(\theta_M\).

In several previous papers it has been observed, in the context of BC models, that the dominant media lose their capacity to attract people opinion, (i.e., the effectiveness of propaganda) after a certain pressure threshold. In Pineda & Buendía (2015), the external media pressure has been modeled as a heterogeneous open mindedness distribution and some interesting particularities are reported, due to the specific conditions considered. In Carletti et al. (2006), the mass media has been modeled as a periodic perturbation. In this paper, the authors divided the systems response into four regimes, where the efficiency of the message is explained in terms of the people open-mindedness threshold, \(\epsilon\), and the period of the message. In this work, the authors stress the importance of the collapse into clusters before the exposure to propaganda, given the influential role that community structures can develops to profile the opinions around a message. This phenomenon is a natural connection with our work, where the effect of the dominant message faces a strong community interaction.

Opinion dynamics with media is an asymmetrical opinion update, meaning that, after an agent interacts with media, she can change her opinion, while the opinion of the media (\(\theta_M\)) will remain identical. We extend to this asymmetrical framework the structure of the BC model:

$$if |\theta_i-\theta_M|<2\varepsilon\Rightarrow\begin{cases} \theta_i=\theta_i+\mu (\theta_M-\theta_i)\\ \theta_M=\theta_M\end{cases}$$

(4)

In the following, we will fix \(\mu\)=0.5, as in the previous case, and the opinion of the media, \(\theta_M\)=1. The Python function defining this asymmetrical opinion update is described in Fig. 8 in the appendix.

To analyze the effect, we introduce a parameter \(p_m\) representing the exposure to dominant media messages. If \(p_m\) = 0 the agents have no probability to interact with the media, while if \(p_m\) = 1 the agents will interact only with the media.

The model evolves according to the following steps (for a Python implementation see Fig. 10 in the appendix):

• A random uniform opinion distribution and a network structure (with \(N\) nodes and with a \(\beta\) parameter) are created.
• At each time step, for \(N\) times, an agent \(i\) and a real number in the interval \(r\in\) [0; 1] are randomly extracted.
• If \(r < p_m\) : agent \(i\) makes opinion dynamics with the media according to Eq. 4.
• If \(r ≥ p_m\): a second agent \(j\) is selected and an opinion dynamics update according to Eq.3 is performed on the pair (\(i, j\)).
• The loop is halted when, on all the edges no more successful interactions are possible (\(|\theta_i-\theta_j|\geq2\varepsilon\) or \(|\theta_i-\theta_j|=0\)).

In order to compare the same scenarios according to the unforced opinion dynamics, first we will consider the case \(\epsilon\) = 0.5 where, without forcing, consensus is obtained both for homophilous (\(\beta\) = 30) and non-homophilous (\(\beta\) = 0) situations. In a second step, we will extend these results to a larger spectrum of values for the tolerance threshold.

Results

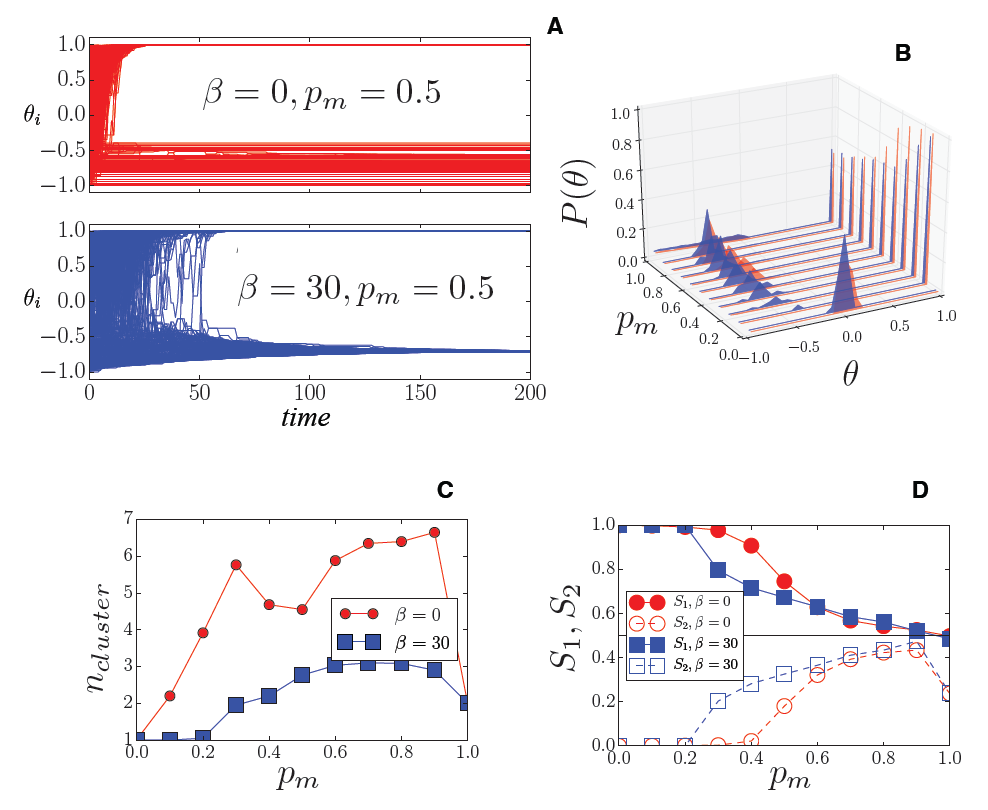
Our results are reported in Fig. 4. In Fig. 4A, we show the result of the evolution of a single replica in the case where the media pressure is fixed to \(p_m\) = 0.5. When agents are highly affected by mass-media, like in this case (\(p_m\) = 0.5), several opinions remains in opposition to the dominant message. This effect has been observed over BC models in all the previously cited papers (Pineda & Buendía 2015; Carletti et al. 2006; Gargiulo et al. 2008) as well as in the Axelrod model (Gandica et al. 2011).

Note, however, that when homophily is not present in the social network (see Fig. 4A), these counter-messages remain a non-homogeneous set of separate opinions (the parallel red lines in the Figure) because the agents carrying these opinions are not connected by the social network and therefore cannot interact among them. The presence of homophily in the social network makes more probable that individuals with radical opinions opposing to the media cluster are connected among them by the social network. The interactions between these radical agents are therefore possible allowing the recomposition of a secondary composite opinion counter-cluster (the final blue state in the Figure), describing a real situation of opinion polarization.

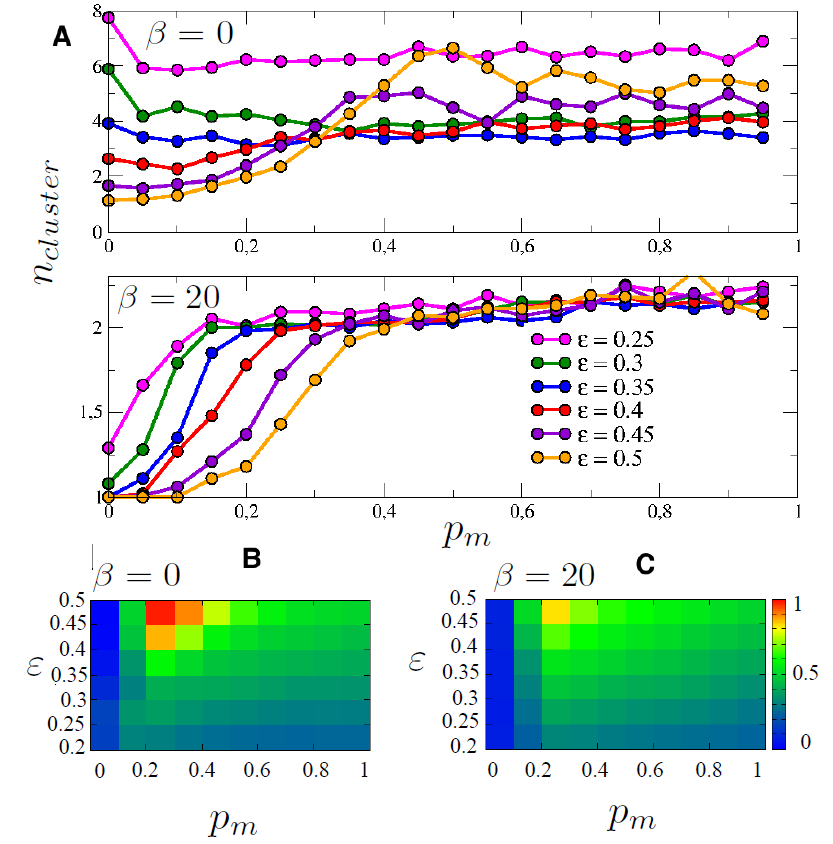
In the following, we analyze this effect more deeply as the result of aggregate replicas of the model and for various values of the media pressure parameter \(p_m\). Fig. 4B shows the probability density function for the final states in terms of mass-media intensity. The red shapes represent the case for \(\beta\) = 0, the blue shapes represent the case for \(\beta\) = 30, where homophily strongly influence the network structure. Fig. 4C and D show respectively the number of opinion clusters and the size of the two largest clusters as a function of the media pressure, \(p_m\).

In general, we observe that the alignment of all the agents to the mass media state (an unique opinion cluster at \(\theta\) = \(\theta_M\)) occurs, counterintuitively, only for low values of the media intensity, as previously found in several works, and explained in the introduction. This happens because the fast drift toward media opinion leaves several isolated agents that cannot find a peer to interact with. For networks without homophily, the threshold value for the mass-media to have this self-defeating effect is around \(p_m\) = 0.4, when some very small non-aligned states start to appear Fig. 4C and become macroscopic Fig. 4D. A first effect of the presence of homophily in network morphogenesis is the lowering of the threshold for the media to be effective. In the case where homophily is present we observe the formation of counter messages (and the decrease of the size of the cluster aligned with the media) already for \(p_m\) = 0.2 Fig. 4B.

At the same time, if we look at the blue plots in Fig. 4B, for high values of \(p_m\), it is clear how the homophily-based networking structures the non-aligned states around one powerful cluster (as we observed for the single replica plot in Fig. 4A). The fact that the cluster has a larger amplitude than the single peak observed in Fig. 4A is due to the statistical fluctuations of the position of the second cluster among the different replicas of the system (for each replica the single cluster observed in Fig. 4A has a different position), but we can observe, as well, that the final opinions are much less sparse than in the case without homophily. This effect can be better observed in Fig. 4C and D. The community structure resulting from the homophily effect during the network morphogenesis, re-organizes all the small non-aligned states into a macroscopic one, competing with the dominant message: for the homophilous case, for \(p_m\) ≥ 0.4 the size of the second cluster is much larger while the number of cluster is much smaller. At the same time, we can observe a relevant reduction of the size of the dominant cluster (aligned to the media).

In Fig. 5, we extend the analysis to other values of the tolerance threshold \(\epsilon\). Note however that in these cases the output of the model is a priori different already at the level of the opinion dynamics without media. The number of clusters (in upper panel) and the fraction of agents aligned with the external mass-media (in the bottom panel) are shown, varying the media pressure pm but also for several values of tolerance.

This global picture first shows that, as in the case where media are not present, when the tolerance is low more clusters are formed 5A. This effect is more pronounced for the case where community structures is not present (\(\beta\) = 0). In this case the effect of the media pressure on the number of clusters is remarkable only for high values of the tolerance (\(\epsilon\) > 0.4), when high values of the media pressure produce the increase of the number of opinion clusters.

When community structures is present (\(\beta\) = 20), the basic scenario of the loss of control by the strong mass media exposure, takes a different shape: First we can observe that the tuning of media pressure has the general role of creating, when a media pressure threshold is reached, a general bi-polarized configuration as previously described for the \(\epsilon\) = 0.5 case.

In Fig. 5B-C, we display the fraction of agents aligned with the media opinion \(\theta_M\). For both the network topologies (non homophilous, Fig. 5B, and homophilous, Fig. 5C), lower values of tolerance create a stronger resistance to the dominant media independently from its pressure. At same time, we observe that the maximum power of attraction of the mass media is obtained around \(p_m\) = 0.2 and it monotonically decreases as the media pressure increases. However, Fig. 5C shows that as a consequence of the community structures, when homophily is present, this maximum value no longer reaches all the population. Therefore, in this case, the large mass of the counter-cluster is able to subtract support to the media.

Central result:

In general, independently of the network topology, the media messages are less effective if the media pressure is too high. In the case where homophily is present in the network structure, the threshold where the media become ineffective is lower, showing that these structures are more resistant to propaganda. Furthermore, the community structures resulting from the homophily-based networking, when facing a dominant message, aggregate the non-aligned states into just one second strong opinion counter-cluster, decreasing the size of dominant one.

Conclusions

In this work, three related subjects have been addressed. First, we showed how a network morphogenesis model, including at the same time the preferential attachment mechanism and a homophily effect, can structure networks with the same power-law degree distribution as the BA networks, but with marked communities of nodes sharing similar opinions.

Second, the bounded confidence model has been used on such topology showing that, contrary to established ideas, homophily in social networks favors consensus formation: we show that the critical value of tolerance (\(\epsilon_c\) = 0.5), previously reported as the threshold for BC models to shift between total consensus and different opinions, loses its "universal" character when considered in more realistic networks, as the ones formed with community structures. In the case where homophily is present consensus is reached also for lower values of the tolerance parameter (less open-minded societies).

Finally, the effect of mass media over the BC models with homophily scale-free networks has been reported. We showed that homophily has a double effect: first, it decreases the effectiveness of the media pressure, facilitating the emergence of counter opinions also for lower values of the media pressure. On the other hand, we showed that, when the community structures (typical of homophily-based networks) face dominant messages, disaggregated non-aligned states converge into just one (or few) strong counter-opinion cluster, representing a strong polarization of the opinions in the societies. Moreover, the strong polarization against the dominant message is promoted by low values of tolerances.

Social networks and social media are nowadays the backbone of the diffusion of controversial subjects. Using data analytics tools (to personalize the advertisements) and new tools of the digital economy like the click-farms (to increase visibility to a content), new debates, often deviant from the dominant vision of the state authorities, spread everyday on the web. In several cases, when these debates, can trigger risky behaviors, the authorities answer with strong media campaigns (think for example to the case of vaccines).

According to our findings, these risky opinions would be naturally controlled, on long time scale. If the subject is too risky and an immediate response is needed, media campaigns are probably the worst method. Probably the best solution would be to use the same social networks to propagate the counter-messages.

A first further direction of analysis concerns this last point: if traditional media apparently have lost their centrality in the communication, how counter-messages to prevent risky behaviors should be conveyed? A second point is the role of the click-market on the opinion formation. How do the new instruments to capture users’ attention differ from tradition media? Is the click economy responsible for the fact that opinions that once were considered deviant are now dominating?

References

APOLLONI, A. & Gargiulo, F. (2011). Diffusion processes through social groups’ dynamics. Advances in Complex Systems, 14(02), 151–167 [doi:10.1142/S0219525911003037]

BARABASI, L. & Albert, R. (2007). Statistical mechanics of complex network. Reviews of Modern Physics, 7, 47–97

BIANCONI, G., Darst, R. K., Iacovacci, J. & Fortunato, S. (2014). Triadic closure as a basic generating mechanism of communities in complex networks. Physical Review E, 90(4), 042806 [doi:10.1103/PhysRevE.90.042806]

BLONDEL, V. D., Guillaume, J.L., Lambiotte, R. & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008(10), P10008 [doi:10.1088/1742-5468/2008/10/P10008]

BRAMSON, A., Grim, P., Singer, D. J., Fisher, S., Berger, W., Sack, G. & Flocken, C. (2016). Disambiguation of social polarization concepts and measures. The Journal of Mathematical Sociology, 40(2), 80–111 [doi:10.1080/0022250X.2016.1147443]

CARLETTI, T., Fanelli, D., Grolli, S. & Guarino, A. (2006). How to make an efficient propaganda. Europhysics Letters, 74(2), 222–228 [doi:10.1209/epl/i2005-10536-9]

CASTELLANO, C., Fortunato, S. & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of modern physics, 81(2), 591 [doi:10.1103/RevModPhys.81.591]

CONOVER, M., Ratkiewicz, J., Francisco, M. R., Gonçalves, B., Menczer, F. & Flammini, A. (2011). Political polarization on twitter. ICWSM, 133, 89–96

DEFFUANT, G., Neau, D., Amblard, F. & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(1), 87–98 [doi:10.1142/S0219525900000078]

DEL VICARIO, M., Bessi, A., Zollo, F., Petroni, F., Scala, A., Caldarelli, G., Stanley, H. E. & Quattrociocchi, W. (2015). Echo chambers in the age of misinformation. arXiv preprint arXiv:1509.00189 .

DELAONË, A. & Galam, S. (2014). Modeling a controversy in the press: The case of abnormal bee deaths. Physica A: Statistical Mechanics and its Applications, 402, 93–103 [doi:10.1016/j.physa.2014.01.054]

FESTINGER, L. (1954). A theory of social comparison processes. Human relations, 7(2), 117–140 [doi:10.1177/001872675400700202]

FLACHE, A. & Macy, M. W. (2006). Why more contact may increase cultural polarization. arXiv preprint physics/0604196.

FORTUNATO, S. (2004). Universality of the threshold for complete consensus for the opinion dynamics of Deffuant et al. International Journal of Modern Physic C, 15(09), 1301–7 [doi:10.1142/S0129183104006728]

FORTUNATO, S. (2010). Community detection in graph. Physics Reports, 486(3), 75–174 [doi:10.1016/j.physrep.2009.11.002]

GANDICA, Y., Charmell, A., Villegas-Febres, J. & Bonalde, I. (2011). Cluster-size entropy in the axelrod model of social influence: Small-world networks and mass media. Physical Review E, 84(046109) [doi:10.1103/physreve.84.046109]

GARGIULO, F. & Huet, S. (2010). Opinion dynamics in a group-based society. EPL (Europhysics Letters), 91(5), 58004 [doi:10.1209/0295-5075/91/58004]

GARGIULO, F. & Huet, S. (2012). New discussions challenge the organization of societies. Advances in Complex Systems, 15(7), 1250033 [doi:10.1142/S0219525912500336]

GARGIULO, F., Lottini, S. & Mazzoni, A. (2008). The saturation threshold of public opinion: are aggressive media campaigns always effective? arXiv preprint arXiv:0807.3937 .

GARGIULO, F. & Mazzoni, A. (2008). Can extremism guarantee pluralism? Journal of Artificial Societies and Social Simulation, 11(4), 9: https://www.jasss.org/11/4/9.html.

GONZÁLES-AVELLA, J. C., Cosenza, M. G. & Tucci, K. (2005). Nonequilibrium transition induced by mass media in a model for social influence. Physical Review E, 72(6), 065102 [doi:10.1103/PhysRevE.72.065102]

GROUCUTT, J., Leadley, P. & Forsyth, P. (2004). Marketing—Essential Principles. New Realities. Kogan

HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.

HEIDER, F. (1946). Attitudes and cognitive organization. The Journal of psychology, 21(1), 107–112 [doi:10.1080/00223980.1946.9917275]

HEIDER, F. (1958). The psychology of interpersonal relation. New York: Wiley, . [doi:10.1037/10628-000]

IYENGAR, S. & Hahn, K. S. (2009). Red media, blue media: Evidence of ideological selectivity in media use. Journal of Communication, 59(1), 19–39 [doi:10.1111/j.1460-2466.2008.01402.x]

KOZMA, B. & Barrat, A. (2008). Consensus formation on adaptive network. Physical Review E, 77(1), 016102" [doi:10.1103/PhysRevE.77.016102]

LAZARFELD, P. & Merton, R. K. (1954). Friendship as a social process: A substantive and methodological analysis. Freedom and control in modern society, 18, 18–66

LORENZ, J. (2007). Continuous opinion dynamics under bounded confidence: A survey. International Journal of Modern Physics C, 18(12), 1819–1838 [doi:10.1142/S0129183107011789]

MANZO, G. (Ed.) (2014). Analytical sociology: actions and networks. John Wiley & Sons

MCPHERSON, M., Smith-Lovin, L. & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual review of sociology, 27(1), 415–444 [doi:10.1146/annurev.soc.27.1.415]

MOUSAVI, S. & Gu, B. (2014). The role of online social networks in political polarization. Association for Information Systems

MUNNIKSMA, A., Verkuyten, M., Flache, A., Stark, T. H. & Veenstra, R. (2015). Friendships and outgroup attitudes among ethnic minority youth: The mediating role of ethnic and host society identification. International Journal of Intercultural Relations, 44, 88–99 [doi:10.1016/j.ijintrel.2014.12.002]

NEUMANN, P. R. (2013). The trouble with radicalization. International Affairs, 89(4) [doi:10.1111/1468-2346.12049]

NEWMAN, M. E. (2006). Modularity and community structure in networks. Proceedings of the national academy of sciences, 103(23), 8577–8582 [doi:10.1073/pnas.0601602103]

NEWMAN, M. E. (2012). Communities, modules and large-scale structure in networks. Nature Physics, 8(1), 25–31 [doi:10.1038/nphys2162]

PINEDA, M. & Buendía, G. (2015). Mass media and heterogeneous bounds of confidence in continuous opinion dynamics. Physica A, 420, 73–84 [doi:10.1016/j.physa.2014.10.089]

PULICK, E., Korth, P., Grim, P. & Jung, J. (2016). Modeling interaction effects in polarization: Individual media influence and the impact of town meetings. Journal of Artificial Societies and Social Simulation, 19(2), 1: https://www.jasss.org/19/2/1.html. [doi:10.18564/jasss.3021]

RIVERA, M. T., Soderstrom, S. B. & Uzzi, B. (2010). Dynamics of dyads in social networks: Assortative, relational, and proximity mechanisms. Annual Review of Sociology, 36, 91–115 [doi:10.1146/annurev.soc.34.040507.134743]

STARK, T. H. & Flache, A. (2012). The double edge of common interest: Ethnic segregation as an unintended byproduct of opinion homophily. Sociology of Education, 85(2), 179–199 [doi:10.1177/0038040711427314]

STEHLÉ, J., Voirin, N., Barrat, A., Cattuto, C., Isella, L., Pinton, J., Quaggiotto, M., Van den Broeck, W., Régis, C., Lina, B. & Vanhems, P. (2011). High-resolution measurements of face-to-face contact patterns in a primary school. PLoS ONE, 6(8), e23176 [doi:10.1371/journal.pone.0023176]