Countries as Agents in a Global-Scale Computational Model

Introduction

Powerful nations rise and fall, many nations today did not exist 75 years ago. What allows a nation or empire to rise to power? We build upon Kennedy’s (1989) analysis of this question by empirically modeling the link between political agreements, wealth, and war. A nation, through networks of political affiliation or lack thereof, can secure its position in the world as a superpower or fall into chaos and collapse. Most and Star (1984) argue that countries can select and utilize various policy options to their advantage, depending on the problems they face. In this paper, we examine outcomes that arise from the networks of formal defense agreements. These agreements are one type of foreign policy option that countries often use to gain prominence and protection on the global scene.

In this paper, we focus specifically on how defense agreements serve as a foreign policy tool to garner protection and tribute. We employ the Correlates of War (CoW) dataset to provide historical data of formal defense agreements since 1945 (Gibler 2009). In the tradition of Cusack and Stoll (1990), we use computer simulation to investigate outcomes of international systems, specifically agreements and conflict. By constructing an agent-based model that builds upon Axelrod’s Tribute model (Gilbert and Conte 1995), we examine how formal defense agreements and alliances shape the success and failure of various countries. This analysis is based on Schelling’s (1960) foundational work that finds that the threat of retaliation can be more effective than a single country’s defense capabilities. We investigate how much defense alliances play into this retaliation threat dynamic.

Axelrod’s original model began with ten actors arranged on a line whose ends meet to form a circle so each actor would only have one neighbor on each side. Political power would grow and diminish as the neighbors next to each actor interacted. Our network model moves beyond simply trying to understand the emergence of higher-level coordination from the elementary interactions of the lower level agents. We take the existing networks and wealth of countries and treat them as having already emerged. In the framework of our tribute model, we use this information to simulate interactions between countries.

Agent-based modeling has previously been used for this type of alliance examination (Cederman 2003; Cederman and Girardin 2007; Bennett and Stam 2000). We build upon this literature, and Kennedy’s (1989) work on the capacity of countries to sustain war, by taking the empirical Correlates of War data as the initial conditions of defense agreements, running our model forward, and examining which countries become dominant through their ability to produce and extract wealth. We set four years as initial conditions, 1945, 1960, 1980, and 2007. Our model employs historical data to simulate similar decision-making conditions. Cederman and Girardin (2007) employ empirical data to simulate local conflicts. They integrate GIS data with computational models to analyze civil wars. Our model makes a similar contribution on an international level. We identify the emergence of patterns of international conflicts and distributions of power. Our paper makes a contribution to the conflict dynamics and resolution literature using a methodology that is informed by agent-based modeling^[1] and the economic analysis of conflict^[2].

Section 2 provides the theoretical basis on which our model stands. Our model, methods, and data are laid out in Section 3. The results and conclusions from our agent-based model are shown and discussed in Section 4.

Theory

Jouvenel (1963), in Pure Theory of Politics, introduces the problem of political exchange and reciprocation. At its root, politics is the art of moving “other men in pursuit of some design cherished by the mover” (Jouvenel 1963, 38). Agent A suggests some action H by agent B. Agent A may promise agent B gain for cooperation, penalty for defiance, or both. The principle extends to foreign policy where state power is exercised against other states through various channels. Morgan and Palmer (2003) show that foreign policy is goal directed, either to accomplish a certain task or destroy a particular state. Alliances involve “both costs and benefits, and the only alliances we observe are those in which the benefits outweigh the costs” (Morgan and Palmer 2003, 200). Costs and benefits that govern diplomatic outcomes are those born and received by political decision-makers: those who have influence over the evolution of society’s power structure (Wagner 2016; Salter and Wagner 2018). Depending on a nation’s institutional arrangement, political decisions may or may not lead to desirable outcomes for the public. We integrate this understanding at a high level, considering states to make decisions in light of costs and benefits of war. While tension of internal social and institutional dynamics may not always lead to the welfare maximizing outcome (Arrow 1950; Buchanan 1954; Boettke and Leeson 2002; Caplan 2011; Decanio 2014), deal-making within democracy can move society closer to this outcome (Buchanan and Tullock 1962; Wittman 1989, 1995). To account for generally imperfect rationality among actors, we include a random parameter that influences the efficiency of democratic decision-making in its decision to war.

In economic interactions two agents engage in exchange because both parties expect to realize a state superior to the one that would arise absent exchange (Menger 1983). This requires that agents, as legal persons, are not so inequitable that one can, owing to a privileged position, use force or the institutions of force to manipulate the terms of exchange to benefit himself at the cost of another agent. This is not the historical norm. For most of human history, the Hobbesian “natural state” embodied the dominant form of political relationships^[3]. Even when the “natural state” is superseded by robust institutions of governance, relationships between agents of different states are prima facie exposed to the risk of poorly constrained violence. In the “natural state”, whether domestic or international, asymmetries in power allow a stronger agent to employ force or the threat of force as a tool to transform his relationships with other agents. The weaker agent, sensing a threat, may choose to cooperate under such circumstances (Buchanan 1985, 68-69). Alliances that embody substantial political inequity, are the fruit of this type of power relationship. They can breed the discontent that gives rise to future conflicts (Benson 2011). In this anarchic world, peace and security are especially rare.

We generalize this sort of behavior with a derivation of a game of war. Table 1 demonstrates the payoffs for this scenario. Given the payouts in Table 1, both agents will typically be incentivized to avoid conflict. There are cases where either agent might not avoid conflict; these include games where payouts for engaging in conflict differ between agents. Imagine that agent A is substantially stronger than agent B and that the rule of law is not firmly established. Agent A might destroy agent B. More likely agent A will promise not to harm agent B. Instead, agent A proposes to agent B “something similar to the slave contract, in which the ‘weak’ agree to produce goods for the ‘strong’ in exchange for being allowed to retain something over and above bare subsistence (Buchanan 1975, 78).” Agent A may offer to agent B the opportunity to keep a portion of his income by a formal agreement.

Table 1: Game Theoretic Payoffs for Agents of Equal Strength

		B
		Altruism	Fight
A	Altruism	a, a	-b, b
	Fight	b, -b	-c, -c

In their analysis of the development and constraint of state power, North, Wallis, and Weingast (2009) describe the emergence of early forms of political organization. Development begins from “the natural state.”

”The natural state reduces the problem of endemic violence through the formation of a dominant coalition whose members possess special privileges. The logic of the natural state follows from how it solves the problem of violence. Elites – members of the dominant coalition – agree to respect each other’s privileges, including property rights and access to resources and activities. By limiting access to these privileges to members of the dominant coalition, elites create credible incentives to cooperate rather than fight among themselves. Because elites know that violence will reduce their own rents, they have incentives not to fight. Furthermore, each elite understands that other elites face similar incentives. In this way, the political system of a natural state manipulates the economic system to produce rents that then secure political order. (North et. al. 2009, 18).”

From this process arises a system of government that maintains a monopoly on the use of force. This logic can be extended to the formation of international order. Agents on both sides who influence government recognize that they will be better off if both governments reach an agreement with one another, which will constrain the use of force in their interactions (Olson 1965).

The scenario we have described is the starting point from which agreements between governments must emerge. Interaction between agents from different nations includes a peculiar problem that is not present among interactions within a nation. Besley and Persson (2008) find that external war typically leads to much larger investments in fiscal capacity than do civil wars. In nations where the rule of law has reached an appreciable level of maturity, the position of any two agents in the legal system is much closer to equality than in a system where the rule of law is absent, thus reducing costs that arise due to legal uncertainty (Hayek 2010). The formation of legal equality promotes predictability within the system as agents can not only form expectations about the governing system’s response to their own actions, but also its response to the actions of other agents (Koppl 2002). Under the rule of law, an agent can expect that the legal system will respond symmetrically and, by implication, predictably to his own action as it would to the same action taken by any other agent (Hayek 1982, 112-13).

In order for the rule of law to extend beyond a single nation, whether in piecemeal or in whole, different nations must form enforceable agreements with one another. These agreements can also manifest themselves in common institutions as the “institutional arrangements of political systems influence the incentives of leaders to provide different kinds of policies” (Bueno de Mesquita et al. 1999, 41). Countries with similar institutions, democracies for example, interact differently and often times more cordially with each other than they do with autocracies. Discrepancies in the power of nations will play a significant role in determining the extent to which the rule of law plays a role in international relations. Alliances may also be used as a tool of increased control for the stronger party. Given power asymmetries between nations, Benson’s (2011) findings that alliance formation can even create incentives for alliance members to initiate and perpetuate conflict are unsurprising. Our model integrates these attribute of alliances in their willingness to respond to conflict.

Model

This section provides a description of our Network Tribute model as well as a background on the data and methods used to conduct our analysis.

We identify our agent as the nation-state. In doing this, we assume an equilibrium condition within political markets in each state. Each agent involved in enacting state policy knows the expected costs and benefits of the potential action and chooses their most preferred option. We allow for inefficiencies in collective decision-making to arise and test the effects of such a systematic deficiency (Arrow 1950).

The process of becoming an active agent who has the potential to go to war is random. At the core of the model, the decision of whether to attack or not and the decision to attack certain countries or not, however, is strategically calculated. Activated agents make their decisions whether or not to threaten another country by the potential amount of tribute they can garner from their threat. Countries do not threaten their allies. They engage in a cost benefit analysis for each decision. These decisions are much like the decisions modeled in Cederman’s model (2003). He poses that due to increased globalization and technological advancements, stochastic decisions to wage war are based on the specific contexts, costs, and benefits. Agent utility is based on accumulated wealth, and their foreign policy decisions are based upon future expected utility (Bennett and Stam 2000). Deviations from this norm are dependent upon the efficiency of collective decision-making.

As the model runs, agreements between countries are created and are strengthened or weakened based upon the interactions of the actors. In our model, agents are nodes that comprise an existing network of countries. These actors may or may not have connections to other countries. Although this model can be run on any variety of simulated networks, the analysis of this paper is concerned with the dynamics of specific real-world networks drawn from certain points in time.

The data used for our global network model experiments come from the Correlates of War Project. The networks for the countries are created using data on formal defense alliances, where one state has signed a defense pact to protect another (Gibler 2009). These defense networks convey information about the structure of global relationships as they represent a high level of commitment to another country. They are directed connections that represent an explicit public promise that one country will commit some level of resources to another country should they come under attack. The Network Tribute model takes the formal defense alliance networks of years 1945, 1960, 1980 and 2007 and treats them as having already emerged from the previous interactions of the individual countries. These years were chosen because they allow us to compare model results from time periods before during and after the cold war, a time of international tumult. In the model, alliances are preexisting conditions that are taken as given and are fixed as the simulation is run forward each time.

New links between previously unlinked countries arise when one country pays tribute to another country. These new links do not represent formal defense agreements. They represent a “non-aggression” agreement between the two countries. They signify that neither country, should they become active again, will target the other in the future. They do not represent a promise to commit any resources to another county in the future.

The CoW project has detailed data on the national material capabilities of countries throughout much of the 20^th century. In the globalized model, each country is instantiated with a proxy for wealth that is based on data for that country in that year. We use CoW data on yearly steel production are used as a proxy for wealth. One might argue that certain countries, Japan in particular, did not have adequate steel production of their own to sustain their growing army in the 1920s-1940s. Although this is true, Japan did have three principal mines in the early 1900s that provided an ample amount of iron and steel to the country (Journal of the Royal Society of Arts 1908). As Berglund (1922) states, “the iron and steel industry of Japan is closely bound up with that country’s continental policies. Military power is dependent upon this industry, the political situation in the Orient will be better appreciated as the conditions governing Japan’s iron and steel industry are understood (Berglund 1922, 623).” Iron and steel production is closely linked with levels of industrial activity. This measure provides a valuable proxy for military potential (Rogers 1948, 41; Inwood and Keay 2013, 1265; Shone and Fisher 1958; Wayman, Singer and Goertz 1983) ^[4]. Production of steel is required to fight wars and sustain infrastructure for a modern society. Trade during, before, and after war is crucial to military success, however a country’s own iron and steel production indicates its ability to acquire this significant input independently during a time of war (Birkett 1920, 353; Zimmern 1918, 7-10).

Previous models have used arbitrary thresholds for when actors are to become active during a simulation. Some literature suggests that the frequency of wars worldwide has been increasing since 1870, due to economic globalization and democratization (Harrison and Wolf 2012, 1055). In order to define a year in our model we look to the CoW Militarized Interstate Dispute data (Palmer et al. 2015). The average number of disputes in the four years considered in this model was calculated at 23.25 disputes, Table 2 shows the number of disputes each year. Therefore, in our globalized model, 23 countries are asked to become active each year. These active agents could potentially enter into a conflict. The selection of the countries to become active is random.

Table 2: Number of Global Disputes Each Selected Year

Year	Number of Disputes
1945	14
1960	30
1980	30
2007	19
Average	23.25

In our model, there are two parameters that may be chosen by the modeler. The experiments for our model include a parameter sweep of the tribute rate as well as the cost efficiency of democratic decision-making. The tribute payment is a parameter that can be modified to see the effect that various levels of tribute have on the outcome of the model. The democratic efficiency parameter adds the notion of irrationality to the model.

Agent decision-making and interaction

An active country must decide whom to target and it does this by assessing a possible target’s vulnerability and multiplying it by their possible tribute payment. The greater the costs of tribute, the more likely a threatened country will choose to fight. Vulnerability is defined by Axelrod according to the following formula:

$$\text{Vulnerability of a Possible Target (with no allies)} = \frac{ W_A - W_T }{ W_A }$$

Where W_A and W_T are the wealth of the active actor and the target, respectively. In order to take into account the networks of targeted countries we need to add a term to this formula that will allow the Active Country to incorporate this information. This term is called AC_T and it represents the weighted wealth contribution of all countries that have a link to the targeted country. Only countries that have a network will calculate the modified vulnerability calculation:

$$\text{Vulnerability of Possible Target (with allies)} = \frac{ W_A - ( W_T + AC_T ) }{W_A}$$

The AC_T term is calculated by each actor in the defense network of a targeted country. Each country in the defense network multiplies the alliance strength it has with the targeted country by its own wealth. This is the amount that each country is willing to contribute to the defense of the targeted country.

When an agent becomes activated, it will look at all the countries that it doesn’t have a link to and from those countries it will find the county that maximizes the product of vulnerability and payment. The country with the maximum attack score becomes the targeted country. At this point the active actor will have made its decision based on the information available to them. Not all decisions to go to war are rational and it is not guaranteed that the active country will carry out its threat to fight. Previous models made unrealistic assumptions about a countries decision to go to war but the democratic efficiency parameter adds this element of irrationality to our model.

The targeted country is faced with two options: they can either choose to pay the tribute to the active country (in which case they transfer a certain percent of their total wealth to the demander) or they can refuse the demand and war will occur. The targeted county will decide to pay tribute if the amount demanded in tribute is less than the cost of going to war. The threatened country engages in a cost minimization calculation in which they calculate whether losing wealth equal to 25 percent of the attacking countries wealth or losing the amount demanded in tribute is less costly.

Our model uses a proxy for alliance strength that is calculated using data from the CoW dataset. This measure exists for each defense agreement in each year considered. It contains information on the length of time the two countries have had a formal defense agreement with each other as a proxy for the strength of the relationship between the two countries. Alliances can, however, create some unintended consequences themselves. Historically, various alliance groups actually increased the probability of a conflict within the alliance. Because of this fact, many alliance groups started to add caveats to their alliance agreements that countries would only be obliged to come to the aid of another country if they were attacked by a country outside the alliance (Benson et. al. 2013, 47).

Alliance strength in our model is bounded between 0 and 1 and is used in the calculation of how much assistance a targeted country would receive from each country that has agreed to protect it if attacked. In the globalized model the strength of alliances is thought to have already emerged from real world processes. These link weights are treated as given and are fixed for the duration of all simulations, therefore, the weights and network connections do not update as the model runs.

The new links created in the model are not to be confused with defense agreements. They are created when one county decides to pay tribute to another country. After the tribute is paid and the link is created, those two countries will not target each other (in either direction) again. They do not commit any resources from one country to another.

If war occurs and the targeted country has no network, the attacking country has its wealth reduced by 25 percent of the targeted countries wealth and the targeted country has its wealth reduced by 25 percent of the attacking countries wealth.

If war occurs and the targeted country has a network, each country in the defense network multiplies the alliance strength it has with the targeted country by its own wealth. The sum of the amount that all countries will contribute is added to the wealth of the targeted country and this sum represents the total alliance contribution to be put toward the defense of the targeted country. Damage is done to the attacking country that is equal to 25 percent of the sum of the contributed wealth of all countries in the defense network plus the targeted countries own wealth. Damage is done to the targeted country equal to 25 percent of the wealth of the attacking country. Each country in the defense network of the targeted country has its wealth reduced by the total amount they contributed to the defense of the targeted country.

Technical background

The code for preparing the data, running the simulation and experiments, and visualizing outcomes is available in a GitHub repository at the following link: https://github.com/hwalbert/Countries-as-Agents-in-a-Global-Scale-Computational-Model. This repository contains a static version of an R package that contains the raw data use for instantiating the model as well as the functions that allow creation of the different empirical instantiations of countries, networks, and attributes. The standard R documentation for this package is also included as a pdf file. The simulation model was created in NetLogo and is also available in the repository. The experiments for the model are included in the behavior space tool within NetLogo. Python scripts for analysis and visualization of results are also included.

Results

We run experiments for the years 1940, 1960, 1980, and 2007. We sweep values from .1 to 1 in increments of .1 for the rate of tribute and democratic efficiency. For all parameter combinations, we run 100 trials. We also sweep values between .01 and 1 in increments of .01 to observe the results with finer texture. For each pair of exogenously determined parameter values we run 20 experiments. We use this set of experiments to generate heatmaps that include the mean values generated for variables for each pair of exogenously determined parameters. In the results we consider the average values generated in each set of runs. We discuss results that are representative of experiments across years.

Results of the experiments share many of the same characteristics of the original model. Axelrod notes that model runs show significant variation. Model runs show significant variation. Each set of parameters is usefully described by the mean values they generate. When agents do not perfectly maximize their expected wealth holdings, conflict can arise late in the model. Across runs, there tends to emerge a dominant player. There also can emerge two powerful, yet opposing players, as is the case between Russia and the United States in many runs. Nations with relatively greater levels of wealth tend to accumulate the greatest levels of wealth, but a nation’s initial endowment does not guarantee it success in any given run (Gilbert and Conte 1995, 28).

Axelrod found that his model could see devastating wars and other large events long into a model run. A typical run of the network tribute model will see an initial period of turbulence in which many wars of varying size are fought. This behavior can continue many years into the run of the model but after a time a sort of equilibrium will emerge and wealth will only grow at the rate of wealth increase in the model. This result is unique and different from one of the characteristics of the original Axelrod model where the model never settled down. This difference is probably due to the fact that this model takes the existing network as given, alliance strength is not dynamic in this model, and ties are not broken. Thus, a rigid hierarchy of tribute payments is inevitably formed, and with especial swiftness when tribute rates are relatively high.

We test varying combinations of values for democratic efficiency and tribute rates in the model. We expect to see that higher rates of tribute lead to relative impoverishment of society, including those who are collecting tribute, as defending nations have a significant incentive to go to war to prevent themselves from being subject to high rates of extraction.

The democratic efficiency parameter influences the likelihood that an aggressor who would profit from going to war actually follows through. The defending country decides whether to pay tribute or fight. In this case, the democratic efficiency parameter influences whether the defending nation will fight even when it expects that paying tribute would be cheaper. Since the aggressor is the first to act, we expect the effect of democratic efficiency on the frequency of war to be generally positive. We expect that increased democratic efficiency – i.e., only going to war when it is profitable – will tend to have welfare enhancing effects when tribute rates – that is the incentive to go to war – is relatively low.

High tribute rates lead to lower levels of welfare across the system

The results show a generally negative correlation between tribute rates and the level of global wealth. The highest levels of wealth, for both the system and for individual states, occurs with the lowest rates of tribute (Figure 1). In cases where there is one agent whose holdings of iron and steel are multiples larger than the next most powerful country, this negative correlation reverses as the rate of tribute approaches 100%. Wars under this scenario are fought early on and lead to complete or nearly complete extraction of a losing nation’s resources. Having lost most or all of their resources, these nations are unable to engage in war later in the experiment. This finding is consistent with Kennedy’s (1989) work which concludes that a country’s economic resources are a prerequisite for sustained conflict. Although the level of wealth that develops at a tribute rate of 100% is relatively high for experiments in 1945 and 2007, this is an artifact of initial conditions where one nation – the United States in 1945 and China in 2007– is much wealthier than all others. In 1945, for example, not much wealth is lost from war since no nation is able to effectively oppose rule of the United States. This set of experiments exhibit an implicit hierarchy due to these discrepancies. Further, the model’s assumption that wealth extracted as tribute is efficiently invested within the recipient nation is independent from the productivity and welfare of other nations. In data from other years, such a discrepancy in power does not exist. High levels of tribute tend to lead to impoverishment across the system.

It is tempting to think of this result as reflecting an upward-sloping supply curve for war. As the expected return to war increases, more wars are fought (Figures 2 and 4). This is true for individual countries in the short-run, but the effect is complex. We must also consider that willingness for a nation to defend itself increases as the rate of extraction increases. Thus the cost of war increases significantly and wealth plummets at the beginning of runs where the tribute rate is relatively high (Figures 1 and 3). It takes a significant period of time for wealth to recover in these cases. This suggests a corollary to the Laffer curve, as tribute is essentially tax. Rather than substitute leisure for labor, nations attempt to avoid tribute payment in the model by engaging in war (Laffer 1981). Nations are more willing to submit to low rates of tribute than high rates. If aggressing nations agree to limit their rates of extraction, the growth rate of the system is improved. This tends to improve the growth of nations across the system, including more powerful nations. Likewise, acts of aggression that might lead to war are limited when the return to war is relatively small.

In terms of war, the effects of democratic efficiency may be ambiguous. We expect that less efficiency will lead to lower levels of wealth extraction by more powerful countries. This means that poorer countries may perform relatively well in cases of lower levels of democratic efficiency. Since our model shares with Axelrod’s model that the country that initiates war is only concerned with its financial ability to wage war, more wars are initiated under the original decision criteria compared to less efficient democratic decision-making where aggressive nations avoid war.

The expectation of less war occurring at low rates of democratic efficiency is observed as the rate of democratic efficiency approaches 0. As democratic efficiency falls below a level of .1, the number of wars experienced in the system collapses and the level of wealth in the system quickly rises. This is true even at the highest rates of tribute. At a rate of democratic efficiency of 0, we expect that, according to the model, there would be no wars.

Alliance structure matters

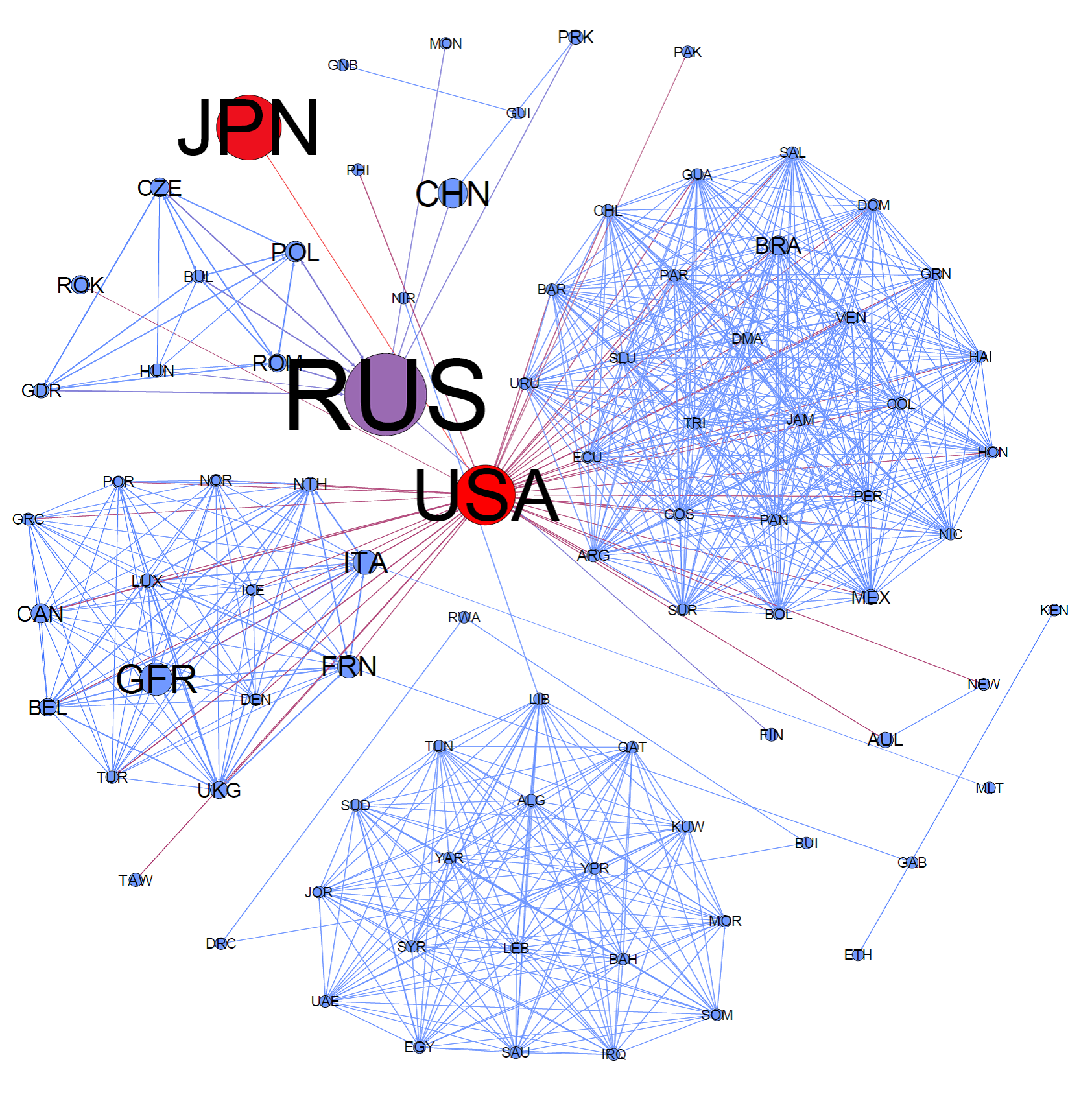
In concordance with Schelling’s (1960) work, outcomes in each experiment depend largely upon alliance structure. This alliance structure has direct consequences for a country’s retaliatory capacity. A powerful country that attempts to attack a weaker country that whose alliance is able to repel the stronger country finds imperial expansion an unviable option. Figure 5 and 6 show cases where the most powerful nation is not opposed by a relatively strong alliance. Under every circumstance, the most powerful nation – the United States – is able to expand. The cost of war for the winning nation is offset by tribute from weaker nations. In the case that the tribute rate is relatively low (.1) and democratic efficiency is relatively high (1), a sustainable structure of tribute is established, allowing all nations to experience a positive, even if negligible, rate of growth.

Only in the case where the most powerful country can be opposed by a strong alliance do we see that conflict is either abated or that the nation that starts with the greatest resource capacity loses that position (Figure 7 and 8). The finding is consistent with Axelrod’s finding that alliance network can consist of have more than one powerful actor. This is the case in 1980 where the most powerful nation, Russia, is opposed by an alliance between Japan and the United States. If Russia attempts to extract from these nations at a high rate, United States and Russia respond by entering into conflict with Russia. Since these two, together, have greater resources than Russia, Russia loses these wars. In the case where Russia extracts a low rate of tribute and democratic efficiency is high, a tribute structure is formed early on that allows all nations to experience positive rates of growth.

Conclusion

Perhaps our main result is not surprising. Societies are best served when the extent to which they extract wealth (i.e., steal) from their neighbors is relatively low. Our model assumes that society experiences an equilibrium level of extraction for those who are successful in such endeavors. This feature allows us to investigate the relationship between rates of extraction of tribute and the predisposition toward war and welfare levels that result. Higher levels of tribute lead to more war, except under the premise that powerful nations are able to extract the entirety of another nation’s wealth. Further, we find that large discrepancies in power between the most powerful nations tend to lead to a single dominant player in the network.

We have provided a general model of international conflict and negotiation. Our model is not a predictive model in the sense that it accurately predicts future alliances and levels of wealth in each country. The model shows the relationship between the efficiency of decision-making processes and the incentive to engage in conflict as represented by the tribute rate. It is conceivable, however, that the model could be calibrated to reflect past levels of extraction or integrate other variables of significance that may make it useful for predicting future conflicts.

Extensions for future work include an extension similar to Mearsheimer’s (Toft 2005) work. Just as he focuses on the role of power and geography in world politics in his theory of offensive realism, we wish to expand our model by adding geographical components to the decisions that the agents make when deciding whether or not to go to war. There is also potential to include to a more in-depth network-based theory of alliance formation that relies on a more expansive data environment for the country-agents to use in decision making. Networks and structure also exist within a nation-state. Our model does not consider such structure, however, there is no reason why these structures cannot be simulated using voting models and other complex simulations of decision-making within government.

References

ARROW, K. (1950). A Difficulty in the Concept of Social Welfare. Journal of Political Economy 58(4) 328-346. [doi:10.1086/256963 ]

AXELROD, R. (2006). Agent-Based Modeling as a Bridge Between Disciplines. Handbook of Computational Economics, 2, 1566-1583.

BENNETT, D. S., & Stam, A. C. (2000). A Universal Test of an Expected Utility Theory. International Studies Quarterly, 44(3), 451-480. [doi:10.1111/0020-8833.00167 ]

BENSON, B. (2011). Unpacking Alliances: Deterrent and Compellent Alliances and Their Relationship with Conflict, 1816-200. The Journal of Politics, 73(4), 1111-1127.

Benson, B. V., Bentley, P. R., & Ray, J. L. (2013). Ally provocateur: Why allies do not always behave. Journal of Peace Research, 50(1), 47-58. [doi:10.1177/0022343312454445 ]

BERGLUND, A. (1922). The iron and steel industry of Japan and Japanese continental oolicies. Journal of Political Economy, 30(5) 623-654.

BESLEY, T. & Persson, T. (2008). Wars and State Capacity. Journal of the European Economic Association, 6(2-3). 522-530. [doi:10.1162/JEEA.2008.6.2-3.522 ]

BHAVNANI, Ravi & Dan Miodownik. (2009). Ethnic polarization, ethnic salience, and civil war. Journal of Conflict Resolution, 53(1), 30-49.

BIRKETT, M. S. (1920). The iron and steel trades during the war. Journal of the Royal Statistical Society, 83(3), 351-400. [doi:10.2307/2340957 ]

BOETTKE, P. J., & Leeson, P. T. (2002). Hayek, Arrow, and the problems of democratic decision-making. Journal of Public Finance and Public Choice, 20(1), 9-21.

BUCHANAN, J. M. (1954). Individual choice in voting and the market. Journal of Political Economy 62(4), 334-343. [doi:10.1086/257538 ]

BUCHANAN, J. M. (1975). The Limits of Liberty: Between Anarchy and Leviathan. Chicago: University of Chicago Press.

BUCHANAN, J. (1985). Liberty, Market, and State: Political Economy in the 1980s. New York, New York: New York University Press.

BUCHANAN, J. M., & Tullock, G. (1962). Calculus of Consent: Logical Foundations of Constitutional Democracy. Liberty Fund, Inc.

DE MESQUITA, B. B., Morrow, J. D., Siverson, R. M., & Smith, A. (1999). An institutional explanation of the democratic peace. American Political Science Review, 93(4), 791-807. [doi:10.2307/2586113 ]

CAPLAN, B. (2011). The Myth of the Rational Voter: Why Democracies Choose Bad Policies. Princeton, NJ: Princeton University Press.

CEDERMAN, L. E. (2003). Modeling the size of wars: from billiard balls to sandpiles. American Political Science Review, 97(1), 135-150. [doi:10.1017/S0003055403000571 ]

CEDERMAN, L. E., & Girardin, L. (2007). Toward realistic computational models of civil wars. Presentation at the Annual Meeting of the American Political Science Association, Chicago, IL.

CUSACK, T. R., & Stoll, R. J. (1990). Exploring Realpolitik: Probing International Relations Theory with Computer Simulation. Boulder CO: Lynne Rienner.

DECANIO, S. (2014). Democracy, the market, and the logic of social choice. American Journal of Political Science 58(3), 637-652.

GARFINKEL, M. R., & Skaperdas, S. (2007). Economics of conflict: An overview. Handbook of Defense Economics, 2, 649-709. [doi:10.1016/S1574-0013(06)02022-9 ]

GILBERT, N., & Conte, R. (Eds.) (1995). Artificial Societies: The Computer Simulation of Social Life. London, England: University College Press.

GIBLER, D. M. (2009). International military Alliances, 1648-2008. CQ Press. [doi:10.4135/9781604265781 ]

HARRISON, M., & Wolf, N. (2012). The frequency of wars. The Economic History Review, 65(3), 1055-1076.

HAYEK, F.A. (1982). Law, Legislation and Liberty. London: Routledge.

HAYEK, F.A. (2010). The Constitution of Liberty. Westminster, London: The Institute of Economic Affairs.

HIRSHLEIFER, J. (1995). Anarchy and its breakdown. Journal of Political Economy, 103(1), 26-52. [doi:10.1086/261974 ]

INWOOD, K., & Keay, I. (2013). Trade policy and industrial development: iron and steel in a small open economy, 1870− 1913. Canadian Journal of Economics/Revue canadienne d'économique, 46(4), 1265-1294.

JOURNAL of the Royal Society of Arts (1908). Royal Society for the Encouragement of the Arts, Manufacturers and Commerce.

JOUVENEL, B. (1963). Pure Theory of Politics. New Haven, Connecticut: Yale University Press.

KENNEDY, P. (1989). The Rise and Fall of the Great Powers. New York: Random House.

KOPPL, R. (2002). Big Players and the Economic Theory of Expectations. New York, New York: Palgrave Macmillan.

LAFFER, A. B. (1981). Government exactions and revenue deficiencies. Cato Journal 1(1).

MENGER, C. (1883). Investigations into the Method of the Social Sciences with Special Reference to Economics. With a new introduction by Lawrence H. White & Louis Schneider. New York and London: New York University Press.

MORGAN, T. C., & Palmer, G. (2003). To protect and to serve: Alliances and foreign policy portfolios. Journal of Conflict Resolution, 47(2), 180-203. [doi:10.1177/0022002702251028 ]

MOST, B. A., & Starr, H. (1984). International relations theory, foreign policy substitutability, and “nice” laws. World Politics, 36, 383-406.

NORTH, D. C., Wallis, J. J., & Weingast, B. R. (2009). Violence and Social Orders: A Conceptual Framework for Interpreting Recorded Human History. Cambridge University Press. [doi:10.1017/CBO9780511575839 ]

OLSON, M. (1965). The Logic of Collective Action: Public Goods and the Theory of Groups. Cambridge, MA: Harvard University Press.

OSTROM, E. (1990). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge, UK: Cambridge University Press. [doi:10.1017/CBO9780511807763 ]

PALMER, G., d’Orazio, V., Kenwick, M., & Lane, M. (2015). The MID4 dataset, 2002–2010: Procedures, coding rules and description. Conflict Management and Peace Science, 32(2), 222-242.

ROGERS, A. (1948). The Manchurian iron and steel industry and its resource base. American Geographical Society, 38(1), 41-54. [doi:10.2307/210738 ]

SANDLER, T. (2000). Economic analysis of conflict. Journal of Conflict Resolution, 44(6), 723-729.

SALTER, A. W., & Wagner, R. E. (2018). Political entrepreneurship, emergent dynamics, and constitutional politics. Review of Social Economy, 1-21. [doi:10.1080/00346764.2018.1425897 ]

SCHELLING, T. (1960). The Strategy of Conflict. Cambridge, MA: Harard University Press.

SHONE, R., & Fisher, H. R. (1958). Industrial production and steel consumption. Journal of the Royal Statistical Society. Series A (General), 121(3), 269-311. [doi:10.2307/2342902 ]

TOFT, P. (2005). John J. Mearsheimer: an offensive realist between geopolitics and power. Journal of International Relations and Development, 8(4), 381-408.

WAGNER, R. (2016). Politics as a Peculiar Business: Insights from a Theory of Entangled Political Economy. Cheltenham, UK and Northampton, MA: Edward Elgar Publishing. [doi:10.4337/9781785365485 ]

WAYMAN, F. W., Singer, J. D., & Goertz, G. (1983). Capabilities, allocations, and success in militarized disputes and wars, 1816–1976. International Studies Quarterly, 27(4), 497-515.

WITTMAN, D. (1989). Why democracies produce efficient results. Journal of Political Economy 97(6), 1395-1424. [doi:10.1086/261660 ]

WITTMAN, D. (1995). The Myth of Democratic Failure: Why Political Institutions Are Efficient. Chicago: University of Chicago Press.

WITTMAN, D. (2000). The wealth and size of nations. Journal of Conflict Resolution, 44(6), 868-884. [doi:10.1177/0022002700044006010 ]

ZIMMERN, D. M. (1918). The wool trade in war time. The Economic Journal, 28(109), 7-29.