Indirect Reciprocity with Contagious Reputation in Large-Scale Small-World Networks

Markus Neumann

doi:10.18564/jasss.4392

Introduction

Altruism is a great behavioral puzzle. People help the homeless, donate blood, or give to charity - with no discernible reward for themselves. In spite of the many incentives to defect, humans choose to cooperate with one another on a daily basis. The progression of evolutionary research on this phenomenon can be characterized as a path from small- to large-N explanatory power.

‘Inclusive fitness’ provides an explanation for altruism between family members (Hamilton 1964a). In order to pass on its genes, an organism’s best chance is to reproduce, and failing that, to aid its closest relatives in doing so. However, Hamilton’s theory does not account for altruism outside the family.

Indirect reciprocity fills this role by adding reputation into the equation: I scratch your back, and while you don’t necessarily have to scratch mine, my reputation built in the process will ensure my back will get scratched by someone. Using this ‘image score’ approach, Nowak & Sigmund (1998) show altruism can be evolutionarily stable in populations of up to 100. More recent research, often relying on networks – and aided by greater computational power – has studied altruism in larger populations. But even here (see, for example, Peleteiro et al. 2014), this number rarely exceeds 1,000-2,000 – the population of a small village. Humans have congregated in much bigger cities for thousands of years, a trend that has only accelerated since the Industrial Revolution. Consequently there is a need to study the circumstances under which altruism can exist in larger populations.

I address this problem by bringing together two different strands of the literature. On the one hand, students of network reciprocity have investigated the effect of topology – which translates to population density and clustering (i.e., neighborhoods) – and shown that it can have a profound effect on cooperative behavior (Santos et al. 2008). However, I argue that due to the common assumption of perfect information across the network, the effect of topology is not yet fully understood. Researchers such as Mohtashemi & Mui (2003) have shown that the spread of information through a network can be modeled and that it has an effect on the level of reciprocity. This idea is supported by the experimental literature, which has demonstrated the contagious effect of prosocial behavior (Ito et al. 2016; Kang et al. 2015; Tsvetkova & Macy 2014).

I integrate these ideas and model them as a contagion mechanism through which information spreads throughout the network. Then, I compare random networks generated with the Watts-Strogatz algorithm (Watts & Strogatz 1998), which, depending on the model parameters, can produce a small-world network, with a number of neighborhoods within which players are very densely connected. Connections between the neighborhoods themselves however are much more sparse. As such, it realistically mimics social structures formed by humans, such as families, neighborhoods, or villages: people living within these structures are much more closely connected to other members of these structures and interact with them on a more frequent basis, but nevertheless maintain some level of contact with the outside world as well. This means that the small-world network alleviates the problem a large population poses to altruism, as it essentially consists of a number of smaller sub-populations, which are much more amenable to altruistic behavior.

I begin by situating my analysis within the body of research on indirect and network reciprocity. A new contagion-based method for handling image scores is introduced, designed to be more realistic and receptive to different network topologies. This leads to a set of novel results: altruistic behavior is demonstrated in populations of up to 20,000, and shown to be strongly dependent on the structure of the network. Substantively, this means that strongly clustered societies with distinct sub-populations are at an advantage when it comes to encouraging selfless behavior among their members. Large-scale groups without any such neighborhoods on the other hand face difficulties when it comes to fostering altruism.

Altruism between nonhuman animals can be explained through ‘inclusive fitness’. Conceived by William (1964a), one of Darwin’s most famous successors, this theory accounts for selflessness through the bonds of family: The parents, siblings and children of an organism have a 50 percent chance of sharing an allele for any one gene. In order to pass on its genes, an organism’s best chance is to reproduce, and failing that, to aid its closest relatives in doing so. Ergo, costly altruistic behavior towards these individuals is rational because it increases their reproductive fitness.

A good showcase for this concept is provided by animals warning their relatives when sighting a predator. Examples include the “thumping” of rabbits, as well as warning cries by birds and monkeys (Hamilton 1964b). The sentry reduces its own chances of survival, as it attracts the attention of the predator and spends time alerting its family rather than fleeing immediately. However, it also increases the reproductive fitness of its kin, and thus makes it more likely that its own genes will be passed on.

This concept is expressed in the simple equation \(rB > C\). If the benefits \(B\) of an altruistic action, controlling for the degree of relatedness \(r\) (the probability of sharing any one gene), are greater than the costs \(C\), said action is worth undertaking.

In principle, inclusive fitness also applies to humans. However, it does not have the same explanatory power as for other animals (Abbot et al. 2011). While altruistic behavior between unrelated nonhuman animals is extremely rare, it occurs frequently among homo sapiens (Axelrod & Hamilton 1981; Fehr & Gächter 2002). Evolutionary game theory offers several alternatives to kin selection: Direct reciprocity, group selection, altruistic punishment, tag systems, indirect reciprocity and network reciprocity number among the most prominent ones.

Direct reciprocity frames cooperative behavior as a simple quid pro quo interaction: you scratch my back and I will scratch yours. This theory features strongly in the economist tradition and is useful for explaining a wide range of behaviors (Axelrod & Hamilton 1981; Fehr & Gächter 2002). However, it falls short when dealing with sporadic encounters in large-scale societies, where it is unlikely that two individuals will meet twice. In reality, people are usually willing to help a stranger in need even if it is unlikely that this person will ever get the chance to reciprocate. Under the concept of direct reciprocity, both parties receive an immediate benefit. As a result, true altruism, which would presuppose unconditional benevolence, is not present here (Fehr & Gächter 2000). Consequently I do not make use of this mechanism.

The same is true for group selection. Originally conceived in the 1960s, this theory has been picked up again by some scholars and posits that groups or colonies of (not necessarily related) animals which contain selfless individuals are at a competitive advantage compared to other groups which do not (Wilson & Sober 1994). Therefore, groups that do not contain selfless individuals go extinct and even though the altruists are at a fitness disadvantage compared to other members of their group, they still get ‘carried’ by the overall more successful collective (Okasha 2013). While somewhat controversial in evolutionary biology (Abbot et al. 2011), in human societies, group selection is facilitated by culture and the existence of mechanisms such as conformity, imitation, or punishment of norm violators (Boyd & Richerson 1985; Henrich et al. 2003; Richerson et al. 2016 ; Soltis et al. 1995). Hence, cultural group selection can account for some forms of prosocial behavior among humans, but it is not pertinent for my own argument.

Another common strand of research attempts to supplant altruistic cooperation with altruistic punishment. Punishing non-cooperators incurs a cost, but pays off in the long run because it decreases the number of defectors (Boyd et al. 2003; Fehr & Gächter 2002). However, Nowak (2006) rightfully points out that while altruistic punishment may be a flourishing research area of its own, it ultimately relies on the mechanisms of indirect and network reciprocity, or group selection. Introducing altruistic punishment into a given situation is likely to increase cooperation even in larger populations (Tang & Ye 2016), but it is by no means necessary.

Tag-based systems are another way to change the rules of the game in a way that generally increases reciprocity (Axelrod et al. 2004; Cohen 2012; Hamilton 1964a; Shutters & Hales 2013; Spector & Klein 2006). Here, actors only engage in cooperative behavior if their partner matches them in some attribute, e.g., a green beard (Dawkins 1976). Tags can manifest either discretely (only direct matches lead to cooperation) (Axelrod et al. 2004), or as a continuous value, where a tolerance threshold determines how far a partner may deviate before cooperation is precluded (Shutters & Hales 2013, 2015). This approach can be very effective, as in the case of ( Shutters & Hales 2015), cooperative behavior even increases with population size.

The focus of this paper however lies on indirect reciprocity, which adds reputation into the equation: one person helps out another at his own detriment, but benefits in the form of an improved reputation. Therefore he is more likely to receive help from someone else in the future. Nowak & Sigmund (1998) theorize that the complex social dynamics involved in this process (keeping track of who has helped whom) might even have been one of the driving forces of human evolution.

The donation game is the classical example for this mechanism. In a well-mixed population (meaning that every player can interact with every other player), every participant \(i\) possesses an image score \(s_i \in [-5,5]\) and a strategy \(k_i \in [-5,6]\). Here, \(k_i=-5\) corresponds to complete altruism and \(k_i=6\) to defection no matter what. Finally, every player also has a fitness score, measuring his success in the game. Then, two players are randomly selected. If the strategy of player 1 \(k_i\) is lower or equal to the image score of player 2 \(s_j\) (meaning that player 2’s reputation is not worse than player 1’s level of altruism permits), player 1 donates to player 2. This exchange raises player 2’s fitness score by 1, while lowering player 1’s by 0.1. Additionally, the image score of player 1 is increased by 1. If \(k_i>s_j\), no donation takes place, but player 1 is penalized with a deduction of 1 from his image score. This process is repeated a number of times across the population. At some point, the players spawn a new generation, where the more successful actors (as measured by their fitness score) have a higher probability of producing offspring. Over time, variation in the relative success of different strategies decreases, until an equilibrium emerges.

The standards set by Nowak & Sigmund (1998), such as the concept of image scoring as well as the notation style are still used in recent papers. As such, they also form the foundation of my own research, which builds on and extends this method.

Network methods improve on the unrealistic assumption of a well-mixed population, limiting encounters by spatial (or social) proximity. Introduced by Kearns et al. (2001), this approach is used in conjunction with either indirect reciprocity or altruistic punishment (or both). However, network dynamics can create circumstances under which altruism can exist even without these mechanisms: With some minor modifications to the classical donation game, Santos et al. (2008) show that cooperation strongly depends on societal structure, modeled through network topology. Generally speaking, network structure has been identified as a major driver of whether cooperative behavior can exist. The literature has largely revolved around the comparison of different types of networks, such as the scale-free Barabási-Albert model (Barabási & Albert 1999; Santos & Pacheco 2005; Wu et al. 2005), the small-world (Watts & Strogatz 1998) model, or a simple random network (Erdös & Rényi 1960). However, there is a great degree of variance even within these network types depending on the model parameters, resulting in vastly different network properties (see the discussion below for the effect of the rewiring probability parameter of the Watts & Strogatz (1998) network. Hence, research which compares one manifestation of two types of networks misses part of the story (see for example Peleteiro et al. 2014; Salazar et al. 2011; Shutters & Hales 2015). Instead, I follow an approach laid out by researchers such as Santos et al. (2006), who explore the result of varying the connectivity parameter in a set of scale-free networks (among others). I build on this idea, analyzing the effects of the rewiring probability and neighborhood coefficient in the Watts & Strogatz (1998) network within the context of indirect reciprocity – with one more addition: contagion.

Contagion is a crucial component of many social processes – once an attribute or behavior is adapted by a part of a population, it spreads. Researchers have explored cooperative contagion in a variety of domains – be it friendship networks (Christakis & Fowler 2007), social media (Bond et al. 2012; Centola 2010; Rand et al. 2015), online games (Kang et al. 2015) or open-source software (Khalak 2003), observing the spread of altruism (Tsvetkova & Macy 2014) as well as egoism (Ito et al. 2016). While agent-based modeling is also prevalent among these works (Khalak 2003; Rand et al. 2015), a substantial number of these papers are empirical, based on both controlled experiments (Centola 2010; Ito et al. 2016; Tsvetkova & Macy 2014) and observation (Bond et al. 2012; Kang et al. 2015). However, (Shalizi & Thomas 2011), responding to (Christakis & Fowler 2007) in particular, challenge the notion that contagion can be separated from homophily (i.e., the propensity of similar individuals to form ties) in observational settings. Approaches that rely on agent-based modeling do not suffer from this problem, as the causality of tie formation is controlled by the researcher.

Here, I explore the contagion of the reputation component of the indirect reciprocity mechanism – modeling the spread of information through the network (Mohtashemi & Mui 2003). Contagion is an inherently topology-dependent process (Duan et al. 2005), so I expect variance in network structure to differentially affect prosocial behavior. Thus, the contribution of this paper lies in the exploration of this complex interaction – the contagion-like spread of information through different network topologies, and its effect on cooperative behavior even in large populations.

Model: Contagious Information and Network Topology

I employ simulations to analyze the evolutionary stability of altruism under a variety of conditions.simulations were implemented in R, version 4.0.1.\(^{}\)^[1], ^[2] I follow the methods used by Peleteiro et al. (2014) based on the donation game of Nowak & Sigmund (1998), with the addition of a network component.

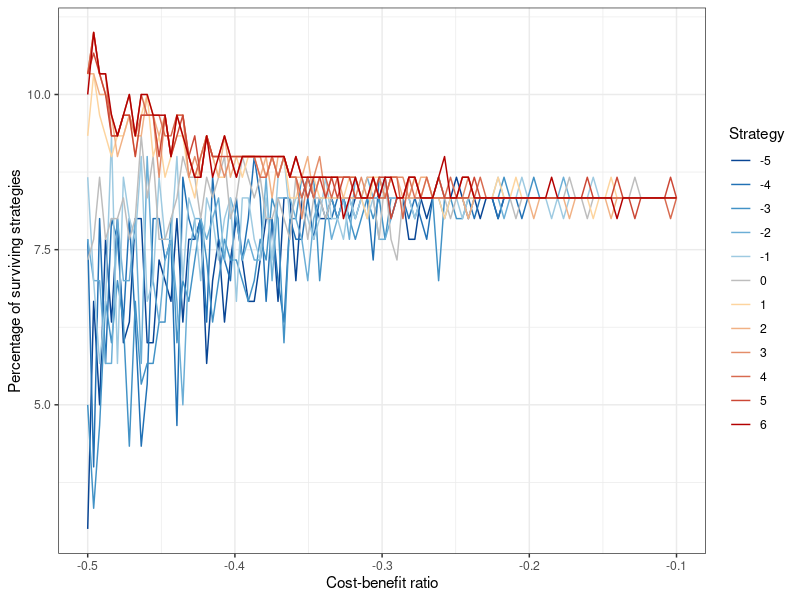
The rules of this game are as following: A population of size \(N\) is arrayed in a network, in which the nodes correspond to the actors and the edges indicate their neighborhood, and thus the possible interactions they can have with one another. In such an interaction, player 1 may be referred to as \(i\) , and player 2 (randomly selected from the neighbors of player 1) as \(j\). The players use strategies \(k \in [-5,6]\) . The notation for the fitness score is \(f \in [-\infty,\infty]\). When a donation takes place, the fitness score of player 2 increases by 2, whereas player 1 incurs a cost of \(-1\). These values are a small departure from Peleteiro et al. (2014), where they are 1 and -0.1. The reason I choose a higher cost relative to the benefit (1/2 rather than 1/10) is because this presents a tougher test for the evolution of altruistic strategies, which could otherwise flourish too easily. However, a robustness test with the original 1/10 cost-benefit ratio is presented in Figure 10 and 11 in Appendix B. When no donation transpires, the fitness scores remain unchanged. The reputational benefit for donating is \(+1\) (for player 1), the cost for refusing to do so is \(-1\) . In Peleteiro et al. (2014), whether a donation actually occurs or not, is determined by comparing the strategy of player 1 \(k_i\) to the image score of player 2 \(s_j \in [-5,5]\). If \(k_i\leq s_j\) , player 1 cooperates.

I argue that in this last regard, scholars have been a bit too faithful to Nowak & Sigmund (1998), especially when adopting their concept into the realm of network reciprocity. In the original notation, the image score \(s_i\) is an objective measure of how much players have cooperated over the course of the game. This variable is known to every actor in the population. Clearly, this notion is based on an unrealistic assumption: In the real world, altruistic actions will only change the opinion of the person directly affected, and perhaps that of those they choose to tell about it. However, the donation game is supposed to be composed of one-shot interactions between individuals who may or may not meet again. It is fairly unlikely that they would already know about the previous actions of a stranger they are encountering for the first time.

Consequently, I introduce a new method for handling image scores. As opposed to a score \(s_i\) for each individual, every player now has their own opinion about every other player they’ve encountered or heard about. ^[3] Rather than an \(N\)-dimensional vector, this can be thought of as a \(N*N\) matrix. The score \(s_{ij}\in [-5,5]\) then reflects the reputation of player \(j\) in the eyes of player \(i\) . ^[4] After one round in which every player gets one chance at playing the game,^[5<]/sup> dissemination of information through the network takes place. For every game played, the receiving player \(j\) is guaranteed to change his opinion on the donor \(i\) . Then, there is a 50% chance for every player \(c\) with whom \(j\) has a tie to take notice as well. Conceptually, this represents either people telling their friends and family about what happened to them, or bystanders witnessing the good or bad deed. Then, there is a 25% probability for every neighbor \(d\) of \(c\) to also receive the information. The consequences of this contagion-based mechanism are demonstrated in Figure 1, which shows the reputation of the black node among other members of the network. Grey nodes have never heard of the black player (or have a neutral opinion), blue nodes have a positive image of the player, whereas red nodes have a negative one. This figure illustrates that when information spreads in a contagion-based manner, closer nodes are more likely to receive the information. ⁶

**Figure 1.** Illustration of how information spreads throughout the network. The plot shows the reputation of the black node among other members of the network. Grey nodes have never heard of the player (or have a neutral opinion), blue nodes have a positive image of the black player, whereas red nodes have a negative one. This figure illustrates that when information spreads in a contagion-based manner, closer nodes are more likely to receive the information.

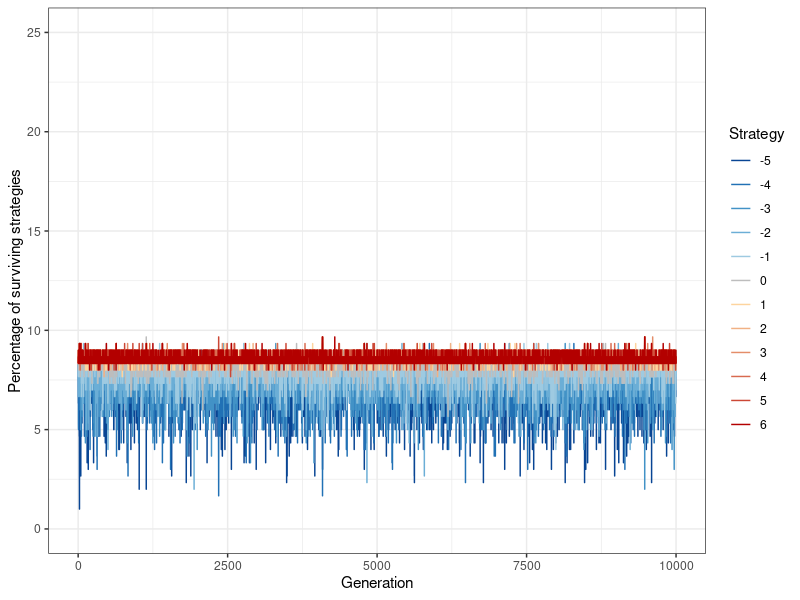
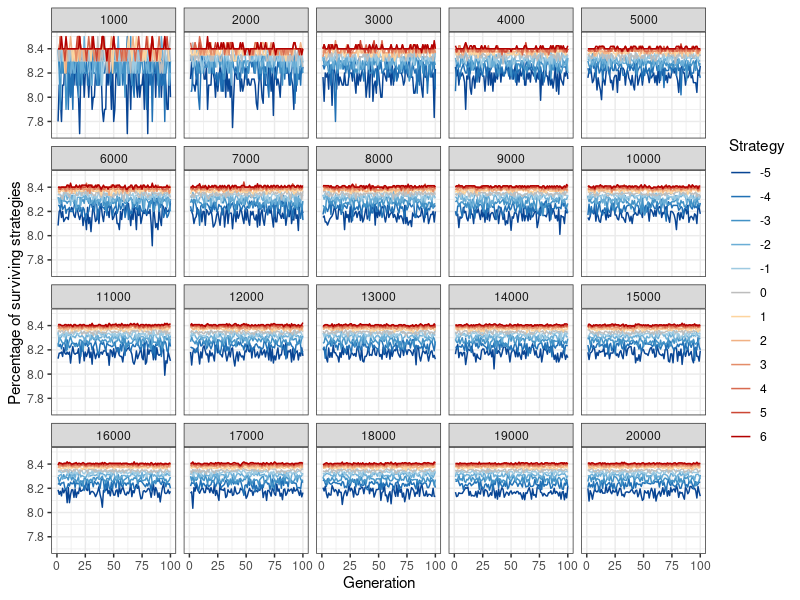
With the new information dissemination mechanism in place, the simulation proceeds as following: In each round, every agent gets to play the donation game as player 1 (the potential donor) once. After one round has been played out and image scores (as well as fitness scores) have been changed, 9 additional iterations are played. These 10 rounds make up 1 generation. The final fitness scores for this generation’s players corresponds to their global payoffs across the 10 rounds – the fitness benefit of all the donations a player has received, minus the fitness cost of all the donations they have given. The prevalence of every strategy (indicated by what proportion of players use it) is recorded at the end of each generation, so that their evolutionary viability, through their stability over time, can be assessed. This corresponds to the data points in Figures 4- 13. Then, the players ‘procreate’ in accordance with their evolutionary fitness: Strategies \(k\) are replicated in a new network of the same size, proportional to the fitness of all players who have adopted that strategy. The more successful a specific strategy compared to all other strategies, the higher its rate of replication. Therefore the ‘children’ carry on the strategy of their ‘parents’. Image and fitness scores are however reset to zero. One set of simulations consists of 100 of these ‘generations’ (Figure 12 shows that nothing changes if a simulation is run for 10,000 generations instead).

Human societies differ not just with regard to sheer size, but also in how dense they are: In a village of 500 inhabitants, the average citizen might regularly interact with 10, 50 or 100 other people. Additionally, those people may know each other at different rates as well. Furthermore, people may only interact with those who live close to them, or also have friends at the other end of the town. All of these factors could potentially affect altruistic behavior, because someone’s propensity to do a good deed may depend on who will learn about it. Or, alternatively, egoistically-minded people might fare better if their fellow citizens haven’t heard about their reputation yet, which could also depend on network density and the spread of information.

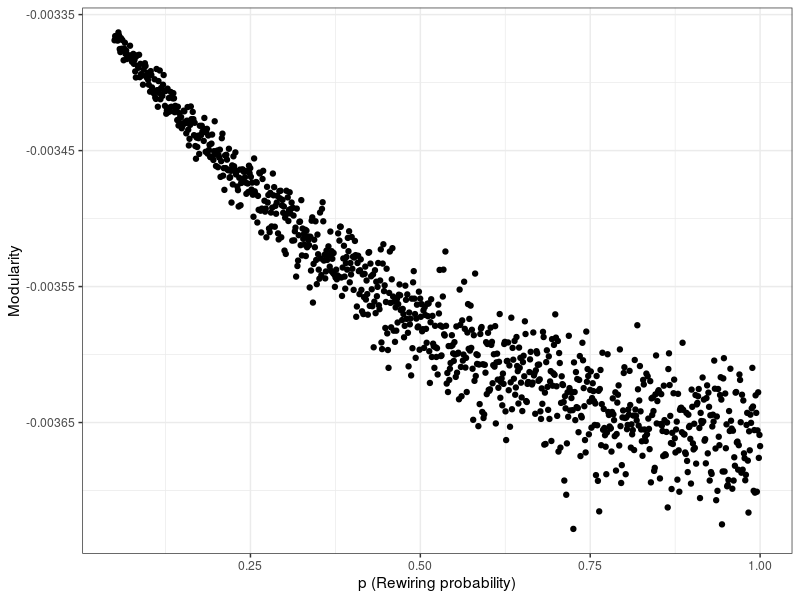
The network is randomly generated via the Watts-Strogatz model (Watts & Strogatz 1998). This algorithm is already customary in the literature because it approximates real population structures (Peleteiro et al. 2014; Santos et al. 2008) . ^[7] ^[8] The Watts-Strogatz model, often referred to as a small-world model, constructs a network as following: All nodes are placed in a ring lattice, in which each node is connected to its \(l\) ^[9] nearest neighbors. Then, each edge is rewired (i.e., one end is connected to a different node) randomly with probability \(p\) (if this leads to the creation of a duplicate edge, said edge is omitted). For low values of \(p\), the original ring lattice is largely preserved and the graph takes on the small-world property - high clustering (i.e., highly localized density) and small path length (i.e., no connections from one end of the network to another). One measure used to illustrate this is modularity, which measures the degree to which a graph is split into subgraphs. Specifically, modularity describes the number of edges that exist in groups within which nodes are heavily connected, compared to the expected number of edges in a random network of equal size (Clauset et al. 2004). Greater modularity corresponds to higher clustering. I illustrate this by simulating 1000 Watts-Strogatz networks, varying \(p\) from \(0.05\) to \(1\). The results are shown in Figure 2 – it is evident that modularity is greater for the more heavily clustered networks resulting from a lower rewiring probability \(p\).

**Figure 2.** 1000 Watts-Strogatz networks are generated, varying \(p\) from \(0.05\) to \(1\). Modularity measures the degree to which the network clusters into small communities. This plot demonstrates that as \(p\) increases, the degree to which these neighborhoods are formed decreases.

As a starting point, I simulate models with parameters similar to Peleteiro et al. (2014): A rewiring probability of \(p=0.1\) and a neighborhood coefficient of \(l=5\) are used. I begin with a population size of 300. Over the course of my analysis, these parameters are varied.

Figure 3 shows examples for the Watts-Strogatz network at two different values of \(p\). For \(p = 0.05\) , individual neighborhoods are clearly visible. By contrast, at \(p = 0.3\), connections between opposite ends of the graph are more common, and local clustering is much less prevalent. The larger \(p\), the more closely the Watts-Strogatz network resembles the Erdős-Rényi random graph, where connections are simply assigned at random. The expectation is that as \(p\) increases and neighborhoods start to vanish, the conditions should become less conducive to altruistic behavior.

**Figure 3.** A comparison of the Watts-Strogatz model with the connectivity parameter \(p = 0.05\) on the left and \(p = 0.3\) on the right. The colors denominate the strategies of the players at the end of a simulation, with blue corresponding to the most altruistic, and red to the most egoistic strategy. Larger nodes have more edges.

**Figure 4.** Every player in a Watts-Strogatz network generated with \(p = 0.2\) and \(l = 5\) plays the donation game once per round. After ten rounds, they replicate at a rate proportional to their relative fitness. The data points correspond to the percentage of players pursuing a particular strategy (with \(k =-5\) being never defect, and \(k = 6\) being always defect) after one such generation.

Results: Altruism Endures in Small-World Societies

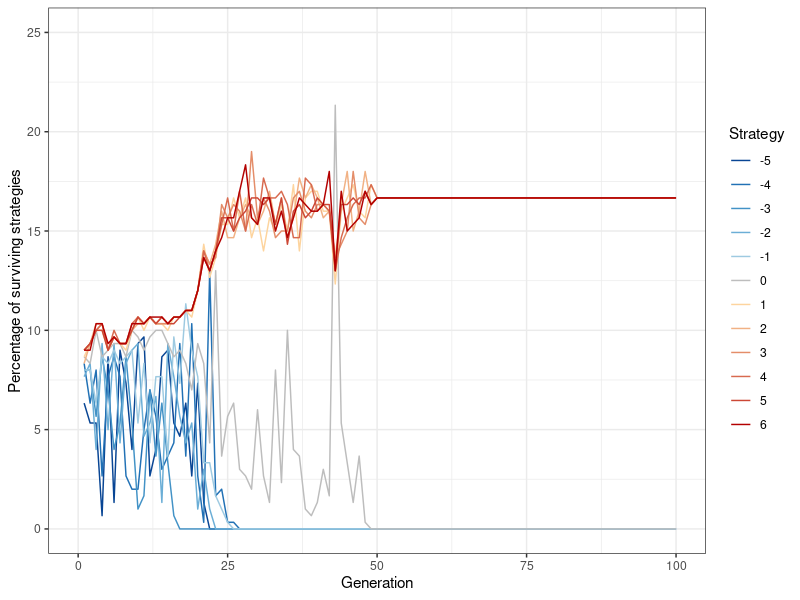
To illustrate how the simulation works, I begin by showing an example in which altruism does not survive, and then move on to exploring conditions under which it becomes a stable strategy. Figure 4 provides an example for how different strategies survive over the course of 100 generations (with N=300, \(p=0.2\) (double the default value) and \(l=5\)). Every point on the x-axis represents one generation, while the y-axis denotes the percentage with which a specific strategy occurs among the population. For example, at the end of the first generation, 24 players, or 8 percent of the population, are playing strategy \(k=-3\).

**Figure 5.** Every player in a Watts-Strogatz network generated with \(p=0.1\) and \(l=5\) plays the donation game once per round. After ten rounds, they replicate at a rate proportional to their relative fitness. The data points correspond to the percentage of players pursuing a particular strategy (with \(k=-5\) being never defect, and \(k=6\) being always defect) after one such generation.

Since strategies are randomly distributed at the beginning of the simulation, it takes a while until they begin to sort themselves out. However, it becomes evident quite quickly that the strategies associated with greater egoism (i.e., \(k>0\) ) are more stable. By contrast, the altruistic strategies \(k<=0\) fluctuate wildly, and after about 20 generations, begin to die out one after another. There are a handful of cases in which the mildly altruistic, or in this case, the neutral strategy (\(k=0\) at generation 43) actually surpass the egoistic strategies for a short while. However, rather than a sustainable trend, this is more of a ‘last hurrah’, after which the strategy quickly flickers out again. This demonstrates that no mutant is able to invade the set of evolutionarily stable strategies (Hamilton 1964b).

Finally, the strategies \(k>0\) quickly become dominant and stay that way for the rest of the simulation. However, among these strategies, no single one emerges as preeminent. Instead, they fluctuate around, and eventually converge to the same value. This behavior is also present in my other simulations and stems from the degree of randomness introduced by the information contagion mechanism.

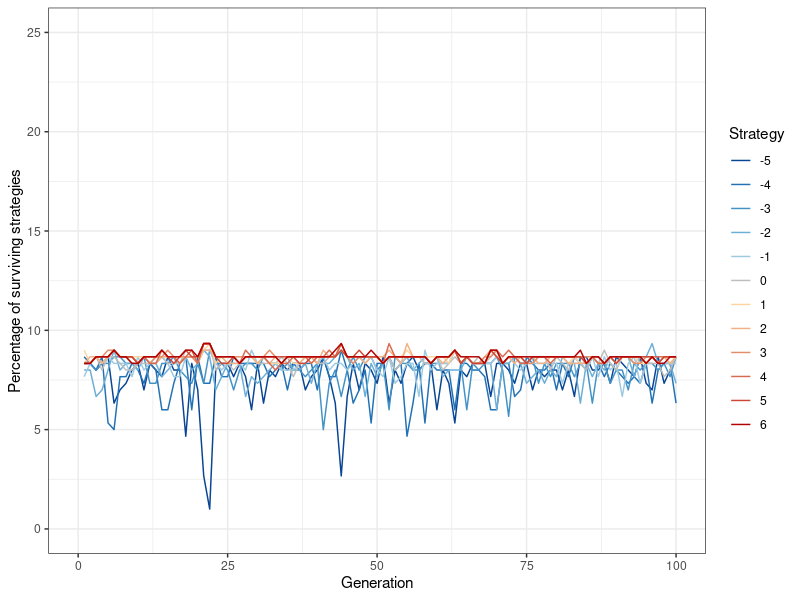
Figure 5 shows the results of a similar simulation, this time using the default value of \(p=0.1\) instead of \(p=0.2\). The differences are quite striking: Convergence occurs immediately, all strategies fluctuate only slightly, and around the same value. None of them are dominant in any way, \(k=-5\) (never defect) occurs just as much as \(k=6\) (always defect).

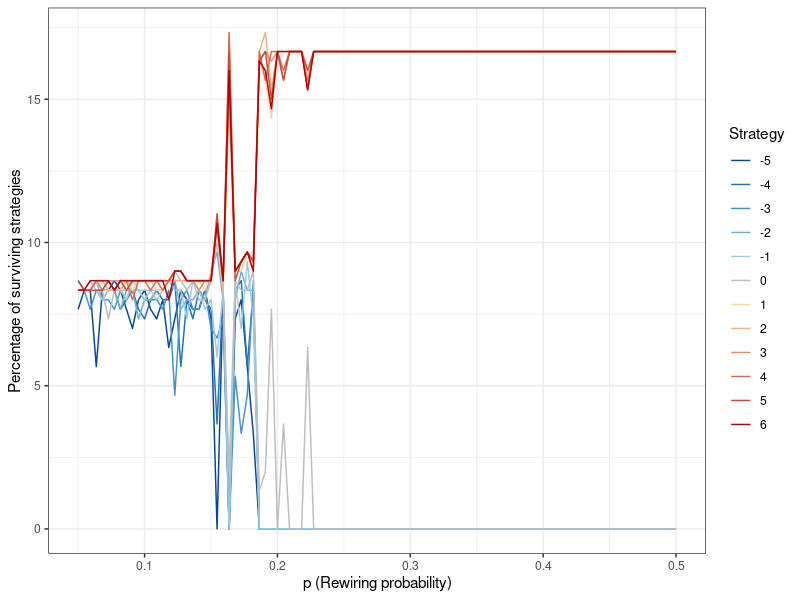
**Figure 6.** The simulation is conducted 100 times, varying the connectivity parameter \(p\) in a Watts-Strogatz network. The data points correspond to the percentage of players pursuing a particular strategy (with \(k=-5\) being never defect, and \(k=6\) being always defect) after the 100th generation in each simulation.

To further elucidate the impact of network topology, and the connectivity parameter specifically, Figure 6 presents the results of 100 simulations using the Watts-Strogatz algorithm, where the connectivity parameter \(p\) is varied. Importantly, this plot is different from Figures 4 and 5: Before, the values described the results after each generation, from only one simulation. Figure 6 on the other hand is the result of 100 individual simulations, each with a different value for \(p\). Here, the values on the y-axis denominate the distribution of strategies after the last generation of each of these simulations (i.e., when they have converged). At comparatively low levels of connectivity (however, it should be noted that even a value of 0.1, as used above, already leads to a fairly dense network) the results mirror Figure 5, but once it gets higher, the altruistic strategies start to fluctuate. Finally, at 0.2, this fluctuation becomes much stronger until one after another, these strategies die out. ^[10]

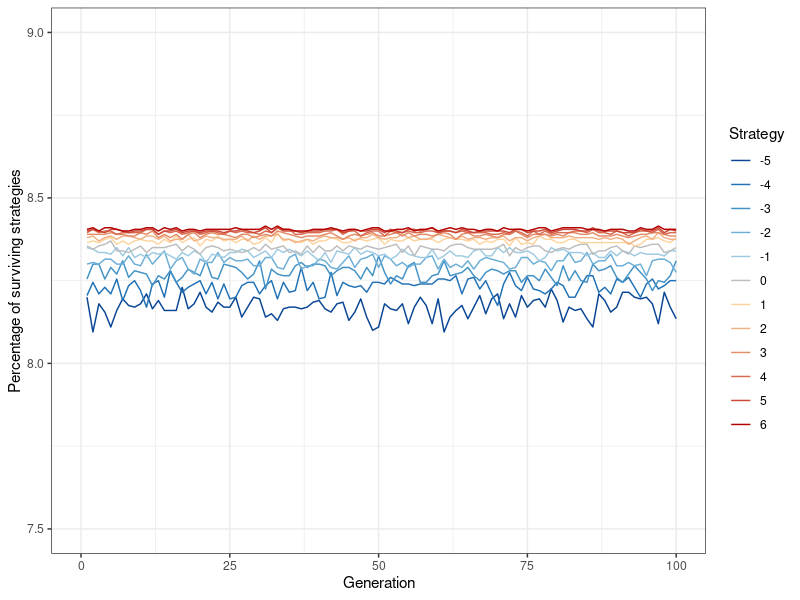
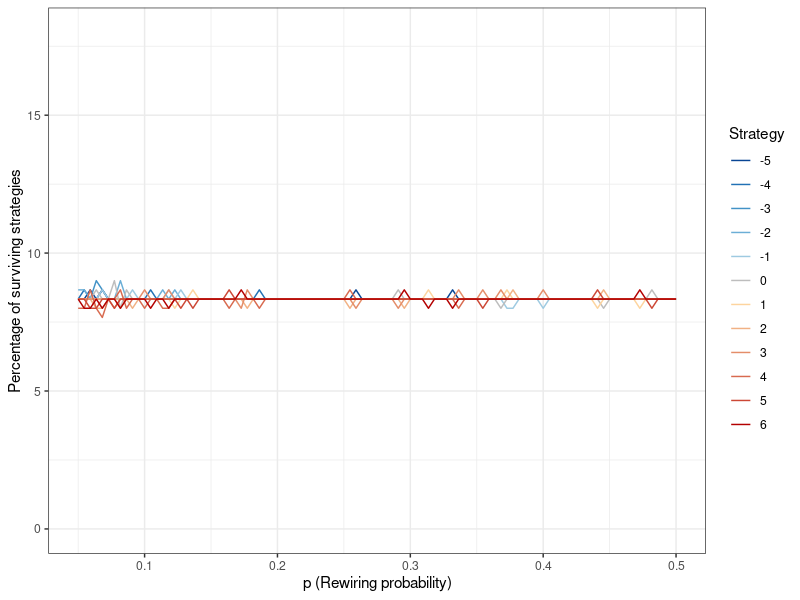
**Figure 7.** Every player in a Watts-Strogatz network with a population of 20,000 plays the donation game once per round. After ten rounds, they replicate at a rate proportional to their relative fitness. The data points correspond to the percentage of players pursuing a particular strategy (with \(k=-5\) being never defect, and \(k=6\) being always defect) after one such generation.

Having established that the extent to which a Watts-Strogatz network forms local neighborhoods, modulated by the rewiring probability \(p\), affects the degree of altruism that is possible in the network, I can now put this knowledge to use in simulating a large random network under conditions amenable to altruism. Figure 7 shows the results of a simulation with the Watts-Strogatz model, using an even lower rewiring probability of \(p=0.05\) (while keeping the neighborhood coefficient at \(l=5\)), and a population of 20,000 (see Figure 13 in Appendix B for population sizes ranging from 1,000 to 20,000). In keeping with my hypothesis, altruistic behavior at such a large population size is now feasible. That being said, while altruistic strategies are viable and stable, pure egoism is the most successful. This result stands in contrast to smaller population sizes, where all strategies were either equally successful, or died out entirely. However, it is very important to note that the differences are small, as even \(k=-5\) still makes up around 8.1 percent of the population at the 100th generation (as opposed to roughly 8.4 percent for \(k=6\) ). The differentiation between degrees of egoism (i.e., \(k<0\)) does not occur anywhere else and appears to be entirely dependent on population size.

Alternative Mechanisms

In addition to the method of information diffusion discussed above, I explore two additional variants to test the robustness of the proposed model. To defend themselves against exploitation, individuals might be more eager to talk about negative than positive experiences. I implement this notion by changing the probability of information transmission. In the original game, this is 0.5 for the first spread, and 0.25 for the second (see above). For negative actions, this is changed to 0.75 (first) and 0.375 (second), and remains the same for prosocial behavior. Ergo, information about antisocial behavior is propagated with a higher probability.

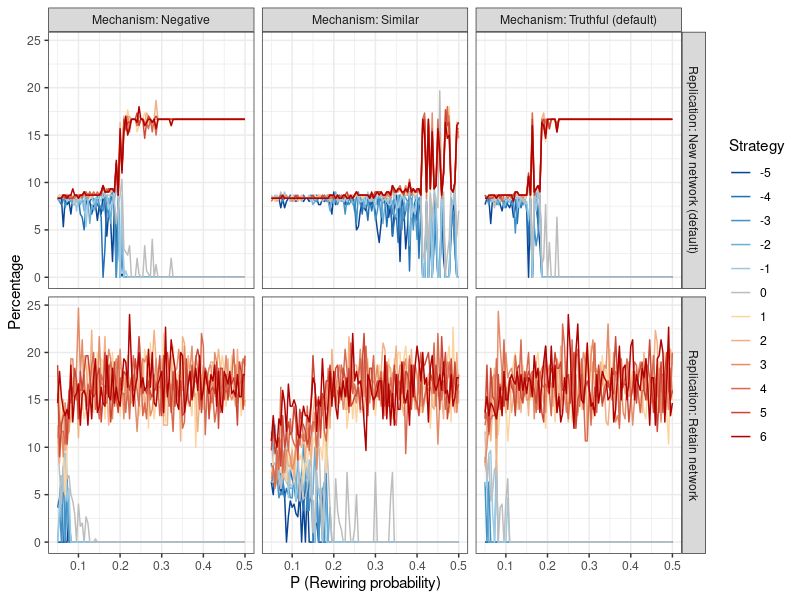
Results can be found in the top left panel of Figure 8, and are presented akin to Figure 6, where the level of cooperation depends on the extent of network clustering. Compared to the default model (shown in the top right panel), the mechanism that spreads information about negative actions with a greater probability leads to very similar results. Altruistic strategies remain viable at slightly higher levels of \(p\), but the difference is marginal.

**Figure 8.** The figure shows how the different mechanisms react to changes in the level of neighborhood clustering (greater clustering corresponds to lower values of \(p\)). The default model (shown in Figure 6) is in the top right panel. By comparison, the similarity-based mechanism can tolerate lower levels of clustering, while the mechanism that assigns a greater probability of information transmission to negative actions behaves about the same. The alternative replication strategy leads to considerably more volatile outcomes, with lower rates of survival for altruistic strategies. However for the similarity-based mechanism coupled with low values of \(p\), survival of moderately altruistic strategies is still possible.

Another plausible variation is that people might be more willing to accept new information about someone if they already hold a similar opinion about them. If Bob and Alice both believe that Mark is a good person, Alice would be more likely to believe Bob that Mark carried out another beneficial act. By contrast, if Bob thinks highly of Mark and Alice does not, she might be less inclined to believe Bob’s stories about Mark. Consequently the likelihood of information dissemination is proportional to the difference in perceptions of two actors of player i. Since the maximum score is 5, and the minimum score is -5, the difference can be, at the most, 10. Hence, the probability of information dissemination \(p_{spread}\) is calculated as following: \(p_{spread}=1-(s_{ij_1}-s_{ij_2})/10\) where \(s_{ij_1}\) is what player \(j_1\) thinks of player \(i\), and \(s_{ij_2}\) is the opinion of \(j_2\) of player \(i\). To avoid extreme behaviors (guaranteed spreading of information, or no chance of spreading information) the probabilities are limited to \(p_{spread}=[0.2,0.8]\). This is particularly important at the start of a generation, where all players have no information, and thus the same opinion about each other. The second round of information dissemination is carried out according to the same rules.

Here, results are shown in the center top panel of Figure 8. Compared to the default model in the top right panel, this form of information dissemination is considerably more conducive to altruism. Cooperative strategies now remain viable at lower levels of clustering (higher values of p) and only start to die out around \(p=0.4\) , compared to roughly \(p=0.2\) in the default and negativity-based mechanisms.

In addition to varying the mechanisms through which information is spread after one round, I also test a modification of the replication mechanism used at the end of a population generation. In the standard version, the survival rate of a given strategy is determined by all players of that strategy, and the network is reset along with the fitness scores of the players. However, realistically, children also tend to inherit the social circles in which their parents have lived. Consequently, I test an alternative reproduction mechanism where the network is retained. Rather than determining reproduction at the population level, a Bernoulli trial is then carried out for every node, determining whether it passes on its ‘genes’ (i.e., its strategy) or not. The probability in this trial is based on the success of the node’s strategy, relative to all other strategies. Nodes where the ‘parent’ failed to pass on its ‘genes’ pick a new strategy in accordance with the original replication mechanism.

The bottom three panels of Figure 8 show that this form of replication leads to considerably more volatile results, with altruistic strategies already dying out at much higher levels of network clustering. Only the similarity-based information dissemination mechanism is able to sustain cooperative behavior until about \(p=0.15\) . Evidently, this form of replication requires conditions to be very favorable in order for altruistic strategies to survive.

Discussion

What can we learn from all this? Clearly, network topology matters a great deal. Networks which cluster into small neighborhoods, where everyone knows everyone else and interacts with them on a regular basis are more conducive to altruism. Essentially, these neighborhoods form smaller sub-networks, and as the literature has shown, smaller populations are more likely to produce selfless behavior. By contrast, when connections exist evenly throughout the graph, altruistic behavior becomes less feasible. This is because in a network with heavy clustering, a node’s neighbor is more likely to be connected to another neighbor of the original node.

This is where my contagion-based information dissemination mechanism comes in. In a conventional network with perfect information, clustering is not as important, as all of a node’s immediate neighbors will always learn about its reputation. But if information about a player spreads on the basis of contagion, its neighbors it did not interact with that turn will be much more likely to find out in a network with high clustering. By contrast, when clustering is low, it does not matter as much if they annoy some of their neighbors through non-cooperative behavior, because there are still enough other players around who have not heard about their exploitative deeds yet.

Once the necessary network structure is in place, scaling up the population to \(N>1000\) without making altruism non-viable becomes less of a problem than it has been in prior research. As long as the rewiring probability is low, the network consists of small neighborhoods, and since the players predominantly interact with other players within their neighborhoods rather than across the network, repeated interactions are common, and information spreads quickly among their neighbors. Consequently, altruistic strategies can survive.

When comparing the effects of varying network topology and size, it becomes clear that while size matters, topology turns out to be another powerful determinant of altruism. This is an important finding, because previous research has not been conclusive in this matter: Santos et al. (2008) and Peleteiro et al. (2014) compare different types of network models, but their simulations do not test for differences within them by varying the network parameters. My model is more sensitive to changes in network topology and thus reveals the full repercussions of variation in it.

In conclusion, my research contributes to the existing literature by improving the widely-used image score mechanism, introducing an element of imperfect information. Furthermore, it demonstrates that a great deal of variation in altruism can be explained through network topology. Finally, I manage to show how selflessness can exist even in larger societies. With that said, I will let the Bard (Shakespeare 1605) have the last word: “How far that little candle throws his beams! So shines a good deed in a naughty world.”

Model Documentation

The full replication code (written in R) is available in the CoMSES Computational Model Library at: https://www.comses.net/codebases/41bc083e-b8d3-4133-83ed-150bb63a4b39/releases/1.0.0/.

Notes

These simulations were implemented in R, version 4.0.1.
The Supplemental Information contains pseudo-code for the simulation, along with a more detailed description.
At the end of an example simulation run, players in a network of \(N=300\) with default parameters hold, on average, non-neutral opinions about 64.8 other players. In a network of \(N=20,000\), this number increases to 72.3. This relatively modest increase is due to the fact that players are clustered, and an increase in population leads to an increase in the number of clusters much more so than an increase in their size. Note that it is possible they also heard both positive and negative things about a few others, which might have balanced out to a score of zero, which wouldn’t be reflected in these numbers. Given that according to Dunbar(1998), humans can only know about 150 people reasonably well, it is quite plausible that the actors in this game manage to keep track of the reputations of about half this number.
Initially, \(s_{ij}=0\) for everyone. This means that not knowing another player corresponds to being indifferent about them.
This is another, albeit much smaller difference to at least some of the literature, in which players are selected randomly, as opposed to everyone getting one shot at the game per round. Conceptually, this really makes no difference, the main reason I handle it this way is because it can be implemented in a more computationally efficient manner. My method of image score dissemination is quite demanding on processing resources, so efficiency is important.
In addition to replacing the flawed concept of perfect information with a much more realistic one, this approach also corrects a minor mathematical artifact in the conventional method: Once a player has attained the highest possible image score, he has no incentive to cooperate further, because it won’t benefit him. Consequently, the only rational choice is to defect (although this strategy is usually not even implemented, which means players are just downright ‘wasteful’ and irrational). Therefore, even an altruistically-minded person would always oscillate between the highest and second highest image score. Clearly, this is a little odd. In my methodology, this never becomes a problem. Even a player who has always cooperated will (virtually) always have someone in his immediate or at least proximate neighborhood who has not heard about his good deeds yet. Consequently there is still an incentive to be cooperative.
For the generation of a network via the Watts-Strogatz model, the R package igraph, version 1.2.5, is used.
Although my argument specifically centers around the Watts-Strogatz model and its small-world property, I also experimented with two other frequently used random graph models: The Barabási-Albert model, and the Erdős-Rényi model. These models do not have the same small-world properties as the Watts-Strogatz model. Since my argument centers around the role of clustering, which requires the small-world property to be controllable (which can be done in the Watts-Strogatz model through the parameter \(p\)), the results are not sufficiently relevant to be included in the paper.
In the original notation style of Watts & Strogatz (1998), this parameter is referred to as \(k\). However, since this letter already denotes the players’ strategies here, I use \(l\) as a substitute.
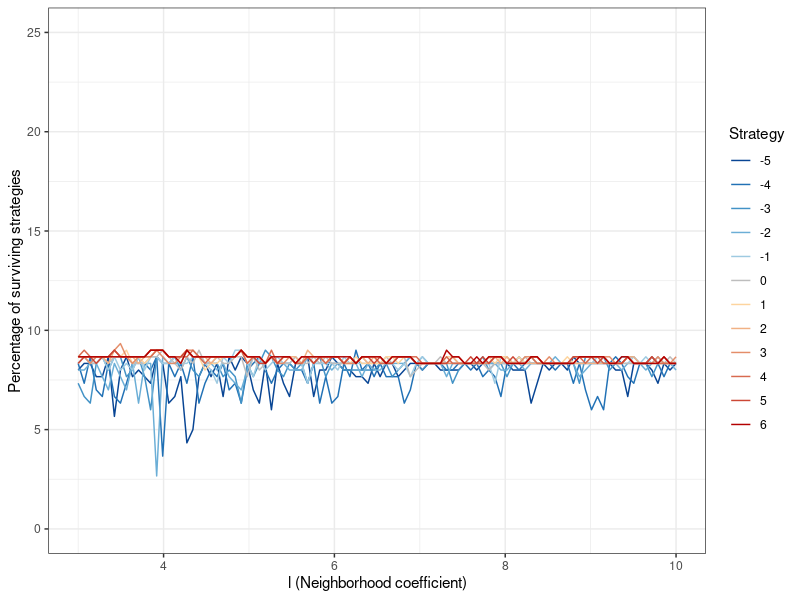
The results for the other network parameter \(l\) can be found in Figure 9 in Appendix B. The neighborhood coefficient does not appear to affect altruism.

Appendix

A: Pseudo-Code

The following pseudo-code provides a simplified overview of the simulation. Algorithm 1 details the overarching framework of the simulation. First, a Watts-Strogatz network is created according to a set of parameters: population size \(N\), rewiring probability\(p\) and neighborhood coefficient \(l\). If any of the players are isolates (i.e., they have no connections), the network is re-generated until all players are properly connected. Then, 100 generations of the population ‘live their lives’. Each of these consist of 10 rounds. In every one of these rounds, the donation game, specified in Algorithm 2, is played. After the completion of this stage, information about the players’ actions is spread through the population according to Algorithm 3. Once 10 such rounds have concluded, the number of players using each strategy is recorded. For example, after 15 generations, the strategy \(k=0\) is used by 25 players. Ergo, 8.3 percent (\(25/300=0.083\)) is the \(y\)-value for \(k=0\) at \(x=15\) in Figure 5. Finally, the players replicate, as denoted in Algorithm 4.

Algorithm 2 describes the donation game. Every member of the population gets to be player 1 once. The first thing he does is to determine who his neighbors (i.e., nodes to which he is connected through an edge) are. Of these, one is randomly selected to be player 2. Then the game begins: Player 1 determines whether his own strategy \(k_i\) is smaller or equal to his impression of his “opponent’s” image score \(s_{ij}\) . If it is, a donation takes place and player 1’s fitness is decreased by \(1\), while player 2’s fitness is increased by \(2\). Furthermore, the variable \(s_i\), which denotes whether or not player 1 has helped, is set to \(1\) . If \(k_i>s_{ij}\), no donation occurs, and \(s_i\) is set to \(-1\). Ergo, as in the classical form of the donation game without the spread of information, \(s_i\) is an objective measure of what player i has done in their role as a potential donor. However, it is only valid for the current round.

Algorithm 3 determines if and how other players actually learn about \(s_i\). For every donation game played in Algorithm 2, information is disseminated through the network as following: Since player 2 was directly involved, he always learns about the donation. His impression of player 1, \(s_{ij}\), is updated by adding \(s_i\) to it. Then his neighbors are determined. For each neighbor, a Bernoulli trial with a 50 percent chance of success is conducted. Every neighbor \(c\) for whom this trial is successful, learns about the donation and updates his image of player 1 (\(s_{ci}\)). Then all players \(h\) repeat this process and spread the information to their neighbors \(d\) with a 25 percent probability for each.

At the end of a generation, all players ‘die’ and pass on their strategies to their ‘children’. This process is outlined in Algorithm 4. Replication is modeled by calculating the relative success of each strategy compared to all others. Then, a new network is created in which the strategies are distributed accordingly. This is done as following: For each strategy \(k\), I determine the average fitness of all players who follow it. The result is a 12-element vector, containing one mean value for each strategy. In order to avoid erratic results due to outliers, I apply the inverse logit function. Then, each value is divided by the sum of the vector, to calculate the relative success of each strategy. This value is multiplied by the population size \(N\), for the number of players who will use that strategy in the next generation. This value is then rounded to the nearest whole number.

If the sum of the resulting values does not equal the population size (due to rounding error), I add or subtract randomly selected strategies until they do. This can lead to the reintroduction of strategies that have already died out (although as noted above, they never survive long). Thus, I explicitly test for the assumption that no mutant can successfully invade an evolutionarily stable strategy distribution (Hamilton 1964b). This concludes the final stage of a generation, the replication.