A Comparative Study on Apprenticeship Systems Using Agent-Based Simulation

, , ,
and
aUniversity of Otago, New Zealand; bNorwegian University of Science and Technology (NTNU), Norway
Journal of Artificial
Societies and Social Simulation 25 (1) 1
<https://www.jasss.org/25/1/1.html>
DOI: 10.18564/jasss.4733
Received: 29-Jun-2019 Accepted: 04-Nov-2021 Published: 31-Jan-2022
Abstract
In this paper, we investigate the effects of different characteristics of apprenticeship programmes both in historical and contemporary societies. Apprenticeship is one of the major means to transfer skills in a society. We consider five societies: the Old Britain system (AD 1300s−1600s), the British East India Company (AD 1600s − 1800s), Armenian merchants of New-Julfa (AD 1600s − 1700s), contemporary German apprenticeship (1990s), and the “Modern Apprenticeship” in Britain (2001). In comparing these systems, using an agent-based simulation model, we identified six characteristics which impact the success of an apprenticeship programme in a society, which we measured by considering three parameters, namely the number of skilled agents produced by the apprenticeships, programme completion, and the contribution of programmes to the Gross Domestic Income (GDI) of the society. We investigate different definitions for success of an apprenticeship and some hypothetical societies to test some common beliefs about apprenticeships' performance. The simulations suggest that a) it is better to invest in a public educational system rather than subsidising private contractors to train apprentices, b) having a higher completion ratio for apprenticeship programme does not necessarily result in a higher contribution in the GDI, and c) governors (e.g. mayors or government) that face significant emigration should also consider employing policies that persuade apprentices to complete their programme and stay in the society after completion to improve apprenticeship efficacy.Introduction
This paper studies apprenticeship as an important tool of skill transfer throughout human history. In this study, we start with two successful contemporaneous historical long-distance trading societies, namely Armenian merchants of New-Julfa (Julfa, AD \(1600s-1700s\)) and the English East India Company (EIC, AD \(1600s-1800s\)). Also, we extend our study by analysing an additional historical case, i.e. old Britain (AD \(1300s-1600s\)). A key to this study is the employment of an agent-based simulation model that is used to explore various factors impacting these societies. To make such an exploration possible, we chose the aforementioned historical societies, because we had access to more studies on their characteristics. The availability of such resources facilitates creating a bigger picture. Also, we contrast two contemporary schemes of apprenticeship (i.e. those of modern Britain (2001) and Germany (1990s)), to learn the reasons for better performance of some societies than others. This study identifies important characteristics for apprenticeship programmes based on the patterns of the investigated societies. This way, we understand mechanisms by “learning from history”, along with investigating two well studied contemporary apprenticeship models.
To clarify the subject, we wish to briefly define apprenticeship. Apprenticeship refers to a set of activities and technical training provided by a skilled practitioner in which inexperienced participants learn a profession or art (Hamilton & Hamilton 1993). Also, as suggested by Purvis et al. (2014) in meta-role modelling of artificial societies, a society needs such institutions to turn agents with the Worker meta-role (ordinary agents) into agents with the Skill meta-role. Skill transfer is a time-consuming task in which an unskilled individual develops skills under the supervision of professionals. The incentives for apprenticeship are diverse: sustainable development (UNESCO-UNEVOC 2006 p. 9), fighting youth unemployment (Plug & Groot 1998), and increasing productivity (King 2009), to name a few. Also, the importance of apprenticeship is identified by historians. For instance, Riello (2009) suggests that the Indian subcontinent lost its cotton market share in 50 years (i.e. from the 1760s to 1810s) to Europeans, because the latter had the opportunity to gradually attain relevant trading skills by accumulating experience and information. He attributes this as an important reason for British economic advancement in addition to the industrial revolution.
Nowadays the importance of apprenticeship programmes is emphasised in many countries. However, there are different frameworks for apprenticeship programmes, such as work-based training and dual systems (i.e., a combination of schools and work-based training; see Davy & Frankenberg 2018). Despite the relative success of programmes in terms of the number of skilled agents and increasing profitability, some apprenticeship programmes are accepted as more efficient than the others. Also, there are several studies on formalising apprenticeship programmes (Allais 2012; Palmer 2009).
The identification and systematic modelling of the impact of characteristics and institutions (i.e. “the rules of the game,” such as restrictions imposed by guilds; North 1990) on the performance of apprenticeship programmes, has not yet been addressed. Therefore the key questions are (a) which one of them is more important and (b) why different societies do not follow the same approach. The main purpose of this study is to address these concerns, and we employ agent-based simulation to improve our understanding of the mechanics that made some apprenticeship programmes in completely different times and locations, such as the Julfan and the German, more efficient in terms of improving societal skill level and the GDI. To achieve this general objective, we employ intuitive numbers in our models based on available shreds of evidence (e.g. discussions and economic studies). There are also other questions posed by earlier studies or policy makers which this study investigates. These questions are: a) why large companies in Britain asked for an apprenticeship programme but would not participate in it (Ryan & Unwin 2001), and b) is it helpful to ask employers for some costs to subsidise the apprenticeship programme (see discussions on South Africa’s levy-grant system).
Other studies conducted in Britain and Switzerland emphasise the importance of apprenticeship programmes in the modern context (Fuller & Unwin 2003; Müehlemann et al. 2009). It has been noted that Germany has a successful apprenticeship programme where companies invest in training apprentices (Büchel 2002; Franz & Soskice 1994). This programme has worked well enough so that it has limited the unemployment rate for under 25-year olds to around 6.7 per cent, versus 17.3 per cent across the EU (Jacobs 2017).
In the agent-based modelling literature, studies that simulated apprenticeship institutions are limited. A prior study identified the importance of apprenticeship as a means of removing untrustworthy agents (Frantz et al. 2015), and a recent study emphasised the importance of apprenticeship in Julfa as a substantial institution to improve skills, but the work did not systematically identify factors involved in apprenticeship (Sedigh et al. 2019).
Note that the present paper addresses apprenticeship for two distinct types of trades with different incentives for training (i.e. artisans and manufactures/traders) and it addresses concerns related to the Overview, Design Concepts and Details protocol that includes human decision-making (ODD + D) (see Appendix D; Müller et al. 2013). In the context of historical cases, although Julfans were known for their long-distance trading societies, they had artisans or worked with artisans who produced items traded. In this study, we concentrate on manufacturers (not traders) and artisans because of more contemporary studies on them.
The rest of this paper is organised as follows. First we concisely review these societies and identify their differences. Then we discuss the modelling approach used to simulate these systems. In the next two sections, we present the results of the simulations for manufacturers and artisans, respectively. Finally, we discuss the findings of this paper and provide future directions.
A Review of Five Systems
In this section, we proceed towards modelling apprenticeship programmes. What follows provides an overview of societies’ background and apprenticeship programmes in five different societies, namely Julfa, Germany, old Britain, the EIC, and modern Britain. We chose these societies, because a) we have access to more information about them, and b) these societies enable us to compare apprenticeship programme characteristics to improve our knowledge about alternatives and develop a more universal apprenticeship approach. First we state societies’ background to get familiar with the chosen systems. Then we compare these systems with respect to six characteristics (elaborated in paragraphs starting from 2.9). These are identified by the similarity of patterns in historical and contemporary apprenticeship programmes and verified by related studies, and they are a) trade types (artisans and manufacturers),1 b) access hurdles, c) guilds and unions, d) trainer type (companies and contractors), e) schools, and f) openness (i.e. opportunities to join the programme from other societies).
Societies’ background
In what follows, we describe the characteristics of the five societies, and how these societies possess the characteristics mentioned above.
Old Britain: In the old British apprenticeship system (AD 1300s-1600s) guilds were in effect that limited skilled agents from joining the workforce society and made apprentices pay premium costs for training (Wallis 2008). Also, bigger cities (e.g. London) hosted recruits from smaller towns who frequently left the system once they had adequate skills to work in their own town.
Armenian merchants of New-Julfa (Julfa): Armenian merchants of New-Julfa were originally from old Julfa in Armenia. They re-established a trader society in New-Julfa (near Isfahan, Iran) after their forced displacement in the early 17th century. Due to their complicated inheritance rules that created tight bonds within extended families (Herzig 1991), they formed a closed society that was run by strong social norms instead of formal rules. Based on the historical data, these traders are known to have had a “merchant school” (Aslanian 2007 p. 171) around the 1680s. A more general apprenticeship system was active in Julfa and Persia (old Iran) to transfer skills in society, wherein skilled agents employed the labour of apprentices and trained them as a substitute of paying higher wages. In Julfa, apprenticeship programmes took place informally by family members, relatives, and friends who hired or recommended trained apprentices.
The EIC: During roughly the same period (AD 1600s-1800s), a parallel system was active in Britain. The British contemporary counterpart of Julfa (i.e. the British East India Company (EIC, AD 1600s-1800s)) had a totally different perspective about managing the society. The EIC hired inexperienced apprentices, asked them to provide signed bonds, and sent them for trading to India to be trained by fellow merchants on a voluntary basis. However, EIC bonds could have been signed by totally unknown people see (Hejeebu 2005, footnote 43). Because of these considerations we do not address it in our model. In addition, we note that the EIC trainers have lower incentives to provide good training. In other words their incentives is questionable for reasons such as the time spent on training a task without any provisioned profit (i.e. they trained for immediate income).
Modern Britain: In the contemporary era, Britain has used a different scheme for apprenticeship programmes. A survey of this system around 2001 referred to the method as a “Training Market” (Ryan & Unwin 2001). During this time the government employed contractors to train apprentices and a subsidy-based system to compensate the training costs incurred. For paying contractors, the government used a weighting system to rank and pay contractors based on: (a) the skill requirement of the society, (b) the trainer’s performance (i.e. how many apprentices were trained and how successful they were in finding a job), and (c) the difficulty-level of the target skill.
Germany: The other contemporary apprenticeship system which is studied extensively is the German dual apprenticeship system (Franz & Soskice 1994). These programmes combine teaching technical knowledge in public schools, coupled with work-based training provided by certified trainers (i.e. companies). In these programmes, the government invests in providing public schools, and work-based training is provided by companies or individuals.
Next, we discuss the characteristics of these systems in detail. In the following sections, we discuss the characteristics of the system mentioned at the beginning of the section.
Characteristics and institutions
This section provides an overview of the aforementioned societies with respect to the characteristics stated earlier, namely trade type, access hurdles, workforce restriction (i.e. guilds and unions), trainer type, schools, and the openness of society. These characteristics are institutional (i.e. they are "humanly devised constraints", North 1991), the only exception is trade type.
Trade type
First we divide systems into two sub-systems based on the trade which is inspired by the German apprenticeship programme (Franz & Soskice 1994), namely ‘artisans’ and ‘manufacturers’. These trades have different requirements for skills, and trainers have distinct incentives for training.
Artisan: An artisan, such as a wood-carver or a hairdresser, trains a potential competitor but can employ the trainee’s services during the apprenticeship. For these reasons, in some societies, artisans consider those services insufficient for compensating for the costs, and ask for some payments from apprentices. In addition, some artisans use guilds as a means of restricting trained agents from getting into the system to guarantee the stability of wages in the future. These trades do not require complicated analytical skills or computations, etc. that are provided by school-based training, and the artisans are the only ones who are eligible to train others (i.e. contractors cannot replace the artisans).
Manufacturer: Alternatively, a trader’s or manufacturer’s trainee does not compete with apprenticeship providers, unlike a trained artisan. For instance, setting up a factory or starting long-distance trades require a large amount of capital when compared to a salon or to buying tools and working at home. Therefore a trained apprentice is a potential employee (not a competitor as in the case of an artisan).
Manufacturers have future benefits in training apprentices. Therefore companies train agents without asking agents for prepayment. These benefits include negotiating for paying slightly lower wages than community norms, hiring the best-trained agents, and providing training in some specific skills required for that particular manufacturing company. Note that these trades require complex knowledge and analytical skills that may require school-based training. Furthermore, these skills can also be transferred by employing third-party trainers (i.e. contractors).
Based on the aforementioned arguments, we assume that it is in the vested interest of manufacturers to put in their best efforts to train apprentices that may potentially work for them. This logic shows itself in efforts put forward to transfer all skills to the apprentices. On the other hand, in the artisan training domain, the disinclination to train artisans well has been observed by Chardin in Persia.2
In the following paragraphs, we choose the most influential characteristics for each society, based on the above-mentioned discussion. These characteristics are shown in Tables 1 and 2 for each trade type and the details of the characteristics would be discussed in the following.
| Characteristics | Julfa | Old Britain | The EIC | Germany | Modern Britain |
| Trainer type | Companies | Companies | Contractor* | Companies | Contractors |
| School | Yes | No | No | Yes | No |
| Openness of society | No | Yes | Yes | No | No |
| * In the EIC, employees trained other agents as a responsibility, so they did not have any expected profits in good training and only faced costs of spending more time. | |||||
| Characteristics | Julfa | Old Britain | Germany | Modern Britain |
| Access hurdles | No | Yes | No | Yes |
| Workforce restrictions | No | Yes | No | Yes |
| Openness of society | No | In big cities | No | No |
Access hurdles (for artisans only)
As discussed earlier, some societies had entry conditions for apprentices by asking them for premiums to compensate for training costs and as a bond to guarantee reliable behaviour on the part of apprentices. However, ‘s travelogue shows no evidence of such requirements in Julfa and more generally, in Persia (i.e. old Iran). Instead, trainers paid wages to the apprentices based on their age and skill, and both parties could freely terminate the programme.3 In contrast, in Old Britain, some rules prohibited masters from paying apprentices during some periods, and it was a norm to ask apprentices to compensate training costs by paying a premium upfront (Wallis 2008). The significant result of asking for a premium was on limiting participants’ access to apprenticeship programmes from less-prosperous individuals, because they may not be able to afford to pay training costs.
In more recent instances (i.e. German and modern British apprenticeship programmes), sometimes there is a payment for eligible apprentices, and there is no evidence of asking for payments from young apprentices4 (Franz & Soskice 1994; Ryan & Unwin 2001). In this paper, the effect of asking for a premium is abstractly considered by limiting the number of participants and imposing costs to the trainees.
Workforce Restrictions (for artisans only)
One of the prominent effects of guilds is restricting skilled people from practising their skills by having exclusive legal privileges for performing that task (Ogilvie 2014). In Old Britain, skilled people were restricted from being “freemen,”(i.e. they were not granted the “freedom of the company)” and this had adverse effects on trainees finishing apprenticeships (Wallis 2008). However, based on Chardin’s observations, no evidence of guilds is available for most skills in Iran (including Julfa).5
Due to the liberalisation of the workforce market in Germany, guilds no longer exist. However, in Britain, the effect of guilds is still present in forms of either guilds themselves or livery companies (London companies comprising trade associations and guilds).6 Unions are a means of introducing another kind of restriction in workforce societies. Unions attempt to regulate wages in a competitive labour market wherein agents are employees of other companies (e.g. in a manufacturer’s society).7 Therefore guilds are established in favour of trade profitability, while unions defend the profits of employees at some costs for trades.8
Trainer Type (for manufacturers only)
Manufacturing systems had certain types of trainers in apprenticeship programmes (contractors or potential employers). In Julfa, masters (the primary owners of the trade) trained and monitored the performance of apprentices (Aslanian 2007). Their simultaneous training and evaluation helped them to identify talented and trustworthy apprentices. On the other hand, in Old Britain, once apprenticeship programmes began, the training could be terminated if apprentices were deemed untrustworthy (i.e. the training contract would have persisted if apprentice is evaluated to have just low attainability).
In Germany, the nature of apprenticeship programmes is more complicated. Apprentices learn technical knowledge (henceforth academic skills) in public schools, and they are assessed there. At the same time, there is also work-based training that takes place by certified companies or craftsmen. After finishing the process, apprentices gain a qualification (Franz & Soskice 1994). The qualification strongly controls whether an agent is eligible to practise a profession.9 Finally, in the modern British programmes, a cost-efficient scheme was designed for training. They subsidised technical trainers, who mostly employed contractors, in addition to some public trainers, based on a scoring scheme (Ryan & Unwin 2001).10
For work-based skills, contractors collaborated with companies willing to provide a work environment for trainers (mostly small companies). This method created tendencies to sacrifice quality of teaching for quantity and to train simpler skills. In this work, we distinguish between training provided by contractors (the ones involved in the modern British programme) and non-contractors (i.e. companies as future potential employers). It should be noted that the contemporary British apprenticeship system officially uses contractors for training apprentices. Furthermore, in the EIC the training was provided by more experienced agents at the destination. The method employed in the EIC worked like that in Modern Britain — there was no motivation for trainers to train their apprentices well.
Schools (for manufacturers only)
An important attribute of these systems is associated with their emphasis on the use of schools (vocational schools) for academic skills and training purposes. Schools’ impact on system performance is twofold. On the one hand, they are a source of declarative knowledge (i.e. facts, information, and descriptive knowledge) transfer. This knowledge can be obtained by studying in schools much more easily than in work-based situations.11
The impact of declarative knowledge on the improvement of learning skills was shown by several scholars (Ahlum-Heath & Di Vesta 1986; Anderson 1982; Williams & Davids 1995).12 In addition, a school attendee obtains some skills through education (academic skills) that are important for companies with frequent revisions in their production processes (Stasz & Brewer 1999).13 This point was neglected in Old Britain, the EIC, and the apprenticeship system employed in Britain in 2001, i.e. the schools were not a compulsory part of programmes.14
Openness versus closedness (for artisans and manufacturers)
Another important attribute of apprenticeship systems concerns the proportion of apprentices that leave the system to work in other communities for reasons such as finding a job with better payments in other places.15 Henceforth, we call such societies as open for training. Some cities in Old Britain were open for training (e.g. London; Wallis 2008), but Julfa was a totally closed system, where apprentices were only employed within their society (Aslanian 2007). Due to the availability of apprenticeship programmes in Germany and Britain (in most cities) and its availability to their own residents, they are considered to be closed (i.e. the trained apprentices stay in the same community for some years).
However, another definition of openness is the availability of agents from other communities (e.g. countries) to work for lower wages than the norm in the community under study (i.e. openness for working). Openness for working is considered as a scenario in our modelling. To summarise, when a society trains apprentices who may leave, it is open for training. Furthermore, when companies of a society have the opportunity to find trained agents from other communities, it is open for work. Henceforth, by openness we mean that the system is open for training (unless stated otherwise).
Tables 1 and 2 show selected characteristics based on the trade type and specifications of various societies considered in this work. Note that the availability of these characteristics is considered to be neither good nor bad, but we consider them with respect to their impact on the decisions made by trainers and apprentices.
Summarising the characteristics associated with the systems, first, we have divided apprenticeship programmes based on the trade type (i.e. artisans versus manufacturers) for a better understanding of the societies’ characteristics. Then the openness of the society has been considered for both trade types. For complicated industries such as manufacturers, we have addressed the impact of two other characteristics: (a) the use of schools in imparting knowledge and academic skills and (b) trainer type which can be a trainer contractor or a company that trains potential employees. For apprenticeship programmes in an artisan trade, we have investigated the impact of access hurdles (i.e. asking for prepayment such as a premium) and the restrictive influence of guilds by limiting the number of authorised skilled agents.
Simulation Model of Two Types of Traders
The integrated simulation presented here is a general representation of an apprenticeship system that is built based on numbers inspired by available evidence, discussions, or empirical notions (e.g. the Pareto Principle, Backhaus 1980). In this simulation, we consider two types of agents (i.e. trainers and apprentices) and two types of trades (i.e. manufacturers and artisans). Apprentices are agents who participate in the programme to attain skills, while trainers are agents who provide training and they have diverse motivations.
The motivations of trainers to participate in the programme are based on the trade and their type; however, all of them optimise their utility functions in terms of expected profits. In a manufacturing trade where apprentices are potential employees, the company (i.e. potential employer) trains for future profits that are earned by the skills of trained agents. However, in the same trade, the contractors train an apprentice for income from the training. Therefore if a company decides to train, it has a motivation for good training. However, a contractor wants to reduce the costs of training by modifying the quality of training (i.e. they choose between good and bad training based on the expected profits). On the other hand, artisans train the agents for their income during the programme and sometimes based on community pressure. Before continuing with the model discussions, we discuss some assumptions made for representatives of the different apprenticeship systems.
Model assumptions
There are some assumptions in this model that should be clarified before further discussions of simulation. These assumptions include system characteristics that impact the expected profits of trainers and apprentices. Therefore we cover the following:
- Parameters and utility functions that are considered in connection with the calculation of expected profits;
- The importance of schools and their impact on different manufacturing companies;
- The attainability of work-based and school-based skills that represent separate aptitudes which are independent of each other;
- Reasons for changes in wages.
In this model, both apprentices and trainers calculate their expected profits over a finite horizon by taking into account a discount factor \((\alpha)\) for anticipated income. A finite horizon reflects the myopic decision-making of agents caused by workforce turnover observed in countries such as Germany (Franz & Soskice 1994). For manufacturers, as formerly discussed, we consider two skills to be obtained (i.e. school-based and work-based skills) that are essential for a good performance for employees in companies. To model the effects of skills on the outcome of companies, we use the idea of Franz & Soskice (1994) in a way that would be applicable for a discrete scenario. The output of a skilled worker \((y)\) is given by:
| \[ y=f(ed,s_{wb}),\] | \[(1)\] |
In our work, we also use Multiple Intelligence (MI) theory as a framework for the two skills discussed above.16 We use this idea by assuming that attainability for work-based skills and school-based skills is different for different individuals. Some studies suggest that motivation (henceforth, passion) and achievements are positively correlated (Kusurkar et al. 2013; Subotnik et al. 2011).17 In our model, the effect is twofold:18
- More passionate agents have a higher chance of enrolling in an apprenticeship (i.e. they are persistent in finding a trainer);
- Passion causes the apprentice to practise more, and hence, gain skills faster than non-persistent ones.
In our model, the degree of acquired work-based skills falls into three categories that are denoted by discrete numbers (these parameters represent weights for \(S_{wb}\) in Equation 1). These discrete numbers reflect classifications of skilled agents, based on the predefined thresholds (e.g. shopfitter and cabinet maker) as follows:
- Excellent (E), the skills acquired fall in the upper range of the requirement (i.e. from \(0.75\) to \(1\)) and has a value of 2,
- Adequate (AD), these agents’ skills fall in the upper-middle range of the skill requirement (i.e. from \(0.5\) to \(0.75\)) and has a value of 1,
- Inadequate which is denoted by a value of 0, wherein the acquired work-based skill is less than 0.5.
For academic skills, we use two categories by employing Boolean numbers (e.g. having or not having a high-school diploma) as follows:
- Academic (A) which is denoted by a value of 1, wherein the apprentice’s acquired academic skill is more than or equal to 0.5.
- non-academic (N) which is denoted by a value of 0, wherein the apprentice’s acquired academic skill is less than 0.5.
Note that a detailed discussion about utility functions used is presented in Appendix A. Another assumption of this model is related to wages and factors that influence them. One of the main assumptions discussed in the field of labour economics concerns the correlations between demand and supply in the market (Borjas 1999). These discussions suggest that there is a correlation between the labour supply, the labour demand, and wages, such that an excessive supply of the labour force initiates a drop in wages and vice versa, and there is a tendency for the labour market to reach an equilibrium in the long run (see Mankiw 2017, Part II for explanations about market equilibrium). On the other hand, there is some empirical evidence for stickiness of wages that suggests that wages are not adjusted quickly based on labour market behaviour for various reasons (see Blinder & Choi 1990; Kahn 1997). This issue (i.e. stickiness of wages) and its influence is addressed in our model by considering a threshold (stickiness threshold) for excess supply and demand below which there is no effect on the wages.
Algorithms
The simulation model is split into three executive procedures. The first procedure is executed with the societal level set-up, including the creation of an appropriate society as artisans or a manufacturing society. The second procedure covers the decision-making of trainer agents. The third algorithm describes the procedure of individual apprentices. In each run, these procedures are executed in sequence. Note that all loops run once per iteration. Figure 1 illustrates how two agent types interact with each other and the decision variables external to them. The trainers compare the profit of training with other alternatives (i.e. they take account of already trained agents and hiring from other communities or graduates). In parallel, agents decide whether or not to participate in the apprenticeships by taking account of demand for the skill, the cost of lost fortune over the training period, and their ability to pay fees. If two agent types decide to participate, based on the rules (e.g. restrictions on the number of trainers) and capacity of trainers, the apprenticeship begins. In each iteration the system parameters are updated, trainees may revise their decision, and new potential trainers are introduced into the system. The following paragraphs present a detail of these decision procedures.
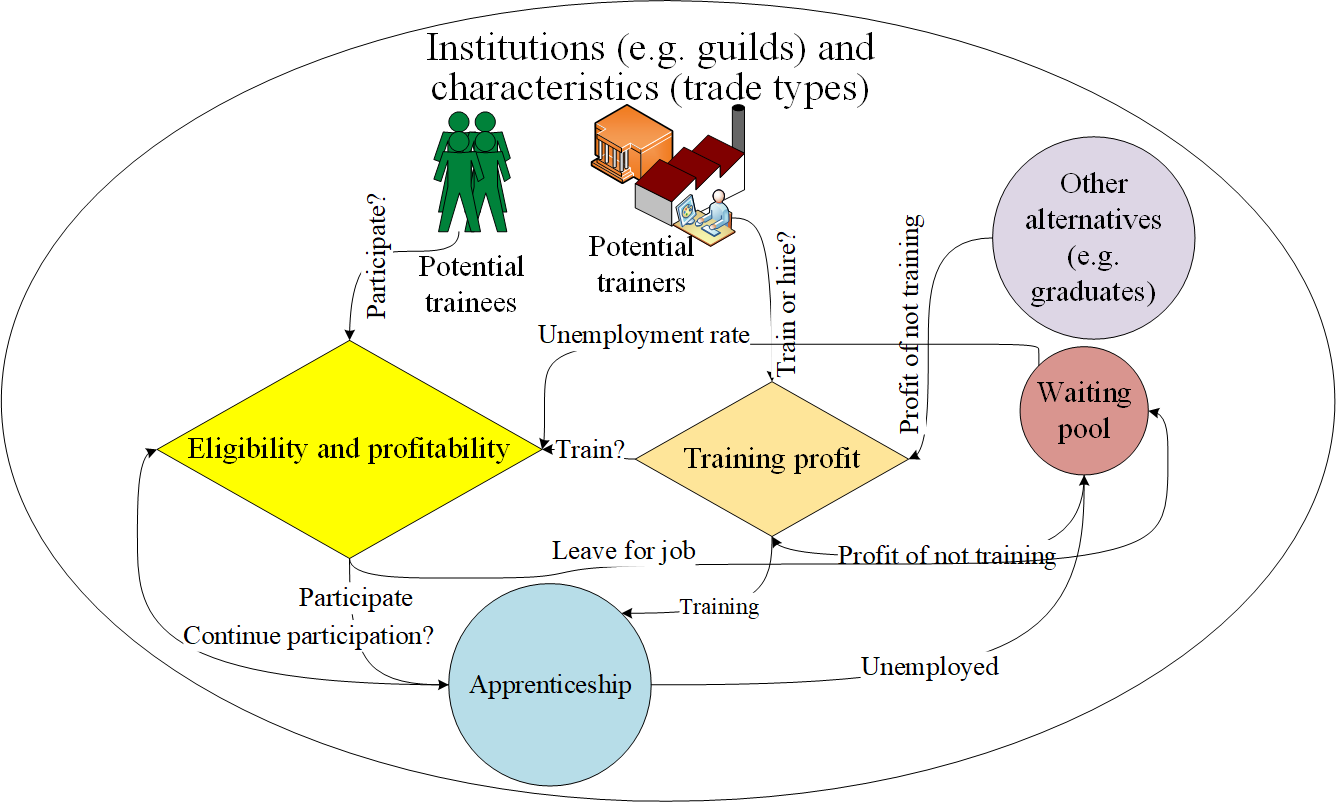
Algorithm 1 presents the steps of the societal level of the simulation. We assume that in each iteration of the simulation (which is one year), \(1000\) new agents are introduced into the apprentice system with random characteristics, and the ones who do not find a trainer leave the society at once (line 1).
Then we divide the system based on the trade type. If the trade deals with artisans, a trainer can accept a new apprentice once the recruited agent’s training has been completed (i.e. once every three years). The number of years reflects apprenticeship programmes’ duration in modern and some historical contexts.19 In each iteration, a fraction (\(R\%\)) of skilled agents are required to replace deceased or retired individuals (lines 2-3).
Furthermore, as mentioned before, the guild prevents an excess supply of skilled agents (lines 4-5). If there is no guild and the surplus supply of skilled agents exceeds its demand in addition to the stickiness threshold, the wages for that particular skill decreases by 1 (lines 6-10). In contrast, if the demand for a skill exceeds its supply and the stickiness threshold, the wages increase by 1 (lines 11-12). Finally, the probability of finding a job will be updated in the society, based on the number of unemployed agents, demand for each skill, and weighting information (line 13).
On the other hand, when the system deals with manufacturers (i.e. an apprentice is trained to be potentially hired by the company), the demand and procedures for skilled agents are relatively different (line 15). In a society where contractors train agents, demand represents the number of companies that find it more profitable to wait and hire employees from the existing apprenticeship society where the employees have already acquired skills, rather than hiring just academically educated agents and training them during work (line 16).
Afterwards, wages associated with skill \(i\) (\(w_i\)) are updated, based on the excess supply or demand, and we assume only large numbers of supply or demand can increase or decrease the wages in society (i.e. deviations of around 30% of potential demand) (lines 17-18). Finally, the outcome of the whole apprenticeship programme is decided, based on the degree of skill possessed by hired apprentices (i.e. supply) and the size of the company that hired them (i.e. demand by small or large companies) and their impact on the value of produced items. These two parameters (i.e. skill of apprentices and type of companies) are utilised to calculate the value of produced items by these skilled agents in the form of the Gross Domestic Income — i.e. the GDI (line 20).
Algorithm 2 represents the trainers’ decision-making. Note that as mentioned before, artisans and manufacturers societies have different incentives for training; hence, they are addressed separately in this algorithm. If some premium is paid by apprentices, it will be taken into account (line 1). Then the trainers are divided, based on the nature of the skill — i.e. artisans (lines 2-7) or manufacturers (lines 8-16). For artisans, the decision to participate in an apprenticeship is based on factors, such as income from trainees’ labours, paid premium, and the trainees’ impact on the workforce market.
Based on these factors, an artisan calculates the expected income of good training, bad training, and abstaining from training (lines 3-6). On the other hand, manufacturers have a different kind of motivation for training apprentices. They first decide what actions to take (i.e. do not train or provide good or bad training). We divide trainers into two subsets, namely potential employers and contractors. Quality of training has a direct impact on potential employers’ future income, so they make decisions based on factors, such as the probability of finding a skilled person, the costs of hiring and training educated agents, and the profits of providing good training.
The profit of good training is decided, based on the probability of an apprentice staying until the end of an apprenticeship programme (lines 8-10). Furthermore, contractors only consider incomes from subsidies in two ways: a) a subsidy paid, based on the number of apprentices trained and b) a subsidy paid based on the trained agents who found a job. Contractors can decrease costs by slightly reducing the quality of training (e.g. hiring low-quality tutors) (lines 12-15). Then based on their calculated profits, trainers decide how to train (lines 18-21). Finally, companies who trained agents will hire the best one (if anyone is left) or they hire academically-educated agents to train them during work (lines 23-29).
Algorithm provides an overview of how agents decide about their attendance in an apprentice programme. First, agents who can afford the programme will update their costs; if there is no premium, then everyone can afford to participate (lines 1-4). Then agents check to see if it is profitable to attend an apprenticeship programme or if it is better to start working in the labour market directly as unskilled labourers (line 5). The rest of the algorithm is about apprentices who attend the programme. Note that if the number of apprentices who find attending the programme profitable exceeds the maximum capacity, the apprenticeship system chooses the ones who are more passionate (i.e. motivated) with a higher chance (line 6).
Then the system checks to find eligible agents (i.e. agents who decided to continue with the programme and who have not completed their apprenticeship period (AP)), and then updates their APs (lines 7-8). The eligible agents first increase their apprenticeship experience and set their speed of learning(s) to 1 (line 9). Then the speed of transferring skills to an agent is updated based on the company’s size, its training policy, and the apprentice’s passion, and whether or not attending school is compulsory (lines 10-12). An example of such a procedure for a contractor who has a policy of ‘good’ training in a society without compulsory schools for a passionate apprentice (who did not attend school this year) with a work-based attainability of \(x\) can be calculated as (for employed factors see Table (???)):
| \[s=( \mathrm{s_{small}}\times \mathrm{s_{NoKnowledge}}\times \mathrm{s_{passion}} \times \mathrm{{work-BasedAttainability}})/3 = (0.85\times0.9\times1\times x)/3=0.255\times x.\] | \[(2)\] |
Furthermore, the availability of schools introduces the possibility of having more educated agents — unavailability of school reduces this opportunity to agents who pursued the education voluntarily (with a totally random chance — 50% — per run) (lines 13-19). When the society is open, each agent may leave the system with a probability of 10% (line 20).20 Moreover, an apprentice may find it more profitable to leave the apprenticeship due to the reductions in demand for skilled labour (lines 21), and with a probability of 20%, 50%, or 80% (which is varied in the experiments) the agent checks to see if it is more profitable to leave sooner and use their current skill in their employment (lines 22).
It is essential to emphasise that agents estimate their provisioned skills optimistically and assume they can attain skills faster than before (10% faster).21 Finally, at the end of their training, apprentices search for a job and at most wait for two years22 (i.e. at most while \(0.5\times waited < 1\)), and when they cannot find any jobs, they leave the waiting list to pursue other labourer jobs afterwards (lines 24-28).
| No | Name | Comment | Distribution/parameter values | Values |
| 1 | Number of potential apprentices | Per run | Constant | 1000 |
| 2 | Attainability | For work-based skill For academic | Uniform | (0.5, 1) (0, 1) |
| 3 | Passion | To learn the skill | Uniform | (0, 1) |
| 4 | Number of companies | Large : Small | Pareto principle | 20 : 80 |
| 5 | Utility function (artisans)* Large:Small | E AD | \(a_{AL}=10^{**}\) \(a_{AS}=1.5^{**}, b_{AS}=10^{**}\) | 20 : 13 10 : 11.5 |
| 5 | Utility function (manufacturers)* Large:Small | A E A AD N E N AD | \(a_{ML}=5^{**}, b_{ML}=10^{**}\) \(a_{MS}=2^{**}, b_{MS}=2^{**}\) \(c_{ML}=8^{**}\) | 30 : 14 15 : 12 10 : 12 5 : 10 |
| 6 | Speed of training | Large : Small companies Good : Bad training School : No school | Constant | 1 : 0.85 |
| 7 | Speed of learning | Passionate (\(\geq0.5\)) Not passionate (\(<0.5\)) | Constant | 1 0.9 |
| 8 | Speed of learning | School No School | Constant Probability per run | 1 0.5 |
| 9 | Initial wages (artisans)* | E AD | Adapted, based on situation | 11 7 |
| 10 | Initial wages (manufacturers)* | A E A AD N E N AD | Adapted, based on situation | 10 8 4 3 |
| 11 | Stickiness threshold | Indicates changes in labour supply/demand that do not impact the wages | Constant | 30*** |
| 12 | Discount factor \((\alpha)\) | All agents | Normal \((\mu, \sigma)\) | (0.9, 0.033) |
| 13 | Years (considered for calculating profit) | Constant | - | 6 |
| 14 | Maximum waiting time (years) | To search for jobs | Constant | 2 |
| 15 | Weight of the past information | Apprentices Companies | Constant | 03 0.5 |
| * Note that A and N indicate having and not having academic skills, respectively. Also, E and AD indicate possessing excellent and adequate work-based skills, respectively (see Appendix B for more explanations). | ||||
| ** These parameters corresponds to utility functions of manufacturers and artisans and are constant coefficients indicating the importance of work-based skills and educations for large and small manufacturers/artisans (see Appendix A for utility function). | ||||
| *** We check the impact of this parameter on simulation (see Appendix C). | ||||
In the simulation, we used parameter values shown in Table 3 (see Appendices B and C for an explanation of chosen values and a sensitivity analysis, respectively). In the following sections, we provide results of this simulation for manufacturers and artisans, respectively. The simulation was initialised with random values for probabilities to be learnt by the agents. Also, row numbers 9 and 10 of Table 3 shows the initial wages that the simulation was started with. Some of the simulation constants (e.g. Pareto principle) are chosen based on empirical studies (see Appendix B for a description of chosen values). Other simulation constants are chosen such that they reflect our information about those societies (e.g. sustainability of apprenticeship programmes). We have performed a sensitivity analysis to test the impact of these values (Appendix C).
We used 30 different runs for each system and then averaged their results. We evaluated the simulation results by averaging different runs to obtain an acceptable statistical inference about the system’s behaviour. Note that the law of large numbers states that the average of performing the same experiment converges to the distribution mean (von Luxburg & Schölkopf 2011). Different scholars have mathematically proved this theory (e.g. see Etemadi 1981). It is suggested that 30 experiments are sufficient (Sedlmeier & Gigerenzer 1997). We assume that each iteration reflects a year. For all these societies we simulated the system for 300 iterations (corresponding to the longest sustained apprenticeship programme).
Results of Apprenticeship for Manufacturers
In this section, we discuss the results of the simulation for manufacturers, considering eight different combinations of three characteristics (indicated in Table 1).
Table 4 indicates characteristics for the eight simulated societies and societies they represent. The set-ups (i.e. societies) are identified by a prefix (M.) that represents the trade type of manufacturing. Additionally, each society can be identified by the first letter of the characteristics, namely S, O, C that are representatives of compulsory school, openness of the system, and company trader, respectively. We used a Boolean index to indicate whether such an attribute is included (i.e. 1) or not (i.e. 0). Likewise, in this table a tick indicates that the society includes that attribute, and a cross indicates the society does not include that attribute.
Moreover, we assumed 20% of agents might check for job opportunities during their apprenticeship, and may leave the programme if they find leaving the apprenticeship more profitable (see Appendix C for a sensitivity analysis). Note that the threshold used for the stickiness of wages is considered to be 30 (other thresholds did not impact the system significantly; See Appendix C). Furthermore, for simplicity, we use academic and non-academic as shorthand for having and not having the school-based skill, respectively. For excellent and adequate skills acquired in a work-based training, we use excellent and adequate, and will not explicitly mention work-based skills any more.
| Characteristics | M.S0O0C1 (Modern Britain) | M.S0O0C1 | M.S0O1C0 (EIC/Old Britain) | M.S0O1C1 | M.S1O0C0 | M.S1O0C1 (Julfa/Germany) | M.S1O1C0 | M.S1O1C1 |
| School | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ |
| Open | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ |
| Company | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ |
What follows discusses three scenarios (A, B, and C) studied for manufacturers. The assessed three scenarios for apprenticeship systems are as follows:
- Training to satisfy the labour market demand;
- Training more than expected labour market demand by relaxing restrictions due to unions’ considerations;
- Openness for skilled agents from other countries to join and work in the society.
The first scenario, Scenario A, is inspired from the German apprenticeship programmes, where some certified companies were allowed to train apprentices (Franz & Soskice 1994). Overall, the unions are the means to try to defend workers’ interests such as guilds in an artisan’s society with different means. This scheme aims to reduce the risks by stabilising the apprenticeship programme (i.e. reducing unemployment risks for trainers) and control the costs of contractors imposed on the governor.
The difference between Scenario B and Scenario A is about relaxing regulations, considering the restrictions on the number of trainers that controls the number of apprentices attending the programme (i.e. unions). In this scheme of the apprenticeship programme, societies invest in training to address two issues raised by the skills shortage in a society, namely: a) high wages and b) costs incurred to the system due to the lack of skilled agents needed by companies. Using a higher number of trainers (i.e. 180 and 200, see Table 2) in Scenario B represents when there is no union to control the companies’ training capacity (to reduce unemployment risks) or the contractors’ appetite to increase their capacity to make the most profits.
| Scenario | Name | Comment | Distribution | Values |
|---|---|---|---|---|
| A–C | Number of contractors | Constant | 10 | |
| A–C | Number of companies | Large:Small | Constant | 20:80 |
| A–C | Capacity for training | Large companies | 5 | |
| A–C | Small companies | Constant | 1 | |
| A&C:B\(^*\) | Contractors | 12:20 | ||
| A&C:B\(^*\) | Maximum number | Companies | Capacity \(\times\) (the maximum | 106:180 |
| A&C:B\(^*\) | of apprentices | Contractors | number of participants) | 120:200 |
| A&B | Probability of leaving\(^{**}\) | Open communities (per run) | Constant | 0.1 |
| \(^{*}\)A&C:B, means A and C have the same parameters versus B with a different parameter. | ||||
| \(^{**}\)Discussed in endnote 20. | ||||
In scenario C, we explore the impact of the influx of workers from other communities. This mirrors the situation of Britain during its modern apprenticeship programme (McCollum & Findlay 2015). This interpretation of openness for Scenario C considers systems that cope with immigration rather than emigration, i.e. some skilled agents move into the community to work instead of leaving apprenticeship programmes to work in other communities. Therefore in these systems, immigrants are not aware of a wage norm (e.g. they moved due to unfortunate situations in their home country). Some studies indicate that the presence of both legal and illegal immigrants in a society triggers tendencies in companies to hire them and pay them lower wages (see McCollum & Findlay (2015; Ruhs & Anderson 2010)). We address the impact of this tendency by considering some negotiation advantages for companies that can hire from other communities (see Appendix B for explanation).
The aim of this systematic exploration is to identify the extent to which workforce liberalisation impacts the market in terms of apprenticeship programmes. The common values employed for these scenarios are presented in Table 3 (see Appendix B for a justification for chosen values).
Impact on programme completion
Before discussing our results, note that results for Scenario C only concern closed societies (i.e. \(O_0\)). Now we discuss the results of programme completion for each of the eight simulated societies considering Scenarios A to C. As can be seen in Figure 2, the systems producing the highest completion ratio for Scenarios A –C are societies \(M.S_0O_0C_1\) and \(M.S_1O_0C_1\) where the systems are closed (i.e. \(O_0\)) and companies train the apprentices (i.e. \(C_1\)). Moreover, Scenario A, \(M.S_0O_1C_0\) and \(M.S_1O_1C_0\) are systems with the least programme completion (see Figure 2). This emphasises the adverse effect of the combination of openness (i.e. \(O_1\)) and contractor trainers (i.e. \(C_0\)) on the decisions made by trainers about finishing the programme.23
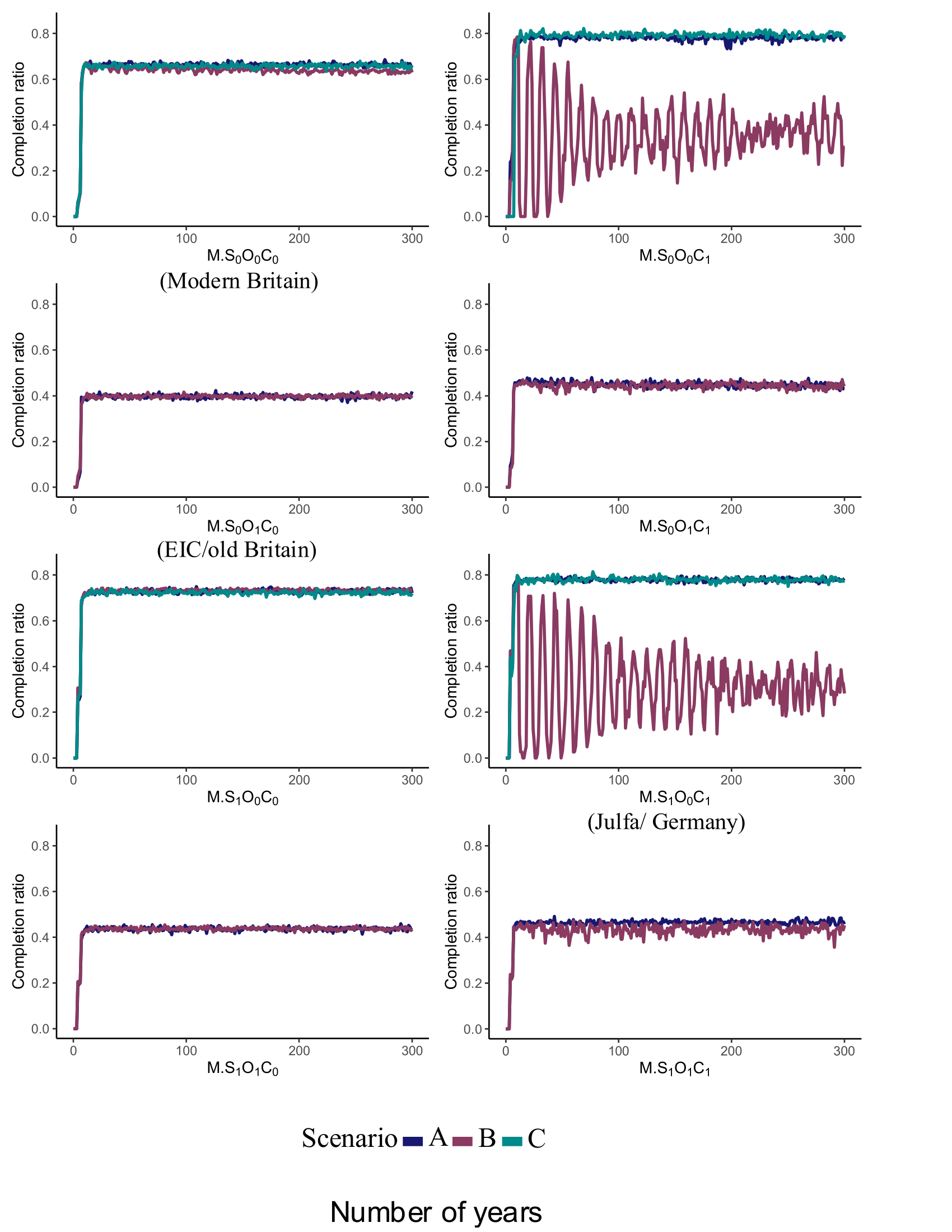
For Scenario B, the same as Scenario A, closed systems had a better programme completion ratio. However, in closed societies those companies that train apprentices (\(O_0C_1\)) had a significant reduction in the programme completion. Also \(M.S_1O_1C_1\)) had a slight decrease in completion ratio in comparison with Scenario A. The programme completion for systems run by contractors perform almost the same as Scenarios A and C. Also, as can be seen in Figure 2, for societies \(M.S_0O_0C_1\) and \(M.S_1O_0C_1\) in Scenario B, there is a significant variation in terms of the programme completion at first. However, these changes decrease over time.
Now let us focus on the systems similar to the German apprenticeship programme and Julfa which is system \(M.S_1O_0C_1\). It can be observed that this system is working well as anticipated, with 77.5% completing the apprenticeship (this is consistent with the German system).24 This consistency stems from factors, such as the requirement to complete the programme to earn a qualification (i.e. low probability of checking for jobs).
We know that in countries such as Britain, such a rule was not in effect, and one can even assume that contractors may encourage trainees to search for a job during the programme to earn their subsidies faster. Therefore such societies are highly likely to behave worse (see Appendix C for a sensitivity analysis).
Impact on the GDI
Another method to measure the success of an apprenticeship programme is assessing its contribution to the Gross Domestic Income (GDI) of the society, based on items manufactured by hired apprentices (see Figure 3).
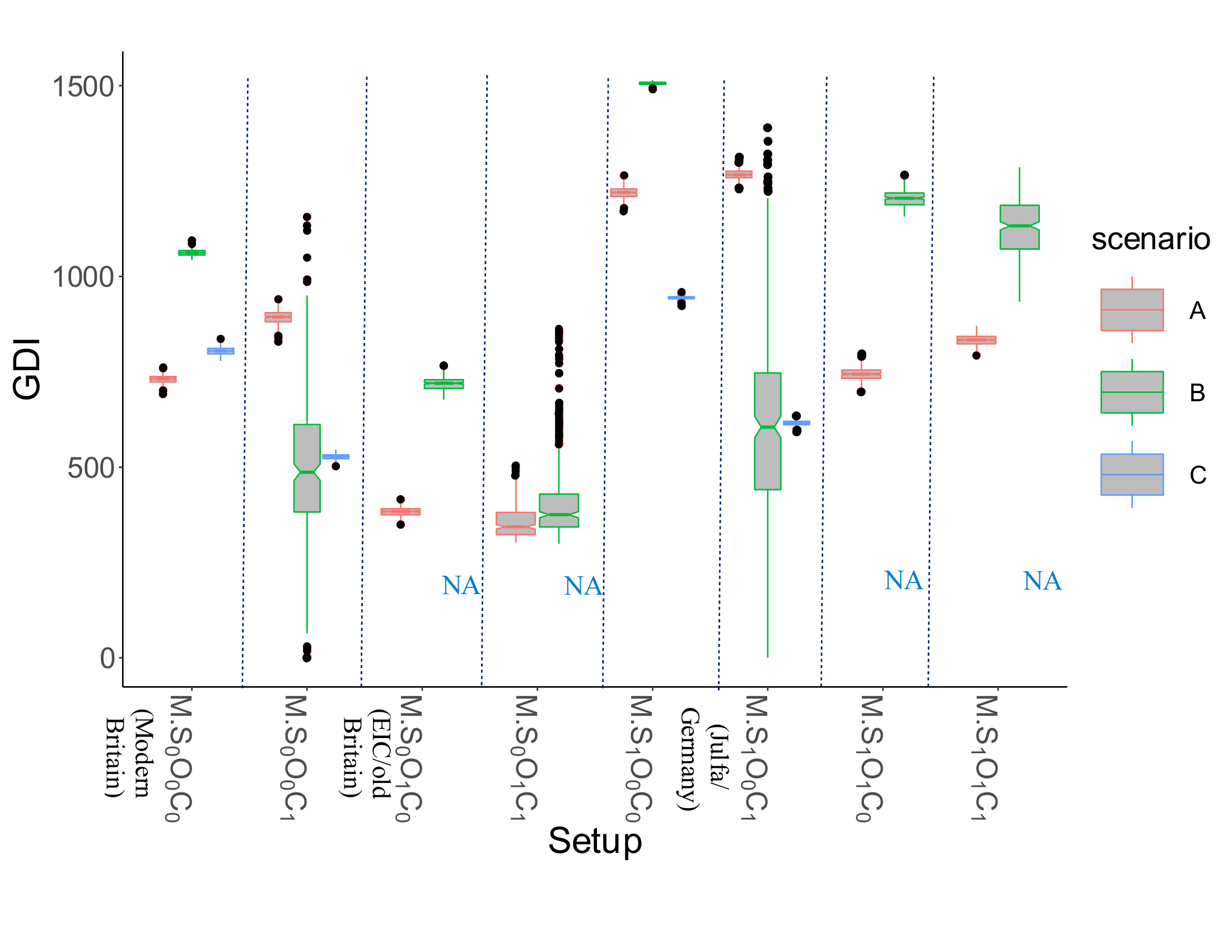
As can be seen, in Scenario A, societies \(M.S_1O_0C_0\) and \(M.S_1O_0C_1\) have a higher GDI (see Figure 3) than other systems wherein compulsory schools (\(S_1\)) are coupled with closedness (\(O_0\)). Furthermore, societies \(M.S_0O_1C_1\) and \(M.S_0O_1C_0\) (the simulated EIC) have the lowest GDI, and the rest of systems perform similarly. To have a better analysis, we also conducted a Wilcoxon test that indicates that: a) the closedness of society (\(O_0\)), b) compulsory schools (\(S_1\)), and c) being trained by companies (\(C_1\)) improves apprenticeship performance (\(p <0.01\)).
As, can be seen, Scenario B changes the patterns of contribution to the GDI. Non-parametric tests25 confirm that the changes in the GDIs for all societies are significant (\(p<0.01\)). However, Scenario B only worsened the contributed GDIs for societies \(M.S_0O_0C_1\) and \(M.S_1O_0C_1\) (i.e. closed societies wherein companies trained apprentices). Note that in both \(M.S_0O_0C_1\) and \(M.S_1O_0C_1\), the GDI decreased to less than 60% of the former scenario.
When we compare Scenarios C and A, it is noted that the only system where its contributed GDI was improved was \(M.S_0O_0C_0\), which is similar to modern Britain. Also, British companies could hire workers from other communities around the same years (see McCollum & Findlay 2015). The opportunity of hiring from other societies and consideration about the costs of free academic training for all apprentices by the government may be some of the reasons for not employing the German scheme in Britain.
Impact on wages and the number of skilled agents
Table 6 shows the total number of skilled agents, including the apprentices who are still attending apprenticeship programmes. As can be seen, in Scenario A, the number of educated agents with excellent skills has the highest value in \(M.S_1O_0C_1\) (61.1), and that is more than the total number of skilled agents in societies \(M.S_0O_1C_0\) and \(M.S_0O_1C_1\). Overall, societies with compulsory schools (\(S_1\)) outperform other systems in developing skilled agents (‘Total Skilled’ in Table 6). Only society \(M.S_0O_0C_1\) (where companies train in a closed system) performs better than \(M.S_1O_0C_1\) and \(M.S_1O_1C_1\) (open societies with schools). System \(M.S_0O_1C_0\) (the EIC) has more poorly skilled agents in comparison with society \(M.S_1O_0C_1\) (Julfa) as stated by Fryer (1698) (as we quoted in the introduction). For Scenario A, a Spearman correlation test indicates a strong and positive correlation (i.e. 0.96) between the number of skilled agents and the GDI (\(p <0.01\)).
| Part 1 (Societies \(M.S_0O_0C_0\)-\(M.S_0O_1C_1\)) | |||||
| Set-up | Scenario | \(M.S_0O_0C_0\) (Modern Britain) | \(M.S_0O_0C_1\) | \(M.S_0O_1C_0\) (EIC/Old Britain) | \(M.S_0O_1C_1\) |
| Non-academic and adequate | A B C | 68.4\(\pm\)6.1 119.4\(\pm\)11.0 67.0\(\pm\)9.7 | 67.2\(\pm\)4.3 47.7\(\pm\)21.1 40.2\(\pm\)6.2 | 45.7\(\pm\)4.0 76.2\(\pm\)6.4 - | 34.9\(\pm\)5.7 41.1\(\pm\)14.1 - |
| Non-academic and excellent | A B C | 4.3\(\pm\)0.4 8.8\(\pm\)0.9 4.2\(\pm\)0.6 | 26.8\(\pm\)1.1 21.9\(\pm\)9.6 15.9\(\pm\)2.2 | 2.8\(\pm\)0.3 4.8\(\pm\)0.4 - | 12.6\(\pm\)2.1 14.7\(\pm\)5.1 - |
| Academic and adequate | A B C | 3.8\(\pm\)0.4 6.4\(\pm\)0.6 3.8\(\pm\)0.6 | 6.9\(\pm\)0.6 5.0\(\pm\)2.2 4.2\(\pm\)0.7 | 2.5\(\pm\)0.3 4.2\(\pm\)0.4 - | 3.4\(\pm\)0.6 4.1\(\pm\)1.3 - |
| Academic and excellent | A B C | 0.4\(\pm\)0.4 0.5\(\pm\)0.3 0.3\(\pm\)0.3 | 16.2\(\pm\)0.5 22.2\(\pm\)1.3 11.1\(\pm\)1.3 | 0.2\(\pm\)0.1 0.3\(\pm\)0.1 - | 1.8\(\pm\)0.6 2.1\(\pm\)1.1 - |
| Total Skilled | A B C | 76.9\(\pm\)6.1 135.1\(\pm\)11.1 75.3\(\pm\)9.7 | 117.1\(\pm\)4.5 96.8\(\pm\)23.3 71.4\(\pm\)6.7 | 51.2\(\pm\)4.0 85.5\(\pm\)6.4 - | 52.7\(\pm\)6.1 62.0\(\pm\)15.1 - |
| Part 2 (Societies \(M.S_1O_0C_0\)-\(M.S_1O_1C_1\)) | |||||
| Set-up | Scenario | \(M.S_1O_0C_0\) | \(M.S_1O_0C_1\) (Julfa/Germany) | \(M.S_1O_1C_0\) | \(M.S_1O_1C_1\) |
| Non-academic and adequate | A B C | 45.5\(\pm\)3.3 79.9\(\pm\)5.2 44.7\(\pm\)5.5 | 51.0\(\pm\)2.9 33.2\(\pm\)17.0 29.7\(\pm\)4.2 | 32.7\(\pm\)2.2 54.7\(\pm\)3.3 - | 41.3\(\pm\)2.4 60.8\(\pm\)5.2 - |
| Non-academic and excellent | A B C | 12.5\(\pm\)1.0 21.8\(\pm\)1.2 12.3\(\pm\)1.6 | 21.6\(\pm\)1.3 16.5\(\pm\)9.1 12.6\(\pm\)1.7 | 8.2\(\pm\)0.6 13.7\(\pm\)0.9 - | 15.3\(\pm\)1.0 22.3\(\pm\)2.1 - |
| Academic and adequate | A B C | 36.8\(\pm\)1.9 78.7\(\pm\)5.0 36.1\(\pm\)4.4 | 32.3\(\pm\)1.5 24.1\(\pm\)11.6 19.2\(\pm\)2.7 | 25.3\(\pm\)1.2 42.1\(\pm\)1.8 - | 24.6\(\pm\)1.3 36.6\(\pm\)3.0 - |
| Academic and excellent | A B C | 0.4\(\pm\)1.9 25.2\(\pm\)2.7 14.8\(\pm\)2.1 | 61.1\(\pm\)13.4 97.5\(\pm\)8.4 49.4\(\pm\)5.4 | 8.5\(\pm\)0.9 14.2\(\pm\)1.3 - | 16.0\(\pm\)1.9 23.7\(\pm\)3.5 - |
| Total Skilled | A B C | 95.2\(\pm\)4.4 205.6\(\pm\)7.8 107.9\(\pm\)7.5 | 166.0\(\pm\)13.9 171.3\(\pm\)24.0 110.9\(\pm\)7.5 | 74.7\(\pm\)2.7 124.7\(\pm\)4.1 - | 97.2\(\pm\)3.5 143.4\(\pm\)7.3 - |
In Scenario B, the tendency to train more agents increases the number of skilled agents in all societies, except for \(M.S_0O_0C_1\). However, this increase is more evident for societies where contractors train apprentices who are identified by \(C_0\). Only \(M.S_0O_1C_0\) performs worse than \(M.S_1O_1C_1\) in terms of increasing the number of skilled agents, which implies a lower impact of the excessive number of skilled agents on contractors’ performance. Note that, comparing the number of skilled agents and the GDI associated with societies in Scenario B (see Figure 3 and Table 6) convinces us that the presence of more highly skilled agents in a society does not necessarily mean a better GDI. This result is intuitive if we keep in mind that high-skilled agents are paid more and cannot increase small companies’ profitability significantly.
However, in Scenario C, the number of skilled agents decreased in all societies, except \(M.S_1O_0C_0\). Interestingly, less demand for skilled agents increases the proportion of agents with academic and excellent skills in \(M.S_0O_0C_1\) and \(M.S_1O_0C_1\) (societies in which companies train agents). Therefore the indicators for Scenario A versus Scenario C, measured by the ratio \(Academic And Excellent / Total Skilled\), show an increase from 14% and 36% to 16% and 45% for societies \(M.S_0O_0C_1\) and \(M.S_1O_0C_1\), respectively. The increase in the number of skilled agents may imply that some of the skilled agents are redundant; hence they cannot participate in productive jobs. Also, the overall decrease in the number of skilled agents indicates a decrease in the number of trained apprentices in the society.
Note that in Scenario B, in comparison with Scenario A, for societies \(M.S_0O_1C_1\) and \(M.S_0O_1C_0\) (EIC), even training a higher number of agents cannot guarantee the availability of enough skilled agents for companies. Also, by training more agents, society \(M.S_0O_0C_1\) faced a shortage of skilled agents. This is because of reactions of apprentices and companies to the supply and demand for trained apprentices (see Figures 1 and 2). This myopia in human decisions is observed by other studies (Farmer 1997).26
Table7 presents wages of skill levels for different societies and scenarios. Comparing Scenarios A and B, only \(M.S_0O_0C_0\) (modern Britain) and \(M.S_1O_0C_0\) had a significant decrease in wages. However, societies \(M.S_1O_0C_1\) and \(M.S_1O_1C_1\) (which are two other societies with more than 130 total skilled agents), did not have a decrease in wages. Note that society \(M.S_1O_0C_1\) has an increase in the number of agents with academic and excellent skills, but who cannot improve small companies’ profits. Therefore the lower bound for wages is determined by the wages of low-skilled agents for whom society faces a shortage. Also, society \(M.S_1O_1C_1\) has a uniform distribution of skills so that individual excessively skilled agents would not meet the threshold. However, this uniform distribution of skills improves the contribution to the GDI, in comparison with \(M.S_1O_0C_1\), by the availability of skilled agents.
| Part 1 (Societies \(M.S_0O_0C_0\)-\(M.S_0O_1C_1\)) | |||||
| Set-up | Scenario | \(M.S_0O_0C_0\) (Modern Britain) | \(M.S_0O_0C_1\) | \(M.S_0O_1C_0\) (EIC/Old Britain) | \(M.S_0O_1C_1\) |
| Wage non-academic and adequate | A B C | 4.0\(\pm\)0.1 2.0\(\pm\)0.2 4.0\(\pm\)0.1 | 4.0\(\pm\)0.1 4.0\(\pm\)0.1 4.0\(\pm\)0.1 | 4.0\(\pm\)0.1 4.0\(\pm\)0.1 - | 4.0\(\pm\)0.1 4.0\(\pm\)0.1 - |
| Wage non-academic and excellent | A B C | 8.9\(\pm\)0.4 6.8\(\pm\)0.4 6.3\(\pm\)0.3 | 8.9\(\pm\)0.4 8.5\(\pm\)0.6 8.9\(\pm\)0.7 | 8.8\(\pm\)0.6 8.9\(\pm\)0.4 - | 8.9\(\pm\)0.4 8.9\(\pm\)0.4 - |
| Wage academic and adequate | A B C | 11.0\(\pm\)0.2 10.8\(\pm\)0.3 10.1\(\pm\)0.3 | 11.0\(\pm\)0.2 11.0\(\pm\)0.2 10.9\(\pm\)0.4 | 11.0\(\pm\)0.2 11.0\(\pm\)0.2 - | 11.0\(\pm\)0.2 11.0\(\pm\)0.2 - |
| Wage academic and excellent | A B C | 13.0\(\pm\)0.2 12.8\(\pm\)0.3 12.1\(\pm\)0.3 | 13.0\(\pm\)0.2 13.0\(\pm\)0.2 12.9\(\pm\)0.4 | 13.0\(\pm\)0.2 13.0\(\pm\)0.2 - | 13.0\(\pm\)0.2 13.0\(\pm\)0.2 - |
| Part 2 (Societies \(M.S_1O_0C_0\)-\(M.S_1O_1C_1\)) | |||||
| Set-up | Scenario | \(M.S_1O_0C_0\) | \(M.S_1O_0C_1\) (Julfa/Germany) | \(M.S_1O_1C_0\) | \(M.S_1O_1C_1\) |
| Wage non-academic and adequate | A B C | 4.0\(\pm\)0.1 4.0\(\pm\)0.1 4.0\(\pm\)0.1 | 4.0\(\pm\)0.1 4.0\(\pm\)0.1 4.0\(\pm\)0.1 | 4.0\(\pm\)0.1 4.0\(\pm\)0.1 - | 4.0\(\pm\)0.1 4.0\(\pm\)0.1 - |
| Wage non-academic and excellent | A B C | 8.9\(\pm\)0.4 6.1\(\pm\)0.1 8.8\(\pm\)0.7 | 8.9\(\pm\)0.4 8.7\(\pm\)0.5 8.9\(\pm\)0.7 | 8.9\(\pm\)0.4 8.9\(\pm\)0.5 - | 8.9\(\pm\)0.4 8.9\(\pm\)0.4 - |
| Wage academic and adequate | A B C | 10.6\(\pm\)0.3 7.2\(\pm\)0.2 9.9\(\pm\)0.2 | 10.9\(\pm\)0.3 10.8\(\pm\)0.3 10.9\(\pm\)0.4 | 11.0\(\pm\)0.2 10.9\(\pm\)0.3 - | 11.0\(\pm\)0.2 11.0\(\pm\)0.2 - |
| Wage academic and excellent | A B C | 13.0\(\pm\)0.2 11.3\(\pm\)0.1 11.9\(\pm\)0.3 | 12.9\(\pm\)0.3 12.9\(\pm\)0.3 12.9\(\pm\)0.4 | 13.0\(\pm\)0.2 13.0\(\pm\)0.2 - | 13.0\(\pm\)0.2 13.0\(\pm\)0.2 - |
Comparing Scenario A and C, only \(M.S_0O_0C_0\) and \(M.S_1O_0C_0\) had a significant decrease in wages. As can be seen, in \(M.S_0O_0C_0\), the wages for agents with academic skills or excellent skills decreased. Also, in society \(M.S_1O_0C_0\), the largest wage difference is associated with academic and excellent skills. This is because of the opportunity of hiring agents with academic skills from other societies. Overall, more demand for low-skilled agents and less participation by large companies causes a lower number of agents to attend an apprenticeship and finish the programme in Scenario C in comparison to Scenario A (see Table (???)).
Results of apprenticeships for artisans
The specific parameters for apprenticeships by artisans are presented in Table 3. As can be seen, artisans have limited training capacity (i.e. they accept only one new apprentice per run). Moreover, for the model to be more realistic, we assumed only some artisans accept apprentices and those who accept them will do so once in three years. The number of trainers considered for the system is for each run, and we considered a trainer as a representative for a group of three possible trainers (i.e. 100 artisans accept participants in each run). The agents already training decide based on the behaviour of similar training agents (i.e. if a similar agent decides not to train, they reduce the quality of training).
What has been discussed earlier (i.e. participation by a limited number of artisans), impacts apprentices’ decisions by assuming a 10% chance of being a trainer in the system in the near future;27 hence, they have an income that is the same as the paid costs in the future. For more explanation about the parameters used see Appendix B.
| Name | Description | Distribution | Values |
|---|---|---|---|
| Number of trainer artisans | Constant | 100 | |
| Capacity | Small companies | Constant | 1 |
| Large companies | 1 | ||
| Probability of leaving the system | When system is open (per run) | Constant | 0.1 |
For modelling apprenticeship programmes with respect to artisans, we chose three characteristics, namely:
- Asking for a premium;
- The degree of openness towards candidates of other communities seeking to join apprenticeship programmes;
- Benefiting from guilds as a mediator to hedge already skilled artisans’ benefits (see Table 9 ).
Table 9 presents characteristics for the eight simulated societies and real societies they represent. The set-ups (i.e. societies) are identified by a prefix (A.) as a representative for the trade type of artisans. In addition, each society can be identified by the first letter of the characteristics, namely P, O, and G that are representatives of the characteristics listed above (premium, openness, guilds). We used a Boolean index to indicate whether such an attribute was included (i.e. 1) or not (i.e. 0). Likewise, in this table a tick indicates the society includes that attribute, and a cross indicates the society does not include that attribute.
Table 10 represents an overview of the results. As can be seen, we do not consider academic skills for artisans (the activities are concerned with making or doing things by hand), and skills are divided into Adequate and Excellent. To obtain the GDI, we employed the values in Table 3 . Simulation started with wages equal to 7 and 11 for agents with adequate and excellent skills, respectively. The following paragraphs discuss the impact of the society’s characteristics on the agents’ behaviour.
| Characteristics | A.P0O0G0 (Julfra/Germany) | A.P0O0G1 (Modern Britain) | A.P0O1G0 | A.P0O1G1 | A.P1O0G0 | A.P1O0G1 (Old Britain) | A.P1O1G0 | A.P1O1G1 (Old Britain) |
| Premium | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ |
| Open | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ |
| Guilds | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ |
| \(^{1}\) Note that in old Britain both closed and open societies were presented. | ||||||||
| Part 1 (Societies \(A.P_0O_0G_0\)-\(A.P_0O_1G_1\)) | ||||
| Set-up | \(A.P_0O_0G_0\) (Julfa/Germany) | \(A.P_0O_0G_1\) (Modern Britain) | \(A.P_0O_1G_0\) | \(A.P_0O_1G_1\) |
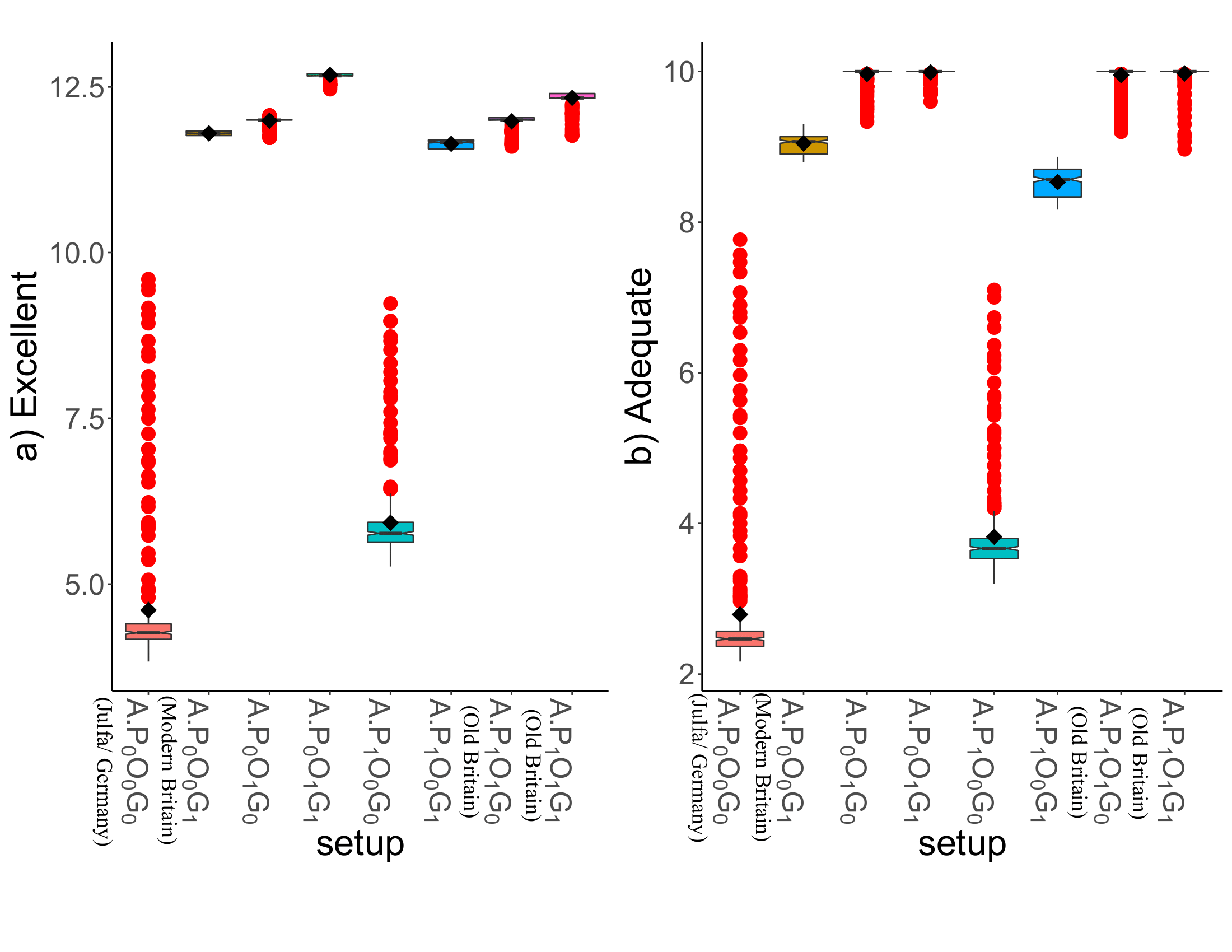
| Wage adequate | 3\(\pm\)1.5 | 9.0\(\pm\)0.2 | 9.9\(\pm\)0.3 | 9.9\(\pm\)0.3 |
| Wage excellent | 4.9\(\pm\)1.6 | 11.8\(\pm\)0.1 | 12.0\(\pm\)0.1 | 12.7\(\pm\)0.1 |
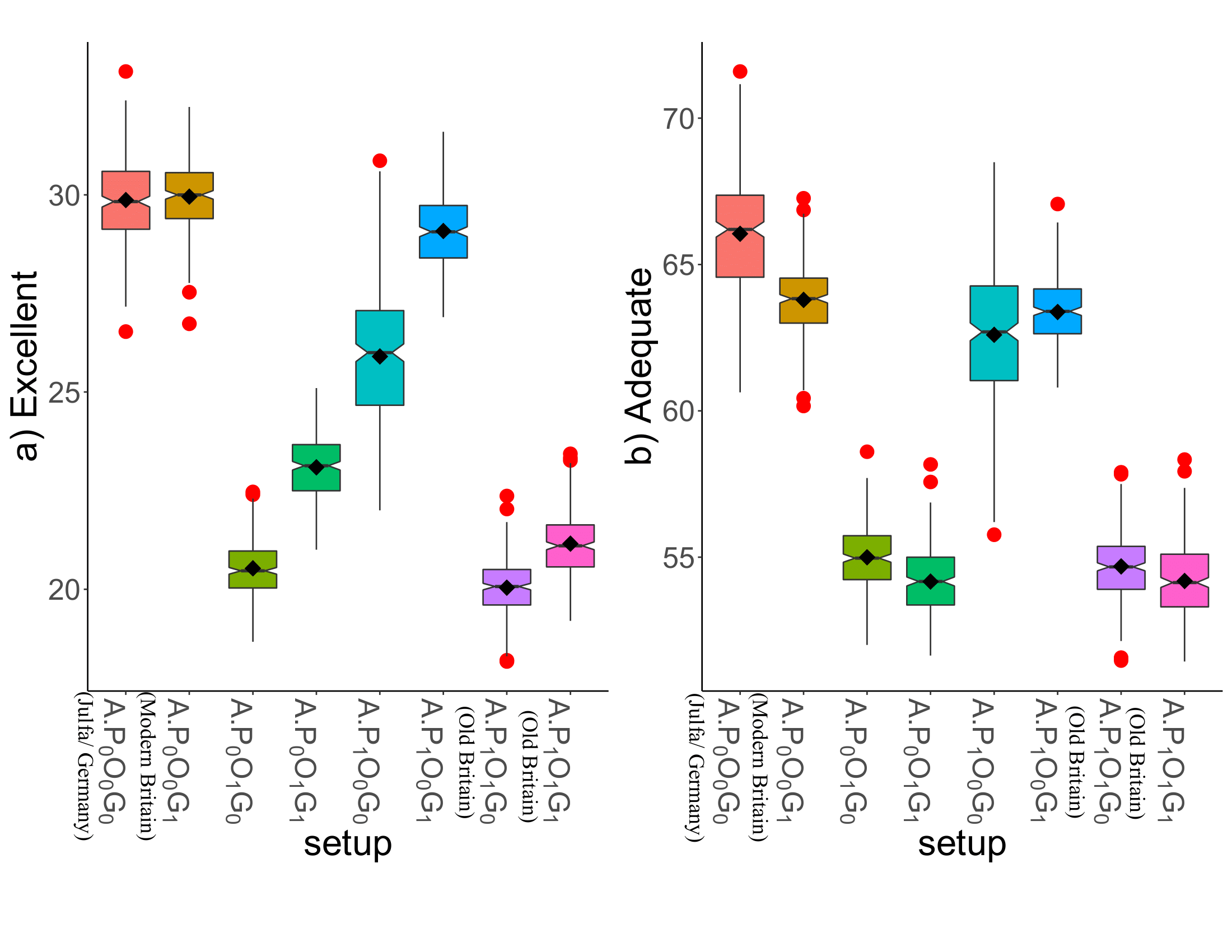
| Number of adequate | 65.7\(\pm\)3.8 | 63.5\(\pm\)2.7 | 54.8\(\pm\)2.0 | 54.0\(\pm\)2.3 |
| Number of excellent | 30.0\(\pm\)1.3 | 30.2\(\pm\)1.5 | 20.7\(\pm\)1.3 | 23.2\(\pm\)1.1 |
| Total Skilled | 95.7\(\pm\)4.0 | 93.7\(\pm\)3.1 | 75.5\(\pm\)2.4 | 77.2\(\pm\)2.5 |
| Programme completion (%) | 70.6\(\pm\)3.4 | 70.9\(\pm\)2.0 | 59.3\(\pm\)1.4 | 58.5\(\pm\)1.2 |
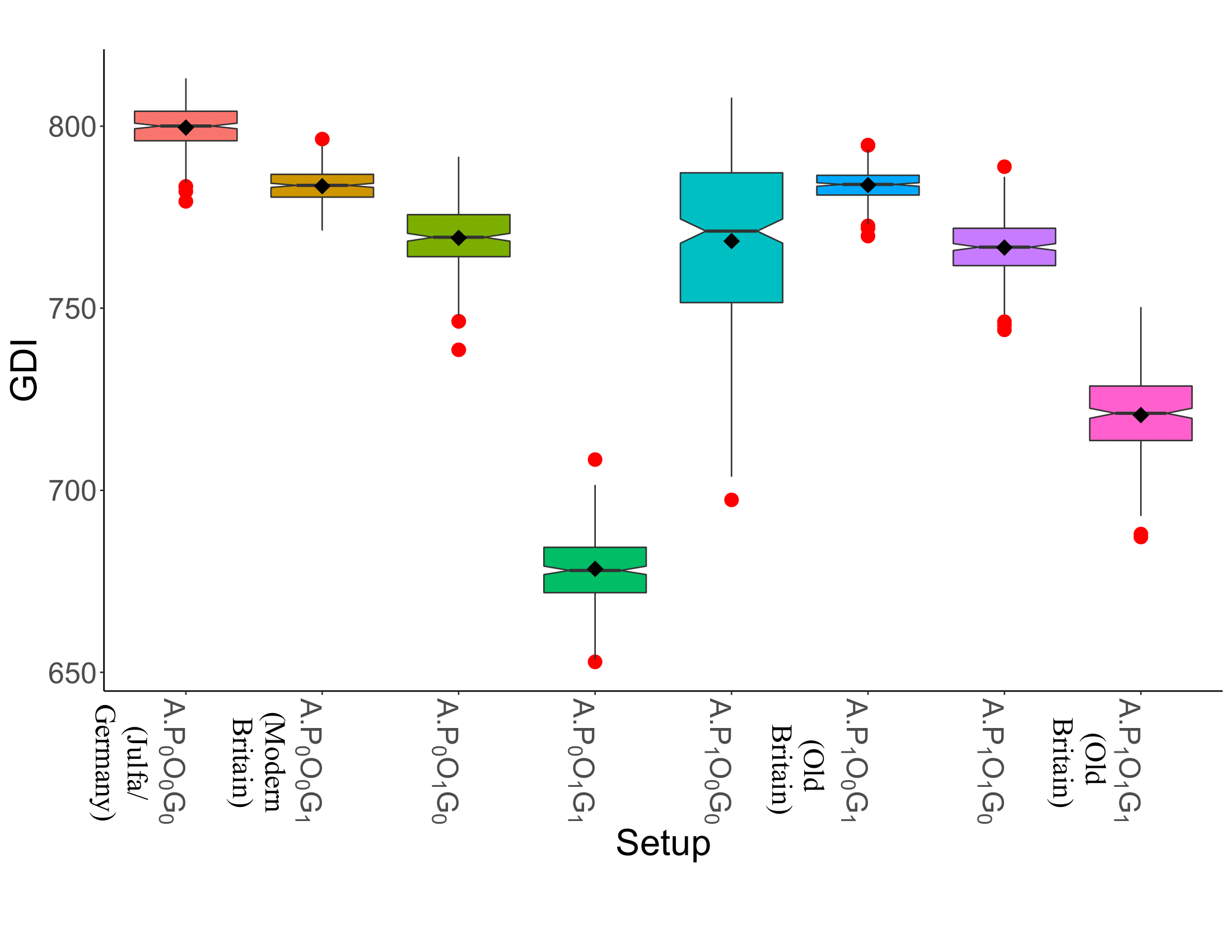
| GDI | 797\(\pm\)28 | 782\(\pm\)18 | 767\(\pm\)22 | 677\(\pm\)19 |
| Part 2 (Societies \(A.P_1O_0G_0\)-\(A.P_1O_1G_1\)) | ||||
| Set-up | \(A.P_1O_0G_0\) | \(A.P_1O_0G_1\) (Old Britain) | \(A.P_1O_1G_0\) | \(A.P_1O_1G_1\) (Old Britain) |
| Wage adequate | 4.0\(\pm\)1.0 | 8.5\(\pm\)0.2 | 9.9\(\pm\)0.3 | 9.9\(\pm\)0.4 |
| Wage excellent | 6.1\(\pm\)1.0 | 11.6\(\pm\)0.1 | 12.0\(\pm\)0.1 | 12.3\(\pm\)0.2 |
| Number of adequate | 62.6\(\pm\)2.9 | 63.2\(\pm\)1.9 | 54.6\(\pm\)1.5 | 54.1\(\pm\)1.5 |
| Number of excellent | 26.3\(\pm\)2.6 | 29.3\(\pm\)1.6 | 20.2\(\pm\)1.5 | 21.4\(\pm\)1.6 |
| Total Skilled | 88.9\(\pm\)3.9 | 92.5\(\pm\)2.5 | 74.8\(\pm\)2.1 | 75.5\(\pm\)2.2 |
| Programme completion (%) | 71.2\(\pm\)2.2 | 70.4\(\pm\)2.1 | 59.1\(\pm\)1.4 | 58.4\(\pm\)1.3 |
| GDI | 769\(\pm\)26 | 782\(\pm\)16 | 765\(\pm\)15 | 721\(\pm\)12 |
Impact on programme completion
Figure 4 indicates programme completion with respect to different set-ups. In these graphs, each horizontal pair groups simulated societies, based on having (left column) and not having (right column) that characteristic (i.e. the same line appears in each pair of characteristics). Furthermore, the societies of interest are highlighted with thicker lines. As can be seen in Table 10, when there is no guild (indicated by \(G_0\)), the overall completion rate increases. The results mirror claim about the impact of guilds on apprenticeships (\(G_1\)).28
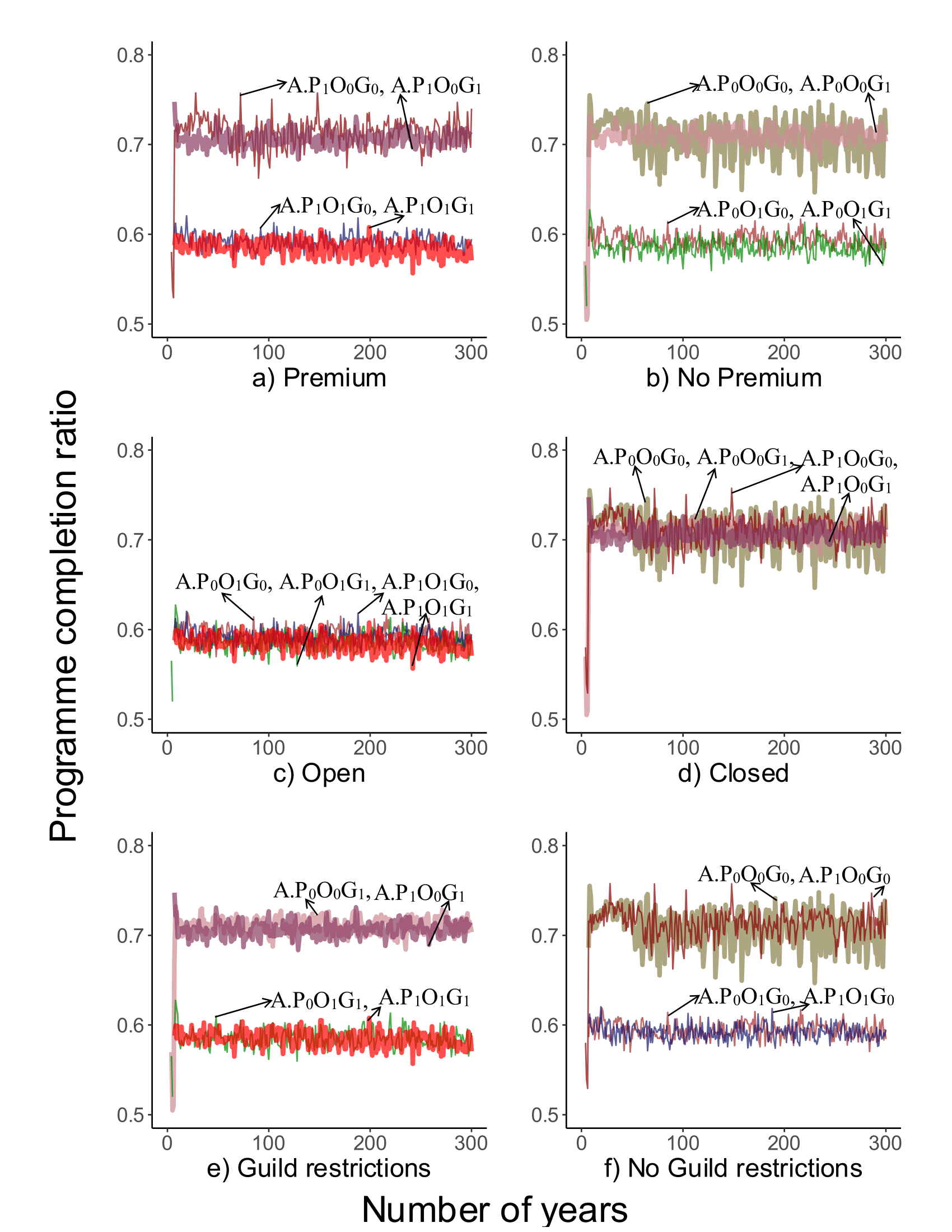
Only in the \(A.P_0O_0G_1\) society does the presence of guilds have a negative impact on programme completion. This is because trainers will not train well to control the workforce supply, and some apprentices may leave the programme because of lower probabilities of finding a job. Just as with the manufacturers’ case, openness decreases the completion rate. Also, the highest completion rate is associated with the \(A.P_1O_0G_0\) society. Finally, the completion ratio of the society \(A.P_1O_1G_1\) is more than the numbers suggested by Wallis (2008 Table 1), which can be caused by factors such as deceased agents. The impact of other factors \((16\%)\)29 justifies differences between the completion rate obtained by simulation (i.e. 58.4%) and the around 40% completion rate observed in Old Britain.
Impact on the GDI
The next step is measuring the contribution of these programmes to the GDI of society. As can be seen in Figure 5, paying a premium may decrease the system’s GDI by limiting the number of participants; hence, it deceases the total value of items produced by them. Only in the \(A.P_1O_1G_1\) society does the GDI improve comparing to its counterpart (i.e. \(A.P_0O_1G_1\)) that is a representative of the big cities in Old Britain. Overall, closed societies (identified by \(O_0\)) produce better GDIs for training apprentices who will serve the society. Finally, for both open and closed societies, when there are free programmes and no guilds, the contribution to the GDI increases (i.e. \(A.P_0O_1G_0\) outperforms \(A.P_0O_1G_1\), \(A.P_1O_1G_0\), and \(A.P_1O_1G_1\), and \(A.P_0O_0G_0\) outperforms all societies).
Impact on wages and the number of skilled agents
Figure 6 presents numbers of excellent (left) and adequate (right) skilled agents in the society. As can be seen in Figure 6 and Table 10, asking for premiums (indicated by \(P_1\)) decreases the number of skilled agents in the system by limiting the number of participants, because of a decrease in the trainees’ motivation. On the other hand, the openness of the system (indicated by \(O_1\)) causes a remarkable drop in the number of skilled agents in the system, because some apprentices leave the system to work in other societies. As depicted in Figure 6, the number of excellent skilled agents slightly increases when there are some guilds (\(G_1\)) in the system, because trainers have less fear of the loss of profit.
Also, Figure 7 presents wages associated with excellent (left) and adequate (right) skilled agents in the society. As can be seen, when there is no guild (identified by \(G_0\)), wages decrease to some extent. The openness of the system (identified by \(O_1\)) increases wages in the societies for skill shortage. Asking for a premium (identified by \(P_1\)) has different impacts on wages. It limits the increase in wages in societies having Guilds (\(G_1\)) but fails to do so in other societies (\(G_0\)). Another interesting observation regards the combination of closedness (\(O_0\)) and the lack of guilds (\(G_0\)) that reduces the wages dramatically. Moreover, not asking for premiums causes more drops in wages. This phenomenon was the reason for what was observed by Chardin (Chardin 1720), i.e. masters were reluctant to train their apprentices.30
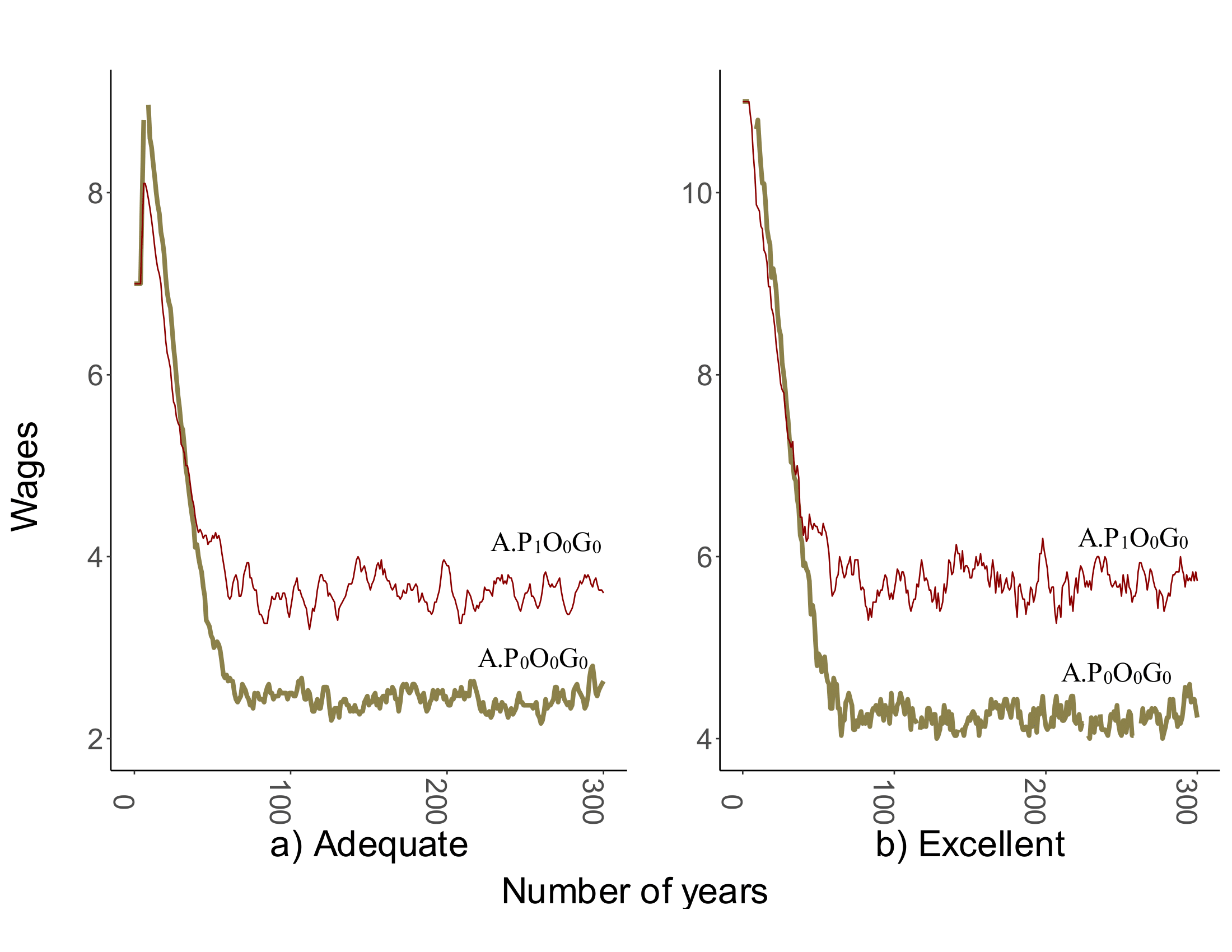
As can be seen in Figure 7, societies \(A.P_0O_0G_0\) and \(A.P_1O_0G_0\) have a significant shift in means in comparison with medians (i.e. their means are placed outside the box). To study the reason for such shifts, Figure 8 presents the line plot for these two societies. Based on the figure, we can conclude that the outliers (i.e. observations outside the first and third quartiles) that caused this shift are representatives for gradual decreases in wages — over time and after more than 50 iterations (i.e. years) wages reach a more stable value (i.e. the value represented by the median in Figure 7).
Summary, discussion, and outlook
This study has investigated the key characteristics of apprenticeship programmes by considering both historical and contemporary cases in several countries. The main aim of the simulation has been to improve our understanding about the impact of institutional mechanisms and social characteristics on the success of these programmes in increasing the number of skilled agents and improving societal level profits (i.e. the GDI). To perform this modelling, we considered two trade types, namely artisans and manufacturers.
Differentiating these two trade types is essential, as their motivations for accepting apprentices were diverse. Artisans trained may have felt threatened by their apprentices, as they were potential competitors. However, the manufacturers train future employees for themselves. For each of the aforementioned trade types, we systematically changed the key characteristics to assess their impacts on societies’ performances. Furthermore, we considered different scenarios for manufacturers because of the more complicated characteristics of those societies.
For the manufacturers, we considered three characteristics: the openness of the society, the utilisation of schools in training apprentices, and the trainer type. We assessed three scenarios for apprenticeship systems as follows:
- Training to satisfy the labour market demand;
- Training more than expected labour market demand by relaxing restrictions due to unions’ considerations;
- Openness for skilled agents from other countries to join and work in the society.
We systematically mapped these characteristics into societal stereotypes which capture intrinsic separate real-world societies. A key difference between the EIC and Julfan traders was utilising schools, and its importance is also emphasised in modern contexts by differentiating between German and British cases. The trainers for manufacturers have two types: contractors (paid trainers), and companies (training potential employees). These two factors, i.e. employing schools and trainer types were considered for all scenarios associated with manufacturers.
The other trades type that has been addressed in this paper is artisans. In both historical and contemporary contexts, some societies use guilds as a mediator to regulate the workforce market (by controlling excessive skill supply). The openness of the society is another characteristic that impacts the workforce supply (i.e. agents may leave the community to work elsewhere). Finally, in Old Britain, trainers asked for some prepayments to compensate for the costs of training. Those costs reduced the number of agents who could access the system to those from more prosperous families, and these expenses reduced the expected profit margins of apprenticeships for agents.
As the results suggest, the success of apprenticeships should not be assessed by programme completion, and the approach taken by Ryan & Unwin (2001) can be misleading. For instance, in Scenario A, \(M.S_0O_0C_1\) society (see Figure 2) has the highest programme completion (about \(78\%\)), but this system has a lower GDI than two other closed societies (\(M.S_1O_0C_0\) and \(M.S_1O_0C_1\) in Figure 3) with about 900 versus about 1200 and 1300. This is because of a lower speed of learning and profitability (\(S_0\) means that schools are not mandatory). Furthermore, in this society, trainees have chances to be hired by the companies under which they are trained and that increases their motivation to complete the programme.
Also, the results of open systems in Scenarios A and B emphasise the importance of some guarantees provided by apprentices about staying in the same society after training, since the openness of systems (i.e. leaving a system by trainees, which is indicated by \(O_1\)) decreases the GDI dramatically (see Figure 3). This drop of the GDI is because of the substantial decrease in either collaboration by large companies to train apprentices or the failure of some companies to find the most appropriate agents to hire.
Also, manufacturing apprenticeships need a scheme that persuades agents to finish the programme instead of leaving it half way through for better jobs (see Appendix C). It should be emphasised that when comparing societies considering trainer type (i.e. contractors or companies), we should consider some other factors that may motivate/demotivate the government to use contractors, such as creating some jobs for trainer contractors, and the expenditures for the paid subsidies.
Systems run by contractors (indicated by \(C_0\)) benefited more from increasing the number of apprentices to a level more than was required (see Figure 3 Scenario B); because the availability of skilled agents would not impact contractors’ motivations for training. However, Scenario B has more public expenditures for the apprenticeship programme compared to Scenario A. Finally, results of Scenario C shed some light on the reasons large companies in Britain asked for an apprenticeship programme but would not participate in it (Ryan & Unwin 2001). If we assume that some skilled agents with lower expectations from outside the country are available (as suggested by McCollum & Findlay (2015)), the main intention of large companies is to stabilise the wages so they do not have to pay so much to hire skilled agents.
Considering obligations for companies to accept apprentices or studying the best ways for reforming an already working system is an example of employing this model to help developing societies: See study on South Africa and study on Ghana. Nevertheless, based on this study, we know that for manufacturers, based on their needs, we can consider two situations:
- When companies themselves need the skilled agents in the future. If that is the case, system characteristics are similar to one of four manufacturing societies (\(M.S_0O_0C_1\), \(M.S_0O_1C_1\), \(M.S_1O_0C_1\), and \(M.S_1O_1C_1\));
- If companies do not need the apprentices they have trained, the system performance would be worse than that of manufacturing societies \(M.S_0O_0C_0\), \(M.S_0O_1C_0\), \(M.S_1O_0C_0\), and \(M.S_1O_1C_0\), since companies only want to reduce their costs and hence decrease the programme’s quality as much as possible.
Given this, the government interventions should focus on providing academic training required by manufacturers in schools and finding some ways to persuade participants to finish the programme. For instance, Brockmann & Laurie (2016) recently conducted a comparative case study between two British apprenticeship systems, engineering and motor vehicle maintenance (MVM), which support the results of this simulation. Their results suggested that the engineering apprenticeship programme, known internationally for its quality, benefited from more motivated trainees with better education backgrounds. Finally, they suggested that even for MVM apprentices who want to be skilled workers, the programme should provide a comprehensive educational opportunity.
Assessing the apprenticeship for artisans reveals that a lack of guilds and prepayments for the programme increases the system’s GDI significantly (see \(A.P_0O_0G_0\) and \(A.P_0O_1G_0\) in Figure 5). The negative impact of prepayments is through limiting the number of potential participants and dissuading them from participation by decreasing the profit of apprenticeship and the degree of societal skill. This was evident in Old Britain where agents had to pay some premium.31 Although guilds improve societal skills, their control over workforce supply make the system biased for trainers’ benefits and fail the self-regulatory behaviour of the system by unilaterally increasing the risks associated with newly trained apprentices finding a job. Therefore on the one hand, trainers will train without considering the number of unemployed skilled agents, and on the other hand, this increase cannot reduce wages to modify demands for highly skilled agents.
We wish to acknowledge some of the limitations of this study. These include not exploring parameters in a continuous range, but only considering a systematic set of discrete values (e.g. for motivation, and bad training), especially in cases where it is predictable that a further decrease in parameter values reduces system performance (e.g. when considering outputs such as the GDI and the number of skilled agents). Furthermore, while more complex functions for the impact of these parameters and letting agents decide about the optimum numbers would have made the system more thorough, it would have increased the complexity of the system and made it more case-dependent (thereby limiting the generalisation of results). This work also did not address the effect of the export and import of items produced on the demand.
Another issue that should be considered in the future is addressing wage differences among different skill levels (we did not consider it to prevent immediate failure of the simulation); however, these are crucial before implementing an apprenticeship programme. Other factors include modelling more than one skill to investigate the agent’s preferences to attend more profitable programmes, companies’ bankruptcy because of a lack of skilled agents, consideration of the mortality of apprentices, and economic depression, to name a few. While we believe we have considered the essential aspects of the system, these nuances can be explored in the future, especially if exploring specific cases.
In conclusion, we have presented a general candidate simulation model for apprenticeship programmes developed based on five societies. We have extracted the essential characteristics of apprenticeship systems in order to gain insights into the potential influences on stimulating growth and to maintain competition. First, we have validated our model based on historical information (see paragraphs 4.11, 5.7, and 5.10). Furthermore, the importance of considered parameters has been emphasised by their presence in general and specific cases (e.g. the German apprenticeship) which performed efficiently in terms of improving societal skill level and the GDI. We believe this simulation model and the employed decomposition incorporates suitable assumptions and can be used as a baseline model to support parameterisation to explore societies – including both existing as well as idealised/hypothetical scenarios. Based on these accommodations of existing societal outcomes, the developed model is thus a candidate for refinement for further exploratory analysis – and for learning more about by the apprenticeship phenomenon and its impact on economic outcomes at large.
Model Documentation
We have utilised NetLogo to perform our simulation (Wilensky 1999). The simulation code is available at link: https://www.comses.net/codebases/d2b4c033-5adc-4c57-9163-99a0bdbfcafe/releases/1.0.0/.Notes
- We believe that other trades (e.g. the service sectors) can be modelled using concepts of this simulation by selecting relevant characteristics from two given trade types.↩︎
- Chardin (1720 Chapter XVII, p. 261) said: “There it is indeed that Knowledge must be stolen; for the Master thinking on the Profit he may reap by his ’Prentice [sic], more than on teaching him his Trade, doth [sic] not trouble himself much with him, but employs him only in those things that relate to his Profit.”↩︎
- For example, a family of three agents in Julfa were paid a lesser extent than the norm. More precisely, a father and his two sons entered into a commenda contract (a profit sharing contract) and asked for 25% share of the profit (instead of \(33\%\)) and part of the profit went to the sons (Herzig 1991).↩︎
- In contemporary British apprenticeship programmes, there is an age restriction for subsidising participants.↩︎
- Chardin (1720 Chapter XVII, p. 260) said: “Whoever is about to set up a Shop in any Trade, goes to the Head of the Trade, gives his Name and Place of Abode to be set down in the Register, and pays some small Fee for it. The Head never enquires of what Country the Tradesman is, nor who was his Master, nor whether he understands his Trade. The Trades likewise have no Restrictions, to hinder one from incroaching [sic] upon another. A Tinker makes Silver Basons [sic], if they are bespoke; every one undertakes what he pleases, and they never Sue one another upon that account.”↩︎
- For instance, see Gwyther (1992) for a report on the power of livery companies in London and Thomas et al. (2013) for a study about guilds in the UK. An example of a guild’s website is https://www.wsd.org.uk.↩︎
- For instance, Johnston & Hancké (2009) discuss how unionised societies that were active under the European monetary union, could negotiate for excessive wage increases when there was a loss of employment.↩︎
- Note that a guild controls the number of skilled agents who can work in the system (i.e. some skilled agents are not permitted to work). However, unions protect their members interests (e.g. they stabilise wages by regulating the number of apprentices to control the number of unemployed agents).↩︎
- In Germany, some freedom in the programme design lets companies give training in some specific skills needed for employees to work in these companies, along with more general skills. This makes participation in such programmes more attractive for both large and small companies (Franz & Soskice 1994).↩︎
- The scoring scheme takes account of a) the skill requirement, b) the complexity of the skill training, and c) the number of trainees combined in a ratio with the ones who find a job.↩︎
- The importance of knowledge is observed in some historical cases, as well as modern instances. For example, Julfans not only provided a pamphlet containing trade information (e.g.routes and conversion of units), but also had a specialised school for training recruits (see Aslanian 2007).↩︎
- For instance, it is shown that improvements in declarative tactical knowledge facilitate skills transfer (Anderson 1982; Williams & Davids 1995). Note that declarative tactical knowledge is a combination of information about rules, tasks, objectives of the game, etc. which is overall knowing what to do (Américo et al. 2017).↩︎
- The importance of different degrees of the school-based skills on performance in various fields are discussed in Stasz & Brewer (1999 Chapter 3, pp. 15-36). They suggest companies that face more frequent changes in their production processes need agents with technical skills obtained in schools. Such issues, along with limited availability of time and resources at hand in a work-based training environment, call for an independent structure to form and enhance academic skills.↩︎
- Note that in Julfa a trader should have basic skills in arithmetic and formal writing before he was considered for employment (Aslanian 2007). In modern contexts, these skills are essentially more extensive. One of the reasons schools are more efficient in transferring academic skills is the time and effort invested by experts to design an appropriate and comprehensive educational system. Therefore in designing courses students’ and the industry’s diverse capabilities and requirements are considered, and the training is concentrated on developing skills that could be transferred to other contexts.↩︎
- Overall, this attribute (i.e. openness) is affected by three characteristics: a) probability of finding a job with better payments in other places which motivates some agents to leave programmes sooner to work in other communities, b) reputation for having high skills so that agents can work in other places with higher payments, and c) reputation of programmes that attracts apprentices from other communities.↩︎
- Gardner (2011 p. 19) argues “intelligence tests rarely assess skill in assimilating new information or in solving new problems. This bias toward ‘crystallized’ rather than ‘fluid’ knowledge can have astounding consequences.” He proposes the idea of MI that splits the intelligence into eight or nine categories (see Gardner 2011 p. xv). He discusses that individuals may be strong in certain types of intelligence and be weak in others. In this study, differentiation among Logical-Mathematical, Bodily-Kinesthetic, and Linguistic intelligence emphasises the separation of agents’ ability to acquire different aspects of skills in school-based and work-based training.↩︎
- For instance, Kusurkar et al. (2013) indicated positive correlations among autonomous motivation (i.e. motivation from within the student), study strategy, and average grades.↩︎
- Some evidence from the German apprenticeship system in the 1980s suggests that some sectors faced deficiencies in the availability of apprenticeship vacancies (Franz & Soskice 1994 see Table 2). Note that being passionate can also be reflected in choices among different programmes in real-world situations, i.e. agents choose the programmes that are more interesting for them. However, a low birth rate in societies with an ever-growing demand for skilled workforce can harm the overall performance of the society. These deficiencies show the importance of being persistent and passionate (e.g. accept to wait for a while) to get into an apprenticeship system.↩︎
- In the German and British instances, programmes duration is three years. In the EIC, after five years, the agents were promoted to factors (i.e. merchants). Note that in the EIC case, apprenticeship programmes were not full-time because the agents already had some tasks to do.↩︎
- Wallis (2008 see p. 840) provided such level of decline in perusing programme for Old Britain.↩︎
- For instance, Grossman & Owens (2012) indicates that participants felt they are unlucky and their score should be higher by about 10%.↩︎
- Worthen (2002) discusses that the Workforce Development committee recommended that enrolling every two years for plumbers’ apprenticeship programme is inefficient because “[high school graduates] won’t wait around 2 years.”↩︎
- We also conducted a Wilcoxon test on simulations results associated with Scenario A. This indicates a positive impact of the studied characteristics on finishing the programme. The test indicates that a) the closedness of society, b) the engagement of schools (i.e. systems with compulsory schools, and c) training by companies improve the apprenticeship performance.↩︎
- Around 75% of apprentices finish the programme in Germany (Ryan & Unwin 2001).↩︎
- We employed Kruskal-Wallis and Pairwise Mann-Whitney tests as post-hoc analysis due to the non-homogeneity of variances that was identified by the Fligner-Killeen test.↩︎
- Farmer (1997) discusses the phenomenon in supply chains and business schools. He states that in the final years of the 1960s, academics in the US believed that purchasing was not a strategic act and had a myopic attitude towards the practice. After a while, through a change in attitude triggered by the efforts of a minority of academics, purchasing was considered as a strategic activity rather than an administrative one. Without doubt, that belief shows the myopia in academia to avoid complexities in their decision-making.↩︎
- It is based on the evidence that suggests that “masters’ experience of training did matter. Masters were able to charge higher premiums with each apprentice they took, with the fourth apprentice paying over 20 per cent more than the first” (Minns & Wallis 2011 p. 12). From the importance of training experience, we can infer that a recently trained person could hardly recruit apprentices.↩︎
- Wallis (2008) claims that “apprenticeship[s] thrived despite, not because of the guilds, therefore we should be more aware of the distinction between the two institutions.”↩︎
- Note that in one instance Wallis (2008) mentioned that the reason for leaving the programme was that 14.6% of apprentices died, and 1.1 per cent wed and left the programme for paid jobs (i.e. 15.7 in total).↩︎
- Note that the masters’ tendency for training will be less if they have to pay wages (as observed in Persia by Chardin). One of the essential tools of masters in such societies is the flexibility of the apprenticeship’s duration. This flexibility helps masters to compensate the costs incurred to them by asking apprentices to assist them in their day-to-day tasks and reducing the speed of training to improve their future income and control the labour supply.↩︎
- In the EIC, agents should have asked two guarantors to sign a bond, which it was not collected upon the fault (Hejeebu 2005 see footnote 43).↩︎
- Estimated based on figures in New Zealand see Figure 3-8, (pp. 9-12).↩︎
- Overall, the Pareto principle expresses Vilfredo Pareto’s statement who experimentally observed the ratio of persons with an income more than \(x\) can be modelled as \(Cx^{-\alpha}\), wherein \(C\) and \(\alpha\) are constants (Arnold 2015 p. 1). This dominance of some companies over market is known as the 80/20 rule by economists, exhibiting phenomena that around 80% of values are produced by 20% of society. This behaviour is also expressed as “probability of measuring a particular value of some quantity varies inversely as a power of that value” (Newman 2005).↩︎
- Some studies such as Brynjolfsson et al. (2011), suggest revisions on 20% market share (i.e. long tail phenomenon), but these revisions are questioned in other empirical studies (Zhong & Michahelles 2013).↩︎
- Franz and Soskice analytically indicated the importance of these costs and their trade-off — see Franz & Soskice (1994), Section 3.1, (pp. 16-17).↩︎
- A \(15\%\) decrease in leaving programmes is observed for cases where the number of cities in which that particular skill could be utilised was limited to 3 (see Wallis 2008 p. 844).↩︎
- Note that the probability of \(X\), where \(x_1<X<x_2\), which follows a uniform distribution in \((a,b)\), is calculated as \((x_2-x_1)/(b-a)\) (see Equation 7). Here it is calculated as \((0.75-0.5)/(1-0.5) =0.5\) and \((1-0.75)/(1-0.5)=0.5\), for probabilities of adequate and high work-based skills, respectively.↩︎
- We know in German apprenticeship programmes, only eligible companies could participate in training that indicates some interventions to control training an excessive number of apprentices (Franz & Soskice 1994). This number can be optimised for a real-world scenario.↩︎
- Around 20 countries face shrinking populations (Wikipedia contributors 2019).↩︎
- It is based on the apprenticeship period in modern instances, namely Modern Britain and German apprenticeships.↩︎
- It is based on the evidence of 1700s England that indicates it took about two years of saving for a farmer to provide the required premium for an apprenticeship in low prestigious industries, such as the metal and footwear industries — £53.6 versus £10 (see Minns & Wallis 2012 Table 2). Also, the more prestigious skills and professions that were not hired by a company asked for higher premiums that were mostly affordable by “sons of professionals and gentlemen”(Minns & Wallis 2011, 2013). On average, these premiums were five times more than that of the metal and footwear industries (Minns & Wallis 2011, 2013).↩︎
Appendix
Appendix A: Utility Functions
Here We discuss the utility function for manufacturers and artisans. Overall, we have six combinations of academic and work-based skills such that two of them have no benefits for employers. Those two are agent types with inadequate work-based skills (irrespective of whether they have adequate academic skills). In the model, we consider two kinds of companies for manufacturers, namely large and small:
- Large companies/traders: These are the leaders in the manufacturing/trading area (e.g. electrical technicians for maintenance sectors in a car manufacturing company such as BMW or General Motors and large trading families in Julfa). They have complicated production systems or trade in valuable items, and their employees need some level of education to understand and handle those complexities (Stasz & Brewer 1999).
- Small companies/traders: These are companies, such as household wiring and small shops which are engaged with less complicated technologies and invest less in infrastructure and tools or do trades which are not engaged in luxurious and international trades that need complex computations (e.g. a lot of conversion to compare prices in different countries).
To compute the total amount of income generated in a society by employing apprentices trained by a system, we model certain utility functions. What follows are utility functions to abstractly model income generated by a manufacturing system that hires apprentices (large and small companies). Items produced by large companies have an income function which is given by:
| \[ U_{Manufacturers}(Large) = (a_{ML}\times s_{wb}) + (b_{ML}\times s_{wb}\times ed)\] | \[(3)\] |
The small-company utility function in the manufacturing section is defined as:
| \[ U_{Manufacturers}(Small) = (a_{MS} \times s_{wb}) + (b_{MS} \times ed\times Boolean(s_{wb})) + (c_{MS}\times Boolean(s_{wb}))\] | \[(4)\] |
As discussed earlier, artisans’ academic educations do not influence the quality of the final product directly. This assumption is a direct result of the fact that the focus of such skills is on how one can utilise his body parts (e.g. hands) skilfully. Therefore an artisan does not need academic skills, and the utility functions are defined as:
| \[ U_{Artisans}(Large) = (a_{AL}\times s_{wb}),\] | \[(5)\] |
| \[ U_{Artisans}(Small) = (a_{AS} \times s_{wb})+(b_{AS}\times Boolean(s_{wb}) )\] | \[(6)\] |
Appendix B: Simulation Parameters
In this section, we discuss the important parameters used (see Table 3) in this simulation and the reasons for choosing the values presented. Note that for both apprenticeship trades (i.e. artisans and manufacturers) we used 300 iterations as a representative for the longest duration that we knew lasted in different societies (Old Britain’s apprenticeship programmes was active between 1300s to 1600s, see paragraph 2.3).
The number of potential apprentices: The simulation creates 1000 new agents per iteration. This number shows the birth rate in a society that introduces new persons who potentially can attend the apprenticeship programme.
Attainability: In our simulation model, we assume that the degree to which agents can acquire different types of skills (i.e. work-based and school-based) are not similar and we call those degrees attainabilities. Apprentices should have a minimum attainability level for a work-based skill to be qualified to enrol in an apprenticeship programme. Therefore we assume that agents have the ability to acquire the minimum required work-based skills if they put sufficient effort into apprenticeship programmes (i.e. 0.5) for a work-based skill. Therefore the work-based attainability for qualified agents has a continuous uniform distribution in the interval (0.5, 1)).
However, the attainability of academic skills is independent of work-based skills and has a continuous uniform distribution in the interval (0, 1). The minimum attainability of 0 reflects the fact that agents may not have any interests or intelligence for school-based training, but they attend that programme because it is a compulsory part of the programme. Note that we employed continuous parameters for attainability to facilitate gradual increments of them in the simulation.
Passion: In the simulation model, each agent has a passion to learn the new skill. This number is randomly generated from the \((0,1)\) interval.
The number of companies: One of the parameters that impacts demand in the labour market is ratio of companies. We assumed the ratio of small companies to large companies in a society to be \(4:1\), inspired by the Pareto principle. This ratio complies with infrastructure to residential building companies presented by the Ministry of Business, Innovation and Employment (2017).32 Furthermore, Geerolf (2017) indicates that under certain production functions and assumptions that are not very restrictive, the Pareto Principle is upheld.33 In our study, we only use the rate as an indicator for the ratio of large to small companies, not a representation of their market share.34
Utility function — artisans: As discussed earlier, different trading societies have different utility functions. Overall, two factors impact these utilities, namely the size of the company (i.e. large or small) and the trade type (i.e. artisan or manufacturing). Overall, a large company has a high potential to make profits for the investments made on providing advanced production processes or buying high-quality raw materials. In an artisan-trading society, the large and small companies are metaphors for budget spent on raw materials by an artisan when producing an item based on their target market (i.e. part of the community is more prosperous and hence, can afford more luxurious items). This phenomenon is also considered in the form of the proportion of demands in a society (i.e. the percentage of prosperous families in a community is limited; hence, the demand for items provided by high-skilled agents is less). Attempts of low-skilled agents for producing decorative items lead to more wastage costs due to their limited ability to perform complicated tasks. On the other hand, high-skilled agents cannot benefit from their skills to perform advanced tasks when their target market includes average families who cannot afford expensive items. The values of items are calculated based on Equations 5 and 6, and the parameters presented in Table (???). For instance, the value of an item produced by an agent with adequate skills (\(s=1\)) in a small company is obtained as \(a_{AS}\times 1+b_{AS}\times 1=1.5+10=11.5\) using Equation 6.
Utility function — manufacturers: In a manufacturing society, the advanced production process means more frequent changes in the process. The academic skills are required to handle these frequent changes in equipment and help the employees to predict some what-if scenarios by utilising their information and analysing skills obtained in schools (Stasz & Brewer 1999). Note that having low work-based skills or not having school-based skills lead to a significant loss in large companies for producing scrapped items and opportunity loss, despite remarkable depreciation costs. Furthermore, small companies utilising simple production processes can benefit from work-based and school-based skills obtained by agents to a limited extent. The values are obtained based on Equations 3 and 4, and the parameters presented in Table 3. For instance, the value of an item produced by an agent with adequate and academic skills (\(s=1\) and \(ed =1\)) in a large company is obtained as \(a_{ML}\times 1+b_{ML}\times 1\times 1=5+10=15\),3 using Equation 3.
Furthermore, as discussed earlier, in some manufacturing apprenticeship schemes, some Contractors were employed to train agents. We assume that contractor processes are similar to that of small companies (i.e. they do not invest in providing resources for an advanced learning environment). Furthermore, note that we know that in the modern apprenticeship in Britain, mostly small companies were interested in providing work-based training. This implies it is not profitable for large companies to invest in training apprentices. Both small companies and contractors use simple procedures; therefore we have assumed that the maximum transferred skill (to an apprentice) is limited to \(85\%\). The lower chance of training highly skilled agents is a consequence of the company’s limited resources (i.e. trainer’s skills and available tools) that decreases the quality of training.
Speed of training and learning: As discussed in the algorithms, training and learning speeds are modified, based on the quality of training and the agent’s characteristics. We assumed that the lack of the following worsens speed of learning and the speed of the training, and reduces these by \(10\%\):
- Passion (e.g. practising beyond the necessary);
- Good training (i.e. putting all efforts towards transferring skills to apprentices);
- Declarative knowledge (i.e. providing guidelines and required rules by experts before starting work-based training).
We have considered small numbers (i.e. 10% reduction) to study the impact of the aforementioned parameters on the speed of learning. The reasons for this small reduction are as follows:
- If the deviation is significant, especially for the passion and quality of training, then it can be recognised by third parties such as the government, unions, and the trainer, and they will interfere to rectify the system.
- Knowledge exclusion by not having attended school can be compensated by providing some guidance during work-based training, but it is time-consuming. This time-consumption slightly decreases the overall quality of training by decreasing the available time for work-based training.
- If small numbers indicate significant impacts, increasing them would not show anything new.
Academic skills: Another important attribute of the apprenticeship programmes for manufacturing societies is the engagement of schools. If systems lack formal schools as a compulsory part of programmes, each apprentice with the probability of 50% gains academic skills per iteration. This percentage reflects arbitrary decisions on attending schools voluntarily made by agents per run, based on their perception about their academic skills and value of such skills.
As stated earlier, in manufacturing societies, contractors are paid for training apprentices. However, training costs for artisans and manufacturing companies are a concern that should be addressed. Based on discussions provided by Franz & Soskice (1994) and Wallis (2008), there are two reasons artisan-trainers accept apprentices despite the apparent costs:
- There are benefits of manual labour provided by the apprentices, at the beginning of apprenticeship along with additional profits associated with their services for acquired skill during their apprenticeship. Wallis (2008) proposes some necessary tasks that are useful in the workplace, such as delivery, cleaning, and shop watching that could be done by apprentices and suggests that youth in Old Britain might have gained some other useful skills, i.e. work-related or general chores, by training provided by their parents.
- Franz & Soskice (1994) mention an additional reason for artisans to accept apprentices. They note there are reasons net costs of training are negligible or negative (i.e. it can be profitable considering the aforementioned incomes). Also, if there exist small costs, especially in small towns, being from the same social circles and knowing the parents of an applicant puts some pressures on artisans to accept applicants. Overall, social circles and friends and family put pressures on artisans to accept these marginal costs to create a good reputation.
In our model, for those artisans who accept apprentices, the motivation for training apprentices is to create a good reputation in addition to utilising apprentice services that also result in some marginal profits. We also considered a small proportion of training costs for manufacturers. However, manufacturers have privilege of negotiation with successful apprentices (i.e. they pay lower wages than the norm of society for that particular skill).
Initial wages — artisans and manufacturers: Another crucial element for having a stable system is paid wages and expected profits of apprenticeship programmes. Former studies indicated that if these numbers are not chosen correctly, the system fails.35 Note that these numbers are chosen, based on the following conditions, by considering utility functions of companies (to avoid making a system unprofitable and eventually fail). Two requirements of agents’ wages that we considered are:
- The wages for a high level of skills should be more than a lower level of skills (e.g. an educated agent with excellent work-based skills is paid more than his uneducated counterparts).
- The wages cannot exceed the price of the item produced using the same skill for both large and small companies (i.e. companies need to have enough income to pay wages).
The openness of the system in terms of being open for training worsens the programme completion ratio. Some may join the apprenticeship system, but may exit earlier to work where a low level of skills is required.36 Another impact of the openness of the system is addressed in one scenario of manufacturers where some skilled agents from other communities may join the system to work for companies (see Equation 11).
Stickiness threshold: This number shows the excessive labour supply or demand for skilled agents beyond which wages in the labour markets change. In other words, wages do not adjust to the market equilibrium for values below this number. For example, if 100 agents are employed and 29 agents are unemployed in a society, the wages do not change. In our model, we have considered 30 as the stickiness threshold; however, we test the impact of other values on the model (see Appendix C).
Discount factor and number of years: Another parameter that impacts trainers and apprentices’ expected profits of the programme is their discount factor and provisioned horizon. The agents use a discount factor to calculate the net present value of future income in a finite horizon (\(6\) years). The number of years reflects the high workforce turnover observed in Germany, the high mortality rate in the EIC, and overall, the time inconsistency of expectation observed in studies such as Ainslie (2015). For a discount factor for money, we used evidence available from Julfa (Herzig 1991). Herzig (1991) discussed that the interest rate norm in Julfa was around 10% per annum. This number suggests how Julfans mentally discounted the value of money.
Another important factor of apprenticeship programmes is their duration. The number of years in apprenticeship programmes is inspired by modern programmes (i.e. 3 years) to make results more applicable. However, this assumption does not comply with some historical cases such as Old Britain and Persia (Old Iran), but is essential in modern contexts where there are minimum age constraints to enter programmes and the availability of alternative programmes with three years duration.
Maximum waiting time: After completing the programme, agents will search for jobs and will not stay unemployed for more than two years (i.e. they will stay in the system for at most two years), and the chance of leaving the waiting pool in the first and second years (if they are unemployed) is 0.5 and 1, respectively. These figures are employed to reflect concerns, such as living cost requirements and family pressures (see also footnote 22).
However, in manufacturing systems run by companies, some of the trained apprentices are hired by companies. If manufacturers train some agents, they hire the qualified agent who possesses the highest degree of skill (i.e. they do not hire agents from the labour market). The reasons for such a decision are listed below:
- Pressures imposed by society and unions that expect companies to hire their apprentices if they need some skilled agents.
- The employees of a company also expect the company to hire one of the trainees because of the friendship bonds formed during the programme.
- The company has a vested interest in hiring its own apprentices, because they attain specific skills that are important for the company, and they are familiar with specific procedures inside the company that are not known to outsiders.
In addition, estimations of probabilities in the system are based on globally known information about the number of hired agents, agents’ skills, the number of trainers, and trainers’ current policy to decide about participating in apprenticeship programmes, and the quality of training. For the number of hired agents and number of traders, we know that currently, countries have official reports on their skills shortages, and unemployment rates, etc. that are indicators for agents to decide the next iterations. In older contexts, for lower population per community, rumours and observed shortages are means that agents can use for an estimation about those figures.
Weight of past information: Furthermore, we parametrise agents’ learning and their behaviours as follows. The agents’ skills and the trainers’ current policy are numbers that can be assessed by asking former trainers and references in both contemporary and historical instances. Apprentices discount past information using a weight of 30% for long past and a weight of 70% for recent information. This reflects the importance of recent information for apprentices, because they do not monitor the system for a long time. On the other hand, companies use a 50% weight for recent information and long past information. Note that companies keep a better track of past information than apprentices, because companies are active in the system for a longer time than apprentices. Therefore we used a different weighting for companies to abstractly reflect their experiential differences that stem from their long term activity in the system.
Trainers estimate the impacts of changing their training policy from good to bad, or hiring from already educated people, based on known parameters. In other words, they assume if they change their policy from good quality to bad quality training, the chances for agents to obtain high skills decreases by 10%. For hiring already educated agents, large companies assume that an agent has a 45% chance of having excellent skills, 45% of having adequate skills, and 10% of having inadequate skills after training. This assumption is based on predicted low motivation for learning new skills by already hired agents on their obtained skills.
Note that hired agents’ attainability is continuously and uniformly distributed over the range \((0.5,1)\), and such agents have low motivation (i.e. they do not practise well); therefore their learning speed decreases by \(\mathbf{0.9}\). Furthermore, an agent has equal chances to obtain adequate or excellent skills (i.e. its work-based attainability may be higher or lower than \(0.75\) with equal chances).37 Therefore a manufacturer predicts that a hired agent obtains each level of the aforementioned skills (adequate or excellent) with equal probabilities. The manufacturer takes account of the hired agent’s work-based attainability in each threshold (i.e. \(0.5\)) decreased by the hired agent’s lack of motivation; therefore the probability is \(0.5 \times 0.9 = 0.45\). Furthermore, the manufacturer notes that the hired agent may not obtain any skills with the probability of \(0.1\) (i.e. \(1 -\) sum of the aforementioned probabilities).
Parameters for Scenario A for manufacturers: Train to satisfy the labour market demand
Here we discuss how we stabilise the programme. We assume each contractor has a capacity to train 12 apprentices per year (i.e. they train \(20\%\) more apprentices than what the labour market needs to address the openness of the society), and when companies initiate training, small companies will not participate in training (i.e. the system starts by training 100 apprentices). They may add to the system when there is some vacant capacity for training, e.g. some large companies are not interested in participating. Note that at most, 6 small companies can participate in training in the next iterations when all large companies accept apprentices to reduce the risks of skill shortages.38 The capacity for contractors is defined to reflect government boundaries on paying subsidies to limit the total number of trained agents. The apportionment of training by large companies is a reflection of the following:
- the higher tendency for agents to be trained by companies with a better reputation;
- Government intervention to enhance the reputation of the apprenticeship system (e.g. the German government let certain certified companies train apprentices, and that restriction limited the number of companies that could have participated in the programme; Ryan & Unwin 2001).
As can be seen in Table 2 and based on the Pareto principle, the maximum number of apprentices per run can be calculated as \(10 \times 12 = 120\) for systems run by contractors and \((20 \times 5) + (6 \times 1)=106\) for systems run by large and small companies.
The capacity for manufacturers is obtained based on their expectations from the system and trade-offs between costs and benefits. In a system benefiting from school training, it is expected that half of the students obtain enough academic skills based on a continuous uniform distribution of the academic attainability of students. The chances of obtaining excellent work-based skills is \(50\%\), considering the distribution of agents’ attainability and the required degree of skill. In other words, an agent needs to obtain \(0.75\) of skill, while the attainability has a continuous uniform distribution in the range \((0.5,1)\), which means half of the trainees have the chance to obtain excellent skills. Note that when \(x\) follows \(U(a,b)\), i.e. \(x\) follows a continuous uniform distribution in \((a,b)\), we have from Ross (2010, p. 195):
| \[ P(x\geq c) = \left\{ \begin{array}{ll} 0 & c\leq a \\ \dfrac{b-c}{b-a} & a<c\leq b \\ 1 & b<c \\ \end{array} \right.\] | \[(7)\] |
| \[P(s_{wb}\geq 0.75)=\dfrac{1-0.75}{1-0.5}=0.5\] | \[(8)\] |
Due to the fact that academic and work-based skill attainability are independent, a random agent with a chance of \(25\%\) can have academic and excellent work-based skills altogether, i.e. he has \(50\%\) chance of obtaining academic skills, and considering the former probability, we have \(0.5 \times 0.5=0.25\). Therefore on average, having four apprentices leads to having one desirable trainee if that one is passionate and finishes the programme. This part is calculated, based on the geometric random variable expected value. This distribution is appropriate to calculate the probability of one success for any trial of games or experiments, such that each trial has a Boolean-value outcome such as tossing a coin. Let \(p\) be the probability of success and the number of required successes is one; then the expected value of the number of trials \(X\) can be obtained as (Ross 2010, pp. 157–159):
| \[\mathrm{E}(X)=\dfrac{1}{p},\] | \[(9)\] |
| \[P(x>n)=\sum_{i=n+1}^{\infty}P\{X=i\}=\sum_{i=n+1}^{\infty}p(1-p)^{i-1}=(1-p)^n.\] | \[(10)\] |
On the other hand, for requirements and costs associated with training, the manufacturers cannot accept many apprentices, so five apprentices are considered to be the maximum capacity for apprenticeship programmes.
The capacity of small companies is defined based on their small budget and workshop space. However, since there is not much difference among incomes obtained by different skills, and the risks only concern the probability of the apprentice leaving the programme or training an apprentice with an attainability lower than \(0.6\) — then in this case, the risks of (i.e. probability for) not finding an ideal agent is around the same number for small and large companies. The chance for small companies is \((0.6-0.5)/(1-0.5)=0.2\), and for large companies, it can be calculated as \(0.75^5\approx 0.24\). Note that we increased large companies’ maximum capacity to five.
The capacity of contractors is calculated using a simple approach. For contractors, most training costs are covered by the government, and to cover the rest of the costs, it is enough that some of their apprentices find jobs. In the current scenario, this capacity is defined to avoid significant differences between the overall capacity of systems run by contractors and companies (see Table 2). However, due to the lower quality of training provided by contractors which is a consequence of their limited investments, we assumed that the government and unions let them have slightly more capacity (i.e. maximum of \(120\) versus \(106\)). Note that either the government had to accept this increase in capacity or grant significant subsidies to trainers to establish much more complicated processes that were not affordable for small companies.
Explanation of parameters for Scenario C for manufacturers
We address the impact of tendency of companies to hire from other societies by considering some negotiation advantages for companies that can hire from other communities (see Equation 11). We assume that in negotiation, large companies can pay average wages for all combinations of non-academic and excellent, academic and excellent, and academic and adequate to immigrants because although they have doubts about the excellence of agents’ work-based skills, they are sure about their academic skills.
For these societies, we considered two factors, namely flexibility of immigrants and large companies’ uncertainties about immigrants’ work-based skills. Therefore we assume that companies suggest an average wage norm for the three types of agent skills as discussed above:
| \[ \mathrm{Wage} = \dfrac{\sum_{i=\mathrm{non-Academic\ and\ Excellent}}^{\mathrm{Academic\ and\ Excellent}} \mathrm{Wage}_{i}}{3}\] | \[(11)\] |
Explanation of parameters used for artisans
In this scenario, the agents assume they can be trainers after finishing the programme in three years (they use simple calculations). The demand in these systems is a function of the following phenomena:
- Formerly active agents retire, pass away, or move to other communities. This indicates the requirement of skilled agents observed or provisioned in some societies. For instance, Neumark et al. (2013) warned that some states in the US will face skill shortages in the near future due to the retirement of the “baby boom cohort.”
- Population growth introduces new demands for the skill. This is a consequence of new demand for services introduced by a new person. In most countries, net population growth is positive; hence, all else unchanged, more skilled agents are required to work in the same sector.39
Note that based on the assumption that all agents would not participate in the training, and the ones who do train participate once in three years,40 the demand can be a significant share of the number of trainers (we assumed that \(R\) in Algorithm 1 is 60%). The impact of asking for a premium (i.e. prepayments by apprentices) is twofold: a) it imposes some initial costs that are considered by apprentices to calculate the profits of attending the programme, and b) the imposed costs limit the share of the society that can afford to attend the apprenticeship to families with higher incomes (around 30% of the society).41 Furthermore, for stickiness of wages (discussed in Section 3.8), we modified the threshold employed for manufacturer societies, considering the new proportion of the demand (i.e. \(60\%\)), to decrease the considered number (i.e. we used 18 instead of 30).
Appendix C: Sensitivity Analysis
Here we present the sensitivity analysis of the output variables and the parameters values. The presented figures show the sensitivity of mean and standard deviation of output variables to the parameters. For this purpose we took 1500 random samples of different combinations (already Aiello-Lammens & Akçakaya 2017; Becker et al. 2018 showed that between 500 and 1000 samples can reasonably represent the real model). The range of parameters was defined so that they can present some real-world scenarios (e.g. we considered a lower bound of 0.5 for agents’ discount factors). Also, we considered relationships between the wages and profits as stated in other studies (Stasz & Brewer 1999). Table 4 explains parameters and variables shown in Figures 9–14. Also, apprenticeships without any contribution to the GDI after iteration 100 were considered as failed and removed from sensitivity analysis. The number of such instances for artisans, company trainers, and contractor trainers were 80 (5.3%), 36 (2.4%), and 80 (5.3%), respectively.
| No. | Abbreviation | Explanation |
|---|---|---|
| 1 | #No ed Adeq | Number of not educated/adequate |
| 2 | #Adeq | Number of adequate |
| 3 | #Apprentices | Number of potential apprentices |
| 4 | #Large | Number of large companies |
| 5 | #Ed Adeq | Number of educated/adequate |
| 6 | #Ed Exc | Number of educated/excellent |
| 7 | #Exc | Number of excellent |
| 8 | #Inadeq | Number of inadequate |
| 9 | #No ed Exc | Number of not educated/excellent |
| 10 | #Small | Number of small companies |
| 11 | #Small Trainers | Percentage of small companies who train |
| 12 | Ad Thresh | Adequate skill threshold |
| 13 | Alpha | Discount factor |
| 14 | Bad Train Spd red. | Impact of bad training on speed of learning |
| 15 | Check Job | Percentage of agents who check for jobs |
| 16 | Completion | Completion ratio |
| 17 | Cost Good Train | Cost of good training |
| 18 | Decision Horizon | Decision Horizon |
| 19 | Demand rate | Demand rate for artisans |
| 20 | Ed Thresh | Threshold for academic skills |
| 21 | Ex Thresh | Threshold for excellent skills |
| 22 | Guild? | Is there a guild in effect |
| 23 | Info Apprentice | Weight of recent information for apprentices |
| 24 | Info Artisan | Weight of recent information for trainers |
| 25 | Init Wage Adeq | Initial wage for adequate |
| 26 | Init Wage Ed Adeq | Initial wage for educated/adequate |
| 27 | Init Wage Ed Exc | Initial wage for educated/excellent |
| 28 | Init Wage Exc | Initial wage for excellent |
| 29 | Learn Overestim | Overestimation of learning speed |
| 30 | Max Waiting | Maximum waiting years |
| 31 | No passion | Impact of low passion on learning speed |
| 32 | Open? | Open society? |
| 33 | Prepay? | Prepayment requirement |
| 34 | Pr Be Trainer | Probability of being a trainer |
| 35 | Prof Large Adeq | Profit of adequate for large companies |
| 36 | Prof Large Ed Adeq | Profit of educated/adequate for large companies |
| 37 | Prof Large Ed Exc | Profit of educated/excellent for large companies |
| 38 | Prof Large Exc | Profit of excellent for large companies |
| 39 | Prof Small Adeq | Profit of adequate for small companies |
| 40 | Prof Small Ed Adeq | Profit of educated/adequate for small companies |
| 41 | Prof Small Ed Exc | Profit of educated/excellent for small companies |
| 42 | Prof Small Exc | Profit of excellent for small companies |
| 43 | School Speed Accel | Impact of school on accelerating learning |
| 44 | School? | Any school is engaged? |
| 45 | Small Spd Red. | Negative impact pf small companies on skill learning |
| 46 | Stickiness | Stickiness of wages |
| 47 | Train Years | Number of training years |
| 48 | Wage Adeq | Wage of educated agents with adequate skills |
| 49 | Wage Ed Adeq | Wage of agents with adequate skills |
| 50 | Wage Ed Exc | Wage of educated agents with excellent skills |
| 51 | Wage Exc | Wage of agents with excellent skills |
| 52 | Wealthy (%) | Percentage of wealthy families |
Figures 9 and 10, represent the correlation between average (\(\mu\)) and standard deviation (SD) of simulation output variables with parameters/variables of artisans, respectively. We discuss the correlations with an absolute value more than 0.3. As can be seen, the average (\(\mu\)) and standard deviation (SD) of GDI are negatively impacted by an increase in the percentage of agents who check for job. Also, an increase in demand rate increases the average (\(\mu\)) and standard deviation (SD). Also, the average (\(\mu\)) and standard deviation (SD) of the completion ratio are negatively impacted by the number of training years and the percentage of agents who check for jobs. In addition, the averages (\(\mu\)) of wages are positively correlated to initial wages, profits, and demand that mirror studies in economics regarding impact of stickiness of wages, company’s earnings, and demand on system dynamics. The averages (\(\mu\)) of the number of skilled agents is negatively correlated with the thresholds and the percentage of agents checking for jobs.
Figures 11, 13, 12, and 14, represent the correlation between average (\(\mu\)) and standard deviation (SD) of simulation output variables with parameters/variables of companies and contractors, respectively. We discuss the correlations with an absolute value more than 0.3. As can be seen, the average (\(\mu\)) of GDI is negatively impacted by an increase in the percentage of agents who check for job. Also, the engagement of schools increases the average (\(\mu\)) and standard deviation (SD) of GDI. And the average (\(\mu\)) and standard deviation (SD) of completion ratios are negatively impacted by the number of training years and the percentage of agents who check for jobs. The averages (\(\mu\)) of wages are positively correlated with initial wages and profits that mirror studies in economics regarding impact of stickiness of wages and company’s earnings on wages. Also, initial wages for high skilled agents increases the associated SD with them. The averages (\(\mu\)) of the number of skilled agents is negatively correlated to the thresholds. And, engagement of schools improves the educational skills of apprentices.
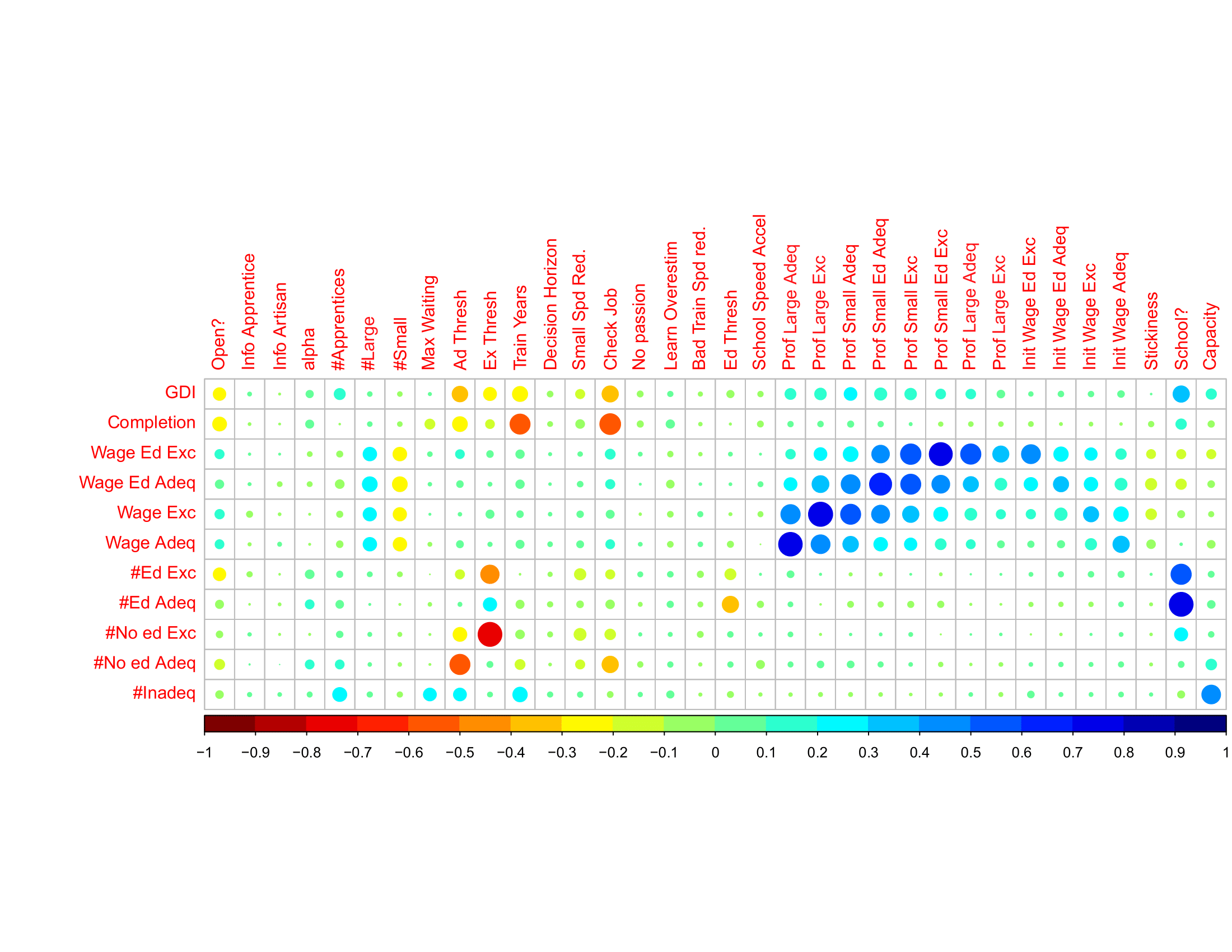
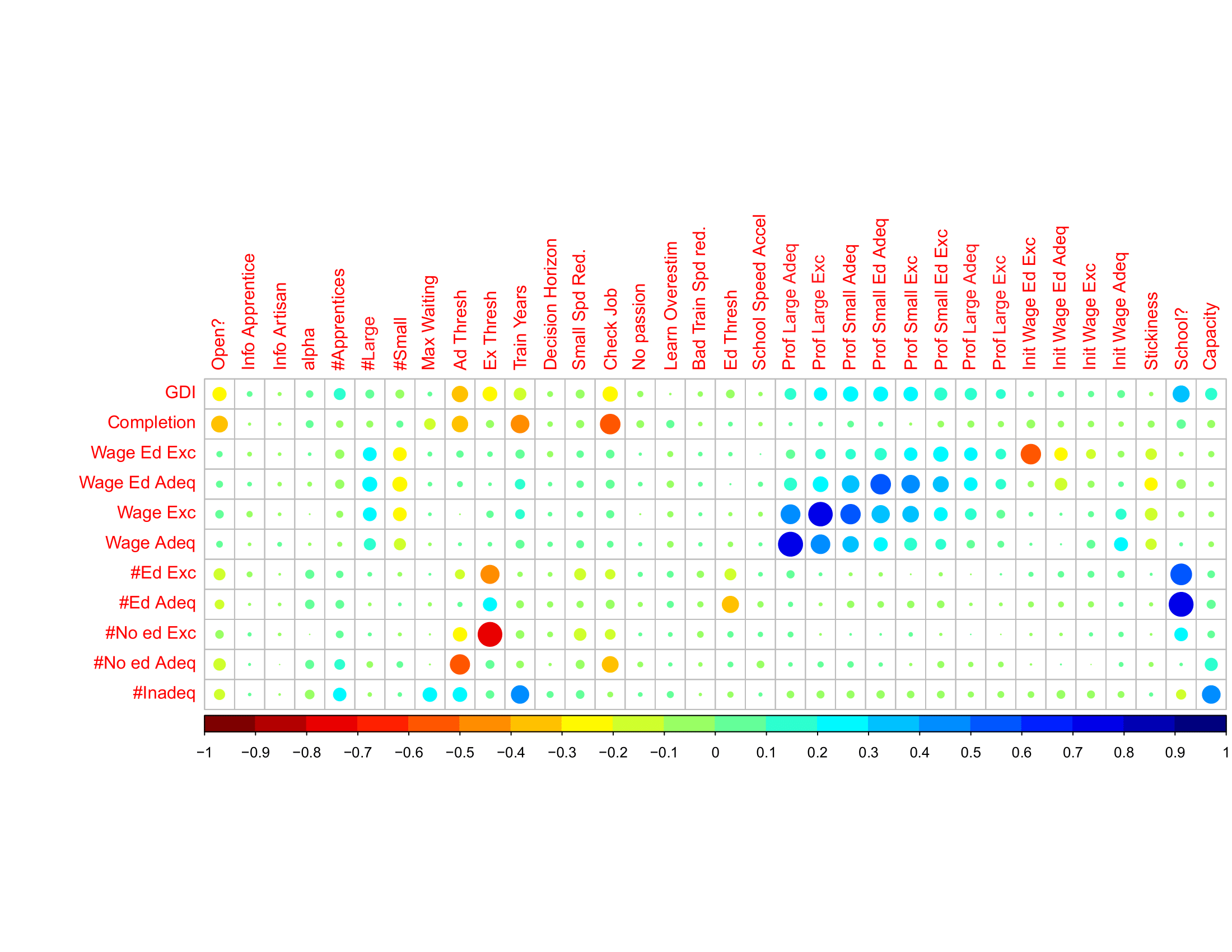
Appendix D: ODD + D Protocol
Table 12 shows where we addressed different aspects of the Overview, Design Concepts and Details protocol that includes human decision-making (ODD + D) (Müller et al. 2013). Noting that the ODD protocol can be lengthy and it is not easy to use for all simulation models (Grimm et al. 2020), we did not structure the paper based on this protocol. As suggested by Polhill et al. (2008), we start the verification and validation by discussing the submodels. In other words, we discuss how different agent types make decisions by discussing their utility functions. First we discuss the utility function and decision procedure associated with trainees.
| No. | Structural elements | Addressed in |
|---|---|---|
| I | Overview | |
| I.i | Purpose | Paragraph 1.3 |
| I.ii | Entities, state variables and scales | Paragraph 2.9 |
| I.iii | Process overview and scheduling | Figure 1 |
| II | Design concepts | |
| II.i | Theoretical and empirical background | Discussed in Model assumptions and Appendix B |
| II.ii | Individual decision-making | The agents maximise their utility functions; therefore it is discussed as a part of Algorithms |
| II.iii | Learning | Appendix B |
| II.iv | Individual sensing | Different agent types sense different information, see Figure 1 |
| II.vi | Interaction | The interaction of agents happens through training, see Figure 1 and Algorithms 2-3 |
| II.vii | Collectives | NA |
| II.viii | Heterogeneity | Agents’ parameters have different values, see distributions and values in Table 1 |
| II.ix | Stochasticity | Agents’ attainability, discount factors, and passions are randomised (see Table3) |
| II.x | Observation | GDI, completion ratio, skill levels, and wages are collected observations |
| III | Details | |
| III.i | Implementation details | The model is uploaded in a repository |
| III.ii | Initialisation | Paragraph 3.21 |
| III.iii | Input data | NA |
| III.iv | Submodels | Appendix D |
Trainees have two distinctive policies, identified by \(\pi_{Trainees}(policy)\), namely not to attend (\(NA\)) and attend the programme (\(A\)). The expected utility function associated with not attending programme over \(y\) years’ decision horizon, \(tr\) years of training, and considering a discount factor of \(\alpha\), \(W_l\) unit income per year for skill \(l\), and a prepayment of \(premium\) is calculated as follows:
| \[\pi_{Trainees}(NA)=\sum_{t=1}^{y}\alpha^t\times W_l,\] | \[(12)\] |
| \[\pi_{Trainees}(A)=\sum_{\forall l}\sum_{t=tr+1}^{y}P_h\times P_l\times\alpha^t\times W_l-Premium+IncomeTrainer(t)\times\alpha^t,\] | \[(13)\] |
| \[IncomeTrainer(t)=(1-P_{Tra}^{t})\times premium ,\] | \[(14)\] |
The agents who attend the programme, decide whether to continue (\(C\)) or not (\(NC\)). The following provides the expected utility of trainees at year \(x\) of training.
| \[\pi_{Trainees}(C)=\sum_{t=tr+1-x}^{y} Pr_{Es}\times\alpha^t\times W_{Es},\] | \[(15)\] |
| \[\pi_{Trainees}(NC)=\sum_{t=1}^{y} Pr_s\times\alpha^t\times W_s,\] | \[(16)\] |
On the other hand, the trainers have three policies to improve their utility functions \(\pi_{Trainers}(policy)\), namely good (\(G\)), bad (\(B\)), and avoid training (\(N\)). Overall, each trainer considers cost of training (e.g. competition and training costs), and profits of training (e.g. paid subsidies and prepayments) based on its type. In the following, we show utility functions associated with different training policies for companies:
| \[\pi_{companies}(G)=\sum_{\forall l}\sum_{t=tr+1}^{y}Pr_{G,l}\times (profit(l)-W_{G,l})\times \alpha^t-n\times\sum_{t=1}^{tr} Cost\times \alpha^t,\] | \[(17)\] |
| \[\pi_{companies}(N)=\sum_{\forall l}\sum_{t=1}^{y}\{Pr_{N,l}\times (profit(l)-W_{l})\alpha^t,\] | \[(18)\] |
Utility functions associated with different training policies for contractors are as follows:
| \[\pi_{contractors}(G)=Pr_{G,Hired}\times subsidy(Hired)+cost(G),\] | \[(19)\] |
| \[\pi_{contractors}(B)=Pr_{B,Hired}\times subsidy(Hired)+cost(B),\] | \[(20)\] |
Utility functions associated with different training policies for artisans are as follows:
| \[\pi_{artisans}(G)=Prepayment+\sum_{t=1}^{tr}(Wage_{labour}\times\alpha^t)-\sum_{t=1}^{y}(Pr_{G,ExcessSupply}\times \alpha^t),\] | \[(21)\] |
| \[\pi_{artisans}(B)=Prepayment+\sum_{t=1}^{tr}(Wage_{labour}\times\alpha^t)-\sum_{t=1}^{y}(Pr_{B,ExcessSupply}\times \alpha^t),\] | \[(22)\] |
Note that, in addition to providing the utility functions for verification and validation, we have earlier discussed some results which mirror the historical observations in paragraphs 4.11, 5.7, and 5.10.
References
AHLUM-HEATH, M. E., & Di Vesta, F. J. (1986). The effect of conscious controlled verbalization cognitive strategy on transfer in problem solving. Memory & Cognition, 14(3), 281–285. [doi:10.3758/bf03197704]
AIELLO-LAMMENS, M. E., & Akçakaya, H. R. (2017). Using global sensitivity analysis of demographic models for ecological impact assessment. Conservation Biology, 31(1), 116–125.
AINSLIE, G. (2015). The cardinal anomalies that led to behavioral economics: Cognitive or motivational? Managerial and Decision Economics, 37(4–5), 261–273. [doi:10.1002/mde.2715]
ALLAIS, S. (2012). Will skills save us? Rethinking the relationships between vocational education, skills development policies, and social policy in South Africa. International Journal of Educational Development, 32(5), 632–642. [doi:10.1016/j.ijedudev.2012.01.001]
AMÉRICO, H. B., Kowalski, M., Cardoso, F., Kunrath, C. A., Gonzalez-Villora, S., & Teoldo, I. (2017). Difference in declarative tactical knowledge between U-11 and U-15 soccer players. Human Movement Special Issues, 18(5), 25–30.
ANDERSON, J. R. (1982). Acquisition of cognitive skill. Psychological Review, 89(4), 369–406. [doi:10.1037/0033-295x.89.4.369]
ARNOLD, B. C. (2015). Pareto Distributions. Oxford: Taylor & Francis Inc.
ASLANIAN, S. D. (2007). From the Indian Ocean to the Mediterranean: Circulation and the global trade networks of Armenian merchants from New Julfa/Isfahan, 1605-1747. PhD Thesis, Graduate School of Arts and Science, Columbia University. [doi:10.1525/9780520947573]
BACKHAUS, J. (1980). The Pareto principle. Analyse & Kritik, 2(2), 146–171. [doi:10.1515/auk-1980-0203]
BECKER, W. E., Tarantola, S., & Deman, G. (2018). Sensitivity analysis approaches to high-dimensional screening problems at low sample size. Journal of Statistical Computation and Simulation, 88(11), 2089–2110. [doi:10.1080/00949655.2018.1450876]
BLINDER, A. S., & Choi, D. H. (1990). A shred of evidence on theories of wage stickiness. The Quarterly Journal of Economics, 105(4), 1003–1015. [doi:10.2307/2937882]
BORJAS, G. J. (1999). Labor Economics. New York, NY: McGraw-Hill Education.
BROCKMANN, M., & Laurie, I. (2016). Apprenticeship in England - The continued role of the academic-vocational divide in shaping learner identities. Journal of Vocational Education & Training, 68(2), 229–244. [doi:10.1080/13636820.2016.1143866]
BRYNJOLFSSON, E., Hu, Y., & Simester, D. (2011). Goodbye Pareto principle, hello long tail: The effect of search costs on the concentration of product sales. Management Science, 57(8), 1373–1386. [doi:10.1287/mnsc.1110.1371]
BÜCHEL, F. (2002). Successful apprenticeship-to-work transitions. International Journal of Manpower, 23(5), 394–410.
CHARDIN, J. (1720). Sir John Chardin’s Travels in Persia. London, UK: J. Smith in Exeter-Change in the Strand.
DAVY, N., & Frankenberg, A. (2018). Typology of apprenticeships in higher vocational education. Mainstreaming Procedures for Quality Apprenticeships in Educational Organisations and Enterprises (ApprenticeshipQ).
ETEMADI, N. (1981). An elementary proof of the strong law of large numbers. Zeitschrift Für Wahrscheinlichkeitstheorie Und Verwandte Gebiete, 55(1), 119–122. [doi:10.1007/bf01013465]
FARMER, D. (1997). Purchasing myopia — Revisited. European Journal of Purchasing & Supply Management, 3(1), 1–8. [doi:10.1016/s0969-7012(96)00006-8]
FRANTZ, C., Purvis, M. K., Nowostawski, M., & Savarimuthu, B. T. R. (2015). 'Analysing the apprenticeship system in the Maghribi traders coalition.' In F. Grimaldo & E. Norling (Eds.), Multi-Agent-Based Simulation XV (pp. 180–196). Berlin Heidelberg: Springer. [doi:10.1007/978-3-319-14627-0_13]
FRANZ, W., & Soskice, D. W. (1994). The German apprenticeship system. Center for International Labor Economics (CILE), University of Konstanz, Discussion Paper.
FRYER, J. (1698). A New Account of East-India and Persia, in Eight Letters: Being Nine Years Travels Begun 1672 and Finished 1681. London, UK: R. Chiswell, at the Rose; Crown in St. Paul’s Church-Yard. [doi:10.1098/rstl.1698.0071]
FULLER, A., & Unwin, L. (2003). Creating a “Modern Apprenticeship”: A critique of the UK’s multi-sector, social inclusion approach. Journal of Education and Work, 16(1), 5–25. [doi:10.1080/1363908022000032867]
GARDNER, H. (2011). Frames of Mind: The Theory of Multiple Intelligences. New York City, NY: Basic Books.
GEEROLF, F. (2017). A theory of Pareto distributions. Working Paper, UCLA, available at: https://fgeerolf.com/pareto.pdf.
GRIMM, V., Railsback, S. F., Vincenot, C. E., Berger, U., Gallagher, C., DeAngelis, D. L., Edmonds, B., Ge, J., Giske, J., Groeneveld, J., Johnston, A. S. A., Milles, A., Nabe-Nielsen, J., Polhill, J. G., Radchuk, V., Rohwäder, M.-S., Stillman, R. A., Thiele, J. C., & Ayllón, D. (2020). The ODD protocol for describing agent-based and other simulation models: A second update to improve clarity, replication, and structural realism. Journal of Artificial Societies and Social Simulation, 23(2), 7: https://www.jasss.org/23/2/7.html. [doi:10.18564/jasss.4259]
GROSSMAN, Z., & Owens, D. (2012). An unlucky feeling: Overconfidence and noisy feedback. Journal of Economic Behavior & Organization, 84(2), 510–524. [doi:10.1016/j.jebo.2012.08.006]
GWYTHER, M. (1992). Gilded cages of the city: These days the ancient livery companies seem to exist for wining and dining and dressing up. So why the secrecy? Matthew Gwyther finds a lot more going on than meets the eye. Independent, http://www.webcitation.org/74ZzVQSld.
HAMILTON, M. A., & HAMILTON, S. F. (1993). Toward a youth apprenticeship system. A progress report from the youth apprenticeship demonstration project in Broome County, New York. Research/TechnicalReports, State University of New York, College of Human Ecology at Cornell University.
HEJEEBU, S. (2005). Contract enforcement in the English East India Company. The Journal of Economic History, 65(2), 496–523. [doi:10.1017/s0022050705000173]
HERZIG, E. M. (1991). The Armenian merchants of New Julfa, Isfahan: A study in pre-modern Asian trade. PhD Thesis, Oxford University.
JACOBS, R. (2017). Apprenticeship scheme success may be hard to replicate abroad. Financial Times, available at: https://www.ft.com/content/1a82e8e0-04cf-11e7-aa5b-6bb07f5c8e12.
JOHNSTON, A., & Hancké, B. (2009). Wage inflation and labour unions in EMU. Journal of European Public Policy, 16(4), 601–622. [doi:10.1080/13501760902872742]
KAHN, S. (1997). Evidence of nominal wage stickiness from microdata. The American Economic Review, 87(5), 993–1008.
KING, K. (2009). Education, skills, sustainability and growth: Complex relations. International Journal of Educational Development, 29(2), 175–181. [doi:10.1016/j.ijedudev.2008.09.012]
KUSURKAR, R. A., Ten Cate, T. J., Vos, C. M. P., Westers, P., & Croiset, G. (2013). How motivation affects academic performance: A structural equation modelling analysis. Advances in Health Sciences Education, 18(1), 57–69. [doi:10.1007/s10459-012-9354-3]
MANKIW, N. G. (2017). Principles of Economics. Boston, MA: Cengage Learning.
MCCOLLUM, D., & Findlay, A. (2015). “Flexible” workers for “flexible” jobs? The labour market function of A8 migrant labour in the UK. Work, Employment and Society, 29(3), 427–443. [doi:10.1177/0950017014568137]
MINISTRY of Business, Innovation and Employment. (2017). Future demand for construction workers - Projections from the national construction occupations model. Ministry of Business, Innovation and Employment New Zealand.
MINNS, C., & Wallis, P. (2011). Why did (pre‐industrial) firms train? Premiums and apprenticeship contracts in 18th century England. Economic History Working Papers, London School of Economics and Political Science, Department of Economic History. [doi:10.1016/j.eeh.2013.02.001]
MINNS, C., & Wallis, P. (2012). Rules and reality: Quantifying the practice of apprenticeship in early modern England. The Economic History Review, 65(2), 556–579. [doi:10.1111/j.1468-0289.2010.00591.x]
MINNS, C., & Wallis, P. (2013). The price of human capital in a pre-industrial economy: Premiums and apprenticeship contracts in 18th century England. Explorations in Economic History, 50(3), 335–350. [doi:10.1016/j.eeh.2013.02.001]
MÜEHLEMANN, S., Wolter, S. C., & Wüeest, A. (2009). Apprenticeship training and the business cycle. Discussion Paper, IZA Institute of Labor Economics.
MÜLLER, B., Bohn, F., Dreßler, G., Groeneveld, J., Klassert, C., Martin, R., Schlüter, M., Schulze, J., Weise, H., & Schwarz, N. (2013). Describing human decisions in agent-based models – ODD + D, an extension of the ODD protocol. Environmental Modelling & Software, 48, 37–48.
NEUMARK, D., Johnson, H., & Mejia, M. C. (2013). Future skill shortages in the U.S. economy? Economics of Education Review, 32, 151–167. [doi:10.1016/j.econedurev.2012.09.004]
NEWMAN, M. E. J. (2005). Power laws, Pareto distributions and Zipf’s law. Contemporary Physics, 46(5), 323–351. [doi:10.1080/00107510500052444]
NORTH, D. C. (1990). Institutions, Institutional Change and Economic Performance. Cambridge: Cambridge University Press.
NORTH, D. C. (1991). Institutions. Journal of Economic Perspectives, 5(1), 97–112.
OGILVIE, S. (2014). The economics of guilds. Journal of Economic Perspectives, 28(4), 169–192.
PALMER, R. (2009). Formalising the informal: Ghana’s national apprenticeship programme. Journal of Vocational Education and Training, 61(1), 67–83. [doi:10.1080/13636820902820048]
PLUG, E., & Groot, W. J. N. (1998). Apprenticeship versus vocational education: Exemplified by the Dutch situation. Working paper TSER/STT, Amsterdam School of Economics Research Institute (ASE-RI).
POLHILL, J. G., Parker, D., Brown, D., & Grimm, V. (2008). Using the ODD protocol for describing three agent-Based social simulation models of land-Use change. Journal of Artificial Societies and Social Simulation, 11(2), 3: https://www.jasss.org/11/2/3.html. [doi:10.18564/jasss.1563]
PURVIS, M. K., PURVIS, M. A., & Frantz, C. K. (2014). CKSW: A folk-sociological meta-model for agent-based modelling. Social Path Workshop, University of Surrey, Guildford, UK.
RIELLO, G. (2009). 'The Indian apprenticeship: The trade of Indian textiles and the making of European cottons.' In G. Riello & T. Roy (Eds.), How India Clothed the World: The World of South Asian Textiles, 1500-1850 (pp. 309–346). Leiden: Brill. [doi:10.1163/ej.9789004176539.i-490.87]
ROSS, S. M. (2010). A First Course in Probability. Bergen County, NJ: Pearson Prentice Hall.
RUHS, M., & Anderson, B. (2010). Semi-compliance and illegality in migrant labour markets: An analysis of migrants, employers and the state in the UK. Population, Space and Place, 16(3), 195–211. [doi:10.1002/psp.588]
RYAN, P., & Unwin, L. (2001). Apprenticeship in the British ‘training market’. National Institute Economic Review, 178(1), 99–114. [doi:10.1177/002795010117800114]
SEDIGH, A. H. A., Frantz, C. K., Savarimuthu, B. T. R., Purvis, M. K., & Purvis, M. A. (2019). 'A comparison of two historical trader societies - An agent-based simulation study of English East India Company and New-Julfa.' In P. Davidsson & H. Verhagen (Eds.), Multi-Agent-Based Simulation XIX (pp. 17–31). Berlin Heidelberg: Springer. [doi:10.1007/978-3-030-22270-3_2]
SEDLMEIER, P., & Gigerenzer, G. (1997). Intuitions about sample size: The empirical law of large numbers. Journal of Behavioral Decision Making, 10(1), 33–51. [doi:10.1002/(sici)1099-0771(199703)10:1<33::aid-bdm244>3.0.co;2-6]
STASZ, C., & Brewer, D. J. (1999). Academic skills at work: Two perspectives. National Center for Research in Vocational Education, MDS-1193, University of California at Berkeley, Berkeley, CA., USA.
SUBOTNIK, R. F., Olszewski-Kubilius, P., & Worrell, F. C. (2011). Rethinking giftedness and gifted education: A proposed direction forward based on psychological science. Psychological Science in the Public Interest, 12(1), 3–54. [doi:10.1177/1529100611418056]
THOMAS, N. J., Harvey, D. C., & Hawkins, H. (2013). Crafting the region: Creative industries and practices of regional space. Regional Studies, 47(1), 75–88. [doi:10.1080/00343404.2012.709931]
UNESCO-UNEVOC. (2006). Orienting technical and vocational education and training for sustainable development (Discussion Paper Series 1). Discussion Paper, UNESCO-UNEVOC International Centre for Technical and Vocational Education and Training.
VON Luxburg, U., & Schölkopf, B. (2011). 'Statistical learning theory: Models, concepts, and results.' In D. M. Gabbay, S. Hartmann, & J. Woods (Eds.), Inductive Logic (Vol. 10, pp. 651–706). Amsterdam: Elsevier. [doi:10.1016/b978-0-444-52936-7.50016-1]
WALLIS, P. (2008). Apprenticeship and training in premodern England. The Journal of Economic History, 68(3), 832–861. [doi:10.1017/s002205070800065x]
WIKIPEDIA contributors. (2019). Population decline. Available at: https://en.wikipedia.org/w/index.php?title=Population_decline&oldid=876453369.
WILENSKY, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University.
WILLIAMS, M., & Davids, K. (1995). Declarative knowledge in sport: A by-product of experience or a characteristic of expertise? Journal of Sport and Exercise Psychology, 17(3), 259–275. [doi:10.1123/jsep.17.3.259]
WORTHEN, H. (2002). 'Joint labor-management apprenticeship programs: The issue of access to multi-employer training programs in Chicago’s construction industry.' In P. B. Voos (Ed.), Industrial Relations Research Association Series - Proceedings of The 54th Annual Meeting (pp. 115–123). Champaign, IL: Industrial Relations Research Association.
ZHONG, N., & Michahelles, F. (2013). Google Play is not a long tail market: An empirical analysis of app adoption on the Google Play app market. Proceedings of the 28th Annual ACM Symposium on Applied Computing, New York City, New York, USA. [doi:10.1145/2480362.2480460]