Klaus Jaffe (2002)
An economic analysis of altruism: who benefits from altruistic acts?
Journal of Artificial Societies and Social Simulation
vol. 5, no. 3
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/5/3/3.html>
Received: 31-Jan-2002 Accepted: 5-Jun-2002 Published: 30-Jun-2002
 Abstract
AbstractTabulating the different possible combinations allows us to define more precisely the different types of mutualistic interactions:
| Uni-directional considerations | Bi-directional considerations | Effect on donor | Effect on recipient | Aggregate effect | Type of interaction |
| K > A | K > B | - | + | ? | Dissipative altruism |
| K < A | K > B | - | + | + or - | Synergistic altruism |
| K = A | K > B | - | + | ? | Efficient altruism |
| K > A | K < B | + | + | + | Dissipative business |
| K < A | K < B | + | + | + | Synergistic business |
| K = A | K < B | + | + | + | Efficient business |
| K > A | K = B | 0 | + | ? | Dissipative mutualism |
| K < A | K = B | 0 | + | + | Synergistic mutualism |
| K = A | K = B | 0 | + | ? | Efficient mutualism |
| K = cost to the donor, A = benefit to the recipient, B = benefit to the donor | |||||
Of the different types of interactions listed, the three related to business, even the dissipative one, may be beneficial to society, as is demonstrated by classical economic theory. Synergistic mutualism is an evolutionarily very successful strategy (Jaffe 2001) and is beneficial to the group, and so is synergistic altruism if the amount of utility gained by the recipient is larger than the amount lost by the donor (K - B < A), as the balance of benefits will be necessarily positive. Efficient altruism and the various kinds of mutualism appear to be cases of rather ideal conditions and thus not likely to be found in nature. However, doubt remains about altruisms and mutualisms of the dissipative and efficient kind regarding their impact on aggregate benefits to the group. Here I present results of simulations, exploring the effect on aggregate wealth, of these kinds of interactions.
dw = -b + wo where wo = 0 if no resources are encountered.b determines the degree of external constraints or of competitiveness of the environment and could vary in the range of 1 to 10/wo
s = 0 indicate a 100% dissipation of the utility donated
s < 1 indicate dissipative altruism: Recipient receives less wealth than the altruistic donor spends
s = 1 indicate equitative altruism: Recipient receives the same amount of wealth as the altruistic donor spends
s >1 indicates synergistic altruism: Recipient receives more wealth than the altruistic donor spends
In the simulations presented here, s = 0 when a = 4.
|
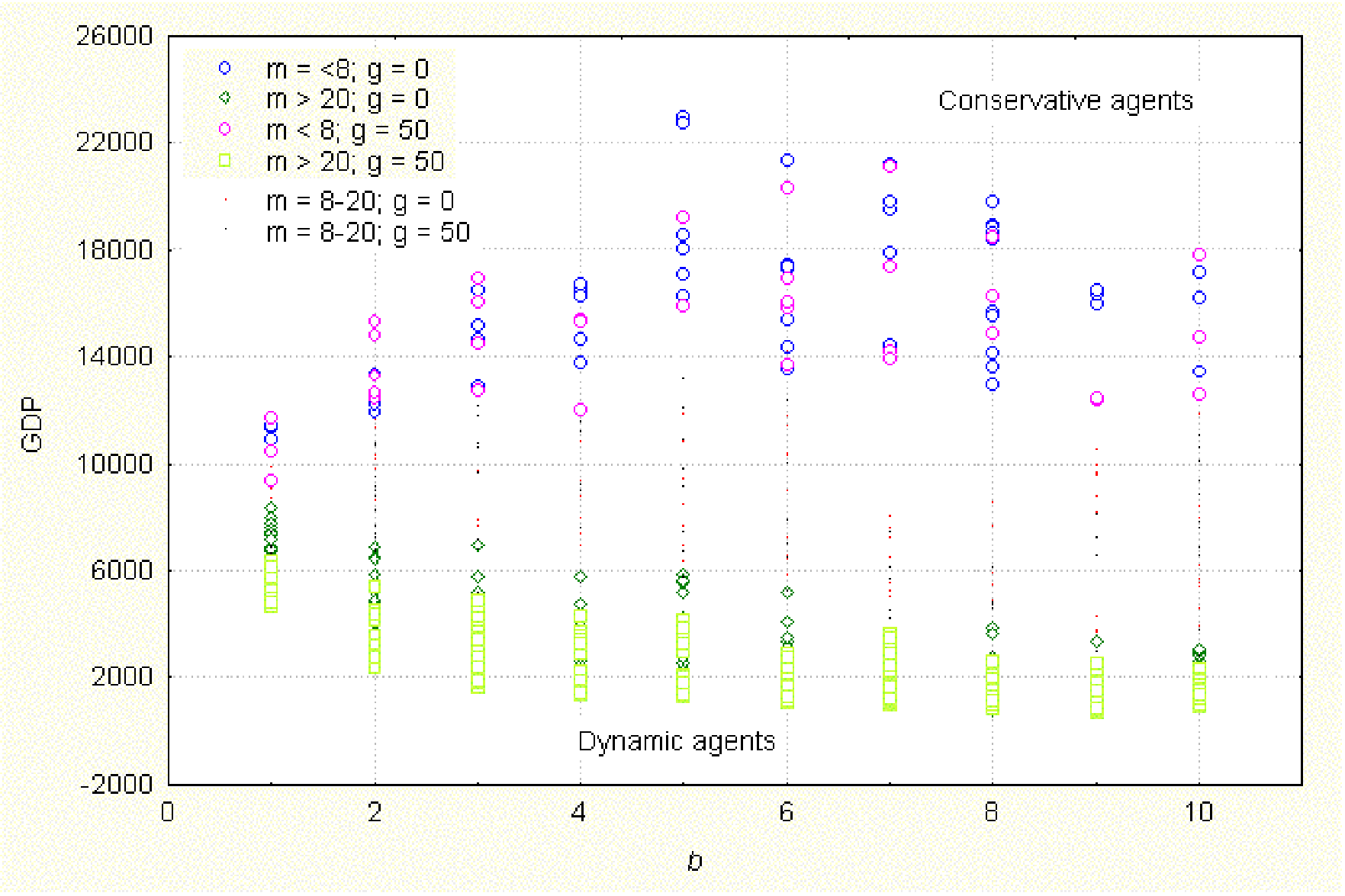
| Figure 1. Effect of b, m and g on total accumulated wealth (GDP). tstep = 40, RD = 1, RN = 1, RS = 100, τ = 2, a = 2 |
|
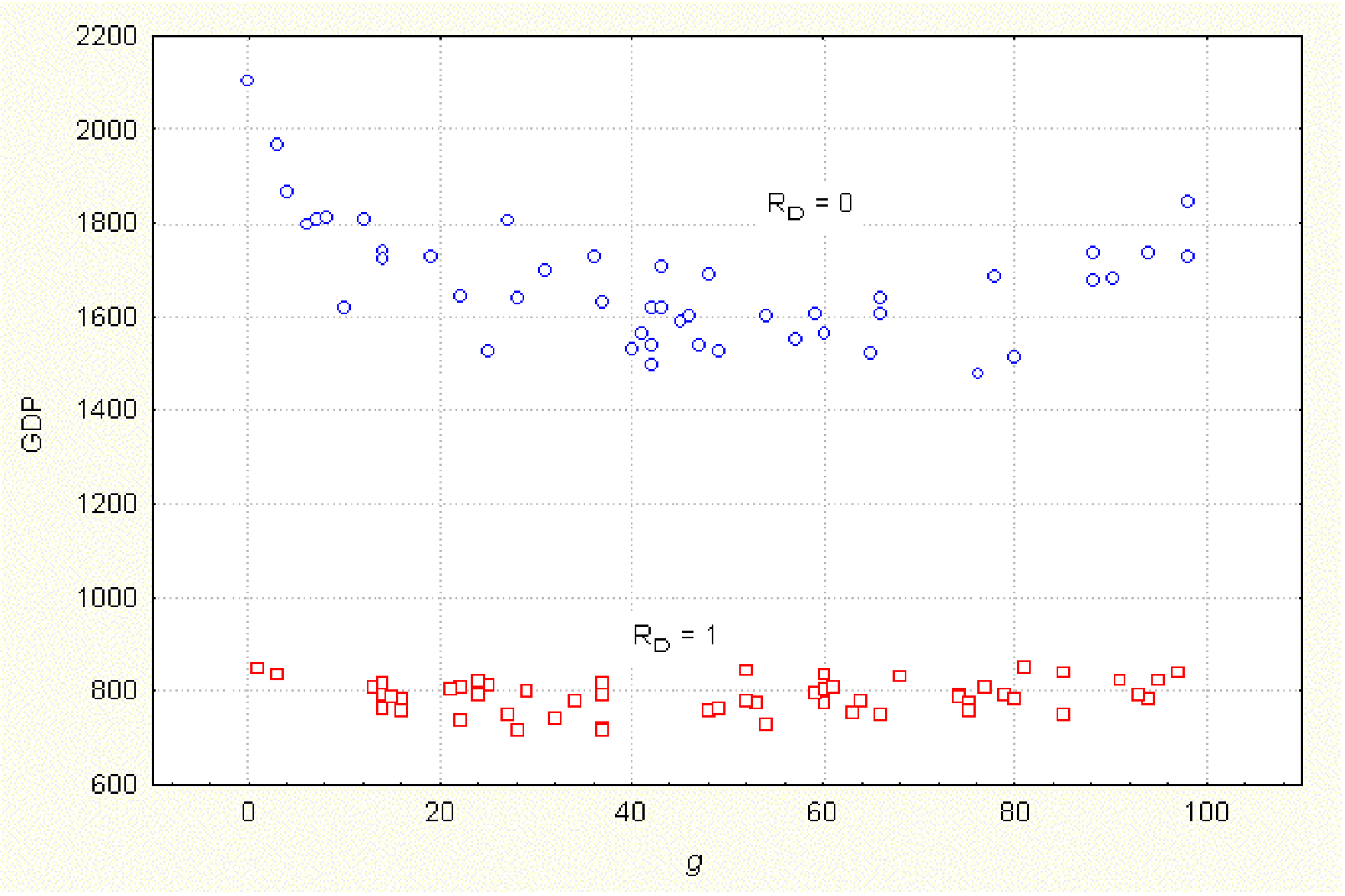
| Figure 2. Total wealth accumulated (GDP) vs. generosity (g). tstep = 80, RN = 1, RS = 100, τ = 2, b = 5, m = 20, a = 2 |
|
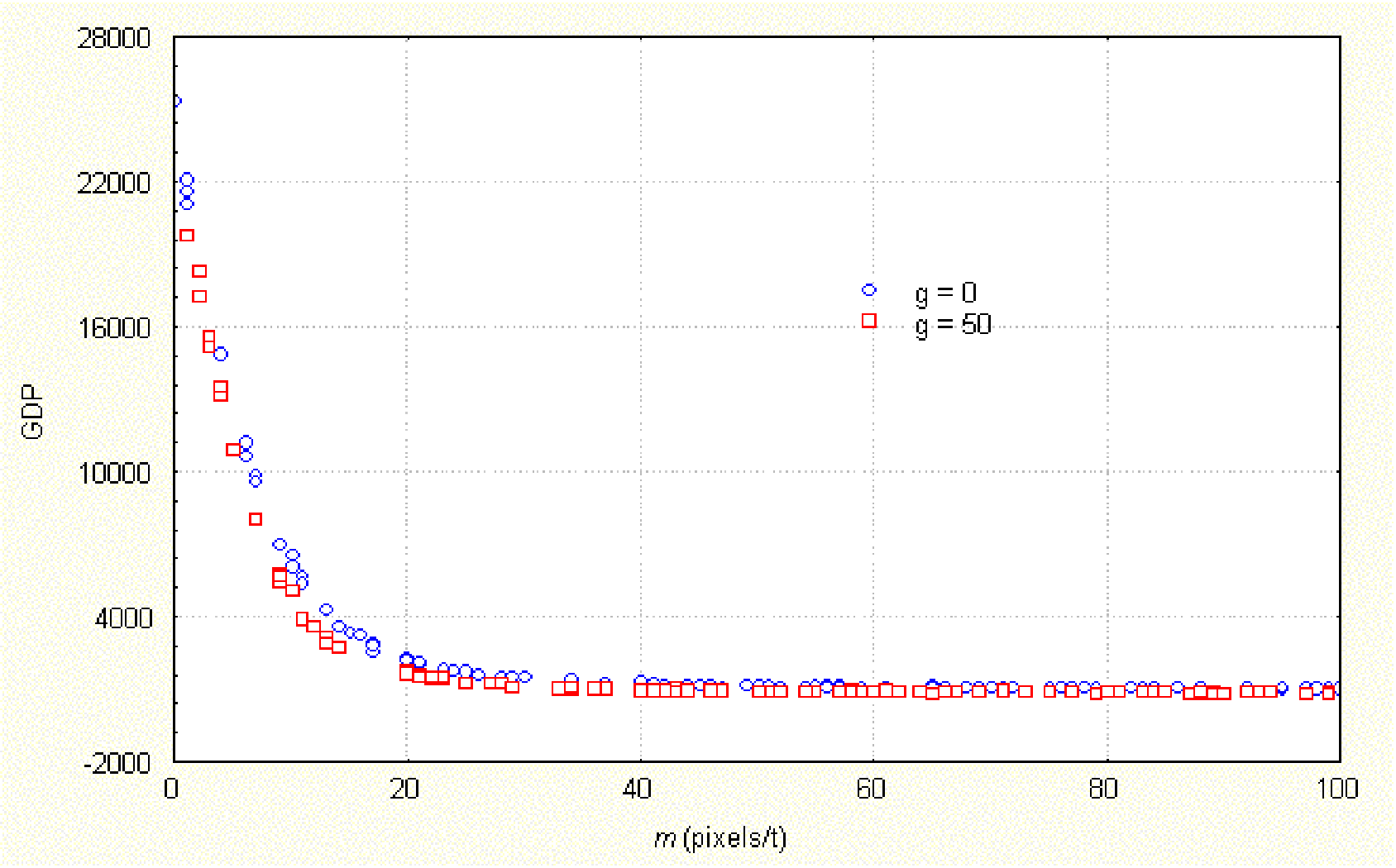
| Figure 3. Total wealth accumulated (GDP) at different speeds of movement (m) of agents. tstep = 80, RD = 1, RN = 1, RS = 100, τ = 2, b = 5, a = 2 |
|
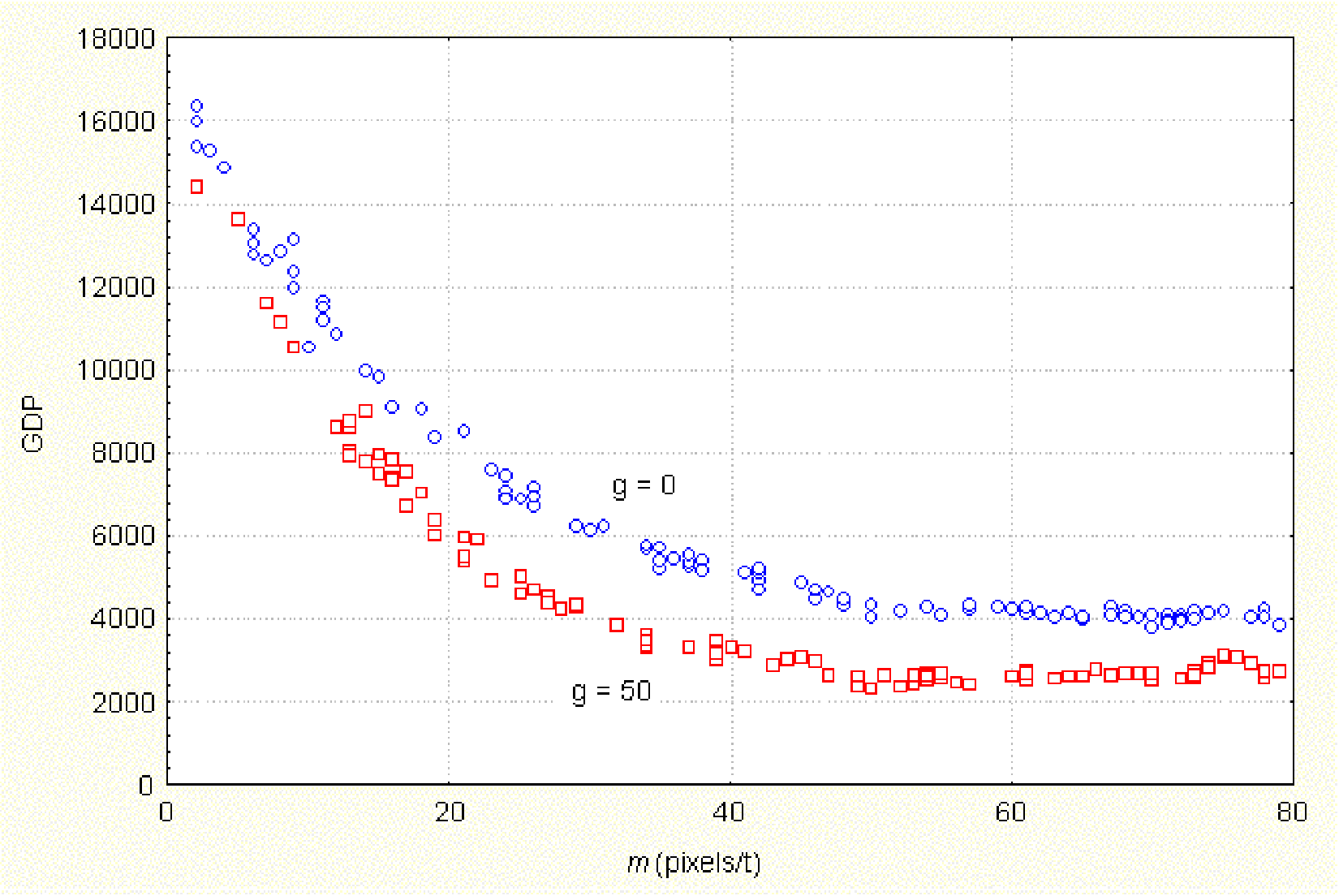
| Figure 4. Effect of the speeds of agents (m) on accumulated wealth (GDP). tstep = 40, RD = 0, RN = 1, RS = 100, b = 2, τ = 2, a = 2 |
|
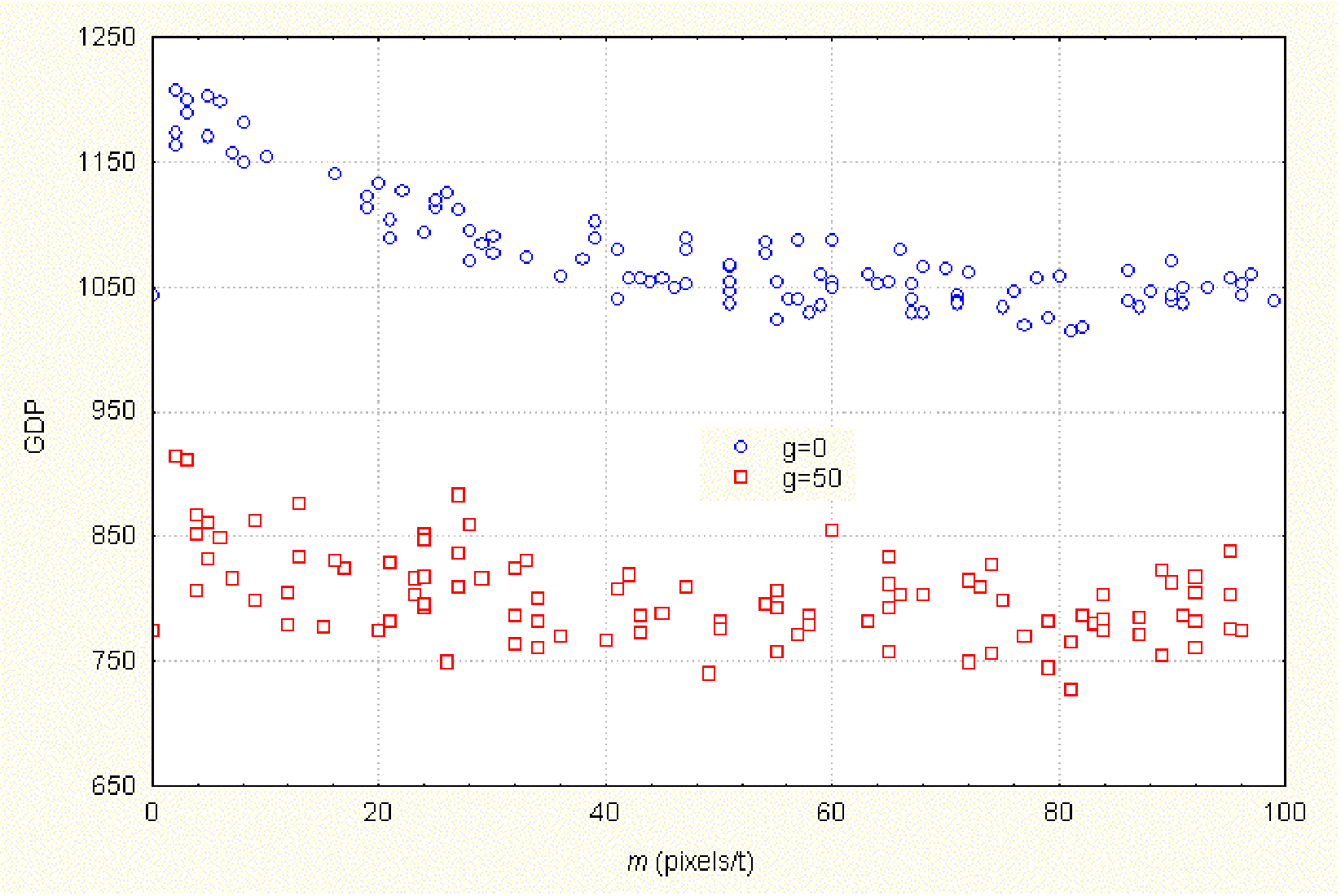
| Figure 5. Accumulated wealth (GDP) vs. speeds of movement (m). tstep = 80, RD = 1, RN = 1, RS = 1, τ = 2, b = 5, a = 1 |
| Table 1: Regression Summary for GDP as Dependent Variable | ||||||
| MULTIPLE R= .59331672 R2= .35202473 Adjusted R2= .34810947, REGRESSION: F(6,993)=89.911 p<0.0000 Std.Error of estimate: 648.25 . Rs * Rn = 100 | ||||||
| N=1000 | BETA | St. Err. of BETA | B | St. Err. of B | t(1000) | p-level |
| Intercept | 2488.398 | 99.57890 | 24.9892 | .000000 | ||
| RN : 1-3 | -.240355 | .025592 | -240.917 | 25.65139 | -9.3920 | .000000 |
| RD : 0-1 | -.230911 | .025619 | -370.639 | 41.12142 | -9.0133 | .000000 |
| b : 1-10 | -.360600 | .025584 | -101.086 | 7.17185 | -14.0948 | .000000 |
| m : 0-80 | -.327687 | .025587 | -11.324 | .88423 | -12.8066 | .000000 |
| g : 0-100 | .039650 | .025594 | 1.103 | .71223 | 1.5492 | .121650 |
| τ: 1-4 | .045711 | .025608 | 32.905 | 18.43378 | 1.7850 | .074562 |
| MULTIPLE R= .68707494 R2= .47207197 Adjusted R2= .46839046 REGRESSION: F(5,717)=128.23 p<0.0000 Std.Error of estimate: 940.28. Rs = 100, Rn = 1 | ||||||
| N=723 | BETA | St. Err. of BETA | B | St. Err. of B | t(723) | p-level |
| Intercept | 3690.323 | 146.0162 | 25.2734 | .000000 | ||
| RD : 0-1 | -.336655 | .027238 | -868.009 | 70.2286 | -12.3598 | .000000 |
| b : 1-10 | -.343743 | .027184 | -154.763 | 12.2391 | -12.6450 | .000000 |
| m : 0-80 | -.485642 | .027274 | -26.208 | 1.4718 | -17.8063 | .000000 |
| g : 0-100 | -.017311 | .027228 | -.785 | 1.2345 | -.6358 | .525139 |
| τ: 1-4 | -.007347 | .027231 | -8.443 | 31.2943 | -.2698 | .787396 |
| MULTIPLE R= .68711002 R2= .47212018 Adjusted R2= .46999805 REGRESSION: F(4,995)=222.47 p<0.0000 Std.Error of estimate: 877.46. Rs = 100, Rn = 1, τ= 2 | ||||||
| N=1000 | BETA | St. Err. of BETA | B | St. Err. of B | t(1000) | p-level |
| Intercept | 3480.976 | 94.02562 | 37.0216 | .000000 | ||
| RD : 0-1 | -.347609 | .023050 | -837.840 | 55.55771 | -15.0805 | .000000 |
| b : 1-10 | -.344063 | .023054 | -144.109 | 9.65599 | -14.9243 | .000000 |
| m : 0-80 | -.479049 | .023048 | -24.835 | 1.19485 | -20.7853 | .000000 |
| g : 0-100 | -.010569 | .023067 | -.439 | .95865 | -.4582 | .646913 |
| Table 2: Regression Summary for GDP as Dependent Variable, when non-economic considerations were included in the model | ||||||
| MULTIPLE R= .82476112 R2= .68023090 Adjusted R2= .66322190 REGRESSION: F(5,94)=39.992 p<.00000 Std.Error of estimate: 1988.3 / Rs = 100, Rn = 1, Ψ ≠ 0 | ||||||
| N=100 | BETA | St. Err. of BETA | B | St. Err. of B | t(94) | p-level |
| Intercept | 13032.57 | 831.8147 | 15.66764 | .000000 | ||
| RD : 0-1 | -.555703 | .058535 | -3807.87 | 401.1005 | -9.49356 | .000000 |
| b : 1-8 | -.266175 | .058561 | -394.37 | 86.7660 | -4.54524 | .000016 |
| m : 0-50 | -.281783 | .060037 | -66.56 | 14.1824 | -4.69348 | .000009 |
| g : 0-50 | .231442 | .059328 | 54.09 | 13.8660 | 3.90107 | .000180 |
| τ: 1-4 | -.508383 | .059106 | -1584.98 | 184.2741 | -8.60123 | .000000 |
| MULTIPLE R= .82476112 R2= .68023090 Adjusted R2= .66322190 REGRESSION: F(5,94)=39.992 p<.00000 Std.Error of estimate: 1988.3 / Rs = 100, Rn = 1 Ψ = 0 | ||||||
| N=202 | BETA | St. Err. of BETA | B | St. Err. of B | t(196) | p-level |
| Intercept | 38912.4 | 1197.985 | 32.4815 | .000000 | ||
| RD : 0-1 | -.709221 | .027455 | -15711.9 | 608.224 | -25.8324 | .000000 |
| b : 1-8 | -.325338 | .027626 | -1472.5 | 125.032 | -11.7766 | .000000 |
| m : 0-50 | -.462689 | .027483 | -361.8 | 21.490 | -16.8353 | .000000 |
| g : 0-50 | -.081932 | .027590 | -60.9 | 20.495 | -2.9696 | .003354 |
| τ: 1-4 | .031644 | .027498 | 325.7 | 283.022 | 1.1508 | .251234 |
Society for Advancement of Behavioral Economics (SABE), Biennial Conference, George Washington University, Washington DC, USA, June 11-12, 2001
Computational and Mathematical Organization Theory Conference, July 5 - 8 2001, Carnegie Mellon University, PA, USA
International Conference on Mathematical and Theoretical Biology, and Annual Meeting of the Society for Mathematical Biology, Joint with Japan Association of Mathematical Biology, Hilo, Big Island, Hawaii, July 16-19, 2001
| A | Utility received by altruistic beneficiary (benefit to the recipient) |
| K | Utility donated by altruistic agent (cost to the donor) |
| B | Long term benefits received by donor of utility (benefit to the donor) |
| b | Degree of external constraints and/or degree of competitiveness |
| m | Maximum distance of random movement of agents |
| g | Degree of generosity Percentage of excess resources donated by agent |
| τ | Threshold in wealth difference that triggers altruistic donation |
| RD | Renewable resources (0) or non renewable (1) resources |
| RN | Number of patches the resource was distributed in space |
| RS | Size of the resource in wo |
| RF | Pattern of the distribution of resource patches 0 random, 1 centered |
| a | Type of altruism simulated |
| wo | Unit for resource |
| wi | Resources accumulated by agent i |
| GDP = Σwi. | Resources accumulated by the whole population |
| Ψ | Domain of non economic utilities |
| w | Work |
| e | Efficiency |
| u | Utility |
| p | Probability |
| κ | Amount of non economic utility |
AXELROD, R. and HAMILTON, W.D. 1981. The evolution of cooperation. Science 211:1390-1396
BECKER, G.S. 1974. A Theory of Social Interactions, J. Political Economics, 82:1063-1091
CABRERA, S. and JAFFE, K. 1998. On the energetic cost of human societies: energy consumption as an econometric index. Interciencia 23: 350-354.
CHENG, S.W. and WAGENER, A. 1992. Altruism and Donations http://www.uni-siegen.de/dept/fb05/vwliv/doks/92-00.pdf
CLARK, K. and SEFTON, M. 2001. The sequential prisoner's dilemma: Evidence on reciprocation. Economic Journal 111: 51-68
FRIEDMAN, D.D. 1987. Does Altruism Produce Efficient Outcomes? Marshall vs. Kaldor." Journal of Legal Studies, Vol. XVII. http://www.daviddfriedman.com/Academic/Marshal_Pareto/Marshal_Pareto.html
FROMING, W.J., ALLEN, L. and JENSEN, R. 1985. Altruism, role-taking and self awareness: The acquisition of norms governing altruistic behavior. Child Development 56: 1223-1228
HAMILTON, W.D. 1964. The genetic evolution of social behaviour I and II. Journal of Theoretical Biology 7: 1-16 and 17-52.
JAFFE, K. 2001. On the relative importance of Haplo-Diploidy, Assortative Mating and Social Synergy on the Evolutionary Emergence of Social Behavior. Acta Biotheoretica 49: 29-42.
NAKAMARU,M., MATSUDA, H. and IWASA. Y. 1998. The Evolution of social interaction in lattice models. Sociological Theory and Methods 12: 149-162.
NOWAK, M.A. and SIGMUND, K. 1998. Evolution of indirect reciprocity by image scoring. Nature, 393: 573
PALMER, C.T.1991. Kin-selection, reciprocal altruism and information sharing among Maine lobstermen. Ethology and Sociobiology 12: 221-235.
RAUT L.K. 1992. Two-sided altruism, Lindahl Equilibrium, and Pareto Optimality in Overlapping Generations Models http://137.151.62.161/Research/Papers/Working/lindahl.pdf
RIOLO, R.L., COHEN, M.D. and AXELROD, R. 2001. Evolution of cooperation without reciprocity. Nature414, 441 - 443.
SIMON, H.A. 1990. A mechanism for social selection and successful altruism. Science, 250: 1665-1668
SILVA, E.R. and JAFFE, K. 2002. Expanded food choice as a possible factor in the evolution of eusociality in Vespidae Sociobiology 39:25-36.
WILSON, E.O. 1976. Sociobiology: A New Synthesis, Harvard University Press.
QUELLER, D.C., ZACCHI, F., CERVO, R., TURRILLAZZI, S., HENSHAW, M.T., SANTORELLI, L.A. and STRASSMANN J.E. 2000. Unrelated helpers in a social insect. Nature 405: 784-787.
QUIGGIN, J. 1997. Altruism, total valuation and benefit cost analysis. Australian Economic Papers 36 (68), 144-155. http://ecocomm.anu.edu.au/quiggin/JournalArticles97/Altruism97.pdf
ZEGGELINK,E.P.H., DEVOS, H. and DONALD, E. 2000. J. Artificial Societies and Social Simulation,https://www.jasss.org/3/3/1.html.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2002]