Ioannis D Katerelos and Andreas G Koulouris (2004)
Seeking Equilibrium Leads to Chaos: Multiple Equilibria Regulation Model
Journal of Artificial Societies and Social Simulation
vol. 7, no. 2
<https://www.jasss.org/7/2/4.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 16-Nov-2003 Accepted: 24-Feb-2004 Published: 31-Mar-2004
 Abstract
Abstract| Table 1: Rescale process: scaling factor according to the range of values of opinions 1 and 2 | |
| Value's range | Scaling factor |
| max>=1 and min<0 | max-min |
| max>1 and min>=0 | max |
| max<=1 and min<0 | 1-min |
| max<=1 and min>=0 | 1 |
| |||||||||||||||
| Table 2. Simulation of MER Model for Ψ = 0.5 and three values of ε | |||||||||||||||
| |||||||||||||||
| Table 3. Simulation of MER Model for Ψ = 1 and three values of ε | |||||||||||||||
| |||||||||||||||
| Table 4. Simulation of MER Model for Ψ = 1.5 and three values of ε | |||||||||||||||
|
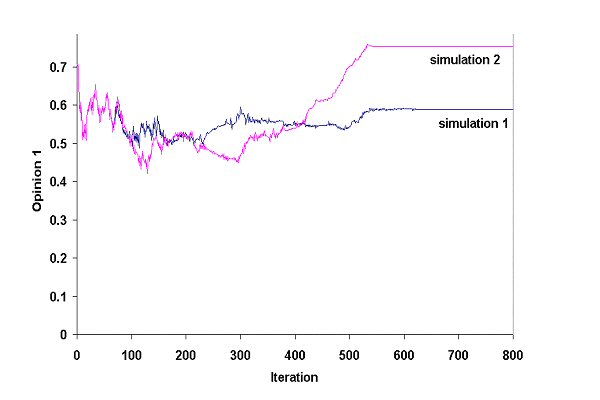
| Figure 1. Opinion 1 of agent 1 in the two simulations (Ψ = 1.5 and ε = 0.1) |
|
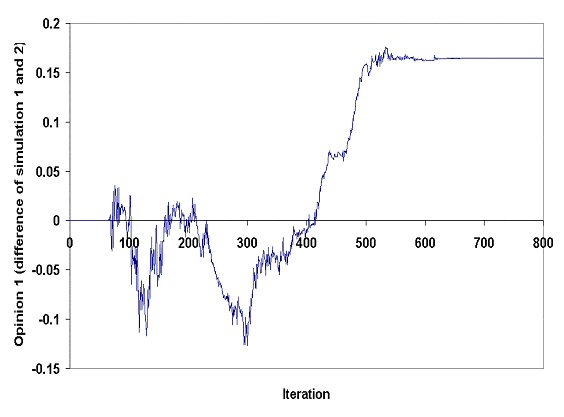
| Figure 2. Differences of opinion 1 of agent (1) in simulations 1 and 2 |
|
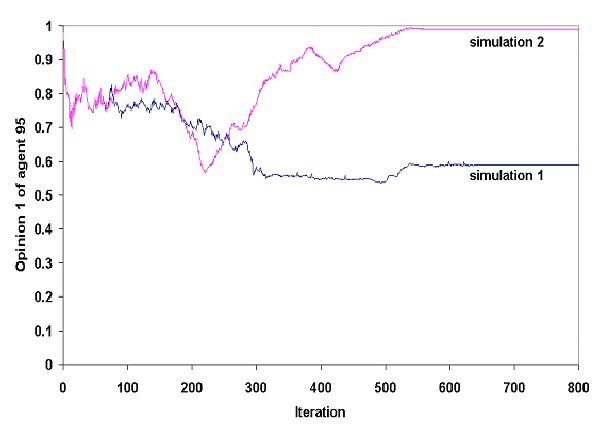
| Figure 3. A minimal change on Agent (1) signifies a major change of Agent (95) -"Personal" history of Agent (95) according to two slightly different (in Agent (1), opinion 1) simulations of the MER model |
| |||||||||||||||||||||||||||
| Table 5. System's dynamics with (simulation 2) or without (simulation 1) a small error (e = 10-10) in the initial opinion 1 of agent 1. Both agents' trajectories and final configurations are different due to sensitivity to initial conditions. | |||||||||||||||||||||||||||
| ||||||||||||
| Table 6. Examining system's nonlinear characteristics: Lyapunov Exponents and Information Entropy |
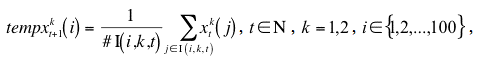
|
where #I(i, k, t) denotes the number of elements of the set I(i, k, t).
|
|
where
|
|
| ε | Bound of confidence |
| Ψ | Intra-regulation factor |
| Opinion (i, p) | Opinion p, p ∈ {1, 2} of agent i at the previous iteration. |
| TemporaryOpinion (i, p) | The mean of the Opinions of agents j that their Opinion differ from agent i less than the Bound of Confidence ε. |
| NewOpinion (i, p) | Opinion p of agent i at the next iteration. |
| Abs | Absolute Value |
For all opinions p
For all agents i
Sum=0: Counter=0
For all agents j
Distance (i, j, p) = Abs (Opinion (i, p) – Opinion (j, p))
If Distance (i, j, p) <= ε Then
Counter = Counter + 1
Sum = Sum + Opinion (j, p)
End If
TemporaryOpinion (i, p) = Sum / Counter
For all agents i
For all opinions p
Change (p)= TemporaryOpinion (i, p) – Opinion (i, p)
Max=Maximum { Abs (Change (1)), Abs (Change (2)) }
If Max= Abs (Change (1)) Then
NewOpinion (i, 2) = TemporaryOpinion (i, 2) - Ψ * Max
If Max= Abs (Change (2)) Then
NewOpinion (i, 1) = TemporaryOpinion (i, 1) - Ψ * Max
For all opinions p
For all agents i
Rescale NewOpinion (i, p) into [0,1]
Calculate Information Entropy
Calculate Lyapunov Exponent
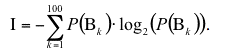
|
2 This conflict is defined as a psycho-logical concept and not on a pure logical basis.
3 These inter-relations among cognitive elements (CE) can be of three kinds: consonant, dissonant and irrelevant (Festinger 1957).
4 In our paradigm, opinions have a sentence-like form: they can be defined as cognitive elements (CE) of the same cognitive space: i.e. if CE A goes up then CE B must go down or vice-versa.
5 Maybe the word "conforming" is more suitable in our case (Sherif 1936; Asch 1951, 1956).
6 Of course, as for social equilibrium, a state of achieved "Intra-individual" equilibrium is purely theoretical (see Introduction on Intra-individual equilibrium). Therefore, to be more exact, a person rather "tries" to attain the equilibrium than "maintaining" an already achieved equilibrium.
7 Just like rhinoceros, one is considered "myopic" in static values but accurate in changes. A rhinoceros is very deficient in seeing static things but he distinguishes motion easily.
8 For the moment, we consider that values above 2 are rather "unrealistic". This means that adding or subtracting the double of the difference found in one opinion to the other can already be characterised as "over-reaction".
9 This procedure is like every time some opinion escapes the interval [0,1] we "photocopy" the opinions by reducing their size proportionally and so we put them into [0,1] again. We have tested for a large number of parameter values that the dynamical behavior of the system is unaltered and thus we obtain similar configurations.
10 Given the expected measurement error produced in every data collection technique concerning social phenomena, the magnitude of "error" can be extremely high (or even "gross") in terms of exact sciences' mathematical analysis. This means that an error of the order 10-10 is simply senseless in socio-psychological research and one considers that social sciences' measurement cannot be "exact", so these sciences could never enter the "exact sciences club".
11 We do not present simulation 2 for Ψ = 0.5 and Ψ = 1, since in these cases the initial error becomes even smaller or disappears. The system gives exactly the same picture for simulation 2, as we can see for simulation 1 in table 2 and apparently does not exhibit sensitivity to initial conditions.
12 Sensitivity, however, does not automatically lead to unpredictability. Indeed, there are sensitive systems that are predictable, e.g. the linear transformations xn+1 = c · x n, c ∈ R, n ∈ N*. An initial error is magnified after we iterate, but the error remains significantly smaller than xn (Peitgen et al 1992, pg.512). In a chaotic system, given the slightest deviation in initial conditions, after a certain number of iterations, it will become as large as the true signal itself. In other words, the error will be of the same order of magnitude as the correct values.
13 For every pair of values for Ψ and ε the system has 200 Lyapunov Exponents since it is defined in R200. In all cases, we compute only the Larger Lyapunov Exponent, which is the best indication for the predictability or unpredictability of the system.
14 We have also tested that the values of the Lyapunov Exponents calculated above are independent of the magnitude of error (when error tends to zero) and independent of different initial conditions.
15"Final configuration" stands for the system position beyond which there is no further change of values.
16 The simplest way of defining methodological individualism is the thesis in which every proposition about a group is, implicitly or explicitly, formulated in terms of behavior or interaction of the individuals constituting the group (Schumpeter 1908).
17 Our model does not include any stochastic process; therefore, the trajectories of our agents are predetermined by means of interaction's algorithms.
18"Zeitgeist" means a trend of a culture and taste characteristic of an era.
ALLIGOOD, K. T., Sauer, T. D. & Yorke, J. A. (2000). Chaos, an Introduction to Dynamical Systems. New York: Springer-Verlag.
ASCH, S. E. (1951). Effects of Group Pressure upon the Modification and Distortion of Judgement. In H. Guetzkow (Ed.). Group, Leadership and Men. Pittsburgh, PA: Carnegie Press. (p. 177-190)
ASCH, S. E. (1956). Studies of Independence and Conformity: 1. A Minority of one Against a Unanimous Majority. Psychological Monographs. 70 (9, No 416)
AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. Complexity, Vol. 3, No 2, p. 16-22.
BECKMANN, T. (1997). Starke und schwache Ergodizität in nichtlinearen Konsensmodellen. Diploma thesis Universität Bremen.
BEN-NAIM, E. Krapivsky, P. & Redner, S. (2003). Bifurcations and Patterns in Compromise Processes. Physica D 183 190.
BILLIG, M. (1991). Ideology and Opinions. London: Sage Pbns.
BUCKLEY, W. (1967). Sociology and Modern Systems Theory. Englewood Cliffs: Prentice-Hall
CAMBEL, A. B. (1993). Applied Chaos Theory: A paradigm for Complexity. Academic Press, Inc.: San Diego, USA.
CASTI, J. L. (1994). Complexification: Explaining a Paradoxical World Through the Science of Surprise. London: Abacus.
DEFFUANT, G. Neau, D. Amblard, F. and Weisbuch, G. (2001). Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 87-98.
DEFFUANT, G. Amblard, F. Gérard Weisbuch, G. & Faure, T. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation vol. 5, no. 4
https://www.jasss.org/5/4/1.html
DITTMER, J. C. (2000). Diskrete Michtlineare Modelle der Konsensbildung. Diploma thesis Universität Bremen.
DITTMER, J. C. (2001). Consensus Formation Under Bounded Confidence. Nonlinear Analysis, 47(7), p. 4615-4621.
FESTINGER, L. (1957). A Theory of Cognitive Dissonance. Evanston, IL.: Row, Peterson.
FISKE, D. W. & Shweder R. A. (1986). Metatheory in Social Science. Chicago and London: The University of Chicago Press.
FLAMENT, C. (1981). L' Analyse de Similitude: Une Technique pour les Recherches sur les Représentations Sociales, Cahiers de Psychologie Cognitive, 4, p. 357-396.
GERGEN, K. J. (1973). Social Psychology as History. Journal of Personality and Social Psychlogy. 26: 309-20.
GILBERT, N. & Troitzsch, K. G. (1999). Simulation for the Social Scientist. London: Open University Press.
HEIDER, F. (1946). Attitudes and Cognitive Organization. Journal of Psychology, 21, 107-112.
HALFPENNY, P. (1997). Situating Simulation in Sociology. Sociological Research Online, vol. 2, No 3.
HEGSELMANN, R. & Flache, A. (1998). Understanding Complex Social Dynamics: A Plea For Cellular Automata Based Modelling. Journal of Artificial Societies and Social Simulation, vol. 1, no 3. https://www.jasss.org/1/3/1.html
HEGSELMANN, R. & Krause, U. (2002). Opinion Dynamics and Bounded Confidence Models, Analysis and Simulation. Journal of Artificial Societies and Social Simulation, vol. 5, no 3. https://www.jasss.org/5/3/2.html
KIEL, L. D. & Elliott, E. (1997/2000). Chaos Theory in the Social Sciences. USA: The University of Michigan Press.
KRAUSE. U, (1997). Soziale Dynamiken mit vielen Interakteuren. Eine Problemskizze. In Krause, U. and Stockler, M. (Eds.) Modellierung und Simualation von Dynamiken mit vielen interagierenden Akteuren. Universitat Bremen, p. 37-51.
KRAUSE, U. (2000). A Discrete Non-linear and Non-autonomous Model of Consensus Formation. In Elaydi, S., Ladas, G., Popenda, J. and Rakowski, J. (Eds.). Communications in Difference Equations. Amsterdam: Gordon and Breach Publ. p. 227-236.
LEWIN, K. (1936). Elements of a Topological Psychology. New York: McGraw-Hill.
LUGAN, J-C. (1993). La Systémique Sociale. Paris: P.U.F. (Q-S-J)
PARETO, V. (1916/1935). Mind and Society, USA: Kensington Publishing Co.
PARSONS, T. (1977). Social Systems and the Evolution of Action Theory. New York: The free Press
PEITGEN, H-O. Jurgens, H. & Saupe, D. (1992). Chaos and Fractals, New Frontiers of Science. New York: Springer-Verlag.
PERELMAN, C. (1979). The new Rhetoric and the Humanities. Dordrecht: D. Reidel.
SCHUMPETER, J. (1908). On the Concept of Social Value. Quarterly Journal of economics, p. 213-232.
SHERIF, M. (1936). The Psychology of Social Norms. New York: Harper and Brothers.
SOROKIN, P.A. (1927). Social Mobility. New York: Harper.
SPROTT, J.C. (1998). Numerical Calculation of Largest Lyapunov Exponent. http://sprott.physics.wisc.edu/chaos/lyapexp.htm
SPROTT, J.C. (2003). Chaos and Time-Series Analysis. Oxford University Press: Oxford.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2004]