Petter Holme and Andreas Grönlund (2005)

Modelling the Dynamics of Youth Subcultures

Journal of Artificial Societies and Social Simulation vol. 8, no. 3
<https://www.jasss.org/8/3/3.html>

For information about citing this article, click here

Received: 05-Feb-2005    Accepted: 25-Apr-2005    Published: 30-Jun-2005

Abstract

What are the dynamics behind youth subcultures such as punk, hippie, or hip-hop cultures? How does the global dynamics of these subcultures relate to the individual's search for a personal identity? We propose a simple dynamical model to address these questions and find that only a few assumptions of the individual's behaviour are necessary to regenerate known features of youth culture.

Keywords:

Youth Culture, Adolescence, Multiagent Systems, Complex Networks, Social Networks

Introduction

1.1

One can often distinguish youths from adults, not only by their faces, but also by their jargon, clothing, gait and posture. Their relative lack of experience and generally different position in life have probably always separated the youth and adult worlds (Brake 1985). The prosperity of Western societies during the 20th century has postponed the entry of adulthood. This has increased the importance of youth culture in the search of identity. It has also diversified youth culture so that one (in academia since Hall and Jefferson 1979) speaks of youth subcultures rather than one youth culture. Whereas "subculture," in general, refers to a social group with particular behaviours or beliefs, this paper specifically focuses on youth subcultures. Today, youth subcultures are conspicuous features of Western and other societies of the world. We note that youth subcultures, as known in the West, often require some economic strength from the follower. Many aspects of our discussion are probably ubiquitous, but to simplify we focus on youth culture in wealthy democracies. Subcultures may be long lived like the hip hop or punk cultures, or die out almost as soon as they have a name. They may be centred on music, sports (such as the surf or snowboard culture, Rinehart and Sydnor 2003) or literature (such as the Beat generation, Polsky 1971), religion (Damrell 1978), etc. The reason a subculture may flare up and vanish soon is related to that adolescents in search of an identity are very adaptive in terms of the defining traits of a subculture. An adolescent's formation of a personality is both an individual and a social process (Conger 1973, Erikson 1968). For the social part the subcultures often play a major role. In this study we attempt to model the dynamics of subcultures based on a few assumptions about the rationale behind the subcultures' roles in the formation of a personal identity. Our goal is to observe the skewed distribution of sizes of the subcultures - like Thornton's example about the club subcultures of late-eighties Britain: "Hundreds of dance genres are coined every year. While most fail, acid house prospered." (Thornton 1995, p. 156.) "Genre" refers to a division of an art form, in this case club music. Just as music can be classified hierarchically, one can divide subcultures into sub-subcultures. Since, in the club music world of Thornton, the subcultural identity is closely tied to the music, it is natural to associate the genre with a subculture. This is, of course, a very fine distinction of a subculture; henceforth, we will not explicitly state the level of the hierarchy we are discussing, but presume that the same precepts govern subcultures at all different hierarchical levels. To model youth subcultures is, no doubt, an exceedingly complex problem; and any approach runs the risk of either being an over-simplification or so complex the actual mechanisms become indecipherable. Since this question is, to our knowledge, not earlier addressed, we propose a simple framework that can easily be extended to more elaborate future models. We mention that this model can be applied to different social and economic systems. In this paper, however, we focus solely on the question of youth subcultures.

Dynamical model

2.1

Our model is based on five major assumptions:

1. The dynamics of the underlying social network is negligible. This is probably our least realistic assumption - as a youth takes up a new subculture she, or he, will likely meet and get acquainted with other aficionados. On the other hand, there are many factors that inhibit the dynamics of one's social network: the classmates, neighbours and relatives do not change that rapidly. We anticipate future models that will include an adaptive network dynamics. For this work we will use static underlying networks. Some evidence that youths retain some of their social network after the entry into adulthood can be found in (Degenne and Lebeaux 2005).
2. An adolescent belongs to one subculture at a time. This is natural since, belonging to many subcultures at the same time would conflict with the subculture as a basis for a personal identity. Furthermore, for many subcultures, a member is expected to be devoted to it. That much said, it is sometimes more appropriate to represent the identities in a multi-dimensional space (McPherson 1983). Certainly our study can be extended to incorporate this framework (someone can be a hip-hopper in a music dimension and a basketball player in a sports dimension). Note that, if the dimensions are weakly coupled (interrelated), each dimension can be treated as a separate, one-dimensional system. For the present study we assume one-dimensional identities.
3. If the fraction of friends that have adopted a certain subculture is big enough then an adolescent will adopt that subculture too. This assumption lies behind much of modelling for the spread of fads (Watts 2002). It is known that friends play a great role for an individual's adoption of subcultures (Conger 1973, Erikson 1968). If many friends of a youth follow a new fad, naturally she, or he, will be interested in the new thing and may also feel left behind.
4. The attractiveness of a subculture decreases with its age. Youths do not want to be old-fashioned, so a subculture on its decline certainly seems less appealing to potential followers than a subculture on its rise. 5. There is a certain resistance to changings subcultures. To take up a subculture requires an effort - one needs to learn the unstated rules and most likely buy various paraphernalia - i.e. acquire subcultural capital (Thornton 1995). Then, of course, the followers of a subculture must like what they are doing, if they are not tired and dissatisfied with what they are doing they would not change.

2.2

Many subcultures define themselves against the "mainstream" - the commercialised culture promoted by media (Thornton 1995, Brake 1985). It has been argued that this dichotomy - the subcultures vs. the mainstream - is more a way of maintaining individuality (Grönlund and Holme 2004) than a relevant social distinction. In our work we assume the mainstream can be regarded as a collection or set of subcultures, kindred with the other subcultures, though in reality of course by far the biggest. Media (though, by definition, not the most used channels) has, of course, a role in the spreading of more obscure subcultures too. A youth may adopt a subculture only as a result of a media report. In the real world there is a coupling from the youth to the media and back again. This paper assumes the personal coupling is stronger when it comes to identity formation and thus considers the spread through friends only.

2.3

Now we turn to the definition of our model. We use the framework of graph theory and consider N vertices connected pairwise by M edges. The vertices represent the youths and the edges represent their social ties. At time t the vertex i has a unique identity, or subculture, c(i,t). Time, in our simulation, is discrete. It is represented by an integer number from 1 to t_max (we have t_max = 12800 for all runs of our simulations) corresponding to the number of the iteration of the update of c(i,t). The central part of the updating procedure is the score function s_c(t,i) that is intended to represent the attractiveness of subculture c to person i at time t. If the score-function value of a subculture c exceeds a threshold T (which is a model parameter) the individual will replace her/his current subcultural identity by c. As mentioned, a high number of neighbours adopting c should make c attractive. We make the simplest choice and let s_c(t,i) be a linear function of n_i(c), the number of neighbours of i with the identity c. That the attractiveness of a subculture decreases with time is implemented by making s_c(t,i) proportional to the age difference between c and c_i, i's current subculture, divided by the current age of c_i. The last ingredient of the score function is a normalisation factor, k/k_i, k = 2M/N is the average degree (number of neighbours of a vertex) and k_i is i's degree. This factor is included to compensate for the varying degrees, so that the same threshold value can be used for all vertices. To sum up, the score function is

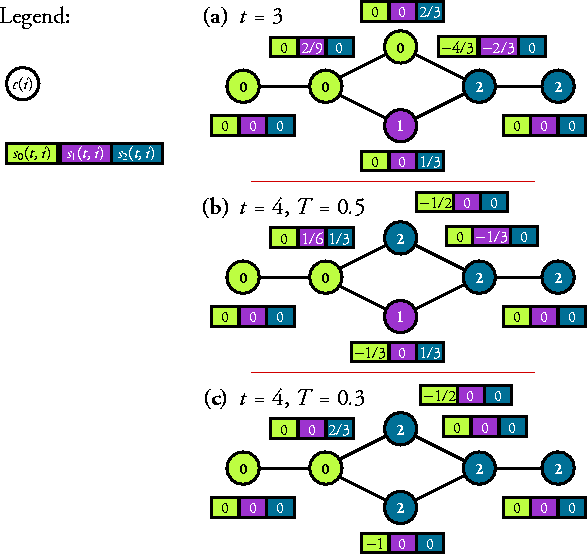
sc(t,i) = (k/ki) ni(c) [t(c)-t(ci)]/[t-t(ci)] ,

(1)

where t(c) is the age of c (note that if t has no argument it refers to the current simulation time). The iterations are as follows:

1. For every vertex i (chosen sequentially) calculate the score s_c(t,i) of all subcultures c for the individual i at time t.
2. Go through the vertex set sequentially once again. If the score is higher than a threshold T for some identity c, then i change its identity to c. If more than one subculture has a score above the threshold then the individual adopts the subculture with the highest score.
3. With a probability R a new identity is assigned to a vertex. So, on average, NR fads are introduced per time step.

Figure 1 Illustration of the model on a small example graph. The colour and number in the circles indicates the current subculture of the vertex. The bar next to the circle shows the vertex' score-function values for the three subcultures (0, 1, and 2) the current time t. The starting time of a subculture t(i) is, in this particular example, identical to i. (b) shows the time-step after (a) in with the threshold value T = 0.5. In this case no other subculture is introduced, no vertex will change subculture as time tends to infinity. (c) is the corresponding plot with T = 0.3. In this case the system will, as time progress, reach a state where every vertex adopts subculture 2.

2.4

An example of the propagation of subcultures on a small test graph can be found in fig. 1. The C++ source code can be found at http://www.tp.umu.se/forskning/networks/fads/.

Substrate networks

3.1

We will use two kinds of network models as underlying networks in our study - one very basic model, the Erdős-Rényi (ER) model (Erdős and Rényi 1959, Rapoport 1957); and one modern model of acquaintance networks, the networked seceder model (Grönlund and Holme 2004). We note that, over the last decade, an abundance of network models have been proposed, the reason we chose these two in particular is that they represent two ends of the spectrum between generality and specificity. The ER model is the simplest possible random graph model - simple in the sense that it is maximally random with no structural biases: One iteratively adds the edges between pairs of vertices so that multiple edges and loops (self-edges) are avoided.

3.2

The seceder model is intended to generate networks with community structure - densely connected subnetworks (communities) with relatively few connections between the subnetworks. We will sketch how this model works, for the exact details we refer to (Grönlund and Holme 2004). One starts from an ER model network and successively rewires (detach one side of an edge and attach it to some other vertex) the edges according to the following approximate rules: 1. Choose three vertices. 2. Select the one i of these with the highest eccentricity (maximal distance to any other vertex, Buckley and Harary, 1989). 3. Choose another vertex j at random and rewire j's edges to i and i's neighbourhood. 4. With a probability r (the only parameter of the seceder model) re-rewire one of j's edges to a randomly chosen vertex. With the parameter r one can tune the randomness of the model - with r = 1 the networks are of ER-type, with r = 0 the community structure is most strongly pronounced.

Figure 2 Examples of network realisations of the ER (a) and the seceder (b) models. Both graphs have N = 50 vertices and M = 150 edges, the seceder graph has the randomisation parameter value r = 0. For the seceder model we indicate the communities, as identified by the algorithm of (Newman 2004), by different symbols.

The ER model networks are characterised by a Poissonian degree distribution, a vanishing clustering (fraction of triangles) and no pronounced community structure. The seceder model networks have an exponentially decaying degree distribution, high clustering and strong community structure. Two example networks are displayed in fig. 2.

Simulation results

Figure 3 Example of a run for ER networks with sizes N = 400, M = 800, and threshold value T = 0.8. The plot shows the size of a few fads as a function of simulation time.

4.1

To get an impression of how subcultures are born, evolve and die, we plot the time evolution of the number of adopters S of different fads. One typical run is seen in fig. 3. We observe that, a subculture can most often be divided into a growth stage, a quasi-stationary stage and a final decline. We note that this distinction of three stages is rather common (Thornton 1995, Damrell 1978). The shape and slope of the growth and decline, the life-length and the maximal size are all distinct for different subcultures. Some fads have more complex time evolution with more than one quasi-stationary state. The time evolution for the seceder model is more complex than for the ER model networks seen in fig. 3. We note that two leading time-scales of this model are the life-length of subcultures and the mean time between introductions of new subcultures. If we have a scale separation (i.e. that, either the life-length is much larger than the introduction time, or vice versa), then the model can be simplified. In the limit of short time between the introductions of new subcultures, every individual will have a new subculture with each time step. In the opposite limit the model essentially reduces to the threshold model of Watts (2002). But in the real world these two time scales are not separable - some subcultures may flare up and vanish within the life-span of others. Our model is thus relevant in this intermediate region and our choice of R = 1/6400 (that we use throughout the simulations) as seen in fig. 3, ensures this. Henceforth, we will study quantities averaged over ~250 realisations of the graph models, this means that there will be ~ 250 t_max RN = 500N fads introduced per point in parameter space.

Figure 4 The probability density function of the largest size of a subculture S_max for the ER (a) and seceder (b) models, and the probability density function of the life-length (t_dur) of subcultures for ER (a) and seceder (b) models. The network sizes are N = 1000 and M = 2000, for the seceder model we have the randomness-parameter value r = 0.1. Errorbars are smaller than the symbol sizes.

4.2

In fig. 4 (a) and (b) we display the distribution plots of the maximal size of the subculture S_max. We see that different threshold values give qualitatively different distributions of S_max. For small threshold values p(S_max) grows with S_max. This means that most subcultures will, at their peak, affect most of the population. For small T-values, or T = 0, S_max is decaying sharply (with an exponential tail). For intermediate values of T there will be a very broad distribution of the maximal subculture-size - a situation where some subcultures grow to involve almost every individual, while many others die out without gaining many followers. Note that such a broad distribution is not a trivial result of the introduction dynamics - a new subculture, in our model, enters the population according to the sharp Poisson-distribution. The two different underlying networks - the ER model of fig. 4 (a) and seceder model of fig. 4 (b) - do not cause any qualitatively different behaviour. (This conclusion - that the result is qualitatively independent of the underlying network structure - is confirmed in preliminary tests on different network models.) There seceder model curves are slightly flatter indicating that there is a larger probability for small subcultures for low T-values and a larger chance for population wide subcultures if T is high. A natural explanation for this lies in the community structure of the seceder model. Since these communities are highly interlinked, the probability that a vertex is neighbour to more than one vertex of the same subcultural identity is higher. Therefore, a new subculture can more easily overcome the threshold and spread within a community. For the same reason it is harder for a subculture to spread between communities. The blurring of the curves of fig. 4 (b) (compared with those in fig. 4 (a)) is thus to some extent due to the community structure. This conclusion is consistent with the plots of the total life time of subcultures t_dur shown in fig. 4 (c) and (d). The seceder model curves (fig. 4 (c)) shows a broader distribution of life-lengths than the ER model (fig. 4 (d)), which can be explained by that the fate of a subculture is, to some extent, determined by the community in which it has started. Another observation regarding the t_dur-distribution is that the peaks come later on the seceder model. This can be explained by the higher clustering (fraction of complete triangles with respect to connected vertex-triples) of the seceder model. A high clustering gives a correction to the number of individuals m step away from a given vertex (Newman 2003) - this number is smaller for a network of high clustering, which means that the number individuals reached (in a person-to-person spreading process) after a certain time is also decreases with the clustering.

Figure 5 The average maximal size <S_max> of a subculture as a function of the degree of the first adopter k₁. The network is of ER type with sizes N = 1600 and M = 3200. Errorbars are of the order of the symbol size.

4.3

So the broad distribution of subculture sizes can be explained by the model, but can anything be said how a large subculture is initiated? Intuitively one expects that if the first adopter has higher degree then the subculture has a higher chance of being a population-wide fad. In fig. 5 we plot the average peak-size <S_max> as a function of the degree of the first adopter k₁. As expected <S_max>(k₁) is an (sublinearly) increasing function. If the threshold is lower the influence of high-degree vertices increases. This is an effect of the larger average peak sizes of lower T-values. (For higher T-values more subcultures coexist, so the peak sizes are smaller but the life-length longer.)

Figure 6 The distribution of the frequency of subcultures per individual v as a function of degree (a) and eccentricity (b). The underlying networks are of ER type with N = 1000 vertices M = 2000 edges and threshold value T = 1.0.

4.4

In addition to the phenomenon that subcultures can be central for the formation of a youth's personal identity, some adolescents shift such characteristics more frequently than others. This can of course be modelled by a varying threshold, but may also be an effect of the structure of the social network. In fig. 6 (a) we plot the frequency v of subcultures per individual, i.e. the number of subcultures that can be expected to be adopted during one time step. Since only one new subculture can be adapted per time step v is also the probability that an individual will adopt a new identity a particular time step. We see a sharp peak of v for small k-values. Low-degree vertices are thus, by this property alone, more prone to changing their identity. In fig. 6 (b) we plot v as a function of the eccentricity e (the maximal distance to any other vertex in the network) of the vertex. We observe that v is an increasing function of e. To summarise, individuals that have few acquaintances and are peripheral in the social networks changes identity more often. One observation in favour of this finding is Thornton's study (Thornton 1995) of British club cultures where many adopters change as soon as a specific style has been adopted by the mainstream. Apart from this we have not found any empirical observations of this phenomenon. Even if the non-constant v of fig. 6 would be dismissed as an artefact of our model, it still exemplifies that it is not only individual characteristics that create the social network - one's identity may also be formed by the social network structure.

Summary and conclusions

5.1

We have presented a model for how subcultures spread in a population of adolescents. Using five main assumptions of a youth's response to the subcultures of others to whom they are socially close, we construct dynamical rules for subculture diffusion. This dynamical model is then put on networks intended to represent acquaintance ties. The model is sketchy, but contains, we believe, many of the important mechanisms for the evolution of the youth subcultures. Even if each individual has a very complex rationale for her, or his, response to the social environment, the fact that individuals, on average, respond in certain ways makes it possible for only a few mechanisms to govern the system-wide properties (Schelling 1978). One problem with the particular question we address, is the lack of quantitative empirical data. Unlike the related issue of memberships in voluntary organisations (Liljeros 2001) an adolescent is not required to register in any way. One can, as we do, compare qualitative model behaviour with qualitative observations. But for future studies it should be possible to perform quantitative studies; either directly by longitudinal interview surveys, or indirectly by e.g. measuring the frequency of related key words in the press.

5.2

One characteristic our model shares with real world observations is that, for certain parameter values, a few subcultures have a much larger staying-power than the average, whereas most subcultures die out very soon. The punk music scene of the 1970s (Hall and Jefferson 1979) is an example of a long-lived and large subculture. The other end, that of short-lived and small subcultures, is less well-defined: one can imagine peculiar habits of a circle of friends, maybe even one person, to define a subculture. Such short-lived fads can be great in number and still remain largely unheard of just because the total number of practitioners is small. We find that the maximal size of the networks is strongly correlated with the degree of the first adopter. Another outcome of our model is that fringe groups change identity more frequently than central and well-connected vertices. This may or may not reflect a real situation, but it serves as an example of how traits of individuals can result from the social structure, as well as vice versa. The qualitative behaviour of our dynamical rules is the same for our two network models. This means that the result is stable for moderate changes of the underlying network topology, and therefore is likely to remain valid for large ranges of real social networks.

5.3

Many studies separate subcultures and the commercialised mainstream youth cultures. It has been argued that this dichotomy, rather than being an accurate social description, stems from members of smaller subcultures and their need to profile themselves as different opposed to a larger mainstream culture (Thornton 1995). In our model, we would like to interpret the largest subcultures as forming the mainstream. Naturally, these subcultures, rather than smaller subcultures, tend to be the focus of commercial interests.

5.4

Many extension and versions of this and similar threshold models are possible. We anticipate future work proposing, just as we (in this paper) and e.g. (Upal 2005) do, fine tuned models for information dissemination on more specific social systems than more general sociodynamic models of e.g. information diffusion and opinion formation (see e.g. Sznajd-Weron and Sznajd 2000, Ben-Naim et al. 2003, Dodds and Watts 2004 and references therein).

Acknowledgements

Thanks for comments and partial financial support is due to Beom Jun Kim, Ajou University, Suwon, Korea

References

BEN-NAIM E, Krapivsky P L, Redner S (2003) Bifurcations and patterns in compromise processes, Physica D, 183: 190-204.

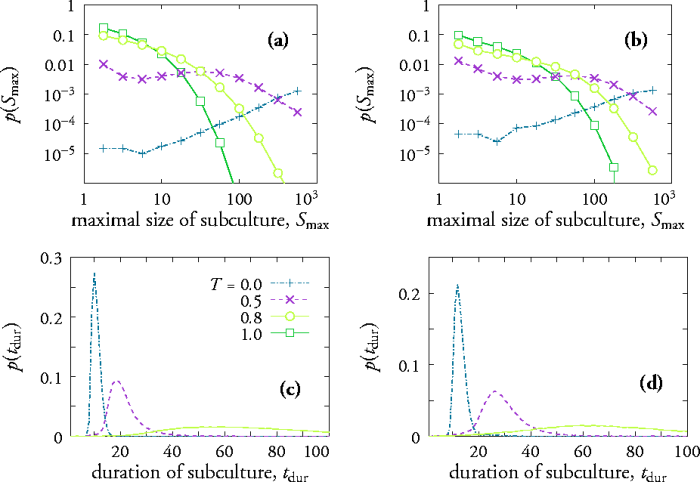
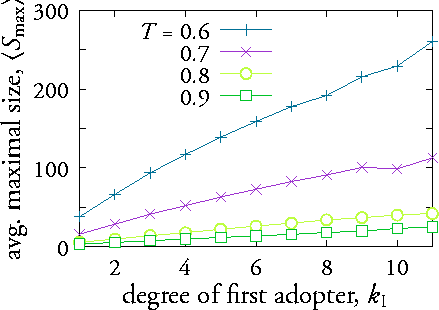
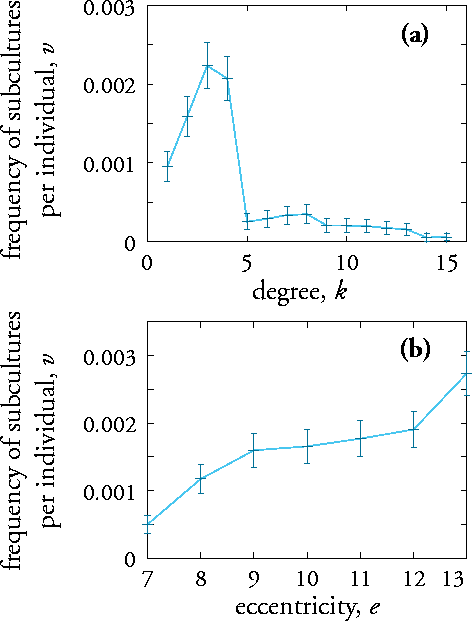
BRAKE M (1985) Comparative Youth Culture: The Sociology of Youth Cultures and Youth Subcultures in America, Britain and Canada, London: Routledge & Kegan Paul.

BUCKLEY F and Harary F (1989) Distance in graphs, Redwood City, CA: Addison-Wesley.

CONGER J J (1973) Adolescence and Youth: Psychological development in a changing world, New York, NY: Harper & Row.

DAMRELL J (1978) Search for Identity: Youth, Religion and Culture, Beverly Hills, CA: Sage Publications.

DEGENNE A and Lebeaux M O (2005) The dynamics of personal networks at the time of entry into adult life, Social Networks, (to be published).

DODDS P S and Watts D J (2004) Universal behavior in a generalized model of contagion, Physical Review Letters, 92: 218701.

ERDŐS P and Rényi A (1959) On random graphs I, Publicationes Mathematicae Debrecen, 6: 290-297.

ERIKSON E H (1968) Identity: Youth and crisis, New York, NY: Norton.

GRÖNLUND A and Holme P (2004) Networking the seceder model: Group formation in social and economic systems, Physical Review E, 70: 036108.

HALL T and Jefferson T (eds.) (1979) Resistance through rituals, London: Hutchinson.

LILJEROS F (2001) The Complexity of Social Organizing, PhD thesis, Stockholm University, Stockholm, Sweden.

MCPHERSON J M (1983) An ecology of affiliation, American Sociological Review, 48: 519-532.

NEWMAN M E J (2003) Ego-centered networks and the ripple effect, Social Networks, 25(1): 83-95.

NEWMAN M E J (2004) Fast algorithm for detecting community structure in networks, Physical Review E, 69: 066133.

POLSKY N (1971) Hustlers, Beats and Others, Harmondsworth: Penguin.

RAPOPORT A (1957) Contribution to the theory of random and biased nets, Bulletin of Mathematical Biophysics, 19: 257-277.

RINEHART R E and Sydnor S (eds.) (2003) To the Extreme: Alternative Sports, Inside and Out, Albany, NY: State University of New York Press.

SCHELLING T C (1978) Micromotives and macrobehavior, New York, NY: W. W. Norton & Company.

SZNAJD-WERON K and Sznajd J (2000), Opinion evolution in closed community, International Journal of Modern Physics C, 11: 1157-1165.

THORNTON S (1995) Club Cultures: Music, Media and Subcultural Capital, Cambridge: Polity Press.
UPAL M A (2005) Simulating the emergence of new religious movements, Journal of Artificial Societies and Social Simulation, 8(1).

WATTS D J (2002) A simple model of global cascades on random networks, Procedings of the National Academy of Sciences of the United States of America, 99: 5766-5771.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2005]