Shah Jamal Alam, Frank Hillebrandt and Michael Schillo (2005)

Sociological Implications of Gift Exchange in Multiagent Systems

Journal of Artificial Societies and Social Simulation vol. 8, no. 3
<https://www.jasss.org/8/3/5.html>

For information about citing this article, click here

Received: 23-Aug-2004    Accepted: 04-Apr-2005    Published: 30-Jun-2005

Abstract

In this paper, the implications of applying the idea of gift exchange mechanism, inspired from Pierre Bourdieu's sociological theories, into a market-based multiagent system are explored. Our work is directed in the continuation of investigations by Knabe (2002), who addressed the formation of different organizations structures between providers in a profit-oriented market. We nevertheless scrutinize various hypotheses centered to gift exchange in which an agent sacrifices its profit for a long-term binding relationship. The idea is to aim a larger profit through alliances that are formed as an effect of gift exchange. Our suggestion is that a multiagent system (MAS) based on the social mechanism of gift exchange performs a high level of robustness and durability. The market in our case comprises of customers and providers agents. The former calls for proposals for the tasks they introduce in the market, while the latter proceed with the execution of tasks based on their abilities and other circumstances. In well defined cases, the providers are able to delegate tasks to other providers. This allows them to give presents to other providers so that the gift exchange mechanism becomes possible. The agents are either profit-oriented or the ones who prefer exchanging gifts and are in pursuit of others who also practice this mechanism. A number of interesting scenarios are examined that include preservation of a hierarchical structure in the market, situations resulting in the forming of an alliance between two providers, and split of profit-oriented and gift-giving agents.

Keywords:

Gift Exchange, Multiagent Systems, Habitus-Field Theory, Social Simulation

Introduction

1.1

While the idea of gift giving in real-world is very ancient, it is found to be an important sociological concept even today, especially in the corporate world. As outlined by Bourdieu, the gift exchange mechanism also structures the practice in modern societies and furthermore even the practice in the economic field of the contemporary highly differentiated society (Bourdieu 2000). The very essence of reciprocity and the accompanying sense of gratitude are pivotal in almost all societies. In his Habitus-Field Theory, Pierre Bourdieu explained the sociological basis of gift exchange in the real-world where individuals as well as organizations exchange gifts; the practical sense behind this practice is to build reliable partnerships in order to survive and accumulate capital in the market where competitions are fierce (Bourdieu and Wacquant 1992). The practice of gift exchange enables the agents to bear smaller losses in order to build a stable and long-term relationship with one another. Another practical reason behind gift giving, also explained by Bourdieu, is to attain supremacy over other individuals or organizations keeping them indebted to the favor granted in the form of a gift. Appendix A presents some related work about the modeling of gift exchange.

1.2

In this paper we introduce gift exchange in an "artificial society" modeled through a multiagent system in a market-based scenario. The single agents of the MAS are self-interested and compete with each other to accomplish tasks introduced in the system and consequently earning profits. This work contributes to a model for gift exchange in a market-based multiagent system and identifies the major parameters surrounding the phenomenon of gift exchange based on Pierre Bourdieu's Habitus-Field Theory. To investigate the effects of gift exchange in our system, we tested the model on the hypotheses that center upon the performance of agents who practice gift exchange, and those who are only interested in earning profits via economic exchange. The observations obtained from the experiments are reported.

1.3

Our model provides the social mechanisms for building the relationships among agents who practice gift exchange. Interaction diagrams for gift exchange are also presented which maybe useful for future extensions. Gift exchange was found to be an important mean for agents to build long-term associations due to the reciprocal structure of gift giving. The performance of such agents was found to be better than the one of the others. Practices of gift exchange not only provided less powerful agents a better chance to survive in the market, it also helped them to accumulate more wealth than they had earned without it.

Sociological Basis

Agents

2.1

Although the term 'agent' has no single definition, we present two definitions of agents that are closer to the notions of agents used in our work. Wooldridge and Jennings (1994) define it with respect to the computer science's perspective as:

• Autonomy: Control over its internal states and is autonomous in its actions.
• Reactivity: Able to perceive its environments and respond accordingly.
• Sociality: Able to interact with other agents and make necessary coalitions.
• Proactivity: Should be able to exhibit opportunistic and goal-directed behavior.

2.2

A more social sciences related definition is given by Ferber (1999), which discusses an agent's ability to communicate with other agents, having its own resources and capabilities which it can offer as services, and is capable of perceiving its environment up to some extent. For a more detailed overview, the reader is referred to one of the several books on the topic (Ferber 1999; Weiß 1999; Wooldridge 2002).

MAS and Social Simulation

2.3

In the multiagent systems (MAS), agents are (usually) different entities that can possess different motives individually (or collectively in case of groups of agents), can adopt different strategies, cooperate and collaborate to facilitate their goals which could be self-centered or group based. The way individuals organize themselves in a society to form groups with various types of organizations leading to clusters and community structures has been studied by sociologists and researchers in distributed artificial intelligence (DAI), see (Carley and Gasser 1999). The idea that intricate problems could be solved by means of the cooperation of many autonomous entities (agents) have inspired vast research opportunities especially in the research field of socionics concerned with the investigation of human societies that are versatile, stable and fault-tolerant (Malsch 2001).

2.4

Gift exchange is one of the only two social phenomena that have been found to be universal among societies throughout the history; the other being the incest taboo (Gouldner 1960). For sociologists, the crux of gift-giving lies in the notion of sacrifice; which is an offering of something dear in order to gain a long standing relationship and intimate ties. There is a sharp difference between economic exchange and social exchange (e.g. gift exchange) as sociologist Peter Blau pointed out:

The most basic difference (between social and strictly economic exchange) is that the obligations incurred in social transactions are not clearly specified in advance. [...] In social exchange, by contrast, one party supplies benefits to another, and although there is a general expectation of reciprocation, the exact nature of the return is left unspecified. Indeed, it must remain unspecified, since any attempt to specify it in advance destroys the social meaning of the transaction by transforming it into a merely economic one. Doing a favor has an entirely different social significance from making a bargain. (Blau 1974)

The aim of gift exchange is to build stronger relationship, which may be beneficial in the long-run. As Schillo (2004) explains,

the results of gift-giving are increased social bonds that may not be (economically) rational but help to stabilise social systems in otherwise brittle environments, e.g. in the absence of formal rules. In economic exchange, a good or task is exchanged for money, assuming that the value of both is of appropriate similarity. Gift exchange, however, is the negation of this concept: the mutually deliberate deviation from the economic exchange. The motivation for the gift exchange is the expectation of either reciprocation, or the refusal of reciprocation.

Bourdieu's Habitus- Field Theory

2.5

The sociological basis of our model draws its stimulus from Bourdieu's sociological concept of habitus and social fields. In his theory, Pierre Bourdieu defines a "field" as an objective structure developed historically and consisting of objective relations between positions, setting aside inter-subjective links. A position is characterized by the determinations imposed upon the agents, by the present and potential composition of all sorts of capital (i.e., economic, cultural, social and symbolic) and by its relation to other positions. According to Bourdieu, an agent is the force behind the development, change and reproduction of the social structure of any field (Bourdieu and Wacquant 1992). As described by Schillo et al. (2002), "The social structure of an organization as a field is a cultural as well as a political construction of dominant and dominated agents." In a dynamic environment like a market, some agents are more powerful with respect to their assets and use of their economic, cultural and social capital. Social structures would then be agents' objectives, the use of their capital helping their interests and the rules of interaction that constrain their activities.

2.6

To model the central aspects of gift exchange we correlate this social mechanism with the mechanism of delegation of tasks. Task delegation in MAS is a well-known notion for DAI researchers and has undergone scrupulous studies recently, its definition, however, may vary for different scenarios. Schillo et al. (2001) describe it as, "task delegation is a delegation of a sequence of (autistic) goals to be achieved". As we use the multiagent system to model gift exchange, the high relevance of delegation in MAS makes it a favorable choice. Hillebrandt (2004) and Schillo et al. (2002) provide detailed sociological justification of choosing the delegation mechanism. In this paper, we restrict ourselves to economic exchange and social (gift) exchange based task-delegation mechanisms, which we shall discuss in the next section.

Temporal Aspects

2.7

One of the major aspects of Bourdieu's idea of exchange is to highlight the temporal aspect, which leads to a cycle of unconscious obligations to give, and to give in return. Hence failure to respond with a counter-gift at some point possibly abolishes any chance of exchange of gifts in future (Acciaioli 1981). As Bourdieu emphasizes, for a gift exchange to get underway the counter-gift must be delayed and different. An immediate return of gift (though different) would be a signal of no further gifts to be given or returned.

2.8

In our model, agents observe time-lag for the gift to be conceived. As argued by Bourdieu, a proper time-lag is essential which is concealed by agents from others and so it remains for the receiver to choose the course of future interactions (Bourdieu 1977). Choice of the time-lag is crucial as an immediate counter-gift implies resentment for building long-term ties, and hence brings no social gain. In the words of Bourdieu:

In symbolic exchanges like gift exchange time plays a decisive role. The inaugural act that institutes communication (by addressing words, offering a gift, issuing an invitation or a challenge, etc.) always entails a kind of intrusion or even a calling into question ... In addition, it always inevitably contains the potentiality of a hold, a bond. It is true, contrary to what the structuralists' mechanical model would suggest, it implies uncertainty and therefore a temporal opening: one can always choose not to reply to the interpellation, invitation or challenge or not to reply immediately, to defer and to leave the other party in expectation. (Bourdieu 2000).

Dyadic Relationship

2.9

Gift exchange is not primarily a global activity in a society and is often a highly local process. It becomes interesting to incorporate and to study its ramifications in a multiagent system testbed, where agents exchange gifts in a pure dyadic fashion but one could look forward to an overall emergent behavior. As explained by Schwartz, a dyadic gift exchange always leads to a situation where one of the participants comes in debt of the other (Schwartz 1967). Sociologically, equilibrium between the two participating agents must never be realized, as the dyadic relationship would be reduced to an economic one rather than an exchange of social capital. One can view the notion of 'indebtedness' as a range of choices bounded by complete and inadequate reciprocity; it is 'somewhere' within this range that an agent giving a counter-gift must decide to choose the value for its gift.

Building Trust and Showing Sacrifice

2.10

Offering a gift to another agent in the society^[1] reflects the identity of the giver (and the receiver) of the gift. With respect to DAI, offering a gift serves as a 'signaling device' that reveals the identity of the giver as an agent who exchanges gifts, in addition to mere economic exchange. Certainly this revelation remains private to the receiver. On the contrary, it imposes a challenge on the receiver who is compelled to show its own interest in building an enduring mutual relationship. In MAS, trust can be regarded as an expectation that an agent 'ascribes' to another agent such that the latter will cooperate with the former in a certain situation and thus let agents decide whom to cooperate and with whom not (Marsh 1994). Our notion of gift exchange relies on building trust as compared to reputation. Trust is a central sociological concept investigated by evolutionary biologists, economists and DAI researchers. Our work restricts to the relationship of trust with gift exchange, which Fley and Florian (2004) discuss as the process-based trust. According to them, dyadic interpersonal practice of gift exchange is 'a crucial practice for the accumulation of social and symbolic capital'. A counter-gift not only reciprocates a gift but also incurs new obligation, since sending gift is an act of free-will. Giving gift to an agents whose type is unknown, involves the risk that the receiver is not interested in reciprocating gift at all. Thus, as Fley and Florian (2004) explain, trust between two agents remains intact as long as 'the reciprocal interest of the social relation is confirmed by a perpetual process of exchanging gifts'.

2.11

For Bourdieu, trust is intertwined with an agent's accumulated social capital based on symbolic exchange of commodities (e.g. gift exchange) (Bourdieu 2000). Nevertheless, on one hand Bourdieu assumes agents to be self-interested in maximizing their profits and thus achieving a higher rank in the society, thus taking a selfish role; but interestingly on the other hand, they presume long-term mutual relationships (both symmetric and asymmetric) through exchange of symbolic goods. Hence agents sacrifice their profits momentarily, anticipating larger profits in a longer run as a result of building stronger relationships.

2.12

In our work, agents evade from making high expectation in terms of gift exchange initially, because sending a gift implies loss of donor's economic resources. However as time passes, agents looking for gift exchange partners broaden their quest. The agents are unaware of the number of rounds (time-steps) the market remains active, making the scenario interesting. In the context of MAS, dyadic gift exchange is advantageous as first the initial gift is marked as a signal of trustworthiness and the risk the giver of the gift has undertaken. The initial gift serves as a gesture and thus is of a size (or value) such that it does not result in a big loss to the sender of the gift. This is because, there always remains a chance that the receiver of the gift is opportunistic in nature and does not return a gift. In case of an exchange, however, there is a symmetric transfer of trust for a future exchange.

The Delegation Matrix

2.13

Four distinct social mechanisms are given for task and social delegations. We discuss a crucial basis for modeling gift exchange: the delegation matrix that defines the relationship between the modes and the mechanisms. As Schillo maintains, in principle all possible combinations of the two modes and the four mechanisms are possible in dealing with organizations in multiagent systems (Schillo 2002).

2.14

Figure 1 presents the matrix that not only allows a decentralized coordination of task assignment, but also provides the basis for the propagation of cooperation between agents in carrying out tasks jointly (Hillebrandt 2004). The entries in the matrix explain that in principle all possible combinations of the two modes and the four mechanisms are possible in dealing with organizations in multiagent systems. In this paper, we discuss only the Economic Exchange and Gift Exchange delegation mechanisms (which are discussed in the next section); an outline of the four mechanisms is as follows:

• Voting: decisions made by plurality of votes
• Authority: Use of hierarchical structure for distributed problem-solving
• Economic Exchange: Some agents offer tasks to other agents who compete for their acquisition and are paid on completion of the assigned task.
• Social Exchange (gift exchange): As stated by Bourdieu this concerns the exchange of favors as gifts; the idea is to accumulate social capital that is an important resource in the HFT.

Figure 1. The delegation matrix with Task Delegation and Social Delegation

2.15

The social mechanism of gift exchange in our system works as follows: In the first step, an agent A offers a gift to another agent B. The gift giving agent cannot be sure to get back a gift in return. Thus it offers a gift with an economic loss. In the second step of the mechanism, the agent B may accept the gift. If it does not, the gift exchange fails. If agent B accepts the gift the third step is possible: Agent B gives a counter-gift to agent A. In this third step it is most important that there is a time lag between gift and counter-gift. Otherwise, the exchange works like an economic exchange and cannot be defined as gift exchange. During the time lag between which the gift and the counter-gift happen, is what makes the gift exchange interesting for sociological research. Expecting a counter-gift structures the situation between agent A and agent B. If there is a counter-gift from agent B to agent A, the latter has to accept the offer from agent B as a counter-gift (step four of the gift exchange mechanism). After that the gift exchange is fulfilled. The counter-gift cannot be quantified and there cannot be any economic strategy behind the exchange, since if there is any economic interest inside of the transaction one cannot define the exchange as gift exchange. There is a minimum size of the gift in our model, which can be anticipated by the receiver of a gift.

The Model

Assumptions and Settings

3.1

The system is a market-based multiagent system (MAS) consisting of two distinct types of agents, i.e. customers and providers. The customers are characterized with respect to the type of tasks they introduce in the market. The market runs for, (say) T number of rounds, and at each round, a subset of customers put their respective tasks on auction and calls for bids. The delegation of tasks from the customer to the provider is based on the English auction, in which each bidder is free to raise their bids. In case when no more bids are raised, the bidder with the highest bids wins with the last offered bid. Our system builds upon the testbed used by Knabe (2002), in which they implement the English auction mechanism augmenting the Contract Net Protocol (CNP) as defined by the FIPA (Foundation for Intelligent Physical Agents) (FIPA 2003). The task delegation mechanism used by the customers is the Contract Net Protocol with Confirmation (CNCP), which is an extension to the FIPA's auction mechanism and based on the economic exchange. Knabe et al. (2002) describe the CNCP and other related issue concerning task delegations via economic exchange. An agent initiating an auction is referred as initiator, while those taking part in the auction are referred to as participants. Our system supports introduction of new agents during the simulation, however, we restricted to fixed market population for the tests reported in this article. Appendix C provides the FIPA definition for the contract net protocol.

3.2

The customers are characterized with respect to the complexity of tasks they put on auction in the he market; a task may be atomic, for example of types A, B or C etc or a compound of distinct or a compound of distinct atomic tasks such as AB, BC, or ABC etc. Each type of task is configured with the number of iterations (time-steps) it requires to accomplish it. Time is modeled in terms of number of rounds and customers taking part in a particular round send calls for proposals for their respective tasks to the providers in the market. The role of customers in our setting is limited to introducing the tasks to a number of providers in the auction and delegating the task via the economic exchange.

3.3

The number of customer agents and their respective characteristics are stated in a configuration file and are loaded in the system before running it. The structure is based on the one used by Knabe et al. (2002) in their work. Figure 2 shows a customer agent's characteristics that can be stated in a configuration. 'Entry round' is the round from which the customer start placing the tasks, e.g. the second group in Figure 2 starts introducing tasks of type 'ABC' from round 10 till the end of simulation.

Figure 2. Example of a configuration where two different groups of customers are introduced

3.4

Two distinct types of providers are introduced: those that only perform economic exchange and make profits, and those who look for other agents with whom they can exchange gifts in addition to practicing economic exchange. We call the former as economic exchange providers (EE), and the latter as the gift exchange providers (GE). Given the population of providers as Providers in the system, we have, |Providers|=|EE|+|GE| such that ∀p∈ Providers, p∈ EE ∨ p∈ GE and EE ∩ GE=∅. Beginning with the simulation, the providers are aware of each other in terms of their abilities; the providers' type is hidden.

3.5

The customer agent picks the provider based on economic exchange and only after the selected provider confirms the task, the task is delegated. The introduction of task by a customer and its delegation to a provider occurs in the same round. Provider agents who receive the customer's request for a task first check if they can process the task on their own. Those who cannot process the entire task on their own, begin their own auction in which they delegate a part of task (that which is beyond their capabilities) to other providers. If the provider agents who receive the cfp, are able to find other providers that can contribute in accomplishing the task, the total cost for the task is calculated and the customer agent is sent the proposal. The EE providers use CNCP delegation mechanism for economic exchange (like the customers), for auctioning partial tasks to other providers. The GE provider agents, on the other hand, practice both economic exchange and gift exchange for which the delegation mechanism is discussed in the next section.

3.6

Figure 3 illustrates the attributes common to all providers in the market. For the GE provider agents, we introduce parameters that control gift-giving practice discussed later. A provider agent with a higher 'resource type' can accomplish tasks of same and lesser types. 'Resource capacity' indicates the number of resources a provider has for its resource type. In our tests, we kept the 'profit' and 'entry round' fixed for all providers. Evaluation of task's cost and profits' cost are mentioned in Appendix 'B'. The basic characteristics were introduced by Knabe (2002).

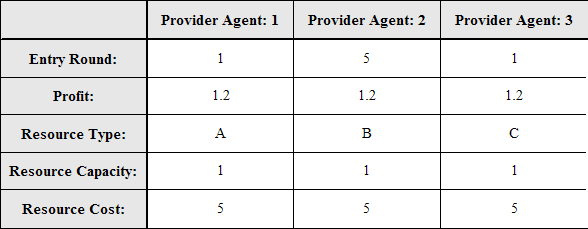
Figure 3. Example of a configuration where three different types of providers are introduced

3.7

The system's general settings are presented in Figure 4. The settings that can be adjusted within the testbed's graphical user interface (GUI), developed for the system. The maximum number of rounds is unknown to the agents. It is crucial that the agents remain unaware of the number of rounds the simulation runs as this information can distort the sociological ideas of reciprocity and building of trust.

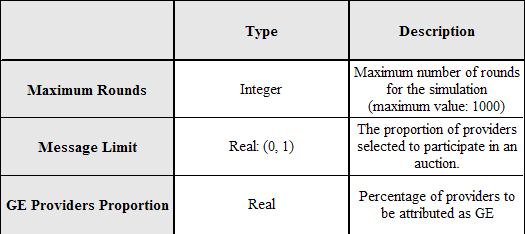
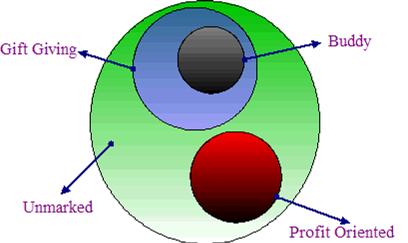
Figure 4. General settings for the system

3.8

It would be useful to define the notion of gift that we have used in our system. We define gift as, A 'gift' is a utility, e.g. a task (or subtask) or capital entrusted by a gift-giving provider to any another provider it chooses in the system. By identifying gift as a utility, we only mean, the gift to be a tangible entity. This is important for both the sender and the receiver, in order to recognize a gift as a gift and know its worth.

3.9

GE providers send gifts in the form of a task such that the profit earned through it remains with the receiver. Similarly, a gift can also be given as some proportion of an economic capital earned by the sender of the gift. The idea of gift can be extended to any form of an agent's capital that it possesses. Given the case when a task is delegated as a gift, a sender of a gift is not allowed to delegate the entire task; instead, a proportion of the task is delegated while the remaining is carried on by the sender itself. An immediate return of a gift or a counter-gift with almost the same worth implies an end of any further gift exchange. A sender of a gift expects reciprocation later on as a signal indicating that the provider receiving the gift is also a GE. It becomes pertinent to have definite way of sending a gift so that the recipient of a gift is able to identify a gift when it is given. As Fley and Florian (2004) explain, it is important in MAS that agents possess abilities to recognize a gift in the system.

Parameters for Gift-Exchange

3.10

The model provides the basis for gift exchange and a number of controlling parameters are introduced that govern the behavior of the system. These parameters are known to the GE provider agents. The values of these parameters are varied so that a satisfactory number of experiments could be performed in order to accumulate statistical measures.

3.11

Initial Rounds: This parameter defines the time limit during which the GE agents experiment gift exchange and after which they build up the future course of action accordingly. It is possible that the simulation ends within the initial rounds or continue for a very long time beyond this threshold.

3.12

Chance of Gift through CNCP: This provides the chance for a GE provider to pick a committed participant of an auction as recipient of the gift. Since the GE providers need to earn profits besides gift exchange initially, the parameter controls the frequency of delegating a subtask as a gift or earning profit via economic exchange, especially during the initial rounds.

3.13

Receiver Selection Strategies: While selecting a committed bidder as recipient of its gifts, a GE provider picks one or more participants of its auction based on the following strategies:

Counter-Gift Receiver Strategy: A GE agent in our model is conscious of reciprocating a gift that it had received from another provider in the past, especially if it had not sent any counter-gift at all. Having such a provider to whom it is indebted, participating in its auction, provides the chance to reciprocate a gift and therefore proving itself as a gift-giving agent. Care is taken that the value of the gift should be different and that 'some' time is passed since the gift was received. Since the CNCP auction is an opportunity to offer gifts to providers in order to know their types, this strategy is not selected always, and the following strategy is chosen:

Best-Bidder Strategy: Gives the chance of picking among the committed participants, the provider with the highest bid. If not, any of the bidders is selected uniform randomly.

3.14

Deadline Strategies: The deadline set when a gift is offered is dependent upon the gift sender's status that in turns reflects the degree of urgency for searching for another GE agent. It also depends upon the size of the task allocated to the recipient in case it is offered as a gift. For instance, a very highly resourceful GE agent may offer gift in order to maintain the structure in the society, which we introduce later on, and hence does not need a partner for its survival. In such case, a longer deadline is set. On the contrary, a GE provider with having limited resources cannot afford to wait long for a counter-gift, therefore requires a response to its gift soon. We introduce four strategies for setting a deadline until a counter-gift is expected. The names for these strategies are inspired from the article by van de Ven (2000), who specified different motivations for giving a gift based on the economic theories.

• Altruistic: This gives a maximum possible deadline and selected as the strategy, when asymmetric gifts are offered.
• Egoistic: Much lesser than altruistic but higher than strategic, chosen when there is a strong dyadic gift exchange between the sender and the receiver of the gift.
• Strategic: Chosen mostly during the 'initial rounds' when GE providers attempt to build relationships via gift exchange.
• Survival: Picked when a sender of a gift desperately needs a reliable partner and time when the gift is sent within the initial rounds.

3.15

Send Further Gift: Typically, no further gift is sent to a provider whose type is unknown unless it reciprocates. This parameter provides a bound to the number of gifts a GE provider sends to a provider before it receives a counter-gift or loses its hope.

Gift-Giving Agents' Relationships

3.16

The relationships built by a GE provider reflect its intentions and the choices it makes under the given circumstances. Being independent from an EE agent can be explained as an intention of a GE provider. For a GE provider with limited abilities, long-term binding relationships are vital. While for a powerful agent, knowledge of providers' types provides opportunities for asymmetric gifts and thus maintaining a hierarchy in the system. In the beginning, no provider knows about the type of others and as the rounds proceeds, their knowledge increases resulting in a grouping of the providers in various relationships. Figure 5 depicts a GE provider's perception of the market at any time t ≥ 1.

3.17

The Gift Giving Relationship: The set of GE providers who are included if at least one gift is received from them, or had sent a counter-gift at least in reciprocation to a gift offer. When a GE provider participating in an auction initiated by a provider receives a gift from the auctioneer, it includes the sender of the gift in this set. If it is a counter-gift, the sender is added into this list. The sender of the counter-gift is thus recognized as the one to be considered for future gift exchange. With the handling of this counter-gift, the return is not awaited any further and the records are updated. On the other hand, if the received gift is found to be an opening gift from an agent, this implies that the sender of the gift has shown itself to be worthy of trust by identifying itself as a gift giving agent, taking the risk of losing a profit. In such case, the receiver acknowledges the sender in this set and tries to reciprocate the gift later on. For the sender, the receiver of its gift is not marked as a member of this group unless a counter-gift is made.

Figure 5. A GE provider's perspective of other providers in the market

3.18

The Buddy Relationship: A GE provider agent acknowledges another as 'buddy', as the one with whom a stable gift exchange is established. This is ensured with the consistent fulfillment of reciprocating the gift. The relationship is specified as a dyadic relationship. An agent can exclusively be a 'buddy' or not with no scalar value attached characterizing the level of being a 'buddy'. In our specification, the number of gifts exchanged between the two GE providers must be at least higher than a threshold value (which is a positive integer) before they acknowledge each other as a 'buddy'. The value of the threshold can be varied for different configurations of the simulation runs. Not only this specification is simple and straightforward, it allows the relationship to be defined as symmetric and dyadic. That is, given two GE providers X and Y we can define the relation buddy as:

3.19

The relation is symmetric since the condition is just the total number of exchanges; however, in order to introduce the dyadic structure, a minimum number of gifts (say, n) need to be sent to the other such that both agents contribute fairly to the establishment of the relation. Hence,

3.20

A dyadic gift exchange provides continuity of relationship between two GE agents, though the mutual obligations of reciprocation remains with the two parties and the resulting trust cannot be generalized to third parties (Fley and Florian 2004). On the other hand, when such dyadic exchange of gifts among agents increases, a network emerges separating the gift-giving agents (having dyadic reciprocal relationship) from others. One possible extension to this relation maybe suggested as plausible in the context of 'a friend of a friend is a friend', where it becomes a transitive relation.

3.21

The Profit Oriented Relationship: A gift giving agent attempts to identify as many profit-oriented or EE agents as possible at the earliest. Gift giving strategy helps in this search as GE agents experiment with unknown providers via CNCP. An agent is attributed as profit oriented if no gift sent to them is reciprocated at all within the deadline. To such agents no further gift is offered, though the economic exchange remains open. Given the fact that our model permits gift exchange via CNCP during the initial rounds, an agent marked as profit oriented is removed from this set and is recognized as gift giving if it returns the gift after the deadline passed. This choice is made only when the gift was offered during the initial rounds, as the recipient of the gift may well possibly fail to reciprocate via the CNCP even though it had desired to send a counter-gift. The idea is to gain some knowledge of other agents' types during the initial rounds so that when later on a gift is sent, it is particularly aimed at the receiver and no one else.

3.22

Unmarked Agents: The group represents the providers whose type is yet to be guessed. Initially every other agent is regarded as an unmarked and thus the set has all providers in the market for each GE agent. As the knowledge about providers is gained, the size of this set reduces as the number of agents whose types are guessed increases. The unmarked agents are a major source of uncertainty in the system and interaction with these agents gives rise to information asymmetries^[2]. The challenge for the gift giving agents is therefore to guess the type of these agents correctly and interact accordingly. 2

Mechanisms for Gift Exchange

4.1

Two mechanisms for gift exchange have been introduced, referred as weak gift exchange and strong gift exchange mechanism. The weak gift exchange is in essence based on the auction-based mechanism and is practiced during the initial rounds of the simulation. We suggest the strong gift mechanism as a special channel for sending a gift without CNCP, carrying the gesture of a strong affinity for the recipient with whom a stable gift exchange is established.

Weak Gift Exchange Mechanism

4.2

The primary distinction of this mechanism is that gift exchange is made possible through the contract-net protocol that is a standard recommended by FIPA. This mechanism facilitates both making gifts and counter-gifts, in which the gift is a subtask on the auction. Moreover, it introduces a challenge for the receiver to disclose its identity as well by sending a counter-gift which is both different and sent at some time later. We take into account the time lag between a gift and a counter-gift as described earlier in this paper. Figure 6 gives the general recipe used for sending a gift.

4.3

A GE provider when receiving a call-for-proposal cfp from a customer evaluates what can be done on its own and in case it is able to perform only a part, initiates a new auction for the subtask which is beyond its capabilities and cfp are sent to the providers. This follows from the approach used by Knabe et al. (2002) for task delegation via CNCP. In the beginning of the simulation, the gift giving auctioneer has little or no knowledge of other providers' type. As this knowledge increases, a GE auctioneer further sends the cfp to the providers from whom a gift had been received in previous rounds; within the initial rounds. Within the initial rounds, this case occurs only occasionally. The idea is to give a chance of participation to the known GE providers so that their wealth increases. More importantly, the motive is to introduce the possibility for reciprocating a gift when the simulation is in the initial rounds. Since the weak gift exchange is the only channel through which GE providers communicate during the initial rounds, the model provides a parameter Chance-Offering-Gift which restricts a GE provider to offer a gift each time it is an initiator of an auction.

4.4

Once a provider is chosen, a gift offer is made and the response is awaited. For the weak gift exchange mechanism, the gift as a utility is a subtask whose value is calculated based on the size of the original task and the bid offered. A gift is only delivered when the payment is made since for various reasons, a committed bidder may fail to accept the auctioneer's request. The gift's size also depends upon whether the market is in the initial rounds during which a small gift is preferred. Such gifts do not have much value instead they serve as gestures for future binding relationships. This prevents a GE auctioneer from big losses in the initial rounds, in case the recipient of the gift turns out to be profit oriented and does not reciprocate at all. A deadline is set depending upon the auctioneer's current status, i.e. the need to find another GE provider. Additionally, the size of the subtask allocated to the gift recipient is also taken into account.

4.5

A GE participant receiving the gift through the weak gift exchange acknowledges the sender as gift giving and keeps record of the incoming gift to be used for sending a counter-gift later on. During the initial rounds a GE receiver of a gift attempts to reciprocate the gift through weak gift exchange and on gaining such opportunity sends a counter-gift with a different value after some time lapse. A GE provider earlier identified as profit oriented due to the fact that it failed to send a counter-gift within the deadline, is removed from this relationship and recognized a gift giving if it sends a counter-gift later on. This occurs only when the gift was sent during the initial rounds. If the number of gifts exchanged between GE providers passes the buddy criterion, a GE provider is promoted to buddy and is informed; the same holds for the former agent (see figures 19 and 20). Figure 7 shows interaction of agents based on UML (Unified Modeling Language) Activity Diagrams, which is an agent's interaction modeling approach developed by Lind (2002).

Figure 6. Scheme for sending gift via Weak Gift Exchange

4.6

The preference criteria set by a GE provider when handling proposals follows an ordering in which a bid from a buddy provider is most preferred; i.e. if there is a proposal from a buddy, its proposal is accepted anyway and kept in the current solution. If the bid is not the best among those who had responded to the call, the loss is calculated as the gift to be given to the buddy. Next, a proposal from a gift giving provider who is not a buddy is preferred given preference if it proposes the highest bid. In case the proposal is not among the best, preference is given when the auctioneer owes a counter-gift to the GE bidder. An unmarked bidder is always preferred over a profit-oriented bidder.

Strong Gift Exchange Mechanism

4.7

In sociological sense gift exchange carries special gestures of individuals sending gifts to others. A gift taking the route through an auction has profound advantages with regards to the problem-solving abilities in artificial societies. There remains a need for an additional mechanism separate from the mechanism which in its basic structure commences economic exchange. We introduce such channel where gifts can be exchanged as utilities, i.e. as tasks or profits earned etc, and call this mechanism Strong Gift Exchange (SGE).

4.8

A strong gift can be given via a special channel without CNCP. The strong gift exchange mechanism comes into action when the market passes through the initial rounds since gift giving agents are required to build strong and stable buddy relationships in order to practice gift exchange via this mechanism.

4.9

Sometimes a GE provider is unable to send a counter-gift to an agent from whom it had received a gift and it is likely that the sender marks it as a profit oriented agent if the deadline passes. Sociologically, it is unfair that an agent is unable to reciprocate constraint by the process which requires task delegation, in spite of the fact that the agent desires it most. The purpose of the counter-gift via the strong gift exchange is to provide such GE providers a chance to send a counter-gift if they had received a gift earlier but could not reciprocate. Figure 8 illustrates sending of a counter-gift via SGE.

Modeling Asymmetric Gift Exchange

4.10

The practice of making gifts does not always involve the element of reciprocation in societies; the entities in real and artificial societies (e.g. individuals in extended families or clans, business organizations etc) can be classified with respect to a hierarchical system. The inequality among the agents emerges as a result of the differences in the capital (e.g. economic, social, symbolic etc) that the agents earn during the course of their interactions. Usually it is the desire of powerful entities in a market or in other words those who rank high in the hierarchy, to maintain their status of being strong and dominating over lesser powerful agents. In his treatise on the sociology of gift, Mauss (1967) refers this phenomenon as a general fact whereby people belonging to the upper class in a society distribute gifts as a means of sustaining prestige to their kith and kin lower in status. As Hillebrandt (2004) explains, in a social field some agents dominate others with respect to their earned capital in order to maintain the structures and regularities in the society.

Figure 7. Interaction of agents using Weak Gift Exchange shown using UML Activity Diagrams

Figure 8. Counter-gift via strong gift exchange

4.11

In this paper, we suggest modeling of such phenomenon is handled by means of the strong gift exchange. In scenarios when the gift is delivered asymmetrically, we refer it to as a strong gift, while when this channel is used as means of reciprocation; we call it a strong counter-gift. For the SGE to take place the market should have passed the initial rounds and any participating agent of SGE must have earned some profit until then. Hence when defining powerful agents, power does not simply mean the ability to carry on a task but also the ability to give a gift and the economic capital earned. Since even for an asymmetric form of a gift, the receiver must be known as a GE by the sender, there should be at least one gift from the receiver so that its type is confirmed.

4.12

In our suggestion for asymmetric gift exchange, the objective of powerful provider agents is to maintain the structure in the society. Hence when they receive a task from either a customer or another provider, they offer a portion of it, i.e. a subtask to a lesser powerful GE provider using the strong gift exchange channel, as shown in Figure 9. A gift giving provider receiving a strong gift makes a decision whether to remain dependent upon a powerful agent for tasks or not. This decision is based upon the number of tasks the receiver acquired via CNCP, the number of buddy relationships it developed earlier on and the frequency of the subtasks it receives from the powerful agent. This strategy is kept simple, but is extendible to more complex strategies.

4.13

When a GE provider initiates an auction and the participants include more than of its buddies, one buddy is preferred over another if the number of strong gifts sent by one is greater than others. In case of a tie, a buddy is preferred randomly. Occasionally, the regular receiver of a SGE sends a counter-gift which is some proportion of the economic capital earned taken care that the counter-gift is different in terms of time and worth. This approach is part of our ongoing study on gift exchange.

Figure 9. An illustration of triggering strong gift exchange

Testing of Hypotheses

5.1

Our market-based testbed encase the model's parameters (introduced in Section 4) that can be varied so that a variety of interesting scenarios can be run and can be investigated. We report tests conducted on some hypotheses relevant to modeling gift exchange in MAS. A number of hypotheses from sociological point of view can be tested on the model; some of them are presented in the discussion.

Hypothesis I: In scenarios where the message-limit (number of call for proposals sent by an auctioneer) and the market size are low, the number of gift exchanges among the gift-giving agents is reduced.

5.2

This hypothesis is primarily concerned with the computation aspect of the effects of gift exchange. The idea that the number of gifts exchanged is proportional to the market-size is not a surprising one and intricate; albeit, it is helpful in testing the workflow of the system. The incentive behind the testing of this hypothesis is to make sure that the practice of gift-giving can be scaled in terms of message-limits as well as in terms of proportion of GE providers in markets of varying size.

5.3

We setup three sets of provider agents' population with sizes 20, 30 and 60 respectively. For each of the three sets three separate configurations were designed, i.e., where the gift giving agents are in minority, same number as that of the profit oriented agents and where the number of gift giving agents is in majority. The experiments were run for 100 rounds and the numbers of gifts exchanged were calculated at the message limits ranging from 10-30% of the population size with 1% step for each experiment.

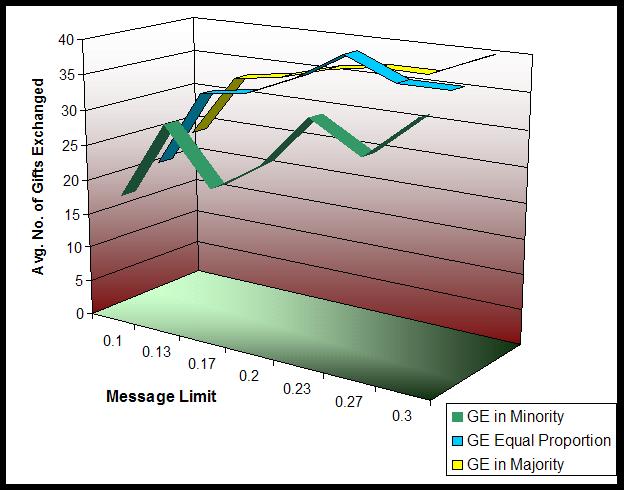
Figure 10. Series plot showing average number of gifts for the three cases with varying message-limit

5.4

Figure 10 summarizes the experiments conducted for this hypothesis based on the given scenario. For the two cases when the gift giving agents are not in minority, the number of gifts exchanged increases with respect to the message limits. One can observe that being in almost equal number or in greater number, provides the gift giving agents sound opportunity to practice gift exchange as the search for other gift giving agents becomes less difficult. Also for the weak gift exchange, there are better chances to return a gift within the initial rounds. On the other hand, when the gift giving agents are in minority, one does not observe an increasing behavior, although for higher value of the message-limit, the number of gifts exchanged increases. The opportunity for gift exchange is inhibited when there are more profit oriented agents in the market and therefore the practice appreciates only when the gift giving agents are able to acquire more tasks than the others during the simulation.

Hypothesis II: We present the hypotheses in two parts, as they may appear correlated to the reader.

II- A: In homogenous market scenarios where all agents are gift-giving, there is no long-term distinct grouping of the agents.

5.5

While the first part 'II-A' may seem trivial, it is helpful in testing the system where the parameters of the model related to gift exchange can be analyzed. The idea of grouping arises from the scenario whereby a GE provider initiating an auction and receiving proposals, prefers a buddy over other respondents to its call for proposals. For a homogenous environment, i.e. where all provider agents are gift giving, stable and long-term ties among the providers is not expected to persist permanently. Since a stable and regular relationship of the delegation of tasks depends upon the exchange of gifts between two agents, a homogenous environment does not permit such phenomenon to occur. When such stability is achieved, it is expected to be limited to a smaller proportion of the providers.

5.6

We selected three different configurations of provider agents each of size 20. All providers were initialized as gift giving agents. A number of experiments were carried out for each of the three configurations and the maximum number of rounds was set to 100. The initial-rounds parameter was fixed to 50% of the simulation rounds. The hypothesis was tested for three different criteria for the buddy selection.

5.7

We build the graph over the buddy relationship which the gift giving agents build after some gifts are exchanged. Since this relation is symmetric, the graph constructed is an undirected and so there is less overhead for updating the graph after each round and calculating its connected components. The standard algorithm for calculating the strongly connected components presented by Cormen et al. (2001) requires two depth-first traversals of the graph and thus the time complexity is O(|GE - Providers|), which does not put significant burden on the simulation.

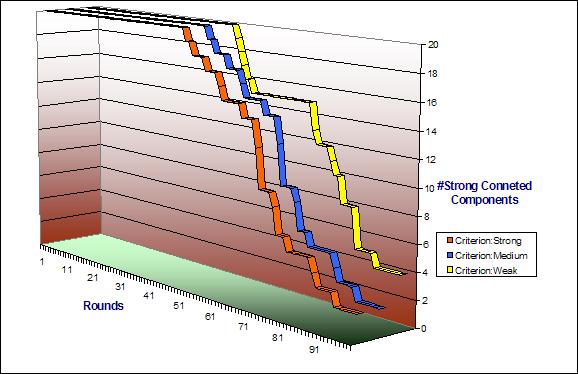
Figure 11. Number of strongly connected components from buddy network based on three different criteria for buddy selection

5.8

Figure 11 presents the outcome of the experiments where simulation begins with all gift giving providers isolated with each other and thus the forest built has |GE-Providers| disjoint single node trees. The number of strongly connected components decreases very gradually during the initial rounds for all the three criteria. Nevertheless we observe a sharp decline in the number of isolated gift giving agents once the simulation goes beyond the initial rounds; the prime factor behind this increase in the connectivity is the counter-gift via strong gift exchange. As the population was homogenous, i.e., all providers were gift giving the number of distinct groups decreases further as the simulation approaches the end and the trend continues. Most of the agents were therefore able to build the buddy relationship with each other.

II- B: In heterogeneous market scenarios, introduction of gift exchange partitions the provider agents into two groups over a long run.

5.9

Three distinct sets of providers' population were used of sizes 20, 30 and 60. We set three distinct configurations for gift giving proportions in the market. The message-limit was fixed to 30% of the population size and the experiments were run for 100 rounds. The number of customers was set to be 20% of providers' population with each customer emitting orders of type ABC in the market. Also we kept the Bias-Bidder-Preference parameter to 100%, i.e., with maximum preference by the gift giving agents for agents of their own type. The Buddy-Criterion was set as moderate while the agents used CNCP to send counter-gifts 70% of the time.

Figure 12. Interactions of GE agents with providers of both types with the GE providers in majority

5.10

We attempt to investigate how well the gift giving agents perform in relying more on other gift giving agents in the market and less on those known to be as the profit oriented ones. Since the gift giving agents look for providers of their own types throughout the simulation, their reliance on agents of their own types is expected to increase. Although each gift giving agent attempts to prefer interactions with other gift giving agents, they practice economic exchange with others when there is no other option. Figures 12 and 13 show the plots of two series, the first series represents the average number of interactions of the gift giving agents among themselves; while the other denotes the average interactions of the gift giving agents with the providers who they know as the profit oriented ones.

5.11

In Figure 12, the graph represents the experiments in which the gift giving agents were in greater number than the profit oriented ones. It may be noticed that in the beginning agents do not know about the types of others and this knowledge is expected to increase during the simulation. With a greater number of GE providers in the market, a majority of gift offers turned out to be successful (i.e., the gift giving agents were able to exchange gifts) due to the fact that the gift giving agents had ample opportunities to return gifts. Thus on average, the knowledge about the other GE providers increased throughout the simulation rounds. On the other hand, it took some rounds for the GE providers to know about the presence of the profit oriented agents in the market. It is relevant to mention here that the gift giving agents interacted with the profit oriented agents right from the start, but they marked them as the EE agents when they did not receive a counter-gift within the anticipated deadline. With a greater proportion, the interaction of the gift giving agents among themselves continued to increase as well as their knowledge about the profit oriented agents, with the rounds. Nonetheless, the former clearly outperformed the latter, i.e. the GE agents kept on increasing their interactions among each other.

Figure 13. Interactions of GE agents with providers of both types with the GE providers in minority

When the GE providers were in minority their knowledge about other GE providers increased gradually during the rounds, as shown in the Figure 13. It is understandable that with a lesser number of GE providers in the market, the number of interactions among themselves is expected to remain low. One also witnesses a sharp rise in the second series, showing the increase in the knowledge of GE agents about the EE provider agents.

5.12

With a greater or equal proportion in the market, the GE providers were able to interact more frequently than in the second case. Nevertheless, their knowledge about the other providers increased during the simulation in both the cases.

Hypothesis III: In heterogeneous market scenarios, if the population of GE agents is greater, the EE agents will not be as successful as in the case when the population of GE agents is low. The higher the populations of GE, the higher are the chances of GE agents of being successful.

5.13

For the third and the fourth hypotheses, we set a heterogeneous population of providers. The experiments were conducted varying the Chance-Weak-GE and the Initial Rounds parameters. The message-limit was fixed to 30% of the population and the simulations were run for 100 rounds. The number of customers was configured to be 25% of the providers' population. We tested the hypotheses with two customers' configurations; one emitting same type of orders, while the other with orders of heterogeneous types. We present the results of our experiments in two phases. First we compare the performance of the gift giving providers (GE) with the profit oriented ones (EE) and then deepen our evaluation in the second phase.

5.14

Figure 14 shows the first part of the experiment in which the parameters Counter-Gift Strategy and Strong Gift were kept low and the message-limit was fixed to 30% of the population's size. The performance was evaluated in terms of the average profit earned by the two types of the providers at the end of each simulation and are shown in the graph as the two series, corresponding to the varying proportion of GE agents. Figure 14(a) shows the graph with an intense criterion for buddy selection, while in Figure 14(b) the criterion is set to be moderate. It maybe noticed that in a heterogeneous population and limited number of rounds, not all GE providers can be expected to build the buddy relationship with others. In the experiments represented by Figure 14, we maintain no distinction within the GE agents.

5.15

With a high criterion, we observe a steady profit gain by the GE providers with a slow increase in the average wealth as their proportion increases in the market. At the same time, the average wealth of the EE agents declines though at a slow rate. Since we keep a stricter criterion for the buddy relationship, the number of GE providers unable to find buddies is more, especially when the GE proportion is in minority. It is due to such GE providers that the average wealth of all the gift giving agents is pulled back. Consequently, we repeated the experiments with a moderate criterion such that more GE agents find opportunities to build up the buddy relationship; Figure 14(b) shows the graph for the second example. With more gift giving agents having long-term gift exchange with others, the increasing trend of their average wealth is more vivid than in the first example. Not only does the chances for gift giving agents to accumulate wealth increases with respect to their proportion, the profit oriented agents lose their average wealth at a faster rate. As the experiments were carried out for a limited number of rounds, one may expect better performance from the gift giving agents when the number of rounds goes higher.

5.16

In the second phase, we went into further study by analyzing the average performances of the gift giving agents with and without buddies separately. Once again, we split the experiments into two cases: i.e., with intense and moderate buddy selection criteria. The Counter-Gift Strategy for weak gift exchange was set high and the Initial Rounds were set to 40% of the total number of rounds. Likewise in the first phase, we set the message-limit to 30% of the population size, while the customers introduced heterogeneous types of orders to the market. Figures 15 and 16 summarize the experiments for the second phase.

Figure 14. A comparison of average profit earned by GE and EE provider agents with varying proportion of GE agents: (a) with high criterion for buddy selection; (b) with moderate criterion

5.17

In both Figures 15 and 16, three series are shown; the first GE Money refers to the average wealth of those GE providers successful in making some buddies during the simulation. The second, i.e. Buddyless GE corresponds to those GE providers without any buddy at all through the simulation. Finally, the third series shows the average wealth attained by the EE providers.

5.18

In the experiments represented in Figure 15, the Buddyless GE providers were found to be more successful than those with buddies when the GE providers were in lesser proportion. This is due to the fact that the GE providers had very few opportunities to practice gift exchange and thus a larger fraction of the gift giving agents remained without any buddy relation; also because the criterion was set to be high. Nevertheless with steady increase in the proportion the GE providers outperformed the Buddyless GE subsequently. Between the GE proportions of 40 - 60, the gap between the first and the second series is less while for the third series the average wealth remained less than the others. One also observes a decreasing trend for the Buddyless GE agents mainly due to the fact that the average wealth of the EE and the GE agents with buddy relations increases at a rapid rate.

Figure 15. A comparison of average wealth earned by the GE providers classified into two groups and EE agents with a high criterion for buddy selection

Figure 16. A comparison of average wealth earned by the GE providers classified into two groups and EE agents with a moderate criterion for buddy selection

5.19

With more GE providers able to build the buddy relationships, they performed better than the others in most of the cases as shown in Figure 16. One might understand the rise of wealth these agents because GE agents preferred their buddies over the potential gift giving agents. When the market was composed of the GE agents in majority, their chance for success were greater than otherwise. The rise and fall of the average wealth for the first series in the middle is possibly because of the change in the number Buddyless GE providers within that interval. Moreover, success of the GE agents also depends upon their ability to build stronger ties with each other; those without such were found to gain lesser wealth than others. The inflation seen in Figures 15 and 16 draws attention to a comprehensive testing of this hypothesis and deeper analysis of the phenomenon.

Hypothesis IV: If the survival of provider agents with lesser capabilities is difficult, the practice of gift exchange will be intensive. Such GE agents would build buddies in order to gain more capital even though they suffer early losses from the gifts they give.

5.20

We look into the proportions of the less powerful GE agents among the total gift giving agents and their corresponding share in the number of gifts exchanged. Three different sets of experiments were conducted for different values of the initial rounds, i.e. 40, 50 and 60% of the total number of the rounds. We assume less powerful agents as the ones whose abilities were of atomic task types A and B whereas the powerful agents as those with abilities of types C and D. For each set, different proportions of the less powerful GE agents were tested. In this scenario, we set a 'strong buddy criterion' and 'send further gift = 2'. The values over which the experiments were conducted were based on the three values of the 'initial round' since the initial round plays a role in determining the surge of gift giving agents to build their relationships and restricts their interactions. Figure 17 shows the series plots for the three sets of the experiments with respect to the respective values of the initial rounds.

5.21

Since the less powerful GE agents are in much need for buddies than those with greater abilities, they are expected to practice gift exchange more often especially when they are in lesser proportion. Furthermore, the gifts offered by them also reflect the surge for their search for long-term relationships. Consequently, the deadline set by them for expecting a counter-gift is also shorter than the others; i.e., either a Survival or Strategic strategies are chosen for the deadline in most cases. For the first two sets of experiments one does not see an increasing trend, though for the smaller proportions the number of gifts exchanged rises. On the other hand when the value for the initial rounds was highest in the third set of experiments, a clear increase can be seen as predicted. As the proportion of less powerful GE agents was reduced, their contribution to the overall gifts exchanged went higher; supported by the higher value for initial rounds. Not only the less weak GE agents could wait longer for a counter-gift, they also had better opportunities to return gifts within the initial rounds than the other two preceding cases. However, more experiments maybe required to test this hypothesis comprehensively.

Discussions and Future Work

6.1

The hypotheses selected for investigating the various effects of gift exchange were tested in our market-based multiagent system. Gift exchange was used by the gift giving providers to build trust and long-term relationship with others, making use of its reciprocal structure. Not only was gift exchange used to search for the other gift giving agents in the market, it also helped in singling out the profit oriented agents; i.e., those agents who do not practice gift exchange at all. The time-lag between a gift and a counter-gift was crucial and the agents used various strategies to estimate such time-lag depending upon their strength. Moreover, gift giving agents were able to build stable relationships earned as much wealth as the profit oriented agents and in several cases outperformed the others.

Figure 17. Series plots for percentage proportion of less powerful agents versus their contribution to total gifts exchanged, for different initial rounds

6.2

When more provider agents were sent the calls for proposal, the practice of gift exchange increased accordingly. Although it is an expected resulted, it not only helps in checking the working of the system, but also provides cue for further work with regards to number of messages exchanged during agents' interactions. In a homogenous environment where there were no profit oriented agents, most gift giving agents were able to find buddies, though, a small number of agents remained isolated at the end of the simulation runs. This shows that in a homogenous population, the symmetric exchange of gifts does not offer significant advantages to some agents over others. This leads to the investigation of the asymmetric mechanism for gifts exchange, which is briefly introduced in this paper. For a heterogeneous provider population, the gift giving agents did tend to successfully avoid interactions with the profit oriented agents when they were at least half the proportion of the total population. However the result was unexpected when the gift giving agents were in lesser number and they remained dependent on interactions with the profit oriented ones.

6.3

Gift giving agents able to build stable relationships with others were found to be more successful than those who could not. Moreover, their chances of accumulating more profit increased with respect to their proportion in majority of the tests. Gifts exchanged by the less powerful agents only seemed to have increased steadily with respect to the reduction in their proportion when the value for the initial rounds was set as high. For lesser values for the initial rounds, the results did not support the hypothesis. The outcome of our experiments show that gift exchange as a sociological concept is important for the emergence of inter-relationships among the agents and can provide the synergy for the agents to remain committed to each other on a long-term basis.

6.4

One of the contributions of our work is that it provides a model for gift exchange among providers in a market-based framework. Many other hypotheses maybe tested in addition to those discussed in this paper. We have also devised mechanisms through which agents could interact in order to exchange gifts. These mechanisms have been specified through the interaction protocols which help in understanding the agents' interactions in the system. These protocols have been specified according to the FIPA standard mentioned in Appendix C. Also the control flow of the gift exchange mechanisms has been presented through UML Activity diagrams using an approach developed by Lind (2002) at the German Research Center for AI [DFKI].

Future Work

6.5

Testing Asymmetric Gift Exchange: We have already implemented in our testbed the mechanism through which powerful agents could dominate the less powerful agents by means of asymmetric gifts. The gift giving agents can use the available mechanism in order to preserve hierarchical structures within the system. Preliminary testing of this phenomenon provides basis for an in-depth study as a potential future research work.

6.6

Further Sociologically Interesting Hypotheses: As mentioned above, a number of hypotheses maybe tested using the testbed. We however present two of such hypotheses that we may be tested in the line of this work.

1. If there is a high population of very strong profit oriented agents, the gift giving agents especially those who are less powerful would try to build co-operations with the agents of similar power. The rate of gift exchange turns to get high in such case.
2. If there is a high population of strong gift giving agents together with a high population of weak profit oriented agents, the rate of exchanged gifts would not be as high as in the above case.

6.7

Incorporating Multiagent-based Organizations: Having dealt with gift exchange for the market-based scenarios, the model can be used to apply gift exchange in more complex multiagent organizations. Markets are complex structures and the framework specified by Schillo et al. (2002) supports gift exchange and the model can be augmented to further investigate the social characteristics of the various organizational forms. Gift exchange among provider agents may also be integrated to the research work by Hahn et al. (2003) and Schillo (2004), which provides a detailed analysis of organizations in a holonic multiagent system. Kerber and Saam (2001) in their work, discuss Friedrich Hayek's concept of "competition as a discovery procedure", where competition in the market is seen as the accumulation of knowledge and 'mutual learning by the competing firms'. Studying Hayek's work on organizations is important in the line of our future work.

6.8

Utilizing Reinforcement Learning: Hogg and Jennings propose a framework for making decisions based on the agents' social welfare function that combines their collective and individual perspectives in a flexible manner (Hogg and Jennings 2001). A realization of such framework was shown successful via Q-learning, a method used for reinforcement learning. The choice for the deadline strategies maybe based on this method, i.e. each GE agent improves its reasoning by exploiting the available information and estimating the response from the others.

Appendix A: Related Work

A.1

Over the years, computer scientists and sociologists have been investigating the possibilities of modeling gift exchange with the sociological perspective. As argued earlier, MAS is well-suited to serve as the means for simulating such social phenomena and finding out whether the outcome of analyses could be beneficial in the area of DAI. Modeling gift exchange is an open field for MAS and DAI researchers, although there have been some contributions to formalizing it.

A.2

Van de Ven (2000) presents various theories that lead to motivation behind gift exchange mechanism. These theories center on market-oriented economics guided by gift exchange but it does not pursue a MAS approach. An important contribution is the presentation of scenarios where reciprocating a gift is not necessary and more importantly the possible gift exchange models presented along with their explanation in the context of economics theories.

A.3

Another significant related work is by Rouchier et al., which is interesting in the sense that it employs an agent-based methodology in investigating certain aspects of gift exchange (Rouchier et al. 2001). For building their artificial society they used MAS approach as they found this methodology "to be effective in representing agents and for observing the result of the repetition of their interactions in time". The society modeled by Rouchier et al. consisted of gift-giving agents who are either giving gifts when they have the capital to do so or (exclusively) work when they lack such resources. Gift-giving is controlled by two parameters, 'esteem' and 'prestige'; the former being self-confidence of an agent while the latter being its motivation to enhance its reputation. Agents observe reputations of every other agent and choose their actions accordingly. A major assumption of this model is that each agent does not worry about to whom its gift is going to go or whether it will get one in return. Our model in this paper circumvents such assumptions as they differ from basis discussed in Section 2. Another aspect of their approach from which we differ, is the global nature of gift-giving phenomena. As argued earlier, the dyadic nature of gift exchange is more rational and has a strong sociological basis.

A.4

Several researchers have reported results of their simulations concerning gift exchange and related concepts. Younger (2004) report about their study of reciprocity and normative reputation in the development of mutual obligations in societies where gift giving is practiced. Jaffe (2002) provide an analysis of altruism in aggregate economic terms. The effects of interaction between populations based on different criteria for aggression control were explored by Castelfranchi et al. (1998).

Appendix B: Profit Calculation and Tasks Composition

B.1

We use the same method for the calculation of provider agents' profit and composition of a complex task that was developed by Knabe (2002), for our model for gift exchange. As introduced in Section 3, the costs for an atomic and a complex task are set in a system. Also all providers have their own costs for the respected 'resource types' that they possess. A provider agent receiving a cfp for a task from a customer, checks if it needs to delegate part of the task to other provider(s) or if it can process it on its own. The bid is then prepared as follows:

where Contribution (i) is the cost of the i^th provider contributing to the task, times the profit. The profit for provider agents can be set in their configuration as shown in Figure 3 and the money earned is profit times the provider's own cost.

B.2

Knabe (2002) defined the atomic tasks to be that of power of 2. That is, the simplest task is A with the resource of 1 unit, followed by B with 2 units, C with 4 units and so on. The complex tasks are simply the sum of the units of the constituent atomic tasks. For example, task AB has 3 (= 1+2) units, ABC has 7 (=1+2+4) and so on. A provider agent decomposes a task into two parts: the part that it can process on its own, and calculates its cost; and the part it decomposes into atomic subtasks and delegate them to other providers. This delegation is done either via economic exchange or given as gift. An example of task decomposition is shown in Figure 9.

Appendix C: Communication Protocols

FIPA Definition of Contract Net Protocol

C.1

Originally proposed by Smith (1980), the contract net protocol (CNP) has been widely applied to task allocation problems and has received momentous popularity within the DAI community. The CNP has become a built-on standard for numerous multiagent platforms. Figure 18 presents the CNP definition by the FIPA.

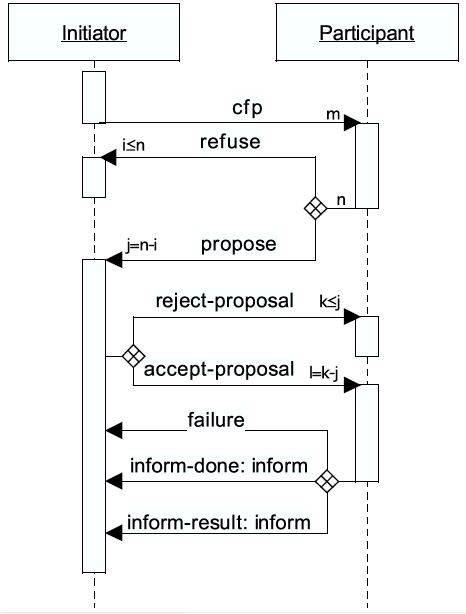
Figure 18. The FIPA definition of the Contract Net Protocol (Schillo 2004)

Interaction Diagrams for Gift Exchange Agents

C.2

In Figure 19 we present the protocol for weak gift exchange mechanism based on the CNCP using the Unified Modeling Language (UML) sequence diagrams. We follow the FIPA nomenclature and call the GE provider offering the gift and the provider taking part is the auction as GE Initiator and Participant respectively. The sequence of events follow from sending the cfp after which a participant either responds with a proposal or refusal; in case of no response and the deadline passes, the communication ends. Figure 20 presents the interaction sequence for Buddy protocol.

Figure 19. CNCP interaction protocol for Weak GE Mechanism

Figure 20. Buddy Inform Protocol

Acknowledgements

We are thankful to the editor and the anonymous referees for their suggestions. We would also like to thank Klaus Fischer, Christian Hahn and Ingo Zinnikus from DFKI, and Michael Florian, Bettina Fley and Daniela Spresny from the Technical University of Hamburg-Harburg. This work was done under the Sozionik_2 project, funded by Duetsche Forschungsgemeinschaft (DFG), in the priority program Socionics. SJA wishes to thank Naveed Ahmed for providing the feedback on the initial draft.

Notes

¹Here by society we mean the population of agents in MAS at any given time.

²The notion of 'information asymmetries' was suggested by one of the anonymous referees. They can be defined as conditions “in which at least some relevant information is known to some but not all parties involved” (InvestorWorld 2005).

References

ACCIAIOLI, G.L., 1981, Know What You're Doing: A Review of Pierre Bourdieu's Outline of a Theory of Practice, Canberra Anthropology, vol. I, pp. 23-51.

BLAU, P. M., 1974, Social Exchange, In: On the Nature of Organizations, John Wiley & Sons, New York, London, Sydney, Toronto, pp. 204-214.

BOURDIEU, P., 1977, Outline of a theory of practice, R. Nice (English Trans.), Princeton University Press, Princeton NJ, USA.

BOURDIEU, P., 2000, Pascalian Meditations, English Trans., Polity Press, Cambridge, UK.

BOURDIEU, P., Wacquant, L., 1992, An Invitation to Reflexive Sociology, Polity Press, Cambridge, UK.

CASTELFRANCHI, C., Conte, R., and Paolucci, M., 1998, Normative reputation and the costs of compliance, Journal of Artificial Societies and Social Simulation, vol. 1, no. 3, http://www.soc.surry.ac.uk/JASSS/1/3/3.html

CARLEY, K., Gasser, L., 1999, Computational Organizational Theory, in Gerhard Weiss (Ed.), Multiagent Systems: A Modern Approach to Distributed Artificial Intelligence, The MIT Press, Boston MA, USA.

CORMEN, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.D., 2001, An Introduction to Algorithms, 2nd Edition, The MIT Press, Boston MA, USA.

FERBER, J., 1999, Multi-Agent Systems: An Introduction to Distributed Artificial Intelligence, Addison-Wesley, Boston MA.

FIPA, 2003, Foundation for Intelligent Physical Agents, http://www.fipa.org.

FLEY, B., Florian, M., 2004, Trust and the Economy of Symbolic Goods: A Contribution to the Scalability of Open Multi_agent Systems", in Fischer, K., Florian, M., Malsch, T. (Ed.), Socionics: Its Contributions to the Scalability of Complex Social Systems, Springer-Verlag, Berlin et al., (to appear).

GOULDNER, A. W., 1960, The norm of reciprocity: A preliminary statement, American Sociological Review, vol. 25, pp. 161-178.

HAHN, C., Fley, B., Schillo, M., 2003, Strategic Adaptation in Self-organizing Multiagent Systems, in Proceedings of the 4th International Workshop on Modelling Artificial Societies and Hybrid Organizations (MASHO'03), Hamburg 2003.

HILLEBRANDT, F., 2004, Sociological Foundation of the Holonic Approach Using Habitus-Field-Theory to improve Multiagent Systems", in Fischer, K., Florian, M., Malsch, T. (Ed.), Socionics: Its Contributions to the Scalability of Complex Social Systems, Springer-Verlag, Berlin et al., (to appear).

HOGG, L.M.J. and Jennings, N.R., 2001, "Socially Intelligent Reasoning for Autonomous Agents", IEEE Transactions on Systems, Man and Cybernetics – Part A: Systems and Humans, vol. 31, no. 5, IEEE Press.

INVESTORWORLD, 2005, Investing Glossary, http://www.investorwords.com/2461/information_asymmetry.html

JAFFE, K., 2002, An economic analysis of altruism: who benefits from altruistic acts?, vol. 5, no. 3, Journal of Artificial Societies and Social Simulation, https://www.jasss.org/5/3/3.html

KERBER, W. and Saam, N.J., 2001, Competition as a Test of Hypotheses: Simulation of Knowledge-generating Market Processes, Journal of Artificial Societies and Social Simulation, vol. 4, no. 3, http://www.soc.surrey.ac.uk/jasss/4/3/2.html

KNABE, T., 2002, Business Organizational Forms in Self-organizing Multiagent Systems, Diplomarbeit, Department of Computer Science, Saarland University.

KNABE, T., Schillo, M., Fischer, K., 2002, "Improvements to the FIPA Contact Net Protocol for Performance Increase and Cascading Applications", in Proceedings of the International Workshop for Multi-Agent Interoperability, the 25th German Conference on Artificial Intelligence (KI-2002) Aachen, Springer-Verlag, Berlin et al.

LIND, J., 2002, Specifying Agent Interaction Protocols with Standard UML, in Proceedings of the 2nd International Conference on Autonomous Agents, Lecture Notes in Computer Science, vol. 2222, pp. 136-147, Springer-Verlag, Berlin et al.

MALSCH, T., 2001, Naming the unnamable: Socionics or the sociological turn of/to distributed artificial intelligence, in Proceedings of Autonomous Agents Multi-Agent Systems (AAMAS), pp. 144-186, New York, USA: ACM Press.

MARSH, S., 1994, Formalising Trust as a Computational Concept, PhD Thesis, Department of Computer Science, University of Stirling.

MAUSS, M., 1967, The Gift, I. Cunnison (English Trans.), Norton Press, New York, USA.

ROUCHIER, R., O'Connor, M., and Bousquet, F., 2001, The creation of a reputation in an artificial society by a gift system, Journal of Artificial Societies and Social Simulation, vol. 4, no. 2, http://www.soc.surry.ac.uk/jasss/4/2/8.html

SCHILLO, M., Bürckert, H., Fischer, K., and Klusch, M., 2001, "Towards a Definition of Robustness for Market-Style Open Multi-Agent Systems", in Proceedings of the 5th International Conference on Autonomous Agents (AA'01), New York, USA: ACM Press.

SCHILLO, M., 2002, Self-Organization and Adjustable Autonomy: Two Sides of the Same Medal?, Connection Science, vol. 14, no. 4, Taylor & Francis.

SCHILLO, M., Fley, B., Florian, M., Hillebrandt, F., Hinck, D., 2002, Self-Organization in Multiagent Systems: From Agent Interaction to Agent Organization, in Proceedings of the 3rd International Workshop on Modeling Artificial Societies and Hybrid Organizations (MASHO'02), Workshop at KI2002, the 25th German Conference on Artificial Intelligence Aachen, pp. 47-56.

SCHILLO, M., 2004, Multiagent Robustness: Autonomy vs. Organisation, PhD Thesis, Department of Computer Science, Saarland University.

SCHWARTZ, B., 1967, The Social Psychology of the Gift, American Journal of Sociology, vol. 73, no. 1, pp. 1-11, The University of Chicago Press.

SMITH, R. G., 1980. The Contract Net Protocol: High Level Communication and Control in a Distributed Problem Solver, IEEE Transactions on Computers, vol. 29, no. 12, pp. 1104-1113, IEEE Computer Society Press.

van de VEN, J., 2000, The Economics of the Gift, available at http://cwis.kub.nl/~few5/center/phd stud/ven

WEISS, G., 1999, Multiagent Systems: A Modern Approach to Distributed Artificial Intelligence, MIT Press, Cambridge, Massachusetts.

WOOLDRIDGE, M., 2002, An Introduction to Multiagent Systems, John Wiley & Sons, New York.

WOOLDRIDGE, M., and Jennings, N.R., 1994, Intelligent agents: Theory and Practice, available at citeseer http://www.citeseer.ist.psu.edu/97055.html

YOUNGER, S., 2004, Reciprocity, Normative Reputation, and the Development of Mutual Obligation in Gift-Giving Societies, Journal of Artificial Societies and Social Simulation, vol. 7, no. 1, http://www.soc.surry.ac.uk/JASSS/7/1/5.html

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2005]