©Copyright JASSS

JASSS logo ----

Juan Carlos González-Avella, Mario G. Cosenza, Konstantin Klemm, Víctor M. Eguíluz and Maxi San Miguel (2007)

Information Feedback and Mass Media Effects in Cultural Dynamics

Journal of Artificial Societies and Social Simulation vol. 10, no. 3 9
<https://www.jasss.org/10/3/9.html>

For information about citing this article, click here

Received: 11-Jan-2007    Accepted: 18-May-2007    Published: 30-Jun-2007

PDF version

* Abstract

We study the effects of different forms of information feedback associated with mass media on an agent-agent based model of the dynamics of cultural dissemination. In addition to some processes previously considered, we also examine a model of local mass media influence in cultural dynamics. Two mechanisms of information feedback are investigated: (i) direct mass media influence, where local or global mass media act as an additional element in the network of interactions of each agent, and (ii) indirect mass media influence, where global media acts as a filter of the influence of the existing network of interactions of each agent. Our results generalize previous findings showing that cultural diversity builds up by increasing the strength of the mass media influence. We find that this occurs independently of the mechanisms of action (direct or indirect) of the mass media message. However, through an analysis of the full range of parameters measuring cultural diversity, we establish that the enhancement of cultural diversity produced by interaction with mass media only occurs for strong enough mass media messages. In comparison with previous studies a main different result is that weak mass media messages, in combination with agent-agent interaction, are efficient in producing cultural homogeneity. Moreover, the homogenizing effect of weak mass media messages is more efficient for direct local mass media messages than for global mass media messages or indirect global mass media influences.

Keywords:
Agent Based Model, Culture, Dissemination, Mass Media

* Introduction

1.1
In an influential paper, Robert Axelrod (1997) addressed the question
if people tend to become more alike in their beliefs, attitudes, and behavior when they interact, why do not all differences eventually disappear?

1.2
To investigate this problem, Axelrod introduced an agent-based model to explore mechanisms of competition between the tendency towards globalization and the persistence of cultural diversity (see the applet at http://ifisc.uib.es/research_topics/socio/culture.html). Culture in this model is defined as a set of individual attributes subject to social influence. The state of an agent is described by a set of $F$ cultural features, each with $q$ possible values or traits. The parameter $q$ gives a measure of initial culture diversity for a random distribution of trait values. The local interaction between neighboring agents follows two basic social principles. The probability of interaction is determined by a principle of homophily: it is proportional to the cultural overlap between the agents, that is, to the amount of cultural similarities (number of features) that they share. The result of the interaction is determined by a principle of social influence, so that similarity is enhanced when interaction occurs. In a typical dynamical evolution, the system freezes in a multicultural state with coexisting spatial domains of different cultures, illustrating how a simple mechanism of local convergence can lead to global polarization. Later systematic studies of Axelrod's model have identified a globalization-polarization transition depending on the value of $q$ for a fixed $F$ (Castellano et al., 2000,Klemm et al., 2003,San Miguel et al., 2005,Klemm et al., 2003,Klemm et al., 2005). There is a threshold value $q_c$ such that for $q<q_c$ globalization (cultural homogeneity) occurs, while for $q>q_c$ a persistent multicultural state (polarization or cultural diversity) is reached.

1.3
Several extensions of this model have been investigated, some of them already suggested in Axelrod's paper. For example, it has been shown that frozen polarized configurations are not robust against cultural drift modeled as random perturbations (Klemm et al., 2003). Other extensions include the consideration of quantitative instead of qualitative values for the cultural traits (Flache & Macy, 2006), the extension of the model to continuous values of the cultural traits and the inclusion of heterophobic interactions (Macy et al., 2003), the simulation of technology assimilation (Leydesdorff, 2001), the consideration of specific historical contexts (Bhavnani, 2003), or the effect of a fixed external cultural influence (Gonzalez-Avella et al., 2005). A number of works have addressed the issue of the role of the social network of interactions. The existence of long range links of interaction in a social network with a small world structure naturally promotes cultural globalization (Klemm et al., 2003). However, a study of the increase in the range of interaction (Greig, 2002) suggests that an increase in communication promotes the emergence of a global culture, but it can also function to maintain areas of cultural uniqueness. A related question is the co-evolution of the social network of interaction and the dynamics of cultural changes, so that possible social interactions are not fixed from the outset (Centola et al., 2006). Within this general context of the studies of the effects of different forms of social interactions, Shibanai et al. (2001) considered the process of information feedback into the social system. Such feedback mechanism is one of the functions of mass media. From a general perspective, this question can be addressed as the competition of local agent interactions with mechanisms of global coupling (Gonzalez-Avella et al., 2006). Shibanai et al. concluded that "mass media, contrary to lay beliefs of their strong uniforming power, would rather contribute to creating differences in the long run."

1.4
This result is certainly surprising since mass media are believed to be powerful instruments to influence people's attitudes and opinions to homogenize society. Conclusions in reference (Shibanai et al., 2001) are based on the analysis for a single value of the parameter $q$ and a few values of the intensity of the influence of mass media. In this paper we consider the full range of values of $q$ when addressing the general question of the effects of different forms of information feedback on cultural dynamics in the framework of Axelrod's model, including the study of local feedback. We consider information feedback mechanisms as different types of mass media influences acting on a social system. This extension of Axelrod's model was referred to as "public education and broadcasting" (Axelrod, 1997). Our aim is to explore mechanisms, and their efficiency, by which mass media modifies processes of cultural dynamics based on local agent interactions. We investigate two main mechanisms that differ on how the information feedback affects the agents (Shibanai et al. 2001): (i) direct mass media influence, and (ii) indirect mass media influence. In the first case, mass media acts as an additional element in the network of interactions of each agent. As applications of direct mass media influence we study models of global and local mass media and compare their effects on the system. In the second feedback mechanism, mass media acts as a moderator or filter of the influence of the existing network of interactions of each agent. The assumption of this second model is that mass media have indirect influential power which reinforces the effect of personal networks. In particular, we focus on a model of indirect influence of global mass media.

1.5
We deal with states of the agents and mass media influences described by vectors whose components can take discrete values. We consider mass media influences that originate endogenously but can act either directly or indirectly on the system. In the first case, the agent-agent interaction and the interaction of the agents with the mass media are two independent processes and both are based on the same homophily and social influence principles of Axelrod's model. This scheme constitutes a model for a social system interacting with global or local mass media that represent endogenous cultural influences or plurality information feedback at different levels. In the case of indirect action, agent-agent interactions are not independent of the state of global mass media, the interaction being reinforced when the states of the agent and mass media message are connected.

1.6
Our results show that the conclusions of Shibanai et al. (2001) are not generally valid, but that different effects are obtained for different values of the parameters of the system. We find that cultural diversity builds up by increasing the probability of interaction of the agents with the mass media, in agreement with Shibanai et al. (2001). This occurs independently of the form of action (either direct or indirect) of the mass media message. However, a new finding that follows from our simulations is that cultural diversity is only promoted by strong enough mass media messages, while weak mass media messages, in combination with agent-agent interaction, are efficient in producing cultural homogenization. Moreover, this homogenizing effect in the way to globalization turns out to be much more efficiently implemented by direct local mass media messages, as for example local or regional TV (narrowcast) than by direct global mass media messages as worldwide TV channels (broadcast), or by an indirect influence of global mass media as in a filtering process of local interactions.

1.7
The model of direct mass media influence, including the description of the local and global mass media, is presented in Section II. This section shows the effects of the direct action of these two types of mass media. We describe different effects occurring in the culturally homogeneous state of the system ($q<q_c$) as well as in the multicultural state ($q>q_c$). Section III describes the model of indirect global mass media influence and the effects of this mechanism in the collective states of the agents. Section IV contains the conclusions of our work, including a comparison of the effects of the different models of information feedback that we have considered.

* Models of direct mass media influence

2.1
We consider a system of $N$ agents at the nodes of a two-dimensional regular lattice. The state $c_i$ of agent i is defined by a vector of $F$ components $\sigma_i= (\sigma_{i1},\sigma_{i2},\ldots,\sigma_{iF})$. In Axelrod's model, the $F$ components of $c_i$ correspond to the cultural features (language, religion, etc.) describing the $F$-dimensional culture of agent i. Each component $\sigma_{if}$ can take any of the $q$ values in the set $\{ 0, 1, \ldots, q-1 \}$ (called cultural traits in Axelrod's model). As an initial condition, each agent is randomly and independently assigned one of the $q^F$ possible state vectors with uniform probability. We introduce a vector $M$ representing the mass media message, with components $(\mu_{i1},\mu_{i2},\ldots,\mu_{iF})$. We distinguish two types of direct mass media influences, schematically shown in Fig. 1.

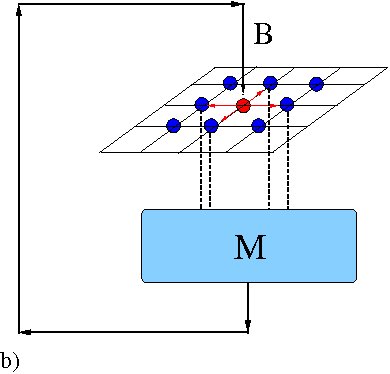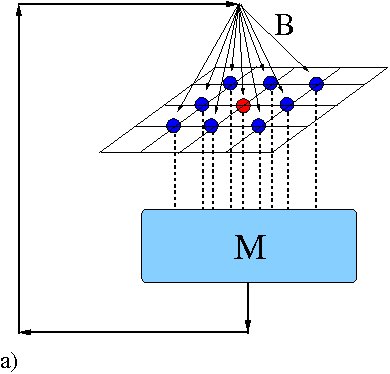
Figure Figure
Figure 1: Diagrams representing two types of direct, endogenous mass media influences acting on the system. a) Global mass media. b) Local mass media

2.2
(i) The global mass media is spatially uniform and may vary in time. Each $\mu_{if}$ is assigned the most abundant value exhibited by the $f$-th component of the state vectors of al the agents, which we denote by $\mu_f$. If the maximally abundant value is not unique, one of the possibilities is chosen at random with equal probability. In this type of influence the same global information is fed back to each agent at any given time. The components of $M$ may change as the system evolves. In the context of cultural models, this represents a global mass media influence shared identically by all the agents and containing the most predominant trait in each cultural feature present in a society (a "global cultural trend") (Shibanai et al., 2001).

2.3
(ii) The local mass media is spatially non-uniform and non-constant on time. Here the component $\mu_{if}$ is assigned the most frequent value of the $f$-th component of the state vectors of the agents belonging to the von Neumann neighborhood of agent i. If there are two or more maximally abundant values of component $f$ one of these is chosen at random with equal probability. This type of influence can be interpreted as a local mass media conveying the "local cultural trend" of its neighborhood to each agent in a social system.

2.4
Systems subject to either local or global mass media describe social systems with endogenous cultural influences. Cultural influences generated endogenously represent a plurality information feedback, which is one of the functions of mass media (Shibanai et al. 2001), but this can occur at a global (''broadcast") or at a local (''narrowcast") level.

2.5
The strength of the coupling to the mass media is controlled by a parameter $B \in [0,1]$ that measures the probability of interaction of the agents with the mass media message. We shall assume that $B$ is uniform, i.e., the mass media influence reaches all the agents with the same probability. The parameter $B$ can be interpreted as the probability that the mass media message attracts the attention of the agents in the social system. The parameter $B$ takes into account factors of the mass media influence that can be varied, such as its amplitude, frequency, attractiveness, etc. At any given time, we assume that any agent can either interact with the mass media message or with other agents in the system. Each agent in the network possesses a probability $B$ of interacting with the message $M$ and a probability $(1-B)$ of interacting with its neighbors.

2.6
Formally, we treat the mass media acting on each agent i as an additional neighbor of i with whom an interaction is possible. The mass media message is represented as an additional agent $\phi(i)$ such that $\sigma_{\phi(i) f} = \mu_{if}$ in the following definition of the dynamics. The dynamical evolution proceeds iterating the following steps:

(1) Select at random an agent i on the lattice (called active agent).

(2) Select the source of interaction $j$. With probability $B$ set $j=\phi(i)$ as an interaction with the mass media vector. Otherwise, choose agent $j$ at random among the four nearest neighbors of i on the network.

(3) Calculate the cultural overlap (number of shared features) $l(i,j)=\sum_{f=1}^{F}\delta_{\sigma_{if},\sigma_{jf}}$. If $0<l(i,j)<F$, sites i and $j$ interact with probability $l(i,j)/F$. In case of interaction, choose $h$ randomly such that $\sigma_{ih}\neq \sigma_{jh}$ and set $\sigma_{ih} = \sigma_{jh}$.

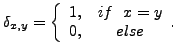
Here we use the definition of the Kronecker's delta function image

(4) Update the mass media vector $M$ if required. Resume at (1).

2.7
The role of mass media can be seen as an additional neighbor of each agent i with whom an interaction can take place. This "fifth" neighbor competes with the other four neighbors to influence an active agent i. $B$ is the probability of capturing the attention of any agent to interact with either the global or the local mass media message $M$. The effect of that interaction on each agent depends on the specific cultural overlap between the agent and the message $M$. The total probability to interact with the mass media is $B p_{iM}$, where $p_{iM}=l(i,M)/F$, and $l(i,M)$ is the overlap between agent i and the message. On the other hand, the active agent i has a probability $\frac{1}{4}(1-B) p_{ij}$ to interact with a randomly chosen neighbor $j$. Therefore, the parameter $B$ weights the influence of the mass media with respect to the influence of the neighbors on an agent i. This dynamics is based on the same principles of Axelrod's model, namely homophily or similarity and social influence. But now the agents interact either between them or with M. The competition of these interactions is measured by $B$.

2.8
To characterize the collective final state reached by the dynamics, we calculate the average fraction of cultural domains $g=\langle N_g \rangle /N$. A cultural domain is a set of contiguous sites with identical cultural traits. $N_g$ is the number of cultural domains formed in the final state of the dynamics for a given realization of initial conditions. A culturally homogeneous state is characterized by values $g \rightarrow 0$. When the system settles into a culturally diverse state we have $\langle N_g \rangle \gg 1$. Our numerical results in this work are based on averages over $50$ realizations for systems of size $N=50 \times 50$, and $F=5$.

2.9
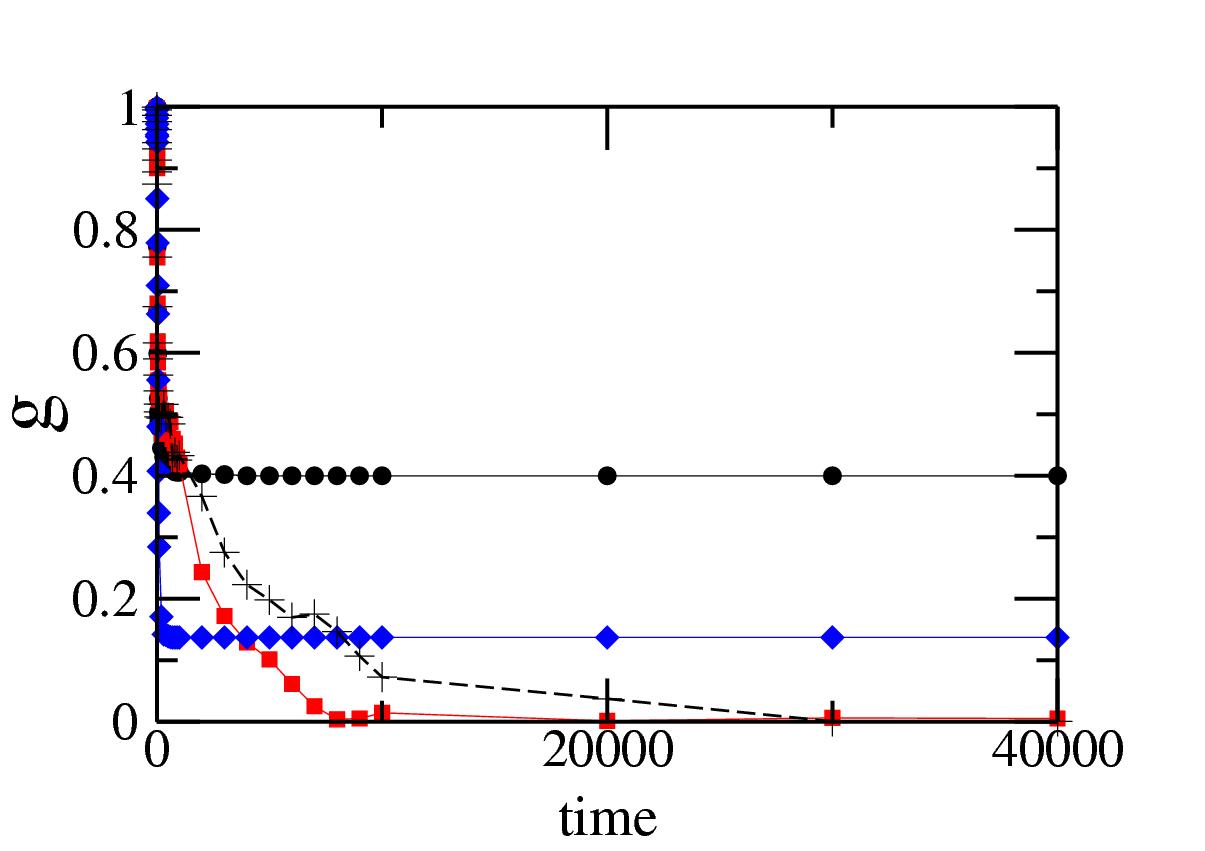
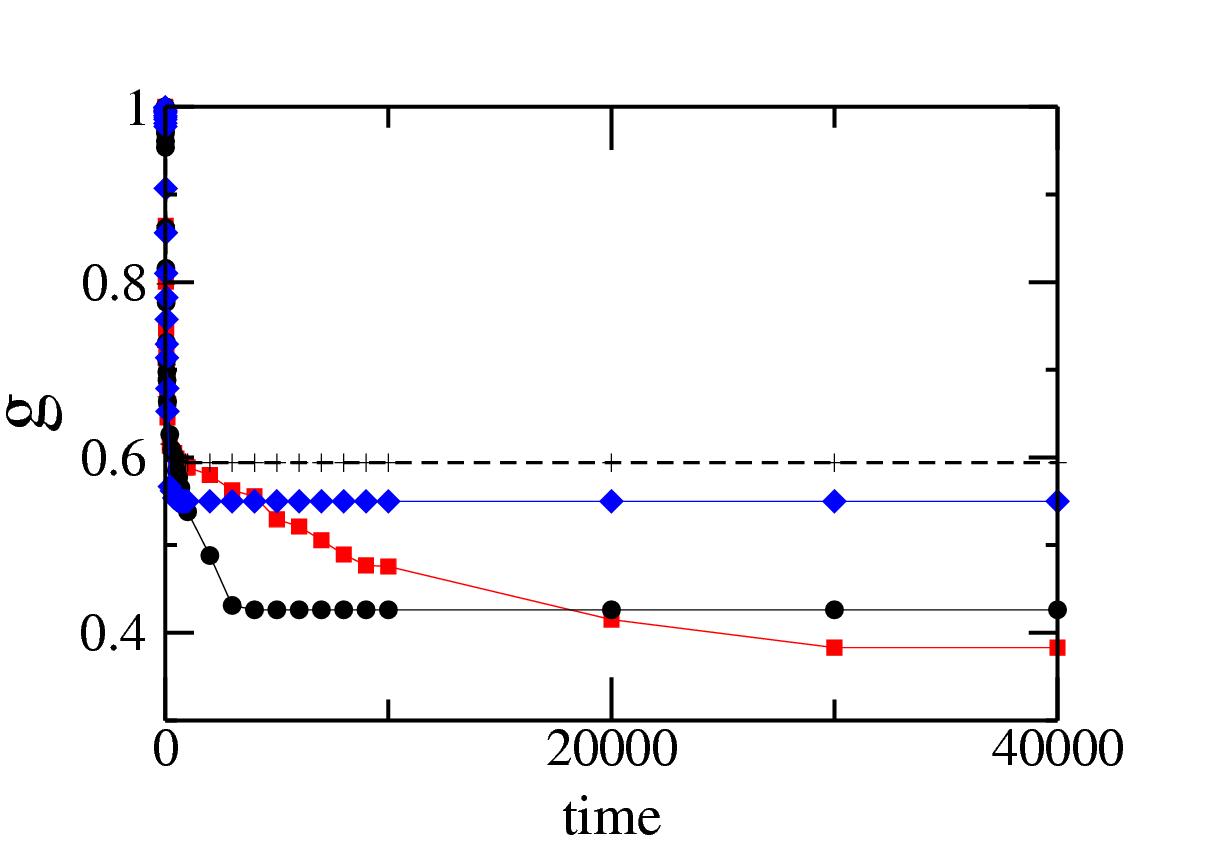
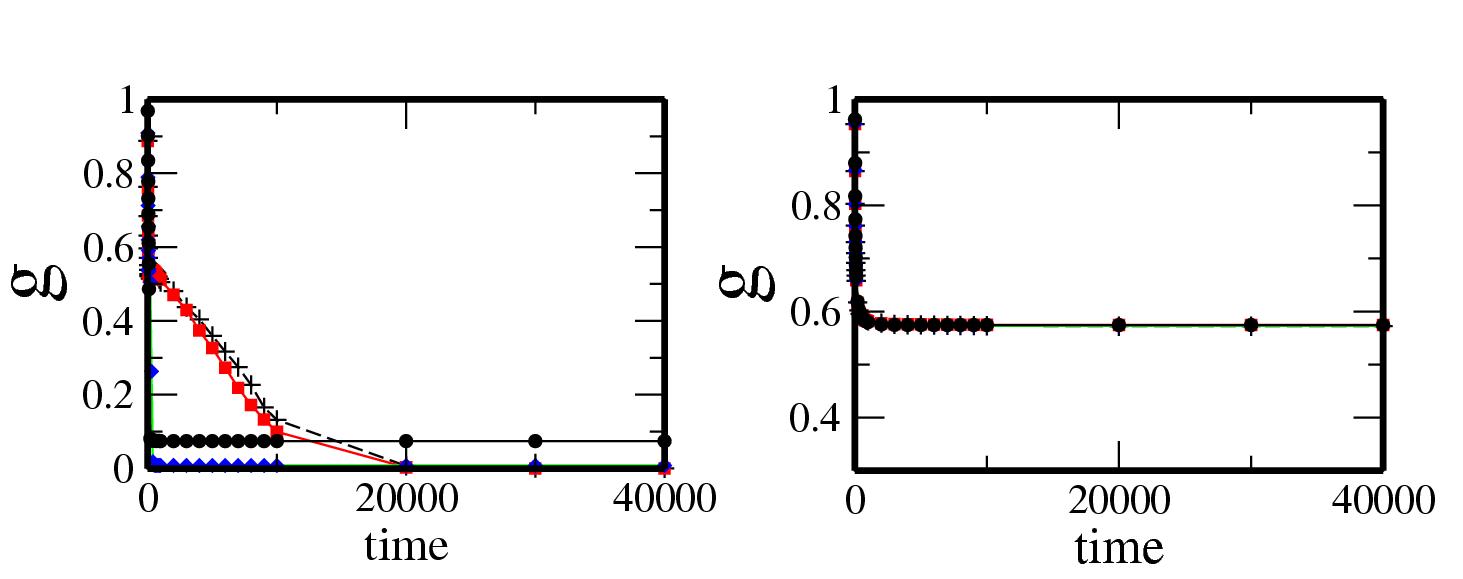
Figure 2 shows the average fraction of cultural domains $g$ as a function of time under the direct action of global mass media, for two values of the number of traits $q$ with $F=5$, and for different values of the probability $B$. Fig. 2 (left): for small values of $q$ the system reaches a culturally homogeneous state in absence of mass media influence ($B=0$) and also for small values of $B$. When the probability $B$ increases, we see that global mass media is able to induce cultural diversity in the system. This result agrees with the results obtained by Shibanai et al. (2001) about the ability of global mass media to induce cultural diversity in the system ($g\neq 0$). However we observe in Fig. 2 (right) that, for larger values of $q$, where the system would be in a culturally polarized state with no mass media influence ($B=0$), small values of the probability $B$ can reduce the number of cultural groups. Effects similar to those shown in Fig. 2 are observed when a local mass media message interacts with the system. We therefore conclude that mass media can increase or decrease cultural diversity depending on the value of the parameter $q$.

Figure Figure
Figure 2: Evolution of $g$ in a system subject to a global mass media message for different values of the probability $B$, with fixed $F=5$. Time is measured in number of events per site. System size $N=50 \times 50$. Left: $q=10$; $B=0$ (crosses); $B=0.0005$ (squares); $B=0.15$ (diamonds); $B=0.6$ (circles). Right: $q=30$; $B=0$ (crosses); $B=0.0005$ (squares); $B=0.005$ (circles); $B=0.1$ (diamonds).

2.10
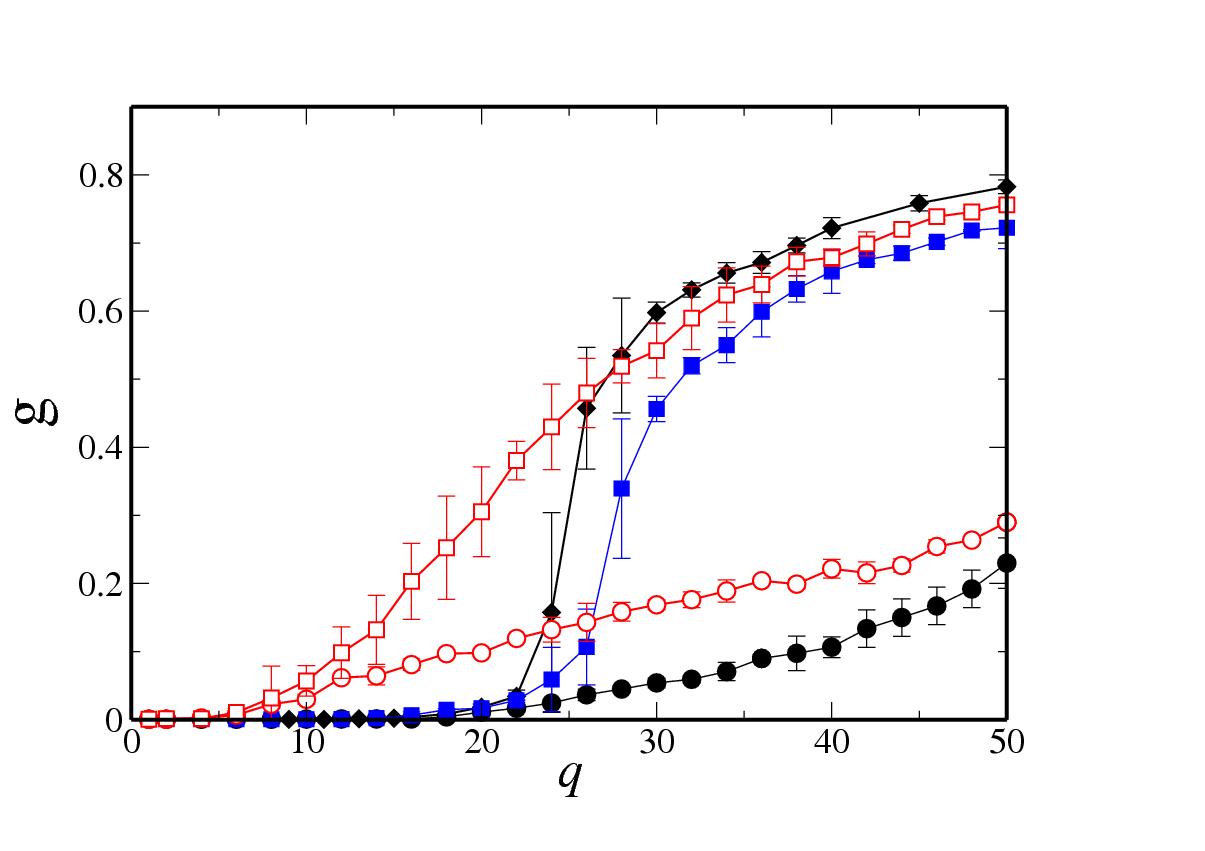
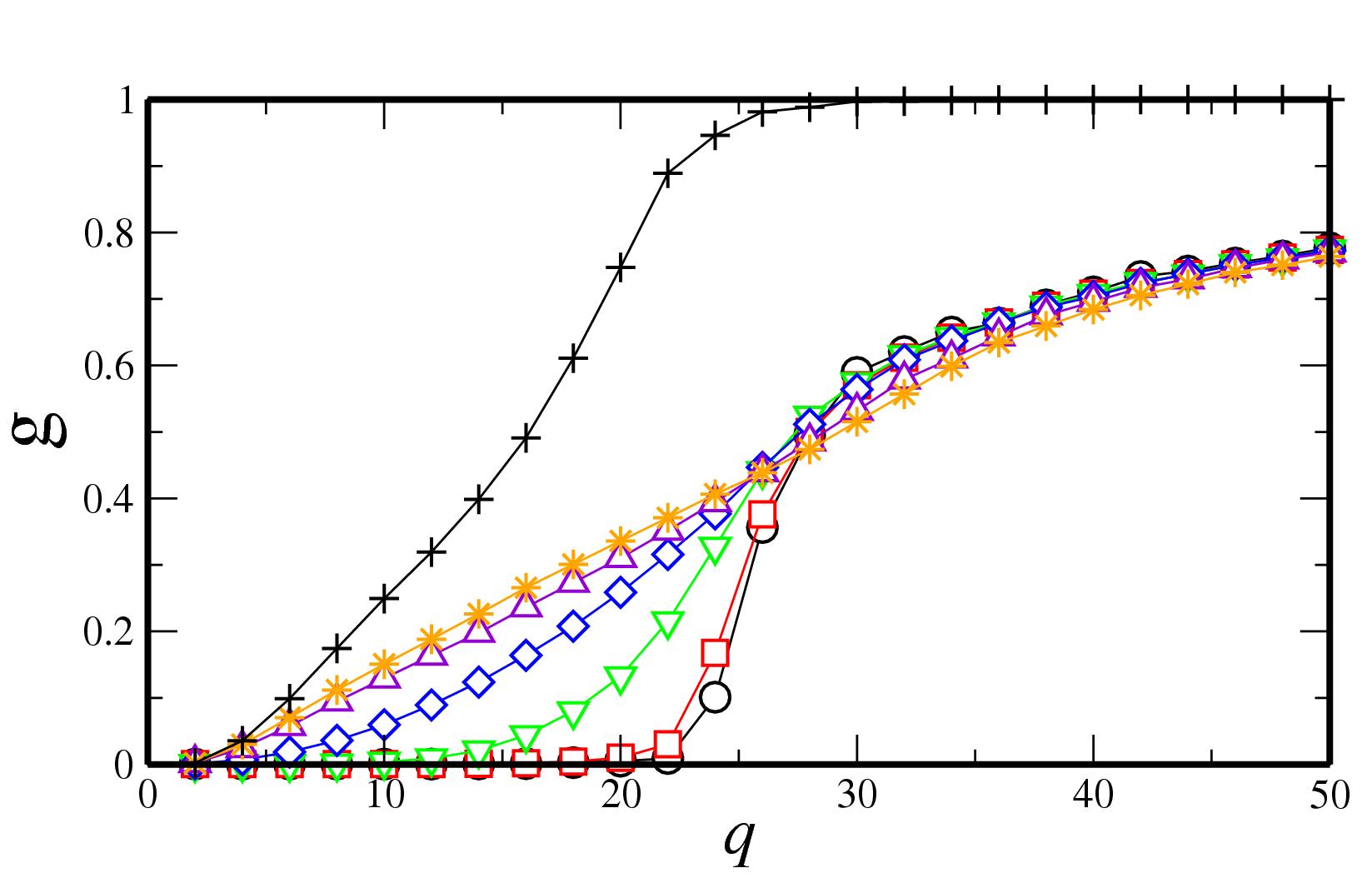
A global picture of direct mass media influences is provided by Figure 3, which shows the asymptotic value of $g$ for long time as a function of $q$, with $F=5$, for different values of the probability $B$. In absence of any mass media influences ($B=0$) there is a threshold value of the number traits $q_c \approx 25$, such that for $q<q_c$ dynamical evolution always leads to one of the possible $q^F$ homogeneous states $(g\rightarrow0)$. On the other hand, for values of $q>q_c$, the behavior of the system changes and it settles into a multicultural state when $B=0$. When the probability $B$ is increased, the threshold value of qc decreases. There is a value $q_c(B)$ below which the system still reaches in its evolution a homogeneous cultural state ( $g \rightarrow 0$) under the action of any of these mass media messages.

Figure
Figure 3: Asymptotic value of the fraction of cultural domains $g$ as a function of $q$, for different values of the probability $B$ and for different types of mass media influences. $B=0$ (diamonds); $B=0.0005$ (solid squares, direct global mass media); $B=0.6$ (empty squares, direct global mass media); $B=0.0005$ (solid circles, direct local mass media); $B=0.1$ (empty circles, direct local mass media).
2.11
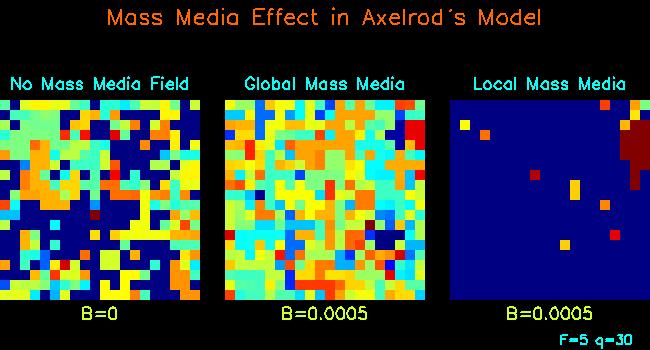
A color code can be assigned to each cultural state for visualization of the spatial patterns during simulations, as shown in Figure 10 in the Appendix. Figure 4 shows the spatial configurations of the final states of the system subject to a global mass media message, when $q<q_c$. In the absence of mass media influence, i.e., $B=0$, the system settles into any of the possible $q^F$ homogeneous cultural states. When the probability $B$ is increased, the system is driven towards a homogeneous cultural state that depends on the evolution of the global mass media from the initial conditions. Thus, for small values of $B$, global mass media contributes to maintain a state of global culture in the system, as one may expect. However, there is a value of the strength $B$ above which there is no convergence to a homogeneous state, but a state of cultural diversity emerges in the system. A similar behavior is observed when the system is under the influence of local mass media. These results describe for $q<q_c$ a transition at a threshold value of $B$ from a culturally homogeneous state to a state of cultural diversity characterized by an increasing number of cultural domains as $B$ is increased. Thus, we find the counterintuitive result that for $q<q_c$, above some threshold value of the probability of interaction, mass media induces cultural diversity in a situation in which the system would be culturally homogeneous under the effect alone of local interactions among the agents.

Figure
Figure 4: Asymptotic cultural configurations for different values of the probability $B$ for a direct global mass media influence, for $F=5$, $q=10$, and $N=50 \times 50$. Top left: $B=0$; top right: $B=0.01$; bottom left: $B=0.1$; bottom right: $B=0.9$
2.12
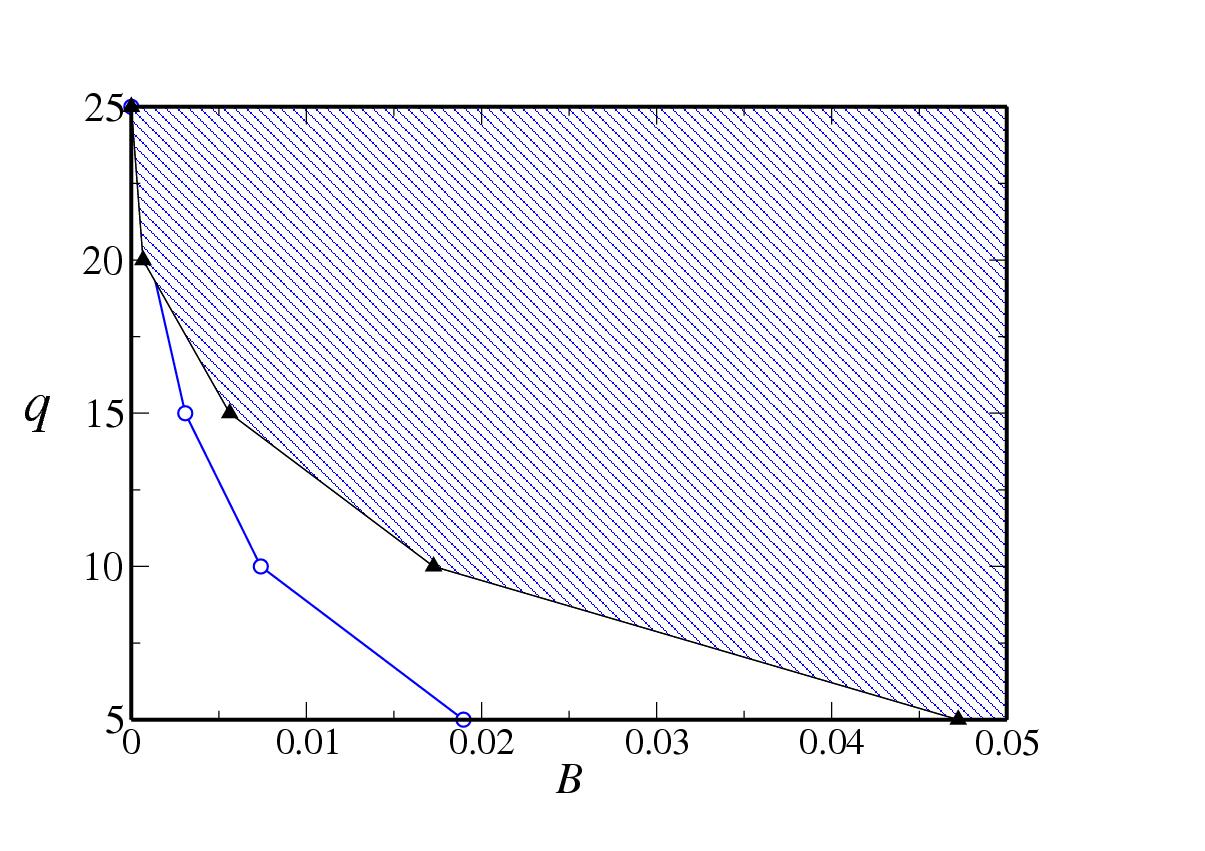
Figure 5 shows $q_c$ as a function of $B$. The threshold value $q_c$ for each type of media decreases with increasing $q$ for $q<q_c$. In each case, the threshold curve $q_c$ vs. $B$ in Fig. 4 separates the region of cultural diversity from the region where homogeneous, monocultural states occur on the space of parameters $(B,q)$. Figure 5 can also be understood as a threshold curve of $B$ vs. $q$. For each value of q, there is a critical value $B_c(q)$, such that for $B < B_c(q)$, a homogeneous state is reached by the system while for $B >B_c(q)$ multiculturality sets in. For values of $B$ above this curve, the interaction with the mass media dominates over the local interactions among the individual agents in the system. Consequently, agents whose states exhibit a greater overlap with the state of the mass media have more probability to converge to that state. This process contributes to the differentiation of states between neighboring agents and to the formation of multiple cultural domains in the system for large enough values of the probability $B$.

Figure
Figure 5: Threshold boundaries $q_c(B)$ vs. $B$ for $q<q_c$ corresponding to the global and mass media. Each line separates the region of cultural diversity (above the line, in grey) from the region of a global culture (below the line) for direct global (circles) and local (triangles) mass media influences.
2.13
When there are no mass media influences ($B=0$), the system always freezes into culturally polarized states for $q>q_c$. Figure 3 shows that the effect of mass media for $q>q_c$ depends on the magnitude of $B$. For the two types of mass media messages that we consider, small values of $B$ produce a drop in $g$ to values below the reference line corresponding to its value when $B=0$. Thus, the limit $B\rightarrow 0$ does not recover the behavior of the model with only local agent-agent interactions. The fact that for small values of $B$ the interaction with mass media promotes cultural homogeneity is related to the non-stable nature of the inhomogeneous states in Axelrod's model. When the probability of interaction $B$ is very small, the action of mass media can be seen as a sufficient perturbation that allows the system to escape from polarized states with frozen dynamics. The role of mass media in this situation is similar to that of cultural drift (Klemm et al., 2003).

2.14
The drop in the asymptotic values of $g$ for small values of $B$ from the reference value ($B=0$) that is observed for the local mass media in Fig. 3 is much more pronounced than the corresponding drops for global mass media. This can be understood in terms of a greater efficiency of a local mass media influence as a nonuniform perturbation that allows the system to escape from a frozen inhomogeneous configuration. Increasing the value of $B$ results, in both types of mass media, in an enhancement of cultural polarization in the system, but the local mass media always keeps the amount of cultural diversity, as measured by $g$, below the value obtained for $B=0$. Information feedback at the regional level is more efficient in promoting cultural homogenization. Figure 6 shows configurations reached under the influence of the direct local and global mass media in the multicultural region $q>q_c$. A smaller number of cultural domains (smaller $g$) than for $B=0$ are observed for global mass media field. But this number is much smaller under the action of local mass media field. In addition, the time to reach the final state is much longer for a local than for a global field (see Movie 1). Local mass media does not lead to an early frozen state, leaving room for agent-agent interactions that result in a culturally homogenized state.

Figure
Figure 6: Cultural configurations for different values of the probability $B$ for different mass media influences in the multicultural region, for $F=5$, $q=30$, and $N=50 \times 50$. Left: no mass media $B=0$; center: Global mass media with $B=0.0005$; right: Local mass media with $B=0.0005$. (see Movie 1)
2.15
We have focused on the effects of information feedback when both the probability of interaction with mass media $B$ and the number of options $q$ are varied, since they give rise to different qualitative behavior. Variations of other parameters, such as the number of neighbors or the system size, have little effect. In particular, the system size may become relevant only in the limit of very small values of $B$ for $q < qc$, when the role of mass media is similar to that of noise added to the system (Klemm et al., 2003).

* Model of indirect global mass media influence: the filtering of local interactions

3.1
In this section we analyze a model of global information feedback where the global mass media acts as a moderator or filter of the local influence of neighbors, as proposed by Shibanai et al. (2001). In the original Axelrod's model one feature with different traits for two neighboring agents is chosen, and the trait of the active agent is changed to that of the neighbor. This is modified in the model of indirect global mass media influence analyzed here, taking into account the agreement of the chosen trait of the neighbor and that of the global mass media or the plurality of the population. If the trait of the neighbor is concordant with the dominant one, that is, the same as that of the global mass media message $M$, the feature of the active agent will be changed to that of the neighbor. But if the feature of the neighbor is different from that of the global mass media message $M$, then, with probability $R$ the active agent will not change. Thus, this model assumes that agents are more likely to adopt a trait from those neighbors that are concordant with the plurality.

3.2
We use the definition of a uniform global mass media as in Section II, $M=(\mu_{i1},\mu_{i2},\ldots,\mu_{iF})$. The dynamical evolution of the filter model can be described in terms of the following iterative steps:

(1) Select at random an agent i on the lattice (active agent).

(2) Select at random one agent $j$ among the four neighbors of i.

(3) Calculate the overlap $l(i,j)$. If $0<l(i,j)<F$, sites i and $j$ interact with probability $p_{ij}=l(i,j)/F$. In case of interaction, choose $h$ randomly such that $\sigma_{ih}\neq \sigma_{jh}$. If $\sigma_{jh}=\mu_{h}$, then set $\sigma_{ih} = \sigma_{jh}$; otherwise with probability $R$ the state of agent i does not change and with probability $1-R$ set $\sigma_{ih} = \sigma_{jh}$

(4) Update the global mass media vector $M$ if required. Resume at (1).

3.3
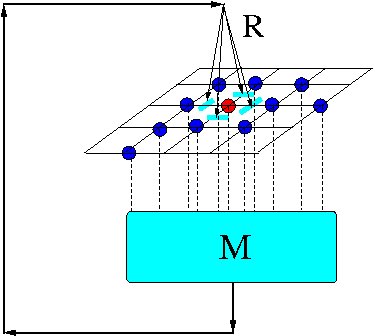Figure 7 shows a diagram of the filter model. The parameter $R$ describes the intensity of the filtering effect of the global mass media on the local interactions. The case $R=0$ corresponds to the original Axelrod's model, while $R=1$ implies that cultural interaction only causes a change if the chosen trait of the neighbor was equal to that of the global mass media. The overall probability of interaction between an active agent i and a chosen neighbor $j$ is $p_{ij} (1-R)$ if the chosen trait of $j$ is different from that corresponding to $M$, and $p_{ij}$ if the chosen trait is equal to that corresponding to $M$.

Figure
Figure 7: Diagram representing the filter model.
3.4
Figure 8 shows the average fraction of cultural domains $g$ as a function of time in the global mass media filter model, for two values of $q$ with $F=5$, and for different values of the filtering probability $R$. In Fig. 8 (left), when $q<q_c$ the system reaches a homogeneous state for $R=0$ as well as for small values of $R$. However, when the probability $R$ increases, the filtering influence of the global mass media can induce cultural diversity. Our results for $q<q_c$ support the results obtained by Shibanai et al. (2001) about the ability of the filtering process to induce cultural diversity in the same fashion as the model with direct global mass media influence. But comparison with Fig. 2 (left) shows that direct interaction with global mass media is more efficient in promoting cultural diversity than the filtering mechanism of agreement with the global plurality. The analysis of reference (Shibanai et al., 2001) was restricted to a single value of $q<q_c$. We have also explored values of $q>q_c$, where the system would be in a heterogeneous cultural state in absence of any filtering ($R=0$). For these values of $q$ we find (Fig. 8, right) that the filtering mechanism has no appreciable effects for small $R$, in contrast with the case of direct global mass media influence where for small values of the probability of interaction $B$ with the media message, the number of cultural groups is reduced as a consequence of this interaction.

Figure
Figure 8: Time evolution of the average fraction of cultural domains $g$ in the filter model for different values of the probability $R$, with fixed $F=5$. Time is measured in number of events per site. System size $N=50 \times 50$. Left: $q=10$; $R=0$ (crosses); $R=0.0005$ (squares); $R=0.15$ (diamonds); $R=0.6$ (circles). Right: $q=30$; $R=0$ (crosses); $R=0.0005$ (squares); $R=0.005$ (circles); $R=0.1$ (diamonds).
3.6
A systematic analysis of the filtering effect for different values of $q$ is summarized in Figure 9 which shows the asymptotic value for long times of the average fraction of cultural domains $g$ as a function of $q$, with $F=5$, for different values of the filtering probability $R$. When no filtering acts on the system ($R=0$) the behavior is that of the original Axelrod's model and also coincides with the direct mass media models for $B=0$.

3.7
The effect of the filtering process in the culturally homogeneous region, i.e., for parameter values $q<q_c$, is similar to that of a direct influence of endogenous mass media. When the probability $R$ is increased, the threshold value qc decreases. There is a value $q_c(R)$ below which the system still reaches a homogeneous cultural state under the influence of the filter. An increase in $R$ for parameters $q < q_c(R)$ leads to cultural diversity. Thus, both mechanisms of feedback information, either direct or indirect, promote multiculturality in the region of parameters where globalization prevails in the absence of any feedback. The similar behavior found for the three types of mass media influences considered here suggests that the phenomenon of mass media-induced diversity should be robust in this region of parameters, regardless of the type of feedback mechanism at work.

3.8
However, in the region of parameters $q>q_c$ where multiculturality occurs for $R=0$ or $B=0$, the results of the filter model differs from those of the direct mass media influence. The filtering mechanism has little effect for values of the probability $R<1$. As $R \rightarrow 1$ there is a small decrease in the number of cultural groups formed in the system. But at $R=1$ a discontinuity appears: the fraction of cultural groups $g$ jumps from a value close to the one for $R=0$ to a value close to $g=1$ corresponding to maximum multiculturality (number of cultural groups equal to the number of agents in the system). The case $R=1$ corresponds to an extreme restriction on the dynamics, when no adoption of cultural features from neighbors is allowed unless the state of the neighbor coincides with the one of the global mass media. Since we are considering random initial conditions, when $q$ is large enough, the probability that the features of any agent coincide with those of the global mass media message $M$ is quite small, making the convergence to globalization, i.e., a common state with the media, very unlikely. As a consequence, the random multicultural state subsists in the system and manifests itself as a maximum value of $g$. The small probability of interaction with the global mass media for large values of $q$ when $R=1$ is also reflected in the very long convergence time needed to reach the final multicultural state as compared with the convergence time for $R<1$.

3.9
We note that the case $B=1$ in the model of direct global mass media influence is less restrictive than the condition $R=1$ in the filter model. Although local agent-agent interactions produce negligible effects in both cases, in the model of direct influence, an agent can still interact with the global mass media when there is some cultural overlap between the agent and the mass media message.

Figure
Figure 9: Average fraction of cultural domains $g$ as a function of $q$, for different values of the probability $R$ for the filter model. $R=0$ (circles); $R=0.01$ (squares); $R=0.1$ (triangles down); $R=0.5$ (diamonds); $R=0.9$ (triangles up); $R=0.99$ (stars); $R=1.0$ (plus signs).

* Conclusions

4.1
We have studied the effects of different forms of information feedback on a social system in the framework of Axelrod's model for cultural dissemination, including a model of local mass media influence. Two basic mechanisms of information feedback have been interpreted as models of direct or indirect mass media influence on the system (Shibanai et al., 2001). For the direct information feedback mechanism we have considered the cases of global mass media and local mass media influences (Gonzalez-Avella et al., 2006). The dynamics of direct interaction with the mass media is based on the similarity or overlap between vector states. Although their origin is different, at the local level the direct global and local mass media influences act in the same manner, as a "fifth" effective neighbor whose specific source is not essential. Consequently they produce similar effects in the system. First, we find the nontrivial result that direct mass media can enhance cultural diversity, in agreement with the results of (Shibanai et al., 2001): for parameter values for which the system reaches a global culture due to the local interaction among the agents, there is a threshold value of the probability of interaction $B$ with mass media. For values of $B$ above this threshold cultural diversity emerges. This happens because there is a competition between the consequences of the similarity rule applied to the agent-agent interactions, and applied to the agent-mass media interaction. This competition leads to the formation of cultural domains and to polarized states. Secondly, we find another surprising effect at variance with the conclusions of (Shibanai et al., 2001): for parameter values for which the dynamics based on the local interaction among the agents produces a frozen multicultural configuration, very weak directly interacting mass media produces cultural homogeneity. This range of parameters was not explored in Ref. (Shibanai et al., 2001), and we find here that mass media interaction for $q>q_c$ produces the opposite effect of the one described before. That is, it favors cultural homogenization. The limit $B\rightarrow 0$ is discontinuous and the homogenizing effect for $B<<1$ occurs because the interaction with the mass media acts as a perturbation on the non stable multicultural configurations with frozen dynamics that appear for $B=0$. As a general result for any value of $q$, we find that for small values of $B$, the interaction with mass media promotes cultural homogenization: for $q<q_c$ this interaction preserves homogeneity, while for $q>q_c$ it causes a drop in the degree of cultural diversity in the system as measured by the average fraction of cultural domain $g$. We have calculated, for the two types of direct mass media influences considered, the corresponding boundary in the space of parameters $(B,q)$ that separates globalization and polarization states. The spatially nonuniform local mass media has a greater ordering effect than the uniform global mass media in the regime $q>q_c$. The range of values of $B$ for which globalization occurs for $q<q_c$ is also larger for the nonuniform local mass media.

4.2
The effect of the indirect global mass media influence as a filtering process in the culturally homogeneous region, i.e., for $q<q_c$, is similar to that caused by a direct influence of mass media. For small values of the filtering probability $R$ the system reaches a culturally homogeneous state. For values of $R$ greater than a threshold value the system converges to a state of cultural diversity. Thus, both mechanisms of feedback information, either direct or indirect, promote multiculturality in a region of parameters where it would not be present in the absence of any feedback. In the region of parameters $q>q_c$ where multiculturality occurs for either $B=0$ or $R=0$, the filtering mechanism has, for values of the probability $R<1$, a very weak effect in comparison to the one caused by a direct mass media influences: there is only a small decrease in the number of cultural groups formed. However, when the extreme restriction $R=1$ is imposed, the number of cultural groups jumps discontinuously to a value corresponding to maximum multiculturality.

4.3
The similarity of the behaviors of the different types of mass media influences considered here suggests that the phenomenon of mass media-induced diversity should be robust, regardless of the type of feedback mechanism. In spite of the differences mentioned between direct and indirect information feedback processes as well as between uniform and nonuniform mass media influences, it is remarkable that the collective behavior of the agents displays analogous phenomenology for the three types of mass media considered.

4.4
Generally speaking, our analysis unveils the delicate compromise between direct agent-agent interactions and feedback processes. Mass media reflects local or global cultural trends created by local agent-agent interactions, but mass media information is processed by agent interactions, while the agent-mass media interaction is conditioned by the overlap of the cultural features of the agent and the mass media message. We have analyzed the effect of different forms of mass media for the full range of the parameter $q$ that measure an initial cultural diversity. Our results indicate qualitatively different effects when globalization $(q<q_c)$ or polarization $(q>q_c)$ would prevail when no mass media feedback is taken in account. In summary, we find that, when the probability of interacting with the mass media is sufficiently large, mass media actually contribute to cultural diversity in a social system, independently of the nature of the media. But direct mass media influences are found to be efficient in promoting cultural homogeneity in conditions of weak broadcast of a message, so that local interactions among individuals can be still effective in constructing some cultural overlap with the mass media message. Strong media messages do not lead to cultural homogenization because agent-agent interaction becomes inefficient. These results identify the power of being subtle in mass media massages. In addition, direct local mass media appear to be more effective in promoting uniformity in comparison to direct global broadcasts, which identifies the importance of local media (feedback at regional levels) in the cultural globalization path.

* Appendix

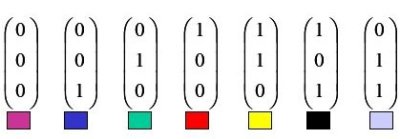Color code for visualization of dynamics. A different color can be assigned to each cultural state. Cultural domains correspond to sets of elements that share the same color. Figure 10 illustrates the case for $F=3$ and $q =2$. In general for $q >2$, q weights the basic colors (R,G,B): $0 \leq \sigma_{if} / (q-1)\leq1$.

Figure
Figure 10: For $F=3$ and $q =2$, there are $q^F = 8$ different cultural states that can be assigned different colors as shown.
Table 1: Key to formulae employed
1. $ l(i,j) = \sum_{f=1}^{F} \delta_{\sigma_{if},\sigma_{jf}}$ Number of shared features between agent i and agent j

2. $ p_{ij} = l(i,j)/F $ The probability that the agent i interacts with the agent j

3. $B \cdot p_{iM}=B \cdot \frac{l(i,M)}{F} $ The total probability that the agent i interacts with the mass media

4. $ l(i,M) = \sum_{f=1}^{F} \delta_{\sigma_{if},\sigma_{Mf}}$ The overlap between agent i and the mass media messages

5. $g = \frac{\langle N_{g} \rangle}{N} $ The average fraction of cultural domains

6. 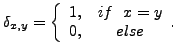image Definition of Kronecker's delta function

* Acknowledgements

J. C. G-A., V. M. E. and M. SM acknowledge financial support from MEC (Spain) through project CONOCE2 (FIS2004-00953). M. G. C. acknowledges support from FONACIT (Venezuela) under grant F-2002000426. K K. acknowledges support from DFG Bioinformatics Initiative BIZ-6/1-2 and from Deutscher Akademischer Austausch Dienst (DAAD).

* References

AXELROD R, (1997), The Dissemination of Culture: A Model with Local Convergence and Global Polarization. J. Conflict Res. 41 pp. 203-226.

BHAVNANI R, (2003), Adaptive Agents, Political Institutions and Civic Traditions in Modern Italy. Journal of Artificial Societies and Social Simulation, 6, no 4, https://www.jasss.org/6/4/1.html.

CASTELLANO C, MARSILI M, and VESPIGNANI A, (2000), Nonequilibrium Phase Transition in a Model for Social Influence. Phys. Rev. Lett. 85, pp. 3536-3539.

CENTOLA D, GONZALEZ-AVELLA J C, EGUILUZ V M, and SAN MIGUEL M, (2006), Homophily, Cultural Drift and the Co-Evolution of Cultural Groups. http://arxiv.org/abs/physics/0609213.

FLACHE A and MACY M,(2006), What sustains cultural diversity and what undermines it? Axelrod and beyond. http://arxiv.org/abs/physics/0604201.

GONZALEZ-AVELLA J C, COSENZA M G, and TUCCI K, (2005), Nonequilibrium transition induced by mass media in a model for social influence. Phys. Rev. E, 72, 065102(R).

GONZALEZ-AVELLA J C, EGUILUZ V M, COSENZA M G, KLEMM K, HERRERA J L, and SAN MIGUEL M, (2006), Local versus global interactions in nonequilibrium transitions: A model of social dynamics. Phys. Rev. E 73, 046119.

GREIG J, (2002), The End of Geography? Globalization, Communications, and Culture in the International System. J. Conflict Res. 46, pp. 225-243.

KLEMM K, EGUILUZ V M, TORAL R, and SAN MIGUEL M, (2003), Global culture: A noise-induced transition in finite systems. Phys. Rev. E. 67, 045101(R).

KLEMM K, EGUILUZ V M, TORAL R, and SAN MIGUEL M, (2003), Role of dimensionality in Axelrod's model for the dissemination of culture. Physica A, 327, pp. 1-5.

KLEMM K, EGUILUZ V M , TORAL R, and SAN MIGUEL M, (2003), Nonequilibrium transition in complex networks: A model of social interaction. Phys. Rev. E. 67, pp. 026120.

KLEMM K, EGUILUZ V M , TORAL R, and SAN MIGUEL M, (2005), Globalization, polarization and cultural drift. J. Econ. Dyn. Control 29, pp 321-334.

LEYDESDORFF L, (2001), Technology and Culture: The Dissemination and the Potential 'Lock-in' of New Technologies. Journal of Artificial Societies and Social Simulation, 6(4)5, https://www.jasss.org/4/3/5.html.

MACY M W, KITTS J, FLACHE A and BERNARD S, (2003). Polarization in Dynamic Networks: A Hopfield Model of Emergent Structure. In Dynamic Social Network Modeling and Analysis. R. Breiger, K. Carley and P. Pattison (Eds.), National Academies Press (Washington, 2003), pp. 162-173.

SAN MIGUEL M, EGUILUZ V M, TORAL R, and KLEMM K, (2005), Binary and Multivariate Stochastic Models of Consensus Formation. Computing in Science & Engineering. 7, pp. 67-73.

SHIBANAI Y, YASUNO S, and ISHIGURO I, (2001), Effects of Global Information Feedback on Diversity: Extensions to Axelrod's Adaptative Culture Model. J. Conflict Res. 45, pp. 80-96.

----

ButtonReturn to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2007]