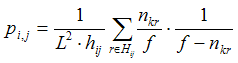
where nkr denotes the number of cultural features for which agents k and r have the same trait.
Here we analyse Axelrod's (1997) model of dissemination of culture using our THMC framework. Axelrod (1997) uses the word 'culture' to denote "the set of individual attributes that are subject to social influence". He argues that culture "is something people learn from each other", and hence something that evolves through social influence. To study the process of cultural diffusion Axelrod builds a model based on two simple assumptions:
An illustrative example given by Axelrod is language: "a person is more likely to talk to someone who speaks a similar language than one who speaks a dissimilar language, and the very act of communication tends to make their future patterns of speech even more similar". Axelrod then notes that this reasoning begs the question: "If people tend to become more alike in their beliefs, attitudes, and behavior when they interact, why do not all such differences eventually disappear?". Thus, the objective of this model is to study why cultural diversity persists even though people tend to approach each other culturally through a self-reinforcing mechanism of 'more interaction' <-> 'more similarity'.
Axelrod's (1997) model has had a significant impact in the scientific world, and several authors have analysed the model and some of its structural assumptions in depth. For instance, Klemm et al. investigate the effect of introducing noise in the model (Klemm et al. 2003a), the role of dimensionality (Klemm et al. 2003b; Klemm et al. 2005), and the impact of changing the network topology (Klemm et al. 2003c). Castellano et al. (2000) use computer simulation to study the transition phase between a mono-culture and a polarized cultural situation as the model parameters change value. More recently, Centola et al. (2007) analyse an extended version of Axelrod's model where they introduce "network homophily" into the dynamics of cultural interaction, i.e. in this extended model the network of social interactions is not arbitrarily fixed, but it co-evolves with the individuals' actions as a function of their changing cultural similarities and differences.
Axelrod's (1997) model has also been extended, modified and used in other contexts: for instance, Gatherer (2002) explores new modes of transmission and selection of cultural traits, Bhavnani (2003) studies the historical process of formation of civic communities, González-Avella et al. (2007) consider the effect of mass media in processes of cultural diffusion, and Leydesdorff (2001) investigates the evolution of competing technologies.
In this model there is a L×L square lattice of cells. Each cell represents a stationary individual who is endowed with a certain culture. An individual's culture is characterised by a list of f features, or dimensions of culture (e.g. language, religion, style of dress...); for each feature there is a set of q traits, which are the alternative values the feature may have. All agents share the same value for f, and all features have the same value q. Thus, individual i's culture is represented by a vector xi of f variables, where each variable takes an integer value in the range [0, q - 1]. Initially, individuals are assigned a random culture. Therefore parameter q, which defines the possible traits in each cultural dimension, can be seen as a measure of the initial disorder or cultural variety in the system.
A time-step in the model is defined by the following activities:
The process outlined above continues until no cultural change can occur. This happens when every pair of neighbouring agents have cultures that are either identical or completely different.
Axelrod explores the aggregate behaviour of this model by studying the spatial distribution of the emergent cultural regions: sets of spatially contiguous agents who share an identical vector of culture. Naturally, parameters f and q influence the probability with which the system evolves to a mono-culture (only one cultural region) or to global polarization (several multicultural regions).
In this model lattice cells and agents are equivalent, so the state of the system can be characterised by a L×L array where each element corresponds to one cell of the grid and stores its agent's cultural vector. With this definition, the number of possible states is qf·L2. As Axelrod (1997, footnote 6) points out, this number is enormous for most parameterisations of some interest.
Deriving the whole transition matrix for a system of such a dimension is quite an effort. Having said that, note that the transition matrix is very sparse, and it is not difficult to calculate any given transition probability. In particular, the transition probability between any two states that differ in more than one agent's cultural feature is necessarily zero. The following explains how to calculate the transition probability from state i to state j in general:
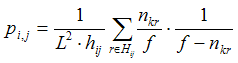
where nkr denotes the number of cultural features for which agents k and r have the same trait.
Note that a state is absorbing if and only if every pair of neighbouring agents have cultures that are either identical or completely different. It is also clear that –as long as there can be different cultures (i.e. f > 1 or q > 1)– the THMC has several absorbing states (note that e.g. every mono-culture state is absorbing). Furthermore there isn't any absorbing class that contains more than one state. This is straightforward to prove when one realises that it is possible to reach (at least) one absorbing state from any given state. Thus, in particular, there are no periodic classes in this model.
Hence using Proposition 2 we can partition the state space as follows: S = {abs1} ∪ {abs2} ∪ … ∪ {absk} ∪ T, where abs1, abs2, … , absk are absorbing states, and T is the union of all non-closed communicating classes. Taking into account Proposition 3 we can conclude that sooner or later the THMC will enter one of the absorbing states and stay in it forever. Naturally, the probability of ending up in any particular absorbing state depends on the initial conditions.
AXELROD R (1997) The dissemination of culture - A model with local convergence and global polarization. Journal of Conflict Resolution 41(2), pp. 203-226.
BHAVNANI R (2003) Adaptive agents, political institutions and Civic Traditions in Modern Italy. Journal of Artificial Societies and Social Simulation 6(4)1. https://www.jasss.org/6/4/1.html.
CASTELLANO C, Marsili M & Vespignani A (2000) Nonequilibrium phase transition in a model for social influence. Physical Review Letters 85(16), pp. 3536-3539.
CENTOLA D, González-Avella J C, Eguíluz V M & San Miguel M (2007) Homophily, Cultural Drift, and the Co-Evolution of Cultural Groups. Journal of Conflict Resolution 51(6), pp. 905-929.
GATHERER D (2002) Identifying cases of social contagion using memetic isolation: Comparison of the dynamics of a multisociety simulation with an ethnographic data set. Journal of Artificial Societies and Social Simulation 5(4)5. https://www.jasss.org/5/4/5.html.
GONZÁLEZ-AVELLA J, Cosenza M G, Klemm K, Eguíluz V M & San Miguel M (2007) Information feedback and mass media effects in cultural dynamics. Journal of Artificial Societies and Social Simulation 10(3)9. https://www.jasss.org/10/3/9.html.
KLEMM K, Eguíluz V M, Toral R, and San Miguel M (2003a) Global culture: A noise-induced transition in finite systems. Physical Review E 67(4), 045101.
KLEMM K, Eguíluz V M, Toral R, and San Miguel M (2003b) Role of dimensionality in Axelrod's model for the dissemination of culture. Physica A 327, pp. 1-5.
KLEMM K, Eguíluz V M, Toral R, and San Miguel M (2003c) Nonequilibrium transitions in complex networks: A model of social interaction. Physical Review E 67(2), 026120.
KLEMM K, Eguíluz V M, Toral R, and San Miguel M (2005) Globalization, polarization and cultural drift. Journal of Economic Dynamics & Control 29(1-2), pp. 321-334.
LEYDESDORFF L (2001) Technology and culture: The dissemination and the potential 'lock-in' of new technologies. Journal of Artificial Societies and Social Simulation 4(3)5. https://www.jasss.org/4/3/5.html.
1 Axelrod begins his investigation considering the von Neumann neighbourhood of radius 1, and then he relaxes this assumption to study the effect of larger neighbourhoods in the dissemination of culture.