 Abstract
Abstract
- In the spatial prisoner's dilemma game, an agent's strategy choice depends upon the strategies he expects his neighboring agents to adopt. Yet, the expectation of agents in the games has not been studied seriously by the researchers of games in complex networks. The present paper studies the effect of the agents' adaptive expectation on cooperation emergence in the prisoner's dilemma game in complex networks from an agent-based approach. Simulation results show that the agents' adaptive expectation will favor the emergence of cooperation. However, due to agents' adaptive behavior, agents' initial expectation level does not greatly affect the cooperation frequency in the experiments. Simulation results also show that the agents' expectation adjustment speed significantly affects the cooperation frequency. In addition, the initial number of cooperation agents on the network is not a critical factor in the simulations. However, together with a bigger defection temptation, a larger neighborhood size will produce greater cooperation frequency fluctuations in a Barabási and Albert (BA) network, a feature different from that of Watts and Strogatz (WS) small world networks, which can be explained by their different networks degree distributions. Simulation results show that the cooperation frequency oscillating on the WS network is much smaller than that of the BA networks when defection temptation becomes larger. This research demonstrates that agent's adaptive expectation plays an important role in cooperation emergence on complex networks and it deserves more attentions.
- Keywords:
- Prisoner''s Dilemma Game, Complex Network, Adaptive Expectation, Agent-Based Simulation
 Introduction
Introduction
- 1.1
- In many social dilemmas, an agent's rational choice is at odds with his payoff maximization and social welfare. Such dilemmas are universal in the real world; therefore, the emergence of cooperation has become one of the hottest issues for current scientific research (Axelrod 1985, Pennisi 2005). In the past decades, the emergence of cooperation and its maintenance have drawn much attention from various research disciplines such as physics, economics, biology, and political science. As one of the most well-known games, the prisoner's dilemma game has been regarded as a perfect metaphor for the study of the evolution and emergence of cooperation among a large population. Currently, the prisoner's dilemma game remains one of the most intensely studied games in literature.
- 1.2
- In the present paper, the focus is placed on the prisoner's dilemma game in complex networks, while agents choose the strategy of cooperation or defection according to adaptive expectation regarding neighboring agents' strategies. In the original form of prisoner's dilemma game, two agents must decide whether to cooperate (C) or defect (D). They will receive a reward (R) if both of them choose to cooperate, and receive punishment (P) if both choose to defect, while the cooperator will receive S when he confronts a defector, who in turn will get T, where T > R > P > S and 2R>T+S. This condition means that a player is always tempted to defect no matter whether the opponent takes C or D strategy in the one shot prisoner's dilemma game. Therefore, the dominant strategy in prisoner's dilemma game is that both agents choose to defect, although both agents will be better off if they choose to cooperate. Contrary to the theoretical prediction, cooperation behaviors are commonplace in society and are frequently observed in experimental game laboratories. Thus, the question is, how can this dilemma be resolved? How does cooperation emerge from prisoner's dilemma game?
- 1.3
- In the past two decades, many extensions on the prisoner's dilemma game have been proposed to resolve the prisoner's dilemma and to explain the emergence of cooperation in the prisoner's dilemma game (Szabó and Fáth 2007). Axelrod (1981; 1985; 1997) first studied the emergence of cooperation in prisoner's dilemma game from the perspective of evolution and computer simulation; however, in Axelrod's work, the agents' interactions are stochastic. Nowak and May (Nowak and May 1992; Nowak and May 1993; Nowak, Bonhoeffer and May 1994) first studied the spatial prisoner's dilemma game by placing agents on a grid wherein each agent could interact with his neighboring agents. In addition, phase diagrams for evolutionary prisoner's dilemma game on two-dimensional lattices were studied by Szabó et al. (Szabó and Toke 1998; Szabó and Hauert 2002). With the rapid development of network science, the prisoner's dilemma game on a structured network has been widely studied among the scientific population. From the perspective of network science, network structures provide a convenient way to describe the interconnection among agents in the system. The relationship between network structure and evolutionary game theory has attracted much attention (Szabó et al. 2000; Szabó, and Hauert 2002) and research on the prisoner's dilemma game has been extended to various complex networks. Abramson and Kuperman (2001) studied the prisoner's dilemma game on the small world network and observed that different topologies, ranging from regular lattices to random graphs, produced a variety of emergence behaviors. Ohtsuki et al. (2006) found that if the ratio of benefit of the altruistic act and the cost exceeds the average number of neighbours, cooperation can evolve as a consequence of 'social viscosity', no matter the underlying network is cycles, spatial lattices, random regular graphs, random graphs or scale free networks. Vukov et al. (2008) studied the maintenance of cooperation in the prisoner's dilemma game with agents located on a one-dimensional chain and their payoffs came from the games with nearest and next-nearest-neighbors. Wu et al. (2005) studied the cooperation on NW (Newman Watts) network, where agents can voluntarily participate in the game. While the WS and NW small world networks are, in general, moderately homogeneous, Fu et al. (2007b) introduced heterogeneity in network structure to investigate the effect of agent heterogeneity on cooperation emergence on NW networks. The work done by Santos et al. (2005, 2006a, 2006b, 2006c) pointed out that scale-free networks can promote the emergence of cooperation due to network heterogeneity, especially the degree heterogeneity.
- 1.4
- In addition to the effect of network structure on the spatial prisoner's dilemma game, factors such as the game micro-updating rule, the way agents interact, and the means by which agents make decisions also affect the cooperation frequency. Moyano's work (2008) implied that when an agent's strategy and updating rule can both evolve, the evolutionary outcome always leans towards defection. Chen et al. (2008a) showed that interaction stochastically supports cooperation in spatial prisoner's dilemma game. Fu et al. (2009) found that partner-switching stabilizes the cooperation in co-evolutionary prisoner's dilemma game. Other factors such as agent teaching activity (Szolnoki and Perc 2009), agent payoff computation mechanism (Yu-Jian et al. 2009), initial strategies distribution (Chen et al. 2008b), agent tag mechanism (Kim 2010), agent's other-regarding preference (Bo 2011), agent's willingness to participate in the game (Szabó and Hauert 2002), other network structure such as agents' Socio-Geographic Community (Power 2009) and co-evolution between agents and network structure (Fu, et al. 2007a) have also received much attentions. These studies showed that cooperation emergence in the prisoner's dilemma game in a network are affected by many factors. Now it is commonly accepted that network structure plays an important role in the cooperation emergence in the prisoner's dilemma game, but due to the complexity of the problem, there is no agreement about which factor is the most important for cooperation emergence and which model is more suitable for the human society. As to the agent learning algorithm and its role in evolutionary process, many researches have different views. It can be concluded that the current researches in prisoner's dilemma are much diversified.
- 1.5
- Agents' learning algorithm is a critical factor in the research of network game. In current literature, many types of learning are used, such as reinforcement learning, genetic algorithm, Bayesian learning and best response learning, etc. It should be pointed out that agents are always assumed to adopt the imitation strategy in the majority of the literature. For example, an agent will imitate the strategy of his neighboring agents, who acquires the best payoff, or perhaps imitate the strategy of a randomly chosen agent from his neighboring agents according to the probability calculated from their utility difference, or follow other similar evolutionary tactics. In fact, this learning algorithm in the evolutionary prisoner's dilemma game is rather simple and agents display little intelligence. In evolutionary game theory, it is reasonable to use such learning algorithm. Nevertheless, human agents are not merely animals who only follow evolutionary biology. Once the agents become smarter, it will be more difficult for cooperation to emerge. Even if agents adopt the best response strategy, a very common strategy used in the game theory and economics, it is found that the cooperation frequency will still be much lower. Previous studies always use the imitation learning method, which, in many cases, indeed leads agents to choose the cooperation strategy. But if agents have more intelligence, it will be also totally unreasonable for an agent to choose the cooperation strategy. If all agents adopt the cooperation strategy, the opportunistic character of agents is neglected; however, opportunistic behavior is the most salient feature of agent behavior in the prisoner's dilemma game. It is well known that agents living in a society seldom use imitation algorithm when they play prisoner's dilemma game with other agents if they have more information about the game played. Given a more realistic view about the prisoner's dilemma game or about agents' behavior, how can we explain the cooperation emergence in prisoner's dilemma game on networks?
- 1.6
- Besides, we found that when the payoff matrix used in prisoner's dilemma game is changed, such as the payoff agents will get when both agents choose defection strategy is set to a non-zero value, the cooperation is difficult to emerge when the imitation learning is used by agents. Therefore, we need another approach to address the cooperation emergence problem in prisoner's dilemma game.
- 1.7
- Also due to the assumption of evolutionary game theory, some critical factors in games such as information or agent expectation are generally ignored by existing models. In existing models, agents always look backward or only care about the current situation. Since the agents' payoffs depend upon the strategies of other agents, it is crucial how agents think about the strategies their neighboring agents will use. That means that human agents do not merely passively react to other agents' strategies, they can form an expectation regarding the strategies their neighboring agents may choose. Agents will decide to cooperate or defect according to this expectation. Therefore, expectation is critical for human agent's strategy selection. On the other hand, agents' expectation regarding other agents' strategy is also an evolutionary or learning process. Agents will adjust their expectations according to the current status and previous expectations experience. Thus, agents' expectation should be adaptive; agents can learn from past experience and adjust their expectations accordingly.
- 1.8
- Given the limitation of present research on the explanation of the cooperation emergence in prisoner's dilemma game, adaptive expectation can be considered and we propose a model which agents' expectation is a critical factor in agents' strategy decision. This paper aims to extend existing approaches in the study of evolutionary prisoner's dilemma game in a complex network by introducing the agents' heterogeneous adaptive expectations into the game model using an agent-based simulation approach. In the network, some agents are supposed to make choices according to adaptive expectations. Agents with adaptive expectations will choose a strategy according to their expectation of how many other agents will cooperate among his neighborhood agents. Although not every agent in the system makes decisions through expectation, there are still some agents choosing strategies according to the expectation payoff. Therefore, it is worthwhile to introduce agents' expectations into the prisoner's dilemma game model and to study its effect on the emergence of cooperation in networks. It is well known that expectations, including rational expectation, play an important role in modern economics. It will be interesting to study the effect of expectation when agents play the prisoner's dilemma game on complex networks. This study anticipates that the expectation will affect the cooperation in many ways and its effects are related to different network structures.
- 1.9
- Similar to other spatial prisoner's dilemma game models, the present model limits agents' expectation among their local neighborhood. Agents can only interact with their neighborhood agents, and other agents' strategies will not affect their payoff directly; therefore, agents only need to form expectations regarding their neighboring agents. The present paper tries to study whether or not adaptive expectation will promote the cooperation among the population, and tries to answer the questions such as when and how this may occur. This research also studies whether or not adaptive expectation will converge, and when and how if it does. In addition, the effect of different network topologies on cooperation frequency is also studied. This paper's results will provide researchers with insights regarding the effect of agents' adaptive expectation on the emergence of cooperation in complex networks. It can be helpful to understand how different expectations and expectation adjustment speed affect cooperation emergence on networks. As we know, agents' expectation is a salient feature of human being; deep understanding of its effects on the cooperation behaviors among human society will be beneficial to the research of human society.
 The Model
The Model
- 2.1
- In the present paper, the evolutionary prisoner's dilemma game on complex network is studied. The BA scale-free and the WS small world networks are used here. In literature, many studies have proven that the scale-free network favors cooperation emergence in many situations. Both kinds of networks are constructed according to the original papers. In the scale-free network construction (Barabási and Albert 1999), a small full-mesh network is first built. Each time a new node is added, the model adds a given number of edges that connect the new node to existing nodes, according to the probability proportional to the node degree of the network. The WS small world network is implemented according to the standard algorithm (Watts and Strogatz 1998).
- 2.2
- The model consists of a set of N agents connected through a complex network. As in the usual case, agents are located on the vertices of the network. This network defines the neighborhood for each agent in the system. In every simulation step, agents interact with other agents within their own neighborhood. The agent can choose only from two strategies: cooperation (C) or defection (D). The status of Agent i at time t is a vector x i that can be described by one of the following two values:
.png) ,
, .png)
(1) indicating cooperation or defection strategy respectively. Following common practice but with some modifications, the payoff matrix is transformed into a simplified form as follows:
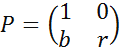
(2) Here, b signifies the defection temptation in prisoner's dilemma game. In addition, 1≤ b <2 means that the defection temptation is no larger than the total payoff received from cooperation, therefore if both agents choose cooperation, their welfare will be better. r is the payoff when both agents choose defection. In many models, r is set to zero; however, this makes the agent indifferent to both cooperation and defection when his opponent chooses defection strategy. Therefore, r is set to a value slightly larger than zero, which means that agents would prefer defection to cooperation when his opponents choose defection, as it is a more reasonable choice. (In our model, setting r to zero will make the cooperation more easily emerge; however, in many models, set r to a value lager than zero will make the cooperation emergence more difficult. We have tested these settings in the simulations. These results show that the agents' expectation will promote the cooperation emergence even if r is larger than zero.)
- 2.3
- In each step, every agent interacts with his neighbor agents: the real payoff he will get from the prisoner's dilemma game at time t can be described as follows:
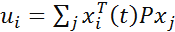
(3) j is the agent who is directly connected with agent i on the network.
- 2.4
- If agent i makes decisions according to his expectation, things will become slightly different, and the computation of the expectation payoff is needed for this agent. It is assumed that the number of neighboring agents expected to take cooperation strategy is ei t at time t, and agent i has ni neighboring agents in the network. Agent i expects that there are agents taking defect strategy; therefore, if agent i takes the cooperation strategy, the expected payoff that he will receive next time is set as follows:
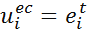
(4) Agent i's expected payoff, which he will receive next time if he takes the defection strategy, is set as follows:
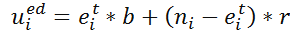
(5) In addition, as previously noted, agents are adaptive about their expectations. They will learn from experience and adjust their expectations accordingly. The number of agents actually adopting cooperation strategy is denoted by rit . The expectation adjustment formula is thus set as follows:
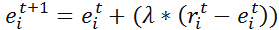
(6) This means that if current cooperators among his neighboring agents are more than his expectation, then agent i will increase his expectation; if current cooperators among his neighboring agents are less than his expectation, he will decrease his expectation. Otherwise, expectation will be kept unchanged. λ is the expectation adjustment speed; the larger the value, the faster the expectation adjustment, and more closely the expectation will be adjusted to the current number of real cooperators among the agents' neighborhood. If λ is 1, the player's current expectation will be equal to the real number of cooperators in the previous round, which means that the player will react to the situation passively. If λ is 0, the player's expectation will never change once it was set at the beginning, that is to say, she will never change her belief regardless of the actual number of cooperators. The updated expectation according to formaluae (6) will be used to calculate the next-round expected payoff by formaulae (4) and (5).
- 2.5
- During the evolutionary process of prisoner's dilemma game, every agent needs to decide whether he should change his strategy in each iteration step. If agent i does not choose a strategy according to the expectation of his neighboring agents' strategies, he will then compute uio , the payoff of adopting opposite strategy given his neighboring agents' strategies remain unchanged. Agent i will then replace his strategy with an opposite strategy based on a probability, which is calculated by their utilities difference. The transition rule or probability ( si replaced by So) is shown in the following formulae.
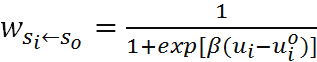
(7) Here, si and Soare the current strategy and its opposite strategy respectively. β relates to the noise in the choice. If β equals to 0, the updating results will be stochastic. If β approaches infinity, the updating rule will definitely choose the strategy, which will bring the agent more payoffs. Though noise may have a significant effect on the evolutionary process, it is not this paper's main focus; therefore, we choose a reasonable value for β. As to the issues of selection intensity and noise, Santos et al. (2006) can be used as a reference. In addition, in the present paper, all agents update their strategies synchronously.
- 2.6
- If agent i forms expectation regarding his neighboring agents' strategies, then the strategy transition rule is modified to reflect the effect of agents' expectation. Agent i will compare the expected payoff if he changes his strategy with the payoff he currently receives. Therefore, the transition rule ( si replaced by so) is set as the following formulae.
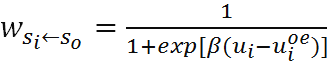
(8) Here, uioe is the expected payoff if this agent changes his strategy when his neighboring agents' strategies remain unchanged. The difference between formulae (7) and (8) lies in whether agents' expectation is taken into account; therefore the utilities of different agents are calculated differently.
- 2.7
- By using the expectation payoff in the transition rule or probability calculation, this model addresses the issue of how expectation affects an agent's strategy selection. If the agent with expectation expects that he will get more payoffs when he switches his strategy, he will be more likely to change his strategy. Otherwise, he may prefer to retain his current strategy. Furthermore, this transition rule is more similar to the best response updating strategy and avoids the limitation of imitation learning. In the present model, the agent is more conscious of the fact that he is playing the prisoner's dilemma game with his neighboring agents. In this sense, agents have more intelligence than the agents who can only imitate other agents' strategies, and are able to utilize the more complete knowledge about the details of the prisoner's dilemma game.
 Simulation results and discussion
Simulation results and discussion
- 3.1
- The simulations are carried out on two kinds of complex network: BA scale free network and WS small world network. In these simulations, we will study the effects of agents' expectation and other related parameters on cooperation emergence in complex networks.
- 3.2
- In simulations, two thousand agents located on the network vertices are connected by this complex network. In its initial status, 50% of the total agents are cooperators and they are distributed randomly in the network. The average degree of the nodes of BA network and WS small world network is 4. The β in agent strategy selection process is set to be 0.1. b or the defection temptation is varied in the interval [1, 2). λor the adjustment speed of expectation is set to be 0.2, which means that agents do not adjust their expectations very quickly. The payoff r agent will receive when both agents defect is set to be 0.1, a small but reasonable value.
- 3.3
- Agents' initial expectations can be set to the same value for all agents, or are randomly drawn from an interval if agents' heterogeneity is taken into account. Here, another scheme is used--- agents use a variable to represent how many percent of their neighboring agents will take the cooperation strategy, which is a random value drawn from [0, 1]. This random variable multiplied by the number of neighboring agents (the integral part) is the number of agents expected to adopt the cooperation strategy in the next iteration. The random values corresponding to all agents constitute the initial expectation distribution. The number of agents with expectation about neighboring agents' strategies lies in [0, 2000]. The default values for model parameters are summarized in Table 1.
Table 1: Simulation parameters initial cooperator number average degree β λ r initial expectations 50% 4 (BA, WS) 0.1 0.2 0.1 [0,1] number of agents having expectation b network nodes number [0,2000] [1,2] 2000 - 3.4
- During these simulations, we adjust model parameters to test their effects on cooperation emergence. Nerveless, it should be pointed out that in the simulation process, all agents will continuously update their strategies according to the expectations regarding neighboring agents' strategies. Therefore, in some cases the system may not evolve to a static status because of randomness in strategy selection and adaptation of expectation, though the fluctuation may vary along with time. This is also a feature which is derived from the introduction of expectation into the model. In order to present the reasonable results in the situations where the cooperation frequency fluctuates greatly, the average results are not used in present paper. The average results may hide the fluctuation pattern of cooperation frequency. However, it should be noted that stochastic factors may affect the simulations results, such as the location of these agents on the networks. In this situation, the statistical results may be more reasonable. But this concern does not entail serious problem in our research, because it is found that the location of agents with expectation will not affect the simulation result greatly as shown in simulation results (perhaps due to the fact that the number of agents with expectation is big enough compared to hub node number in BA network). So the statistical results are not provided in our research (we have provided the source code in the Open ABM forum).
The emergence of cooperation with adaptive expectation
- 3.5
- In the first experiment, testing about the effect of agent expectation on the emergence of cooperation is conducted among heterogeneous agents who make decisions according to expectation of other agents' strategies. Different numbers of agents who can form expectations about their neighboring agents' strategies are used to test the effect of agent expectation. At the same time, different defection temptations or values of b are also used in the experiment.
- 3.6
- The simulation results from BA network are shown in Figure 1. To make the results more clear and easy to compare, the results from the experiment with no agents forming expectation regarding other agents' strategy are also displayed. The results from the experiment with the same number of agents with expectation are plotted in the same graph, which is composed of curves corresponding to different values of b.
- 3.7
- From these simulation results, it can be easily seen that the cooperation frequency is very low when no agents form expectations regarding their neighboring agents' strategies given the present transition rule. However, when some agents act according to their expectations and update their expectations based upon their performance, the situation is different.
- 3.8
- In all the cases, the cooperation frequencies are much higher than the situation with no agent forming expectation about neighboring agents' strategies. The main factor accounting for this difference is that the existence of agents' with expectation will promote the cooperation strategy if the number of these kind agents is not very large; therefore, some agents will find that the cooperation strategy will bring them more utilities than defection. In this case, expectation will maintain itself. But as shown in the simulations, a too-large number of agents with expectation will make cooperation unstable in the situation when the defection temptation becomes bigger.
- 3.9
- Naturally, if the agent expect few neighboring agents adopting the cooperation strategy, the emergence of cooperation will be difficult. Thus, the expectation level and cooperation frequency will converge to a low level.
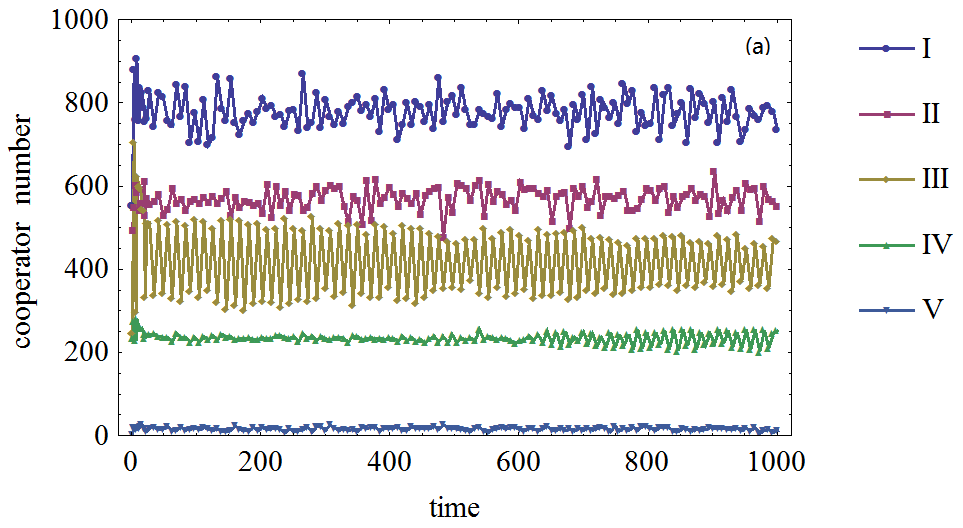
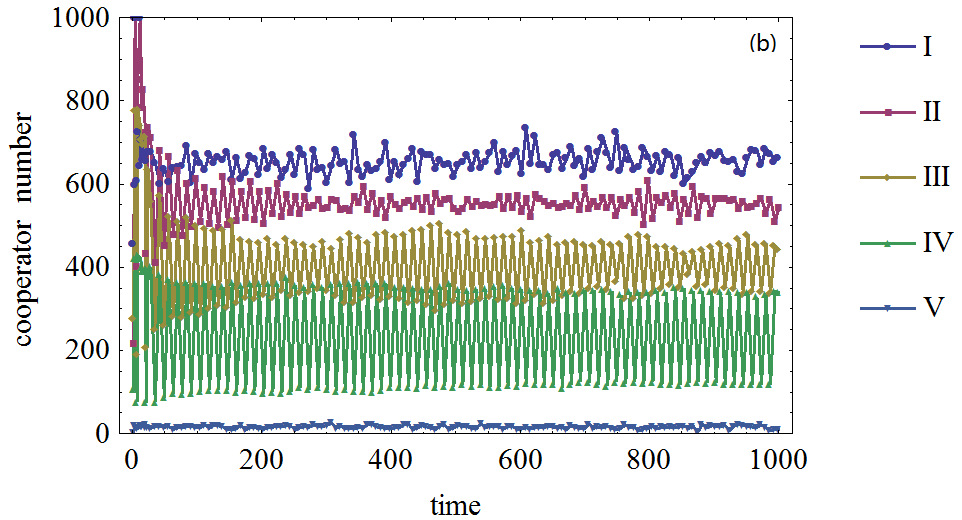
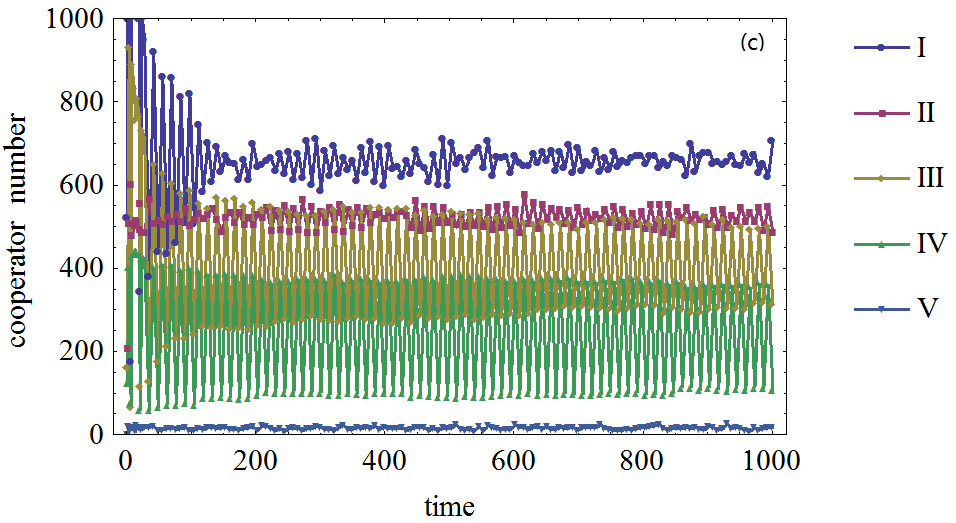
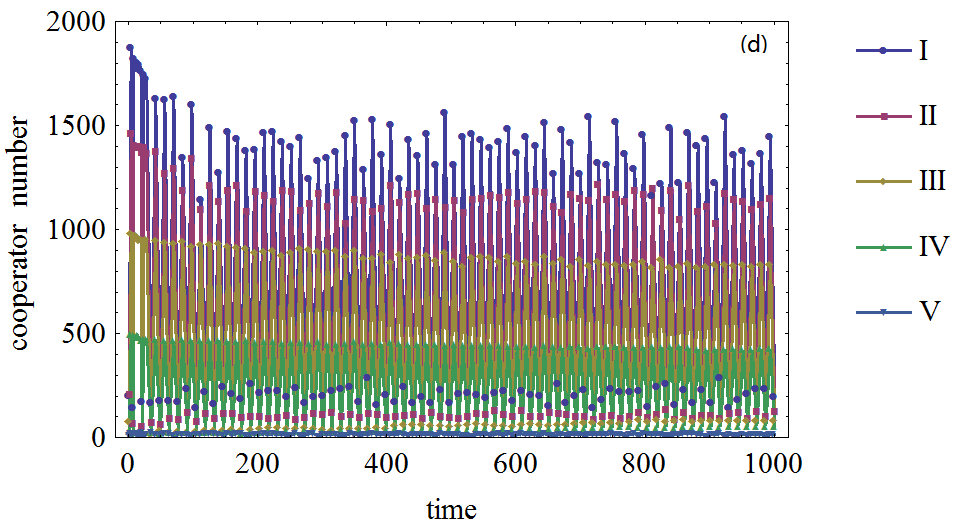
Figure 1. Figure 1. The effect of agents' expectation on the cooperator frequency in prisoner's dilemma game on BA network, (a), (b), (c), (d) : The defection temptation is 1.2,1.5,1.7,1.95, respectively. Different curves correspond to different number of agents who form expectation about their neighboring agents' strategies. I, II, III, IV and V denote 2000, 1500, 1000, 500, 0 agents who form expectations about their neighboring agents' strategies respectively.
- 3.10
- Furthermore, the simulation also shows that the more agents act according to their expectations, the higher cooperation frequency will emerge on the BA networks. Therefore, the agents' adaptive expectation will favor the emergence of cooperation in present model.
- 3.11
- It should be pointed out that not all agents will simultaneously choose the cooperation strategy. It is reasonable to assume that if all or most of their neighboring agents choose the cooperation strategy, the best choice for the agent is to choose defection strategy. In fact, this is determined by the nature of the prisoner's dilemma game. In our simulations, the highest cooperation frequency is approximately 0.4, which is also affected in a very small extent by the randomness of the model, such as the distribution of cooperators on networks.
- 3.12
- Another feature shown in the simulations is the fluctuation of cooperation frequency, especially in the case when the defection temptation is large or not all agents in the system form expectations regarding neighboring agents' strategies. This feature relates to expectation and its adaptive adjustment. This happens when some agents think it is in their best interest to switch their choices but one step later find that switching back to their previous strategy is the best choice when decisions are based upon the adjusted expectations. In this way, some periodical fluctuations appear.
- 3.13
- However, the cooperation frequency fluctuation on WS small world network is quite different, although the existence of agents with adaptive expectation also favors the emergence of cooperation. The simulation results are shown in Figure 2.
- 3.14
- It is conceivable that high defection temptation creates more cooperation frequency oscillations because agents will be more likely to defect to get more payoffs. But from these simulation results, we found that even if the defection temptation is very high, the cooperation frequency emerged in the WS network is not very low. The fluctuation is also small compared to those of BA network. The rationale for this difference relates to the different network topologies. In BA scale-free network, the changing of hub nodes' strategies affects many neighboring agents' behavior, while in WS small world network, nodes are almost homogeneous; therefore, the effect of node's strategy switching on other agents will not be significant. From these simulations, it can be concluded that the WS small network promotes the emergence of cooperation more than the BA scale-free network if defection temptation is high.
- 3.15
- In fact, another factor or parameter r will also affect the dynamic of the cooperation. In our simulations, it is found that the bigger the value of r, the more difficult the cooperation to emerge.
- 3.16
- Another issue that needs attention is the agents' initial expectation level or expectation distribution. The agents' expectation may be homogeneous or heterogeneous. Since expectation is a critical factor in the emergence of cooperation in prisoner's dilemma game, it is natural that its distribution may, to some extent, affect the evolutionary outcome. We tested different initial expectation levels, and the simulation results on the BA scale-free network are displayed in Figure 3. The experiments in the WS small world network have similar results; thus, they are omitted here.
- 3.17
- These results are a little different from our previous opinion; they show that the initial expectation distribution has no obvious influence on cooperation frequency. This is also due to the agents' adaptive expectation. The initial difference may not be significant, simply because agents can update their expectations. Furthermore, the expectations are not self-reinforcing in this prisoner's dilemma game. If more agents choose the cooperation strategy, the best choice for the agents is to defect. Given the initial cooperation agents unchanged; the effect of initial expectation distribution is not a critical factor. The initial difference will be smoothed by the agents' adaptive behavior and the evolutionary process.
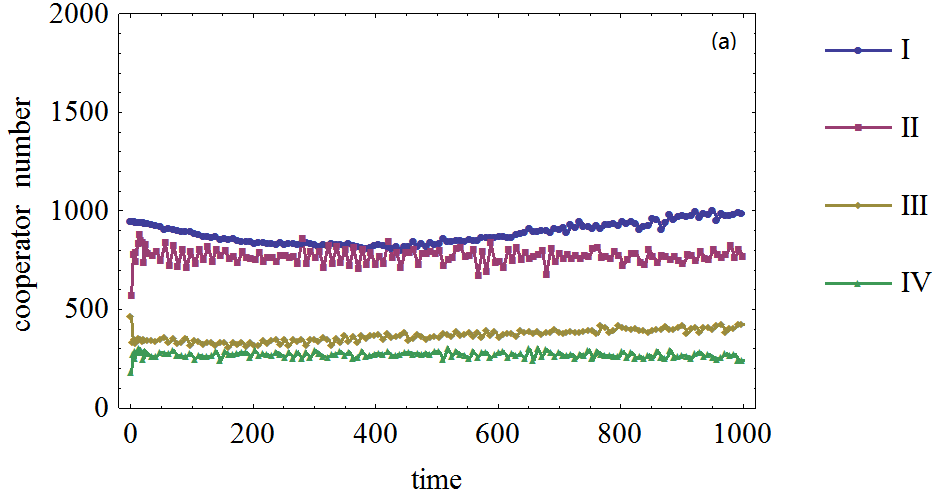
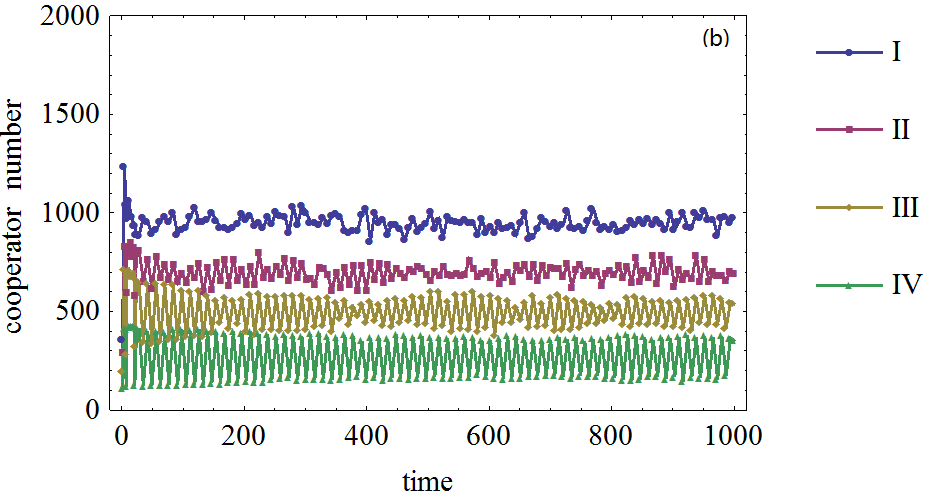
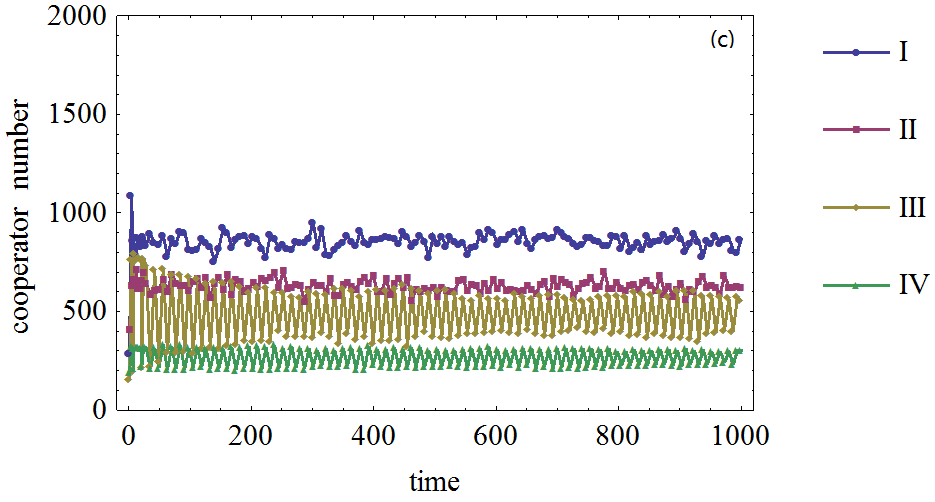
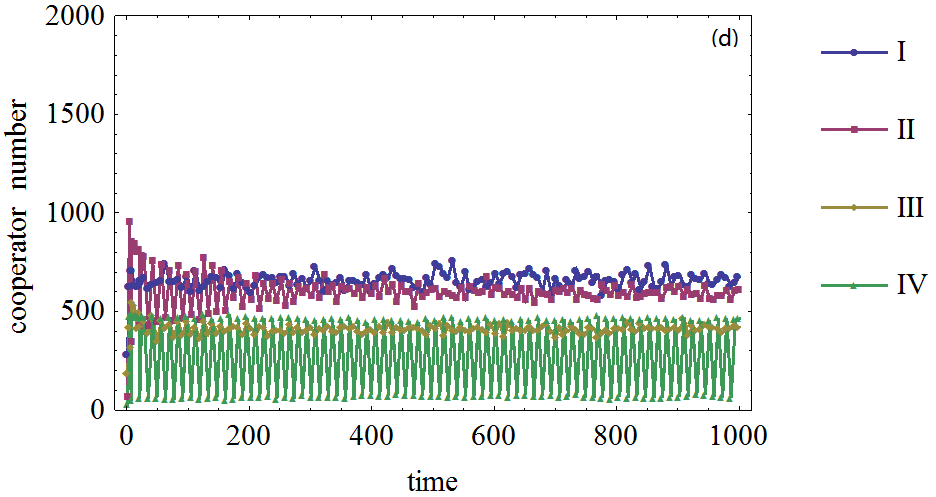
Figure 2. Figure 2. The effect of agents' expectation on the cooperator frequency in prisoner's dilemma game on WS small world network, (a), (b), (c), (d): The defection temptation is 1.2, 1.5, 1.7, 1.95, respectively. Different curves correspond to different number of agents who form expectation about their neighboring agents' strategies. I, II, III and IV correspond to 2000, 1500, 1000, 500 agents who form expectations about their neighboring agents respectively.
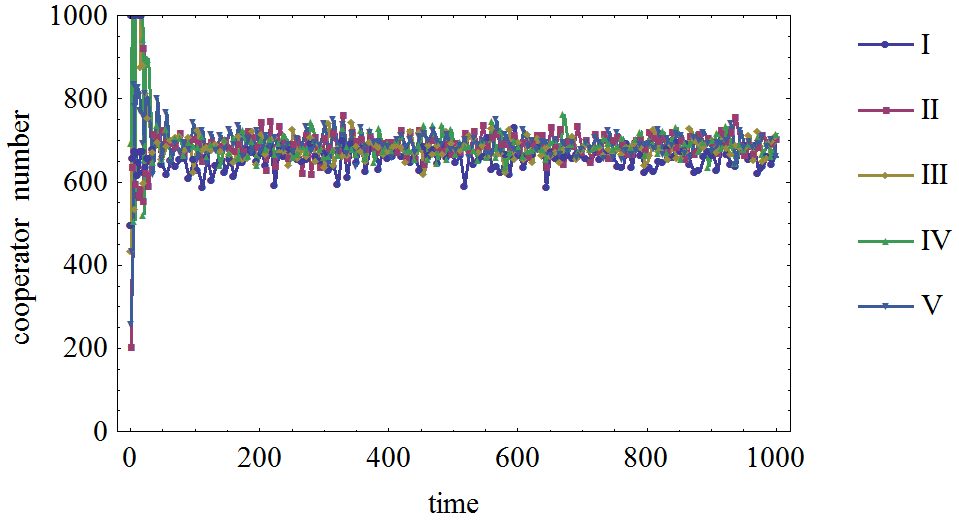
Figure 3. Figure 3. The effects of agents' expectation distribution on the cooperator frequency in prisoner's dilemma game on BA network. (I): The initial expectation of agents is 0.3. (II): The initial expectation of agents is 0.5. (III): The initial expectation of agents is 0.8. (IV): The initial expectation of agents is 1. (V): The initial expectation of agents is randomly drawn from [0; 1]. The number of agents with expectations about their neighboring agents' strategies is 2000.
- 3.18
- Therefore, all simulation results imply that agents' adaptive expectation regarding other agents' strategies plays an important role in the prisoner's dilemma game in the complex network and it can promote cooperation frequency. However, given agents will use a more intelligent transition rule in complex network, agents will not choose the cooperation strategy at the same time. A somewhat surprising result is that the agents' initial expectation level slightly affects the cooperation frequency due to the adaption of agents. This also implies that agents' heterogeneous expectation level does not affect the cooperation frequency in the situations discussed above.
The cooperation frequency with different expectation adjustment speeds
- 3.19
- The second experiment is to test the effect of different expectation adjustment speeds. Mainly through adjusting the expectation adjustment speed, we try to find its relationship with cooperation emergence in networks.
- 3.20
- In the present model, the agents' expectation adjustment speed is an important factor for the evolution dynamics and cooperation frequency achieved in complex networks. The adjustment of expectation embodies the adaptation and learning ability of the agents in the evolution process. Obviously, too fast or too slow expectation adjustment speed will make the expectation ineffective. In the simulations, we tested different effects of agents' expectation adjustment speeds given that other parameters in the model keep unchanged.
- 3.21
- The simulation results are shown in Figure 4.
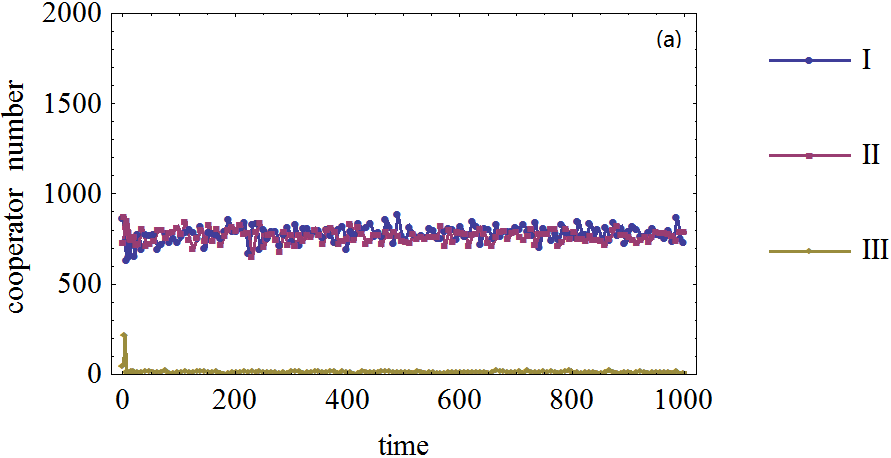
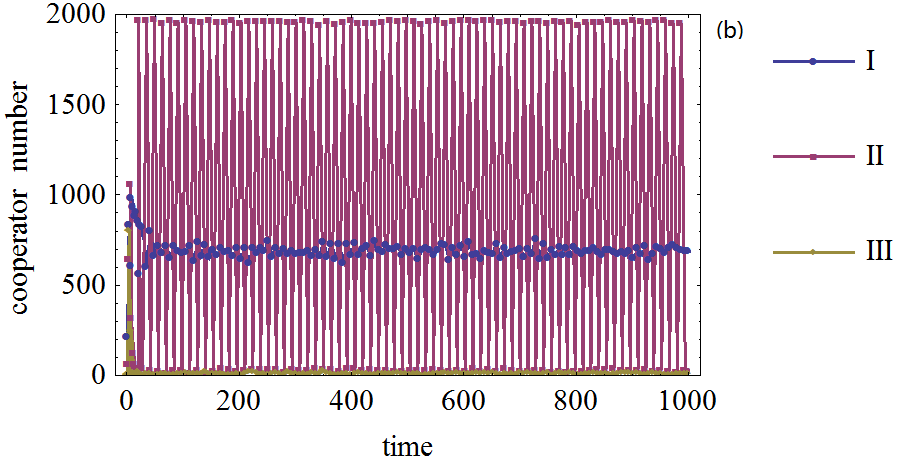
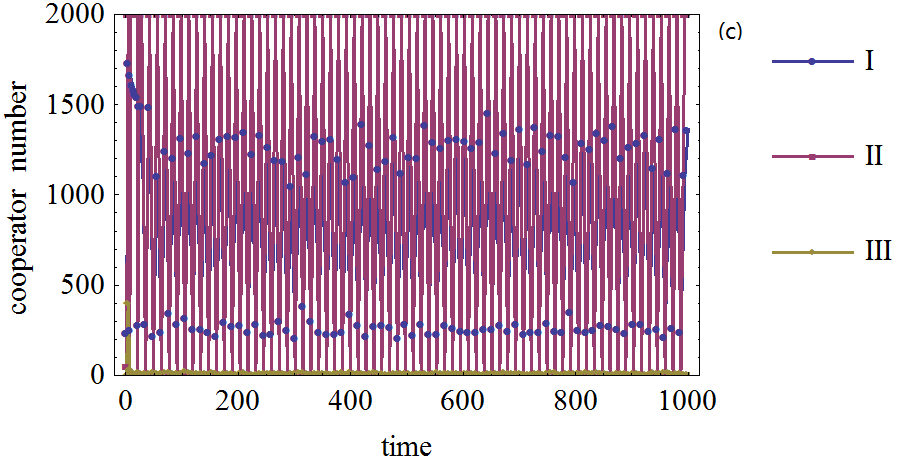
Figure 4. Figure 4. The effect of agents' expectation adjustment speed on the cooperator frequency in prisoner's dilemma game on BA network. (a): The defection temptation is 1.1. (b): The defection temptation is 1.5. (c): The defection temptation is 1.9. (I): The expectation adjustment speed is 0.2. (II): The expectation adjustment speed is 0.5. (III): The expectation adjustment speed is 0.8. The number of agents with expectations about their neighboring agents' strategies is 2000.
- 3.22
- From the simulation results, it can be seen that the cooperation frequencies are very low even if the defection temptation is small when agents quickly adjust their expectations, for example, agents' expectation adjustment speed is 0.8 or 0.5. This experiment is similar to the situation agents do not make decisions according to the expectations. When expectation adjustment speed is slow, the cooperation will emerge from agents' interaction. When defection temptation becomes larger, cooperation will be difficult to emerge when agents' expectation adjustment speed is not very high, such as lower than 0.5. The cooperation level will fluctuate between a very low value and a high value. The underlying mechanism for this is that when defection temptation is high, agents tend to choose defection strategy; however, when most agents choose defection strategy, agents' payoff will be very small. At this time, when each agent's expectations is adjusted, the expectations regarding other agents who will choose cooperation strategy are small, but they are still not reduced to zero; therefore, agents will choose cooperation because they expect that cooperation will bring them more payoffs than defection, which only bring them a very low payoff. At this moment, agents find that choosing defection is beneficial since their expectations are also quickly adjusted; therefore they are led to believe that the majority of the agents will choose the cooperation strategy. This fluctuation is mainly resulted from the nature of agents' adaptive expectation and the prisoner's dilemma game. The simulations on WS small world network display the same dynamical pattern; therefore, the details are omitted here.
- 3.23
- Simulations show that it is necessary to keep the expectation adjustment speed relatively small for cooperation to emerge on the BA networks in many situations. It implies that not all adoption of agents' expectation will be helpful for cooperation emergence on complex networks. The effect of agents' expectation depends upon the suitable expectation adjustment speed.
The cooperation frequency with different network average node degrees
- 3.24
- The third experiment is conducted to test the relationship between network node average degree and cooperation frequency. The network node degree varies in experiments while other parameters keep unchanged.
- 3.25
- In complex networks, the network average node degree defines the neighborhood size and may affect the agents' learning and evolution process. In many previous models, a larger neighborhood size of agents will bring more opportunities for agents to learn; therefore, the neighborhood size affects the cooperation frequency. The test of the effect of network average node degree is also conducted here and the simulation results are displayed in Figure 5.
- 3.26
- The simulation results show that it is more difficult for cooperation to emerge when the average node degree increases in BA network. The high average node degree, combined with high defection temptation or b, introduces more fluctuations into the dynamic process of cooperation frequency. In the present model, the agents' decision is based on the expectations regarding other agents' strategies. When hub agents interact with more neighboring agents, these agents' expectations are affected by more agents or more agents' choices are affected by hub agents; therefore, more agents need to adjust their strategies when defection temptation is large. It has been observed that there are more fluctuations in the evolution process than the situations where the average neighborhood size is smaller. In addition, the cooperation frequency is a slightly lower with larger average network node degrees if the cooperation frequency volatility is not very high. Since agents have more opportunities when network average node degree increase, these results seem reasonable.
- 3.27
- We also conducted simulations on WS small world network. The effect of neighborhood size is much smaller, which can be observed from Figure 6. As there is little difference between results from different defection attraction values, we simply displayed the results when defection value is 1.95-a very high value which will make great oscillation in cooperation frequencies in the BA scale-free network.
- 3.28
- The simulation results imply that the effect of neighborhood size is rather small on the WS network compared to that of the BA network. Therefore, the results reveal that the oscillation is mainly resulted from the heterogeneity of the BA scale-free network.
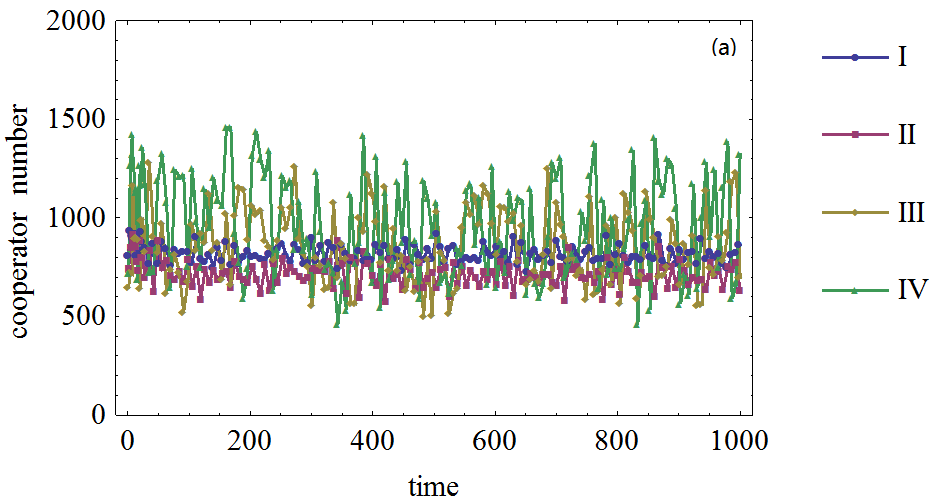
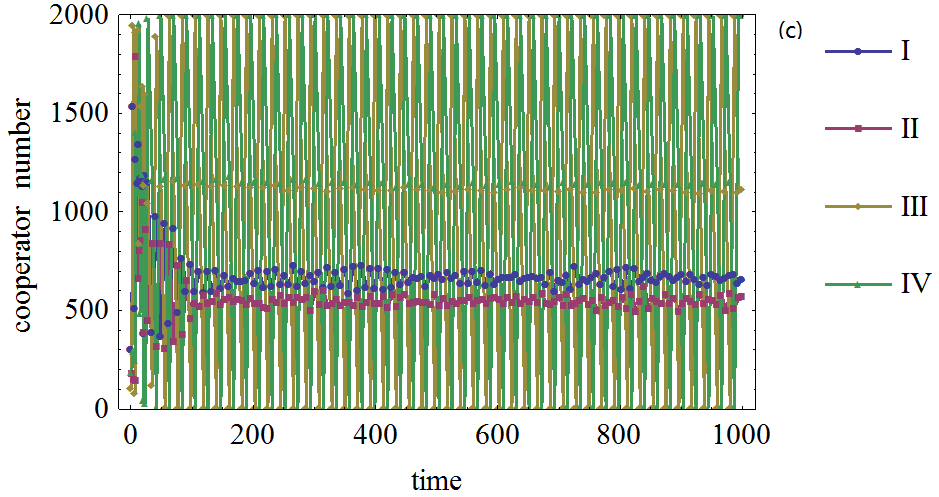
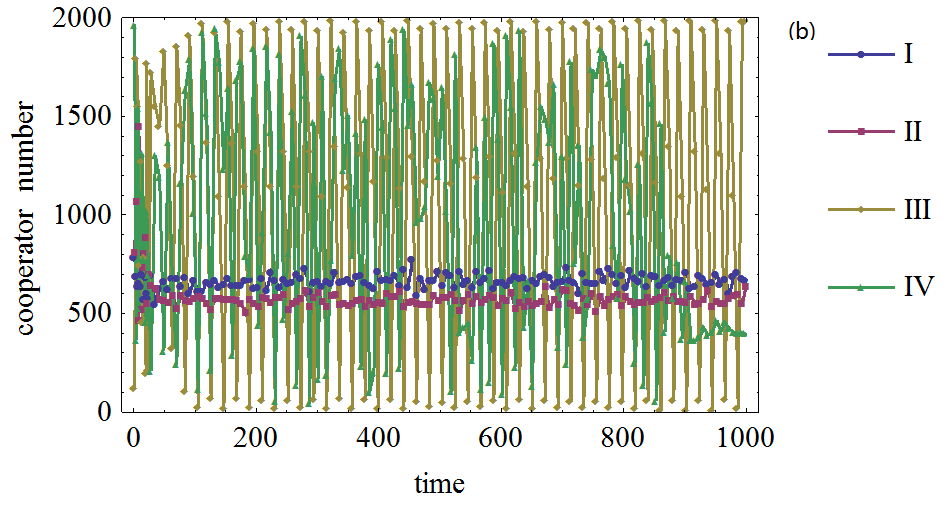
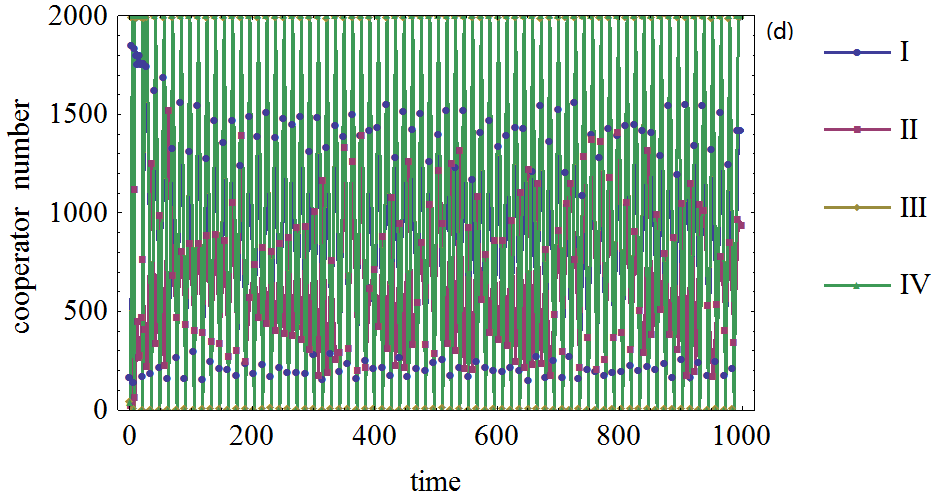
Figure 5. Figure 5. The effect of network average node degree on the cooperator frequency in prisoner's dilemma game on BA network. (a): The defection temptation is 1.1. (b): The defection temptation is 1.4. (c): The defection temptation is 1.7. (d): The defection temptation is 1.95. (I): Network average node degree is 4. (II): Network average node degree is 6. (III): Network average node degree is 8. (IV): Network average node degree is 10.
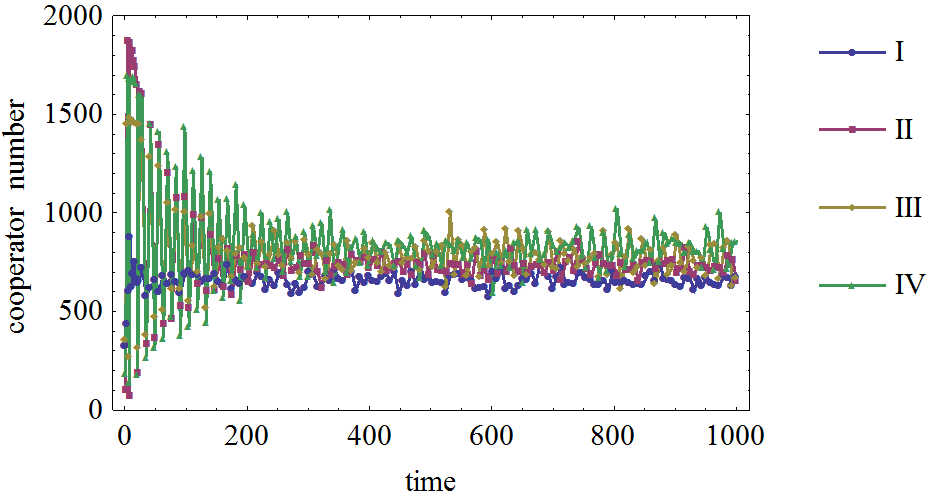
Figure 6. Figure 6. The effect of network average node degree on the cooperator frequency in prisoner's dilemma game on WS network, the defection temptation is 1.95. (I): Network average node degree is 4. (II): Network average node degree is 6. (III): Network average node degree is 8. (IV): Network average node degree is 10.
- 3.29
- In summary, the larger the network degree, the harder the cooperation emerges in BA network when the defection temptation increases. This feature relates to the heterogeneous degree of BA network nodes, the hub nodes' strategies will affect many other nodes' strategies. So it is not surprising that this feature does not exist in the WS small network which has a more homogeneous nodes' degree distribution.
The effect of different initial number of cooperators on cooperation frequency
- 3.30
- The last experiment focuses on the effect of system initial status, mainly the initial number of cooperators on cooperation emergence. So as the previous experiment, the initial number of cooperators will vary while other parameters keep the default value.
- 3.31
- As we known, in a complex system, the initial status may be a critical factor for the evolution process. The initial number of cooperative agents will affect agents' expectation and its adjustment in the system's initial status. Therefore, it is worthwhile to study its effect on cooperation frequency. Several different numbers of initial cooperative agents are then chosen to test their effects. Keeping all other factors unchanged, the simulation results for different initial numbers of cooperative agents are displayed in Figure 7.
- 3.32
- It is surprising that the simulation results show that, in most cases, the initial number of cooperative agents has little effect on the cooperation frequency. Even with different numbers of initial cooperators, the curves are very close; this is true even when the defection temptation varies greatly. Given the agents' initial expectation level and their adaptive adjustment, the higher number of initial cooperators will not lead to a higher cooperation frequency, because given the opportunistic nature of prisoner's dilemma game, agents will choose defection if most of the neighboring agents choose cooperation strategy. As agents can learn and adjust their expectations, the difference between initial cooperative agents is mediated and removed in the evolutionary process. The results show that the agents' adaptive expectation plays a more vital role in cooperation emergence than the number of initial cooperative agents. The simulation results on the WS small world network display similar patterns, except that the oscillation is much smaller when the defection attraction is high, a feature which has been noted in previous sections. The simulation results are shown in Figure 8.
- 3.33
- As there is little difference between different defection temptation values, we simply display the results when defection value is 1.7 and 1.95 respectively, which are very high values resulting great oscillations in cooperation frequencies in the BA scale-free network.
- 3.34
- It can be seen that if the defection attraction is 1.7 or 1.95, the oscillation is small in the long-term; although there are great oscillations in the early time. In these experiments, the initial cooperator agent number is not a significant factor for the cooperation emergence.
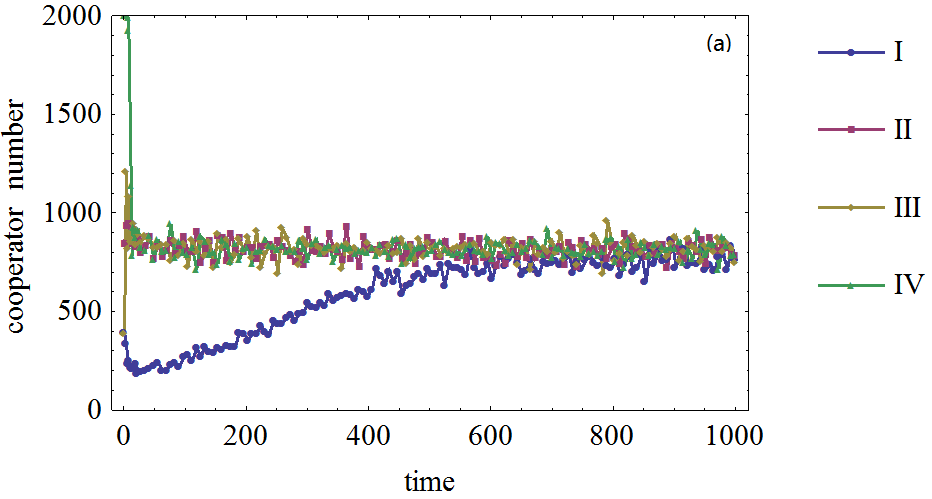
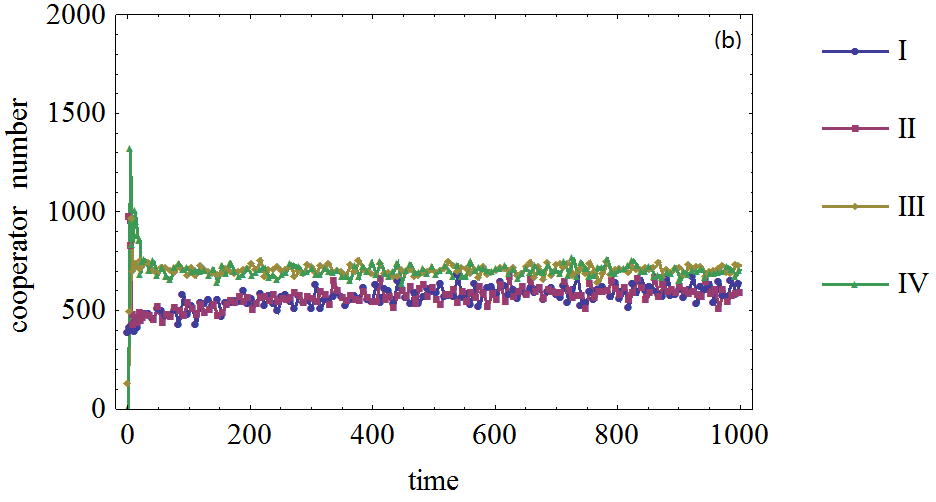
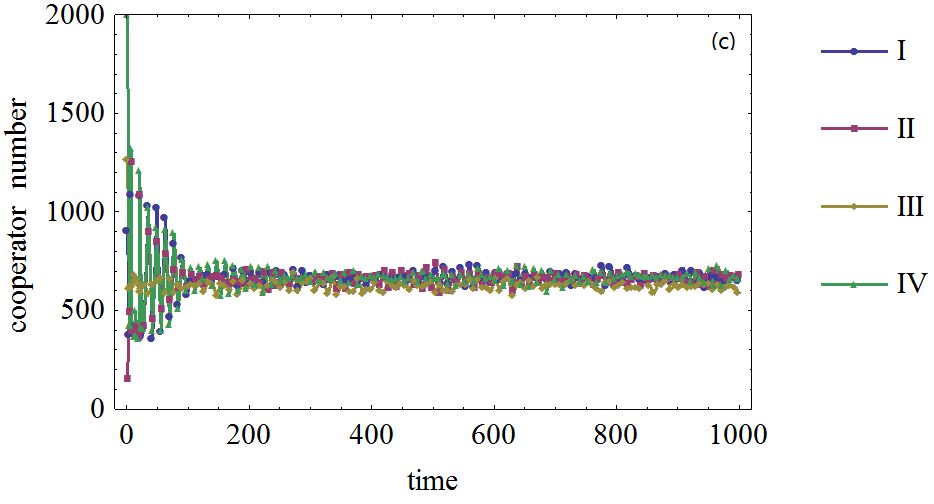
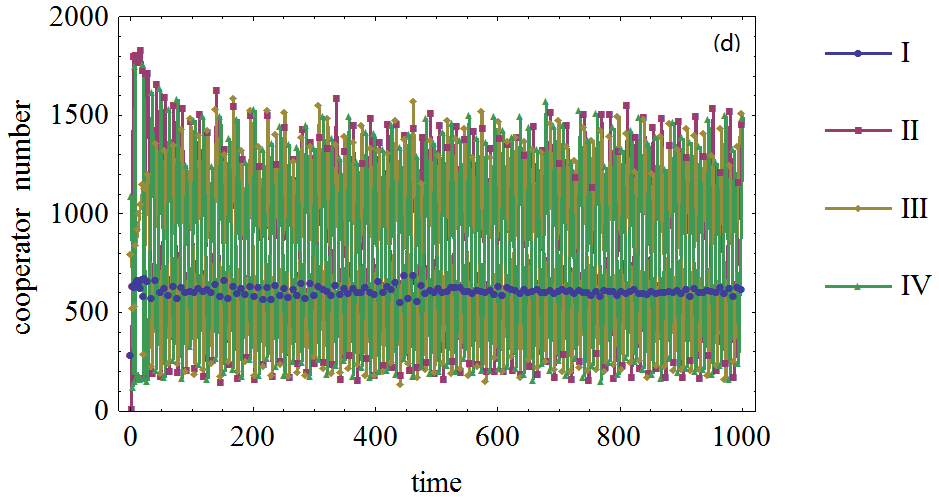
Figure 7. Figure 7. The effect of the number of initial cooperation agents on the cooperator frequency in prisoner's dilemma game on BA network. (a), (b), (c), (d): The defection temptation is 1,1,1.4.,1.7,1.95, respectively. (I), (II), (III), (IV): The initial cooperation agents number is 500, 1000, 1500, 2000, respectively.
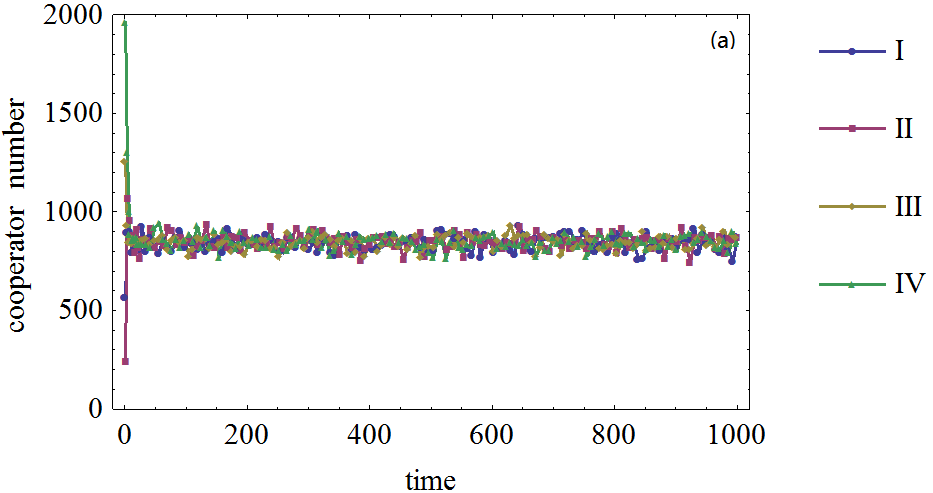
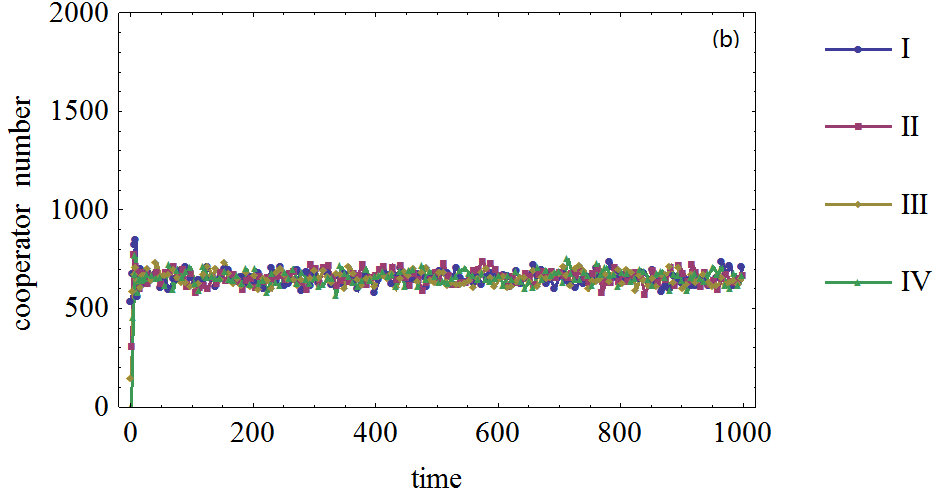
Figure 8. Figure 8. The effect of the number of initial cooperation agents on the cooperator frequency in prisoner's dilemma game on WS network, (a), (b): The defection temptation is 1.7, 1.95, respectively. (I), (II), (III), (IV): The initial cooperation agents number is 500, 1000, 1500, 2000, respectively.
 Conclusion
Conclusion
- 5.1
- As agent's expectation plays an important role in human behavior (such as in the prisoner's dilemma game), it is reasonable to introduce expectation into game model in complex network. In the present paper, we have studied the emergence of cooperation in scenarios where agents can choose strategy based upon expectations regarding their neighboring agents' strategies and adjust their expectations according to past experiences. In present model, we also modify the agent strategy updating rule, which allows agents switching current strategy based on the expectation of strategies of their neighboring agents and the payoffs the opposite strategy will bring about.
- 5.2
- In the previous model of evolutionary prisoner's dilemma game, it was very difficult for cooperation to emerge if agents chose a strategy based upon the best response rule, or if agents were not limited to the strategy of simply imitating neighboring agents. As human agent, such simple learning rule may not be very realistic. When agents' expectation is introduced into the complex network game model, the simulation results show that cooperation frequency is maintained at a relatively high value when the defection temptation is not very high. Our experiments demonstrator that agents' expectation will indeed promote cooperation.
- 5.3
- In addition, because of agents' expectation are different and the nature of prisoner's dilemma, not all agents will choose cooperation strategy at the same time. However, it is reasonable. It means that cooperation agents and defection agents should coexist in the network, a more commonly observed phenomenon. The initial expectation level does not display significant effect due to the agents' adaptive expectation adjustment. The simulations also display that agents' expectation adjustment speed affects the evolution results. The network average node degree affects the cooperation frequency fluctuation in the BA scale-free network, while the initial number of cooperation agents is not a critical factor for the emergence of cooperation in our experiments.
- 5.4
- Another point that should be noted is that cooperation frequency will display more fluctuations because agents will switch their strategies to defection for greater payoffs according to their expectations. Expectation favors cooperation emergence; however, at the same time, when defection temptation is large, expectation also brings more fluctuations in the cooperation frequencies. Due to the network heterogeneity or hub nodes, the oscillation is much greater in the BA scale-free network than that in the WS small world network. When defection attraction is high, the cooperation frequency is more stable on the WS network, which implies a higher cooperation frequency. These results reveal that different topologies have different effects on cooperation emergence.
- 5.5
- In addition, this research shows that expectation is not self- enforcing. Different from other self-enforcing expectations, the cooperation frequency is constrained by the opportunistic behavior of agents. Therefore, not all agents will be cooperators at the same time. Given the simulations results, it can be said that agents' adaptive expectation successfully addresses the emergence of cooperation when agents have more knowledge about the game. Thus, agents' expectations deserve more attentions in evolutionary game research. Besides, since human agents act according to their expectations, our research result may be useful for the researches of cooperation in a society. As to the social policy maker, present research may also deliver some helpful suggestions about how to promote cooperation in a society.
- 5.6
- However, there is still much work to be done in the future. In our model, agents' expectation is exogenously given, therefore, how to endogenously address agents' expectation needs further study.
 Appendix
Appendix
-
The model presented in this work was implemented using Repast Simphony 1.2.
- Create 2000 players, add players into the context;
- Initialize the agents and model's parameters;
- Build the BA scale free or WS small world network; Agents are located on the vertices of the network.
- Set some agents to be the agents with expectation.
- Set agent's initial strategies
- 6.1
- The following methods are defined. They are the methods deployed by the agents during their interactions in the spatial prisoner's dilemma game.
Player( ): //constructor function Initializes agents, Set agent's initial strategy, Set the status whether agent acts according to his expectation; Set the payoff matrix of the game; setInitialExpectation(): //set agent's initial expectation Multiply agent network degree by initial expectation level, get the integer part of it; Set agent's initial expectation; computePayoff( ) computes total payoffs when an agent plays game with neighboring agents according to his current strategy. expectationAdjust( ): //adjust the expectation according to the real situation; If agent acts according to expectation then Count the neighboring agents number using cooperation strategy; Adjust the expectation according to formulae 6; computeExpectationPayoff( ): according to agent's current strategy, compute the expected payoff when expectation is adjusted; chooseStrategy( ): According to agent's current strategy, compare the expected payoff and current payoff; Compute the probability of switching to another strategy#∫prob; Generate a random number between 0 and 1: randomProb; If (randomProb<=prob) then change strategy else keep agent's strategy unchanged; set whether agent is cooperator; postStep( ): update the agent's current strategy status when strategy was chose.
Model class:
Context build ( ):
Build the simulation schedules as follows:
// because in the simulation process, each agent needs to get some neighboring agents' information,
// thus it is needed to make sure that each agent's change of status will not affect other agents'
// decision during the same step or tick in simulation, therefore the loops are separated to
// several parts.
// t signifies time step or tick
If t=0 then {
//Prepare to begin the model
Add all agents to be processed into the list;
Set Initial Expectation of agents;
}
// t[stop] is the time step or tick when simulation stops.
for t = 1 to (t[stop]-1)
{
for each agent on the network {
// Compute the payoff each agent has received, here no social preference involved.
computePayoff();
}
for each agent on the network{
// adjust the expectation and compute the payoff expected;
expectationAdjust();
computeExpectationPayoff();
}
for each agent on the network {
// agents choose the strategies
chooseStrategy();
}
for each agent on the network {
// update the status of this agent after the work in one step is done.
postUpdate();
}
}
If t=t[stop]{
Perform data recording work, write needed data to output file.
End the model;
}
Agent class:
 Acknowledgements
Acknowledgements
- The author is supported by National Natural Science Foundation of China (Grants No. 71071061, No. 61173019) and the Major Subject of Research Project in Philosophy and Social Science, Ministry of Education (No. 10JZD0006). The author thanks the referees for their great suggestions.
 References
References
-
ABRAMSON, G.,Kuperman, M. (2001). Social games in a social network. Physical Review E, 63, pp:030901. [doi:10.1103/PhysRevE.63.030901]
AXELROD, R. (1985). The Evolution of Cooperation. New York, Basic Books.
AXELROD, R. (1997). The Complexity of Cooperation. Princeton University Press, Princeton.
AXELROD, R.,Hamilton, W.D. (1981). The evolution of cooperation. Science, 211(4489), pp:1390-1396.. [doi:10.1126/science.7466396]
BARABÁSI, A-L.,Albert, R. (1999). Emergence of scaling in random networks. Science, 286, 509-512. [doi:10.1126/science.286.5439.509]
BO, X.Y.(2011). Other-regarding preference and the evolutionary prisoner's dilemma on complex networks. Physica A, 389(5), 1105-1114. [doi:10.1016/j.physa.2009.11.032]
CHEN, X., Fu, F., and Wang, L. (2008a). Influence of initial distributions on robust cooperation in evolutionary prisoner's dilemma. Physics Letters A, 372, 1161-1167. [doi:10.1016/j.physleta.2007.09.044]
CHEN, X, Fu, F, and Wang, L (2008b). Interaction stochasticity supports cooperation in spatial prisoner's dilemma. Physical Review E, 78, 051120. [doi:10.1103/PhysRevE.78.051120]
FU, F., Chen, X., Liu, L., and Wang, L. (2007a). Promotion of cooperation induced by the interplay between structure and game dynamic. Physica A, 383, 651-659. [doi:10.1016/j.physa.2007.04.099]
FU, F, Liu, L, and Long, W (2007b). Evolutionary prisoner's dilemma on heterogeneous newman-watts small-world network. European Physical Journal B, 56, 367-372. [doi:10.1140/epjb/e2007-00124-5]
FU, F., Wu, T., and Wang, L. (2009). Partner switching stabilizes cooperation in coevolutionary prisoner's dilemma. Physical Review E, 79, 036101. [doi:10.1103/PhysRevE.79.036101]
KIM, J-W. (2010), A Tag-Based Evolutionary Prisoner's Dilemma Game on Networks with Different Topologies. Journal of Artificial Societies and Social Simulation, 13(3) 2 https://www.jasss.org/13/3/2.html
MOYANO, L.G. and Sanchez, A. (2008). Spatial prisoner's dilemma with heterogeneous agents: Cooperation, learning and co-evolution. http://arxiv4.library.cornell.edu/abs/0805.2071v1.
NOWAK, M.A., Bonhoeffer, S., and May, R.M. (1994). Spatial games and the maintenance of cooperation. Proceedings of the National Academy of Sciences of the United States of America,91, 4877-4881. [doi:10.1073/pnas.91.11.4877]
NOWAK, M.A.,May, R..M. (1992). Evolutionary games and spatial chaos. Nature 359, 826-829. [doi:10.1038/359826a0]
NOWAK, M.A. ,May, R.M. (1993). The spatial dilemmas of evolution. International Journal of Bifurcation and Chaos, 3, 35-78. [doi:10.1142/S0218127493000040]
OHTSUKI, H., Hauert, C., Lieberman, E. and Nowak, M.A. (2006) A simple rule for the evolution of cooperation on graphs and social networks. Nature, 441, 502-505. [doi:10.1038/nature04605]
PENNISI, E. (2005). How did cooperative behavior evolve? Science, 309, 93. [doi:10.1126/science.309.5731.93]
POWER C. (2009). A Spatial Agent-Based Model of N-Person Prisoner's Dilemma Cooperation in a Socio-Geographic Community. Journal of Artificial Societies and Social Simulation,12(1) 8. https://www.jasss.org/12/1/8.html.
SANTOS, F. C. and Pacheco, J M (2005). Scale-free networks provide a unifying framework for the emergence of cooperation. Physical Review Letters, 95, 098104. [doi:10.1103/PhysRevLett.95.098104]
SANTOS, F.C. ,Pacheco, J.M. (2006a). A new route to the evolution of cooperation. Journal of Evolutionary Biology, 19, 726-733. [doi:10.1111/j.1420-9101.2005.01063.x]
SANTOS, F.C., Pacheco, J.M., and Lenaerts, T.(2006b). Evolutionary dynamics of social dilemmas in structured heterogeneous populations. PNAS, 103, 3490-3494. [doi:10.1073/pnas.0508201103]
SANTOS, F.C., Rodrigues, J.F., and Pacheco, J.M.(2006c). Graph topology plays a determinant role in the evolution of cooperation, Proceedings of the Royal Society B: Biological Sciences, 273, 51-55. [doi:10.1098/rspb.2005.3272]
SZABÓ, G., Antal, T., Szabó, P., and Droz, M.(2000). Spatial evolutionary prisoner's dilemma game with three strategies and external constraints. Physical Review E, 62, 1095-1103. [doi:10.1103/PhysRevE.62.1095]
SZABÓ, G. ,Fáth, G. (2007). Evolutionary games on graphs. Physics Reports, 446 (97) 216. [doi:10.1016/j.physrep.2007.04.004]
SZABÓ, G.,Hauert, C.(2002), Evolutionary prisoner's dilemma games with optional participation. Physical Review E, 66, 062903. [doi:10.1103/PhysRevE.66.062903]
SZABÓ, G. ,Toke, C.(1998). Evolutionary prisoner's dilemma game on a square lattice. Physical Review E, 58, 68-73. [doi:10.1103/PhysRevE.58.69]
SZOLNOKI, A.,Perc, M. (2009). Promoting cooperation in social dilemmas via simple co-evolutionary rules. European Physical Journal B, 67, 337-344. [doi:10.1140/epjb/e2008-00470-8]
VUKOV, J., Szabó, G., and Szolnoki, A. (2008). Evolutionary prisoner's dilemma game on the Newman-Watts networks. Physical Review E, 77, 026109. [doi:10.1103/PhysRevE.77.026109]
WATTS, D. ,Strogatz, S. (1998). Collective dynamics of 'small-world' networks. Nature, 393, 440-442. [doi:10.1038/30918]
WU, Z. X., Xu, X. J., Chen, Y., and Wang, Y. H. (2005). Spatial prisoner's dilemma game with volunteering in newman-watts small-world networks. Physical Review E, 71, 7103. [doi:10.1103/physreve.71.037103]
YU-JIAN, L., Bing-Hong, W., Han-Xin, Y. Xiang, L., Xiao-Jie, C., and Rui, J. (2009). Evolutionary prisoner's dilemma game based on pursuing higher average payoff. Chinese Physics Letter, 26, 01871. [doi:10.1088/0256-307X/26/1/018701]