Introduction
Groupware is often effectively employed for sharing information in many types of groups such as companies and organizations. Some communication tools including Yammer[1] and Slack[2] provide advantages for knowledge sharing in system development. When using these tools users must actively provide information to the system. However their users have little incentive to provide information through the media because they benefit from such knowledge as free-riders. According to a previous survey (Yamamoto & Kanbe 2008) several bad examples of groupware or enterprise SNSs have been adopted for sharing knowledge in certain firms.
Although knowledge sharing among members of an organization is an important issue for knowledge management, organizational knowledge can also be considered a public good as discussed in previous work (Cabrera & Cabrera 2002). In order to overcome such a social dilemma it is necessary to appropriately design groupware as an infrastructure of the knowledge-sharing system. Our challenge is significant because we propose an operational model for groupware while most related studies focus on case studies.
These observations support the idea that these tools are regarded as public-goods games (Fulk et al. 1996, 2004). Using this analogy cooperative behavior in public-goods games corresponds to providing effective information on groupware and non-cooperative or defecting behavior corresponds to not providing them. Non-cooperative regimes are dominant among rational participants in public-goods games. This theory suggests that actual groupware might provide incentives to encourage cooperative behaviors because it has appropriate knowledge.
The managers of successful groupware could employ a system in which content providers would get such responses as comments and feedback from other users. This system corresponds to providing rewards in public-goods games. Reward mechanisms can be analyzed as meta-reward games which are related to meta-sanction games (Fujio et al. 2014)[3] . While previous works have shown that meta-reward games effectively provide information in social media meta-sanction games which are an extension of meta-reward games include a function that promotes cooperation not only by reward systems but also by punishment systems. On the one hand it seems unrealistic to punish information non-providers in social media. On the other hand it does seem possible to punish non-cooperators in a knowledge-sharing site or groupware. What is the most effective system for robustly promoting cooperation in any sanction system including reward and punishment?
In this paper we addressed that question by modeling a groupware system as a meta-sanction game and simulating its complete configuration. Although previous studies theoretically show that meta-reward games effectively provide information in social media no analysis has been made of the punishment aspect of meta-sanction games.
Related Works
Studies on groupware often point out that it is an effective tool for managing knowledge (Ferreira & Du Plessis 2009; Yamamoto & Kanbe 2008; Leonardi et al. 2013; Majchrzak et al. 2013; Neto & Choo 2011). Such groupware as wikis knowledge repository Slack and Yammer are effective forms of media for knowledge sharing and active open communication. Thom et al. (2011) tested the effectiveness of a Q & A system and Cross et al. (2012) supported participants who wanted to collaborate by visualizing the analysis of a social network. The negative side of groupware has also been pointed out (Gibbs et al. 2013; Wang & Kobsa 2009) privacy concerns. While earlier work (Fulk et al. 1996, 2004; Leonardi et al. 2013) argued that information behaviors in groupware resemble a feature of public goods few studies of such behaviors have regarded them as public-goods games.
Many researchers continue to focus on the evolution of cooperation in public-goods games. Some have granted sufficient ability to those playing public-goods games to remember their direct experiences (Fehr et al. 2002) or indirect experiences (Nowak & Sigmund 2005) using tags (Riolo et al. 2001) or reputation systems (Ohtsuki & Iwasa 2007). They insist that such additive information generates cooperative regimes due to (in)direct reciprocity. Other works have focused on the interaction of players. Spatial structure (Helbing et al. 2010) and network structure (Nakamaru & Iwasa 2005; Hirahara et al. 2014) imposed on players are alternatives that encourage cooperation. Another group which gave players other choices in addition to contributing or doing nothing proposed a loner who does not participate in the game (Hauert et al. 2002; Sasaki et al. 2007) or a malicious prankster who destroys public goods (Arenas et al. 2011).
Other researchers (Axelrod 1986; Nowak 2012) have devised another sort of game that promotes cooperation by explicitly incentivizing players. Rewards and penalties are important incentives for the evolution of cooperation (Balliet et al. 2011). Our approach integrates such positive incentives as rewards and such negative ones as penalties into a system that promotes cooperation.
Galan & Izquierdo (2005) exposed the vulnerability of the metanorm game proposed by Axelrod (1986). They demonstrated its dynamics with different types of selection mechanisms and concluded that meta-norms cannot be sustained in wide parameter spaces for long runs. While this work mathematically analyzed the evolutionary stable states (ESS) of the system they also showed by computer simulation that such ESSs are not necessarily stable for super-long runs through mutations. Although they argued in a pioneering and counterintuitive way for the vulnerability of meta-norms they only treated punishment and meta-punishment systems as defections. However as Rand et al. (2009) clearly showed the analysis of both reward and punishment systems must be considered. We address a meta-sanction game that integrates reward punishment meta-reward and meta-punishment (Toriumi et al. 2012; Fujio et al. 2014). Using this game we capture a bird’s-eye view of the effect of meta-sanctions (rewards and punishments) on the evolution of cooperation. Our work comprehensively analyzes the effect of meta-sanction systems while Galan & Izquierdo (2005) scrutinized punishment systems.
Groupware Model as Meta-Sanction Games
Public-goods Games
Generally the information behaviors in groupware consist of accepting knowledge posted by users and letting other members access it. The users who browse the knowledge get benefits but the users who post it incur both making and posting costs. Here providing appropriate knowledge is defined as cooperative behavior C and providing inappropriate knowledge is defined as non-providing behavior (defective behavior) D. When users make and post appropriate knowledge they incur costs. Let κ0 be the cost for C let p0 be the benefit for browsing the knowledge and let N0 be the number of other users who provide appropriate knowledge. For simplicity in our model D users provide nothing without any cost and the other users get nothing. The payoff of the cooperators is represented as − κ0 + p0 N0 , and the expected payoff of the defectors is represented as p0 N0 .
Let us compare the payoffs of the cooperators and the non-cooperators when N0 > 0. Since the non-cooperator does not pay κ0, she always has a higher payoff than a cooperator. This situation does not change even when N0 = 0, because the new cooperator s payoff is − κ0 if a non-cooperator changes her strategy. Consequently all of the players choose non-cooperative behaviors and N0 becomes saturated at 0. Therefore information behaviors in groupware resemble a kind of public-goods game.
Meta-Sanction Games
A sanction system is a scheme that promotes cooperation in public-goods games. Rewarding cooperators and punishing non-cooperators are external incentives for players who cooperate in the games.
We regard groupware as a sanction system that gives rewards and punishments. First consider a reward system. In some cases groupware users who provide knowledge might obtain rewards. Next we consider users who browse knowledge without providing it or free-riding. Such users might be punished when they do not provide any knowledge. A punishment system also works as an external incentive system that allows users to provide appropriate knowledge. We clarify the essential mechanism of providing appropriate knowledge in groupware by developing a model that is an extension of both public-goods and meta-sanction games.
We employ a meta-sanction game (Toriumi et al. 2012; Fujio et al. 2014) as a generalized model of the sanctions in public-goods games. This scheme is an extension of Axelrod’s metanorm game (Axelrod 1986) and devises not only punishments of defects but also the configurations of meta-sanctions including punishments and rewards.
3.6 The following six systems are the sanctions in our meta-sanction game
- Punishment of defectors (System P)
- Reward for cooperators (System R)
- Punishment of free-riders who punish defectors (System PP)
- Reward for punishers who punish defectors (System PR)
- Punishment of non-rewarding of cooperators (System RP)
- Reward for rewarders who compensate cooperators (System RR)
Since those who play meta-sanction games incur costs and accrue benefits for their actions we set parameters. As mentioned in Section a cooperator pays κ0 in a public-goods game and all of the players receive p0. κp is the cost when performing System P and κr is the cost when performing System R. Likewise κpp, κpr, κrp and κrr are the costs when performing Systems PP, PR, RP and RR. The benefits of sanctions pp, pr, ppp, ppr, prp, and prr are defined using the same rule. Since these costs and benefits include not only pecuniary matters but also psychological aspects kt > pt is possible. On a Q & A system in groupware for example an answer might be quite valuable for the questioner even if it is trivial for the respondent. In this case κr > ρr, is satisfied because respondent s cost κr is less than questioner's benefit pr[4].
Basic Framework of Meta-Sanction Game
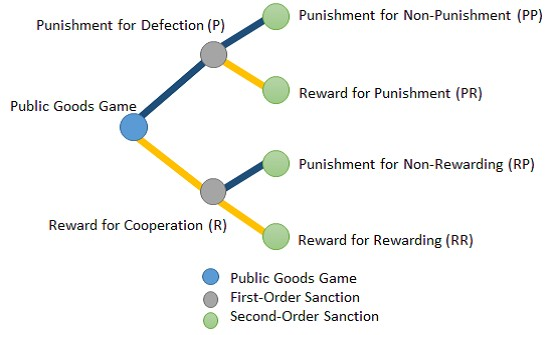
As shown in Fig. 1 a meta-sanction game has trilaminar parts that consist of the part of a public-goods game in which the player strategies are defect and cooperate. In a first-order sanction game the player strategies are punishing defectors and rewarding cooperators. In part of a second-order sanction game the player strategies are punishing free-riders for using first-order sanctions and rewarding first-order sanction performers.
A meta-sanction game can be understood through various types of games that restrict the possible sanctions. For example it has a reward system (System R) that players can use to reward cooperators. Not all of the players necessarily reward others if a game has System R. If the players are not allowed to punish the defectors in a game the game does not have a punishment system (System P).
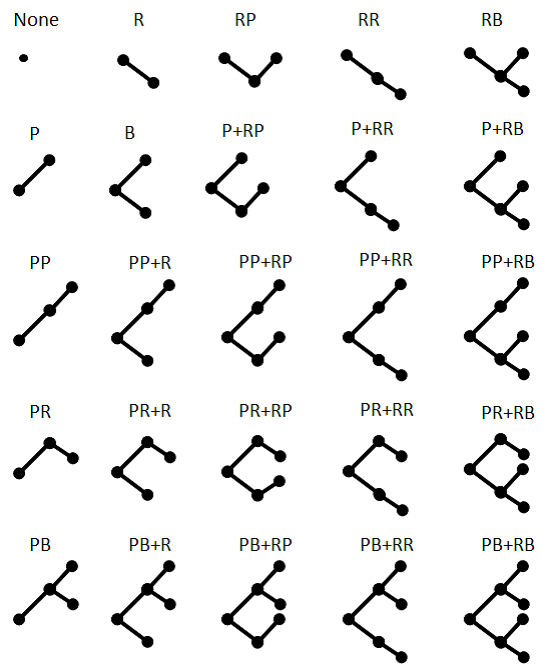
We define all 25 possible configurations of meta-sanction games in Fig. 2. The name of the game type represents the system name of the deepest level of sanctions. System B is defined as a game with both Systems P and R at the same level of sanctions. For example the PB 十 R-type game has Systems P, R, PP and PR.
Unfortunately not all combinations of the six systems in the meta-sanction game are feasible. For example neither System PP nor PR can be included in the game if it does not have System P conversely the game must have System P when it includes System PP or PR.
Groupware Simulation using Meta-sanction Games
In this section we develop and simulate an agent-based groupware model using meta-sanction games to demonstrate the dominant conditions in cooperative regimes.
Simulation Overview
We set a model that consists of N agents as users in a groupware system. The simulation flow proceeded as follows
- Public-goods game phase Each agent plays the public-goods game and either provides beneficial knowledge (cooperation = C) or does nothing (defect = D).
- First-order sanctions phase Each agent decides whether to perform first-order sanctions on the actions of all other agents in the public-goods game phase. When the game has System R each agent has an opportunity to give reward (R) to the cooperators. When the game has System P it also has an opportunity to punish non-cooperators (P).
- Second-order sanctions phase Each agent decides whether to perform second-order sanctions on the actions of all other agents in the first-order sanction phase. If the game has System RR each agent has an opportunity to reward first-order rewarders (RR). If the game has System PR each agent also has an opportunity to reward first-order punishers (PR). Moreover the punishment of non-rewarders (RP) is possible if the game has System RP while the punishment of non-punishers (PP) is possible if the game has System PP.
- Learning phase Each agent evolves his own strategy as explained below.
Each agent repeatedly plays the meta-sanction game and evolves its own strategy to maximize profit in the learning phase. By analyzing our model we clarified what types of game structures are likely to facilitate cooperation.
Agent Model
Parameters of agent strategies
Let ai( i = 1, · · · , N) be the agents in the simulation. All agents have two parameters that describe their strategies. Cooperation rate bi is the probability that an agent posts appropriate content in the groupware and reaction rate ri is the probability that an agent gives a prosocial sanction (reward or punishment) to another user who is randomly chosen. In the public-goods game phase each agent cooperates based on the probability of its behavior rate (the probability of non-cooperation is defined as 1 − bi). In the first-order sanction phase each agent performs its sanction with the probability of its reaction rate (the probability of non-performing is also 1 − ri). In the second-order sanction phase each agent also performs its sanction using the probability of its reaction rate as well as in the first-order phase where the probability of non-performing is 1 − ri. To overcome the higher-order social dilemma we assume a correlation between the first- and second-order sanctions. Kiyonari & Barclay (2008) experimentally established a linkage between them in a one-shot public-goods game. Therefore like Axelrod (1986) we set the parameter value of the first-order sanctions equal to that of the second-order ones.
Agent payoffs
Players pay costs and get benefits as a consequence of the game. Let N0 be the number of cooperators. The payoffs of public-goods game (u i0) are
| $$u_{i0}= \begin{cases} \rho_0 N_0 \kappa_0 & \text{if cooperator,} \\ \rho_0 N_0 & \text{if defector.} \end{cases}$$ | (1) |
In the first- and second-order sanction games each agent aj gives one proper sanction &Tau of possible sanction behaviors { P, R, PP,PR, RP, RR} to every other agent with probability rj. If giving a sanction aj pays the cost for giving it to aj , who receives a fine or a benefit. The payoffs of ai and aj are
| $$u_{i\tau}=\rho_{\tau}$$ | (2) |
| $$u_{j\tau}=\kappa_{\tau}$$ | (3) |
Summing up each agent ais total payoff ui, in every simulation step is calculated as
| $$rho_0 = N_c - \gamma_{i0} \kappa_0 + \sum_{t} \rho_{\tau} N_{\tau} - \sum_{\tau} \gamma_{it} \kappa_{\tau}$$ | (4) |
Evolution process
In our model an agent learning function in the fourth phase is represented using an evolutionary algorithm. Although many evolution algorithms have been tested (Galan & Izquierdo 2005) we employ roulette selection as a selection mechanism because it is one of the most basic selection methods.
Each agent ai has an opportunity to change strategy parameters bi and ri. Agent ai randomly selects two parent agents among the others by roulette selection as in the following algorithm. The probability that ai is randomly chosen by ai is defined as
| $$p_j = \frac{(u_j - u_{min})^2 + \epsilon}{\sum_{\kappa \neq i} (u_k - u_{min} + \epsilon)^2}$$ | (5) |
Installing Intermediate Parameters
According to pioneering work on meta-sanction games (Fujio et al. 2014) cooperation rates depend on the parameters for player costs and benefits. Here we confirm the cooperation rates and the parameters in all game types.
The parameters defined in Section 3.2 are κ0,p0 , κp , κr , κpp , κpr , κrp , κrr , pp , pr , ppp , ppr , prp , and prr . Since we cannot analyze all of them we analyze them using two new intermediate parameters \(\mu\) and \(\delta\). We defined all of the parameters as follows using \(\mu\), \(\delta\)
| $$\kappa_0=1, \rho_0=\mu\kappa_0,$$ | (6) |
| $$\kappa_1=\delta \kappa_0, \rho_1=\mu\kappa_1,$$ | (7) |
| $$\kappa_2=\delta \kappa_1, \rho_2=\mu\kappa_2,$$ | (8) |
Simulation Results and Discussion
Parameter Settings
We ran simulation scenarios by controlling \(\mu\) and \(\delta\) which were respectively changed at 0.1 steps between 0 to 2 and 0 to 1. All of the simulation lengths were 1000 steps and we ran 100 episodes for each scenario. Cooperation rate C R is calculated as the averages of agent cooperation rates bi at the 1000th step to evaluate each scenario. The number of agents is fixed to 20 in all simulations. The initial values of parameters bi, ri of each agent are set to the following by the uniform random distributions of [0 − 1].
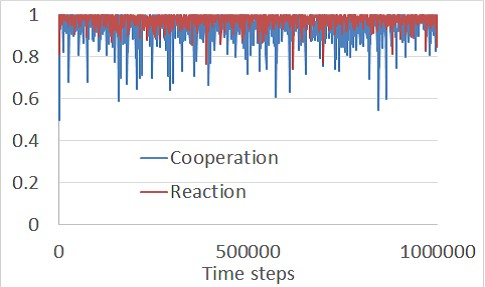
Figure 3 shows the cooperation ratios of the long generations with \((\mu, \delta)=(1.5,0.8)\). After verifying that runs of 1000 steps are satisfactory for the system to reach equilibria we set the simulation steps to 1000.
Influence of Incentive Cost/Effect Ratio and Discount Factor of Costs
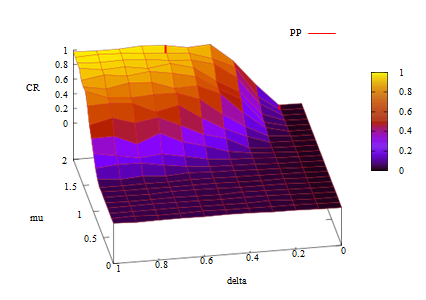
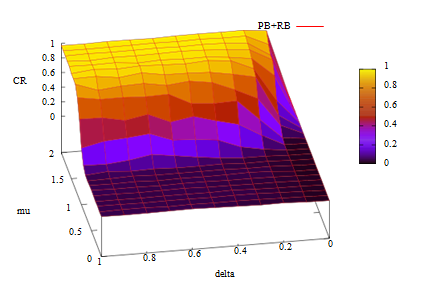
First we confirmed the influence of incentive cost/effect ratio \(\mu\) and discount factor of costs \(\delta\). Figures 4 and 5 show the cooperation rates (CR) with respect to the values of \(\mu\) and \(\delta\) in PP- and PB+ RB-type games. The X- Y- and Z-axes of these figures are \(\mu\), \(\delta\) and CR.
As defined above in PP-type games which have the same structure as Axelrod’s metanorm game (Axelrod 1986) agents are permitted to punish defecting agents as first-order sanctions and non-punishers as second-order sanctions.
The PB+RB-type game in Figure 5 is the most complex system of meta-sanction games. Both figures demonstrate that the cooperation rates basically have positive correlations to \(\mu\) and \(\delta\). Cooperative regimes cannot be dominant if the values of these two intermediate parameters are too small in the framework of meta-sanction games.
Influence of Game Types
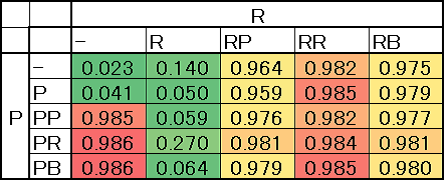
We tested the game types in which cooperators are dominant. Figure 6 shows the maximum values of the cooperation rates in each game type when \(\mu\) and \(\delta\) move in the range described in Section 5.2. For example in P P -type games the maximum cooperation rate is 0.985 which is reached when \(\mu\) = 2.0 and \(\delta\) = 0.7. In R-type games the maximum cooperation rate is 0.140 and thus the game cannot reach cooperative regimes despite the values of \(\mu\) and \(\delta\).
The figure shows that some game types (None, P, R, B, PP+R, PR+R, and PB+R) never facilitate cooperation. We can also derive which second-order sanctions are necessary for facilitating cooperative regimes. The figure also indicates the importance of following the first-order rewards. This is because games with first-order rewards and without second-order sanctions of rewards (e.g. PB+R-type games) cannot become cooperative regimes even though other games can achieve this with the same systems except for the first-order rewards (e.g. PB-type games). These mechanisms are discussed in the following Section.
Robustness of Cooperative Regimes
We confirmed the raobustness of the cooperative regimes using 231 simulation scenarios when \(\mu\) and \(\delta\) change as explained in Section 5.2.
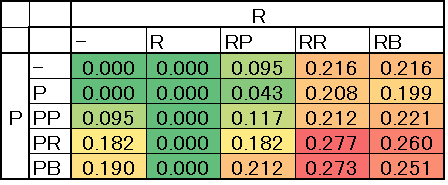
Figure 7 shows the proportion of scenarios that achieve C R > 0.9. The game types with Systems PR and RR are important because their robustness rates for cooperation exceed 25% (Figure 7). In other words these games can reach cooperative regimes even if \(\mu\) and \(\delta\) are relatively small. The figure also shows that the rate of PB-type games is close to that of PR-type games as with the relationship of Systems RB and RR suggesting that Systems PR and RR are critical for robust cooperation.
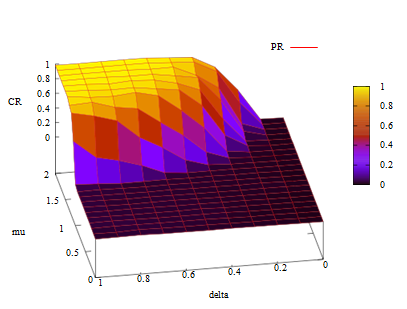
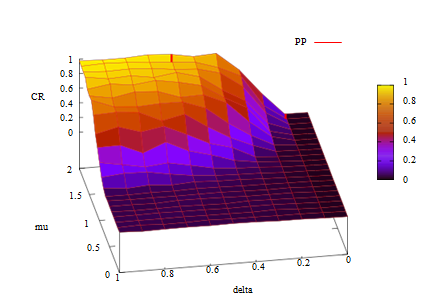
Figures 8 and 9 show a PR-type game which is highly robust for cooperation and a PP-type game which is mildly robust for cooperation. In a PR-type game small \(\mu\) and \(\delta\) values are likely to facilitate cooperation. Cooperative regimes can be achieved at low cost in the game because \(\mu\) denotes the cost/benefit ratios for sanctions. From the figure we find that in P R games cooperation becomes dominant even when \(\mu\) and \(\delta\) are low. Notice that \(\mu\) shows the cost and profit ratio. The ability of a smaller \(\mu\) to facilitate cooperation indicates that in such systems a cooperative society can be formed at relatively smaller cost.
These insights highlight the importance of selecting the sanction system to be employed for groupware management. A system has different \(\mu\) and \(\delta\) thresholds if it can reach cooperative regimes. A groupware designer favors a simple system with low costs. Therefore we evaluate whether an RR system that adopts many actual examples of social media (Toriumi et al. 2012) is relatively suitable from this viewpoint.
Discussion
Disturbance by Reward System
Generally more complex sanction systems promote cooperative regimes. Our results however do not support this expectation which we discuss using PP + R−, PR + R- and PB + R-type games.
In these games even though agents can reward the cooperative behaviors of other users second-order sanctions are not permitted for rewarding behaviors. As shown in Figure 6 cooperation is never dominant under any condition. Surprisingly even though the PP −, PR- and PB-type games are simpler the players in them can reach cooperative behaviors. Furthermore a policy that allows rewards for cooperation but prohibits meta-sanctions for rewards inhibits cooperation.
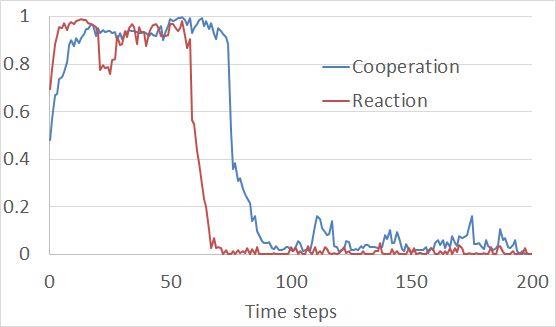
Next we explain our mechanism. Figure 10 shows the relationship of the cooperation and reaction rates in an episode of a PB+R-type game where the parameters are as effective as in Section when \(\mu\) = 2.0 and \(\delta\) = 1.0. In the initial steps the reaction rates rise to 1.0 and the cooperation rates follow them. At the 50th step however they begin to decline and finally reach 0.0 and the cooperation rates follow them. This situation continues to the end of the simulation.
Why does the reaction rate increase at the beginning? This is because in the initial simulation period the cooperation rate is near 0.5 and thus half of the agents are not cooperating in the public-goods game. If an agent with a high reaction rate detects a non-cooperator that non-cooperator must pay punishment cost κP. The game permits second-order sanctions where the agent has a chance to receive reward pPR while an agent with a low reaction rate may be punished and pay pPP. Since agents with high reaction rates have an advantage non-cooperators cannot survive most sanctions and a cooperative regime is established.
In this game however a cooperative regime confers an advantage on agents with low reaction rates because they must reward the other agents with κR costs. Meta-rewards for these rewards are also prohibited and do not increase their (first-order) rewards. Therefore the learning process supports agents with low reaction rates. At that time a mutant occasionally becomes a defector and the agent receives no punishment. Consequently the cooperative regime disappears.
PB+R-type games are less likely to facilitate cooperation PB-type games are more likely to facilitate it. This is because the former games have System R in which agents can reward cooperators and cooperation rates are allowed to decrease. This result is critical because a more complex system does not necessarily improve the cooperative regimes. Accordingly a system designer must carefully choose and construct a sanction system that achieves cooperative and active groupware.
Applying Groupware
According to previous social media analyses (Toriumi et al. 2012; Fujio et al. 2014) RR-type games would be effective in meta-sanction games. Facebook is an appropriate example because it employs first- and second-order reward systems. Providing comments from users to other user posts corresponds to first-order rewards while pushing Like! buttons corresponds to second-order rewards.
Our findings suggest that PR+RR-type games are more likely to facilitate cooperation than RR-type games and thus groupware that adopts the former type is more effective than more complex systems such as PB+RB from the viewpoint of cost/profit ratios. Few groupware approaches have implemented this finding which suggests a new path for groupware designers.
Conclusion
In this paper we demonstrated a model of information behaviors in groupware using a meta-sanction game and an agent-based simulation and also theoretically analyzed the necessary conditions for facilitating cooperative and active behaviors. Our simulation shows that some game types promote cooperative regimes and that second-order sanctions are not a sufficient condition for cooperation. For example a PB-type game[5] can reach cooperative regimes and be activated prosocially because groupware users have opportunities to give first-order punishments to other users inappropriate behaviors (providing inadequate knowledge or free-riding) meta-punishments for shirking first-order punishments and meta-rewards for performing first-order punishments. However a PB+R-type game cannot reach cooperative regimes in which participants in a groupware have opportunities for first-order punishments, meta-punishments meta-rewards as well as PB-type games and first-order rewards for the appropriate behaviors of other users. This result suggests that groupware designers must design their systems carefully.
In future extensions we must relax the parameter restrictions. In this paper for simplicity we adopted two intermediate parameters to analyze all of the configurations of a meta-sanction game. We might sensitively analyze the conditions for cooperative regimes by assigning degrees of freedom to the parameters.
The present version of our model does not consider antisocial punishment or retaliation. However several experimental studies (Herrmann et al. 2008; Rand & Nowak 2011) have shown that such behaviors are commonly observed in real public-goods games. Although our model can be extended to capture these behaviors as punishing cooperators or (meta-) punishing punishers an analysis of this factor remains a future work.
Notes
- Yammer is a freemium enterprise-type social networking service for private communication within organizations: https//www.yammer.com/
- Slack is a cloud-based team collaboration tool: https://slack.com/.
- This game is extended to the original version of the previously proposed metanorm game (Axelrod 1986).
- In this case the question corresponds to cooperation in public-goods game C and the answer is first-order reward R.
- A meta-sanction game allows punishments for cooperation rewards for performing punishments and meta-punishments for non-punishments.
References
ARENAS, A. Camacho J. Cuesta J. A. & Requejo R. J. (2011). The joker effect cooperation driven by destructive agents. Journal of Theoretical Biology, 279(1), 113-119. [doi:10.1016/j.jtbi.2011.03.017]
AXELROD, R. (1986). An Evolutionary Approach to Norms. American Political Science Review, 80(4), 1095-1111. [doi:10.1017/S0003055400185016]
BALLIET, D. Mulder L. B. & Van Lange P. A. (2011). Reward punishment and cooperation a meta-analysis. Psychological Bulletin, 137(4), 594. [doi:10.1037/a0023489]
CABRERA, A. & Cabrera E. F. (2002). Knowledge-sharing dilemmas. Organization studies, 23(5) 687-710. [doi:10.1177/0170840602235001]
CROSS, R., Borgatti, S. P., & Parker, A. (2012). Making Invisible Work Visible: Using Social Network Analysis to Support Strategic Collaboration. California Management Review, 444(2), 25 46.
FEHR, E. Fischbacher U. & Gächter S. (2002). Strong reciprocity human cooperation and the enforcement of social norms. Human nature, 13(1) 1-25. [doi:10.1007/s12110-002-1012-7]
FERREIRA, A. & Du Plessis T. (2009). Effect of online social networking on employee productivity. South African Journal of Management, 11(1), 1-16. [doi:10.4102/sajim.v11i1.397]
FUJIO T. Hitoshi Y. & Isamu O. (2014). Influence of payoff in meta-rewards game. Computational Intelligence and Intelligent Informatics, 18(4), 616-623. [doi:10.20965/jaciii.2014.p0616]
FULK, J. Flanagin A. J. Kalman M. E. Monge P. R. & Ryan T. (1996). Connective and communal public goods in interactive communication systems. Communication Theory, 6(1) 60-87. [doi:10.1111/j.1468-2885.1996.tb00120.x]
FULK, J. Heino R. Flanagin A. J. Monge P. R. & Bar F. (2004). A test of the individual action model for organizational information commons. Organization Science, 15(5), 569-585. [doi:10.1287/orsc.1040.0081]
GALAN, J. M. & Izquierdo L. R. (2005). Appearances can be deceiving: Lessons learned re-implementing Axelrod’s evolutionary approach to norms. Journal of Artificial Societies and Social Simulation, 8(3) 2: https://www.jasss.org/8/3/2.html.
GIBBS, J. L. Rozaidi N. A. & Eisenberg J. (2013). Overcoming the “Ideology of Openness” Probing the Affordances of Social Media for Organizational Knowledge Sharing. Journal of Computer-Mediated Communication, 19(1), 102-120. [doi:10.1111/jcc4.12034]
HAUERT, C. De Monte S. Hofbauer J. & Sigmund K. (2002). Replicator dynamics for optional public good games. Journal of Theoretical Biology, 218(2), 187-194. [doi:10.1006/jtbi.2002.3067]
HELBING, D. Szolnoki A. Perc M. & Szabó G. (2010). Evolutionary establishment of moral and double moral standards through spatial interactions. PLoS computational biology , 6(4), e1000758. [doi:10.1371/journal.pcbi.1000758]
HERRMANN, B. Thöni C. & Gächter S. (2008). Antisocial punishment across societies. Science, 319(5868), 1362-1367. [doi:10.1126/science.1153808]
HIRAHARA, Y. Toriumi F. & Sugawara T. (2014). Evolution of cooperation in SNS-norms game on complex networks and real social networks. Social Informatics , 112-120. [doi:10.1007/978-3-319-13734-6_8]
KIYONARI, T. & Barclay P. (2008). Cooperation in social dilemmas free riding may be thwarted by second-order reward rather than by punishment. Journal of Personality and Social Psychology, 95(4), 826. [doi:10.1037/a0011381]
LEONARDI, P. M. Huysman M. & Steinfield C. (2013). Enterprise Social Media Definition History and Prospects for the Study of Social Technologies in Organizations. Journal of Computer-Mediated Communication, 19(1), 1-19. [doi:10.1111/jcc4.12029]
MAJCHRZAK, A. Faraj S. Kane G. C. & Azad B. (2013). The Contradictory Influence of Social Media Affordances on Online Communal Knowledge Sharing. Journal of Computer-Mediated Communication, 9(1), 38–55. [doi:10.1111/jcc4.12030]
NAKAMARU M. & Iwasa Y. (2005). The evolution of altruism by costly punishment in lattice-structured populations score-dependent viability versus score-dependent fertility. Evolutionary ecology research, 7(6), 853-870.
NETO R. C. D. d. A. & Choo C. W. (2011). Expanding the concept of Ba managing enabling contexts in knowledge organizations. Perspect. ciênc. inf., 16(3), 2-25.
NOWAK, M. A. (2012). Evolving cooperation. Journal of Theoretical Biology, 299(0), 1-8. [doi:10.1016/j.jtbi.2012.01.014]
NOWAK, M. A. & Sigmund K. (2005). Evolution of indirect reciprocity. Nature, 437(7063), 1291-1298. [doi:10.1038/nature04131]
OHTSUKI H. & Iwasa Y. (2007). Global analyses of evolutionary dynamics and exhaustive search for social norms that maintain cooperation by reputation. Journal of Theoretical Biology , 244(3), 518-531. [doi:10.1016/j.jtbi.2006.08.018]
RAND, D. G. Dreber A. Ellingsen T. Fudenberg D. & Nowak M. A. (2009). Positive interactions promote public cooperation. Science, 325(5945), 1272-1275. [doi:10.1126/science.1177418]
RAND, D. G. & Nowak M. A. (2011). The evolution of antisocial punishment in optional public goods games. Nature Communications, 2, 434. [doi:10.1038/ncomms1442]
RIOLO, R. L. Cohen M. D. & Axelrod R. (2001). Evolution of cooperation without reciprocity. Nature, 414(6862), 441-443. [doi:10.1038/35106555]
SASAKI T. Okada I. & Unemi T. (2007). Probabilistic participation in public goods games. Proceedings of the Royal Society B Biological Sciences, 274(1625), 2639-2642. [doi:10.1098/rspb.2007.0673]
THOM J. Helsley S. Y. Matthews T. L. Daly E. M. & Millen D. R. (2011). What Are You Working On ? Status Message Q & A in an Enterprise SNS. In Proceedings of the 12th European Conference on Computer Supported Cooperative Work (pp. 313-332).
TORIUMI, F. Yamamoto H. & Okada I. (2012). Why do people use social media? Agent-based simulation and population dynamics analysis of the evolution of cooperation in social media. In Proceedings of the The 2012 IEEE/WIC/ACM International Joint Conferences on Web Intelligence and Intelligent Agent Technology , Volume 02, 43-50. [doi:10.1109/WI-IAT.2012.191]
WANG Y. & Kobsa A. (2009). Privacy in Online Social Networking at Workplace. 2009 International Conference on Computational Science and Engineering, 6, 975-978. [doi:10.1109/CSE.2009.438]
YAMAMOTO S. & Kanbe M. (2008). Knowledge Creation by Enterprise SNS. The international journal of knowledge culture and change management, 8(1), 255-264.

