Introduction
The bounded-confidence model (Hegselmann & Krause 2002; Deffuant et al. 2000) is one of the success stories of formal modeling work in the social sciences. It is build on very few, simple assumptions about individual behavior but generates complex and surprising dynamics and clustering patterns. This is certainly the main reason why it has attracted impressive scholarly attention in fields as diverse as sociology, physics, computer science, philosophy, economics, communication science, and political science.
The bounded-confidence model proposes a prominent solution to one of the most persistent research puzzles of the social sciences, Abelson’s diversity puzzle (Abelson 1964)[1]. Building on Harary (1959), Abelson studied social-influence dynamics in networks where connected nodes exert influence on each others’ opinions in that they grow more similar through repeated averaging. He analytically proved that social influence will always generate perfect consensus unless the network consists of multiple unconnected subsets with zero influence between them. This result was later extended to a theory of rational consensus in science and society (DeGroot 1974; Lehrer & Wagner 1981). Stunned by his finding, Abelson formulated an intriguing research puzzle: “Since universal ultimate agreement is an ubiquitous outcome of a very broad class of mathematical models, we are naturally led to inquire what on earth one must assume in order to generate the bimodal outcome of community cleavage studies.” Abelson’s puzzle is challenging, because consensus is a very robust pattern. For instance, Abelson (1964) showed that consensus is inevitable even when one also includes the assumption that social influence between actors is weaker when they hold very discrepant opinions prior to the interaction, an assumption that was supported by laboratory studies (Fisher & Lubin 1958; Aronson et al. 1963)[2].
Panel (a) of Figure 1 illustrates the inevitable trend towards perfect uniformity that social influence generates in a fixed network with 100 agents. For this ideal-typical simulation run, we assumed that agents’ initial opinions are randomly drawn from a uniform distribution ranging from zero to one. Agents with an initial opinion distance of less 0.15 were connected by a fixed network link. In each time step, agents update their opinions, adopting the arithmetic mean of their own opinion and the opinions of their network contacts. The figure shows that opinions converge to consensus despite the high initial opinion diversity and the relatively sparse influence network. Clustering of opinions can only be observed transiently.
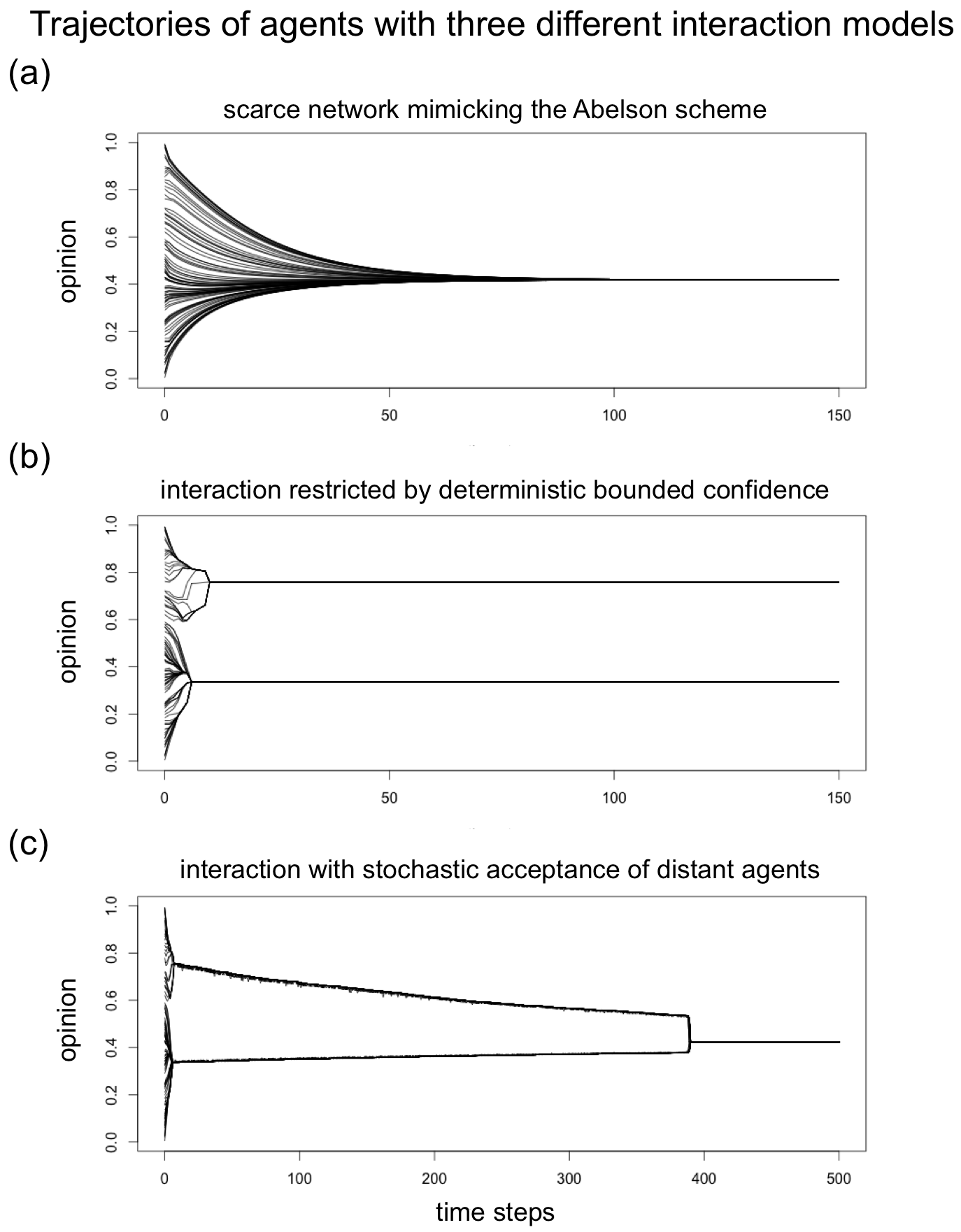
The solution to Abelson’s puzzle proposed by the bounded-confidence model is strikingly simple, because it sharpens just one of Abelson’s own modelling assumptions: The influence of the opinions of others on the individual is not only declining with opinion discrepancy[3] but individuals ignore influence by actors when opinion discrepancy exceeds a threshold – the bound of confidence. Panel (b) of Figure 1 shows opinion dynamics of the bounded confidence model of Hegselmann & Krause (2002) with initial conditions identical to the one from Panel (a). The crucial difference between the two simulation runs is that the influence network in Panel (b) is not fixed. New ties are created when two agents’ opinion distance has decreased to a value below the bounded-confidence threshold of \(\epsilon\) = 0.15, and ties are dissolved whenever opinion differences exceed 0.15. Panel (b) illustrates that the bounded-confidence models predicts the emergence of increasingly homogenous clusters, which at some point in time adopt opinions that differ too much from each other. As a consequence, opinions cannot converge further and clusters remain stable.
Other approaches to Abelson’s puzzle included assumptions about negative social influence (Macy et al. 2003; Mark 2003; Salzarulo 2006; Flache & Mäs 2008), the communication of persuasive arguments (Mäs et al. 2013; Mäs & Flache 2013), biased assimilation (Dandekar et al. 2013), information accumulation (Shin & Lorenz 2010), striving for uniqueness (Mäs et al. 2010), attraction by initial views (Friedkin 2015), influences by external forces such as media and opinion leaders (Watts & Dodds 2007) and the assumption that opinions are measured on nominal scales (Axelrod 1997; Liggett 2013). However, none of these approaches has attracted as much scholarly attention as the bounded confidence model.
The bounded-confidence assumption has also been subject to important criticism (Mäs et al. 2013; Mäs & Flache 2013). To be sure, the assumption that individuals tend to be influenced by similar others is certainly very plausible in many social settings and has been supported by sociological research on homophily (McPherson et al. 2001; Lazarsfeld & Merton 1954) and social-psychological studies in the Similarity-Attraction-Paradigm (Byrne 1971). However, bounded-confidence models assume that individuals always ignore opinions that differ from their own views, which is an extreme and unrealistic interpretation. In other words, it is certainly plausible that individuals’ confidence in others is bounded but it is certainly not plausible that individuals are never influenced by actors with very different opinions[4].
In fact, even a tiny relaxation of the bounded-confidence assumption fundamentally changes model predictions, as Panel (c) of Figure 1 illustrates. These dynamics were generated with a model identical to the model of Panel (b) but with a slightly relaxed bounded-confidence assumption. We included that with a tiny probability of 0.001 also agents with otherwise too big opinion differences (difference exceeds 0.15) take each others’ opinions into account when they update their views. Panel (c) shows that this seemingly innocent relaxation of the bounded-confidence assumption results in the emergence of opinion consensus and, thus, suggests that the bounded-confidence assumption might not be a satisfactory solution to Abelson’s puzzle.
Even though we emphasize this criticism of bounded-confidence models, we show here that the model’s ability to solve Abelson’s puzzle can be regained if another model assumption is relaxed. In particular, we relax the common assumption of social-influence models that actors’ opinions are only affected by social influence. Inspired by modelling work published in the field of statistical mechanics (Pineda et al. 2009, 2013; Carro et al. 2013), we include the assumption that an agent’s opinion might sometimes happen to switch to another, new opinion not as a result of social influence but at random. These random opinion changes might reflect, for instance, influences on agents’ opinions from external sources, or turnover dynamics in an organization where employees leave the organization and are replaced by new workers who hold opinions that are unrelated to the opinion of the leaving person. We study the conditions under which this mechanism leads to the emergence and persistence of opinion diversity and opinion clustering even when the bounded-confidence assumption is implemented in a weaker fashion as in its original strict way but accompanyied by random opinion replacement.
The model
We adopt an agent-based modeling framework and assume that each agent i of N agents is described by a continuous opinion xi (t) ranging from 0 to 1. At every time step t agents’ opinions are updated in two ways. First, agents are socially influenced by the opinions of others, as assumed by classical social-influence models and the bounded-confidence models. Second, we included that agents’ opinions may also change due to other forces. To this end, we added that agents can adopt a random opinion as studied in models inspired by statistical mechanics (Pineda et al. 2009, 2013; Carro et al. 2013) .
Social influence is implemented as follows. First, the computer program identifies those agents who will exert influence on i’s opinion. To this end, the program first calculates what Fishbein & Ajzen (1975) called the probability of acceptance, i.e. the probability that an agent j is influential, using Equation 1. Next, agent i updates her opinion, adapting to the average of the opinions of the influential agents and i’s own opinion.
Following psychological literature on opinion and attitude change (Abelson 1964; Fishbein & Ajzen 1975; Hunter et al. 1984, e.g.), we define opinion discrepancy between agents i and j as the distance in opinion D(i, j) = |xi(t) - xj(t)| and assume that the probability that i is influenced by j declines with opinion discrepancy. To that end, we define the probability of acceptance for i and j as
| $$ P(i,j) = \begin{cases} \max\{\beta, \displaystyle{\left(1 - \frac{D(i,j)}{\varepsilon}\right)^{1/f}}\} & \text{if } D(i,j) \leq \varepsilon,\\ \\ \beta & \text{otherwise,} \end{cases} $$ | (1) |
The update of the opinion of agent i is modelled as follows
| $$x_{i}(t+1) = \frac{1}{n}\sum_{j'}x_{j'}(t)$$ | (2) |
For \(\varepsilon\) = 1 and \( \beta\) = 0, the definition of P is identical to the definition in the seminal model in social psychology of Fishbein & Ajzen (1975) from which also the concept “probability of acceptance” is adopted.
The second model ingredient are random opinion replacements. We implemented that agents adopt a randomly picked opinion with probability m. The new opinion is a random value in the range of [0,1] and is drawn from a uniform distribution (Pineda et al. 2009, 2013; Carro et al. 2013). The rate of random opinion influx is given by \(m\cdot N\) per N time steps. This means that \(m\cdot N\) independent opinion renewals would occur on average during N interdependent opinion renewals, hence m gives the ratio, or relative importance, of independent opinion replacement.
In a nutshell, the simulation program proceeds as follows. In the iteration from time step t to t + 1, the program decides for each individual agent i whether each of the other agents exerts influence on i by random events with respect to the probability of acceptance. Next, the program computes the updated opinion of agent i at time step t + 1 as the average of all those agents that have been selected to exert influence. Next, the program decides through a random event with respect to the probability of random opinion replacements whether this updated opinion is replaced by a completely new, randomly drawn opinion. The order in which agents are updated does not matter in this process, because we always use the opinions from time step t to compute the opinion for time step t + 1 (synchronous updating).
In the following we assumed one thousand randomly distributed agents along the entire opinion axis for the initial state (N = 1000). Effects of di erent initial conditions (i.e., hysteresis problems) are not discussed here.
Results
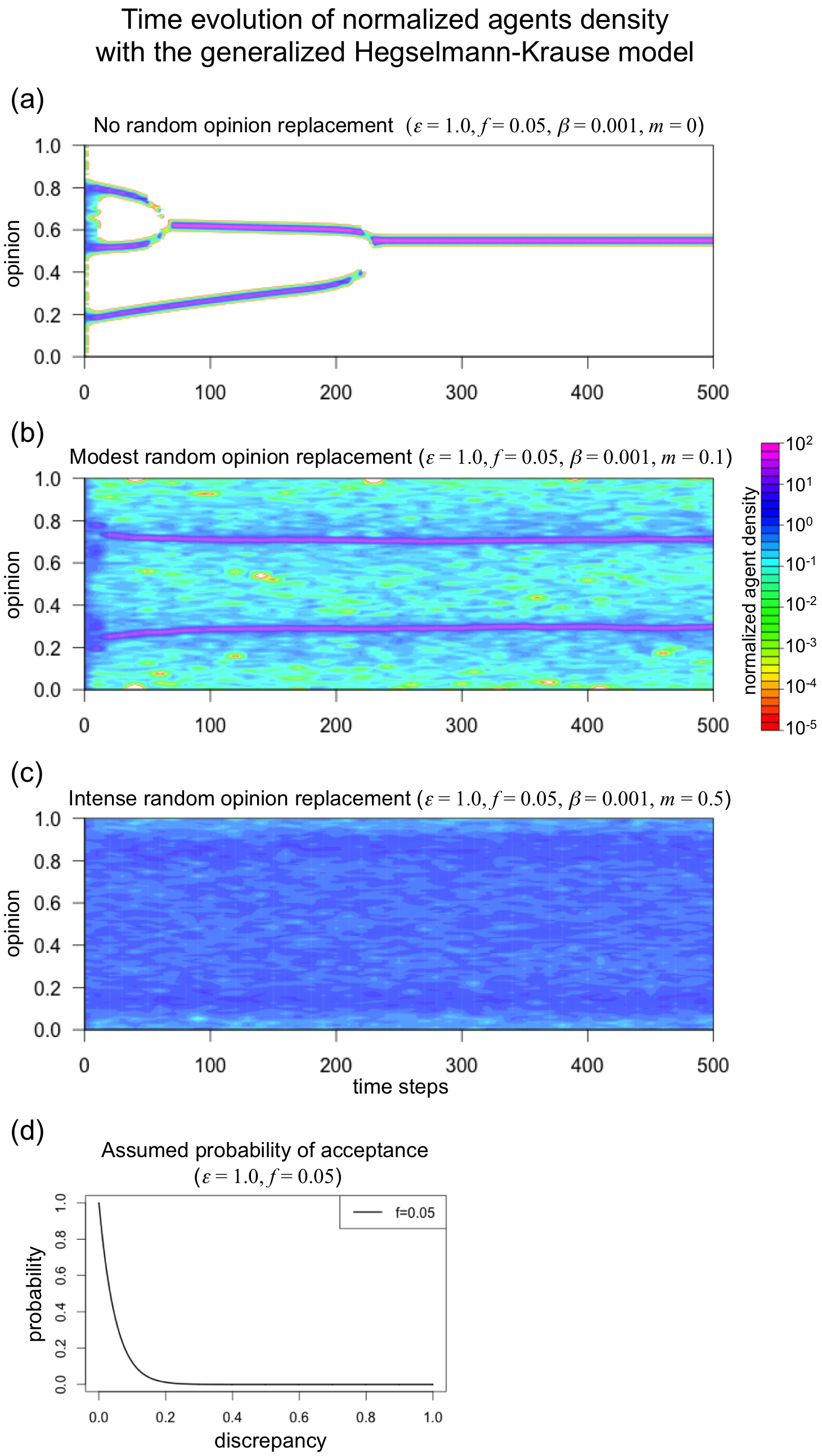
Figure 2 shows three ideal-typical opinion dynamics to illustrate the effects of random opinion changes on opinion dynamics. In the figures, the agent distribution is shown as the probability density, which is estimated by the kernel density estimation with the bandwidth of 0.005. For all three simulation runs, we assigned positive values to parameters \(\beta\) and f, implementing that there is always a small but positive probability that an agent j exerts influence on i’s opinion. When agents’ opinions only depend on social influence and there are no random opinion changes (m = 0), then this parameter setting implies that dynamics will always generate opinion consensus. Panel (a) of Figure 2 shows that social influence leads to the formation of clusters. However, as there is always a positive chance that members of distinct clusters exert influence on each other, clusters merge and the population reaches a perfect opinion consensus.
Panel (b) of Figure 2, in contrast, shows that including random opinion replacements (m = 0.1) leads to a very different outcome. Like in the dynamics shown in Panel (a), social influence leads to the formation of clusters of agents with similar opinions. However, these clusters remain stable. This result is obtained even though there is always a positive probability of acceptance and even though the opinion replacements are entirely random.
The intuition is simple. Social influence leads to the formation of clusters, but due to the random opinion replacements, clusters also loose members from time to time. These agents will first adopt a random opinion but will sooner or later join one of the clusters. Thus, all clusters have an input and an output of agents and remain stable when in and output are balanced. To be sure, it is possible that a cluster happens to disappear in this dynamic. However, randomness in tandem with social influence will lead to the formation of a new cluster (Pineda et al. 2009, 2013; Carro et al. 2013) and the collective pattern of opinion clustering will reemerge.
Panel (c) of Figure 2 shows that clusters disappear, however, when random opinion replacements happen too frequently. For this run, we imposed that opinions adopt random values with a probability of 0.5. Under this condition, social influence is too weak to generate stable clustering.
Figures 3 and 4 extend the observations from the three ideal-typical runs to broader parameter spaces, using opinion pattern diagrams[6] to visualize aggregated agent-distributions for quasi-steady states (except for the Panel (a) of Figure 4, as we discuss below) in twenty independent simulation runs per parameter combination. The number of simulation events (Tmax) required for the quasi-steady states greatly depends on parameter settings, hence we adjusted Tmax for each Panel empirically to save computation time.
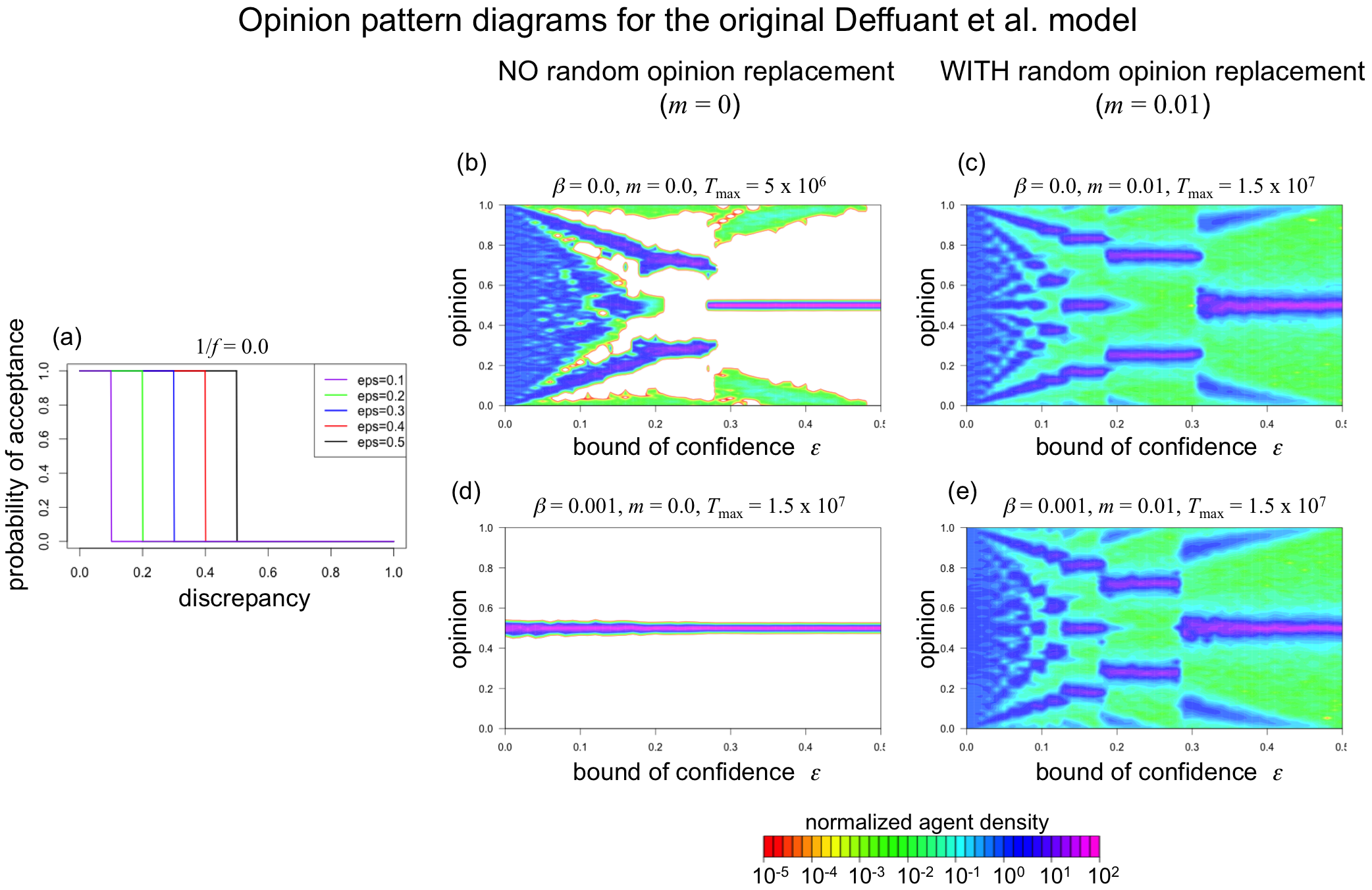
Figure 3 focuses on the original implementation of confidence bounds, where the probability of acceptance is either zero or one (see Panel (a)). Panel (b), thus, replicates the findings from earlier studies with the original bounded-confidence model (Lorenz 2007), showing that the bounded-confidence model can explain the emergence and stability of opinion clustering when agents’ confidence is sufficiently bounded. When \(\varepsilon\) exceeds a value of 0.23, agents arrive at consensus, forming one big cluster close to the center of the opinion space. However, agents form multiple clusters, when they have narrower bounds of confidence (\(\varepsilon\) < 0.23). These clusters are stable because the probability that an agent is influenced by an agent from another cluster is zero. The number of clusters forming is roughly \(1/(2\varepsilon)\) (e.g., Deffuant et al. 2000; Ben-Naim et al. 2003). Note that Panel (b) fails to visualize the emergent clustering for very small values of \(\varepsilon\), as the model generates a large number of opinion clusters with only small (but stable) opinion differences between clusters. When \(\varepsilon\) = 0.05, for instance, dynamics typically settle when about eight distinct clusters have formed. Random differences in the initial opinion distributions of the twenty realizations per parameter combination, however, lead to small differences in the exact positions of the clusters between simulation runs. As a consequence, the differences between clusters are not visible in the aggregated opinion distributions shown in Panel (b) of Figure 3.
The predictions of the standard bounded-confidence model are robust to including random opinion replacements (m = 0.1), as Panel (c) of Figure 3 shows. When agents sometimes happen to adopt a random opinion (drawn from a uniform distribution), clustering can be stable when the bounds of confidence are sufficiently small.
However, the ability of the bounded-confidence model to generate stable clustering breaks down when one slightly relaxes the bounded-confidence assumption in that one allows also agents with otherwise to divergent opinions to exert influence on each other with a small probability of \(\beta\) = 0.001. Demonstrating this, Panel (d) of Figure 3 shows that the initial opinion diversity decreases and the agent populations arrive at a consensus, even when agents have very narrow bounds of confidence.
Strikingly, the ability of the bounded-confidence model to explain clustering is regained when both forms of randomness are included (see Panel (e) of Figure 3). That is, when agents sometimes adopt random opinion values (\(\beta\) = 0.001) and when random violations of the bounded-confidence assumption are included (m = 0.1), opinion clustering remains stable when agents’ confidence in others is sufficiently bounded.
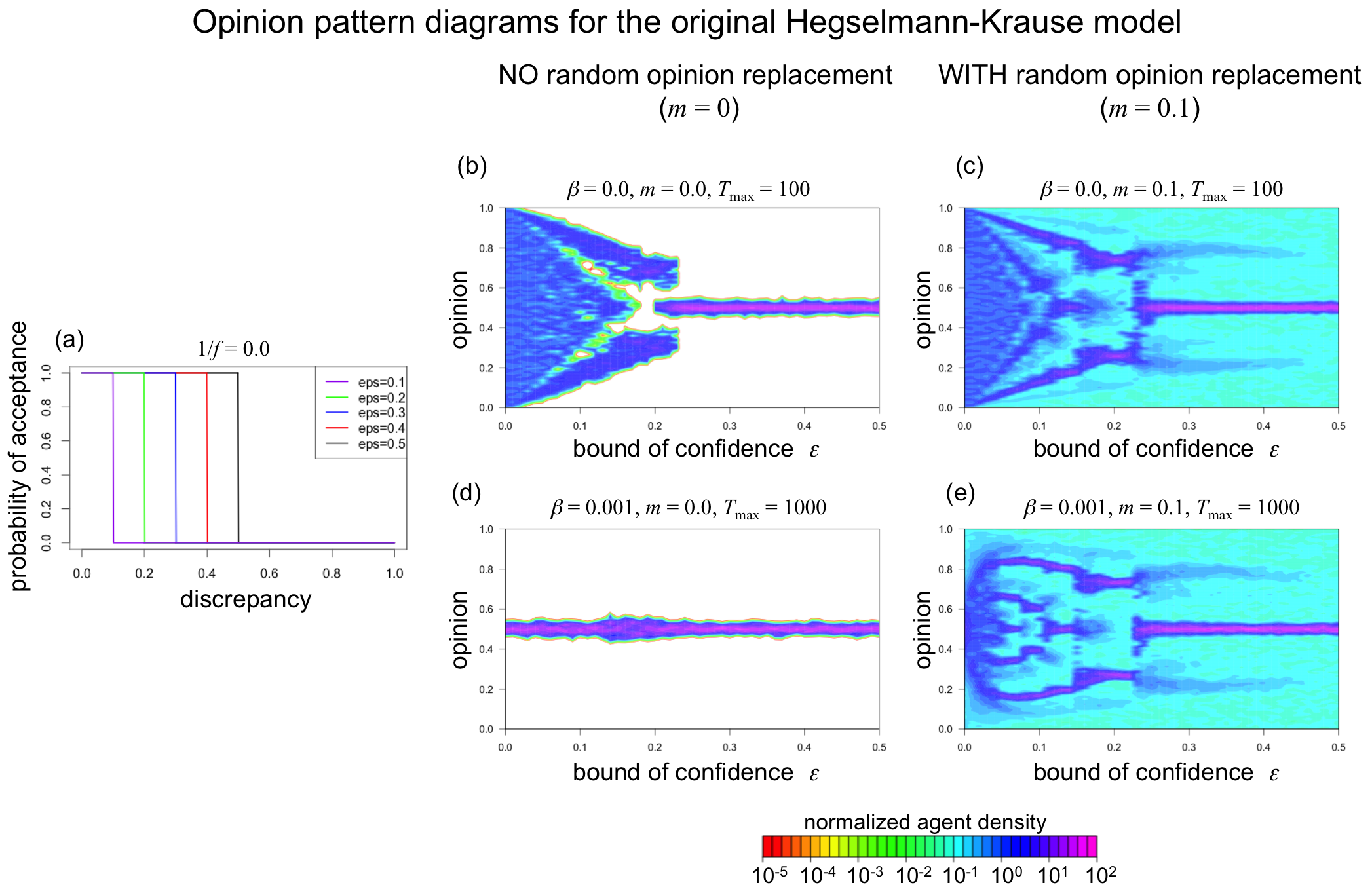
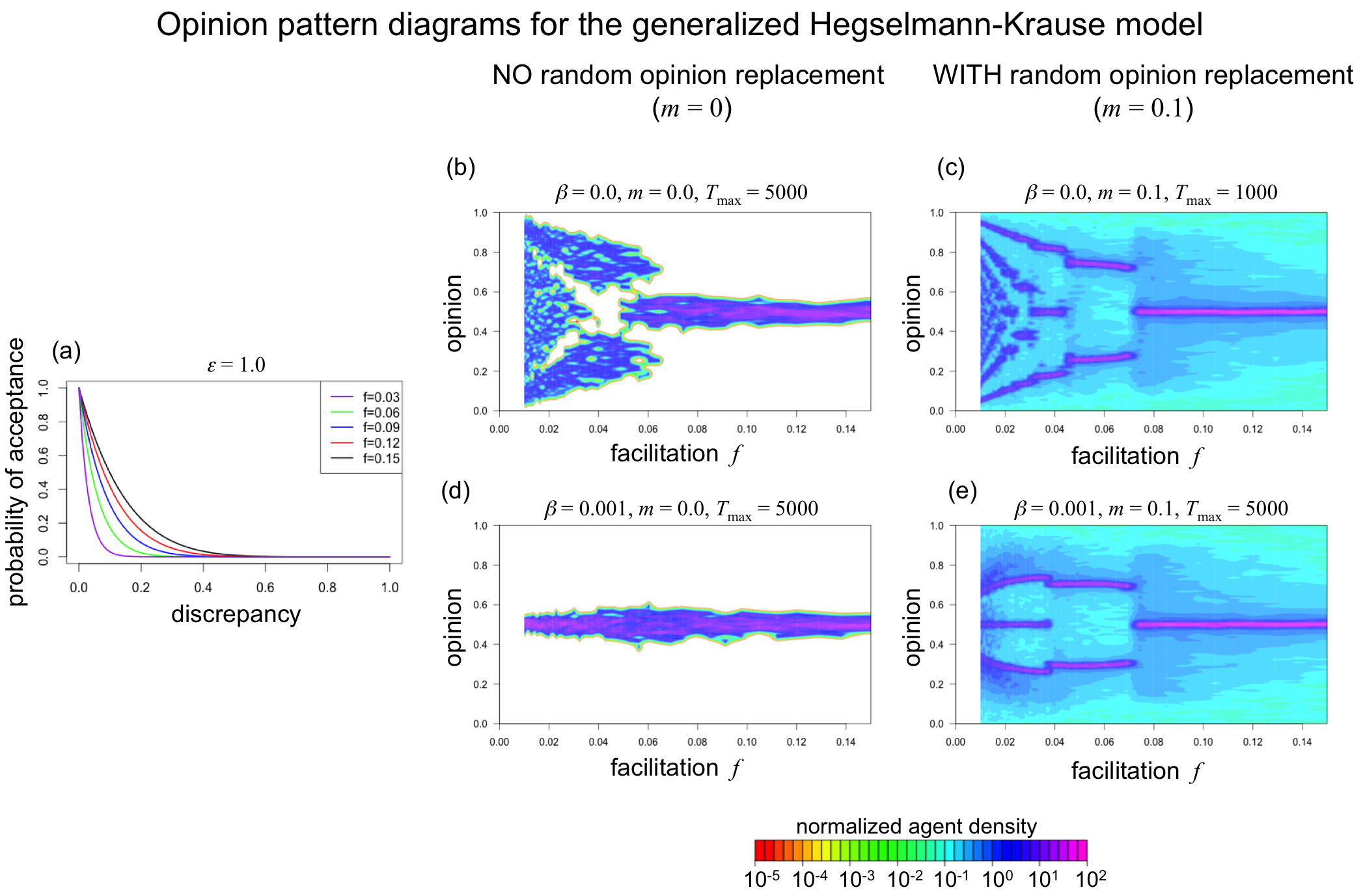
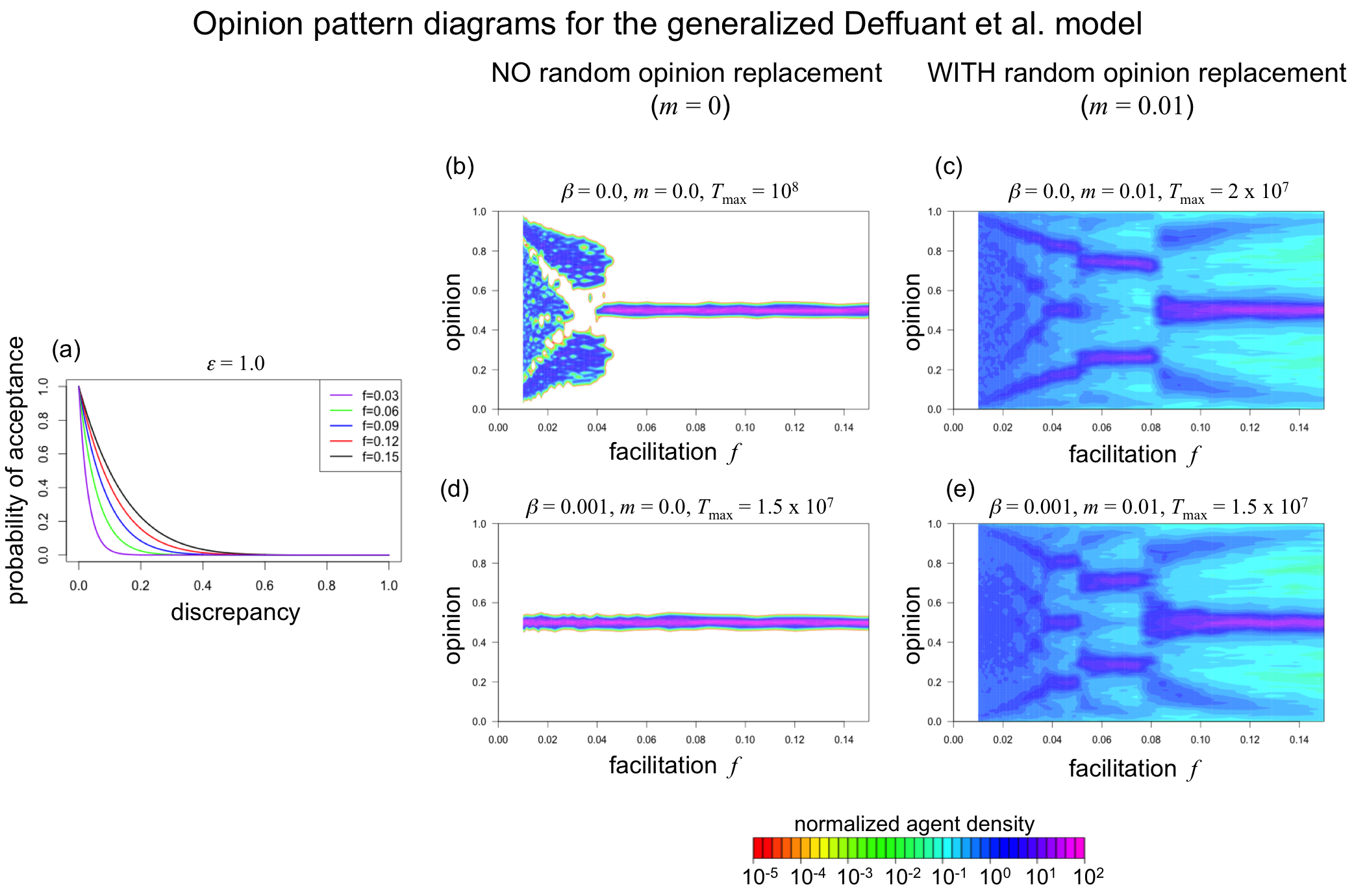
Figure 4 shows the same analyses as Figure 3 but focuses on the less restrictive interpretation of the bounded-confidence assumption, where the probability of acceptance is not modelled as a step function. To generate these figures, we assumed that \(\varepsilon\) = 1 and varied parameter f (see Panel (a)). Accordingly, the x-axis represents parameter f rather then \(\varepsilon\).
Panel (b) of Figure 4 focuses on the condition without random opinion changes (m = 0) and without random deviations from the bounded-confidence rule (\(\beta\) = 0). It is important to understand that the opinion variance shown in the left part of Panel (b) is an artifact of our decision to run simulations for “only” 5000 simulation events and of floating point precision close to zero. Even under small facilitation values the probability of acceptance is always positive, which implies that populations will always reach a consensus, because every possible interaction will continue to occur ad infinitum although quite rarely. However, small f values lead to probabilities of acceptance that are so small that agents with distant opinions hardly influence each other or are even represented by zero due to floating point imprecision. As a consequence, consensus is not reached with in the limit of 5000 simulation events and will perhaps not even do without technical modifications dealing with floating point precision.
In order to test whether our intuition that the model generates consensus also for small facilitation values, we ran twenty additional simulations with f = 0.05 and without a predefined simulation end (m = 0, \(\beta\) = 0). Supporting our intuition, we observed that all twenty populations generated a consensus. On average, it took systems approximately 30,000 iterations to decrease the value range of opinions to less then 10-10.
Panel (d) of Figure 4 is based on the same parameter conditions as Panel (b) but adds a small default acceptance probability of \(\beta\) = 0.001, which excludes the artifact observed in Panel (b). Accordingly, Panel (d) shows that all simulation runs generated consensus, independent of the degree f of facilitation. This shows again that the bounded-confidence model fails to generate opinion clustering when the bounded-confidence assumption is implemented in a less restrictive way than in the original contributions.
However, system behaviour differs very much when random opinion replacements are included (m = 0.1), as Panels (c) and (e) of Figure 4 show. In particular, Panel (e) shows that the model generates phases of opinion clustering even though there is always a positive probability of acceptance and even though independent opinion changes are added.
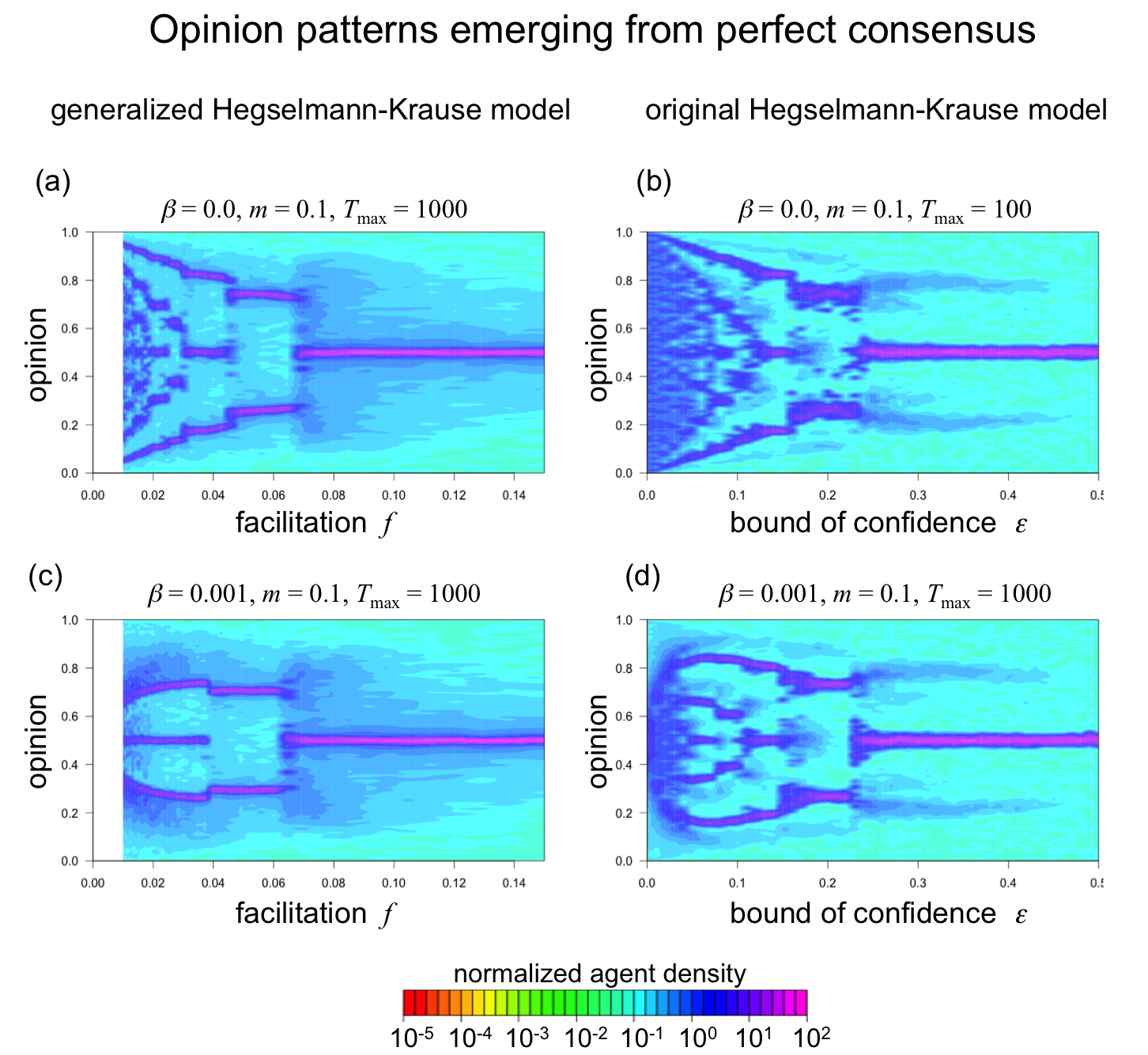
In order to demonstrate that the opinion clustering observed in the simulation runs with random opinion replacements (Panels (c) and (e) of Figure 4) is not an artifact of a limited duration of the simulations and/or floating point issues, we reran the simulation experiment for these experimental treatments assuming that all agents held the same opinion at the outset of the dynamics (xi (0) = 0.5 for all i). In Appendix B we show that the resulting opinion pattern diagrams are virtually identical to those generated in the main simulation exper-iment where simulations departed from a uniform opinion distribution. This shows that the opinion diversity shown in Panels (c) and (e) of Figure 4 also emerges when dynamics start from perfect consensus, showing that these results are not artifacts.
So far, we focused on the bounded-confidence model developed by Hegselmann & Krause (2002) which assumes that agents consider the opinions of multiple sources when they update their opinions. The alternative bounded-confidence model by Deffuant et al. (2000), in contrast, assumed that influence is dyadic in the sense that agents always consider only the opinion of one other agent for opinion update. We focused our analyses on the Hegselmann-Krause model mainly because it is more similar to the original work of Abelson (1964). We demonstrated in Appendix , however, that our conclusions also hold under the dyadic influence regime proposed by Deffuant et al. (2000).
We provide a NetLogo implementation of our model which allows readers to produce trajectories of all model variations presented here (Lorenz et al. 2016) . The reader can use it to observe and explore our claims on the basis of independent simulation runs. The model also includes “example buttons”, which set the model parameters to the values studied in our examples.
Summary and conclusions
Bounded-confidence models proposed the most prominent solution to Abelson’s puzzle of explaining opinion clustering in connected networks where nodes exert positive influence on each other. However, the models have been criticized for being able to generate opinion clustering only when the assumption that agents’ confidence in others is bound is being interpreted in a maximally strict sense. When one allows agents to sometimes deviate from the bounded-confidence assumption, clustering breaks down even when these deviations are rare and random.
Even though we echoed the criticism that the predictions of the original bounded-confidence models are not robust to random deviations, we showed the models’ ability to explain clustering can be regained if another typical assumption of social-influence models is relaxed. Building on modeling advances from the field of statistical mechanics (Pineda et al. 2009, 2013; Carro et al. 2013), we showed that a bounded-confidence model that takes into account random deviations from the bounded-confidence assumption is able to explain opinion clustering when one includes that agents’ opinion are not only affected by influence from other agents. If, in addition, opinions can change in a random fashion, clustering can emerge and remain stable. Thus, our results demonstrate that the bounded-confidence model does provide an important answer to Abelson’s puzzle, despite the criticism.
Our findings illustrate that in complex systems seemingly innocent events can have profound effects, even when these events are rare and random. One important way to deal with the problem is to base models on empirically validated assumptions. With regard to the bounded-confidence model, however, too little is known about how bounded individuals’ confidence actually is. How is this boundedness distributed in our societies and under what conditions can bounds shift and increase or decrease openness to distant opinions? Under which conditions do individuals deviate from the bounded-confidence assumption? Are these deviations random or do they follow certain patterns? Our finding that deviations have a decisive effect on the predictions of bounded-confidence models shows that empirical answers to these questions are urgently needed.
What is more, empirical research is needed to inform models about how to formally incorporate deviations from model assumptions. For instance, we adopted from earlier modeling work (Pineda et al. 2009, 2013; Carro et al. 2013) the assumption that agents sometimes adopt a random opinion and that this random opinion is drawn from a uniform distribution. This is certainly a plausible model of turnover dynamics, where individuals may happen to leave a social group or organization, making space for a replacement with an independent opinion. However, this model of deviations appears to be a less plausible representation of other influences, such as social influences from outside the modelled population or the empirically well documented striving for unique opinions (Mäs et al. 2010). For instance, deviations have also been modelled as “white noise”. That is, rather than assigning a new, random value to the agent’s opinion, a random value drawn from a normal distribution with an average of zero was added to agents’ opinions (Mäs et al. 2010). This “white noise” leads on average to much smaller random opinion changes, which generates very different opinion dynamics, as it does not make agents leave and enter clusters as observed with the uniformly distributed noise. In contrast, white-noise deviations at the level of individual agents aggregate to random opinion shifts of clusters. As a consequence, it is possible that clusters happen to adopt similar opinions and merge, a process that will inevitably generate global consensus and not clustering as observed with uniformly distributed noise (Mäs et al. 2010). In sum, deviations from model assumptions can be incorporated in different ways and model predictions often depend on the exact formal implementation. Theoretical and empirical research is, therefore, needed to identify conditions under which alternative models of deviations are more or less plausible. Empirical research in the field of evolutionary game theory has shown, for instance, that deviations tend to occur more likely when they imply small costs (Mäs & Nax 2016). Similar research should be conducted also in the field of social-influence dynamics.
The bounded confidence model is yet another example of a theory that makes fundamentally different predictions when its assumptions are implemented probabilistically rather than deterministically (Macy & Tsvetkova 2015). It is, therefore, important that theoretical predictions, independent of whether they have been derived formally or not, are tested for robustness to randomness. To be sure, there is no doubt that deterministic models are insightful, as they allow the researcher to analyze theories in a clean environment without any perturbations. This often simplifies analyses, making it easier to understand the model’s mechanisms and their consequences. Nevertheless, a model prediction that only holds for deterministic settings is of limited scientific value, because it cannot be to put to the empirical test in a non-deterministic world. The notion that individual behaviour is deterministic may be useful but it is not an innocent assumption.
In sum, we studied a new answer to Abelson’s question of how to generate the empirical finding of bimodal opinion distributions. Abelson’s approach to assume that influence declines with opinion discrepancy is supported by empirical research but turned out to not solve his puzzle. The original bounded-confidence models were able to explain opinion clustering by assuming that the influence network is not fixed, and by further strengthening Abelson’s assumption, implementing a threshold in discrepancy beyond which influence vanishes completely. We showed here that Abelson’s weaker implementation of influence declining in discrepancy does generate opinion clustering when it is combined with random independent opinion replacements.
Notes
- Abelson’s diversity puzzle is called “community cleavage problem” by Friedkin (2015).
- This observation was later generalized by Davis (1996).
- Formally opinion discrepancy is nothing else than distance in opinion and this notion is usually used in the social simulation literature. We use "discrepancy" here because it is the original notion used by Abelson and well established in psychological models (see e.g. Hunter et al. 1984). In this paper discrepancy is the same as distance, which is also the case for a large part of the psychological literature.
- Another criticism was that there are no “hard” bounds but “smooth” ones. Therefore, already some early variations of bounded confidence models on the evolution of extremism (Deffuant et al. 2002, 2004) introduced different kinds of smoother bounds. Both studies did not analyse the impact of smoothness itself.
- Mäs & Bischofberger (2015) use the same function for the definition of similarity and interaction probability. They use a parameter h = 1/f quantifying the degree of homophily in the society. In our parametrization they further used \(\beta\) = 0 and \(\varepsilon\) = 2 for an opinion space where opinion can take values between -1 and 1.
- Based on Ben-Naim et al. (2003) these diagrams are called “bifurcation diagrams” in the physics literature e.g. by (Lorenz 2007; Pineda et al. 2009, 2013; Carro et al. 2013).
Appendix
Appendix A: Model based on Deffuant et al
The conclusions drawn from our analyses do not only apply to the bounded-confidence model proposed by Hegselmann & Krause (2002) but also hold for the model by Deffuant et al. (2000), as Figures 5 and 6 show. In this alternative model, the agent-interaction scheme is divided into two subprocesses. First, two agents i and j are randomly picked. Second i and j influence each other and adjust their opinions with a given probability of acceptance P if their opinions do not differ too much.
When agents i and j are selected for interaction and accept each other, they adjust their opinions towards each other by averaging their current opinions. This leads to the following dynamic equation
| $$ x_{i}(t+1) = \begin{cases} \displaystyle{\frac{x_{i}(t)+x_{j}(t)}{2}} & \text{with a probability } P(i,j) \\ \\ x_{i}(t) & \text{otherwise.} \end{cases}$$ | (3) |
Appendix B: Opinion patterns
The experiments described in the main text cannot exclude the possibility that the opinion patterns shown in Panels (c) and (e) of Figures 3 and 4 also result from the fact that we did not run simulations long enough. To ensure that the diagrams in those Panels are not suffering from insuficient simulation length, we conducted additional simulations that started with a perfect consensus (i.e., all agents have an opinion of 0.5 at the initial state). The additional simulations resulted in very similar general opinion patterns (Figure 7), which shows that our discussion in this study is valid. This holds for both version of the bounded-confidence model.
Panel (a) of Figure 7 should be compared to Panel (c) of Figure 4 and Panel (c) of Figure 7 should be compared to Panel (e) of Figure 4. Likewise, Panel (b) of Figure 7 should be compared to Panel (c) of Figure 3 and Panel (d) of Figure 7 should be compared to Panel (e) of Figure 3.
References
ABELSON, R. P. (1964). Mathematical models of the distribution of attitudes under controversy. In Contributions to mathematical psychology, (pp. 142–160). Holt, Rinehart & Winston, New York.
ARONSON, E., Turner, J. A. & Carlsmith, J. M. (1963). Communicator credibility and communication discrepancy as determinants of opinion change. The Journal of Abnormal and Social Psychology, 67(1), 31–36. [doi:10.1037/h0045513]
AXELROD, R. (1997). The dissemination of culture. Journal of Conflict Resolution, 41(2), 203–226. [doi:10.1177/0022002797041002001]
BEN-NAIM, E., Krapivsky, P. L. & Redner, S. (2003). Bifurcation and patterns in compromise processes. Physica D, 183, 190–204. [doi:10.1016/S0167-2789(03)00171-4]
BYRNE, D. E. (1971). The attraction paradigm. New York: Academic Press.
CARRO, A., Toral, R. & San Miguel, M. (2013). The role of noise and initial conditions in the asymptotic solution of a bounded confidence, continuous-opinion model. Journal of Statistical Physics, 151(1), 131–149. [doi:10.1007/s10955-012-0635-2]
DANDEKAR, P., Goel, A. & Lee, D. T. (2013). Biased assimilation, homophily, and the dynamics of polarization. Proceedings of the National Academy of Sciences, 110(15), 5791–5796. [doi:10.1073/pnas.1217220110]
DAVIS, J. H. (1996). Group decision making and quantitative judgments: A consensus model. In E. H. Witte & J. H. D. Mahwah (Eds.), Understanding Group Behavior: Consensual Action by Small Groups, (pp. 35–59). Lawrence Erlbaum.
DEFFUANT, G., Amblard, F. & Weisbuch, G. (2004). Modelling Group Opinion Shift to Extreme: The Smooth Bounded Confidence Model. Arxiv preprint cond-mat/0410199: https://arxiv.org/ftp/cond-mat/papers/0410/0410199.pdf.
DEFFUANT, G., Neau, D., Amblard, F. & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 87–98. [doi:10.1142/S0219525900000078]
DEFFUANT, G., Neau, D., Amblard, F. & Weisbuch, G. (2002). How Can Extremism Prevail? A Study Based on the Relative Agreement Interaction Model. Journal of Artificial Societies and Social Simulation, 5(4), 1: https://www.jasss.org/5/4/1.html.
DEGROOT, M. H. (1974). Reaching a consensus. Journal of the American Statistical Association, 69(345), 118–121. [doi:10.1080/01621459.1974.10480137]
FISHBEIN, M. & Ajzen, I. (1975). Belief, attitude, intention and behavior: An introduction to theory and research. Reading, MA: Addison-Wesley.
FISHER, S. & Lubin, A. (1958). Distance as a determinant of influence in a two-person serial interaction situation. The Journal of Abnormal and Social Psychology, 56(2), 230–238. [doi:10.1037/h0044609]
FLACHE, A. & Mäs, M. (2008). How to get the timing right. A computational model of the effects of the timing of contacts on team cohesion in demographically diverse teams. Computational & Mathematical Organization Theory, 14(1), 23–51. [doi:10.1007/s10588-008-9019-1]
FRIEDKIN, N. E. (2015). The problem of social control and coordination of complex systems in sociology: A look at the community cleavage problem. IEEE Control Systems, 35(3), 40–51. [doi:10.1109/MCS.2015.2406655]
HARARY, F. (1959). A criterion for unanimity in French’s theory of social power. Studies in social power, 6, 168.
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence, models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.
HUNTER, J. E., Danes, J. E. & Cohen, S. H. (1984). Mathematical Models of Attitude Change. Human communication research series, Academic Press.
LAZARSFELD, P. F. & Merton, R. K. (1954). Friendship as a social process: A substantive and methodological analysis. In M. Berger & T. Abel (Eds.), Freedom and control in modern society, (pp. 18–66). Van Nostrand.
LEHRER, K. & Wagner, C. (1981). Rational Consensus in Science and Society. D. Reidel Publishing Company, Dordrecht, Holland. [doi:10.1007/978-94-009-8520-9]
LIGGETT, T. M. (2013). Stochastic interacting systems: contact, voter and exclusion processes, vol. 324. Springer Science & Business Media.
LORENZ, J. (2007). Continuous Opinion Dynamics under bounded confidence: A Survey. International Journal of Modern Physics C, 18(12), 1819–1838. [doi:10.1142/S0129183107011789]
LORENZ, J., Kurahashi-Nakamura, T. & Mäs, M. (2016). ContinuousOpinionDynamicsNetlogo: Robust clustering in generalized bounded confidence models. http://doi.org/10.5281/zenodo.61205.
MACY, M. W., Kitts, J. A., Flache, A. & Benard, S. (2003). Polarization in dynamic networks: A Hopfield model of emergent structure. In Dynamic Social Network Modeling and Analysis, (pp. 162–173). National Academies Press.
MACY, M. & Tsvetkova, M. (2015). The signal importance of noise. Sociological Methods & Research, 44, 2, 306-332.
MARK, N. P. (2003). Culture and competition: Homophily and distancing explanations for cultural niches. American Sociological Review, 68(3), 319–345. [doi:10.2307/1519727]
MÄS, M. & Bischofberger, L. (2015). Will the personalization of online social networks foster opinion polarization? SSRN. Available at SSRN: http://ssrn.com/abstract=2553436.
MÄS, M. & Flache, A. (2013). Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PLoS ONE, 8(11), e74516. [doi:10.1371/journal.pone.0074516]
MÄS, M., Flache, A. & Helbing, D. (2010). Individualization as driving force of clustering phenomena in humans. PLoS Comput Biol, 6(10), e1000959. [doi:10.1371/journal.pcbi.1000959]
MÄS, M., Flache, A., Takacs, K. & Jehn, K. A. (2013). In the short term we divide, in the long term we unite: Demographic crisscrossing and the effects of fault lines on subgroup polarization. Organization science, 24(3), 716–736. [doi:10.1287/orsc.1120.0767]
MÄS, M. & Nax, H. H. (2016). A behavioral study of “noise” in coordination games. Journal of Economic Theory, 162, 195–208. [doi:10.1016/j.jet.2015.12.010]
MCPHERSON, M., Smith-Lovin, L. & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual Review of Sociology, 27, 415–444. [doi:10.1146/annurev.soc.27.1.415]
PINEDA, M., Toral, R. & Hernandez-Garcia, E. (2009). Noisy continuous-opinion dynamics. Journal of Statistical Mechanics: Theory and Experiment, 2009(08), P08001 (18pp).
PINEDA,, M., Toral, R. & Hernández-García, E. (2013). The noisy Hegselmann-Krause model for opinion dynamics. The European Physical Journal B, 86(12), 1–10. [doi:10.1140/epjb/e2013-40777-7]
SALZARULO, L. (2006). A continuous opinion dynamics model based on the principle of meta-contrast. Journal of Artificial Societies and Social Simulation, 9(1) 3: https://www.jasss.org/9/1/13.html.
SHIN, J. K. & Lorenz, J. (2010). Tipping diffusivity in information accumulation systems: More links, less consensus. Journal of Statistical Mechanics: Theory and Experiment, 2010(06), P06005. [doi:10.1088/1742-5468/2010/06/p06005]
WATTS, D. J. & Dodds, P. S. (2007). Influentials, networks, and public opinion formation. Journal of Consumer Research, 34, 441–458. [doi:10.1086/518527]

